
Contributed by Theodore H. Geballe, November 8, 2020 (sent for review August 31, 2020; reviewed by Antonio Bianconi, Jochen Mannhart, and Naurang Saini)
Author contributions: S.D.C., T.H.G., and C.-Q.J. designed research; S.D.C., C.Q.-J., L.-P.C., A.G., M.K., G.B., W.-M.L., and J.M.J. performed research; L.-P.C., A.G., M.K., W.-M.L., E.G., M.L., O.M., and V.N. contributed new reagents/analytic tools; S.D.C., C.-Q.J., L.-P.C., A.G., M.K., G.B., and W.-M.L. analyzed data; and S.D.C., T.H.G., C.-Q.J., and E.G. wrote the paper.
Reviewers: A.B., Rome International Center for Materials Science Superstripes; J.M., Max Planck Institute for Solid State Research; and N.S., Sapienza University of Rome.
- Altmetric
The Cu extended X-ray absorption fine structure of YSr2Cu2.75Mo0.25O7.54 (with superconducting critical temperature, Tc, = 84 K) and Sr2CuO3.3 (Tc = 95 K) through their superconducting transitions demonstrates that the common factor in superconductivity in cuprates, including those prepared by high-pressure oxygenation, is an internal quantum tunneling polaron in its dynamical structure. In addition, Sr2CuO3.3 is the first material to show a concomitant transformation in this structure involving atom displacements >1 Å that would be expected to modify its Fermi surface, which would complicate the transition beyond a purely electronic one consisting of the pairing of electrons of opposite momentum across fixed electronic states.
A crucial issue in cuprates is the extent and mechanism of the coupling of the lattice to the electrons and the superconductivity. Here we report Cu K edge extended X-ray absorption fine structure measurements elucidating the internal quantum tunneling polaron (iqtp) component of the dynamical structure in two heavily overdoped superconducting cuprate compounds, tetragonal YSr2Cu2.75Mo0.25O7.54 with superconducting critical temperature, Tc = 84 K and hole density p = 0.3 to 0.5 per planar Cu, and the tetragonal phase of Sr2CuO3.3 with Tc = 95 K and p = 0.6. In YSr2Cu2.75Mo0.25O7.54 changes in the Cu-apical O two-site distribution reflect a sequential renormalization of the double-well potential of this site beginning at Tc, with the energy difference between the two minima increasing by ∼6 meV between Tc and 52 K. Sr2CuO3.3 undergoes a radically larger transformation at Tc, >1-Å displacements of the apical O atoms. The principal feature of the dynamical structure underlying these transformations is the strongly anharmonic oscillation of the apical O atoms in a double-well potential that results in the observation of two distinct O sites whose Cu–O distances indicate different bonding modes and valence-charge distributions. The coupling of the superconductivity to the iqtp that originates in this nonadiabatic coupling between the electrons and lattice demonstrates an important role for the dynamical structure whereby pairing occurs even in a system where displacements of the atoms that are part of the transition are sufficiently large to alter the Fermi surface. The synchronization and dynamic coherence of the iqtps resulting from the strong interactions within a crystal would be expected to influence this process.
More than 30 y after the discovery of unconventional superconductivity in cuprates (1) and subsequently in analogous materials its underlying mechanism and in particular the role of the lattice are still under debate. Proposed microscopic theories range from purely electronic Mott–Hubbard and t-J approaches at one extreme to Bose–Einstein condensates of bipolarons at the other (23–4). Experimentally, however, anomalous isotope effects (5), resonant ultrasound (6), angle-resolved photoemission spectroscopy (78–9), femtosecond optical pump terahertz (10)/megaelectron-volt transmission electron microscopy probe (11), infrared pump (12), and so on have demonstrated that specific phonons not only couple to the superconductivity but correlate directly with the gap energy and may even transiently induce it well above the superconducting critical temperature, Tc. Cuprates also exhibit a plethora of superstructures indicative of strong electron–lattice coupling, stripes that have been proposed to stabilize the superconductivity (13), and charge-density waves (14, 15) and the pseudogap (PG) (16) that compete with it. Another possibility is mechanisms that boost Tc from a low value expected within a conventional Bardeen-Cooper-Schrieffer (BCS) scheme. That this question remains unanswered suggests considering more unconventional approaches (4). One candidate is the dynamical structures of cuprates, S(Q, E) or experimentally S(Q, t = 0), specifically their internal quantum tunneling polarons (iqtp). An iqtp is a set of atoms oscillating between two structures that possess different geometries, energy levels, and charge distributions (1718–19). A chemist would describe these endpoints as separate species, adapting this term that applies more intuitively to solutions to the atoms in crystalline solids. Neutron scattering and X-ray absorption fine structure (XAFS) measurements identified O-centered iqtps and their correlation with the superconductivity 30 y ago (1718192021222324–25). We now present Cu K edge extended XAFS (EXAFS) results from “overdoped” YSr2Cu2.75Mo0.25O7.54 (YSCO-Mo) that is isostructural with YBa2Cu3O7 (Fig. 1A and SI Appendix, Fig. S1), Tc = 84 K (26) and hole doping p (excess charge on the planar Cu2 site) = 0.3 to 0.5 (27) and Sr2CuO3.3 (SCO) that is structurally analogous to La2CuO4 (Fig. 1B and SI Appendix, Fig. S1), Tc = 95 K (28, 29), and p = 0.6, both synthesized via high-pressure oxygenation (HPO) (30, 31). In YSCO-Mo the Cu2-apical O (Oap) double-well potential is degenerate in the normal state but renormalizes below Tc with the energy difference between its two minima increasing with decreasing temperature by ∼6 meV. SCO is already unique among cuprates in not having intact CuO2 planes (32, 33). Its Cu EXAFS demonstrate that it is unique among superconductors in that its Oap shift by >1 Å at its superconducting transition, challenging our conception of superconductivity as an electronic transition that is incompatible with structural transformations.

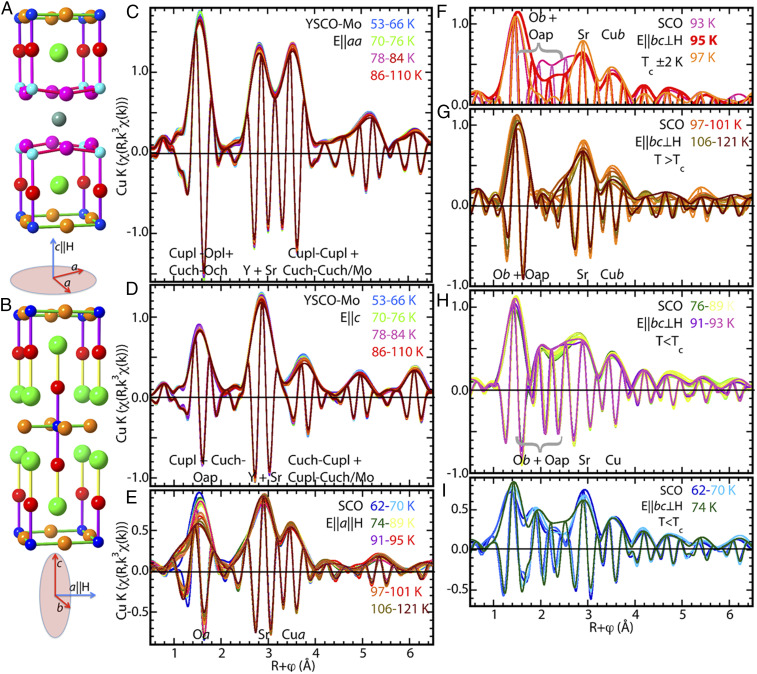
Structures and modulus and real components of the Fourier transforms of the EXAFS spectra, χ(R), of YSCO-Mo and SCO across temperature ranges bracketing their superconducting transitions. (A) Structure representation of YSCO-Mo. The CuO2 planes are turqoise (Cu2) and magenta (Opl), Cu-O chains are blue (Cu1) and gold (Och), Oap is red, and Sr is green. In the actual structure one-fourth of Cu1 are substituted by Mo. The orientation is shown underneath. (B) The same as A for SCO, except a significant number of Oap and half of the O sites in the a direction in the CuO2 planes are vacant. The CuO2 planes are blue (Cu) and gold (O). For the χ(R) spectra the blue traces denote the lowest temperatures, then green to yellow, purple, and red-orange to brown at the highest ones. (C) YSCO-Mo spectra for E of the X-ray probe beam in the aa plane, with the modulus peaks labeled with their principal sources. The first temperature above Tc is red. (D) YSCO-Mo spectra for E||c, with the Cu1- and Cu2-Oap contributions overlapping at R = 1.6 Å. The peaks at higher R are a combination of direct, two-leg path contributions from more distant neighbor atom shells and ordered multiple scattering paths. (E) SCO spectra for E||H used for the orientation that is assigned to the a direction of the orthorhombic O sublattice. Tc is red and double width. (F–I) SCO over the designated temperature ranges for E⊥H spectra that will be the contributions in the bc plane defined by the orthorhombic O sublattice. (F) The extent of the change in the spectra, and by inference in their originating structures, across the superconducting transition. The features appearing at R = 2 to 2.5 Å below Tc result from the ∼2 Å shift of the O depicted in Fig. 3 B–D. In G the first temperature above Tc is orange and double width.
We have recently shown that HPO cuprates are described by their own phase diagram (34). The principal feature of the well-known one for non-HPO cuprates is the superconducting “dome” that begins at p ∼0.06, peaks at p ∼ 0.16, and ends at p ∼ 0.27. Subsequent augmentations with the microstrain in the planes (35) and hole density on the O atoms (36) explain some of the material specificity but do not modify this overall pattern. For HPO compounds the superconductivity may begin at p < 0.06 and continues to increase beyond p = 0.27 with possible flattening but no reduction in Tc. Although we have found that the excess O in YSCO-Mo is mostly taken up by domains enriched in octahedral Mo(VI) substituting in the Cu(1) chains, much of the extra charge resides in the CuO2 planes (27) and some of the carriers constitute a normal Fermi liquid that coexists with the superconductivity (26). The inherent inhomogeneity (37) in YSCO-Mo and SCO was probed by EXAFS, which is arguably the most incisive experimental method for characterizing short-range order and is especially sensitive to its changes. Diffraction patterns originate in the long-range average structure of a material and provide precise information on the symmetry and symmetry-constrained locations of the atoms that dominate the Bragg peaks. In contrast, EXAFS—and pair distribution function (pdf) analysis—are sensitive to local order separate from the crystallographic symmetry. The element selectivity of EXAFS provides further advantages by separating the atom pairs comprising the distribution function. Especially important for this study, EXAFS measures the instantaneous structure factor, S(Q, t = 0), that incorporates the dynamic structure components, S(Q, E), observed with inelastic scattering. EXAFS therefore accesses time and energy scales corresponding to collective dynamical phenomena (25, 38, 39). Dynamical structures such as the iqtp are demonstrated when S(Q, E/t = 0) gives locations for atoms that differ from those (19, 38) obtained from diffraction and elastic scattering measurements (2021–22, 40). This complementarity was the basis for the original identification of the Cu-Oap two-site distribution (41) and its assignment to the double-well potential of the iqtp (17, 19, 42).
Results
For YSCO-Mo one-fourth of the Cu1 atoms in the CuO3 chain are replaced by Mo (26). The EXAFS of the sample of the c||H||E orientation of tetragonal YSCO-Mo is composed of the Cu1-Oap-Cu2 pairs and the c-axis projections of the Y/Sr pairs. The (c||H)⊥(aa||E) sample contains the contributions of the CuO2 planes–CuO3 chains (34) and Y/Sr projections in the aa plane (Fig. 1A and SI Appendix, Fig. S1). Crystallographically tetragonal SCO (Fig. 1B and SI Appendix, Fig. S1) is unique in that its a-axis that contains half-filled -Cu-O- chains aligns with the field, its b axis in the bc plane perpendicular to the field contains intact -Cu-O- chains, and its Oap sites are only partly occupied (33). Its EXAFS corroborates that its Cu-Sr sublattice is locally tetragonal as found by diffraction.
The EXAFS spectra, χ(k), are presented as their Fourier transforms, χ(R), where the modulus peaks correspond to the contributions of the neighbor atom shells in an approximate representation of the partial pair distribution. This interpretation is modified by the phase shift that causes the locations of the modulus peaks to be below the actual distances and the finite data range that causes the peaks to be much wider than the actual resolving capability of the analysis. The overlap of the modulus peaks from adjacent neighbor shells therefore does not relate to the actual π/2kmax = 0.11 Å resolution in this analysis. Since the EXAFS signal includes both an amplitude and phase, the modulus represents only half of the information with the remainder contained in the real/imaginary component of χ(R). The E||aa (Fig. 1C) and E||c (Fig. 1D) spectra of YSCO-Mo are dominated by the contributions from the nearest-neighbor O, Sr, and Cu (34, 434445–46). The increased thermal Debye–Waller factors at higher temperatures cause the small reductions in the amplitudes of the spectral features. Although the EXAFS spectra of SCO show the expected features from the nearest-neighbor O, Sr, and Cu, it differs from that of the La2CuO4 family (37, 47) since the spectra originate in the structures along the a axis and in the bc plane. In contrast to the expected behavior demonstrated by the YSCO-Mo spectra, the E||a spectra of SCO are complicated, showing a large reduction with increasing temperature for the Cu-O feature and an anomalous diminution of the Sr modulus amplitude with decreasing temperature (Fig. 1E).
The focus of this paper, however, is the behavior of the E||bc spectra of SCO in the region R = 1.5 to 2.8 Å that contains the contributions of Cu-O pairs at ∼2.2 to 3 Å. In contrast to the relatively subtle effects on the EXAFS resulting from the partial collapse of the iqtp double-well potential at Tc (20, 23, 42), these spectra have minimal amplitude in this region down to 97 K but at the onset of superconductivity at 95 K a complex pattern of large-amplitude features abruptly appears (Fig. 1F). This indicates the formation throughout the crystal of a structural moiety in the bc plane consisting of O ions displaced over long distances from their positions in the normal state into new ones in the superconducting state. That the crystal structure shows O atoms in symmetry-constrained positions that do not give these distances and no change in the structure across Tc (28, 29) indicates its dynamical origin. Smaller, continual changes divide the remaining spectra into temperature regions (Fig. 1 G, J, and I), demonstrating that the Cu environments undergo additional stepwise transformations.
Curve fitting (SI Appendix, Figs. S2–S70) confirms that the EXAFS gives the crystallographic positions for the cations and the YSCO-Mo plane and chain O atoms (33, 34). It also gives detailed depictions of the anomalous temperature dependence of Oap in YSCO-Mo and the entire O sublattice in SCO. The behavior of the Cu2-Oap in YSCO-Mo is visualized in the EXAFS of this pair isolated by subtracting the contributions of the other neighbors determined by the curve fits. The two-site distribution is evident in the two peaks in the residual χ(R) (Fig. 2A). The R = 1.75 Å peak increases continuously with increasing temperature, with a significant jump at Tc. The trend in position and amplitude of the R = 1.95 Å peak is more complicated, being relatively high at the lowest temperatures, then diminishing until near Tc it melds with the R = 1.75 Å one at a higher amplitude. This behavior reflects the sensitivity of χ(R) to the details of the two-site distribution, which are unraveled by the curve fits to reveal a consistent pattern. The two Cu–O distances and occupancies for the Cu2-Oap pair (Fig. 2 B and C and SI Appendix, Figs. S71–S86) divide into four regions: 1) the normal state for T > 87 K, 2) a fluctuation region from 77 to 85 K in the distances and 77 to 94 K in the numbers of the two O, 3) a first superconducting region from 68 to 77 K, and 4) a second superconducting region for T < 68 K. Although the distances and numbers are all obtained independently, the stepwise shifts in distances and numbers occur at the same temperatures, delineating the boundaries of temperature regions where the two-site distribution and its double-well potential change.

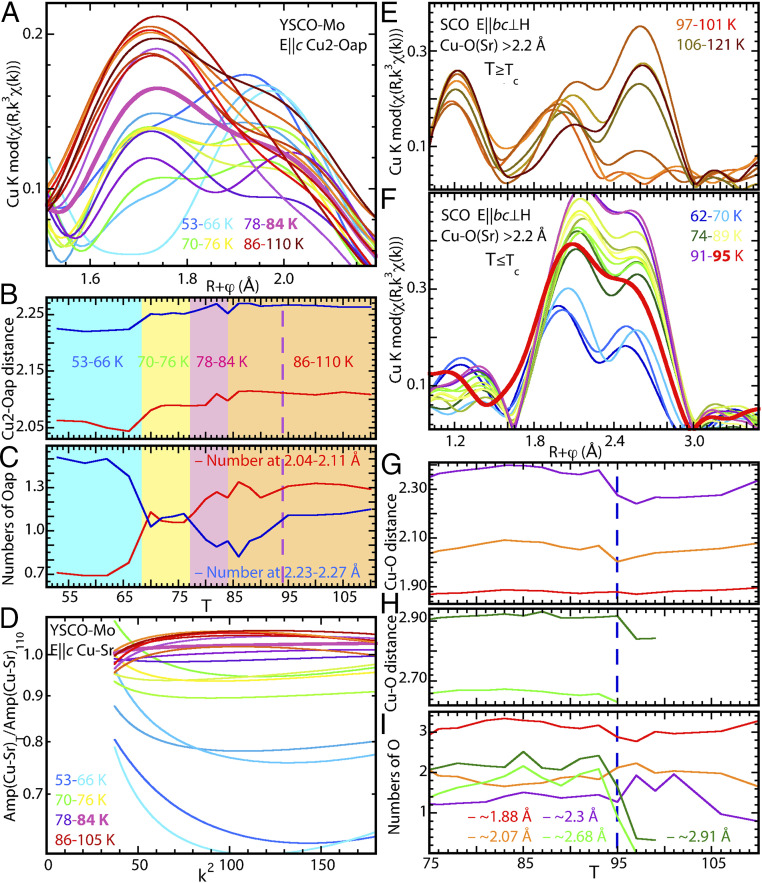
Results characterizing the Cu2-Oap and Cu-Sr components of the dynamical structure of YSCO-Mo through its superconducting transition (Left) and the Cu-O bc oriented Cu-O pairs in SCO (Right). (A) Moduli of χ(R) of the isolated Cu2-Oap EXAFS spectra showing its two features at R = 1.7 and 1.95 Å. The color scheme is as in Fig. 1, with the Tc ∼ 84 K curve in magenta plotted using a double-width line. (B) The two Cu2-Oap distances and (C) their corresponding numbers independently determined by curve fits of the EXAFS spectra (SI Appendix, Figs. S1–S40 and S71–S87). Discontinuous changes in these three values at the same temperatures divide the temperature range into the four regions, above Tc (orange), a fluctuation region (magenta) that begins at a somewhat higher temperature for the numbers (dashed line), below Tc (yellow), and farther below Tc (blue). The uncertainties for the three parameters can be taken as the SD from a line fit through the points in each region. (D) The anharmonicity of the Cu-Sr E||c pair, represented by the curvature of the logarithm of the ratio of the amplitude of the Cu-Sr wave at the designated temperatures divided by this amplitude at the maximum temperature of 110 K. (E and F) The corresponding χ(R) moduli of the isolated Cu-O waves for Cu-O > 2.1 Å, divided into above and below Tc because of the substantial change in the spectra and structure. The feature at R = 2.6 Å for T > 101 K is fit better by Sr than O, the one at R = 2.5 Å for T < 96 K is definitely O (SI Appendix, Fig. S87). (G and H) The Cu–O distances between 75 and 110 K with Tc indicated by the dashed blue line. (I) The numbers of O atoms at these distances, with the O at 2.68 and 2.91 Å appearing only below Tc because of the ∼2-Å shift of the O as in Fig. 3 B–D.
Another quantity showing coupling to the superconductivity is the anharmonicity of the c-oriented Cu2-Sr pair. This is evaluated from the EXAFS from the logarithm of the amplitude divided by the amplitude of the selected baseline spectrum vs. k2 (Fig. 2D). Since the Cu-Sr sublattice is conserved the linear part of this function is the difference in the Gaussian Debye–Waller factor and the curvature and deviation of the intercept from zero reflects the change in the anharmonic component of the pair distribution (48). The conservation of the Cu-Sr distribution in the normal state is demonstrated by these ratios being essentially horizontal lines with extrapolated intercepts of 1 from 85 to 110 K. At Tc these ratios begin to decrease continuously, at a faster rate and with greater curvature as the temperature becomes lower. This pattern implies that the polarizability of the Sr scales with the superfluid density.
The most remarkable component in the structure of SCO is the entity that forms in the bc plane at Tc to give the spectral features at R = 1.8 to 2.6 Å in the superconducting phase. Curve fits confirm the absence of significant numbers of O neighbors beyond 2.4 Å in the normal state. Subtracting the contributions of the two O neighbors with Cu–O distances <2 Å and the Sr and Cu visualizes the relevant portion of the spectrum (49) (Fig. 2 E and F). The radical change in the full spectrum from 93 to 97 K is the result of a reduction in the amplitude of the feature at R = 2.0 Å to half its size at Tc and a complete loss of the feature around R = 2.6 Å in the normal phase (Fig. 2 E and F). The shifts of the lower feature and the recovery of the higher one beginning at 106 K is complicated and may result from the displacement of an Sr atom rather than the resumption of the 93 K structure (SI Appendix, Fig. S88). Below Tc the overall shape is retained, albeit with shifts in the positions of the peaks, and the amplitude that is at a maximum just below Tc diminishes, with a large reduction between 74 and 70 K (Fig. 2F). The spectrum in this region is fit by an O neighbor around 2.3 Å and larger, approximately equivalent numbers of O neighbors with Cu–O distances of 2.6 Å and 2.9 Å in the bc plane (Fig. 2G, H, and I and SI Appendix, Figs. S56–S70). These two neighbors are not present in the normal phase (Fig. 2I) and must result from a large displacement of an O atom from one position in the lattice to another. The other changes occurring at the transition are the substantial reduction in the amplitude of the O at 2.3 Å along with the 0.13 Å expansion of its Cu–O distance and a 0.06 Å expansion of the Cu–O at 2.05 Å.
Discussion
Descriptions of the structural transformations in YSCO-Mo and SCO consistent with these results begin with the previously described environments of the relevant O atoms (33, 34) (Fig. 3). The two-site apical O distribution in YSCO-Mo is simple (Fig. 3A), here showing the positions synchronized along the chain. SCO is much more complex. Interpreting the high degree of disorder and the large change at Tc as a random distribution of the apical and chain vacancies, there are three types of Cu, all with two b chain but distinguished by having zero, one, or two a chain O neighbors. The square planar geometry of Cu(II) dictates that the 2a+2b conformation would have its Oap either vacant or with one or two Oap at >2.1 Å and the 0a+2b conformation two Cu-Oap distances at <2 Å. The 1a+2b Cu with its long or short Cu-Oap and distorted environment would then be the Cu(III) required for charge balance. This combination of occupied and vacant Oap sites explains the EXAFS spectra of the normal phase, with the low Cu-Oap amplitude caused by the range of Cu-Oap distances (Fig. 3B). At Tc an Oap adjacent to an Oap-vacancy shifts ∼2 Å in the b direction to form a Cu2O2 unit with an asymmetric bridge that gives the Cu–O distances of 2.6 and 2.9 Å (Fig. 3 C and D). The other O of the Cu2O2 shifts along c away from this Oap, buckling the original -Cu-O-Cu- chain. This O would also move away from the Cu with the shorter, 2.6 Å Cu–O distance, splitting the original distance into two distances at 1.85 and 2.05 Å. The expansion of the 2.05 Å Cu–O distances at Tc would therefore be a response to the formation of these asymmetrically bridged Cu2O2 units. The expansion of the 2.3 Å distance assigned to a long Cu-Oap (Fig. 3G) would result from the modified charge distribution and the increased homogeneity of the Cu sites, whereby ones with and without Oap become more uniform. The 1.9-Å Cu–O distances are unaffected because they are not involved in this transformation.

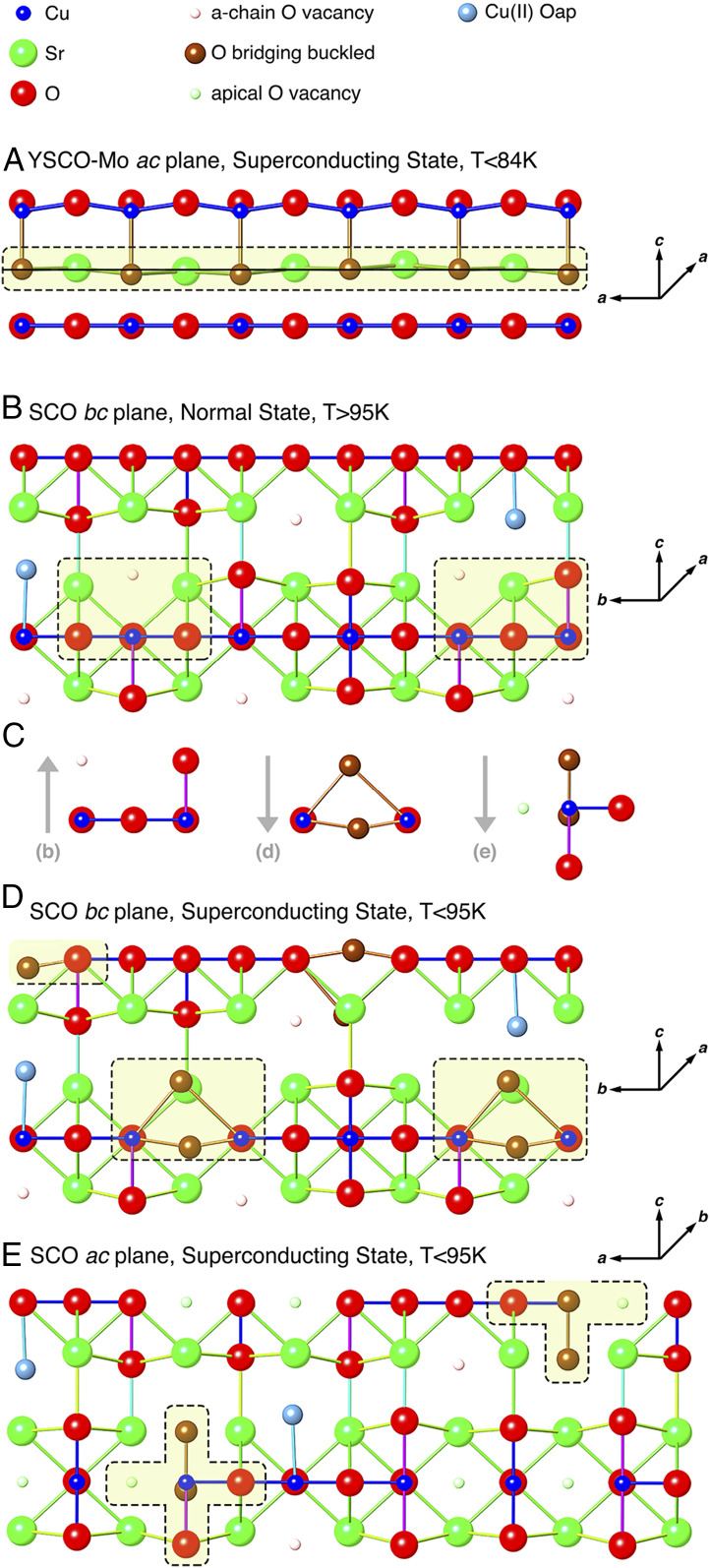
Conceptual structures of the dynamical structure transformations. The results from SCO are derived from the EXAFS results. The shaded areas highlight the atoms of the iqtps whose structure will change across Tc. (A) Cu2-Oap two-site distribution in YSCO-Mo, organized in pairs with corresponding displacements of the Sr. (B) The bc plane in the normal state of SCO. There are some Oap vacancies, and the b-oriented Cu-O chains are fully occupied. As described in the text the half-vacant O sites in the a-oriented Cu-O chains give three types of Cu: 1) zero O along a, two O along b, two Oap with Cu-Oap ∼1.9 Å; 2) two O along a, two O along b, 0 to 2 Oap with Cu-Oap > 2.1 Å; and 3) Cu(III) with one O along a, two O along b, and variable Oap. (C) The Cu2O2 unit in SCO whose structure changes across Tc. (Left) In the bc plane in the normal state (B) showing the two Cu sites, one of which has an O vacancy in the a direction, and one with an Oap vacancy. In the superconducting state (Center, D) the Oap has shifted toward the Oap vacancy to give the 2.7- and 2.9-Å Cu–O distances and the O in the Cu has moved slightly downward. (Right) The same set of atoms viewed in the ac plane as in E. (D) The bc plane in the superconducting state of SCO, showing the doubly bridged Cu2O2 units. (E) The ac plane in the superconducting state of SCO, showing the three types of Cu.
Analogous to YBa2Cu3O7, the Cu2-Oap two-site distribution in YSCO-Mo is assigned to the iqtp of the dynamical structure. This is corroborated by the single site distribution found for Cu1-Oap that shows that the correlated motion of the Cu2-Oap pair differs from the Cu1-Oap pair. Assignment of the asymmetrically bridged Cu2O2 unit in superconducting SCO to an iqtp is supported by the difference with the crystallographic structure determined by neutrons (28, 29) that also show no change across Tc. The dynamical component of the iqtp would be the oscillation of the O atoms between their two equivalent positions across the Cu2O2 midpoint.
Iqtps coupled to the superconductivity are the first significant finding of this paper. Recent reports by the authors have shown that the common attribute in cuprate superconductivity is not the superconducting “dome” of the phase diagram(34) or CuO2 planes (33) or the prolate geometry of the Cu in these planes (50). A remaining factor is the dynamical structure of specific Cu-O pairs, the iqtps. The identification of iqtps as a ubiquitous factor in exotic superconductivity follows from their identification by EXAFS measurements in all classes of cuprates, La2-xBa/SrxCuO4+δ (42, 47, 5152–53), YBa2Cu3O7 (20, 46), Bi- and Tl-based layered cuprates (23, 24, 54, 55), and even related Bi- and Fe-based compounds (5657–58). The basis for this superiority of EXAFS for revealing iqtps is unclear—perhaps it is simply easier than neutron pdf measurements—but it is empirically incontrovertible. YSCO-Mo and SCO therefore exemplify the prevalence of the iqtp even under constraint. The Cu1-Oap iqtp in YBa2Cu3O7 wholly switches to Cu2-Oap when obstructed by the 25% Cu1-Mo substitution of YSCO-Mo, and in disordered SCO the host Cu2O2 unit forms at Tc by an ∼2-Å lateral displacement of an Oap.
EXAFS has previously identified iqtps in both the Oap and the CuO2 planes (52, 53, 55). Their appearance concomitant with the (PG) at T* is explained as the initial freezing out of polarons that in underdoped cuprates self-assemble into the PG and other aggregates (25, 59). Their response to the reduction of Tc by compositional changes that repress both polarons and superconductivity implicate them in the pairing-condensation process (42). The iqtps have the following additional properties that are independent of their location as Oap or in the planes, their host compound, and the Cu–Oap distance. Namely, 1) with the exception of SCO, the separation of the two Cu–O distances is 0.14 to 0.18 Å, 2) the double-well potential collapses at Tc but is subsequently restored as the temperature is further lowered, 3) the change in energy calculated from their tunneling frequencies or relative occupancies is 5 to 15 meV (25), 4) and at optimum doping they constitute 60 to 100% of the sites in the crystal. These common characteristics imply that the iqtp is largely a property of the O and the Zhang–Rice singlet state that occurs on Oap despite the 3dz2 level’s being lower in energy than the 3dx2-y2. However, the relationship of the iqtp to the superfluid quasiparticles is unclear insofar as, pending more complete data, the forms and populations of the double-well potentials do not appear to track the phase diagram with the exception of the softening at Tc.
The second remarkable result is the ∼2-Å displacement in the dynamic structure of Oap coincident with the superconducting transition. Changes in the structure across Tc in response to charge screening by the superfluid are only a few parts per thousand in the lattice constants of conventional BCS-type superconductors. Percent shifts occur in the Cu2-Oap distributions in cuprates. The O displacement in SCO would be the first observation of a rearrangement of the atoms sufficiently large to effect a change in the Fermi surface at the transition. This is a substantial departure from the standard depiction of BCS as a pairing of electrons of opposite momentum across a conserved Fermi surface in which the mediation of this pairing by a soft lattice mode prevents that mode from providing a path for a structural transformation. The caveat in this result is that this transformation occurs in the dynamic and not the static structure. Recent inelastic neutron scattering results in other systems have confirmed that such structural features demonstrate dynamic pair correlations not present in the static structures that originate in processes such as tunneling (39). An outstanding question is the effects of the HPO synthesis that results in compounds displaying a very much different superconducting region in their phase diagram than the “dome” of conventional cuprates prepared with O2 (34, 60). The 84 K Tc of YSCO-Mo, which EXAFS shows conforms very closely to the typical structure of cuprates without substantial disorder, is one-third higher than that of its parent YSr2Cu3O7+δ despite a measured p of 0.5 (27). It nevertheless possesses the same two-site Cu-Oap distribution found in other cuprates, differing in that the relative occupancies change instead of converging at Tc. The 95 K Tc of this phase of Sr2CuO3.3 is over 2.5 times higher than its La1.85Sr0.15CuO4 structural analog (32). Its unique Cu charge, structure, magnetism, and very high degree of disorder in its O sublattice (33) could be expected to convey additional unique behaviors, for example the structural transformation we have identified and described here.
These results provide evidence for a direct role in cuprates for nonadiabatic lattice dynamics that manifests itself as anharmonic oscillations of the atoms and charges (61) coupled to the superconductivity. Analogous to, for example, monolayer FeSe on SrTiO3 (62) and Li2CuO2 (63), our analysis demonstrates that collective behaviors of iqtps most likely have an equally significant role in pairing and condensation. For the iqtp, this collective action is easily assigned to the dynamic synchronization of the O oscillations over distances of the order of the superconducting coherence length. The interaction of the oscillators occurs not only through their dipoles but also directly through their neighbors, for example the Sr that bridges the Oap atoms in YSCO-Mo. Oscillating charge and a significant role for the inert cations have not been previously reported or proposed. In addition, the dynamical structure we report here is of substantial interest as a mechanism for the collective integration of lattice dynamics and charge that derives from a charge-coupled structural instability that does not culminate in static transformation. It is thereby consistent with the original rationale for superconductivity in cuprates, stabilizing the Cooper pairs by increasing the electron–lattice coupling beyond the adiabatic approximation while simultaneously frustrating incipient structural phase transitions (1, 5), but also constitutes a significant extension to high temperature superconductivity.
Materials and Methods
The samples, data acquisition, and analysis are the same as in our recent reports (33, 34) with the addition of having been measured at multiple temperatures and are detailed in SI Appendix. The two compounds were synthesized and samples prepared by magnetic orientation and characterized by standard methods as described in those reports and others that they cite. XAFS measurements were performed at the Stanford Synchrotron Light Source in the continuous scanning transmission mode on end station 2-2. χ(k) spectra were obtained after the standard energy calibration, conversion to absorbance, normalization, and approximation of the smooth atomic background with a sum of a fraction of the absorption peak at the edge plus a spline polynomial with a sufficiently low number of knots and polynomial orders to avoid fitting EXAFS oscillations and that minimized frequencies lower than those of the structural features. The spline parameters were also held to narrow ranges within each of the four sets of spectra to ensure the absence of any artifacts from this procedure. Metrical parameters were obtained by curve fitting of the χ(k) data using amplitudes and phases calculated with the feff9 code (64). Debye–Waller factors and E0 values were constrained to narrow ranges determined by inspection of the results from unconstrained fits on the spectra from all temperatures. Debye–Waller factors for the separable Cu-neighbors pairs were also evaluated by the logarithm-amplitude ratio method as in Fig. 2D, often showing analogous correlations with the superconducting transition. These will be reported later.
Acknowledgements
We acknowledge the financial support from the Slovenian Research Agency (research core funding no. P1-0040). Work at Washington State University is partially supported by the US National Science Foundation Division of Materials Research Early Concept Grants for Exploratory Research Grant 1928874. Work at Institute of Physics, Chinese Academy of Sciences was supported by the Ministry of Science and Technology and National Natural Science Foundation of China. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract DE-AC02-76SF00515. Work at Stanford and SLAC is supported by the Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, under Department of Energy, Office of Basic Energy Sciences Contract DEAC02-76SF00515. We thank A. R. Bishop, I. Bozovic, A. Bussmann-Holder, S. A. Kivelson, D. Mihailovic, and C. Varma for helpful discussions and presubmssion reviews of this manuscript.
Data Availability.
In the absence of an appropriate institutional open access data repository, the original data can be obtained by contacting the first author at st3v3n.c0nrads0n@icloud.com.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
 Nonadiabatic coupling of the dynamical structure to the superconductivity in YSr2Cu2.75Mo0.25O7.54 and Sr2CuO3.3
Nonadiabatic coupling of the dynamical structure to the superconductivity in YSr2Cu2.75Mo0.25O7.54 and Sr2CuO3.3
