
Edited by Jean-François Joanny, Institute Curie, Paris, France, and accepted by Editorial Board Member Brigid L. Hogan December 29, 2020 (received for review August 10, 2020)
Author contributions: D.B.B., J.O.R., and C.P.B. designed research; D.B.B., N.A., and A.F. performed research; P.R. contributed new reagents/analytic tools; D.B.B. and N.A. analyzed data; and D.B.B. and C.P.B. wrote the paper.
- Altmetric
- Two-State Micropatterns Provide Minimal Cell Collider
- Cell Pairs Exhibit Mutual Exclusion
- MCF10A and MDA-MB-231 Cells Exhibit Distinct Collision Behavior
- Contact Acceleration Maps Reveal Dynamics of Cell–Cell Interactions
- Interacting Equation of Motion Captures Experimental Statistics
- Interaction Behavior Space: A Theoretical Framework for Cell–Cell Interactions
- Discussion
- Materials and Methods
- Supplementary Material
- Data Availability.
When cells migrate collectively, such as to heal wounds or invade tissue, they coordinate through cell–cell interactions. While much is known about the molecular basis of these interactions, the system-level stochastic dynamics of interacting cell behavior remain poorly understood. Here, we design an experimental “cell collider,” providing a large ensemble of interacting cell trajectories. Based on these trajectories, we infer an interacting equation of motion, which accurately predicts characteristic pairwise collision behaviors of different cell lines, including reversal, following, or sliding events. This data-driven approach can be used to quantitatively study how molecular perturbations control cell–cell interactions and may be extended to larger cell collectives, where the inferred interactions could provide key insights into multicellular dynamics.
The migratory dynamics of cells in physiological processes, ranging from wound healing to cancer metastasis, rely on contact-mediated cell–cell interactions. These interactions play a key role in shaping the stochastic trajectories of migrating cells. While data-driven physical formalisms for the stochastic migration dynamics of single cells have been developed, such a framework for the behavioral dynamics of interacting cells still remains elusive. Here, we monitor stochastic cell trajectories in a minimal experimental cell collider: a dumbbell-shaped micropattern on which pairs of cells perform repeated cellular collisions. We observe different characteristic behaviors, including cells reversing, following, and sliding past each other upon collision. Capitalizing on this large experimental dataset of coupled cell trajectories, we infer an interacting stochastic equation of motion that accurately predicts the observed interaction behaviors. Our approach reveals that interacting noncancerous MCF10A cells can be described by repulsion and friction interactions. In contrast, cancerous MDA-MB-231 cells exhibit attraction and antifriction interactions, promoting the predominant relative sliding behavior observed for these cells. Based on these experimentally inferred interactions, we show how this framework may generalize to provide a unifying theoretical description of the diverse cellular interaction behaviors of distinct cell types.
Collective cellular processes such as morphogenesis, wound healing, and cancer invasion rely on cells moving and rearranging in a coordinated manner. For example, in epithelial wound healing, cells collectively migrate toward the injury and assemble to close the wound (12–3). In contrast, in metastasizing tumors, cancer cells migrate outward in a directed fashion and invade surrounding tissue (4). At the heart of these emergent collective behaviors lie contact-mediated cell–cell interactions (3, 56789–10), which are apparent in two-body collisions of cells (101112–13). These cellular interactions depend on complex molecular mechanisms, including cadherin-dependent pathways and receptor-mediated cell–cell recognition (5, 10, 11, 141516–17). At the cellular scale, this molecular machinery leads to coordinated, functional behaviors of interacting cells (3, 56789–10), which are highly variable and may take distinct forms in different biological contexts (10, 181920–21).
Achieving a quantitative understanding of the stochastic migratory dynamics of cells at the behavioral level could yield key insights into both the underlying molecular mechanisms (22, 23) and the biological functions (10) associated to these behaviors. For noninteracting, single migrating cells, data-driven approaches have revealed quantitative frameworks to describe the behavior of free unconstrained migration (2425–26) and confined migration in structured environments (2728–29). However, it is still poorly understood how the migratory dynamics of cells are affected by cell–cell interactions and a quantitative formalism for the emergent behavioral dynamics of interacting cells is still lacking (30). Indeed, it is unclear whether cellular collision behaviors follow a simple set of interaction rules and, if so, how these rules vary for different types of cells.
The study of interacting cell dynamics is complicated by the complex settings in which they take place, confounding contributions of single-cell behavior, interaction with the local microenvironment, and cell–cell interactions. Thus, simplified assays have been developed where cells are confined by one-dimensional micropatterned patches (31, 32) or tracks (19, 20, 33, 34), microfluidics (35), and suspended fibers (36). In these systems, cells exhibit characteristic behaviors upon pairwise collisions, including reversal, sliding, and following events. Upon contact, many cell types exhibit a tendency to retract, repolarize, and migrate apart—termed contact inhibition of locomotion (CIL) (10, 13, 37). Indeed, diverse cell types, including epithelial and neural crest cells, predominantly reverse upon collision (19, 33, 34). In contrast, the breakdown of CIL is commonly associated with cancer progression (11, 18, 19, 38), and cancerous cells have been observed to move past each other more readily than noncancerous cells (19). However, it is unclear how to describe these distinct collision behaviors in terms of physical interactions.
Models for collective cell migration often assume repulsive potentials or alignment terms (9, 30, 394041–42), but the form of these interactions is not derived directly from experimental data. Such data-driven approaches have been developed for single-cell migration (2425262728–29), but have not yet been extended to interacting systems. The search for unifying quantitative descriptions of the dynamics of interacting cell trajectories is further complicated by their intrinsic stochasticity, resulting in highly variable migration and collision behavior (19, 33, 34, 36). Thus, developing a system-level understanding of cell–cell interactions requires a quantitative data-driven approach to learn the full stochastic dynamics of interacting migrating cells.
Here, we develop a theoretical framework for the dynamics of interacting cells migrating in confining environments, inferred directly from experiments. Specifically, we confine pairs of migrating cells into a minimal “cell collider”: a two-state micropattern consisting of two square adhesive sites connected by a thin bridge. Both noncancerous (MCF10A) and cancerous (MDA-MB-231) human breast tissue cells frequently migrate across the bridge, giving rise to repeated cellular collisions. In line with prior observations (19), we find that while MCF10A cells predominantly reverse upon collision, MDA-MB-231 cells tend to interchange positions by sliding past each other. To provide a quantitative dynamical framework for these distinct interacting behaviors, we focus on a simplified, low-dimensional representation of these collision dynamics by measuring the trajectories of the cell nuclei. The cell collider experiments yield large datasets of such interacting trajectories, allowing us to infer the stochastic equation of motion governing the two-body dynamics of interacting cells. Our data-driven approach reveals the full structure of the cellular interactions in terms of the relative position and velocity of the cells. Specifically, the dynamics of MCF10A cells are captured by repulsion and friction interactions. In contrast, MDA-MB-231 cells exhibit surprising dynamics, combining attractive and “antifriction” interactions, which have no equivalent in equilibrium systems. This inferred model quantitatively captures the key experimental observations, including the distinct collision phenotypes of both cell lines. Our framework can be generalized to provide a conceptual classification scheme for the system-level dynamics of cell–cell interactions and is able to capture various previously observed types of cell–cell collision behaviors.
Two-State Micropatterns Provide Minimal Cell Collider
To investigate the two-body interaction dynamics of migrating cells, we designed a micropatterned system in which two cells repeatedly collide. The micropattern confines the cells to a fibronectin-coated adhesive region, consisting of a narrow bridge separating two square islands. Outside this dumbbell-shaped region the substrate is passivated with poly(L-lysine)-graft-poly(ethylene glycol), to which the cells do not adhere. We first confine single cells to these patterns, as described in previous work (27). Here, we identify cells which undergo division from which we obtain confined, isolated pairs of daughter cells (Fig. 1A). We employ phase-contrast time-lapse microscopy to study the homotypic interactions of pairs of noncancerous (MCF10A) and cancerous (MDA-MB-231) human mammary epithelial cells. The confining bridge between the two islands leads to two well-defined configurations, with both cells either on the same island or on opposite sides of the pattern, between which the system repeatedly switches (Fig. 1 C and D and Movies S1–S4). During these switching events, the cells interact with each other. Therefore, our experimental setup offers a simple platform to study the interactions of confined migrating cells in a standardized manner: a minimal cell collider.

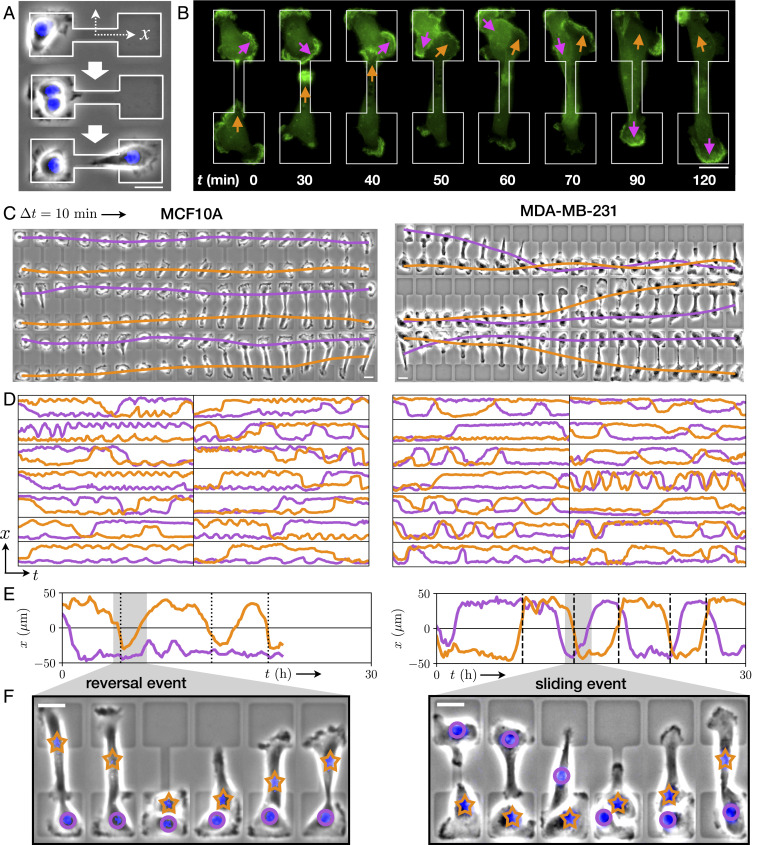
Stochastic switching dynamics of confined cell pairs. (A) Experimental design. Single cells are confined to two-state micropatterns (white outline). We track cell pairs resulting from cell divisions. The stained nucleus is colored in blue. (B) Time series of two interacting MDA-MB-231 cells transfected with LifeAct-GFP. Arrows highlight regions of pronounced actin activity, and the arrow color indicates the cell identity. (C) Brightfield image series with overlaid nuclear trajectories (orange, violet). Images are taken at a time interval = 10 min. (D) Sample set of nuclear trajectories
Within this cell collider, cells are highly motile and exhibit actin-rich lamellipodia-like protrusions forming at the cell periphery (Fig. 1B and Movie S5). As a simplified, low-dimensional representation of the interaction dynamics, we use the trajectories of the cell nuclei, which reflect the long-timescale interacting behavior of the cells (Fig. 1C). These coupled cell trajectories are highly stochastic. Using this assay, we monitor the stochastic two-body dynamics of hundreds of cells over long periods of time (up to 40 h per cell pair) in standardized microenvironments, yielding an unprecedented amount of statistics on cell–cell interactions (Fig. 1D). Importantly, we find that most of the interactive behavior is captured by the
Cell Pairs Exhibit Mutual Exclusion
A key feature of the trajectories for both cell lines is the apparent preference for the configuration in which the cells are on opposite islands (Fig. 1D). Indeed, the positions of the two cells are strongly correlated: The cross-correlation function

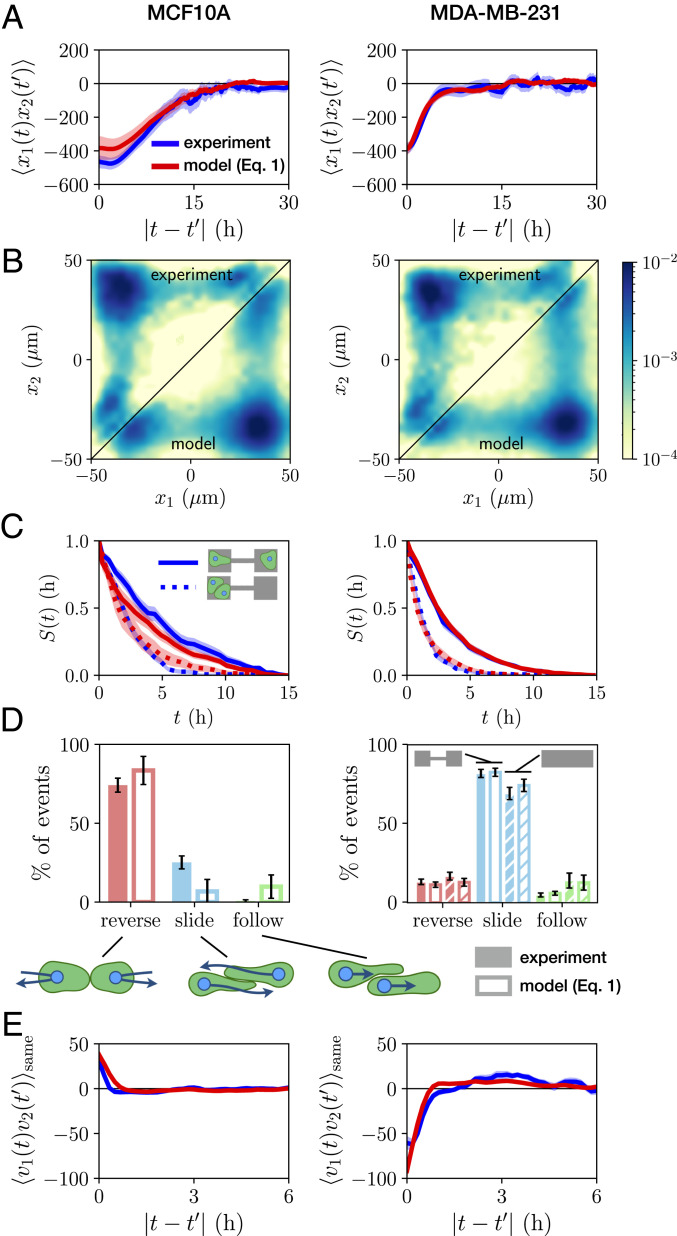
Statistics of the stochastic interaction dynamics. (A) Cross-correlation function of cell positions
MCF10A and MDA-MB-231 Cells Exhibit Distinct Collision Behavior
While the cells mutually exclude each other, they are also highly migratory and thus frequently transit the constricting bridge. This results in repeated stochastic collision events, providing statistics for how these cells interact during a collision. Following a collision, we observe three distinct types of behaviors: reversal events, where the cells turn around upon collision; sliding events, where the cells interchange positions by sliding past each other; and following events, where the cells remain in contact and perform a joint transition (Fig. 1 E and F and SI Appendix, section 3). These three behaviors have been previously used as observables of cell–cell interactions in one-dimensional and fibrillar environments (19, 33, 34, 36, 43).
To quantify the interaction behavior of MCF10A and MDA-MB-231 cells, we identify collision events and measure the percentage that result in reversal, sliding, or following events (Fig. 2D). Both cell lines exhibit only a small fraction of following events. Remarkably however, we find that collisions of MCF10A cells predominantly result in reversals, while MDA-MB-231 cells typically slide past each other upon collision, in line with observations in other confining geometries (19). To further explore the generality of this result, we perform additional experiments with MDA-MB-231 cells on micropatterned tracks without constrictions, but the same overall dimensions of the two-state micropatterns (Movies S6 and S7). We find that sliding events similarly dominate for MDA-MB-231 cells on this pattern, with similar overall event ratios (Fig. 2D). The different responses to cell–cell contacts are also reflected by the velocity cross-correlation of the two cells when occupying the same side of the two-state micropatterns:
Contact Acceleration Maps Reveal Dynamics of Cell–Cell Interactions
Here, we aim to describe the underlying interaction dynamics that capture the full stochastic long-timescale behavior of repeatedly colliding cell pairs. The dynamics of single migrating cells are well described by an equation of motion that is second order in time (2425262728–29), making accelerations the natural quantity to describe cell motility. Specifically, we previously showed that the migration dynamics of single cells in confinement can be described by the average acceleration as a function of cell position
Strikingly, we find that MCF10A and MDA-MB-231 cells exhibit qualitatively different contact acceleration maps (Fig. 3 A and D). Indeed, for MCF10A cells, the contact acceleration exhibits a clear dependence on the relative position, while MDA-MB-231 cells exhibit accelerations that mainly depend on the relative velocity. We investigate these differences by measuring the one-dimensional (1D) dependence of the contact accelerations as a function of just

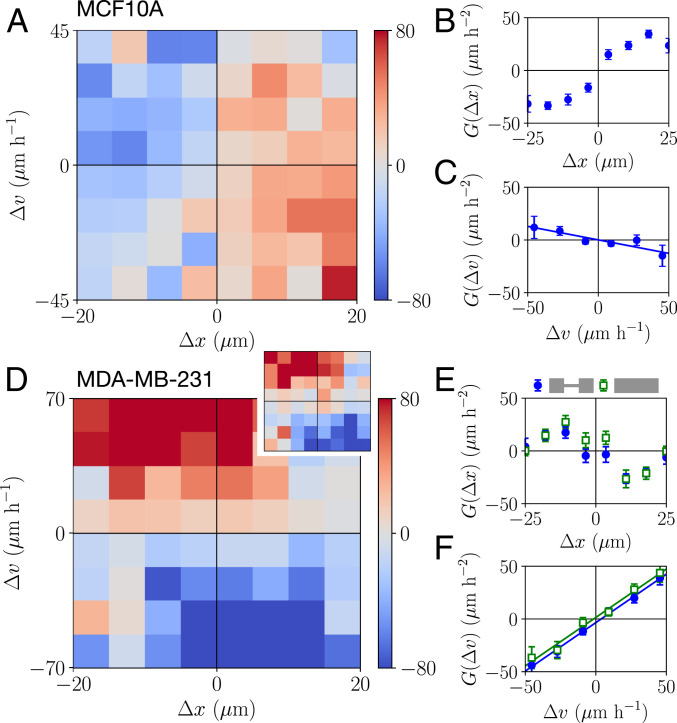
Contact acceleration maps. (A and D) Contact acceleration maps
Interacting Equation of Motion Captures Experimental Statistics
To investigate whether the interacting dynamics of MDA-MB-231 and MCF10A cells can be described by the physical interactions implied by the contact acceleration maps, we consider a simple model for cell–cell interactions in confining environments. Motivated by the structure of the contact accelerations, we postulate that the dynamics of the cells can be described by a stochastic equation of motion of the form
To investigate this model, we first require a systematic approach to infer the systems’ stochastic dynamics and delineate single-cell (one-body) and interactive (two-body) contributions to the dynamics. Thus, we employ a rigorous inference method, underdamped Langevin inference (ULI) (44), to infer the terms of this equation of motion from the experimentally measured trajectories. In this approach, the inferred terms are completely constrained by the short-timescale information in the measured trajectory, i.e., the velocities and accelerations of the cells (Materials and Methods and SI Appendix, section 4).
Importantly, there is no a priori reason why Eq. 1 should provide a reasonable ansatz to correctly capture cell–cell interactions, which could require a more complex description. Thus, we investigate the predictive power of our model by testing whether it correctly captures experimental statistics that were not used to constrain the terms in Eq. 1. Specifically, while the model is learned on the experimental short-timescale dynamics, we aim to make predictions for long-timescale statistics such as correlation functions. To this end, we simulate stochastic trajectories of interacting cell pairs based on our model (Fig. 4 D and H) to make a side-by-side comparison with the experiments. Remarkably, we find that the model performs well in predicting key experimental statistics for both cell lines, including the joint probability distributions (Fig. 2B); the distributions of switching times (Fig. 2C); and the cross-correlations of positions and velocity (Fig. 2 A and E); as well as the relative fractions of reversal, sliding, and following events (Fig. 2D). In contrast, performing the same inference procedure with simpler models than Eq. 1, e.g., with only cohesive or friction interactions, shows that simulated trajectories of these models do not capture the observed statistics (SI Appendix, section 4). To further challenge our approach, we test whether we can use the interactions learned from experiments on two-state micropatterns to predict the collision behavior in a different confinement geometry. Specifically, we use the single-cell term

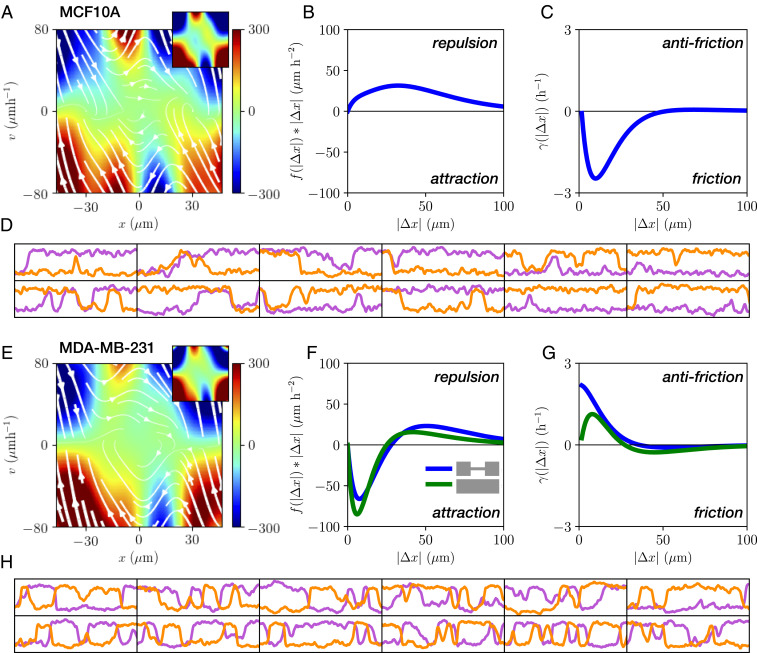
Equation of motion for interacting cells. (A and E) Single-cell contribution
Remarkably, our inference approach reveals that the inferred single-cell contributions
Interaction Behavior Space: A Theoretical Framework for Cell–Cell Interactions
To conceptualize the distinct interactions of MCF10A and MDA-MB-231 cells, we propose an interaction behavior space, spanned by the amplitudes of the cohesive and frictional contributions (Fig. 5). Based on our inference, the two cell lines occupy diagonally opposed quadrants in this space. To investigate whether our model (Eq. 1) is able to capture cellular interaction behaviors more broadly, we predict trajectories for various locations within this interaction map. For interactions consisting of repulsion and friction, we find that collisions predominantly result in reversal events, as we have observed for MCF10A cells. In contrast, for positive friction coefficients, corresponding to effective antifriction, we find that sliding events dominate for all parameter values. This regime thus corresponds to the dynamics we have observed for MDA-MB-231 cells. Finally, attractive interactions with regular friction result in a dominance of following events. The interaction behavior space thus provides an insightful connection between the inferred interaction terms governing the instantaneous dynamics of the system and the emergent macroscopic, long-timescale collision behavior.

![Interaction behavior space. We construct an interaction space by varying the amplitude of the cohesive and friction interactions, f0 and γ0, respectively. Contact acceleration maps for purely attractive, repulsive, frictional, and antifrictional interactions are indicated on the axes. Based on the inferred short-range interactions, we place MDA-MB-231 and MCF10A cells into diagonally opposed quadrants. Predicted behaviors in the interaction space are obtained by varying the cohesion and friction interactions in our model. Specifically, we simulate a model including the inferred MDA-MB-231 single-cell term F(x,v) together with a cohesive term f(|Δx|)=f0gc(|Δx|) and an effective friction term γ(|Δx|)=γ0gf(|Δx|), for varying f0 and γ0. The distance-dependent functions gc,f are positive and monotonically decreasing. These results do not sensitively depend on the specific choice of F(x,v) or gc,f (gc,f=exp[(−|Δx|/R0)] is used here) (SI Appendix, section 5). For each parameter combination, reversal, sliding, and following events were identified. At each point, the dominant behavior is indicated by the color scheme, and white regions correspond to states where no single behavior contributes more than 50% of events. Numbered Insets show sample trajectories from different parts of the interaction map and the corresponding percentages of reversal (red), sliding (blue), and following events (green).](/dataresources/secured/content-1765902912889-a37d7d54-3062-4838-a2f7-9dab5e8f2f1a/assets/pnas.2016602118fig05.jpg)
Interaction behavior space. We construct an interaction space by varying the amplitude of the cohesive and friction interactions,
Discussion
In this study, we introduced a conceptual framework for the stochastic behavioral dynamics of interacting cells. To this end, we designed a micropatterned cell collider in which pairs of cells repeatedly collide with each other, providing large amounts of statistics on the long-timescale interactions of migrating cell pairs. A key advantage of this setup is that it yields a large number of collisions under controllable conditions. Moreover, the dynamics of single cells migrating in this confinement are well understood (27), providing a benchmark for the dynamics inferred for interacting cells. We compare the homotypic interaction behavior of the nonmalignant MCF10A and the metastatic MDA-MB-231 mammary epithelial cell lines. While phenomenological bottom–up models have been developed to describe cell–cell interactions (30, 32, 43, 4546–47), we propose an alternative, top–down approach to learn the interacting stochastic equations of motion governing cell migration from the experimentally observed trajectories. Such an effective model captures the emergent dynamics at the cellular scale which are driven by underlying mechanisms, including the intracellular polarity machinery. Our inferred models for interacting cells quantitatively capture the distinct behaviors of the two cell lines. This inference reveals that the dynamics can be decomposed into a one-body motility component, which qualitatively matches that observed in single-cell experiments (27), and a two-body interaction term.
The interaction terms we inferred from experiments take qualitatively different forms for the two cell lines: While MCF10A cells exhibit repulsion and effective friction, MDA-MB-231 cells exhibit attraction and a surprising effective antifriction interaction. At the single-cell level, MDA-MB-231 cells are known to be more invasive than MCF10A cells (48, 49) and express lower levels of the cell–cell adhesion protein E-cadherin (19, 50), possibly underlying the different friction-like interactions we found for these cell lines. These two cell lines also display remarkably different collective behaviors (5152–53): MCF10A cells in two-dimensional (2D) epithelial sheets exhibit aligned, directed motion and form compact spheroids in three-dimensional (3D) culture, with few invasive branches. In contrast, MDA-MB-231 cells in 2D epithelial sheets exhibit nonaligned, random motion and form invasive, noncontiguous clusters in 3D culture, with significant single-cell dispersion from the cluster. These differences in collective behavior may relate to the distinct types of interactions we have inferred from the two-body dynamics of these cell lines.
Based on the inferred equation of motion, we predict an interaction behavior space to link the interaction terms, which govern the instantaneous stochastic dynamics, to the emergent collision behaviors. The three distinct regimes emerging in our model correspond to specific behaviors observed in experiments for various cell types: Predominant reversal behavior on 1D lines has been termed contact inhibition of locomotion (33, 34), a common type of cell–cell interaction (5, 8, 10, 13). By inhibiting intracellular Rho signaling in neural crest cells, this reversal-dominated behavior could be tuned to following-dominated behavior (34). Such following behavior has also been identified as an important mechanism in collective migration (12, 20, 21, 54) and was termed contact following locomotion (20). Finally, previous work has shown that reducing the expression levels of E-cadherin enables otherwise reversing cells to mainly slide past each other (19). For this regime of predominant sliding interactions, we propose the term contact sliding locomotion. Based on our interaction behavior space, we find that the antifriction interactions we identified for MDA-MB-231 cells promote such sliding behavior. The interaction behavior space could thus provide a quantitative classification of distinct modes of interaction that may be achieved through molecular perturbations in experiments (19, 34). On the other end of the scale, the antifriction interaction type we find here could play a role in collective systems such as the fluidization of tissue in tumor invasion (53, 55, 56). The form of the interaction terms we inferred from experiments may thus inform models for collective cell migration (9, 30, 3941–42). Furthermore, the inference framework we have developed for the dynamics of interacting cell pairs can be extended to infer the dynamics of more complex collective systems, such as small clusters of cells (32, 41, 57), epithelial sheets (42, 58), or 3D organoids (55, 56). In summary, our model, which we rigorously derive directly from experimental data, could potentially describe the diversity of previously observed cell–cell interaction behaviors in a unifying quantitative framework.
Materials and Methods
Sample Preparation and Cell Culture.
Fibronectin micropatterns are made by microscale plasma-initiated protein patterning as described previously (27).
MCF10A cells (American Type Culture Collection) are cultured at
MDA-MB-231 cells (DSMZ) are cultured in minimum essential medium (MEM, c.c. pro), containing 10% FBS (Gibco) and 2 mM L-glutamine (c.c. pro). Cells are grown in a 5%
Microscopy and Cell Tracking.
All measurements are performed in time-lapse mode for up to 50 h on an IMIC digital microscope (TILL Photonics) or on a Nikon Eclipse Ti microscope using a 10× objective. The samples are kept in a heated chamber (ibidi GmbH or Okolab) at
Contact Acceleration Maps.
To gain insight in the general structure of the accelerations due to cell–cell interaction, we introduce contact acceleration maps. We estimate the single-cell component of the dynamics from the accelerations observed at time points where the cells are far apart,
Underdamped Langevin Inference.
From the short-timescale dynamics of the measured cell trajectories
Acknowledgements
We thank Ricard Alert, Edouard Hannezo, and Joris Messelink for inspiring discussions. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project-ID 201269156–SFB 1032 (Projects B01 and B12). D.B.B. is supported in part by a DFG fellowship within the Graduate School of Quantitative Biosciences Munich and by the Joachim Herz Stiftung. P.R. is supported by a Center for the Physics of Biological Function fellowship (NSF Grant PHY-1734030).
Data Availability.
All study data are included in this article and/or SI Appendix.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
 Learning the dynamics of cell–cell interactions in confined cell migration
Learning the dynamics of cell–cell interactions in confined cell migration
