Suspensions of colloidal particles are widely spread in nature and technology and have been studied intensely over more than a century. When the density of such suspensions is increased to high volume fractions, often their structural dynamics are arrested in a disordered, glassy state before they can form an ordered structure. While this puts limits on technical applications, knowledge gained from investigations of phase transformations of colloidal suspensions provides insight into similar phenomena in a broad range of complex glass-forming materials, ranging from metals to biological cells (2–). The colloidal glass transition has therefore been considered a model that features many of the glass transition phenomena found in atomic and molecular systems (). Being big enough to allow their real-space observation using optical microscopy, but small enough to remain suspended over extended periods, colloids in such model systems are employed as “big atoms” () that can be investigated on an individual particle basis (, ). By analyzing the trajectories of thousands of particles, detailed insights into glass phenomena, such as dynamic heterogeneities of collectively rearranging structures, have been obtained (, ).
To date, most experiments of this type have been done using spherical colloids. The recent interest in synthetic colloids as material building blocks (, ), however, has led to the development of a multitude of novel techniques for the synthesis of colloidal particles with specific geometries and interactions (13–). This now allows investigations of the phase transformations in dense suspensions of shape-anisotropic particles, which promises to give unique insight into structural dynamics of complex systems. Highly elongated colloidal rods, for instance, show arrested texture dynamics in suspensions far in the nematic regime (, ). The simplest deviation from spherical symmetry is uniaxial stretching to prolate ellipsoids (, ). Already, for these simple particles, theory and simulations predict a rich phase diagram (), including jammed states (), and complex glass formation (2223–) due to the presence of translational and rotational degrees of freedom. These predictions also have implications for molecular liquid crystalline materials (, ). However, the few investigations of glass-forming suspensions of ellipsoids have all been focused on static structures obtained by driving particles in external gravitational or electric fields (2829–). The only investigations on steric effects of ellipsoid shape have been performed in two-dimensional (2D) films (, 32–). To date, hardly any experimental data on the influence of steric factors on the phase transformation in three-dimensional (3D) ellipsoidal suspensions exist.
Here, we present particle-resolved studies of the structural dynamics of concentrated ellipsoidal colloid suspensions at a nonequilibrium phase transformation. The experiments were performed on a large range of different volume fractions. Mode coupling theory (MCT) predicts that, in systems of this type, a liquid glass should exist in which particle rotation is frozen whereas their translation is still liquid (). We used quantitative optical microscopy in combination with a novel type of core–shell particles () to simultaneously track translational and rotational particle motion with high precision (). Upon increasing the volume fraction , we find that rotational degrees of freedom undergo a glass transition before translational dynamics are arrested, such that a liquid glass is formed. To understand the nature of the observed rotational and translational glass transitions, we further corroborate our results with an MCT analysis and Brownian dynamics simulations and find that long-range correlations are the cause for the emergence of this unique state. Detailed image analysis reveals that hitherto unknown nematic precursors exist as the characteristic structural elements of the liquid glass. They consist of ramified aligned regions intersected by differently ordered or disordered regions and appear to mediate the long-range correlations present in the liquid glass state of particle suspensions. Our experiments give a first impression of the complex behavior of colloidal suspensions arising from the introduction of the simplest geometrical distortion of the particles’ shape from sphericity. They show how sterical factors lead to the emergence of peculiar local structures mediating long-range spatial correlations which result in the formation of amorphous states preempting the globally ordered state.
Results and Discussions
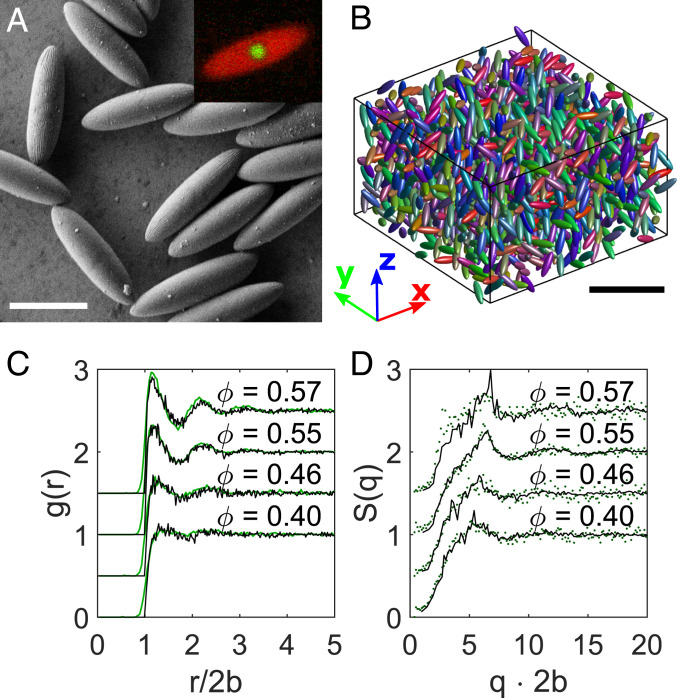
In our experiments, we used ellipsoidal polymethylmethacrylate (PMMA) colloids with a long semiaxis of a=4.32 μm and a short semiaxis of b=1.23 μm, that is, an aspect ratio of a/b=3.5 (Fig. 1A). The particles were sterically stabilized and suspended in a density- and refractive index-matched solvent mixture (). Tracking of particle positions and orientations was facilitated by using particles with core–shell geometry where the spherical core and the ellipsoidal shell were labeled with different fluorophores (). Using confocal laser scanning microscopy, we typically recorded the temporal development of the 3D particle positions and orientations for more than 6,000 particles with accuracies of 60 nm and 5°, respectively () (Fig. 1B). Since volume fractions ϕ are the pivotal variable in all of the experiments, we took utmost care in their determination (see Materials and Methods for details). In order to validate the experimental results, we performed event-driven Brownian dynamics (ED-BD) simulations that model overdamped dynamics of hard ellipsoids (). The system consisted of N nonoverlapping ellipsoids in a cubic simulation box of length L that was varied depending on the desired ϕ. Results from experiments and computer simulations were analyzed using MCT.
Fig. 1.
Characterization of ellipsoidal colloids and their packings. (A) Scanning electron microscope image of the ellipsoidal colloids with aspect ratio a/b=3.5. Inset shows a confocal microscopy image, highlighting the core–shell structure. (Scale bar, 5 μm.) (B) Computer rendered 3D reconstruction of a subset of a sample volume at ϕ=0.57 with the red–green–blue value of the color indicating the particle orientations. (Scale bar 20 μm.) (C) Pair correlation function g(r) and (D) structure factor S(q) for ϕ from experiment (green points) and simulation data (black lines). Distances r are rescaled by the ellipsoid width 2b.
Structural Correlations and Lack of Order.
To gain insight into the systems’ behavior, we first extracted the pair correlation functions g(r) and equilibrium structure factors S(q) from the 3D particle positions at different ϕ (Fig. 1 C and D). With increasing ϕ, we observe the emergence of next-neighbor and second next-neighbor peaks in g(r) while long-range correlations are absent. At the same time, in S(q), the inverse peak position 2π/qmax, indicating the average particle separation, becomes smaller with increasing density. All observations are typical for liquid-like structural correlations and show that the systems remained in a disordered state without translational order for all investigated ϕ. The excellent coincidence between the measured g(r) and S(q) with those obtained by the ED-BD simulations confirms that, in the suspensions, our elliptical colloids interacted like hard particles. A further support for the hard particle potentials of our system comes from the lack of formation of nematic or smectic phases known from charged particles (compare below) (, ).
The equilibrium phase diagram of ellipsoids predicts the transition to a nematic state with increasing ϕ (); thus we determined the orientational order of the whole sample. It is probed by calculating the nematic order parameter S (), which is the eigenvalue possessing the largest absolute value of the nematic order tensor Qij. The nematic order tensor is given by
where
u→ is an eigenvector representing the orientation of the ellipsoid. The order parameter
S for different measured
ϕ shows no indications for nematic order in the probed systems (
Fig. 2A). For all
ϕ, it remains below a value of
S<0.3 which is the commonly accepted criterion for the isotropic–nematic transition in simulations (). The absence of nematic order is confirmed by plotting the changes of the order parameter
S with time (
Fig. 2B) for different
ϕ. It shows no temporal evolution for all
ϕ, indicating the stability of the observed isotropic states.
Fig. 2.
Nematic order parameter S obtained from the nematic tensor Qij. (A) S for different ϕ, indicating the absence of a global particle alignment in the experimental system. (B) Time evolution of the nematic order parameter for different ϕ, again showing no signs of an evolving directional order.
Dynamical Signatures of Glass Formation.
The absence of structural order even in very dense suspensions hints at the possible formation of a glass. To verify this, it is necessary to investigate the structural relaxation dynamics of the suspensions. The translational and rotational dynamics of the system are contained in the temporal evolution of the self part of the density correlation function
and of the orientational correlation functions
respectively. Here,
r→i is the position of the center of particle
i,
θi is its orientation relative to a fixed laboratory direction, and
N is the total particle number. The
Pn are the Legendre polynomials of order
n, and
⟨⟩ denotes averaging over
t′. For the calculation of
Fs(q,t) and
Ln(t), the wave vector
q was set to different values
5.18<q⋅2b<7.90, and
n=2,4, respectively, was chosen.
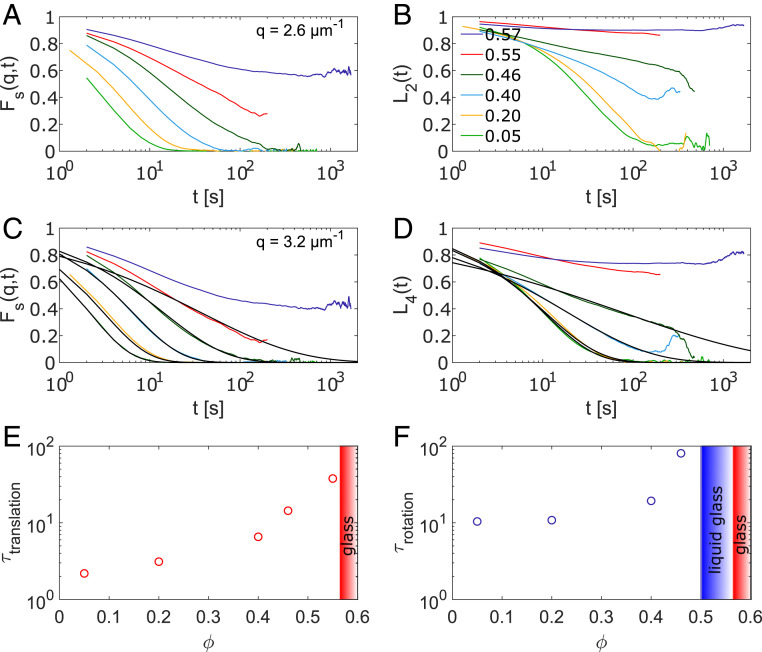
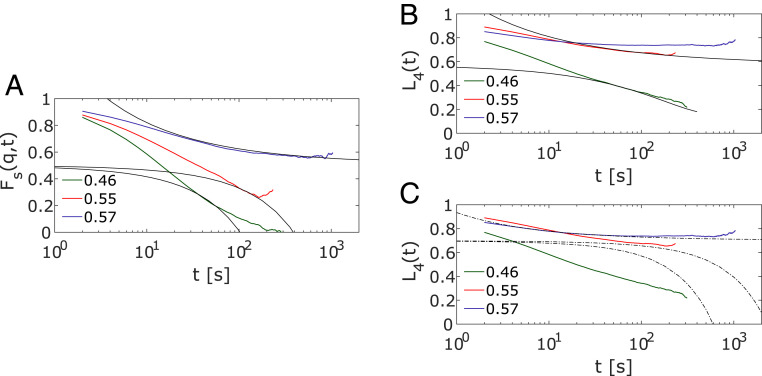
Fig. 3 A, C, and E describes the translation behavior and depicts the experimentally determined Fs(q,t) values for each ϕ. In Fig. 3A, the wavevector is set to q=2.6 μm−1 (namely, 2bq=6.42) which corresponds to the maximum in the static structure factor and thus to the average particle distance. In Fig. 3C, a larger wavevector, q=3.2 μm−1 (2bq=7.90), is selected, where the relaxation is faster and the final decay can be resolved well in fluid states. Correlation functions obtained for different values of q can be superimposed by scaling with log(tq2) for low ϕ as is expected for the dynamics of isolated ellipsoids (SI Appendix, Fig. S1). For a liquid state, one expects the translation correlators Fs(q,t) to decay completely over time. During the measurement time, this is observed for volume fractions up to ϕ=0.46. The curves obtained for ϕ=0.55 are already stretched and thus show a slowing down of the decay dynamics, but one can still assume their complete decay albeit at times longer than those probed. The states at ϕ≤0.55 thus are fluid-like. By contrast, at the highest volume fraction ϕ=0.57, the translational correlator does not decay any more, which is seen by the clear plateau for translational motion typical for a glass state. From these observations, we conclude that, for translational dynamics, a glass transition occurred between ϕ=0.55 and ϕ=0.57.
Fig. 3.
Temporal correlation functions capturing translational and rotational dynamics for different ϕ. A and C depict the self part of the density correlation Fs(q,t) at wavelengths comparable to the average particle separation, namely, 2bq=6.42 (A) and 2bq=7.90 (C), respectively. B and D show the orientational correlation function Ln(t) for n=2 and n=4; the legend in B gives the packing fractions for A–D. Close to the glass transition, the decay of the curves is too slow to be captured within the measurement times. C and D include fits to the correlators in fluid states using the Kohlrausch function . E and F show the relaxation times obtained from the fits. The colored regions mark the glass transitions ϕct and ϕcr which were obtained by the MCT glass stability analysis (see Materials and Methods).
Fig. 3 B and D depicts the temporal relaxation behavior of the rotation correlators Ln(t) for n=2 and n=4, respectively. A comparison with their translational counterparts, illustrated in Fig. 3 A and C, clearly shows the differences in the translational and rotational relaxation of the suspensions. For volume fractions ϕ≤0.46, a complete relaxation of orientational correlation is observed even if the curves for ϕ=0.46 are already stretched significantly. However, for the two highest ϕ, a clear plateau indicative of incomplete relaxation appears in both orientational correlation functions. These frozen orientational correlations are clear signs of glass-like behavior. Plateaus in the orientational correlation functions could also arise from nematic ordering. The observed values for the plateau heights, however, are too large to be compatible with the negligible nematic order of our samples. In nematic states, the relation L2(t→∞)=S2 holds (), and the small values of the order parameter S from Fig. 2 are incompatible with the high amplitudes of frozen-in orientational correlations. We thus conclude that the data show a glass transition in the rotational dynamics occurring between ϕ=0.46 and ϕ=0.55.
The inspection of Fig. 3 leads to the conclusion that two different glass transitions, one in the orientational and a second one in the translational motion, exist. To gain more insight into this phenomenon, we turn to a quantitative analysis. In fully relaxing systems, the long-time decay, often termed α-relaxation, can be fitted with a Kohlrausch function (),
where
fΦ is an amplitude,
τ is the relaxation time, and
β is the so-called stretching exponent. Using this function, we obtain fits that agree very well with our data for curves showing a clear decay within the experimental time window (
Fig. 3 C and
D; fit parameters are collected in
SI Appendix, Table S1). Results for the translational and rotational
α-relaxation times
τt and
τr are depicted in
Fig. 3 E and
F. The rise of the
α relaxation time
τr for rotations sets in at lower
ϕ than the rise in the corresponding translational
τt, and
τr also exceeds the observation time at a lower
ϕ than
τt. This reaffirms the presence of two different glass transitions. We also note that the correlators for translational relaxation at
ϕ=0.55 and for rotational relaxation at
ϕ=0.46 are well fitted, which confirms the fluid-like behavior at these
ϕ, which are the packing fractions of the fluid states closest to the transitions.
A quantitative determination of the ϕ at which the glass transition for translation ϕct and rotation ϕcr occurs is obtained by the glass stability analysis of MCT () (compare Materials and Methods). Performing such an analysis, we find that satisfactory fits to the data (Fig. 3 E and F) can only be obtained assuming two different glass transitions, ϕct=0.56 and ϕcr=0.50. Therefore, also, this analysis shows the existence of two separate glass transitions for rotation and translation in the experiment.
In summary, the analysis of the systems’ dynamics reveals that we observed a density region where orientational motion in the sample was frozen while translational motion persisted. As this state lacks global nematic order, it is properly described as a liquid glass ().
ED-BD Simulations Pointing to Nematic Correlations.
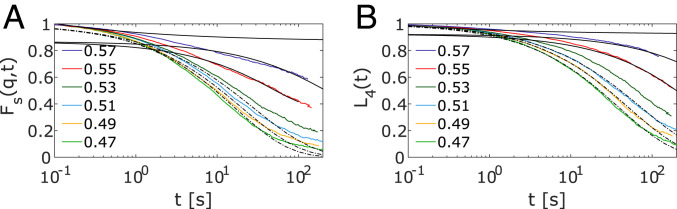
The interpretation of experimental results obtained from colloidal suspensions often is complicated by the fact that the particles possess a certain polydispersity and might carry residual charges. Since these problems are nonexistent in simulations, the latter are an important tool even if the number of particles which can be studied in this manner is typically rather small. To understand the origin of the formation of liquid glass in our system, we performed additional ED-BD simulations. We found that nematic order sets in quickly using monodisperse ellipsoids and periodic boundary conditions (PBCs) in accordance with previous simulation studies (, ). Therefore, we tested different scenarios that could explain the formation of the experimentally observed glass states. First, since the experimental system is inherently polydisperse, we included polydispersity in our simulations. However, we found that a polydispersity of 5 to 15%, well above that of the experimental particle system used, did not affect the structure and dynamics of the system. Second, in order to prevent the formation of nematic order, we introduced rough walls in our simulations. The approach of confining glass-forming liquids has been used experimentally () and in simulations () for studies of polydisperse spheres. Indeed, we find that nematic order is suppressed in systems with rough walls. Results for the dynamics of this system are shown in Fig. 4 for Fs(q,t) and L4(t). Here, L4 is shown, as it exhibits glassy dynamics more clearly than L2. The lines represent the MCT fitting curves obtained from and . Up to ϕ=0.53, both correlation functions decayed to fluid states, while, at ϕ=0.55 and ϕ=0.57, the system was already very close to the glass phase. However, in contrast to the experiments, the simulations still result in a single value for the glass transition of ϕct=ϕcr≈0.57.
Fig. 4.
Glass transition analysis of simulation data. (A) Translational Fs(q,t) for 2qb=6.42 and (B) orientational L4(t) correlation functions from ED-BD simulations, where long-range nematic fluctuations are suppressed by rough walls. An MCT glass stability analysis (black lines for the two highest densities; compare Materials and Methods) finds a single glass transition density in this case. The value ϕc≈0.57 is also supported by a power law fit (with γ=2.5) to the Kohlrausch relaxation times for both translation and rotation.
While the latter discrepancy between the experimental system and simulations appears dissatisfying, it allows us to formulate a working hypothesis on the prerequisites for the formation of a glass and a liquid glass, respectively: It is known, from experiments on suspensions of spherical colloids, that the glass transition at the higher ϕct results from isotropic caging (). This is accessible by simulation if nematic order is suppressed by the introduction of rough walls. Under this condition, the build-up of local neighbor shells leading to caging is possible already in small systems (). The growing fluid structure is reflected in the evolution of the structure factor S(q) shown in Fig. 1D. By contrast, the formation of a liquid glass above ϕcr and below ϕct requires long-range correlations, which cannot be captured in the simulation box sizes currently accessible. This is especially true for shape anisotropic particles, for which it has been shown that simulations are susceptible to finite size effects (). Solvent-mediated interactions, which were neglected in the simulations, could also play a role, but have been shown to be of minor importance in the structural dynamics of spherical colloids (). We therefore conjecture that the discrepancy between experiment and simulations reveals that the nature of the observed liquid glass state is relying on long-range correlations.
Nematic Precursor Analysis.
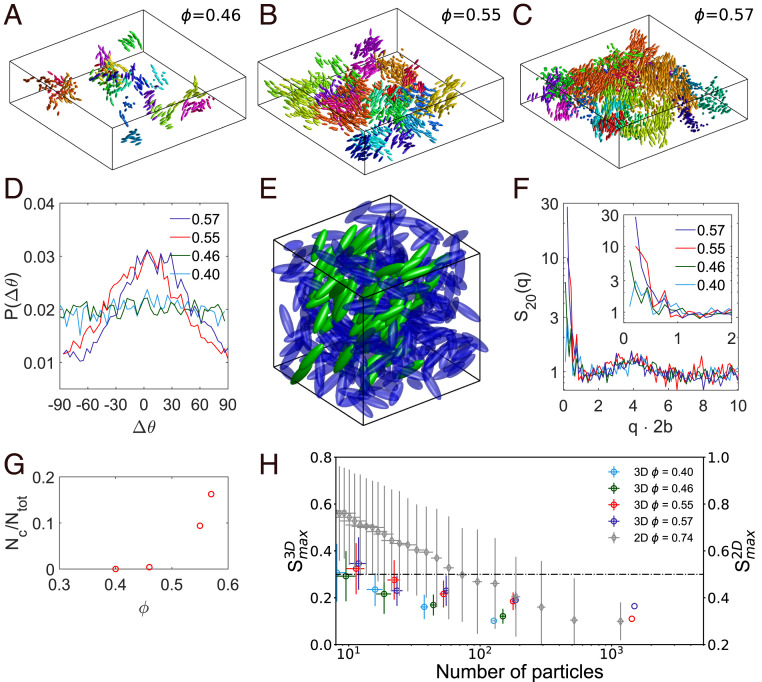
To identify these long-range correlations and to test our hypothesis, we analyzed the spatial correlations in the samples. A close inspection of the imaging data reveals clusters of similarly oriented particles in the system. Two particles are assigned to the same precursor cluster, if they are next neighbors sharing a face of their individual Voronoi cells and have an angular difference in orientation which is less than Δα≤20°. The choice of Δα is based on the half-width of the peak in the probability distribution P(Δθ) of the orientation of all ellipsoids in systems at high ϕ (Fig. 5D). Clusters are defined as nematic precursors, if they contain more than 30 particles. The choice of 30 particles is based on the largest cluster sizes found for ϕ=0.40, which corresponds to an isotropic sample. Since the clusters do not form nematic regions (Fig. 5H), we term them nematic precursors. Fig. 5 A–C depicts the 20 largest nematic precursors for the three highest ϕ studied. In general, we find that the number of particles in nematic precursors increases with growing ϕ, as shown in Fig. 5G. Also, the cluster size distributions become broader with increasing packing fraction. Our findings show that, with ϕ increasing to densities where we find glassy states, more and more particles are found in local structures with a peculiar order. In these, no nematic order is detected even on small length scales, because other particles and clusters intersect the nematic precursors. This is exemplified in Fig. 5E, where the green particles belong to a nematic precursor whereas the blue particles are disordered surrounding particles intersecting the cluster. A local analysis of the nematic order shows this quantitatively. To this end, we divided the sample into equal subboxes and calculated the maximal Smax of the order tensor per subbox. We started with subboxes containing an average of ∼10 particles and gradually increased their size up to ∼103 particles. The mean and variance of Smax vs. the number of particles contained in the subboxes are plotted in Fig. 5H. The results show a quick drop of the local order parameter Smax to low values with increasing particle number. Uniform order does not extend to more than roughly 20 particles. In the vicinity of the glass transition, orientational correlations exist among many particles (Fig. 5G), but still the nematic order parameter remains negligible (Fig. 5H). Nematic order formation is found only for particles with larger aspect ratios (). The existence of the nematic precursors is also visible in the orientational structure factor, S20(q), which reflects the density fluctuations of quadrupolar symmetry, ρl=2,m=0(q), proportional to the spherical harmonic for l=2 and m=0 () (SI Appendix). It is sensitive to the growth of nematic structures, which shows up as a peak for small wavevectors, and has been identified as correlation driving the glass transition at ϕcr in MCT (). Fig. 5F (note the log-linear plotting) shows that the large-q peak in S20(q), which records the orientational alignment of neighboring particles, remains rather unchanged while, upon increasing ϕ, the nematic precursors cause a growing peak at small wavevectors. Its width measures the average size of the clusters, which exceeds the average particle separation by roughly a decade. We have carefully evaluated other possible causes for the appearance of long-wavelength fluctuations and could exclude them for the following reasons: 1) Repulsive or attractive forces between the particles would cause differences in the pair correlation and structure factor data derived from experiment and simulation, which is not the case (Fig. 1). 2) The effect of polydispersity was found to be negligible in additional simulations. 3) Scanning electron microscope images (Fig. 1A) show the particles to be smooth on a scale of tens of nanometers, which rules out surface roughness. 4) Thermal fluctuations were fully included in the simulations, and 5) hydrodynamic interactions are considered insignificant at these volume fractions (). 6) Mermin–Wagner fluctuations, which were suggested to affect glass formation in 2D ellipsoids (), do not exist in 3D systems. Our data therefore suggest that nematic precursors are the hallmark of the long-wavelength fluctuations observed in bulk liquid glass.
Fig. 5.
Analysis of nematic precursors in the experimental system at high densities. (A–C) A 3D representation of the 20 largest clusters with similar orientation, defined as described in the text, for different ϕ showing the existence of nematic precursors which are intercepting each other. Box size is 140×140×40 μm each. All particles are scaled by a factor of 0.8 for better visibility. (D) Probability distribution P(θ) of the orientation of all ellipsoids in the system for different ϕ. For increasing ϕ, a favored orientation is emerging, indicating nematic precursors but no apparent nematic order. (E) The green particles belong to one cluster with similar orientation, while the surrounding blue particles are in an amorphous arrangement or belong to clusters of different orientations. The hindrance between the different precursors prevents global nematic order. Box size is 25×25×25 μm. (F) Orientational structure factor S20(q) obtained from spatially correlating the orientations of all particles. Its dominating small-q peak records the growth of the nematic precursors. Inset shows zoom in on low q values. (G) Normalized cluster size Nc/Ntot for high ϕ, where Nc is the number of particles within a cluster and Ntot the total number of particles within the image volume. The cluster size is increasing for higher ϕ. (H) Dividing the sample into equal subboxes, the mean and variance of 1) nematic order parameter Smax and 2) number of particles per subbox are shown. The 3D liquid glass remains isotropic even for small subboxes. In 2D glasses of ellipsoidal colloids (), nematic domains containing close to 100 particles exist. The dashed-dotted line marks the isotropic–nematic transition; note the different axes for 3D and 2D.
The finding of a liquid glass state and of nematic precursors in a system of colloidal ellipsoids in three dimensions is in stark contrast to experimental and theoretical results for colloidal ellipsoids confined in two dimensions (, ). While, for an aspect ratio of a/b=3.5, the 2D studies also show the appearance of a state in which rotational dynamics is frozen and translational mobility persists, the structural order of this state is very different from the 3D case, as, in two dimensions, domains with high nematic order are found. Repeating the local analysis of the nematic order parameter with 2D data from ref. , Fig. 5H shows that homogeneously aligned nematic subboxes can comprise up to a hundred particles in 2D glasses. For the comparison in Fig. 5H, we used Smax=0.3 and 0.5 as a criterion for the isotropic–nematic transition in three dimensions and two dimensions, respectively (, ). The analysis reveals that pseudonematic domains exist in two dimensions; the local structure in three dimensions, however, remains isotropic even at the lengthscale of the smallest subbox.
Materials and Methods
Experimental Methods.
In a first step, spherical PMMA/PMMA core–shell particles dyed with different fluorophores in the cores and the shells were synthesized according to a route described in refs. and . As fluorophores for the cores, we used the Bodipy dye ((4,4-difluoro-8-(4-methacrylatephenyl)-3,5-bis-(4-methoxyphenyl)-4-bora-3a,4a-diaza-s-indacene), which was synthesized according to ref. . The dye Quasar 670 (LGC Biosearch Technologies) served as a marker for the shells and was used in the form of a 4-vinylbenzylester. For core particle synthesis, the dye was linked to methacrylic acid (Fluka) and copolymerized. The cores were cross-linked using ethylene glycol dimethylacrylate. The resulting particle cores had a diameter of 1 μm. Several seeded dispersion polymerization steps were then used to grow a PMMA shell of the desired thickness onto these cores. The PMMA in the shell material was not cross-linked.
In a second step, the particles were thermomechanically stretched as reported by Keville et al. (), with modifications for the PMMA/PMMA core–shell particles as described in refs. , , and . After the stretching, the ellipsoidal particles were restabilized with polyhydroxystearic acid and dispersed in a mixture of 85:15 (w/w) cyclohexylbromide (CHB) and cis-decalin to match both the density and refractive index of the PMMA colloids (). Since PMMA particles are known to charge in organic solvents, tetrabutylamoniumbromide was added to screen the charges.
The resulting suspensions were placed into a home-built sample chamber. Samples were studied using a confocal laser scanning microscope (TCSP5, Leica Microsystems) equipped with a resonant scanner (8 kHz, bidirectional mode) and a glycerol objective (63×, NA 1.30). An argon laser (wavelength λ=514.5 nm) and a helium neon laser (λ=632.8 nm) were used for excitation of the dyes. The temperature of the whole microscope system was stabilized at 23.0±0.1 °C (Ludin Cube 2, Life Imaging Services), since, at this temperature, the density match between particles and solvent was optimal. Volume fractions up to ϕ=0.46 were prepared by centrifugation at higher temperature and the removal of excess solvent. The highest ϕ were obtained by slightly raising the temperature in a dense sample directly in the measurement chamber for a few days to achieve density mismatch. This led to the slow enrichment of particles at the bottom of the sample.
The temperature was then changed back to 23 °C. After placing a sample onto the microscope, it was allowed to equilibrate for 15 h to minimize drift effects. Remaining drift, which, in all cases, was small compared to the particle movement, was corrected with a routine applied after detection and tracking. To minimize wall effects, all measurements were performed in a depth of 30 μm to 100 μm into the sample. Positions and orientations of all particles in one image volume (144 μm ×144 μm ×40 μm for structural analysis and 144 μm ×36 μm ×20 μm for measurements on the dynamics) containing more than 6,000 particles were identified and linked to trajectories using self-written and tested Matlab algorithms. The core–shell structure facilitates tracking of the ellipsoid position and orientation with accuracies of 60 nm and 5°, respectively () (Fig. 1B). Experimental timescales were limited by the bleaching of the fluorophores after long laser exposure.
Volume fractions are the pivotal variable influencing the structural dynamics of the colloidal suspensions. For their determination, particles were detected and counted in each measured sample, and the related Voronoi volume was calculated to obtain the exact number fraction ρ. Multiplying this with the volume of a particle gives ϕ,
The determination of particle volumes, however, is intricate, since PMMA particles are known to swell in CHB. Therefore, we determined the particle diameter by calculating the pair correlation function for a dense sample of spherical particles before stretching. The volume of a particle is conserved upon stretching, which was proven by cross-checking the obtained value with the width of an ellipsoid acquired by the pair correlation of the elliptical particles.
Glass Stability Analysis.
The values for the glass transitions for translation ϕct and rotation ϕcr are found by the glass stability analysis of MCT in which the collection of all measured correlation functions is used. Close to the glass transition ϕc, a critical decay onto the plateau occurs in a correlation function Φj(t) (e.g., the translation or the rotation correlator functions Fs(q,t) and Ln(t), respectively). Using first-order correction terms (), the decay is given by
where
t0 and
κ(a) are system-dependent constants and
hj,
kj, and
fjc are parameters, which depend on the correlator
j.
Below ϕc, the late plateau and the decay from the plateau is given by the von Schweidler law,
where
τϕ is a time scaling depending sensitively on
ϕ,
and determines the final relaxation time
τ close to and below
ϕc. Importantly, the exponents
a,
b, and
γ are related and determine all universal aspects close to the glass transition. Here, we employ the exponents
a=0.3,
b=0.6 (therefore
γ=2.5) and
B=0.84, and
C=1.54 to represent a repulsive glass-forming system (). For the glass stability analysis, both translation and rotation correlator functions were fitted simultaneously using and for the three highest volume fractions
ϕ=0.46,
ϕ=0.55, and
ϕ=0.57 considering all measured
Fs(q,t) in the range
5.18≤q⋅2b≤7.90 and
Ln for
n=2,4. Results are shown in
Fig. 6 A and
B (again,
L4 is shown because the glassy two-step relaxation is more visible than in
L2). The best fitting results were obtained by keeping
κ(a)=1 and
t0=0.8 fixed and having
fj,
hj,
kj, and
τϕ as free fitting parameters. Satisfactory fits to the data were only obtained assuming two different glass transitions
ϕct=0.56 and
ϕcr=0.50. The gray dotted lines in
Fig. 6C indicate the result when only one glass transition density was assumed for translation and rotation. The failure of this analysis results from the strong slowing down of the rotatory motion between
ϕ=0.46 and
ϕ=0.55 which is absent in the translatory one. Additional background on the MCT states diagram (
SI Appendix, Fig. S6) and the stability analysis is given in
SI Appendix.
Fig. 6.
Glass stability analysis of (A) translational and (B) rotational relaxations: Data from experiment (colored lines) and fits (solid lines) according to and . Two different glass transitions for translation ϕct=0.56 and rotation ϕcr=0.50 are necessary to fit the data. In C, the gray dash-dotted lines indicate the result, when an identical transition density is assumed for translation and rotation. For this condition, poor agreement with the data at ϕ=0.46 is observed.
Simulation Details.
We performed ED-BD simulations (, ) that model overdamped Brownian dynamics of hard ellipsoids. The system consisted of N nonoverlapping ellipsoids in a simulation box of length L and volume V=L3 that was varied depending on the desired ϕ. Similar to De Michele et al. (), we set the moment of inertia to I=2mb2/5. For volume fractions of ϕ=0.05,0.1,0.2, ellipsoids were placed randomly in the simulation box, while, for volume fractions between ϕ=0.4 and ϕ=0.57, the Lubachevsky–Stillinger () technique was used. All systems were equilibrated by Newtonian dynamics, allowing translational and rotational correlation functions to decay to zero. Two types of boundary conditions were modeled. The first case corresponds to systems with PBCs with N=504. The second case corresponds to systems confined within rough walls. For the confined systems, we started from a random configuration of 1,231 ellipsoids and pinned the outermost particles in the range 0<d<Δ and L−Δ<d<L to serve as the wall particles. The remaining 500 particles were free to move. The ED-BD model was first benchmarked for a dilute system of ϕ=0.05, where we reproduced the ratio of translational and rotational diffusion coefficients found in the experiments: Drotb2/Dtrans=1.25, setting the ratio of Brownian time steps Δtrot/Δttrans=0.331 (with Δtrot=2I/kBTDrot=0.0265 short enough to give angular diffusion). This ratio was then applied to all ϕ. At all densities, the timescale, when matching to the experiments, is taken from Dtrans(ϕ). All presented results were averaged from 20 initial configurations of the ellipsoids.








 Observation of liquid glass in suspensions of ellipsoidal colloids
Observation of liquid glass in suspensions of ellipsoidal colloids
