Superoscillations

Essential to this paper is a mathematical structure we call “superoscillation.” Common wisdom assumes that no function can oscillate faster than its fastest Fourier component. Yet, as we show here, there is a large class of functions for which this assumption fails. Indeed, we have found functions that oscillate, on a given interval, arbitrarily faster than the fastest Fourier component. An example of such a function is the following:

Now, consider this function in the region $$ \left|x\right|\le L$$, where $$ L$$ is of order $$ \mathcal{O}\left(N^{\frac{1}{2}-ϵ}\right)$$ with $$ ϵ$$ positive and arbitrarily small. Here, we can approximate the exponentials by their first-order Taylor expansion and obtain (see also SI Appendix, section 1)

Note that there is no contradiction with the Fourier theorem, since the region where this function is (almost) identical to an oscillation of a frequency not contained by its Fourier decomposition does not extend over the entire region where the function is defined.

Although it is not essential for our present paper, it is interesting to note that outside the superoscillatory region, $$ f\left(x\right)$$ increases exponentially. This is a generic property of functions with superoscillatory regions.

The Experiment

The type of effect we describe here is common for all conserved quantities that depend on the shape of the wave function all over the space, including energy, momentum, and angular momentum. Here, we will focus on energy, for which the proof is more intuitive.

Here, we start by presenting the idea intuitively, in terms of a relativistic model, where the arguments are simpler. However, since relativistic quantum-field theory has well-known technical difficulties, we will in subsequent sections formulate a standard nonrelativistic quantum model and do all of the calculations there.

Consider a box of length $$ 2\pi Na$$ (where $$ a$$ is some unit length) that contains a single photon in the state $$ \psi \left(x\right)$$

Fig. 1.

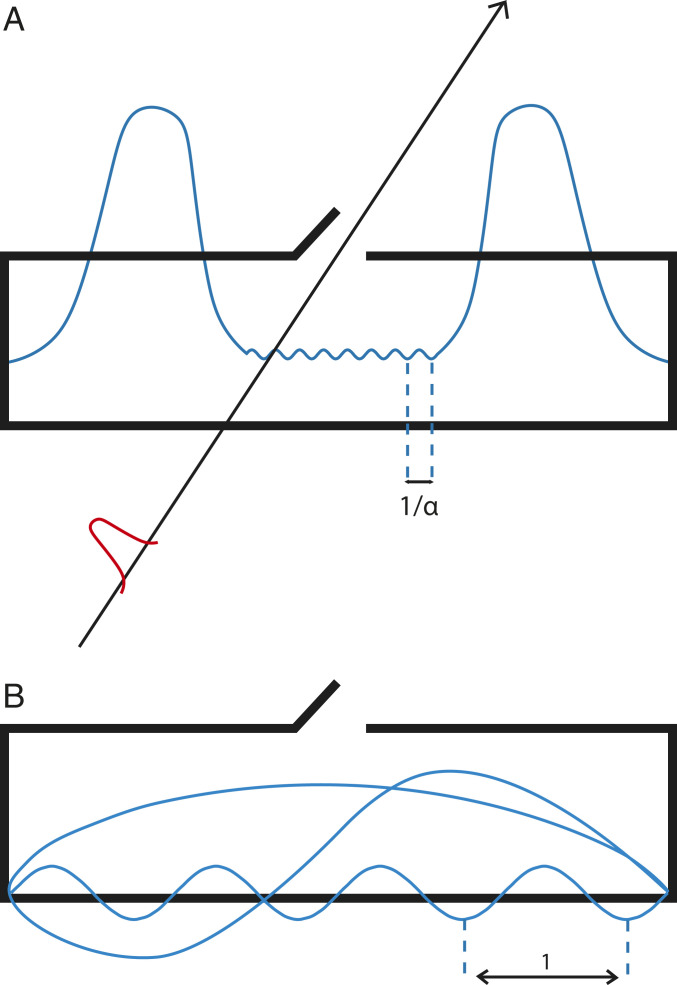
(A) A photon in the box in the specially prepared low-energy quantum state which, in the central region, oscillates with a spatial frequency greater than that of any Fourier components (B). As the opener is passing by, it opens the box and extracts the photon, if the photon is there. The shape of the wave function is not accurate, but simply illustrative; the true wave function is exponentially larger away from the center and has a more complicated shape.

From now on, however, for simplicity, we take $$ a=1$$, and we work in the usual units $$ \hslash =c=1$$.

Given the relation between wavelength, frequency and energy for the photon, the decomposition 2 shows that the photon is in a superposition of different energy eigenstates with wave numbers

Suppose now that a mechanism that we will call the “opener” opens the box in the center and inserts a mirror, such that if the photon hits the mirror, it comes out of the box (as in Fig. 1). The mirror is left inside for a time $$ T$$, then it is extracted out of the box, and the box is closed. The photon could come out of the box only if initially is situated at a distance not larger than $$ T$$ from the mirror; otherwise, it cannot get there while the box is open. The probability for this to happen is at most $$ {\int }_{-T}^T|\psi \left(x\right){|}^{2}dx$$.

Let now the time $$ T$$ be smaller (in units of speed of light $$ c=1$$) than $$ L$$, the length of the region of superoscillations, and suppose that at the end of the experiment, we find the photon out of the box. What is its energy?

Naively, we would think that the emerging photon must have one of the energies $$ E_n=|2n/N-1|\le 1$$ that it had originally in the box—after all, reflection from a mirror doesn’t change the spectrum of light. On second thought, however, we realize that this cannot be so. Indeed, the box was open only for a time $$ T$$. Because any signal propagates, at most, with velocity of light, only information about the wave function in a region, at most, of distance $$ T$$ from the origin can influence what happens at the origin. But we took $$ T<L$$, i.e., smaller than the region where the wave function behaves essentially indistinguishably from a plane wave of high energy $$ \mathcal{E}$$. Hence, the photon that emerges from the box must be in a state which is identical to that in which a genuine photon of energy $$ \mathcal{E}$$ would emerge from the box. Indeed, if this would not be so, we would know that the function far away is different from that of the genuine photon and contradict special relativity. But for a genuine photon of energy $$ \mathcal{E}$$, it is trivial to see what happens: The mirror just reflects the photon out of the box, but it doesn’t significantly change its frequency and energy. All that happens to the wave function of the genuine energy $$ \mathcal{E}$$ photon is that its wave function is chopped into a wave-train of length $$ T$$ by our closing the box after time $$ T$$. Hence, if a genuine photon of energy $$ \mathcal{E}=\alpha $$ emerged from the box, its energy spectrum would have a peak at energy $$ \alpha $$ and a spread in energy of $$ 1/T$$. By increasing $$ N$$, we can increase $$ T$$ and, hence, reduce by as much as we want the disturbance produced by the finite opening time of box; the photon thus emerges as close as we want to its initial energy $$ \mathcal{E}$$. We thus conclude that when our “fake high-energy” photon emerges from the box, it must have energy $$ \mathcal{E}$$ exactly as the genuine high-energy photon, and not the low energies it originally had (Figs. 2 and 3).

Fig. 2.

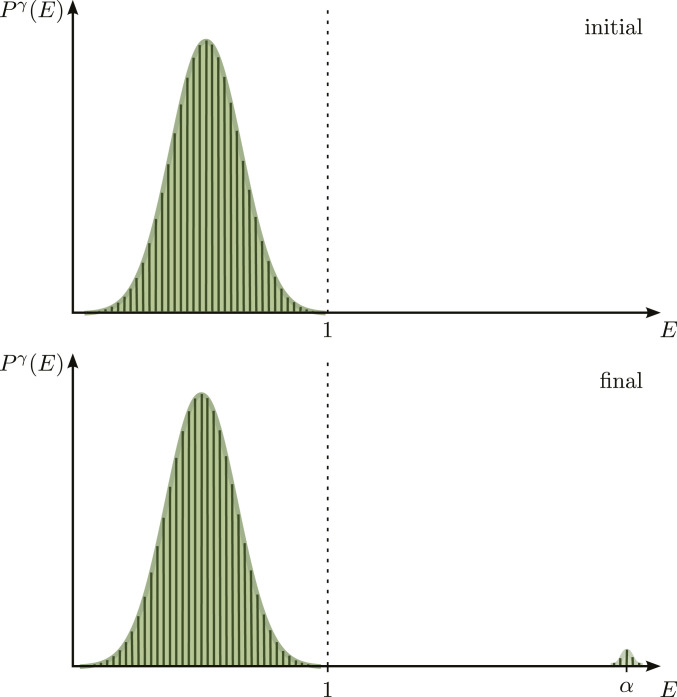
The initial and final distributions of the energy of the photon. Initially, it was a superposition of low energies and strictly no energy higher than one. Finally, a peak at energy $$ \alpha $$ appears, which corresponds to the extracted photons.

Fig. 3.

The initial and final probability distribution $$ P^{\mathrm{\Omega }}\left(E\right)$$ of the energy of the opener for the cases when the photon emerges from the box. One would expect the final energy of the opener to be lower than the initial, to compensate for the increase of the energy of the photon, but this does not happen; instead, the final energy distribution is the same as the initial (up to small perturbations due to the truncation of the photon wave packet).

To summarize, when the photon emerges from the box, it has much higher energy than it initially had. Where did the extra energy come from? This is the question that concerns us in this paper.

The Paradox

Inside the box, the photon was in a superposition of different energy eigenstates, all smaller than one, and out it emerges with the much higher energy $$ \alpha $$. Where does the extra energy come from? A first guess is that the energy comes from the mechanism used for extracting the photon. Indeed, we need to open the box, insert the mirror, and then take out the mirror and close the box. This mechanism, which we call opener, effectively subjects the photon to a time-dependent Hamiltonian, and such a Hamiltonian need not conserve energy.

To put it differently, we can look at the total Hamiltonian, describing the photon and the opener. The total Hamiltonian is time-independent, since it describes the total system, with no parts left outside; the time dependence seen by the photon comes from the time evolution of the opener and its interaction with the photon. The total energy is conserved for time-independent Hamiltonians. Thus, we are tempted to say, all that happens is that the opener and the photon exchange energy: When the photon emerges from the box, and, as we proved, has higher energy than it had inside the box, the opener must have lost the same amount—a trivial case of energy exchange.

We now arrive at the crux of the problem. Although this explanation is the most natural, it is wrong: The photon could not have gotten its energy from the opener. The reason is again causality, as we shall now see.

Consider the case of a monochromatic high-energy photon of energy $$ \alpha $$. When this photon emerges from the box, its energy is unchanged (up to fluctuations of order $$ 1/T$$). Hence, in this case, the opener does not give it any energy. But then the opener cannot give energy to the fake photon, either.

Indeed, recall that the entire difference between the high-energy photon of energy $$ \alpha $$ and our specially prepared low-energy photon lies in regions situated further from the center than $$ L$$; this information cannot arrive at the opener during the time of the experiment, $$ T<L$$. Immediately after the experiment is over, we can measure the energy of the opener. Since the opener is localized in a small region (around the center of the box), we have immediate access to it and can measure its energy in a short time; the measurement can be finished long before information from $$ \left|x\right|\ge L$$ can arrive. If by measuring the opener, we could determine whether the box contained the original low-energy photon or the monochromatic high-energy photon, we would violate relativistic causality. Thus, since the opener didn’t lose energy when the box contained a high-energy photon, it cannot lose energy in the case of the low-energy photon either! We must therefore conclude that the extra energy did not come from the opener.

This is the paradox. The photon emerged from the box with energy much higher than it had inside, but the energy did not come from the opener, the only other system in the problem. Energy seems not to be conserved.

Energy Conservation

Faced with this paradox, one can respond in various ways. The conventional response is that there is no problem whatsoever, and there cannot ever be. In quantum mechanics, the standard formulation of a conservation law is that the probability distribution of the conserved variable over the entire ensemble should not change. This law applies to any time-independent Hamiltonian. On this basis, there should be absolutely no energy nonconservation in our example, either. And, of course, from this point of view, there is none. Indeed, in the preceding sections, we focused on what happens when the photon emerges from the box. But it is also possible (and actually far more probable) that the photon does not emerge from the box. It happens, because the wave function of the photon extends all over the box, so the photon has a nonzero (and, in fact, quite large) probability to be far from the central region. If so, it cannot reach the opening while the box is open; therefore, it cannot leave the box. To see standard energy conservation at work, we must consider these cases as well. What we find in these cases is that, again, the opener didn’t lose any energy (since it did not collide with the photon), but the photon remains in the box with lower energy (as the wave function loses its superoscillatory piece)—again, a paradox. Considering these cases as well, we find that, as expected, the probability distribution of the total energy (photon plus opener) did not change.

But—and this is the main point of our paper—we would like to argue that the standard formulation of conservation laws, though absolutely correct as far as it goes, is simply not enough. The standard conservation law is statistical and says nothing about individual cases. We would like to argue, however, that it is legitimate to ask what happened in a particular individual case. In our example, suppose we have in the box a photon of energy of order 1 eV (more precisely, a photon in a superposition of various energies, but absolutely none of them larger than 1 eV). Yet, when we open the box, the photon emerges with energy of order of 1 GeV. We should definitely be entitled to ask where the energy came from.

What we showed in our example is that this energy cannot come from the mechanism that extracts the photon from the box. Since this is the single other system in the problem, we are faced with energy nonconservation in this individual case. So we do have a problem that needs to be explained.

Furthermore, we also argue that the standard formulation is not only limited in that it cannot address individual cases, it is also unsatisfactory in the meaning of the story it tells.

Suppose that we repeat our experiment a large number of times. Consider a large number of boxes, each box containing just one single photon, prepared in the special low-energy state $$ \psi \left(x\right)$$ of Eq. 5, each box having its associated opener. In some experiments, the photon comes out of the box; in others, the photon remains inside. In each case, the energy of the opener remains unchanged (apart from fluctuations of the order $$ 1/T\ll \mathcal{E}-E_{max}$$). Since the photons that emerge from their boxes have increased energy, for the average energy to remain constant, the photons that stay in their boxes must be left with lower energy. But what this effectively means is that the photons that emerged from their boxes got their energy from the photons in the other boxes. But the experiments are completely independent; they may even happen at different times and in different places. Nevertheless, the photons which stay inside their boxes supply energy to the ones that emerge from the other boxes! Clearly, the idea is absurd, and it cannot be an acceptable resolution of our paradox.

Another possible response to the paradox is to argue that it makes no sense to talk about the energy of a photon as long as it is in a superposition of different energy eigenstates. However, we note that the photon had zero probability to have any energy larger than $$ E_{max}=1$$, yet it emerges with the high energy $$ \mathcal{E}\gg E_{max}$$. So the paradox of the photon’s extra energy remains.

As noted in the introduction, we do not offer any resolution here; we leave the paradox open. But below we provide more details. First, we present an explicit model; then, we analyze in more detail the standard energy conservation as applied to our situation. Although there are no contradictions here, the specific way in which the energy is conserved in the statistical ensemble is extremely unusual and instructive.

Explicit Model

We now give an explicit model. Since relativistic quantum-field theory has well-known technical difficulties, we will formulate a nonrelativistic model. The experiment is the same, the only difference being that, instead of a photon, the box contains a nonrelativistic particle. Of course, we are now no longer allowed to use relativistic causality arguments, and we will prove our statements by explicit calculations. Nevertheless, the intuition for the nonrelativistic model is exactly the same as in the relativistic case, since also nonrelativistic quantum mechanics allows finite time intervals in which a part of a wave function can act, to a good approximation, independently of the rest (8).

Consider the following Hamiltonian to model our experiment:

We let our particle have an internal degree of freedom, a “spin,” which determines whether the particle is in the box or free. The states $$ \left|\uparrow \right.⟩$$ and $$ \left|\downarrow \right.⟩$$ are eigenstates of $$ {\sigma }_z$$. When the spin is $$ \left|\uparrow \right.⟩$$, the potential $$ V\left(x\right)$$ confines the particle inside the box; when the spin is $$ \left|\downarrow \right.⟩$$, the particle is free, since the term in $$ 1+{\sigma }_z$$ multiplying $$ V\left(x\right)$$ vanishes.

The opener’s free Hamiltonian is $$ p_q$$, while the last term in $$ H$$ describes the particle–opener interaction. The interaction takes place when the opener is at $$ q=0$$; at all other times, the opener is free. The opener moves at constant speed $$ \dot{q}=1$$ without spreading, both when it is free and while the interaction takes place. The opener moves from $$ q<0$$ where it is free, through the interaction region, $$ q=0$$, to $$ q>0$$, where it is free again. (One may recognize the opener as the model of an ideal clock that turns on and off an interaction when the “clock time” indicated by the pointer $$ q$$ is $$ q=0$$.)

The interaction term is designed to release the particle if it is situated in a window around the center of the box. This works as follows. The operator $$ {\sigma }_x$$ can release the trapped particle by flipping $$ \left|\uparrow \right.⟩$$ to $$ \left|\downarrow \right.⟩$$. But the particle is released only if it is situated in a window around the center of the box. The window is determined by $$ g\left(x\right)$$, which is zero outside a window of size $$ L$$, of order $$ \mathcal{O}\left(N^{\frac{1}{2}-ϵ}\right)$$, centered around $$ x=0$$, and $$ g\left(x\right)=1$$ inside. The interaction term is, thus, nonzero only when the particle is in this window; hence, the particle can be released only if it is situated here. (Note that this toy model differs slightly from the example in the previous sections: There, the window was taken to be small, but open for a time long enough for a wave-train of length $$ L$$ to emerge through it. Here, the window is open for an infinitesimal time, but is large enough to let a wave-train of length $$ L$$ emerge from it.)

Consider now that at time $$ t=0$$, we prepare the trapped particle in a state $$ \mathrm{\Psi }\left(x,0\right)\left|\uparrow \right.⟩$$ with $$ \mathrm{\Psi }\left(x,0\right)$$ equal to our special state $$ \psi \left(x\right)$$ given by Eq. 5. In the region $$ \left|x\right|\le L$$ with $$ L$$ of order $$ \mathcal{O}\left(N^{\frac{1}{2}-ϵ}\right)$$ , the wave function $$ \mathrm{\Psi }\left(x,0\right)$$ looks like a high-energy state. In relativistic quantum mechanics, when the particle is situated in this region, its time evolution is identical to that of a high-energy particle, since the information that this is not a true high-energy particle is contained only in faraway regions of space, and it takes a finite time to arrive in the center of the box. But, as we mentioned above, and as we show in detail in SI Appendix, section 2, the same is (approximately) true also in nonrelativistic quantum mechanics. That is, in the region of superoscillations, $$ \left|x\right|\le \mathcal{O}\left(N^{\frac{1}{2}-ϵ}\right)$$, the time evolution of the particle (in the absence of the interaction with the opener) is $$ \mathrm{\Psi }\left(x,t\right)=e^{-i{\alpha }^{2}t/2}\mathrm{\Psi }\left(x,0\right)$$—i.e., it just accumulates the same time-dependent phase as the bona fide energy eigenstate $$ \sin \left(\alpha x\right)$$. This approximation is valid for any time $$ T\le \mathcal{O}\left(N^{1/2-\delta }\right)$$ with $$ \delta $$ positive and arbitrary small, and $$ \delta >ϵ$$. During this time, in the limit of large $$ N$$, information from the region $$ \left|x\right|\ge \sqrt{N}$$, where the wave function differs significantly from the high-energy plane wave, cannot reach the region of superoscillations. It is during this time that we extract the particle from the box.

To ensure that the opener opens the box during this time window, we choose its initial state $$ \varphi \left(q\right)$$ to have support only for $$ q$$ within $$ -T\le q\le 0$$.

We now have to calculate the time evolution of the particle–opener system

To see the meaning of Eq. 11, we first note that, since the particle is now free, the energy eigenstates are the plane waves $$ e^{ikx}$$. Hence, as far as the particle is concerned, Eq. 11 is actually the decomposition of the state into energy eigenstates. Everything else being phase factors, the probability of the released particle to have momentum $$ k$$ corresponding to energy $$ k^2/2$$ is $$ |h\left(k\right){|}^2$$. But all we have in 12 are two truncated wave-trains, corresponding to the (untruncated) plane waves $$ e^{\pm i\alpha x}$$. Thus, the most probable final plane-wave state is a free particle in a superposition of eigenstates of momentum $$ \pm \alpha $$ and energy $$ \frac{{\alpha }^2}{2}$$. The particle could also emerge with other energies $$ \frac{k^2}{2}\ne \frac{{\alpha }^2}{2}$$, but with smaller probability. The possibility of coming out with these energies is due to the truncation of the wave-train to $$ \left|x\right|\le L$$. Taking $$ N$$ larger, we can make $$ L$$ larger and, thus, decrease these probabilities, relative to the probability of having energy $$ {\alpha }^2/2$$, as much as we want. As noted before, this is exactly what would have happened had we started in the high-energy eigenstate $$ \sin \left(\alpha x\right)$$.

One’s natural suspicion is that when the particle emerges from the box with energy $$ {\alpha }^2/2$$, which is much larger than the maximal energy it had inside the box, the additional energy of the emitted particle comes from the opener. But the energy distribution of the opener before and after the interaction is the same; $$ \varphi \left(q\right)$$ is merely displaced, as if there had been no interaction. This is the paradox.

Note also that when the particle emerges with an energy slightly different from $$ {\alpha }^2/2$$, because of the truncation of the wave packet, the opener supplies this small difference (mathematically expressed by the $$ q$$-dependent phase accumulated by the opener), but not the difference between the true low energies that the particle originally had and the high energy with which it emerges.

The Standard Energy Conservation

As we discussed before, for any time-independent Hamiltonian, energy is always conserved in the standard sense—that is, the probability distribution of the total energy is time-independent. Since this is a theorem, it holds in our case as well; our paradox appears only at the level of individual cases. Yet, it is worth looking in more detail at the standard account of energy conservation as it applies in our case. As our case has interesting characteristics, the standard account of energy conservation turns out to be interesting as well.

The total Hamiltonian is

The total energy long before the interaction and long after it is simply the sum of the free energies, $$ E=E_p+E_{\mathrm{\Omega }}$$. With this definition, the standard energy-conservation relation is

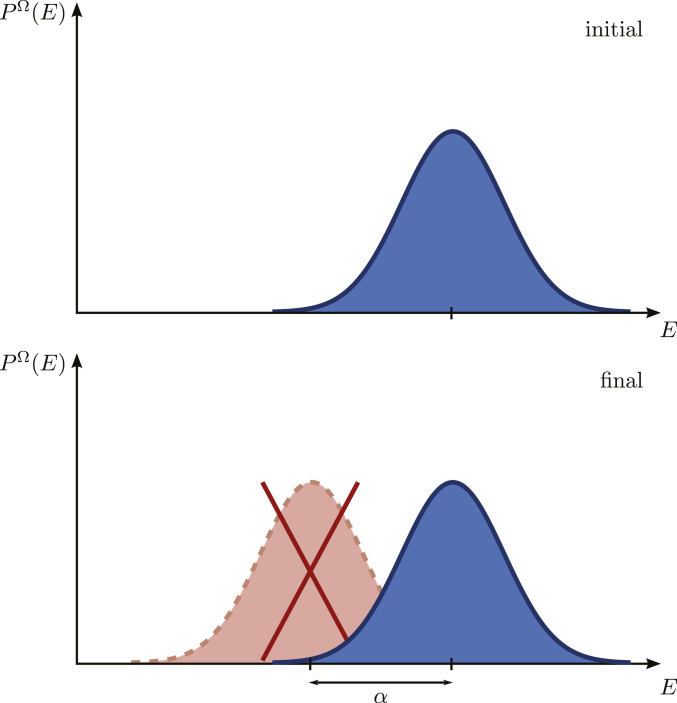
Before the interaction, there is no correlation between the energies of the particle and opener—i.e., the initial joint probability $$ P_i^{p,\mathrm{\Omega }}\left(E_p,E_{\mathrm{\Omega }}\right)$$ of their energies is the product of their respective individual probability distributions

All this leads to a surprising situation: The distribution of the energy of the particle changes without being accompanied by a corresponding change in the distribution of the energy of the opener, yet the distribution of the total energy is conserved.

Although the above situation is surprising, it is mathematically consistent, and it has remarkable implications. Denoting the conserved distributions $$ P_i^{tot}\left(E\right)=P_f^{tot}\left(E\right)=P^{tot}\left(E\right)$$ and $$ P_i^{\mathrm{\Omega }}\left(E\right)=P_f^{\mathrm{\Omega }}\left(E\right)=P^{\mathrm{\Omega }}\left(E\right)$$, we obtain

Eq. 21 can have a solution with $$ {\tilde{P}}_i^p\left(\tau \right)\ne {\tilde{P}}_f^p\left(\tau \right)$$ if and only if for some values of $$ \tau $$, the Fourier transform $$ {\tilde{P}}^{\mathrm{\Omega }}\left(\tau \right)$$ is zero, and the changes in $$ {\tilde{P}}_i^{\gamma }\left(\tau \right)$$ are confined to these $$ \tau $$ values.

To understand the significance of the above results, we first note the general meaning of the Fourier transform of the energy distribution. Consider a particle prepared in the state $$ \left|\mathrm{\Psi }\left(t\right)\right.⟩$$ and evolving according to a Hamiltonian $$ H$$. Then (SI Appendix, section 4),

In our case, we want the opener–particle interaction to take place only for a finite time: The box must be opened, the mirror inserted, then extracted, and the box closed, all before information from remote places in the box can reach the opening. In our explicit model, the opener must, thus, move from far away, going from an initial state in which there is no interaction to an orthogonal state in which there is interaction, and then again to a state with no interaction. This is accomplished by moving through a long sequence of orthogonal states both before and after the interaction (as one can explicitly see in the model). Hence, since the interaction should only take a finite time $$ T$$, it must be the case that the wave function $$ \varphi $$ of the opener, as it evolves, must obey

Note that the opener has the role of a catalyst: Its energy distribution doesn’t change, yet, without it, the particle’s energy distribution could not change, because the energy of the particle would then be the total energy, and changing its distribution would violate the standard energy-conservation law.

Modular Energy Exchange

It is interesting to examine further the changes in the energy distributions. Since neither the total energy distribution nor the opener energy distributions change, it is clear that the average energy of the particle cannot change: Indeed, both before the interaction and after

Furthermore, given that both initially and finally the energy distributions of the opener and particle are uncorrelated, and that the distributions of total energy and opener energy do not change, one can easily derive the fact that all of the moments of the particle energy distribution $$ ⟨H_p^n⟩$$ are unchanged.

We thus arrive at another remarkable conclusion: The energy distribution of the particle changes, although none of its moments change.

At first, it seems that something must be wrong—indeed, it is generally assumed that the moments of a distribution completely define it. This, however, is not so. It is actually perfectly possible for a distribution to change without any of its moments changing. In fact, in quantum mechanics, this behavior characterizes some of the most basic phenomena [such as momentum conservation in the two-slit experiment (9101112–13)]; and many of the “mysteries” of quantum mechanics have this mathematical effect at their core. This behavior generally stems from deep reasons connected with causality and nonlocality—as our present example illustrates.

So, if none of the moments of the particle’s energy distribution change, what changes? It is the average of observables that we call “modular energies” (11, 12), as we now show.

Consider the operator $$ e^{iH\tau }$$; we call this operator modular energy since it depends only on the energy modulo $$ 2\pi /\tau $$. Each $$ \tau $$ defines a different modular energy.

Since $$ H$$ is a conserved operator, so are its associated modular energies:

Note the interesting way in which the conservation of modular energy works. The total modular energy is conserved, so if one of two interacting systems changes its modular energy, this must be accompanied by changes in the modular energy of the other, yet the average modular energy of the particle (for some $$ \tau $$) changes, while the corresponding modular energy of the opener doesn’t. This is possible due to the fact that, as opposed to energy, which is an additive conserved quantity, its modular part is nonadditive but multiplicative, and the modular energy of one of the systems, namely, the opener, is completely uncertain, which makes its average zero.

In concluding this section, we would like to emphasize that the whole issue of exchange of modular energy (or momentum) without any (significant) exchange of any of its moments (or where the exchange of the moments plays a trivial role) is a general characteristic of phenomena in which a localized probe interacts with a system in an extended wave function. At the same time, the particular phenomena described in this paper (the high energy of the particle that emerges from the box) depend on the particular form 1 of the extended wave function. The possibility of exchange of modular energy without changes in any of the moments of the energy distribution simply opens a window of opportunity, through which the phenomena described here can manifest themselves. In other words, the exchange of modular energy without changes in the moments of the energy distribution is just a necessary, but not a sufficient, condition for the phenomena we describe here.

Discussion

To summarize, in our paper, we present an effect that raises questions about what we actually mean by conservation laws. The standard approach is statistical, and it is good as far as it goes. However, our effect begs the question of what happens in individual cases. A particle, prepared in a superposition of low-energy states and with no high-energy component whatsoever, comes out of a box with great energy. It is legitimate to ask where the energy comes from. We showed that the mechanism used for extracting the particle—the only other system in the problem—did not provide this energy, so we are left with a puzzle.

Our example concerned energy conservation. It is, however, clear that one can construct examples involving conservation of other quantities such as momentum or angular momentum (SI Appendix, section 5). The phenomenon is, therefore, a general one. Thus, we argue that the conservation laws of quantum mechanics must be revisited and extended. Without doing this, we will be missing a large part of the message that quantum mechanics is telling us.