Results

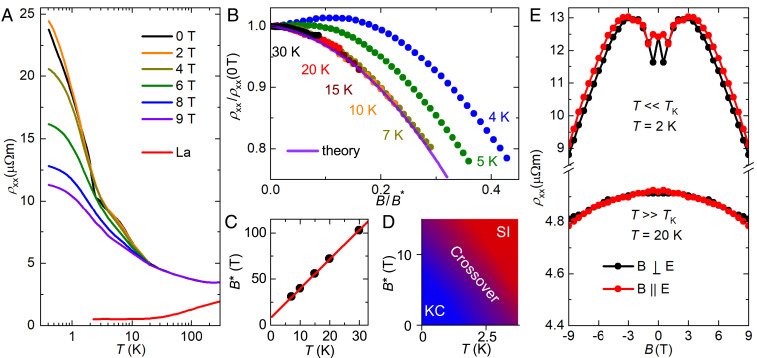
We start by showing that $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ is governed by the Kondo interaction and delineate the temperature and field range of Kondo coherence. The zero-field resistivity of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ increases weakly with decreasing temperature, whereas the nonmagnetic reference compound $$ {\mathrm{L}\mathrm{a}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ is metallic (Fig. 1A). This provides strong evidence that the semimetallic character of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ is due to the Kondo interaction. Below the single-ion Kondo temperature $$ T_{\mathrm{K}}=13$$ K, identified by associating the material’s temperature-dependent entropy with a spin $$ 1/2$$ ground state doublet of the Ce $$ 4f^1$$ wavefunction split by the Kondo interaction (30), a broad shoulder in the resistivity at about 7 K signals the cross-over to a Kondo coherent state (Fig. 1A). As shown in what follows, this is further supported by our magnetoresistance measurements (Fig. 1 B and C).

Fig. 1.

Electrical resistivity and magnetoresistance of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$. (A) Temperature-dependent electrical resistivity $$ {\rho }_{xx}$$ of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ in various magnetic fields applied perpendicular to the electric field ($$ B\perp E$$, transverse magnetoresistance) and of the nonmagnetic reference compound $$ {\mathrm{L}\mathrm{a}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ in zero field (red). The feature in the 0 T data of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ near 3 K is due to the onset of the spontaneous Hall effect (Fig. 2A), which leaves a finite imprint on $$ {\rho }_{xx}$$ because of the giant Hall angle (SI Appendix, section I H) and because of slight contact misalignment (SI Appendix, section I A). (B) Transverse magnetoresistance scaled to its zero-field value vs. scaled magnetic field $$ B/B^{\star }$$, showing the collapses of data above 7 K onto the universal curve (32) (violet) expected for an $$ S=1/2$$ Kondo impurity system in the incoherent regime and a breakdown of the scaling for temperatures below 7 K (shown here by using $$ B^{\star }$$ from the linear fit in C—also, other choices of $$ B^{\star }$$ cannot achieve scaling). (C) Scaling field $$ B^{\star }$$, as determined in B, vs. temperature, showing a linear-in-$$ T$$ behavior as expected for a Kondo system in the single-impurity regime. Fitting $$ B^{\star }=B_0^{\star }\left(1+T/T^{\star }\right)$$ to the data (red straight line) yields $$ B_0^{\star }=10$$ T and $$ T^{\star }=2.5$$ K. (D) Temperature-field phase diagram displaying the single impurity (SI) and Kondo coherent (KC) regime as derived in C. (E) Transverse (black) and longitudinal (red, $$ B\Vert E$$) magnetoresistance for temperatures well below (Top) and well above $$ T_{\mathrm{K}}$$ (Bottom). The data were symmetrized to remove any spurious Hall resistivity contribution and mirrored on the vertical axis for clarity.

Transverse magnetoresistance isotherms (Fig. 1B) in the incoherent regime between 7 and 30 K display the universal scaling typical of Kondo systems (33, 34): $$ {\rho }_{xx}/{\rho }_{xx}\left(0\hspace{0.17em}\mathrm{T}\right)$$ vs. $$ B/B^{\star }$$ curves all collapse onto the theoretically predicted curve for an $$ S=1/2$$ Kondo impurity system (32), provided a suitable scaling field $$ B^{\star }$$ is chosen. The resulting $$ B^{\star }$$ is linear in temperature (Fig. 1C). Fitting $$ B^{\star }=B_0^{\star }\left(1+T/T^{\star }\right)$$ to the data (red straight line) yields $$ B_0^{\star }=10$$ T and $$ T^{\star }=2.5$$ K, which may be used as estimates of the field and temperature below which the system is fully Kondo coherent (blue area in Fig. 1D). Below 7 K, the scaling fails (Fig. 1B), as expected when crossing over from the incoherent to the Kondo coherent regime.

Before presenting our Hall effect results we show that, as anticipated, the chiral anomaly cannot be resolved in the Kondo coherent regime. We find that, at 2 K, the longitudinal and transverse magnetoresistance traces essentially collapse (Fig. 1E, Top). Because the amplitude $$ c_a$$ of the chiral anomaly, being inversely proportional to the density of states (18), is expected to scale as $$ c_a\propto {\left(v^{\star }\right)}^3$$, it is severely suppressed by the strong correlations. The fact that, also at high temperatures, we do not observe signatures of the chiral anomaly (Fig. 1E, Bottom) is consistent with our bandstructure calculations (to be presented later; see Fig. 4A), which reveal that the uncorrelated bandstructure contains Weyl nodes only far away ($$ >100$$ meV) from the Fermi level.

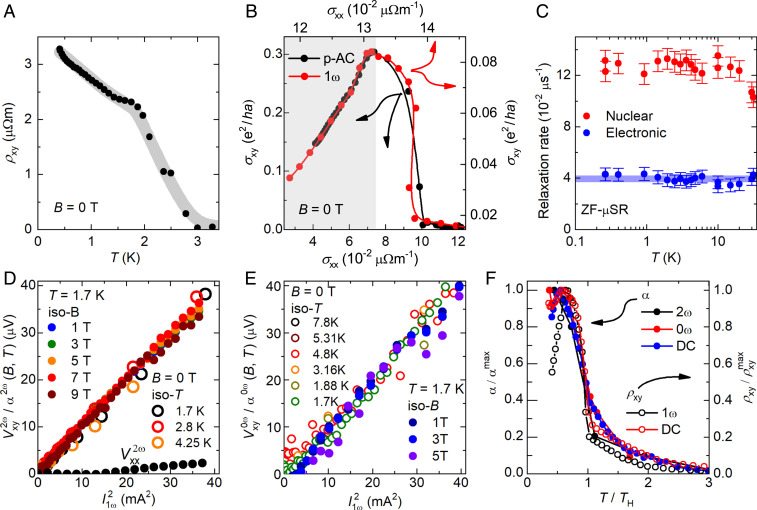
Our key observation, presented next, is a spontaneous (nonlinear, as will be discussed later) Hall effect which appears in $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ as full Kondo coherence is established below $$ T^{\star }$$ (Fig. 2A). The corresponding spontaneous Hall conductivity $$ {\sigma }_{xy}$$ reaches a considerable fraction of the quantum of 3D conductivity (Fig. 2B). The experiment, using a pseudo-AC (alternating current) mode (Materials and Methods), was not only carried out in zero external magnetic field but also without any sample premagnetization process. Hall contact misalignment contributions were corrected for (SI Appendix, section I A and Figs. S1 and S2) and, thus, can also not account for the effect. Moreover, being in the Kondo coherent regime, the local moments should be fully screened by the conduction electrons. The resulting paramagnetic state is evidenced by the absence of phase transition anomalies in magnetization and specific heat measurements (SI Appendix, sections II B and C and Figs. S11 and S12), as well as by state-of-the-art zero-field (ZF) muon spin rotation ($$ \mu $$SR) experiments. The latter reveal an extremely small electronic relaxation rate that is temperature-independent between 30 K and 250 mK (Fig. 2C; for two fully overlapping representative spectra, one well above and one well below $$ T^{\star }$$, see SI Appendix, section II A and Fig. S10). This is unambiguous evidence that, in the investigated temperature range and in particular across $$ T^{\star }$$, TRS is preserved in $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$. In conjunction with the giant spontaneous Hall effect this observation is striking—we are not aware of any other 3D material with preserved TRS that has shown a spontaneous Hall effect.

Fig. 2.

Spontaneous Hall effect of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$. (A) Temperature-dependent direct current (DC) Hall resistivity $$ {\rho }_{xy}$$ in zero external magnetic field, showing a pronounced spontaneous Hall effect below 3 K. Data were taken without prior application of magnetic fields. (B) Spontaneous DC Hall conductivity $$ {\sigma }_{xy}$$ in units of the 3D conductivity quantum vs. longitudinal conductivity $$ {\sigma }_{xx}$$, with temperature as implicit parameter, for the DC response of the sample in A (bottom and left axes, black) and for the $$ 1\omega $$ response in an AC experiment on a sample from a different batch (top and right axes, red), both in zero magnetic field. In the Kondo coherent regime (gray shading), $$ {\sigma }_{xy}$$ is linear in $$ {\sigma }_{xx}$$. (C) Temperature-dependent nuclear and electronic contributions to the muon spin relaxation rate obtained from ZF $$ \mu $$SR measurements. The electronic contribution is extremely small and temperature-independent within the error bars, ruling out TRS breaking with state-of-the-art accuracy. Magnetization and specific heat measurements corroborate this finding (see SI Appendix, sections II B and C and Figs. S11 and S12. (D) Scaled $$ 2\omega $$ spontaneous Hall voltage vs. square of $$ 1\omega $$ driving electrical current in zero magnetic field for different temperatures and at 1.7 K for various magnetic fields. (E) Quantities analogous to D for the $$ 0\omega $$ spontaneous Hall voltage. (F) Scaled coefficients of square-in-current response $$ {\alpha }^{2\omega ,0\omega ,\mathrm{D}\mathrm{C}}$$ from D and E and SI Appendix, Fig. S6, respectively (left axis) and linear-in-current response $$ {\rho }_{xy}^{1\omega ,\mathrm{D}\mathrm{C}}$$ from B (right axis), as function of scaled temperature ($$ T_{\mathrm{H}}$$ is the onset temperature of the spontaneous Hall signal). The absolute values of $$ {\alpha }^{max,i}$$, $$ {\rho }_{xy}^{max,i}$$, and $$ T_{\mathrm{H}}$$ are listed in SI Appendix, Table S1.

We also measured the Hall effect in finite applied magnetic fields. We observe that the field-dependent Hall resistivity isotherms, $$ {\rho }_{xy}\left(B\right)$$, are fundamentally different below (Fig. 3A) and above $$ T^{\star }$$ (Fig. 3B). Whereas above $$ T^{\star }$$, $$ {\rho }_{xy}$$ shows simple linear-in-field behavior consistent with a single hole-like band, strong nonlinearities appear below $$ T^{\star }$$. Most importantly, a large even-in-field component $$ {\rho }_{xy}^{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}=\left[{\rho }_{xy}\left(B\right)+{\rho }_{xy}\left(-B\right)\right]/2$$ is observed (Fig. 3C) that even overwhelms the usual odd-in-field component $$ {\rho }_{xy}^{\mathrm{o}\mathrm{d}\mathrm{d}}=\left[{\rho }_{xy}\left(B\right)-{\rho }_{xy}\left(-B\right)\right]/2$$ (Fig. 3E). The nonlinear part of the latter, that scales with $$ {\left[{\rho }_{xx}-{\rho }_{xx}\left(4\hspace{0.17em}\text{K}\right)\right]}^2$$ and is thus independent of the scattering time (Fig. 3F), is theoretically expected (35) and experimentally observed (36) in TRS broken Weyl semimetals, which is here realized by the finite magnetic field. The exciting discovery, however, is the even-in-$$ B$$ component, which is the finite-field extension of the spontaneous Hall effect. Both are incompatible with the standard (magnetic field or magnetization induced) Hall conductivity mechanism, where the elements $$ {\sigma }_{xy}$$ of the fully antisymmetric Hall conductivity tensor may couple only to a physical quantity $$ G$$ that breaks TRS (i.e., $$ TG=-G$$, where $$ T$$ is the time-reversal operation) (37) and thus have to be an odd function of this quantity [e.g., $$ {\sigma }_{xy}\left(B\right)=-{\sigma }_{xy}\left(-B\right)$$, where $$ G=B$$].

Fig. 3.

Hall resistivity of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ in external magnetic fields. (A) In the Kondo coherent regime below $$ T^{\star }$$ and $$ B_0^{\star }$$ (Fig. 1D), the magnetic field-dependent DC Hall resistivity $$ {\rho }_{xy}\left(B\right)$$ shows a pronounced anomalous Hall effect (AHE) and can be decomposed into an odd-in-$$ B\hspace{0.17em}{\rho }_{xy}^{\mathrm{o}\mathrm{d}\mathrm{d}}\left(B\right)$$ (blue) and an even-in-$$ B\hspace{0.17em}{\rho }_{xy}^{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}\left(B\right)$$ (red) component. (B) Above $$ T^{\star }$$, $$ {\rho }_{xy}\left(B\right)$$ is dominated by a linear-in-$$ B$$ normal Hall effect. (C) $$ {\rho }_{xy}^{\mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}}\left(B,T\right)$$ is suppressed for $$ T>T^{\star }$$ and $$ B>B_0^{\star }$$. (D) Scaled coefficients of the $$ 2\omega $$ and $$ 0\omega $$ Hall voltage in an AC experiment (from Fig. 2 D and F) as function of magnetic field. (E) Below $$ T^{\star }$$ and $$ B_0^{\star }$$, $$ {\rho }_{xy}^{\mathrm{o}\mathrm{d}\mathrm{d}}\left(B,T\right)$$ shows a pronounced AHE on top of a linear background from the normal Hall effect. (F) Amplitude of the odd-in-$$ B$$ AHE, estimated as the total odd-in-$$ B$$ component at 3.5 T (location of extremum) minus its value at 4 K, where the effect has disappeared (see E), vs. the square of the corresponding magnetoresistance difference [$$ {\rho }_{xx}\left(T\right)-{\rho }_{xx}$$ (4 K)] at 3.5 T, with $$ T$$ as implicit parameter. The observed quadratic dependence (red straight line) is in remarkable agreement with expectations for the AHE due to broken TRS as $$ B$$ is applied.

The question, then, is how to understand the Hall response beyond a broken TRS framework. Recent theoretical studies (38) show that in an IS breaking but TRS preserving material, a Hall current (density)

Because $$ {\sigma }_{xy}$$ of Eq. 1 is driven by this TRS invariant Berry curvature and not by an applied magnetic field, it does not need to be odd in $$ B$$, and a finite $$ {\sigma }_{xy}$$ does not even require the presence of any $$ B$$ at all (thus the spontaneous Hall effect). In fact, the only influence the magnetic field has on this topological Hall effect is to successively reduce its magnitude with increasing field (Fig. 3D), similar to what happens when heating the material beyond $$ T^{\star }$$ (Fig. 3C). The observations of a spontaneous Hall effect (Fig. 2) and an even-in-field Hall conductivity (Fig. 3) in $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ are smoking-gun evidence that the physical quantity underlying the phenomenon is not a magnetic order parameter (coupled linearly to $$ B$$), as otherwise $$ {\sigma }_{xy}$$ would necessarily be an odd function in $$ B$$. That the spontaneous Hall current is indeed associated with $$ f\left(\mathit{k}\right)$$ is further supported by the linear relationship between $$ {\sigma }_{xy}$$ and $$ {\sigma }_{xx}$$ in the Kondo coherent regime (Fig. 2B), consistent with a linear dependence on the scattering time ($$ {\sigma }_{xy}\sim \tau $$) and thus the nonequilibrium nature of the effect. As recently emphasized (40), this dependence sharply discriminates this effect from disorder-induced contributions.

Because according to Eq. 1 the topological Hall current is determined by $$ f\left(\mathit{k}\right)$$, $$ {\sigma }_{xy}$$ will depend on $$ {\mathcal{E}}_x$$, and thus the Hall response $$ j_y={\sigma }_{xy}\left({\mathcal{E}}_x\right)\cdot {\mathcal{E}}_x$$ is expected to be nonlinear in $$ {\mathcal{E}}_x$$. By Taylor expanding $$ f\left(\mathit{k}\right)$$ around $$ f_0\left(\mathit{k}\right)$$, a second harmonic response was derived (38), which we have set out to probe by investigating both the dependence of the Hall response on the electric field (or current) strength and by analyzing the different components of the Hall response under AC and DC current drives (SI Appendix, section I D). As we will show in what follows, we do indeed observe this second harmonic response; in addition, however, we also detect terms that go beyond the prediction. The experiments as function of DC current drive reveal that the spontaneous Hall voltage $$ V_{xy}^{\mathrm{D}\mathrm{C}}$$ can be decomposed into a linear- and a quadratic-in-$$ I^{\mathrm{D}\mathrm{C}}$$ contribution (SI Appendix, Fig. S6A, Right). This is in contrast to the longitudinal voltage $$ V_{xx}^{\mathrm{D}\mathrm{C}}$$ that is linear in current, representing an ohmic electrical resistivity (SI Appendix, Fig. S6A, Left). In our AC experiments, in response to an excitation at frequency $$ \omega $$ we detect voltage contributions at $$ 1\omega $$, $$ 2\omega $$, and $$ 0\omega $$. Whereas $$ V_{xy}^{1\omega }$$ is linear in $$ I^{1\omega }$$ (SI Appendix, Fig. S7B), both $$ V_{xy}^{2\omega }$$ and the associated current rectified counterpart $$ V_{xy}^{0\omega }$$ (SI Appendix, Eq. S10) are quadratic in $$ I^{1\omega }$$ (Fig. 2 D and E). These three responses as well as the DC response described above appear simultaneously, as Kondo coherence develops with decreasing temperature (Fig. 2F) and must thus have a common origin.

Discussion

We start by discussing the terms $$ V_{xy}^{2\omega }$$, $$ V_{xy}^{0\omega }$$, and $$ V_{xy}^{\mathrm{D}\mathrm{C}}\sim I^2$$. They can be understood within the perturbative treatment (38) of Eq. 1, where the spontaneous nonlinear Hall conductivity $$ {\sigma }_{xy}$$ is determined by the Berry curvature dipole $$ D_{xz}$$ as

Next, we quantify the terms $$ V_{xy}^{1\omega }$$ and $$ V_{xy}^{\mathrm{D}\mathrm{C}}\sim I$$ that have not been considered in the perturbative approach of ref (38), though odd-in-current contributions can generally appear (SI Appendix, section I F). Intriguingly, these linear contributions show $$ \tan {\mathrm{\Theta }}_{\mathrm{H}}$$ values up to 0.5 (taken as the slope $$ \partial {\sigma }_{xy}/\partial {\sigma }_{xx}$$ in Fig. 2B and SI Appendix, Fig. S8B) and thus are even larger than the $$ 2\omega $$ effect quantified above. Before describing how these new terms as well as the above-discussed spontaneous nonlinear Hall terms may naturally arise in a Weyl–Kondo semimetal picture, we show that other effects can be safely discarded.

Skew scattering, side jump, and multiband effects are investigated via the normal (antisymmetrized) Hall effect and magnetoresistance characteristics and shown to play negligible roles by quantitative analyses (SI Appendix, sections I B and C and Figs. S4 and S5). Spurious Hall contributions due to crystal anisotropies, which may arise in systems with lower than cubic symmetry, can also be ruled out (SI Appendix, section I G). Finally, the reproducibility of the spontaneous Hall effect over various samples (SI Appendix, Fig. S8) confirms the intrinsic nature of this phenomenon.

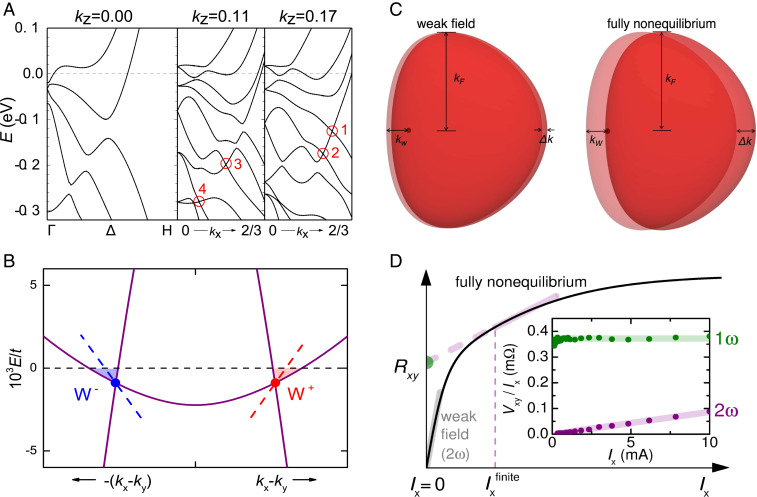
In a Weyl–Kondo semimetal, the Weyl nodes—where the Berry curvature is singular—are essentially pinned to the Fermi level (30, 31). The application of even small electric fields has a nonperturbative effect, in particular in the case of tilted Weyl cones (see SI Appendix, section IV C for an expanded discussion). A simple Taylor expansion of $$ f\left(\mathit{k}\right)$$ around $$ f_0\left(\mathit{k}\right)$$, as done in ref. 38, will therefore fail to describe the effect. Quantitative predictions from fully nonequilibrium transport calculations based on an ab initio electronic bandstructure in the limit of strong Coulomb interaction and strong spin–orbit coupling are elusive to date. Thus, instead, we here present a conceptual understanding. While tilted Weyl cones are present already in the noninteracting bandstructure of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ (Fig. 4A and SI Appendix, section III), it is the Kondo interaction that drives emergent and highly renormalized Weyl nodes in the immediate vicinity of the Fermi level (Fig. 4B), as indicated by calculations for a periodic Anderson model (31) with tilted Weyl cones in the bare conduction electron band (SI Appendix, section IV and Fig. S13) and evidenced by thermodynamic measurements (30). In the resulting tilted Weyl–Kondo semimetal, each Weyl node will be asymmetrically surrounded by a small Fermi pocket. The presence of such small pockets in $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$ is supported by the small carrier concentration ($$ 8\times 10^{19}$$ $$ {\mathrm{c}\mathrm{m}}^{-3}$$, or 0.002 charge carriers per atom) obtained from the normal Hall coefficient (SI Appendix, Fig. S4A). Due to the pinning of the Fermi energy to the Weyl nodes in a tilted Weyl–Kondo semimetal, the smallest distance between node and Fermi surface ($$ k_{\mathrm{W}}$$, see Fig. 4C) can become extremely small. The application of even tiny electric fields will then induce shifts $$ \mathrm{\Delta }\mathit{k}$$ in the distribution function $$ f\left(\mathit{k}\right)$$ that are sizable compared to $$ k_{\mathrm{W}}$$ (and possibly even compared to the Fermi wavevector $$ k_{\mathrm{F}}$$), thus driving the system to a fully nonequilibrium regime (Fig. 4D). In this setting, a nonperturbative approach is needed and will allow for the appearance of terms beyond the second harmonic one predicted by Sodemann and Fu (38), most notably the experimentally observed first harmonic one (SI Appendix, section I D). As the applied $$ \mathcal{E}$$ field can then no longer be considered as a probing field, it introduces a directionality on top of the crystal’s space group symmetry and the selection rules, which hold in the perturbative regime, will be violated.

Fig. 4.

Theoretical description of Weyl–Kondo physics in $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$. (A) Ab initio band structure of $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$, with $$ 4f$$ electrons in the core. In the $$ k_{\mathrm{x}}$$-$$ k_{\mathrm{z}}$$ plane, four different Weyl nodes (1–4) are identified; 1 and 4 are most strongly tilted (SI Appendix, section III). (B) Dispersion across a pair of Weyl ($$ {\mathrm{W}}^{+}$$) and anti-Weyl ($$ {\mathrm{W}}^{-}$$) nodes for a Weyl–Kondo model with tilted Weyl cones (SI Appendix, section IV). Energy is expressed in units of the conduction electron bandwidth $$ t$$. The Kondo interaction pushes the Weyl nodes that are present in the bare conduction electron band far away from the Fermi energy, to the immediate vicinity of the Fermi level (here at $$ E/t=0$$, slightly above the Weyl nodes). (C) Sketch of a Fermi pocket around the Weyl node $$ W^{+}$$ in B (dot) in zero electric field (light red) and its nonequilibrium counterpart with driving electric field (red), in the weak-field regime (left) and the fully nonequilibrium regime (right). (D) Sketch of the driving current-induced Hall resistance $$ R_{xy}=V_{xy}/I_x$$, displaying the weak-field and fully nonequilibrium regimes. The Inset shows experimental results for Ce₃Bi₄Pd₃, demonstrating the simultaneous presence of a spontaneous Hall signal in both the $$ 2\omega $$ ($$ V_{xy}\sim I_x^2$$) and $$ 1\omega $$ ($$ V_{xy}\sim I_x$$) channel. The sum of both contributions corresponds to a linear-in-$$ I_x$$ Hall resistance with a finite offset (violet line with green dot in main panel), which is a characteristic of the fully nonequilibrium regime.

In conclusion, our Hall effect measurements unambiguously identify a giant Berry curvature contribution in a time-reversal invariant material, the noncentrosymmetric heavy fermion semimetal $$ {\mathrm{C}\mathrm{e}}_3{\mathrm{B}\mathrm{i}}_4{\mathrm{P}\mathrm{d}}_3$$. The Hall angle per applied electric field, a figure of merit of the effect, is enhanced by orders of magnitude over values expected for weakly interacting systems, which we attribute to the effect of tilted and highly renormalized Weyl nodes that emerge very close to the Fermi surface out of the Kondo effect. The experiments reported here should allow for a ready identification of other strongly correlated nonmagnetic Weyl semimetals, be it in heavy fermion compounds or in other materials classes, thereby enabling much needed systematic studies of the interplay between strong correlations and topology. Our findings provide a window into the landscape of “extreme topological matter”—where strong correlations lead to extreme topological responses—that awaits systematic exploration. Finally, the discovered effect being present in a 3D material, in the absence of any magnetic fields and under only tiny driving electric fields, holds great promise for the development of robust topological quantum devices.

Materials and Methods