Experimental Results.

The THz absorption spectra from ν = 50 to 450 cm⁻¹ at 293 K were recorded for the water-filled and for the encapsulated [Et₄N]⁺ guest at 20 mM (Fig. 1C), and a second concentration of 10 mM is reported in SI Appendix. These spectra were differenced from the bulk water spectrum to remove the contribution of the background solvent, and to determine the change in absorbance as a function of frequency, ∆α(ν) of the guest-filled complexes (for details, see SI Appendix). We find that the water-filled cavity displays an increased THz absorption with respect to that of the encapsulated salt in the 100 to 270 cm⁻¹ range, which is characteristic of the changes in the intermolecular HB stretching of the water in and around the cage that differs from bulk water at ambient temperatures. In addition, peaks above 270 cm⁻¹ were observed and assigned to the intramolecular modes of the Ga₄L₆¹²⁻ tetrahedral host that overlap with the broad librational band of water. Even so, we are only interested in the confined water signatures that occur at frequencies below 270 cm⁻¹.

Fig. 2 shows a double difference, ΔΔα(ν), between the absorption of the guest–host complex in the presence [Δα(2)(ν)] vs. absence [Δα(1)(ν)] of the [Et₄N]⁺ guest molecule to isolate the THz fingerprint of the water cluster in the cavity:

Fig. 2.

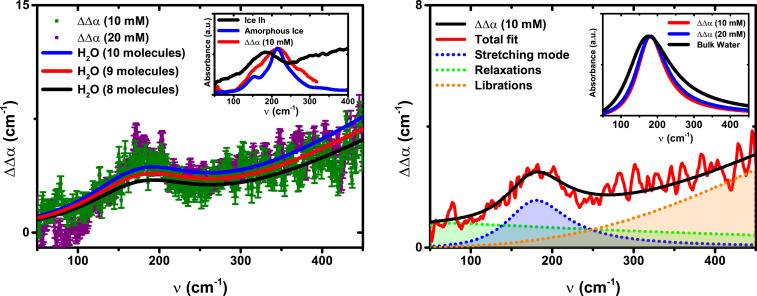
Double difference spectrum, $$ \mathrm{\Delta }\mathrm{\Delta }\alpha \left(\nu \right),$$of the THz fingerprint of the water cluster in the cavity of Ga₄L₆¹²⁻. (A) Experimental data at 10 mM (green points) and 20 mM (purple points) solutions, at 293 K. The data at 10 mM have been rescaled to the 20 mM concentration for comparison. (Inset) Absorbance spectra of ice Ih (blue line) from ref. 38, low-density amorphous ice (red line) from ref. 35, and $$ \mathrm{\Delta }\mathrm{\Delta }\alpha \left(\nu \right)$$ at 10 mM. The maximum intensity of each spectrum has been normalized to unity for the sake of comparison. The error of the absorption coefficients of bulk water, hexagonal ice, and amorphous ice is less than 5%. (B) The different modes of the hydrogen-bonding network are dissected with a fit for intermolecular relaxation, HB stretching, and water librational modes (see text and SI Appendix for details). (Inset) Fit of the intermolecular stretching band of ΔΔα at 10 and 20 mM, respectively, and of bulk water at room temperature. All of the intensities have been rescaled to the maximum absorption of ΔΔα at 10 mM.

The ΔΔα(ν) intensity is then compared to a spectrum of bulk water that has been scaled by a number density to isolate the water count inside the cage. Inspection of Fig. 2A indicates that when compared against the bulk spectrum scaled by 8, 9, or 10 water molecules (black, red, and blue lines, respectively), it is proposed that 9 ± 1 H₂O molecules are dynamically confined inside the cage in the absence of the salt (also see SI Appendix, Fig. S2). This is in agreement with the estimate for the number of water molecules that can be hosted in the cavity, taking into account a total volume of 270 ų (5). Even so, the estimated number of waters has to be considered as an average, resulting from the exchange of water molecules near the host interface with the bulk solvent through the open faces of the cage.

Not surprisingly, the spectrum of the encapsulated water shown in Fig. 2A is very different from the sharp absorption features observed for gas phase water clusters (43). Although the THz absorption spectroscopy is not a direct probe of the structure of a system, these low-frequency spectral signatures are specific fingerprints of the HB network of the isolated water cluster in the [Ga₄L₆]¹²⁻ host compared to other water systems (34, 38). In previous structural studies on supramolecular hosts in the solid state, encapsulated hydrogen-bonded (H₂O)_8–10 water clusters were identified to be similar to the smallest subunit of cubic ice (Ic) (2627–28). Even after soaking a supramolecular host crystal in water for few hours, a crystallized water decamer was observed in the cavity, albeit without a perfectly close-packed arrangement as in ice (44). However, all these previous studies were of crystals and are not directly comparable to those carried out in solution under ambient conditions where the [Ga₄L₆]¹²⁻ capsule can perform catalytic reactions (6, 8, 9).

Thus, to better determine the nature of the encapsulated water, its spectrum was compared to those of hexagonal or amorphous ice (Fig. 2 A, Inset). The spectroscopic fingerprint of the confined water network lacks the characteristic peak at about 220 cm⁻¹ with a shoulder at 150 cm⁻¹ as observed in the case of Ic and hexagonal ice (Ih) (33, 38). In addition, the maximum of the band of water trapped inside the capsule is strongly redshifted with respect to the broad mode of low-density amorphous ice (at about 215 cm⁻¹), indicating a weaker HB than the solid (35). Finally, the librational band of liquid water, i.e., the increased intensity above 250 cm⁻¹, is clearly visible in ΔΔα(ν), while it is missing in ice at these frequencies. Thus the spectrum of the encapsulated water does not resemble the spectrum of amorphous ice nor that of Ih or Ic.

To compare the similarity of capsule-confined water to other water phases, we performed a detailed analysis of the center frequencies, $$ {\stackrel{\sim }{\nu }}_0$$, which indicate the strength of the HBs involved in the vibration, and linewidths, $$ w_0$$, that yield information on the HB network with regards to lifetime and the number of available chemical environments (i.e., the degrees of freedom) (45). Therefore, the dynamics of the encapsulated water network, embodied in ΔΔα(ν), was fitted to a sum of three damped harmonic oscillators, describing the relaxational, the intermolecular HB stretching, and the librational modes with increasing frequency (36). The resulting decomposed spectrum is shown in Fig. 2B.

The broad background extending to low frequencies (<100 cm⁻¹) is attributed to dielectric relaxations and is found to be very similar to bulk water. The maximum of the librational peak (i.e., the hindered rotations) lies outside our experimental frequency range, which stops at 450 cm⁻¹. Thus, for the fits reported in Fig. 2B, the center frequency of the librational modes of the water confined in the cavity was fixed to 650 cm⁻¹ as in bulk water (36). By closer inspection, the increase in absorption with increasing frequency from 180 to 400 cm⁻¹ is smaller than in the case of bulk water: ΔΔα(400 cm⁻¹)/ΔΔα(180 cm⁻¹) = 1.02 to 1.10 for confined water, while ΔΔα(400 cm⁻¹)/ΔΔα(180 cm⁻¹) = 1.45 for bulk water. This is indicative of a blue shift of the librational mode, which can be attributed to a strong steric hindrance encountered by the librations of the water molecules in the proximity of the cage’s internal surface. A similar linewidth narrowing of the librational mode was found for water confined in nanoporous silica glasses, but in that case it exhibited a blueshift of the peak frequency itself due to interaction with the hydrophilic matrix (46).

The most interesting part of the THz spectra arises from the observation of an unperturbed center frequency of the intermolecular HB stretching mode of water confined in the Ga₄L₆¹²⁻ cage. Table 1 provides the values of $$ {\stackrel{\sim }{\nu }}_0$$ and $$ w_0$$ in which the stretch band is centered at 180 cm⁻¹ for confined water, which is (perhaps surprisingly) not shifted with respect to the center frequency of bulk water at 293 K (181 cm⁻¹). The intermolecular vibrations of the confined water are clearly red-shifted by ∼10 cm⁻¹ with respect to the same mode for water cooled to its freezing point (38), and by ∼35 cm⁻¹ with respect to water under high (∼10 kbar) hydrostatic pressures (Table 1 and SI Appendix, Fig. S3) (37). Thus, the nanoconfined water cannot be considered as cold or pressurized water either, but indicates a similar intermolecular HB strength like that of ambient water.

Table 1.

Spectral parameters of the intermolecular stretching band of water confined in the Ga₄L₆ cage and bulk water at different thermodynamic conditions

Fit parameter, cm−1	Water inside Ga4L6	Water (293 K)	Water (273.2 K)	Water (10 kbar)
$$ {\stackrel{\sim }{\nu }}_0$$	180 (4)	181 (2)	193 (2)	216 (4)
$$ w_0$$	249 (18)	537 (3)	557 (4)	542 (9)

Parameters are obtained by fitting a set of damped harmonic oscillators. The statistical 2σ error is given in parentheses. Details and the results of the fit can be found in SI Appendix, Tables S1 and S2, Fig. S3, and Text (see also refs. 37 and 38 for further details).

At the same time, the confined water shows a significant decrease in the damping of the intermolecular stretching mode, characterized as a significant narrowing of the linewidth with respect to bulk water at 293 K (Table 1). Any decrease in linewidth is an indicator for a decreased variance in the fast dynamics (36) (SI Appendix) and has also been ascribable to a reduced number of degrees of freedom, i.e., an entropic signature of a more restricted set of molecular configurations that are available (45). To place the linewidth of the nanoconfined water into perspective, we find that its value of w₀ = 250 cm⁻¹ is greatly reduced with respect to ambient, cold, and pressurized bulk water (∼540 cm⁻¹), as well as with respect to the two hydration bands around the hydrophobic groups of alcohol chains and lightly supercooled water at 266.6 K that exhibit linewidths between 340 and 440 cm⁻¹. Instead, the observed linewidth of the confined water interpolates between that observed for hexagonal ice (w₀ = 80 to 220 cm⁻¹) and clathrate hydrates and amorphous ice (w₀ = 280 to 300 cm⁻¹) (37, 38).

Theoretical Results.

To provide support for the experimental interpretations of the dynamics and structure described above, we have performed AIMD simulations of the solvated [Ga₄L₆]¹²⁻ host to characterize the encapsulated water molecules, using a well-characterized metageneralized gradient approximation (meta-GGA) functional B97M-rV (47), shown to describe bulk water well (48, 49). Fig. 3A provides the AIMD-simulated THz spectra of water inside the cage and the bulk water spectrum compared to experiment (Materials and Methods). The theoretical spectrum reproduces accurately the two main features of the THz measurements: 1) the same position of the intermolecular hydrogen-bonded stretching band at 180 cm⁻¹ for both water inside the cage and in the bulk, and 2) the reduction in linewidth for water inside the cage with respect to bulk water. An AIMD additional simulation with the [Et₄N]⁺ guest does not exhibit differences in interfacial properties near the cage or bulk (SI Appendix, Fig. S4), and thus does not contribute to the difference THz spectra.

Fig. 3.

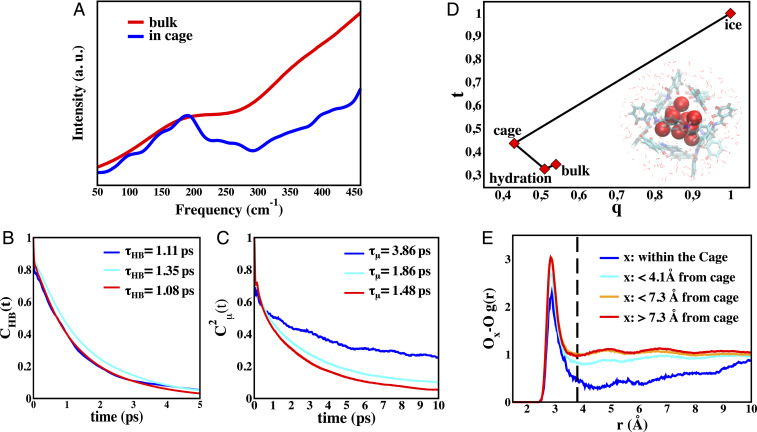
Water HB dynamics inside and outside the Ga₄L₆¹²⁻ cage. (A) Theoretical THz-IR spectra calculated for water inside the cage (blue) and for bulk liquid water taken from previous work (48) (red). The intensities are rescaled in order to have the same intensity for the maximum at ∼180 cm⁻¹ to aid comparison. (B) Hydrogen-bonded lifetimes $$ C_{\mathrm{HB}}\left(t\right)$$ and (C) orientation correlation $$ C_{\mu }^{\left(2\right)}\left(t\right)$$ dynamics inside the cage (blue), in the hydration layer (cyan) and in the bulk liquid (red). The characteristic relaxation times are also reported in the legend (details on defined regions are given in SI Appendix, Text and Fig. S5). (D) The $$ t$$ and $$ q$$ order parameter space showing their values for cubic ice, water confined inside the cage, water in the hydration layer outside the cage (<4.1 Å), and bulk liquid water. The $$ t$$ parameter value for cubic ice (t = 1) is estimated for a fcc crystal (52), while that the q parameter (q = 1) is that of a perfect tetrahedral environment. The Inset illustrates the average position of the nine arrested water molecules with long residence time inside the cage. (E) Oxygen–oxygen radial distribution function g_OO(r) for water inside the cage (blue) compared to the bulk (red).

Given the excellent agreement of the theoretical spectra with experiment, we can now analyze the trajectories to determine the time-averaged number of water oxygen centers inside the salt-free cage is 12.4 ± 0.7, whereas we find an average of 3.4 ± 0.6 water molecules inside the cage when filled with the cationic substrate. However, in the water-filled cage, there are 9 ± 1 water molecules that are dynamically distinct, with long residence times that exceed that of the 1- to 3-ps timescale of bulk water (50, 51) by at least an order of magnitude, and connect directly to what is observed experimentally. The remaining ∼3 waters undergo fast exchange dynamics with the bulk water at the interface (SI Appendix, Fig. S4). These “fast” waters are experimentally subtracted from the THz difference given in Eq. 1, and thus lead to no contradiction with their physical presence in the cage from the simulation.

To quantify the motions for the water-filled Ga₄L₆¹²⁻ cage to connect to the THz observable, we evaluate the intermittent water–water HB autocorrelation function, $$ C_{\text{HB}}\left(t\right)$$, as follows:

To characterize the “phase” of water within the cage, as much as can be said for such a small cluster, we consider two popular structural order parameters used to describe the structure, dynamics, and thermodynamics of bulk water over its phase diagram (details are provided in SI Appendix) (56). Fig. 3D shows that water within the cage is different from the interfacial water near the nanocage interface, bulk (liquid) water, and ice. When considering the order parameters for water inside the cage, one can in particular notice that $$ t$$ is larger than for bulk liquid water, while the opposite is true for $$ q$$. This $$ t-q$$ trend has been shown previously to occur when bulk water is isothermally compressed at a low temperature (56), and from this one would be tempted to correlate the phase of water inside the cage to that of pressurized water. This assumption can be checked by analyzing the $$ g_{\mathrm{OO}}\left(r\right)$$ for water inside the cage and in the bulk as shown in Fig. 3E. In a recent work, it has been shown that when the pressure is increased on the water liquid, the four to five waters residing in the region of the first peak of $$ g_{\mathrm{OO}}\left(r\right)$$ are nearly unchanged, whereas in the region beyond the first peak large structural changes occur with the collapse of the second hydration shell and shifting of higher shells to shorter distances (57). On the contrary, we find that $$ g_{\mathrm{OO}}\left(r\right)$$ for water in the cage shows a less intense peak with respect to bulk water, with no significant density in the outer shells. From this, we can infer that water within the cage is not equivalent to pressurized water, despite the fact that they have some similarities in terms of $$ t-q$$ order parameters. When the aqueous Ga₄L₆¹²⁻ supramolecular tetrahedral assembly is simulated at a low temperature of 260 K, the conclusion that the water inside the cage is remarkably different from bulk water and ice does not change (SI Appendix, Fig. S5).

The $$ t$$ and $$ q$$ order parameters are summarized in SI Appendix, Table S3, for cubic ice, water confined inside the cage, water in the hydration layer outside the cage (<4.1 Å), and bulk liquid water. In SI Appendix, Table S3, we also report the water coordination number as defined by integration under the first peak of the g_OO(r) at various cutoff values, as well as the number of HBs per molecule (53). All of the structural signatures (SI Appendix, Table S3) support that water molecules inside the cage are severely undercoordinated, with greatly reduced hydrogen bonding with respect to bulk liquid water. In particular, water inside the cage forms on average ∼1.8 HBs/molecule compared to ∼3.4 HBs/molecule formed in bulk liquid water. The water undercoordination suggests that, instead of an ice-like structure, water within the cage most likely behaves as an isolated small droplet with a fixed structure unlike other bulk phases. This is in agreement with the conclusion reached from the THz experiment, which finds that the encapsulated water does not resemble any testable phase of water, instead exhibiting mixed spectroscopic signatures of the liquid and solid phases over different parts of the water phase diagram.

THz Spectroscopy.

Spectra of Gallium supramolecular hosts aqueous solutions at 10 and 20 mM were recorded at 293 K in the frequency range from 50 to 450 cm⁻¹ by THz-far infrared (THz) absorption spectroscopy. THz measurements were performed using a Bruker Vertex 80v Fourier-transform infrared spectrometer equipped with a liquid helium-cooled bolometer from Infrared Laboratories as detector. The sample solutions were placed in a temperature-controlled liquid transmission cell with polycrystalline diamond windows and a 25-μm-thick Kapton spacer. In total, 128 scans with a resolution of 2 cm⁻¹ were averaged for each spectrum. The double difference absorption spectra were smoothened with a 2 cm⁻¹ wide (5-point) moving average.

Starting Geometries.

The starting geometry was built by removing the bis(trimethylphosphine) gold cation from Ga₄L₆¹²⁻ capsule of the reported X-ray structure (72), which was further fully optimized with density functional theory (DFT) in vaccum. The structure was then solvated using Gromacs with a preequilibrated normal density water box of size 30 × 30 × 30 Å. To maintain charge neutrality, K⁺ counter ions were also included for the encapsulated system. We ran an additional 3-ps AIMD simulation (300 K, 0.5-fs timestep) in the NVT ensemble to get further equilibration.

AIMD.

All calculations presented in this paper were performed with DFT using the dispersion corrected meta-GGA functional B97M-rV (47, 73, 74) in combination with a DZVP basis set optimized for multigrid integration (75) as implemented in the CP2K software package (76, 77). In all cases, the simulated system consists of 2,572 atoms (including 760 water molecules) in a cubic box of 30 Å. We used periodic boundary conditions, five grids, and a cutoff of 400 Ry. Three independent AIMD simulations were performed for 30 ps in the NVE ensemble after an equilibration period of 6 ps (3 ps in the NVT ensemble with T = 300 K followed by 3 ps in the NVE ensemble). In the NVE trajectories, the average temperature was 318 ± 9 K. All results are based on averages over the three AIMD simulations. The time-averaged number of water inside the cage has been defined for each of the three independent simulations by counting at each step the number of waters within the cage and averaging over all MD steps.

THz Spectra Simulation.

The theoretical IR spectra in the 50 to 500 cm⁻¹ THz frequency range were calculated using the strategy developed recently based on the Fourier transform of the velocity–velocity correlation function modulated by atomic polar tensors (78, 79):

where $$ \beta =1/kT$$; $$ \omega $$ is the frequency; c, the speed of light; V, the volume of the system; $$ \langle \cdots \rangle $$, the equilibrium time correlation function; N, the number of atoms of the system; and $$ v_m$$, the mth element of the $$ \mathit{v}$$vector that collects the 3N cartesian velocities of the N atoms of the system. $$ P_{um}=\partial {\mu }_u/\partial {\xi }_m$$ is the um element of the atomic polar tensor, i.e., the first derivative of the uth component (u = x, y, z) of the total dipole moment $$ \mathit{M}$$ of the system with respect to the mth cartesian coordinate. The above equation takes into account all self- and cross-correlation terms, whether intramolecular or intermolecular, as well as both the charges and the charge fluxes contributions to the IR intensity, and simultaneously reduces the computational cost from the usual Fourier transform of the dipole moment correlation and accelerates signal convergence, without loss in accuracy (79). Velocities $$ \left(v_m\right)$$ are readily obtained from the DFT-MD trajectories, while $$ \mathit{P}\left(t\right)$$ tensors have been parameterized on reference water structures (78). The spectra are calculated including water contributions only, and neglecting contribution from the cage and counter ions. By selecting the Cartesian coordinates of the atoms belonging to a specific vibrational population (class of water molecules with common structural and spectroscopic properties) into the summation in Eq. 4, one gets the individual contribution of the selected population to the IR spectrum by reducing the summation over m = 1,3N to m = 1,3N*, where N* = 9 identifies the waters inside the cage.