
Edited by David A. Weitz, Harvard University, Cambridge, MA, and approved December 14, 2020 (received for review September 2, 2020)
Author contributions: Y.J., S.-i.L., W.K., and H.-Y.K. designed research; Y.J. and S.J. performed research; Y.J., S.-i.L., W.K., and H.-Y.K. analyzed data; and Y.J., S.-i.L., W.K., and H.-Y.K. wrote the paper.
- Altmetric
We provide a biomechanical explanation of how swallows and phoebes can construct strong nests of incohesive mud granules using saliva as a paste. The analysis leads to a hypothesis for why only 57 small light-weighted bird species (of approximately 10,000 species worldwide) can build mud nests on walls by utilizing their saliva. Our comprehensive study, combining experiments on natural and artificial mud nests and mathematical models on granular cohesion, not only elucidates the physical mechanism of this extraordinary animal architecture, but also provides inspiration to three-dimensional printing technology based on environmentally benign granular materials.
Mud nests built by swallows (Hirundinidae) and phoebes (Sayornis) are stable granular piles attached to cliffs, walls, or ceilings. Although these birds have been observed to mix saliva with incohesive mud granules, how such biopolymer solutions provide the nest with sufficient strength to support the weight of the residents as well as its own remains elusive. Here, we elucidate the mechanism of strong granular cohesion by the viscoelastic paste of bird saliva through a combination of theoretical analysis and experimental measurements in both natural and artificial nests. Our mathematical model considering the mechanics of mud nest construction allows us to explain the biological observation that all mud-nesting bird species should be lightweight.
Bird nests come in a variety of forms made from diverse building materials (1, 2). Each type of bird nest is subjected to mechanical constraints imposed by material characteristics. To overcome these constraints, birds have devised brilliant architectural technologies, which provide inspiration for a novel materials processing scheme and help us to better understand animal behavior.
For instance, some birds including storks (Cicioniidae) and eagles (Accipitidae) build nests by piling up hard filamentary materials such as twigs, harnessing their friction as the cohesion mechanism (3). Weaverbirds (Ploceidae) weave soft filamentary materials such as grass and fine leaves into a woven nest tied to a tree branch. Some bird species use their own saliva in nest building, which Darwin considered an example of natural selection (4). An extreme case is the Edible-nest Swiftlets, which build their nest purely of self-secreted saliva so that it can be attached to cliff walls and cave ceilings where the above twig piles and tied leaves are not allowed (5).
Swallows (Hirundinidae), phoebes (Sayornis), and other mud nesters have developed a unique building material, a mixture of mud and their own saliva, in contrast to those made of purely collected or self-secreted materials (6) (Fig. 1). During construction, mud nesters repeatedly pile a beakful of wet mud on the nest, and liquid bridges are formed in the nest due to evaporation. While building a nest usually takes several weeks, a transition from wet to dry structures can occur within a few hours. Hence, the capillary forces of liquid bridges temporarily provide cohesion such as those in sandcastles. However, unlike sandcastles, dehydrated saliva comes into play for permanent cohesion after complete evaporation (SI Appendix, Supplementary Note 1).

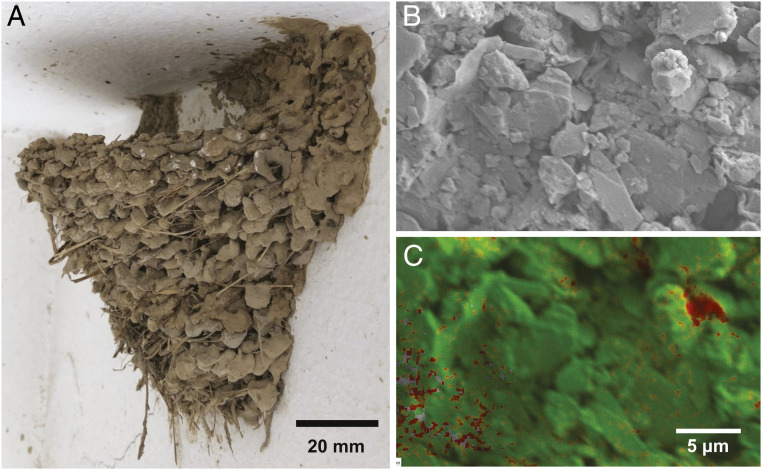
A nest of the barn swallow (H. rustica). (A) Photograph of a barn swallow nest, taken from under the ceiling of a house in Suwon-si, Gyunggi-do, South Korea (37°16′13.5″N 126°59′01.0″E). (B) SEM image of the nest surface. (C) Chemical composition analysis of the surface shown in B by EDS. The red area indicates a region containing mostly carbon atoms, which may originate from bird saliva. The green area indicates a region containing mostly the silicon atoms of clay particles.
Mud itself cannot confer sufficient cohesion and adhesion in mud nests. The ability of mud nests to bear tensile loads originates from the gluing agent in the bird's saliva, which permeates into granules as a liquid and binds them as a solid after solvent evaporation (67–8) (SI Appendix, Supplementary Note 2). The gluing agent is called mucin, a family of large glycoproteins that are ubiquitous in animal organs and form a mucus gel with versatile functionality (9). Fig. 1B shows the scanning electron microscopy (SEM) image of a barn swallow’s mud nest consisting of platelet clay particles and larger grains. Energy-dispersive spectroscopy (EDS) mapping image of Fig. 1C clearly shows regions corresponding to organic material which is presumed to be from bird’s saliva.
Of particular interest and worth biophysical investigation are the tensile strength of the mud nest with hardened saliva, design principles associated with the saliva-originated strength, and the resulting effects on the evolution of these mud-nesting birds. Principles behind cohesion in granular materials, such as wet sands (10), cemented powder aggregates (11), construction materials (12), and pharmaceutical tablets (13), have been studied to date, exploring the stress transmission, elasticity, and failure (14151617–18), and the formation of solidified bridges (1920–21). However, little attention has been paid to the cohesion effects of self-secreted polymer materials upon evaporation and the biologically constructed granular architecture like birds’ mud nests. Here we devised experimental techniques to measure the strength of the relatively small and fragile nest specimens in order to mechanically characterize birds’ mud nests. We elucidate how solutes from bird saliva generate solid bridges that give rise to macroscopic tensile strength, which has long awaited physicochemical explanation since its first observation (4). To characterize the design principle of bird's mud nests, we investigated natural and three-dimensional (3D)-printed artificial nests with various tools for visualization and mechanical testing. Along with the experimental studies, we theoretically investigated the effects of biopolymer concentration on nest strength. This combination of theory and experiment suggests that there is a size limit for mud-nesting birds, which is supported by biological data.
Results
Mechanical Testing of the Barn Swallow’s Nest.
A typical V-shaped nest of the barn swallow (Hirundo rustica) attached to a vertical wall, as shown in Fig. 1A, embodies the mechanical principles required for nest design. To assess the strength of the nest, we attached the nest to a glass plate using a cyanoacrylate adhesive. We applied a vertical load by adding weights to the interior of the nest until it fell. As shown in Fig. 2A, the nest endured 30 N in addition to its own weight of 3 N without any symptom of failure, but it finally failed when the total weight reached 41.5 N (Fig. 2B and Movie S1).

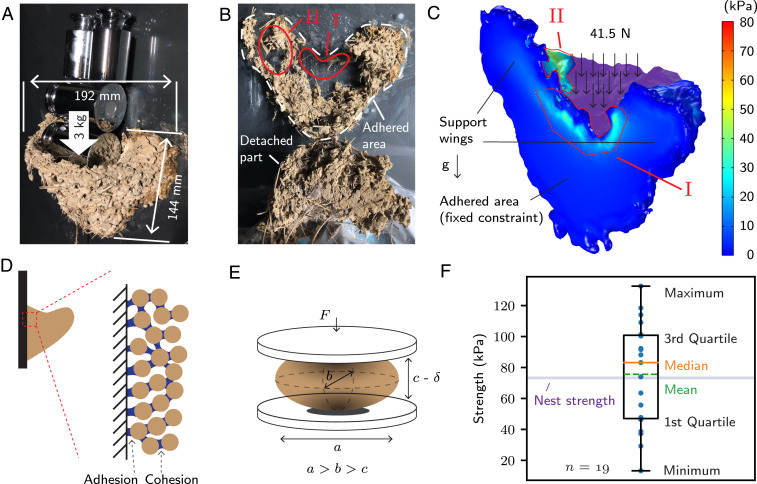
Mechanical tests with a nest of a barn swallow. (A) The nest is attached to a glass plate using a cyanoacrylate adhesive. The nest was able to sustain 33-N weight in the nest interior. (B) Fracture of the attached nest when subjected to a vertical load of 41.5 N. (C) The first principal stress distribution in the attached nest subjected to a vertical loading of 41.5 N. The load is exerted on the purple-shaded area in the image. (D) Adhesion and cohesion of the mud nest. (E) Schematic of measuring the tensile stress of a mud pellet. (F) Strength of mud pellets extracted from the nest.
In this work, we define the adhesion and cohesion strengths of the mud nest as the maximum tensile stress that the substrate–granule and the granule–granule pairs can withstand, respectively (Fig. 2D). After the solvent completely evaporates, a tight agglomerate of the remaining polymer molecules grasps the substrate and granules. The strengths of adhesion and cohesion would depend on the surface characteristics such as roughness as well as the polymer-specific properties, for example, molecular weight and chain structure. Therefore, the two strengths should be comparable in natural settings because natural materials such as mud and the cliff face are anticipated to have similar surface roughness, and both adhesion and cohesion originate from the same type of polymer material. Henceforth, we indicate these as the strength of a mud nest. The maximum weight that the nest endured while attached to the glass plate is associated with the cohesive strength because the artificial adhesive is much stronger (>10 MPa) than the saliva-originated paste.
Based on the force equilibrium, we can estimate the stress distribution in the nest when subjected to vertical loads via computer-aided stress analysis using COMSOL Multiphysics. We used the 3D-scanned mesh geometry of the natural nest shown in Fig. 2C. The computation yielded the stress distribution as shown in Fig. 2C. The fixed constraint condition was applied at the adhered area, and the boundary load condition was applied over the nest interior surface, colored purple in Fig. 2C. The simulated stress distribution explains the nest fracture shown in Fig. 2B. The first principal stress, a typical fracture criterion, reaches its maximum value, 78 kPa in tension, around the uppermost line of the adhered area (denoted as I in Fig. 2 B and C). Due to this high tensile stress over the region, the area was completely disengaged. Another region of high mechanical stress occurred between the nest interior and the support wings (denoted as II). Hence, the interior of the nest and the support wings were separated when failure occurred. Owing to the high strength for compression, the lower part of the adhered area remained intact.
To trace the origin of the nest’s strength that allows it to sustain its structure against external loading, we measured the strength of mud pellets extracted from the nest using the diametrical compression method (Fig. 2E and Methods). The mean value of the measured strength was 75 kPa, as shown in Fig. 2F. For swallows, it is reasonable to use materials providing 50–100 kPa in strength to build their nest so that the nest can endure a vertical load of 40 N. Under usual circumstances, we can assume that a vertical load of ∼4 N is applied on the nest, considering the mass of two adults (<30 g each) with several young (<10 g each) swallows, and the mass of the nest itself (300 g). In this respect, the safety factor of the mud nest amounts to 10. This overdesign strategy for mud nesters is consistent with that of the edible nest swiftlet (Aerodramus fuciphagus), which produces a nest with a safety factor of 5–10 (22). We note that strong winds can exert significant aerodynamic forces. For example, in a storm with a maximum wind speed of 35 m/s, the aerodynamic force on a mud nest is ∼8 N, which is twice the weight of the nest and the birds (SI Appendix, Supplementary Note 3). Even though this aerodynamic force of 8 N is well below the force limit of 40 N, it has been observed that an extremely violent storm could destroy mud nests (23).
Experimental Characteristics of Polymer-Bridged Granules.
Having quantified the strength of a natural bird nest, we investigated its physical origin using artificial systems mimicking the mud nest. The tensile strength, which is the maximum stress that a material can withstand while being stretched, quantifies how a cohesive granular material can maintain its structural integrity. To test the tensile strength of the polymer-bridged granular material, we fabricated test specimens by mixing glass beads with an aqueous polymer solution, shaping it into a rectangular cuboid, and then drying it in ambient conditions for 1 d (Methods). Similar to mud nests, the specimens develop polymer bridges interconnecting the granules as the solvent of the polymer solution evaporates (Fig. 3A). Liquid bridges of the polymer solution provide a mixture with temporary cohesion, and after the complete evaporation of the solvent, the network of solid polymer bridges ultimately binds the granules.

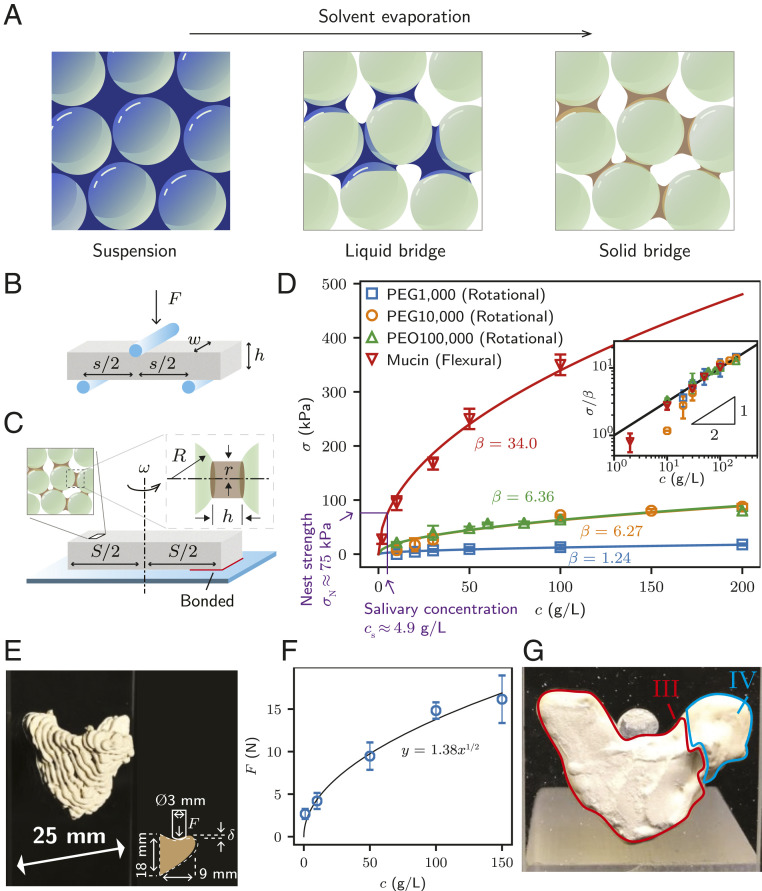
Measurement of the tensile strength of mud-nest–mimicking granular materials and 3D-printed artificial nests made of clay–mucin solution mixture. (A) Formation of solid bridges by solvent evaporation. (B) Schematic of a three-point flexural test setup. (C) Schematic of the custom-built setup for weak tensile strength analysis of fragile specimens. (D) Measured tensile strength, σ, of granular specimens with different initial concentrations of polymer solutions, c. The pores of granular specimens were fully saturated with polymer solution before evaporation began. Solid lines correspond to fitting curves, σ = βc1/2, with β = 1.24, 6.27, 6.36, and 34.0 kPa L1/2 g−1/2 for PEG1,000, PEG10,000, PEO100,000, and mucin, respectively. (Inset) Normalized tensile strength vs. the concentration in the log-log scale. (E) An artificial nest fabricated by the Direct Ink Writing method. (Inset) Test method for the structural stability of artificial nests, where the rod pushes the interior down. (F) Maximum force, F, before nest failure as a function of the concentration of the mucin solution, c. (G) Fracture surface of the artificial nest (mucin concentration: 10 g/L), designated as III. The wings designated as IV remain intact.
We used an aqueous solution of mucin of porcine gastric origins to investigate the effects of the same polymer in a bird’s saliva on the strength of mud nests. In addition to mucin, we carried out comparative experiments using poly(ethylene oxide) (PEO, molecular weight 100,000) and poly(ethylene glycol) (PEG, molecular weight 1,000 and 10,000) to determine how molecule-specific interactions affect the cohesive strength.
We measured the tensile strength of the test specimens using a three-point flexural test and a centrifugal force-based rotational test as schematically illustrated in Fig. 3 B and C, respectively (Methods). Fig. 3D shows that the strength of the polymer-bridged granular samples, σ, increases with the polymer concentration in the interstitial liquid, c. The inset in Fig. 3D reveals that σ grows like c1/2, leading us to write σ = βc1/2, where the fitting coefficient β differs for each polymer solution owing to different polymer strengths, as designated in Fig. 3D in units of kPa L1/2 g−1/2.
As shown in Fig. 3D, β for mucin is the highest among the polymers tested. The superb cohesion reinforcement with the mucin glycoproteins is due to the difference in the ability of entangled polymer chains to resist mechanical stresses. Various structures in the polymer chain networks can occur depending on the polymer type. For example, mucin solution is known to form a gel when the branched carbohydrate side chains of adjacent glycoprotein molecules are forced to interlock and to be cross-linked if they are highly concentrated beyond a critical concentration of ∼50 g/L (24). On the other hand, polymer chains in PEG and PEO solutions are known to form crystalline structures instead of gels during solvent evaporation (25).
The mucin concentration in the bird's saliva, cs, is expected to be cs ∼ 4.9 g/L as shown in Fig. 3D, where σ = βcs1/2 ∼ 75 kPa equals the measured nest strength. At this concentration, the saliva viscosity is close to that of pure water (SI Appendix, Fig. S1C) and thus the transport of saliva from the salivary glands through the salivary ducts is as difficult as that of pure water.
A Mechanical Model for the Polymer-Bridged Cohesion.
Polymer molecules in the interstitial liquid are assembled into bridges between granular pairs, and their volume and cross-sectional area (V and A, respectively) depend on c. Because contact forces are transmitted through A, the strength is a function of A and therefore dependent on c. Based on the relationship between the bridge geometry and the concentration, here we provide a mechanical model that supports this scaling relation between σ and c.
Consider a wet granular pile, which is fully saturated with an aqueous solution of polymer concentration c. Once the solvent is completely removed, solidified polymer bridges emerge in the void space of the bead packing (Movie S3). Since the macroscopic tensile strength of granular materials is determined by the strength of microscopic bridges at contact sites between granules (14, 15), we write
A bridge with a minimal surface area between a pair of identical spheres of radius R is modeled as a cylinder with both ends inward in the shape of a spherical cap (Fig. 3C) (15). If we denote the radius of the cylinder as r, the height h is approximately given by h = r2/(2R) provided that r and h are sufficiently small compared to R. Then the volume V is given by V/R3 = (3π/4)(r/R)4 and area A can be written as
The force threshold of each bridge, f, is an extensive quantity and should scale as the characteristic area of the bond, A. The intensive quantity corresponding to f is the material strength, p, which is a characteristic of the molecular interaction between the deposited polymer chains per unit area; thus, f = pA. Considering that the force transmission area A of a bridge is proportional to the half power of the bridge volume V, or A ∼ V1/2 as shown in Eq. 2, the average force threshold is proportional to the half power of the average volume of the bridges, or ⟨f⟩ ∼ p⟨V⟩1/2. The average volume of the polymer bridges is linearly proportional to the concentration of the polymer solution, c, or ⟨V⟩ ∼ c because the concentration c is simply the mass of the polymer molecules per unit volume of solvent. The volume after solvent evaporation should be linearly proportional to the mass of the polymer molecules. Therefore, we obtain σ ∼ n⟨l⟩⟨f⟩ ∼ ⟨V⟩1/2 ∼ c1/2. Here, n and ⟨l⟩ are independent of V because they are determined solely by the packing characteristics.
This simple model explains why the normalized strength data in Fig. 3D follow the 1/2 power law of polymer concentration. In addition, Eq. 1 implies the scale-free property of σ because n ∼1/l3 and f ∼ l2 provided that the van der Waals (VDW) interactions are negligible. The mud particles in a mud nest and glass beads are so large that the VDW interactions can be negligible (SI Appendix, Supplementary Note 1). The effects of size on σ are absent for both particle types.
Artificial Nest.
We directly related the increased macroscopic tensile strength of granular clusters mixed with the salivary biopolymer to the strength of adherent mud nests by testing 3D-printed artificial nests fabricated using Direct Ink Writing method (26) (Fig. 3E and Methods). This test enabled us to study the characteristics of bird nests while varying polymer concentrations (1–150 g/L) as required. We note that to date, the solute concentration of a bird’s saliva has not been quantitatively and systematically traced. This is probably due to the difficulty in collecting avian saliva.
Vertical loading caused by the nest itself and the residents would be the most important measure of nest strength. To test vertical load-bearing capacity, we depressed the interior part of the printed nests attached to the vertically standing substrate (slideglass) with a 3-mm-diameter rod. We measured the displacement and the force simultaneously using a universal testing machine (Fig. 3E, Inset).
Immediately after the force measurement attained the peak value, artificial nests were severely disrupted. The maximum vertical force F endured by the nest depends on the polymer concentration c, and follows a similar trend to the strength characteristics shown in Fig. 3D. As can be seen in Fig. 3F, the maximum force, F, increased with the half power of concentration, c, such that F = 1.38 c1/2. The support wings of the artificial nest, designated as IV in Fig. 3G, remained relatively intact, similar to those of the natural nest. This implies a similarity in the stress distribution between natural and artificial nests.
Biomechanical Limits on Mud Nest Architecture.
We now turn to the biological significance of the physical constraints imposed on birds to construct mud nests. In order to simply but quantitatively analyze their architectural aspects, we introduce a geometrical idealization of cup-shaped mud nests (2), having three characteristic lengths l1, l2, and l3, as shown in Fig. 4. The geometry of the simplified mud nest is obtained by subtracting a small ellipsoid described by x2/l12 + y2/l22 + z2/l32 = 1 from a large ellipsoid defined by x2/l12 + y2/l22 + z2/[(1+α)l3]2 = 1, and then by taking a quadrant of the subtracted geometry as shown in Fig. 4A. Here α denotes the length of the adhered surface in the direction in units of multiples of

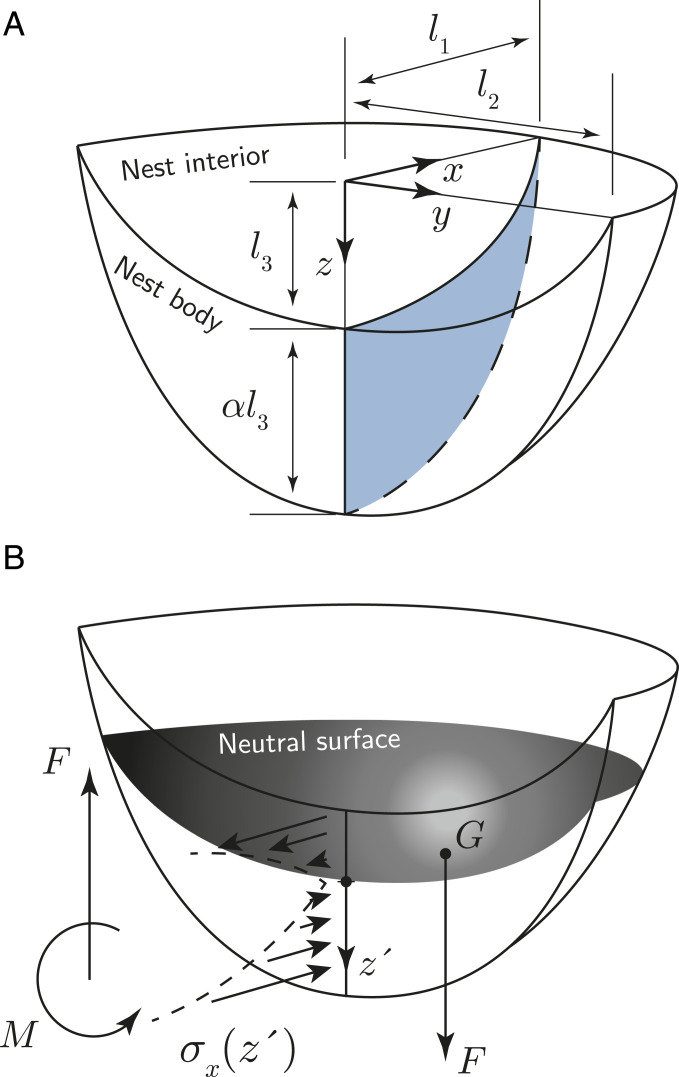
Mud nest architecture. (A) Simplified geometry of half-cup–type mud nests. αl3 is defined as the vertical length of the nest body. (B) Free body diagram of an attached simplified mud nest. z’ is the distance from the neutral surface at the adhered surface. G denotes a point of force application.
For a given size of a bird,
We consider the moment balance for a mud nest attached to a wall. The weight of the nest and birds creates a bending moment
On the other hand, a decrease in
To build a stable mud nest, the maximum tensile stress must be lower than the tensile strength of the material, so that
A clear manifestation of these limits is the restricted scalability of avian mud nests. We plot the number of bird species versus the body mass of 9,307 bird species (28) (Fig. 5 and Methods). Mud-nesters lighter than 100 g occur far more frequently than those heavier than 100 g, with the population peak near 20 g. The number of heavier mud-nesting species abruptly decreases from 19 to 4 after the peak in the mass range of 17.8–22.3 g and never recovers. Most of the heavy mud nesters belong to the Corcoracidae family, which are well known to build coil pot-type mud nests on a stable substrate, such as thick tree branches, rather than on vertical walls (SI Appendix, Supplementary Note 3) (2). Corcorax melanorhamphos of this family are known as the heaviest mud nester (364 g). There are no known bird species heavier than ∼400 g that build nests predominantly made of mud. This scarcity of heavy mud nesters supports our hypothesis of the limited scalability of mud nests as seen in Eq. 8 and Fig. 5.

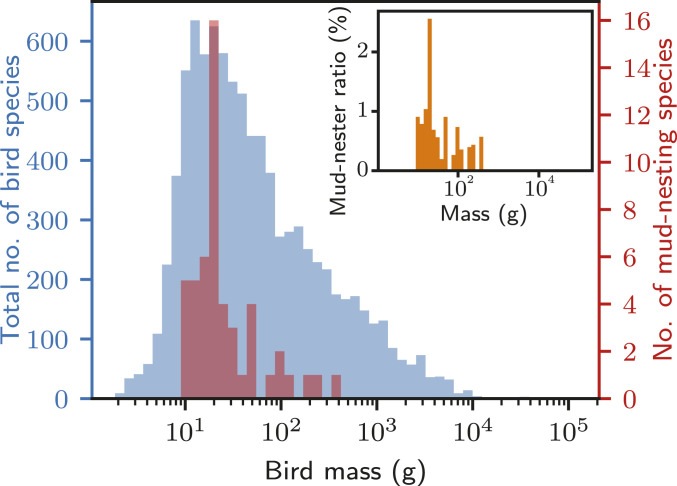
Histogram of masses of 9,307 bird species. Blue bars indicate the number of bird species and red bars indicate the number of mud-nesting bird species. (Inset) Indication of the relative frequency of mud nesters in each bin.
Discussion
Inspired by bird mud nests, we characterized polymer-bridged granular materials using theoretical modeling and mechanical experiments. We identified that the mechanical strength of polymer-bridged granular materials depends on the concentration of the polymer solution; a highly concentrated solution constructs thick bridges.
The fabrication method of the artificial nest was inspired by how birds add nest-building materials (22). This biomimetic 3D printing technology can be applied to a wide range of human-made systems in need of novel materials with the combined advantage of ceramics and polymers (29, 30). The need to develop such novel materials is increasingly important especially in medical applications such as 3D-printable functional prostheses, as well as in conventional ceramic engineering. Our comprehensive study of bird mud nests not only elucidates the physics behind this ingenious and unique animal architecture, but also provides inspiration for 3D printing technology based on environmentally benign granular materials.
Methods
Mechanical Tests of the Nest Material.
We collected mud pellets from the natural nest used in the nest failure experiment. Despite its finite irregularity in shape, we regarded the mud pellets as ideal ellipsoids, having three different diameters which were measured for each mud pellet. Pellets were regarded as ellipsoids of three different lengths of the principal axes, a, b, and c, where a > b > c (Fig. 2C). We measured the dimensions of 19 mud pellets from the collapsed nest. The mud pellets were placed between two flat plates so that the plates compressed them along the shortest principal axis. The force, F, and displacement, δ, during the compression were recorded using a universal testing machine (Instron 3343). The tensile stress developed along the shortest principal axis is approximately σ = kF/(πRe)2 where Re = ab/(2c) and k is a constant that can vary between 2/π and 4/π depending on the geometry of the pellet (3132–33). In our experiment, we kept k = 1 for simplicity.
The irregular shape of the mud pellets is likely to be the source of the large scatter of data because the contact area between the plates and the pellet can vary significantly during the compression process. Conversely, the Hertzian theory of contact between the ellipsoid and plate predicts that the area grows with δ where δ is the displacement of the compression (34). Nonetheless, the mean (75 kPa) and median (83 kPa) values agree with the maximum tensile stress (78 kPa) when the nest is subjected to a vertical load of 41.5 N at the collapse.
Polymer Solution Preparation.
We used commercially available porcine gastric mucin (M2378, Sigma-Aldrich) and PEO (181986, Sigma-Aldrich, MW 100,000), and PEG (MW 10,000; 8.21881, and PEG MW 1,000; 76293, Sigma-Alrdrich). The mucin powder was dissolved in a 1 M sodium hydroxide aqueous solution at 40 °C for 24 h with magnetic stirring at 300 rpm. The PEO and PEG powders were dissolved in deionized water at 70 °C for 24 h with magnetic stirring at 300 rpm.
Preparation of Cuboid Specimen.
In order to fabricate a specimen for tensile strength testing, we mixed glass beads and a polymer solution and shaped the mixture in a rectangular cuboid (w = 10 mm and h = 7 mm; s was varied from 15 to 40 mm; see Fig. 3 A and B). The mixture was dried under ambient conditions for 1 d. The glass beads and polymer solution were mixed in a bulk volume ratio of 5:2 to ensure that the specimen was fully saturated. Specifically, given the porosity of the random close packing of the beads, ψ ∼ 0.4, we added a polymer solution with a volume of ψVb = 0.4Vb in the bead packing of the bulk volume Vb. The dimensions of the specimen are as follows: width w = 10 mm, height h = 7 mm, and length S ranging from 15 to 40 mm (Fig. 3 A and B). The diameter of the glass beads was 0.25 mm.
Measurement of Tensile Strength.
For the mucin-bridged granular specimen, we utilized the three-point flexural testing to measure the tensile strength, using the relation σ = 3Fs/(2wh2) (Fig. 3A). For the PEO- and PEG-bridged granular specimens, we used a customized method to measure the strength using the centrifugal force owing to their fragility (Fig. 3B). A specimen was mounted on a rotational stage with one end adhered to the bottom using a cyanoacrylate adhesive. When the rotational speed exceeded a critical value, ωc, the specimen split into two approximately identical pieces. In this case, the tensile strength σ is given by σ = whS2ωc2/8 (Fig. 3B).
Artificial Bird's Mud Nest: 3D Printing.
We printed artificial bird nests in 3D using a mixture of mucin solution and clay with the Direct Ink Writing technique (26). We initially obtained 3D morphological information of the nest of a barn swallow (H. rustica, Fig. 1A) using a 3D scanning mobile application (Qlone, EyeCue Vision Technologies) to generate a stereolithography (stl) file.
Kaolinite powder (03584, Sigma-Aldrich) and mucin solution at concentrations of 1, 10, 50, 100, and 150 g/L were mixed at a weight ratio of 1:1 with a glass rod. The mixture was placed in a glass syringe. The clay–mucin ink was printed on a glass substrate 0.125 times smaller in length than the real nest (Movie S4). To accelerate the drying process, the syringe and the substrate were heated to 60 °C. Without additional curing, the printed artificial nests adhered well to the substrate, similar to the real nest. We then mechanically tested our bioinspired artificial nests by applying a vertical load on top of the nest using a universal testing machine (Instron 3343).
The grain-size distribution of the mud nest, packed glass beads, and kaolinite powder were different. The kaolinite powder–mucin solution mixture was 3D-printable with syringe needles (20 G) because the grains were small (3 μm) and uniform. Commercially available glass beads and particles in the mud nest were not 3D-printable because of the large particles in the pile. Despite this difference in grain size and polydispersity, we observed the same concentration-dependent strength behavior among nest materials, glass beads (Fig. 3C), and kaolinite powder (Fig. 3E).
Collecting Bird’s Mass Data.
We collated mass data of 9,307 bird species from a single database (28). We used the mean value in the database as representative data of species mass, rather than minimum or maximum values. When multiple mean values were provided for a species, we calculated their mean values. When the mean value is not available in the source, we used the arithmetic average of the minimum and maximum mass of the species.
The following 57 mud-nesting species were chosen according to the classification rule in ref. (7): Petrochelidon pyrrhonota, Petrochelidon rufocollaris, Petrochelidon fulva pallida, Petrochelidon fulva citata, Petrochelidon fulva, Hirundo griseopyga, Hirundo rupestris, Hirundo obsoleta, Hirundo fuligula, Hirundo concolor, H. rustica, Hirundo rustica rustica, Hirundo lucida, Hirundo aethiopica, Hirundo angolensis, Hirundo albigularis, Hirundo tahitica, Hirundo neoxena, Hirundo smithii, Hirundo nigrita, Hirundo nigrorufa, Hirundo atrocaerulea, Hirundo megaensis, Hirundo dimidiata, Hirundo cucullata, Hirundo abyssinica, Hirundo semirufa, Hirundo senegalensis, Hirundo daurica rufula, Hirundo striolata, Hirundo preussi, Hirundo rufigula, Hirundo spilodera, Hirundo nigricans, Hirundo fluvicola, Hirundo ariel, Delichon urbicum, Delichon dasypus, Delichon nipalensis, Grallina cyanoleuca cyanoleuca, Grallina cyanoleucaneglecta, Grallina bruijni, Corcorax melanorhamphos, Struthidea cinerea, Picathartes gymnocephalus, Picathartes oreas, Cichladusa arquata, Cichladusa ruficauda, Cichladusa guttata, Sayornis phoebe, Sayornis nigricans, Furnarius minor, Furnarius rufus, Furnarius cristatus, Furnarius leucopus, Furnarius torridus, Furnarius figlus. See SI Appendix, Table S1 for weights of the bird species listed above.
These species build nests solely or predominantly constructed with mud. We ruled out species who displayed minor use of mud in nest building (7), including using mud to reduce the entrance, lay a base, cement sticks/grass together, and plaster the interior. In addition, puddlelike nests of flamingos were also ruled out because in this case mud does not serve as a building material but as an insulating material.
Acknowledgements
This work was supported by National Research Foundation of Korea (Grant 2018052541) via Institute of Advanced Machines and Design, Seoul National University and DGIST R&D Program of the Ministry of Science and ICT (20-BRP-03). We thank Prof. P. G. Jablonski for helpful comments and Dr. P. Matyjasiak, Mr. J. Ha, Ms. Y. Yoon, and Ms. H. Cho for their assistance with nest collection.
Data Availability.
All study data are included in the article and supporting information.
References
1
2
3
4
5
6
7
8
9
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
30
31
32
33
34
 Avian mud nest architecture by self-secreted saliva
Avian mud nest architecture by self-secreted saliva
