Overview of Our Method

Following the Bayesian paradigm, we view the $$ D$$-dimensional system $$ \mathit{x}\left(t\right)$$ to be a realization of the stochastic process $$ \mathit{X}\left(t\right)=\left(X_1\left(t\right),\dots ,X_D\left(t\right)\right)$$ and the model parameters $$ \mathit{\theta }$$ a realization of the random variable $$ \mathbf{\Theta }$$. In Bayesian statistics, the basis of inference is the posterior distribution, obtained by combining the likelihood function with a chosen prior distribution on the unknown parameters and stochastic processes. Specifically, we impose a general prior distribution $$ \pi \left(\cdot \right)$$ on $$ \mathit{\theta }$$ and independent GP prior distributions on each component $$ X_d\left(t\right)$$ so that $$ X_d\left(t\right)\sim \mathcal{G}\mathcal{P}\left({\mu }_d,{\mathcal{K}}_d\right),\hspace{0.17em}t\in \left[0,T\right]$$, where $$ {\mathcal{K}}_d:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$$ is a positive definite covariance kernel for the GP and $$ {\mu }_d:\mathbb{R}\to \mathbb{R}$$ is the mean function. Then, for any finite set of time points $$ {\mathit{\tau }}_d$$, $$ X_d\left({\mathit{\tau }}_d\right)$$ has a multivariate Gaussian distribution with mean vector $$ {\mu }_d\left({\mathit{\tau }}_d\right)$$ and covariance matrix $$ {\mathcal{K}}_d\left({\mathit{\tau }}_d,{\mathit{\tau }}_d\right)$$. Denote the observations by $$ \mathit{y}\left(\mathit{\tau }\right)=\left({\mathit{y}}_1\left({\mathit{\tau }}_1\right),\dots ,{\mathit{y}}_D\left({\mathit{\tau }}_D\right)\right)$$, where $$ \mathit{\tau }=\left({\mathit{\tau }}_1,{\mathit{\tau }}_2,\dots ,{\mathit{\tau }}_D\right)$$ is the collection of all observation time points, and each component $$ X_d$$ can have its own set of observation times $$ {\mathit{\tau }}_d=\left({\tau }_{d,1},\dots ,{\tau }_{d,N_d}\right)$$. If the $$ d$$th component is not observed, then $$ N_d=0$$, and $$ {\mathit{\tau }}_d=\varnothing $$. $$ N=N_1+\cdots +N_D$$ is the total number of observations. We note that for the remainder of the paper, the notation $$ t$$ shall refer to time generically, while $$ \tau $$ shall refer specifically to the observation time points.

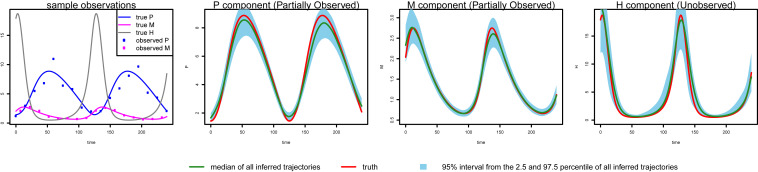
As an illustrative example, consider the dynamic system in ref. 1 that governs the oscillation of Hes1 mRNA (messenger ribonucleic acid) ($$ M$$) and Hes1 protein ($$ P$$) levels in cultured cells, where it is postulated that an Hes1-interacting ($$ H$$) factor contributes to a stable oscillation, a manifestation of biological rhythm (2). The ODEs of the three-component system $$ X=\left(P,M,H\right)$$ are

Fig. 1.

Inference by MAGI for Hes1 partially observed asynchronous system on 2,000 simulated datasets. The red curve is the truth. MAGI recovers the system well, without the usage of any numerical solver: The green curve shows the median of the inferred trajectories among the 2,000 simulated datasets, and a 95% interval from the 2.5 and 97.5% of all inferred trajectories is shown via the blue area.

The goal here is to infer the seven parameters of the system: $$ a,b$$ govern the rate of protein synthesis in the presence of the interacting factor; $$ c,d,g$$ are the rates of decomposition; and $$ e,f$$ are inhibition rates. The unobserved $$ H$$ component poses a challenge for most existing methods that do not use numerical integration but is capably handled by MAGI: The $$ P$$ and $$ M$$ panels of Fig. 1 show that our inferred trajectories provide good fits to the observed data, and the $$ H$$ panel shows that the dynamics of the entirely unobserved $$ H$$ component are largely recovered as well. We emphasize that these trajectories are inferred without any use of numerical solvers. We shall return to the Hes1 example in detail in Results.

Intuitively, the GP prior on $$ \mathit{X}\left(t\right)$$ facilitates computation as GP provides closed analytical forms for $$ \dot{\mathit{X}}\left(t\right)$$ and $$ \mathit{X}\left(t\right)$$, which could bypass the need for numerical integration. In particular, with a GP prior on $$ \mathit{X}\left(t\right)$$, the conditional distribution of $$ \dot{\mathit{X}}\left(t\right)$$ given $$ \mathit{X}\left(t\right)$$ is also a GP with its mean function and covariance kernel completely specified. This GP specification for the derivatives $$ \dot{\mathit{x}}\left(t\right)$$, however, is inherently incompatible with the ODE model because Eq. 1 also completely specifies $$ \dot{\mathit{x}}\left(t\right)$$ given $$ \mathit{x}\left(t\right)$$ (via the function $$ \mathbf{f}$$). As a key contribution of our method, MAGI addresses this conceptual incompatibility by constraining the GP to satisfy the ODE model in Eq. 1. To do so, we first define a random variable $$ W$$ quantifying the difference between stochastic process $$ \mathit{X}\left(t\right)$$ and the ODE structure with a given value of the parameter $$ \mathit{\theta }$$:

Under Bayes’ rule, we have

The first term (1) can be simplified as $$ P\left(\mathit{X}\left(\mathit{I}\right)=\mathit{x}\left(\mathit{I}\right)|\mathbf{\Theta }=\mathit{\theta }\right)=P\left(\mathit{X}\left(\mathit{I}\right)=\mathit{x}\left(\mathit{I}\right)\right)$$ due to the prior independence of $$ \mathit{X}\left(\mathit{I}\right)$$ and $$ \mathbf{\Theta }$$; it corresponds to the GP prior on $$ \mathit{X}$$. The second term (2) corresponds to the noisy observations. The third term (3) can be simplified as

Therefore, the practically computable posterior distribution simplifies to

In practice, we choose the Matern kernel $$ \mathcal{K}\left(s,t\right)={\varphi }_1\frac{2^{1-\nu }}{\mathrm{\Gamma }\left(\nu \right)}{\left(\sqrt{2\nu }\frac{l}{{\varphi }_2}\right)}^{\nu }{B}_{\nu }\left(\sqrt{2\nu }\frac{l}{{\varphi }_2}\right)$$, where $$ l=|s-t|$$, $$ \mathrm{\Gamma }$$ is the Gamma function, $$ B_{\nu }$$ is the modified Bessel function of the second kind, and the degree of freedom $$ \nu $$ is set to be 2.01 to ensure that the kernel is twice differentiable. $$ \mathcal{K}$$ has two hyperparameters $$ {\varphi }_1$$ and $$ {\varphi }_2$$. Their meaning and specification are discussed in Materials and Methods.

With the posterior distribution specified in Eq. 5, we use Hamiltonian Monte Carlo (HMC) (7) to obtain samples of $$ {\mathit{X}}_{\mathit{I}}$$ and the parameters together. At the completion of HMC sampling, we take the posterior mean of $$ {\mathit{X}}_{\mathit{I}}$$ as the inferred trajectory and the posterior means of the sampled parameters as the parameter estimates. Throughout the MAGI computation, no numerical integration is ever needed.

Review of Related Work

The problem of dynamic system inference has been studied in the literature, which we now briefly review. We first note that a simple approach to constructing the “ideal” likelihood function is according to $$ p\left(\mathit{y}\left(\mathit{t}\right)|\widehat{\mathit{x}}\left(\mathit{t},\mathit{\theta },\mathit{x}\left(0\right)\right),\sigma \right)$$, where $$ \widehat{\mathit{x}}\left(\mathit{t},\mathit{\theta },\mathit{x}\left(0\right)\right)$$ is the numerical solution of the ODE obtained by numerical integration given $$ \mathit{\theta }$$ and the initial conditions. This approach suffers from a high computational burden: Numerical integration is required for every $$ \mathit{\theta }$$ sampled in an optimization or Markov chain Monte Carlo (MCMC) routine (8). Smoothing methods have been useful for eliminating the dependence on numerical ODE solutions, and an innovative penalized likelihood approach (9) uses a B-spline basis for constructing estimated functions to simultaneously satisfy the ODE system and fit the observed data. While in principle, the method in ref. 9 can handle an unobserved system component, substantive manual input is required as we show in Results, which contrasts with the ready-made solution that MAGI provides.

As an alternative to the penalized likelihood approach, GPs are a natural candidate for fulfilling the smoothing role in a Bayesian paradigm due to their flexibility and analytic tractability (10). The use of GPs to approximate the dynamic system and facilitate computation has been previously studied by a number of authors (8, 11121314–15). The basic idea is to specify a joint GP over $$ \mathit{y},\mathit{x},\dot{\mathit{x}}$$ with hyperparameters $$ \varphi $$ and then, provide a factorization of the joint density $$ p\left(\mathit{y},\mathit{x},\dot{\mathit{x}},\mathit{\theta },\varphi ,\sigma \right)$$ that is suitable for inference. The main challenge is to find a coherent way to combine information from two distinct sources: the approximation to the system by the GP governed by hyperparameters $$ \varphi $$ and the actual dynamic system equations governed by parameters $$ \mathit{\theta }$$. In refs. 8 and 11, the factorization proposed is $$ p\left(\mathit{y},\mathit{x},\dot{\mathit{x}},\mathit{\theta },\varphi ,\sigma \right)=p\left(\mathit{y}|\mathit{x},\sigma \right)p\left(\dot{\mathit{x}}|\mathit{x},\mathit{\theta },\varphi \right)p\left(\mathit{x}|\varphi \right)p\left(\varphi \right)p\left(\mathit{\theta }\right)$$, where $$ p\left(\mathit{y}|\mathit{x},\sigma \right)$$ comes from the observation model and $$ p\left(\mathit{x}|\varphi \right)$$ comes from the GP prior as in our approach. However, there are significant conceptual difficulties in specifying $$ p\left(\dot{\mathit{x}}|\mathit{x},\mathit{\theta },\varphi \right)$$: On one hand, the distribution of $$ \dot{\mathit{x}}$$ is completely determined by the GP given $$ \mathit{x}$$, while on the other hand, $$ \dot{\mathit{x}}$$ is completely specified by the ODE system $$ \dot{\mathit{x}}=\mathbf{f}\left(\mathit{x},\mathit{\theta },t\right)$$; these two are incompatible. Previous authors have attempted to circumvent this incompatibility of the GP and ODE system: Refs. 8 and 11 use a product of experts heuristic by letting $$ p\left(\dot{\mathit{x}}|\mathit{x},\mathit{\theta },\varphi \right)\propto p\left(\dot{\mathit{x}}|\mathit{x},\varphi \right)p\left(\dot{\mathit{x}}|\mathit{x},\mathit{\theta }\right)$$, where the two distributions in the product come from the GP and a noisy version of the ODE, respectively. In ref. 15, the authors arrive at the same posterior as refs. 8 and 11 by assuming an alternative graphical model that bypasses the product of experts heuristic; nonetheless, the method requires working with an artificial noisy version of the ODE. In ref. 12, the authors start with a different factorization: $$ p\left(\mathit{y},\mathit{x},\dot{\mathit{x}},\mathit{\theta },\varphi ,\sigma \right)=p\left(\mathit{y}|\dot{\mathit{x}},\varphi ,\sigma \right)p\left(\dot{\mathit{x}}|\mathit{x},\mathit{\theta }\right)p\left(\mathit{x}|\varphi \right)p\left(\varphi \right)p\left(\mathit{\theta }\right)$$, where $$ p\left(\mathit{y}|\dot{\mathit{x}},\varphi \right)$$ and $$ p\left(\mathit{x}|\varphi \right)$$ are given by the GP and $$ p\left(\dot{\mathit{x}}|\mathit{x},\mathit{\theta }\right)$$ is a Dirac delta distribution given by the ODE. However, this factorization is incompatible with the observation model $$ p\left(\mathit{y}|\mathit{x},\sigma \right)$$ as discussed in detail in ref. 16. There is other related work that uses GPs in an ad hoc partial fashion to aid inference. In ref. 13, GP regression is used to obtain the means of $$ \mathit{x}$$ and $$ \dot{\mathit{x}}$$ for embedding within an Approximate Bayesian Computation estimation procedure. In ref. 14, GP smoothing is used during an initial burn-in phase as a proxy for the likelihood, before switching to the ideal likelihood to obtain final MCMC samples. While empirical results from the aforementioned studies are promising, a principled statistical framework for inference that addresses the previously noted conceptual incompatibility between the GP and ODE specifications is lacking. Our work presents one such principled statistical framework through the explicit manifold constraint. MAGI is therefore distinct from recent GP-based approaches (11, 15) or any other Bayesian analogs of ref. 9.

In addition to the conceptual incompatibility, none of the existing methods that do not use numerical integration offer a practical solution for a system with unobserved component(s), which highlights another unique and important contribution of our approach.

Results

We apply MAGI to three systems. We begin with an illustration that demonstrates the effectiveness of MAGI in practical problems with unobserved system component(s). Then, we make comparisons with other current methods on two benchmark systems, which show that our proposed method provides more accurate inference while having much faster run time.

Illustration: Hes1 Model.

The Hes1 model described in the Introduction demonstrates inference on a system with an unobserved component and asynchronous observation times. This section continues the inference of this model. Ref. 1 studied the theoretical oscillation behavior using parameter values $$ a=0.022$$, $$ b=0.3$$, $$ c=0.031$$, $$ d=0.028$$; $$ e=0.5$$, $$ f=20$$, $$ g=0.3$$, which leads to one oscillation cycle approximately every 2 h. Ref. 1 also set the initial condition at the lowest value of $$ P$$ when the system is in oscillation equilibrium (1): $$ P=1.439$$, $$ M=2.037$$, $$ H=17.904$$. The noise level in our simulation is derived from ref. 1 where the SE based on repeated measures is reported to be around 15% of the $$ P$$ (protein) level and $$ M$$ (mRNA) level, so we set the simulation noise to be multiplicative following a log-normal distribution with SD 0.15; throughout this example, we assume the noise level $$ \sigma $$ is known to be 0.15 from repeated measures reported in ref. 1. The $$ H$$ component is never observed. Owing to the multiplicative error on the strictly positive system, we apply our method to the log-transformed ODEs, so that the resulting error distributions are Gaussian. To the best of our knowledge, MAGI is the only one that provides a practical and complete solution for handling unobserved component cases like this example.

We generate 2,000 simulated datasets based on the above setup for the Hes1 system. The left-most panel in Fig. 1 shows one example dataset. For each dataset, we use MAGI to infer the trajectories and estimate the parameters. We use the posterior mean of $$ X_t={\left(P,M,H\right)}_t$$ as the inferred trajectories for the system components, which are generated by MAGI without using any numerical solver. Fig. 1 summarizes the inferred trajectories across the 2,000 simulated datasets, showing the median of the inferred trajectories of $$ X_t$$ together with the 95% interval of the inferred trajectories represented by the 2.5 and 97.5% percentiles. The posterior mean of $$ \mathit{\theta }=\left(a,b,c,d,f,e,g\right)$$ is our estimate of the parameters. Table 1 summarizes the parameter estimates across the 2,000 simulated datasets, by showing their means and SDs. Fig. 1 shows that MAGI recovers the system well, including the completely unobserved $$ H$$ component. Table 1 shows that MAGI also recovers the system parameters well, except for the parameters that only appear in the equation for the unobserved $$ H$$ component, which we will discuss shortly. Together, Fig. 1 and Table 1 demonstrate that MAGI can recover the entire system without any usage of a numerical solver, even in the presence of unobserved component(s).

Table 1.

Parameter inference in the Hes1 partially observed asynchronous system based on 2,000 simulation datasets

$$ \mathit{\theta }$$	Truth	MAGI		Ref. 9
		Estimate	RMSE	Estimate	RMSE
a	0.022	0.021 $$ \pm $$ 0.003	0.003	0.027 $$ \pm $$ 0.026	0.026
b	0.3	0.329 $$ \pm $$ 0.051	0.059	0.302 $$ \pm $$ 0.086	0.086
c	0.031	0.035 $$ \pm $$ 0.006	0.007	0.031 $$ \pm $$ 0.010	0.010
d	0.028	0.029 $$ \pm $$ 0.002	0.003	0.028 $$ \pm $$ 0.003	0.003
e	0.5	0.552 $$ \pm $$ 0.074	0.090	0.498 $$ \pm $$ 0.088	0.088
f	20	13.759 $$ \pm $$ 3.026	6.936	604.9 $$ \pm $$ 5084.8	5,117.0
g	0.3	0.141 $$ \pm $$ 0.026	0.162	1.442 $$ \pm $$ 9.452	9.519

Average parameter estimates based on MAGI and ref. 9 across the 2,000 simulated datasets are reported together with the SD. Parameter RMSEs are reported in the following column. Bold highlights the best method in terms of parameter RMSE for each parameter.

Metrics for assessing the quality of system recovery.

To further assess the quality of the parameter estimates and the system recovery, we consider two metrics. First, as shown in Table 1, we examine the accuracy of the parameter estimates by directly calculating the root mean squared error (RMSE) of the parameter estimates to the true parameter value. We call this measure the parameter RMSE metric. Second, it is possible that a system might be insensitive to some of the parameters; in the extreme case, some parameters may not be fully identifiable given only the observed data and components. In these situations, it is possible that the system trajectories implied by quite distinct parameter values are similar to each other (or even close to the true trajectory). We thus consider an additional trajectory RMSE metric to account for possible parameter insensitivity and measure how well the system components are recovered given the parameter and initial condition estimates. The trajectory RMSE is obtained by treating the numerical ODE solution based on the true parameter value as the ground truth: First, the numerical solver is used to reconstruct the trajectory based on the estimates of the parameter and initial condition (from a given method); then, we calculate the RMSE of this reconstructed trajectory to the true trajectory at the observation time points. We emphasize that the trajectory RMSE metric is only for evaluation purpose to assess (and compare across methods) how well a method recovers the trajectories of the system components and that throughout MAGI, no numerical solver is ever needed.

We summarize the trajectory RMSEs of MAGI in Table 2 for the Hes1 system.

Table 2.

Trajectory RMSEs of the individual components in the Hes1 system, comparing the average trajectory RMSEs of MAGI and ref. 9 over the 2,000 simulated datasets

Method	$$ P$$	$$ M$$	$$ H$$
MAGI	0.97	0.21	2.57
Ref. 9	1.30	0.40	59.47

The best trajectory RMSE for each system component is shown in bold.

We compare MAGI with the benchmark provided by the B spline-based penalization approach of ref. 9. To the best of our knowledge, among all of the existing methods that do not use numerical integration, ref. 9 is the only one with a software package that can be manually adapted to handle an unobserved component. We note, however, that this package itself is not ready made for this problem: It requires substantial manual input as it does not have default or built-in setup of its hyperparameters for the unobserved component. None of the other benchmark methods, including refs. 11 and 15, provide software that is equipped to handle an unobserved component. Table 1 compares our estimates against those given by ref. 9 based on the parameter RMSE, which shows that the parameter RMSEs for MAGI are substantially smaller than ref. 9. Fig. 1 shows that the inferred trajectories from MAGI are very close to the truth. On the contrary, the method in ref. 9 is not able to recover the unobserved component $$ H$$ nor the associated parameters $$ f$$ and $$ g$$; SI Appendix, Fig. S1 has the plots. Table 2 compares the trajectory RMSE of the two methods. It is seen that the trajectory RMSE of MAGI is substantially smaller than that of ref. 9. Further implementation details and comparison are provided in SI Appendix.

Finally, we note that MAGI recovers the unobserved component $$ H$$ almost as well as the observed components of $$ P$$ and $$ M$$, as measured by the trajectory RMSEs. In comparison, for the result of ref. 9 in Table 2, the trajectory RMSE of the unobserved $$ H$$ component is orders of magnitude worse than those of $$ P$$ and $$ M$$. The numerical results thus illustrate the effectiveness of MAGI in borrowing information from the observed components to infer the unobserved component, which is made possible by explicitly conditioning on the ODE structure. The self-regulating parameter $$ g$$ and inhibition rate parameter $$ f$$ for the unobserved component appear to have high inference variation across the simulated datasets despite the small trajectory RMSEs. This suggests that the system itself could be insensitive to $$ f$$ and $$ g$$ when the $$ H$$ component is unobserved.

Comparison with Previous Methods Based on GPs.

To further assess MAGI, we compare with two methods: adaptive gradient matching (AGM) of ref. 11 and fast Gaussian process-based gradient matching (FGPGM) of ref. 15, representing the state of the art of inference methods based on GPs. For fair comparison, we use the same benchmark systems, scripts, and software provided by the authors for performance assessment and run the software using the settings recommended by the authors. The benchmark systems include the FitzHugh–Nagumo (FN) equations (17) and a protein transduction model (18).

FN model.

The FN equations are a classic ion channel model that describes spike potentials. The system consists of $$ X=\left(V,R\right)$$, where $$ V$$ is the variable defining the voltage of the neuron membrane potential and $$ R$$ is the recovery variable from neuron currents, satisfying the ODE

$\mathbf{f}\left(X,\mathit{\theta },t\right)=\left(\begin{array}{c}\hfill c\left(V-\frac{V^3}{3}+R\right)\hfill \\ \hfill -\frac{1}{c}\left(V-a+bR\right)\hfill \end{array}\right),$

where $$ \mathit{\theta }=\left(a,b,c\right)$$ are the associated parameters. As in refs. 11 and 15, the true parameters are set to $$ a=0.2,b=0.2,c=3$$, and we generate the true trajectories for this model using a numerical solver with initial conditions $$ V=-1$$, $$ R=1$$.

To compare MAGI with FGPGM of ref. 15 and AGM of ref. 11, we simulated 100 datasets under the noise setting of $$ {\sigma }_V={\sigma }_R=0.2$$ with 41 observations. The noise level is chosen to be on similar magnitude with that of ref. 15, and the noise level is set to be the same across the two components as the implementation of ref. 11 can only handle equal-variance noise. The number of repetitions (i.e., 100) is set to be the same as ref. 15 due to the high computing time of these alternative methods.

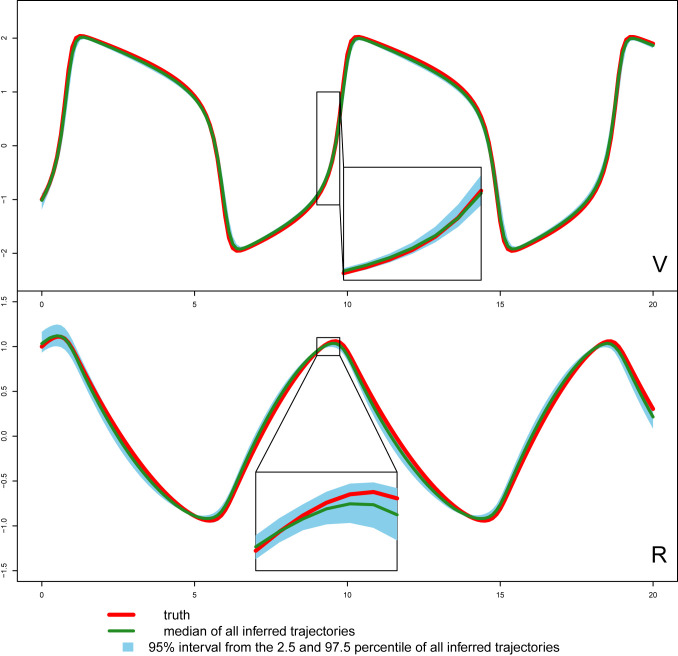
The parameter estimation results from the three methods are summarized in Table 3, where MAGI has the lowest parameter RMSEs among the three. Fig. 2 shows the inferred trajectories obtained by our method: MAGI recovers the system well, and the 95% interval band is so narrow around the truth that we can only see the band clearly after magnification (as shown in Fig. 2, Insets). SI Appendix provides visual comparison of the inferred trajectories of different methods, where MAGI gives the most consistent results across the simulations. Furthermore, to assess how well the methods recover the system components, we calculated the trajectory RMSEs, and the results are summarized in Table 4, where MAGI significantly outperforms the others, reducing the trajectory RMSE over the best alternative method for 60% in $$ V$$ and 25% in $$ R$$. We note that compared with the true parameter value, all three methods show some bias in the parameter estimates, which is partly due to the GP prior as discussed in ref. 15, and MAGI appears to have the smallest bias.

Table 3.

Parameter inference in the FN model based on 100 simulated datasets

$$ \mathit{\theta }$$	MAGI		FGPGM (15)		AGM (11)
	Estimate	RMSE	Estimate	RMSE	Estimate	RMSE
a	0.19 $$ \pm $$ 0.02	0.02	0.22 $$ \pm $$ 0.04	0.05	0.30 $$ \pm $$ 0.03	0.10
b	0.35 $$ \pm $$ 0.09	0.17	0.32 $$ \pm $$ 0.13	0.18	0.36 $$ \pm $$ 0.06	0.17
c	2.89 $$ \pm $$ 0.06	0.13	2.85 $$ \pm $$ 0.15	0.21	2.04 $$ \pm $$ 0.14	0.97

For each method, average parameter estimates are reported together with SD; parameter RMSEs across simulations are also reported. Bold highlights the best method in terms of parameter RMSE for each parameter.

Fig. 2.

Inferred trajectories by MAGI for each component of the FN system over 100 simulated datasets. The Top is the V component and the Bottom is the R component. The blue shaded area represents the 95% interval. Insets magnify the corresponding segments.

Table 4.

Trajectory RMSEs of each component in the FN system, comparing the average trajectory RMSE of the three methods over 100 simulated datasets

Method	$$ V$$	$$ R$$
MAGI	0.103	0.070
FGPGM (15)	0.257	0.094
AGM (11)	1.177	0.662

The best trajectory RMSE for each system component is shown in bold. MAGI reduces the RMSE for 60% in component V and 25% in component R over the best alternative method.

For computing cost, the average run time of MAGI for this system over the repetitions is 3 min, which is 145 times faster than FGPGM (15) and 90 times faster than AGM (11) on the same processor (we follow the authors’ recommendation for running their methods) (SI Appendix has details).

Protein transduction model.

This protein transduction example is based on systems biology where components $$ S$$ and $$ S_d$$ represent a signaling protein and its degraded form, respectively. In the biochemical reaction, $$ S$$ binds to protein $$ R$$ to form the complex $$ S_R$$, which enables the activation of $$ R$$ into $$ R_{pp}$$. $$ X=\left(S,S_d,R,S_R,R_{pp}\right)$$ satisfies the ODE

$\mathbf{f}\left(X,\mathit{\theta },t\right)=\left(\begin{array}{c}\hfill -k_1\cdot S-k_2\cdot S\cdot R+k_3\cdot S_R\hfill \\ \hfill k_1\cdot S\hfill \\ \hfill -k_2\cdot S\cdot R+k_3\cdot S_R+\frac{V\cdot R_{pp}}{K_m+R_{pp}}\hfill \\ \hfill k_2\cdot S\cdot R-k_3\cdot S_R-k_4\cdot S_R\hfill \\ \hfill k_4\cdot S_R-\frac{V\cdot R_{pp}}{K_m+R_{pp}}\hfill \end{array}\right),$

where $$ \mathit{\theta }=\left(k_1,k_2,k_3,k_4,V,K_m\right)$$ are the associated rate parameters.

We follow the same simulation setup as refs. 11 and 15 by taking $$ t=\left\{\mathrm{0,1,2,4,5,7,10,15,20,30,40,50,60,80,100}\right\}$$ as the observation times, $$ X\left(0\right)=\left(\mathrm{1,0,1,0,0}\right)$$ as the initial values, and $$ \mathit{\theta }=\left(0.07,0.6,0.05,0.3,0.017,0.3\right)$$ as the true parameter values. Two scenarios for additive observation noise are considered: $$ \sigma =0.001$$ (low noise) and $$ \sigma =0.01$$ (high noise). Note that the observation times are unequally spaced, with only a sparse number of observations from $$ t=20$$ to $$ t=100$$. Further, inference for this system has been noted to be challenging due to the nonidentifiability of the parameters, in particular $$ K_m$$ and $$ V$$ (15). Therefore, the parameter RMSE is not meaningful for this system, and we focus our comparison on the trajectory RMSE.

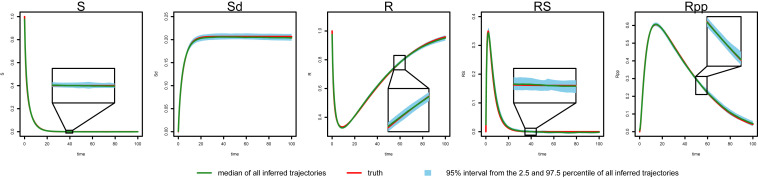
We compare MAGI with FGPGM of ref. 15 and AGM of ref. 11 on 100 simulated datasets for each noise setting (SI Appendix has method and implementation details). We plot the inferred trajectories of MAGI in the high-noise setting in Fig. 3, which closely recover the system. The 95% interval band from MAGI is quite narrow that for most of the inferred components, we need magnifications (as shown in Fig. 3, Insets) to clearly see the 95% band. We then calculated the trajectory RMSEs, and the results are summarized in Table 5 for each system component. In both noise settings, MAGI produces trajectory RMSEs that are uniformly smaller than both FGPGM (15) and AGM (11) for all system components. In the low-noise setting, the advantage of MAGI is especially apparent for components $$ S$$, $$ R$$, $$ S_R$$, and $$ R_{pp}$$, with trajectory RMSEs less than half of the closest comparison method. For the high-noise setting, MAGI reduces trajectory RMSE the most for $$ S_d$$ and $$ R_{pp}$$ ($$ \sim $$50%). AGM (11) struggles with this example at both noise settings. To visually compare the trajectory RMSEs in Table 5, plots of the corresponding reconstructed trajectories by different methods at both noise settings are given in SI Appendix.

Fig. 3.

Inferred trajectories by MAGI for each component of the protein transduction system in the high-noise setting. The red line is the truth, and the green line is the median inferred trajectory over 100 simulated datasets. The blue shaded area represents the 95% interval. Insets magnify the corresponding segment.

Table 5.

Trajectory RMSEs of the individual components in the protein transduction system, by comparing the average RMSEs of the three methods over 100 simulated datasets

Method	$$ S$$	$$ S_d$$	$$ R$$	$$ S_R$$	$$ R_{pp}$$
Low-noise case, $$ \sigma =0.001$$
MAGI	0.0020	0.0013	0.0040	0.0017	0.0036
FGPGM (15)	0.0049	0.0016	0.0156	0.0036	0.0149
AGM (11)	0.0476	0.2881	0.3992	0.0826	0.2807
High-noise case, $$ \sigma =0.01$$
MAGI	0.0122	0.0043	0.0167	0.0135	0.0136
FGPGM (15)	0.0128	0.0089	0.0210	0.0136	0.0309
AGM (11)	0.0671	0.3125	0.4138	0.0980	0.2973

The method achieving the best RMSE for each system component is shown in bold.

The run time of MAGI for this system averaged over the repetitions is 18 min, which is 12 times faster than FGPGM (15) and 18 times faster than AGM (11) on the same processor (we follow the authors’ recommendation for running their methods) (SI Appendix has details).

Discussion

We have presented a methodology for the inference of dynamic systems, using manifold-constrained GPs. A key feature that distinguishes our work from the previous approaches is that it provides a principled statistical framework, firmly grounded on the Bayesian paradigm. Our method also outperformed currently available GP-based approaches in the accuracy of inference on benchmark examples. Furthermore, the computation time for our method is much faster. Our method is robust and able to handle a variety of challenging systems, including unobserved components, asynchronous observations, and parameter nonidentifiability.

A robust software implementation is provided, with user interfaces available for R, MATLAB, and Python, as described in SI Appendix. The user may specify custom ODE systems in any of these languages for inference with our package by following the syntax in the examples that accompany this article. In practice, inference with MAGI using our software can be carried out with relatively few user interventions. The setting of hyperparameters and initial values is fully automatic, although may be overridden by the user.

The main setting that requires some tuning is the number of discretization points in $$ \mathit{I}$$. In our examples, this was determined by gradually increasing the denseness of the points with short sampler runs, until the results become indistinguishable. Note that further increasing the denseness of $$ \mathit{I}$$ has no ill effect, apart from increasing the computational time. To illustrate the effect of the denseness of $$ \mathit{I}$$ on MAGI inference results, an empirical study is included in SI Appendix, Varying Number of Discretization, where we examined the results of the FN model with the discretization set $$ \mathit{I}$$ taken to be 41, 81, 161, and 321 equally spaced points. The results confirm that our proposal of gradually increasing the denseness of $$ \mathit{I}$$ works well. The inference results improve as we increase $$ \mathit{I}$$ from 41 to 161 points, and at 161 points, the results are stabilized. If we further increase the discretization to 321 points, that doubles the compute time with only a slight gain in accuracy compared with 161 points in terms of trajectory RMSEs. This empirical study also indicates that as $$ W_{\mathit{I}}$$ becomes an increasingly dense approximation of $$ W$$, an inference limit would be expected. A theoretical study is a natural future direction of investigation.

We also investigated the stability of MAGI when the observation time points are farther apart. This empirical study, based on the FN model with 21 observations, is included in SI Appendix, FN Model with Fewer Observations. The inferred trajectories from the 21 observations are still close to the truth, while the interval bands become wider, which is expected as we have less information in this case. We also found that the denseness of the discretization needs to be increased (to 321 time points in this case) to compensate for the sparser 21 observations.*

An inherent feature of the GP approximation is the tendency to favor smoother curves. This limitation has been previously acknowledged (11, 15). As a consequence, two potential forms of bias can exist. First, estimates derived from the posterior distributions of the parameters may have some statistical bias. Second, the trajectories reconstructed by a numerical solver based on the estimated parameters may differ slightly from the inferred trajectories. MAGI, which is built on a GP framework, does not entirely eliminate these forms of bias. However, as seen in the benchmark systems, the magnitude of our bias in both respects is significantly smaller than the current state of the art in refs. 11 and 15.

We considered the inference of dynamic systems specified by ODEs in this article. Such deterministic ODE models are often adequate to describe dynamics at the aggregate or population level (19). However, when the goal is to describe the behavior of individuals [e.g., individual molecules (20, 21)], models such as stochastic differential equations (SDEs) and continuous-time Markov processes, which explicitly incorporate intrinsic (stochastic) noise, often become the model of choice. Extending our method to the inference of SDEs and continuous-time Markov models is a future direction we plan to investigate. Finally, recent developments in deep learning have shown connections between deep neural networks and GPs (22, 23). It could thus also be interesting to explore the application of neural networks to model the ODE system outputs $$ \mathit{x}\left(t\right)$$ in conjunction with GPs.

Materials and Methods

For notational simplicity, we drop the dimension index $$ d$$ in this section when the meaning is clear.