Evidence of ideal excitonic insulator in bulk MoS2 under pressure

Evidence of ideal excitonic insulator in bulk MoS<sub>2</sub> under pressure

Evidence of ideal excitonic insulator in bulk MoS₂ under pressure

S. Samaneh Ataei, Daniele Varsano, Elisa Molinari, Massimo Rontani

Edited by Lu Jeu Sham, University of California, San Diego, La Jolla, CA, and approved February 4, 2021 (received for review May 20, 2020)

Author contributions: D.V., E.M., and M.R. designed research; S.S.A., D.V., and M.R. performed research; S.S.A., D.V., and M.R. analyzed data; and S.S.A. and M.R. wrote the paper.

¹S.S.A. and D.V. contributed equally to this work.

https://doi.org/10.1073/pnas.2010110118, Volume: 118, Issue: 13, Pages: 1-11

Article Type: Research Article Article History

Publisher: National Academy of Sciences

- Facebook
- Twitter
- Linkedin
- Whatsapp
Altmetric

Table of Contents

Results
Discussion
Conclusion
Materials and Methods
Supplementary Material
Data Availability

Abstract

We claim that MoS2

under pressure becomes the long-sought “excitonic insulator” (EI). This is a permanent condensate of excitons, electron–hole pairs bound by Coulomb interaction, which form in the absence of optical excitation. A surge of experimental claims has recently addressed layered materials, because of reduced Coulomb screening. However, the transition to the putative EI is ubiquitously accompanied by the softening of a phonon inducing a structural change; therefore it remains unclear whether the observed phase is excitonic or instead stabilized by electron–phonon interaction. Our calculations show that MoS2

for a range of applied pressure is unstable against the generation of excitons but stable against lattice distortion: We predict that the EI is an antiferroelectric, electronic density wave.

Spontaneous condensation of excitons is a long-sought phenomenon analogous to the condensation of Cooper pairs in a superconductor. It is expected to occur in a semiconductor at thermodynamic equilibrium if the binding energy of the excitons—electron (e

) and hole (h

) pairs interacting by Coulomb force—overcomes the band gap, giving rise to a new phase: the “excitonic insulator” (EI). Transition metal dichalcogenides are excellent candidates for the EI realization because of reduced Coulomb screening, and indeed a structural phase transition was observed in few-layer systems. However, previous work could not disentangle to which extent the origin of the transition was in the formation of bound excitons or in the softening of a phonon. Here we focus on bulk MoS2

and demonstrate theoretically that at high pressure it is prone to the condensation of genuine excitons of finite momentum, whereas the phonon dispersion remains regular. Starting from first-principles many-body perturbation theory, we also predict that the self-consistent electronic charge density of the EI sustains an out-of-plane permanent electric dipole moment with an antiferroelectric texture in the layer plane: At the onset of the EI phase, those optical phonons that share the exciton momentum provide a unique Raman fingerprint for the EI formation. Finally, we identify such fingerprint in a Raman feature that was previously observed experimentally, thus providing direct spectroscopic confirmation of an ideal excitonic insulator phase in bulk MoS2

above 30 GPa.

Keywords

Two-dimensional materials, first-principles many-body perturbation theory, excitonic insulator, ferroelectricity, Bose–Einstein condensation

License: CC BY

Ataei,Varsano,Molinari,and Rontani: Evidence of ideal excitonic insulator in bulk MoS2 under pressure

The long-sought excitonic insulator (EI) is a permanent Bose–Einstein condensate of excitons in the absence of optical excitation, hosted in a narrow-gap semiconductor or a semimetal (1 2 3–4). As the exciton condensate shares similarities with the superconductor ground state (5), it may exhibit macroscopic quantum coherence and exotic low-energy excitations (6 7 8 9 10 11–12). These intriguing features are linked to the arbitrariness of the phase of the condensate wave function, $φ$ (defined in Eq. 2 below): Whereas in the superconductor this phase degeneracy is protected by the conservation of electronic charge, in the EI it is contingent on the preservation of excitons (7, 11) and hence lifted by those terms in the Hamiltonian that annihilate or create $e$ - $h$ pairs. This is the case of $e$ -phonon (13) and spin–orbit (14) interactions, which pin $φ$ while hybridizing conduction and valence bands (remarkably, the combination of spin–orbit coupling and other factors may lead to a topological insulator whose character is inherited by the excitonic state) (14). Other mechanisms that act as sources/sinks for excitons include interband hybridization and Coulomb interaction terms allowed by symmetry (11), disorder (15), and environmental fluctuations of the electrostatic potential (8). So far, the most accomplished EIs were realized in bilayer heterostructures in the presence of a magnetic field, requiring both low temperature and complex engineering to maximize the impact of $e$ - $h$ correlations as well as the degeneracy of $φ$ (10, 16). A related concept aims to achieve the temporary condensation of indirect excitons, made of spatially separated $e$ and $h$ , through the optical pumping of artificial bilayers designed to maximize the exciton lifetime (17 18–19).

Recently, layered materials (20 21 22–23) renewed the promise of the EI because of the enhanced Coulomb interactions, and hence exciton binding, due to their reduced dimensionality. In particular, the indirect character of excitons—in reciprocal (20, 21) and real (22, 23) space for ${T i S e}_{2}$ and ${T a}_{2} {N i S e}_{5}$ , respectively—led to inherently weaker screening and hence stronger $e$ - $h$ attraction, thus potentially stabilizing the EI phase. In those systems, the putative transition to the EI was accompanied by a lattice instability (24 25 26 27–28) when lowering the temperature—a singularity in the phonon density of states at vanishing energy—that in turn created $e$ - $h$ pairs through $e$ -phonon interaction. In contrast, the transition to the ideal EI is purely electronic, with only small adjustments of the lattice (4, 29).

Here, we follow an early suggestion by Hromadová et al. (30) and focus on bulk ${M o S}_{2}$ under hydrostatic pressure (30 31 32–33). We use many-body perturbation theory from first principles (34, 35) to demonstrate that ${M o S}_{2}$ is unstable against exciton condensation but stable against lattice distortion. Building a self-consistent effective-mass model on top of ab initio calculations, we show that the true ground state is an ideal, antiferroelectric EI with a distinctive Raman fingerprint that has already been observed (36).

In bulk ${M o S}_{2}$ , the pressure ( $P$ ) closes the indirect gap, $G$ , between the top of the filled valence band, located at the center of the Brillouin zone ( $Γ$ point), and the bottom of the six-degenerate valleys of the empty conduction band—placed at $Λ$ points (approximately midway between $Γ$ and K; see Fig. 1C for $P =$ 34 GPa). The energy landscape along one of the $Γ Λ$ cuts (sketched in Fig. 1A) favors the Coulomb binding of an $e$ , located at $Λ$ , with an $h$ , placed at $Γ$ , creating an exciton of finite momentum $|$ q $| = Γ Λ$ and binding energy $E_{b}$ . Whereas ordinarily $E_{b} < G$ , it may occur that $E_{b} > G$ above a critical pressure, a condition that makes the semiconductor unstable against the condensation of excitons. This is actually the case, as we show below from first principles.

Fig. 1.

Indirect-gap ${M o S}_{2}$ as a candidate excitonic insulator. (A) Sketch of the excitonic insulator instability, adapted from Walter Kohn’s original proposal (4). An exciton binds an electron at the conduction band bottom, located at $Λ$ in k space, with a hole at the valence band top at $Γ$ . If the exciton binding energy, $E_{b}$ , is larger than the indirect gap, $G$ , then the system is unstable against the spontaneous generation of excitons. The reconstructed many-body ground state—a condensate of excitons at thermodynamic equilibrium—is the excitonic insulator. (B) Model of the 2 $H_{c}$ crystal structure from different views. The violet (yellow) color labels Mo (S) atoms. The dashed frame appearing in side and top views is the unitary cell of the layered structure, with $a$ and $c$ being the in- and out-of-plane lattice constants, respectively. (C) Lowest conduction and topmost valence energy band as a function of wave vector in the $k_{z} = 0$ plane, as obtained from first-principles many-body perturbation theory (GW) at a pressure of 34 GPa.

So far, ultrahigh pressure has been used as a handle to make MoS₂ superconducting (33) (at $P \sim$ 90 GPa), although the pairing mechanism remains unclear (37 38–39). The putative EI must be searched at lower pressure ( $P \sim$ 25 GPa), close to the semiconductor–semimetal transition that was observed by several groups (31, 32, 40 41–42). Near this boundary, theory (30, 43)—including our own calculations (SI Appendix, Fig. S1)—predicts an isostructural transition from the 2 $H_{c}$ (Fig. 1B) to the 2 $H_{a}$ (SI Appendix, Fig. S2) phase, which does not affect the crystal space group $D_{6 h}^{4}$ , as the two structures transform into each other through the sliding of the layers in the unit cell (the layer unit is made of one Mo and two S atoms, represented respectively by violet and yellow balls in the sketch of Fig. 1B). Raman and X-ray spectroscopic observations (31, 33, 36, 41, 44) suggest that 2 $H_{c}$ and 2 $H_{a}$ phases coexist in diamond-anvil cells, in a range that varies between 25 and 50 GPa in powders but has narrower extension ( $\sim$ 4 GPa) in single crystals. Importantly, we find that both 2 $H_{c}$ and 2 $H_{a}$ polytypes experience a similar excitonic instability—unrelated to the structural transition, as the electronic bands of the two phases are basically identical close to the Fermi energy. Below, we discuss the 2 $H_{c}$ stacking and leave the analysis of 2 $H_{a}$ to SI Appendix, Figs. S3 and S4.

Results

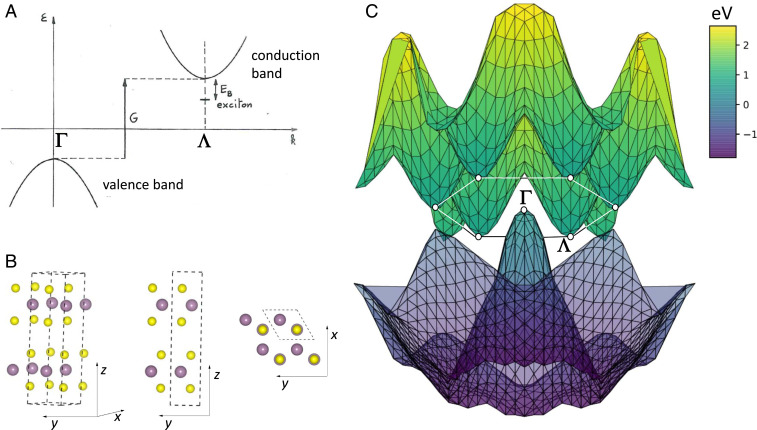
The indirect gap of 2 $H_{c}$ – ${M o S}_{2}$ is sensitive to pressure, as its value drops from 1.31 eV at $P = 0$ (Fig. 2A) to only 9 meV at $P = 34$ GPa (Fig. 2C), close to the semimetal limit. With respect to the accurate band structure calculated within the GW approximation (circles in Fig. 2 A–C) (Materials and Methods), density functional theory (triangles) underestimates the gap of about 0.4 eV at $P = 0$ . However, as pressure reduces the out-of-plane lattice parameter $c$ (SI Appendix, Fig. S1), forcing sulfur orbitals belonging to adjacent layers to overlap (45), virtual $e$ - $h$ pairs start tunneling among layers, screening effectively Coulomb interaction at long wavelength. This reduces the GW energy correction to the density functional theory (DFT) bandgap, as evident in Fig. 2C. Consistently, the conduction band increases its dispersion along the $k_{z}$ direction (Fig. 2F), as well as the other axes of the effective mass tensor (Fig. 2 D and E; dots and lines are GW data and effective-mass fits, respectively). Overall, the semiconductor becomes progressively more isotropic as it turns into a semimetal, losing its two-dimensional character.

Fig. 2.

Closing the gap by applying pressure. (A–C) Band structure along the $Γ - Λ -$ K cut of the Brillouin zone at pressure $P =$ 0 (A), 25 (B), and 34 GPa (C). Band energies obtained from first principles including the quasiparticle GW corrections beyond DFT (circles) are compared to bare DFT data (triangles, PBE functional). Lines are guides to the eye. (D–F) Band dispersion of conduction and valence bands close to $Λ$ and $Γ$ points, respectively, for $P =$ 0 GPa (black color), 25 GPa (red), and 34 GPa (blue). In E and F the conduction band has been rigidly translated by the wave vector $- \vec{Γ Λ}$ . GW predictions (dots) are shown together with effective-mass fits (curves). The directions of the cuts (shown as red arrows in the Brillouin zone) are the principal axes of the effective-mass tensor, two being in the $k_{z} = 0$ plane (D and E) and one being parallel to the $k_{z}$ axis (F).

Exciton Binding and Instability.

The exciton candidate for the instability has a finite center-of-mass momentum q; i.e., it travels in space. We compute its excitation energy—the difference between the GW bandgap and the binding energy—by solving the Bethe–Salpeter equation from first principles (Materials and Methods). The dispersion exhibits a dip for $q = Λ$ , whose energy is first positive at $P = 0$ (1.26 eV, black dots in Fig. 3A) but then quickly lowers with $P$ , eventually changing sign close to the semimetal threshold ( $- 27$ meV at $P = 34$ GPa, blue diamonds). This negative value signals that excitons spontaneously form, which leads to a reconstructed many-body phase of lower energy.

Fig. 3.

Excitonic instability. (A) Excitation energy of the lowest exciton vs. center-of-mass momentum q along the $Γ$ K direction. Data are obtained from first principles for $P =$ 0 (dots), 25 (squares), and 34 GPa (diamonds). Note that the K point position expressed in units of ${B o h r}^{- 1}$ shifts with $P$ . Solid lines are guides to the eye. At $P =$ 34 GPa the excitation energy is negative for $q = Γ Λ$ , which points to the instability against exciton condensation (the dashed line highlights the energy zero). (B) Binding energy of the exciton having momentum $q = Γ Λ$ (black circles, left vertical axis) and macroscopic static dielectric constant (red circles, right axis) vs. $P$ . The latter is obtained through the inverse dielectric matrix, as $1 / {[ϵ^{- 1} (q = 0)]}_{G = G^{'} = 0}$ (G is the reciprocal lattice vector). (C and D) Wave function square modulus of the lowest exciton with $q = Γ Λ$ at $P = 0$ . The plot shows the conditional probability to locate the bound electron (green contour map), provided the hole position is fixed (black dot), either in (C) or out (D) of plane. The violet (yellow) color in the stick-and-ball skeleton points to Mo (S) atoms.

The softening of the exciton shown in Fig. 3A validates from first principles the seminal prediction by des Cloizeaux (2): The binding energy remains finite even if the gap vanishes, as explicitly shown in Fig. 3B (black dots). The reason is that conduction and valence band profiles are almost unaffected by $P$ (Fig. 2), as the band edges are displaced in k space, which prevents the macroscopic dielectric constant from diverging (red dots in Fig. 3B). Were the closing gap direct, metal-like screening would dissociate the exciton.

The square modulus of the exciton wave function is illustrated in Fig. 3 C and D, as the conditional probability density to locate the bound electron (green contour map), provided the hole is fixed (black dot). Note that the center-of-mass motion does not appear in this frame. The probability extends tens of angstroms—the feature of Wannier excitons familiar from bulk semiconductors—both in and out of plane, as apparent in Fig. 3 C and D, respectively (the Bohr radius is 50 Å at 34 GPa, as shown in SI Appendix, Fig. S5). The exciton becomes lighter and more isotropic with pressure, i.e., more delocalized in real space (here shown at $P = 0$ ).

Two-Band Model.

The major source of numerical error is the finite sampling of the Brillouin zone (14), since the exciton is significantly localized in k space while the computational load prevents us from refining the mesh (Materials and Methods). However, the specific features of the exciton provide us with a workaround, since 1) the wave function is spanned essentially by those $e$ and $h$ states that are close to the edges of the lowest conduction and highest valence band, respectively (Fig. 1A) and 2) the spin degree of freedom is irrelevant, the exciton energy being fourfold degenerate within numerical accuracy (spin–orbit coupling is fully included in the calculation). Therefore, we may afford ultradense k-space sampling by replacing the first-principles Bethe–Salpeter equation with its spinless two-band counterpart within the effective mass approximation (35), the mass tensor being extracted from Fig. 2 D–F and the dielectric constant from Fig. 3B (Materials and Methods and SI Appendix, Fig. S5). The resulting excitation energy, at the semimetal threshold, is $\approx - 8$ meV.

The Excitonic Insulator Phase.

Close to the semiconductor–semimetal boundary, the ground state undergoes a reconstruction from the “normal” phase, $|Φ_{0}⟩$ , which is either insulating or semimetallic, to the excitonic insulator, $|Ψ_{EI}⟩$ . In the following, we highlight the essential features of $|Ψ_{EI}⟩$ within the simpler two-band model (as a mnemonic, we adopt the apex “0” to identify quantities of interest defined within this model). Then, we take into account the EI multivalley nature by adapting the theory first proposed for the candidate material ${T i S e}_{2}$ (46).

Within the two-band model (3), $|Ψ_{EI}^{0}⟩$ is formally analogous to the superconductor wave function (5),

|Ψ_{EI}^{0}⟩ = \prod_{k} [u_{k}^{0} + v_{k}^{0} e^{- i φ} {\hat{b}}_{k}^{+} â_{k}] |Φ_{0}⟩,

[1]

provided the Cooper pairs of the metal are replaced with the

e

h

pair excitations of the normal state,

{\hat{b}}_{k}^{+} â_{k} |Φ_{0}⟩

. Here

{\hat{b}}_{k}^{+}

creates an electron with momentum k

+ \vec{Γ Λ}

and energy

ε_{b} (k)

in the conduction band,

â_{k}

annihilates an electron with momentum k and energy

ε_{a} (k)

in the valence band,

u_{k}^{0}

and

v_{k}^{0}

are positive coherence factors [

{(u_{k}^{0})}^{2} + {(v_{k}^{0})}^{2} = 1

], and

φ

is the phase of the condensate wave function,

ζ_{k}^{0} = u_{k}^{0} v_{k}^{0} e^{i φ} = Δ_{k}^{0} / 2 E_{k}

, with

Δ_{k}^{0}

being the excitonic gap function and

E_{k} = {{[ε_{b} (k) - ε_{a} (k)]}^{2} / 4 + | Δ_{k}^{0} |^{2}}^{1 / 2}

. The value of

φ

is—ideally—arbitrary and solely fixed by the spontaneous breaking of the conservation law for

e

h

pairs, as

⟨Ψ_{EI}^{0}| {\hat{b}}_{k}^{+} â_{k} |Ψ_{EI}^{0}⟩ = |ζ_{k}^{0}| e^{i φ} .

[2]

The EI band structure is obtained by solving the pseudo-Bethe–Salpeter equation for

ζ_{k}^{0}

self-consistently,

2 E_{k} ζ_{k}^{0} - \sum_{k^{'}} W (k - k^{'}) ζ_{k^{'}}^{0} = 0,

[3]

where

W (q)

is the screened Coulomb interaction and the minimum value of

2 E_{k}

is the bandgap (Materials and Methods). Reassuringly, turns into the Bethe–Salpeter equation for the zero-energy exciton at the onset of the EI phase (

Δ_{k}^{0} \to 0 +

). As a consequence of the condensation energy gain, the EI conduction and valence bands (circles in Fig. 4A) are flattened and distorted with respect to those of the pristine semiconductor (dashed curves), the gap widening by

\approx 15

meV at

P = 34

GPa.

Fig. 4.

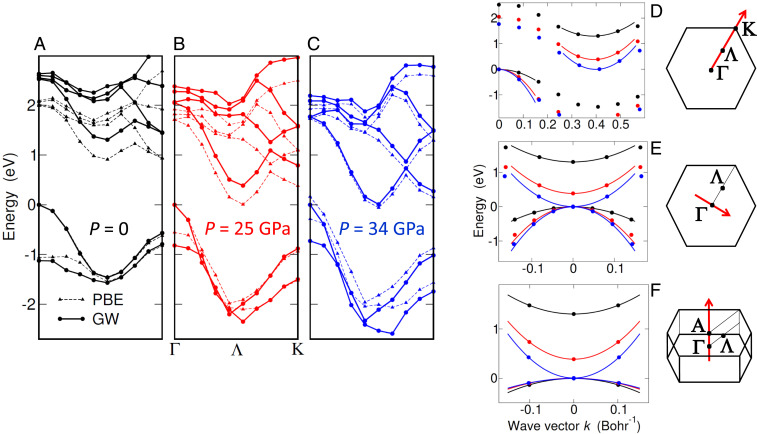
Antiferroelectric excitonic insulator. (A) Band structure of the excitonic (solid curves) and pristine (dashed curves) insulator along one of the six equivalent $Γ - Λ$ directions in the $k_{z} = 0$ plane of the Brillouin zone at $P =$ 34 GPa. The original conduction bands are folded from $Λ$ valleys to $Γ$ and renormalized together with the valence band. The new band structure at $Γ$ is replicated at $Λ$ , since both $Γ$ and $Λ$ points belong to the EI reciprocal lattice. Apart from spin degeneracy, EI renormalized bands exhibit an additional orbital degeneracy reminiscent of the pristine multivalley structure: Bands (solid curves) from top to bottom are respectively one-, three-, two-, and onefold degenerate, respectively. The twofold degenerate band, which overlaps with the pristine conduction band (dashed curve), is actually split due to the tiny anisotropy of $Δ_{k}$ in the $k_{x}$ , $k_{y}$ plane (splitting hardly visible in the plot). Circles point to EI conduction and valence bands obtained within the two-band model. (B) Antiferroelectric structure. A permanent out-of-plane electric dipole, $P_{z} (x, y)$ , spontaneously develops and exhibits an in-plane modulation that breaks inversion symmetry. This dipole, which averages to zero over the unitary cell of the superstructure (solid frame), is perpendicular to the plane and depicted as a red arrow of varying sign and modulus. The superstructure cell contains 72 atoms against 6 of the original cell (dashed frame) (here $Γ Λ \approx 2 π / (3 a)$ ). Violet and blue dots are Mo atoms, respectively, in the top and bottom layer (S atoms are not shown). (C) Overlap charge density of the periodic part of pristine conduction and valence band Bloch states, respectively, at $Λ$ and $Γ$ , shown in the 2 $H_{c}$ cell. The red (blue) color points to a surplus (deficit) of charge. The depicted charge displacement, which is associated with the polarization of condensed excitons, is the origin of the permanent dipole $P_{z}$ shown in B. (D) Maximum local value of $P_{z}$ vs. $P$ .

Multivalley Effects.

As $e$ - $h$ pairs may be formed by exciting an electron from the valence band to any one of the six conduction band valleys, $Λ_{i}$ , the condensate wave function is multicomponent (46), $⟨Ψ_{EI}| {\hat{b}}_{i k}^{+} â_{k} |Ψ_{EI}⟩ = ζ_{i k}$ , with ${\hat{b}}_{i k}^{+}$ creating an electron with momentum k $+ {\vec{Γ Λ}}_{i}$ and energy $ε_{i b} (k)$ in the $i$ th valley ( $i = 1, \dots, 6$ ). In principle, one must solve up to six coupled equations for $ζ_{i k}$ to account for the distortion of the condensate in k space, due to intervalley coupling. Nevertheless, we note that $Δ_{k}^{0}$ has hardly any angular dependence in the $k_{x}$ , $k_{y}$ plane (the maximum amplitude of the azimuthal modulation is smaller than 0.07 meV) (SI Appendix, Fig. S6), whereas $ε_{i b} (k)$ depends on the angle between ${\vec{Γ Λ}}_{i}$ and ( $k_{x}, k_{y}$ ) due to mass anisotropy. As Coulomb interaction protects the cylindrical symmetry of $ζ_{i k}$ , and since the bare-band anisotropy has negligible effect at valley bottom $k \approx 0$ (where the value of $ζ_{i k}$ is largest), we neglect the azimuthal dependence of $ζ_{i k}$ and obtain (Materials and Methods)

ζ_{i k} = ⟨Ψ_{EI}| {\hat{b}}_{i k}^{+} â_{k} |Ψ_{EI}⟩ = \frac{1}{\sqrt{6}} u_{k}^{0} v_{k}^{0} e^{i φ_{i}}, i = 1, \dots, 6 .

[4]

Here only the magnitude of

ζ_{i k}

is fixed (from the self-consistent solution of ), whereas the six phases

φ_{i}

remain undetermined. This is sufficient to compute the band structure of the EI (Fig. 4A), as the ground-state energy is independent from

φ_{i}

(Materials and Methods).

There are now one valence and six conduction bands (solid thin lines in Fig. 4A), in place of the two bands (circles) of the superconductor-like model. Some of the conduction bands are degenerate, the degeneracy being respectively one, three, two, and one, from the topmost conduction to the valence band. Importantly, the band structure at $Γ$ is replicated at $Λ$ , as the electronic charge exhibits a supermodulation in real space that we discuss below, the corresponding unit cell (solid frame in Fig. 4B) being larger than the cell of the crystal lattice (dashed frame). As a consequence, bands are folded into the smaller Brillouin zone (SI Appendix, Fig. S6), changing the gap from indirect to direct. Only the valence and topmost conduction bands repel each other, in agreement with the two-band model (circles), whereas the remaining bands, which are unaffected by the presence of the exciton condensate, replicate at $Γ$ the bare valleys and hence reduce the direct gap. Since the location of the valence band top is slightly displaced from $Γ$ along the $k_{z}$ axis (SI Appendix, Fig. S7), by $\sim$ 0.02 ${B o h r}^{- 1}$ , the actual EI gap is indirect and around $\sim$ 5 meV, smaller than the direct gap at $Γ$ . Note that in Fig. 4A the twofold degenerate band, which almost overlaps with the bare conduction band (dashed curve), splits due to the tiny anisotropy of $Δ_{k}$ in the $k_{x}$ , $k_{y}$ plane (the splitting is hardly visible in the plot).

Antiferroelectric Excitonic Insulator.

The EI ground state is invariant under time reversal, and hence the phases of the condensate components that live in two antipodal valleys must have opposite sign (modulus a multiple integer of $2 π$ ); i.e., $φ_{1} = - φ_{4}$ , $φ_{3} = - φ_{6}$ , and $φ_{5} = - φ_{2}$ (SI Appendix, Fig. S6 and Materials and Methods). This constraint leads to the formation of a purely electronic, self-sustained charge density wave, $Δ ϱ (r)$ , which breaks the inversion symmetry of the pristine crystal (the proof is given in Materials and Methods). The total wave $Δ ϱ$ is the coherent superposition of three contributions, $Δ ϱ = Δ ϱ_{1,4} + Δ ϱ_{3,6} + Δ ϱ_{5,2}$ , each one originating from a couple of antipodal valleys. For example,

\begin{matrix} Δ ϱ_{1,4} (r) & = & \frac{8}{\sqrt{6}} [\sum_{k} u_{k}^{0} v_{k}^{0}] \times \\ Re \{ψ_{Γ} (r) ψ_{Λ_{1}}^{*} (r) \exp [- i ({\vec{Γ Λ}}_{1} \cdot r - φ_{1})]\} \end{matrix}

[5]

exhibits the new periodicity

2 π / | {\vec{Γ Λ}}_{1} |

given by the momentum of those excitons that condense in valleys 1 and 4, and similarly

Δ ϱ_{3,6}

and

Δ ϱ_{5,2}

display an analogous modulation along directions

{\vec{Γ Λ}}_{3}

and

{\vec{Γ Λ}}_{5}

with phase shifts

φ_{3}

and

φ_{5}

, respectively. Here

ψ_{Γ}

and

ψ_{Λ_{1}}

are the periodic envelopes of Bloch states respectively at

Γ

and

Λ_{1}

ψ_{Λ_{4}} = ψ_{Λ_{1}}^{*}

, and the spin has been factored out, since the lattice space group contains a center of inversion and a unique

z

axis (). It is clear that the total amount of charge displaced from the pristine background, as well as the amplitude of the charge modulation, is driven by the condensate through

\sum_{k} u_{k}^{0} v_{k}^{0}

Importantly, the arbitrariness of the phases $φ_{1}$ , $φ_{3}$ , and $φ_{5}$ points to a huge, continuous degeneracy of the ground state. Since the effect of any given two arbitrary phases is merely to rigidly shift the charge pattern $Δ ϱ$ with respect to the frame origin (Materials and Methods), in the following we take $φ_{1} = φ_{3} = φ_{5} = 0$ . The resulting density wave is slightly distorted in the generic case, in which all three phases take arbitrary values (discussion below).

Fig. 4C shows the overlap charge density of the envelopes obtained from first principles, $\sum_{σ} ψ_{Γ σ}^{*} (r) ψ_{Λ_{1} σ} (r) + c.c.$ , which is proportional to $Δ ϱ_{1,4}$ in the unit cell at the origin (we have added the subscript $σ$ to $ψ$ since the numerical envelopes are generically spinors in the presence of spin–orbit coupling). The density wave shows an asymmetric pattern—transferring charge mainly between the two Mo atoms, which breaks the inversion symmetry with respect to the origin of the cell (the red [blue] contour map points to a surplus [deficit] of charge). This charge transfer sets a local electric dipole with an in-plane texture, $P_{1,4} (x, y)$ , as $Δ ϱ_{1,4}$ is modulated by $\exp [i ({\vec{Γ Λ}}_{1} \cdot r)]$ . This dipole may be regarded as the polarization of the excitons coherently built in the condensate (8). Since the contributions to the dipole due to the remaining valleys, $P_{3,6}$ and $P_{5,2}$ , are obtained by rotating $P_{1,4}$ by respectively $2 π / 3$ and $- 2 π / 3$ along the $z$ axis, the total dipole $P = P_{1,4} + P_{3,6} + P_{5,2}$ is parallel to the $z$ axis. We evaluate this parallel component, $P_{z}$ , through direct integration over the unit cell (Fig. 4D and Materials and Methods).

The overall charge pattern, $P_{z} (x, y)$ , exhibits an antiferroelectric texture that breaks inversion symmetry. This is shown in Fig. 4B, where local dipoles, which point out of the plane, are depicted as red arrows having length proportional to $| P_{z} |$ . The electric dipole averages to zero over the unitary cell of the superstructure (solid frame), which contains 72 atoms (with $Γ Λ \approx 2 π / (3 a)$ ) against 6 of the original cell (dashed frame). The reconstructed Brillouin zone, which is again hexagonal in the plane but rotated by $π / 6$ (SI Appendix, Fig. S6D), is spanned by any two independent vectors chosen among the ${\vec{Γ Λ}}_{i}$ s. In the generic, degenerate case that $φ_{1}$ , $φ_{3}$ , and $φ_{5}$ take arbitrary values, we expect a reduction of the maximum local value of $| P_{z} |$ up to $2 / 3$ , together with a variable tilt of the dipole in the plane.

Semiconductor–Semimetal Cross-Over.

The formation of a Fermi surface, made of six $e$ pockets in the $Λ$ valleys and one $h$ pocket at $Γ$ , signals the transition from the semiconductor (Fig. 5B) to the semimetal (Fig. 5D) occurring in the absence of excitonic effects. Fig. 5 B and D shows one of the conduction valleys, displaced by $- \vec{Γ Λ}$ in k space, and the valence band, the filled states being shadowed by gray color. As the free carriers populating the Fermi pockets effectively screen the $e$ - $h$ attraction, we replace the long-range Coulomb force $W$ in Eq. 3 with the vertex interaction proposed by Kozlov and Maksimov (48) to establish self-consistently the range of the force; besides, we extrapolate $P$ -dependent masses from first principles (Materials and Methods).

Fig. 5.

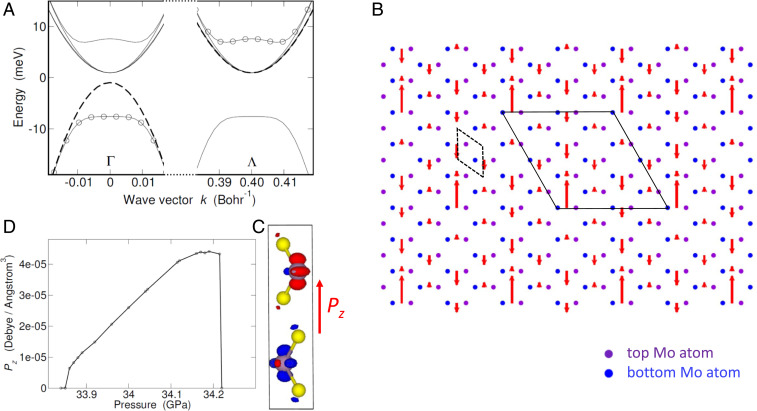
Excitonic insulator phase diagram. (A) Phase diagram in the $P$ – $T$ space. Lines are guides to the eye. The shadowed area highlighted in cyan (green) color is the excitonic gapped (gapless) phase. The vertical dashed line points to the semiconductor–semimetal boundary in the absence of excitonic effects. (B–E) Bare energy bands and wave function of the exciton driving the instability in the $e$ - $h$ center-of-mass frame, evaluated in reciprocal space along the $Γ Λ$ direction. The $e$ - $h$ pair of wave vector $q$ is made of a hole with momentum $- q$ and an electron with momentum $q + Γ Λ$ (in B and D the bare conduction band has been displaced by the vector $- \vec{Γ Λ}$ and the shadowed region highlights occupied states). Going from $P = 34$ GPa (B and C) to $P = 34.12$ GPa (D and E), a Fermi surface forms as conduction and valence band overlap in energy. Consequently, plasmonic features appear in the exciton wave function, the spectral weight accumulating close to the Fermi surface (E). In D the Fermi energy is negative as a consequence of the sixfold valley degeneracy at $Λ$ .

The resulting EI phase extends over a narrow interval of $\approx 0.35$ GPa, reaching a maximum critical temperature of $T \approx 60$ K at $P \approx 34.05$ GPa, which is the semiconductor–semimetal boundary in the normal state (vertical dashed line in Fig. 5A). Importantly, the downward shift of the valence band shown in Fig. 4A opens/widens the gap over a pressure range that extends to values that would lead to a semimetal for $|ζ_{i k}| = 0$ . In the $P - T$ diagram of Fig. 5A, the gapped excitonic phase, highlighted as a shadowed cyan area, is the overwhelming part of the larger region that sustains a finite condensate of excitons, $|ζ_{i k}| > 0$ . The remaining excitonic region—the thin green slice located between $P \sim$ 34.19 and 43.22 GPa—is gapless (SI Appendix, Fig. S7) and ends on the semimetal frontier where $|ζ_{i k}| = 0$ . Here the critical pressure is equivalent to an amount of free carriers (the density per species is $1.1 \cdot 1 0^{- 7} {B o h r}^{- 3}$ ) comparable to the maximum number of excitons in the condensate ( $2.2 \cdot 1 0^{- 7} {B o h r}^{- 3}$ ). This overall behavior is in stark contrast with that of the EI candidate ${T i S e}_{2}$ , which has a multivalley structure similar to that of ${M o S}_{2}$ but remains a semimetal due to the unintentional doping of Ti atoms (46).

The exciton responsible for the instability of the conventional semiconductor exhibits a mixed transverse–longitudinal polarization (49), due to the small $C_{2}$ symmetry of the $Γ Λ$ line (this is also the case of the displacement vectors of the vibrational mode of Fig. 6D). As one moves from the semiconductor to the semimetal, the exciton smoothly turns into a plasmon (4), as illustrated by the wave function in the $e$ - $h$ center-of-mass frame (Materials and Methods). Whereas in the semiconductor (Fig. 5C) the amplitude is Lorentzian-like in k space, similar to that of a familiar Wannier exciton in the bulk, in the semimetal it acquires plasmonic features, as the wave function accumulates close to the Fermi surface (Fig. 5E). Outside the EI phase, this exciton–plasmon dissolves into the continuum of $e$ - $h$ excitations. Note that there may be other long-lived interband plasmons, since small gaps open in the $e$ - $h$ energy continuum due to the degeneracy of $Λ$ valleys. Were there only one valley, then the Fermi energy would be at the crossing of $a$ and $b$ bands (ignoring the mass anisotropy; cf. Fig. 5D) and the $e$ - $h$ excitation spectrum would be gapless.

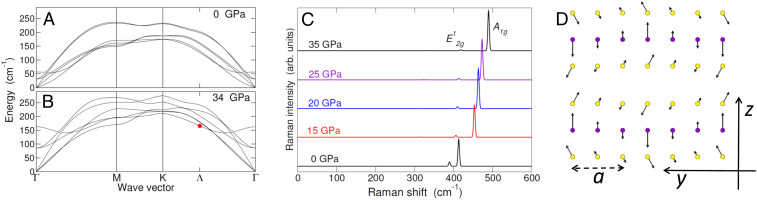
Fig. 6.

Phonon dispersion and Raman fingerprint. (A and B) Dispersion of the lowest-energy phonon modes for $P = 0$ (A) and 34 GPa (B), respectively, computed from first principles. All modes harden with $P$ . The red dot points to the lowest optical mode that is folded from $Λ$ into $Γ$ through the excitonic insulator phase transition. (C) Raman spectrum of the normal phase from first principles, for pressures $P =$ 0, 15, 20, 25, and 35 GPa, respectively, from bottom to top. The peaks are broadened using Gaussians with a standard deviation of 2 ${c m}^{- 1}$ . The bright peak at lower (higher) frequency has $E_{2 g}^{1}$ ( $A_{1 g}$ ) symmetry. The plot compares with figure 4b of ref. 36. (D) Displacement vectors for the mode labeled as a red dot in B, as viewed in the excitonic insulator reconstructed cell along the $Γ Λ$ direction (parallel to the $y$ axis in the adopted frame) (47). The superlattice constant is $3 a$ . The violet (yellow) color labels Mo (S) atoms. This mode is Raman active and degenerate with the one folded from $Λ^{'}$ to $Γ$ .

Raman Fingerprint.

Were ion displacements responsible for the building of electric dipoles in place of excitons, the frequency of the phonon of momentum q $= \vec{Γ Λ}$ and consistent symmetry would soften (or at least exhibit a dip) at the onset of the new phase (50). The phonon dispersion obtained from first principles, respectively at $P = 0$ (Fig. 6A) and 34 GPa (Fig. 6B), shows the opposite behavior, with all low-energy modes hardening with $P$ (see Materials and Methods and SI Appendix, Fig. S8 for the 2 $H_{a}$ phase). Therefore, the antiferroelectricity has a purely electronic origin. This prediction is consistent with recent diffraction measurements, which ruled out any periodic lattice distortion above 40 K (44).

The evolution of Raman spectrum with pressure, as obtained from first principles in Fig. 6C (structure 2 $H_{c}$ ) and SI Appendix, Fig. S9 (2 $H_{a}$ ), compares with observed data with the exception of the $E^{'}$ peak at 174 ${c m}^{- 1}$ (figure 4b in ref. 36), which appears below 150 K and above 30 GPa but is missed by the theory for the normal phase. Cao et al. (36) proposed this mode is a transverse acoustic phonon of finite momentum, which becomes bright at the onset of a charge density wave, due to the reconstruction of the Brillouin zone. Whereas the first-principles spectrum for the excitonic phase is presently out of reach, below we confirm the essence of Cao’s explanation by identifying $E^{'}$ as the lowest optical phonon at $Λ$ . This is the fingerprint of the antiferroelectric charge density wave associated with exciton condensation.

The symmetry group of the antiferroelectric ground state depicted in Fig. 4B includes only the identity operation. Therefore, all 216 vibrational modes are in principle infrared and/or Raman active. However, since the EI critical temperature is relatively low and the $E^{'}$ peak is extremely bright, we expect that the new mode is an optical phonon of momentum $Λ$ , which is Raman active through the folding into the zone center and strongly couples with $P$ . Since $P (x, y)$ originates everywhere in the cell from the interlayer vertical displacement of the charge between two neighbor Mo atoms, it will mainly couple with those optical oscillations of Mo atoms that occur along the $z$ axis. In fact, these vibrations linearly change the Mo-Mo distance and hence the local dipole strength, whereas the amount of displaced charge, which is ruled by the long-range part of Coulomb interaction, changes weakly with the oscillation. From direct inspection of phonon eigenvectors, there is one candidate only below 400 ${c m}^{- 1}$ , i.e., the lowest optical mode of frequency 164 ${c m}^{- 1}$ located at $Λ$ , which is highlighted by a red dot in Fig. 6B. As shown by the displacement vectors in the EI reconstructed cell displayed in Fig. 6D, the Mo atoms oscillate out of phase along the $z$ direction with an in-plane modulation of period $3 a$ along the $\vec{Γ Λ}$ direction (parallel to the vertical axis of Fig. 4B), hence matching the periodicity of $P_{z} (x, y)$ in the plane. This superlattice vibration is twice degenerate, due to the additional folding of the phonon with independent wave vector ${\vec{Γ Λ}}^{'}$ . Note that the observed intensity of the $E^{'}$ mode is constant up to 60 K, which compares with the EI critical temperature. In summary, the $E^{'}$ mode points to the excitonic insulator in the $P - T$ space.

Discussion

Both $2 H_{c}$ and $2 H_{a}$ phases coexist (31 32–33, 41) in the region of visibility of the $E^{'}$ mode, which extends between 30 and 50 GPa at 5 K (36). The lower bound agrees with our prediction, since in the $2 H_{a}$ structure the EI sets in at $P \sim 28$ GPa (SI Appendix, Fig. S4) with a mode frequency of 166 ${c m}^{- 1}$ (SI Appendix, Fig. S8). The upper bound of 50 GPa is larger than our expectation of $\sim 34$ GPa for the $2 H_{c}$ phase. However, recent diffraction measurements on single crystals (44), although available only at temperatures higher than 40 K, suggest that the critical upper pressure could be actually much lower, being artificially enhanced in powders due to the deviatoric stress field applied to randomly oriented crystallites.

In addition, other Raman features unexplained so far (36) point to the EI scenario: 1) the observation of modes supposedly forbidden or silent and 2) the anomalous frequency variation of the out-of-plane $A_{1 g}$ mode accompanying the onset of the $E^{'}$ mode. Since the understanding of the available electrical transport measurements (31, 36) is complicated by the mixture of phases in the high-pressure cell, we do not speculate on the origin of the resistivity peak that was tentatively assigned (31) to the EI.

The huge degeneracy of the EI ground state, associated with condensate phases $φ_{1}$ , $φ_{3}$ , and $φ_{5}$ , points to the emergence of acoustic-like electronic excitations—collective phase modes that, if gapless, would manifest exciton superfluidity (4). Within the two-band model of an isotropic semimetal, Kozlov and Maksimov (51) predicted that the “excitonic sound” velocity, $c_{exciton} = ℏ k_{F} {(3 m_{a} m_{b})}^{- 1 / 2}$ , is proportional to the Fermi wave vector in the normal phase, $k_{F}$ ( $m_{a}$ and $m_{b}$ are valence and conduction band masses). By taking average values at the EI/semimetal boundary, we estimate $c_{exciton} \sim 2 \cdot 1 0^{4}$ m/s, which is much higher than the sound velocity of the stiffest acoustic phonon branch (Fig. 6B), $c_{phonon} \sim 8 \cdot 1 0^{3}$ m/s. Therefore, the phase mode of the exciton condensate should be experimentally accessible, even if it might be gapped due to the mechanisms mentioned in the Introduction and not included in our analysis of the EI phase.

Conclusion

In summary, we have demonstrated that a real excitonic insulator phase sets in between the semiconducting and semimetallic phases of ${M o S}_{2}$ , building on calculations from first principles and available spectroscopic data. These findings call for further investigation of some fascinating possibilities. A first question is the manifestation of the macroscopic quantum coherence of the exciton condensate, which might occur through the observation of low-lying collective modes associated with the oscillation of the condensate phase $φ (r, t)$ . Another issue is whether the superconductivity observed above 90 GPa is related to the excitonic phase, as the overscreening action of surviving exciton–plasmons might act as unconventional glue for Cooper pairs. We hope our study may stimulate further work along these paths.

Materials and Methods

Computational Details of Ground-State Calculation from First Principles.

The lattice parameters and the ground-state electronic structure for the three values of pressure were obtained within DFT, with a plane wave basis set as implemented in the Quantum ESPRESSO package (52, 53), using the generalized gradient approximation Perdew–Burke–Ernzerhof (PBE) parameterization (54). A kinetic energy cutoff of 100 Ry was adopted for the wave functions, and fully relativistic norm-conserving pseudopotentials (55) were used to take into account spin–orbit interaction. van der Waals interactions, included by using the Grimme approximation method, were found to be relevant only at zero pressure, as already shown in ref. 30.

Phonons.

Phonon dispersions were calculated by using a density functional perturbation theory approach (56). We used a 10 $\times$ 10 $\times$ 3 Monkhorst–Pack grid for the integration in the Brillouin zone; the dynamical matrix at a given point of the Brillouin zone was obtained from a Fourier interpolation of the dynamical matrices computed on a 5 $\times$ 5 $\times$ 1 q-point mesh.

Quasiparticles and Excitons.

Many-body calculations (34, 57, 58) were performed by using the Yambo code (59, 60). Quasiparticle corrections to the Kohn–Sham energies were evaluated using the $G^{0} W^{0}$ approximation for the self-energy, the dynamical dielectric screening being accounted for within the plasmon-pole approximation (61). To speed up the convergence of quasiparticle energies with respect to the number of empty bands in the sum over states occurring in the calculation of the polarizability and the self-energy, we have adopted the scheme proposed in ref. 62. Fifty empty bands were used to build the polarizability and to integrate the self-energy (SI Appendix, Fig. S10); the Brillouin zone was sampled by using a 27 $\times$ 27 $\times$ 3 k-point grid. Quasiparticle energies were converged by using 68- and 15-Ry kinetic energy cutoffs for the exchange and correlation parts of the self-energy (SI Appendix, Fig. S11), respectively. Excitation energies and dispersion of the lowest exciton with finite wavevector q were calculated by solving the Bethe–Salpeter equation (BSE) using the Yambo code where the finite-q BSE was implemented as described in refs. 63 and 64. The static screening in the direct term was calculated within the random phase approximation with the inclusion of local field effects; the Tamm–Dancoff approximation for the Bethe–Salpeter Hamiltonian was employed, after having verified that the correction introduced by coupling the resonant and the antiresonant part was negligible for q = 0. Converged excitation energies were obtained considering respectively three valence and five conduction bands in the Bethe–Salpeter matrix, the irreducible Brillouin zone being sampled with a 27 $\times$ 27 $\times$ 3 k-point grid (SI Appendix, Fig. S12).

Computational Details of the Two-Band Model.

The effective-mass framework builds on the knowledge of conduction

ε_{b} (k) = \frac{G}{2} + \frac{ℏ^{2}}{2} [\frac{{(k_{∥} + Γ Λ)}^{2}}{m_{b ∥}} + \frac{k_{⊥}^{2}}{m_{b ⊥}} + \frac{k_{z}^{2}}{m_{b z}}]

[6]

and valence

ε_{a} (k) = - \frac{G}{2} - \frac{ℏ^{2}}{2} [\frac{k_{∥}^{2}}{m_{a ∥}} + \frac{k_{⊥}^{2}}{m_{a ⊥}} + \frac{k_{z}^{2}}{m_{a z}}]

[7]

energy bands. Here

G > 0

(

G < 0

) is the indirect bandgap (band overlap) for pressures below (above) the semiconductor–semimetal threshold—in the absence of excitonic effects—and the momentum components,

k_{∥}

k_{⊥}

k_{z}

, are projected along the principal axes of the effective mass tensor (), the corresponding masses being

m_{i ∥}

m_{i ⊥}

m_{i z}

, with

i = a, b

. These axes are respectively parallel (

k_{∥}

) and perpendicular (in-plane (

k_{⊥}

) and out-of-plane (

k_{z}

)) to the

\vec{Γ Λ}

direction, the axis origin being placed at the band edge. We emphasize that all parameters of the two-band model, for a given pressure, are fixed and obtained from first principles. In particular, the bandgap and the effective masses are extracted from GW bands, as illustrated in Fig. 2 D–F, and hence include the mean-field renormalization due to

e

e

interactions. The (modulus) of the screened

e

h

Coulomb attraction in momentum space,

W (q) = \frac{1}{κ_{r}} \frac{4 π e^{2}}{Ω} \frac{1}{q^{2}},

[8]

depends on the static dielectric constant,

κ_{r}

, which is obtained as the inverse of the first-principles dielectric tensor,

1 / {[ϵ^{- 1} (q = 0)]}_{G = G^{'} = 0}

, in the long-wavelength, macroscopic limit, as illustrated in Fig. 3B (here

Ω

is the crystal volume and G the reciprocal lattice vector).

In the semimetal, the $P$ -dependent values of $G$ , $m_{i ∥}$ , $m_{i ⊥}$ , $m_{i z}$ , and $κ_{r}$ are derived as linear extrapolations of first-principles data at $P =$ 25 and 34 GPa, respectively. Since free $e$ and $h$ carriers effectively screen the interaction by adding a metal-like, intraband contribution to the polarizability, we modify the dressed Coulomb potential as

W (q) = \frac{1}{[κ_{r} + 4 π e^{2} D (ε_{F}) / q^{2}]} \frac{4 π e^{2}}{Ω} \frac{1}{q^{2}} .

[9]

Here the Thomas–Fermi term, proportional to the density of states,

D (ε)

, evaluated at the Fermi energy,

ε_{F}

, removes the long-wavelength divergence of

W

. We obtain numerically

D

through the summation of Gaussian functions over a fine grid in k space, as well as

ε_{F}

by imposing overall charge neutrality (we take into account the sixfold degeneracy of the conduction band).

Two-Band Bethe–Salpeter Equation.

In the semiconductor, the exciton wave function is

|exciton⟩ = \sum_{k} ϕ_{k} {\hat{b}}_{k}^{+} â_{k} |Φ_{0}⟩,

[10]

where

ϕ_{k}

is the probability amplitude of a bound

e

h

pair in momentum space. The Bethe–Salpeter equation of motion for

ϕ_{k}

[ε_{b} (k) - ε_{a} (k)] ϕ_{k} - \sum_{k^{'}} W (k - k^{'}) ϕ_{k^{'}} = ε_{exc} ϕ_{k},

[11]

where

ε_{exc}

is the excitation energy of the exciton, whose negative value signals the instability. We solve this equation by numerical discretization in k space and assess convergence by refining the mesh as well as varying the momentum cutoff. Note that the singularity of Coulomb potential for

|q| \to 0

is harmless, as we integrate

W

over a small parallelepiped, in a semianalytical, accurate manner. We have benchmarked the convergence of our calculations against known analytical or high-precision results, as shown for bulk Wannier excitons in SI Appendix, Fig. S13 and for anisotropic excitons with a well-defined azimuthal quantum number () in SI Appendix, Fig. S14.

In the semimetal ground state, a small area of k space around the origin is populated by electrons in band $b$ and holes in band $a$ . In addition, due to band anisotropy (67), nearby regions exist populated by either electrons or holes only, which prevents from exciting $e$ - $h$ pairs due to Pauli exclusion principle. Therefore, the Bethe–Salpeter equation of motion must be modified as (4)

[ε_{b} (k) - ε_{a} (k)] ϕ_{k} - \sum_{k^{'}} W (k - k^{'}) [n_{a} (k^{'}) - n_{b} (k^{'})] ϕ_{k^{'}} = ε_{exc} ϕ_{k},

[12]

where

n_{i} (k)

is the occupancy factor of the

i

th band in the normal ground state, which takes either 0 or 1 as a value. The “counting” prefactor of

W

[n_{a} - n_{b}]

, removes scattering channels forbidden by Pauli blocking and is responsible of the plasmon-like features shown Fig. 5E. Note that in the semiconductor,

n_{a} (k) = 1

and

n_{b} (k) = 0

, and hence one regains the standard form of .

Self-Consistent Theory of the Excitonic Insulator within the Two-Band Model.

The EI bands (circles in Fig. 4A) are $E_{b k} = [ε_{b} (k) + ε_{a} (k)] / 2 + E_{k}$ and $E_{a k} = [ε_{b} (k) + ε_{a} (k)] / 2 - E_{k}$ , with $E_{k}$ being fixed by the solution of the gap Eq. 3 for $Δ_{k}^{0}$ (through $ζ_{k}^{0}$ ). Eq. 3 is solved self-consistently by numerical recursion, exploiting the exciton wave function $ϕ_{k}$ as a seed (35). If the semimetal is the normal ground state, the gap equation maintains the form 3 of the main text, provided that 1) the summation over k $^{'}$ is limited to those points whose occupancies are such that $[n_{a} (k^{'}) - n_{b} (k^{'})] \neq 0$ to comply with Fermi statistics (67) and 2) the dressed Coulomb interaction $W$ is renormalized by a vertex correction associated with the EI ground state (48), as the opening of the many-body gap significantly enhances the $e$ - $h$ attraction—by suppressing screening—with respect to the gapless normal phase. Therefore, following Kozlov and Maksimov (48), for small momentum transfer $q$ the dressed interaction $W$ appearing in Eq. 3 takes the self-consistent form

W (q) = \frac{1}{[1 + α / {(Δ_{k_{F}}^{0})}^{2}]} \frac{1}{κ_{r}} \frac{4 π e^{2}}{Ω} \frac{1}{q^{2}},

[13]

where the gap function at the Fermi surface,

Δ_{k_{F}}^{0}

, which is determined recursively, removes the long-wavelength divergence as one approaches the EI–semimetal boundary. Here

Δ_{k_{F}}^{0}

is an average value defined as

Δ_{k_{F}}^{0} = {[Δ_{k_{x F}, 0,0}^{0} Δ_{0, k_{y F}, 0}^{0} Δ_{0,0, k_{z F}}^{0}]}^{1 / 3}

, with

k_{x F}

given implicitly by

ε_{F} = ε_{b} (k_{x F}, 0,0)

, and similarly for

k_{y F}

and

k_{z F}

. The constant

α

, for given band overlap

G < 0

, is

α = {[|G_{0}| {(ε_{F} - G / 2)}^{3 / 2}]}^{1 / 2}

, where

|G_{0}| = 9.38

meV is the maximum magnitude of the band overlap at which

e

h

pairing takes place. We neglect the modification of for large momentum transfer, as it turns out to be irrelevant numerically. Whereas the vertex form 13 was originally proposed () for the case of spherically symmetric

e

and

h

pockets, we note that, at the semiconductor–semimetal threshold, the exciton responsible for the instability is essentially isotropic (SI Appendix, Fig. S5). At finite temperature,

T

, the gap equation takes the form

2 E_{k} ζ_{k}^{0} - \sum_{k^{'}} W (k - k^{'}) ζ_{k^{'}}^{0} [f_{F} (E_{a k^{'}} - ε_{F}) - f_{F} (E_{b k^{'}} - ε_{F})] = 0,

[14]

where

f_{F} (x) = 1 / [1 + \exp (β x)]

is the Fermi distribution function, with

β = 1 / k_{B} T

and

k_{B}

being the Boltzmann constant, and we neglect the small renormalization of the chemical potential due to the presence of the exciton condensate.

Multivalley Band Structure.

The calculation of the EI band structure relies on the theory by Monney et al. (46) to include valley degeneracy. This approach, based on Green functions, generalizes to multiple bands the original theory by Jérome et al. (3). For every k point, the EI band energies (solid lines in Fig. 4A and SI Appendix, Fig. S7) are found as the seven roots of the equation

z - ε_{a} (k) - \sum_{i = 1}^{6} \frac{{|Δ_{i} (k)|}^{2}}{z - ε_{i b} (k)} = 0

[15]

(cf. equation 8 of ref. ), after the magnitudes of the excitonic gap components,

Δ_{i} (k)

, are obtained as follows. The gap function is defined as

Δ_{i} (p) = \sum_{k} W (k) ζ_{i k + p},

[16]

with

ζ_{i k}

, apart from a phase factor, being the equal-time interband excitonic coherence

F_{i}^{†} (k, t, t)

defined in equation 4 of ref. ,

ζ_{i k} = - i F_{i}^{†} (k, t + δ, t) = \frac{1}{2 π i} \int_{- \infty}^{\infty} d ω F_{i}^{†} (k, ω) e^{- i ω δ},

[17]

and

δ \to 0^{+}

being a positive infinitesimal quantity. The integral 17 is evaluated through contour integration, the Fourier transform

F_{i}^{†} (k, ω)

being derived from the equations of motion of Green functions () as

\begin{matrix} F_{i}^{†} (k, ω) = - Δ_{i} (k) {[ω - ε_{a} (k) - \sum_{j \neq i} \frac{{|Δ_{j} (k)|}^{2}}{ω - ε_{j b} (k)}]}^{- 1} \times \\ {[ω - ε_{i b} (k) - {|Δ_{i} (k)|}^{2} {(ω - ε_{a} (k) - \sum_{j \neq i} \frac{{|Δ_{j} (k)|}^{2}}{ω - ε_{j b} (k)})}^{- 1}]}^{- 1} . \end{matrix}

[18]

Whereas this expression would generically lead to an intractable system of six coupled equations for the

Δ_{i}

s, we exploit the high symmetry of the problem to simplify the form of

F_{i}^{†} (k, ω)

and recover a single gap equation. As discussed in the main text and SI Appendix, Fig. S6, the symmetrizing effect of

e - h

attraction makes

Δ_{k}^{0}

almost independent from the azimuthal angle

φ_{k}

, with k

\equiv (k, φ_{k}, k_{z})

being expressed in cylindrical coordinates (

k

is the in-plane radial distance and

k_{z}

the component along the

z

axis). Therefore, it is natural to assume that

Δ_{i}

has cylindrical symmetry,

Δ_{i} (k) = Δ (k, k_{z}) e^{i φ_{i}}

. Since we are mainly interested in the region

k \approx 0

, we also neglect the azimuthal dependence of

ε_{i b} (k)

in the denominator of

F_{i}^{†}

, obtaining

F_{i}^{†} (ω) = - \frac{Δ_{i}}{(ω - ε_{a} - \frac{5 {|Δ|}^{2}}{ω - ε_{i b}}) (ω - ε_{i b} - \frac{{|Δ|}^{2}}{ω - ε_{a} - \frac{5 {|Δ|}^{2}}{ω - ε_{i b}}})},

[19]

where we omitted the dependence of terms on k in the notation. is now easily integrated, giving a single self-consistent gap equation. This has the same form as of the two-band model, provided that

Δ_{k}^{0}

is replaced with

\sqrt{6} Δ_{i} (k)

Ground-State Wave Function.

The contour integration of equal-time Green functions provides us with all interband coherences and band populations, i.e., $⟨Ψ_{EI}| {\hat{b}}_{j k}^{+} {\hat{b}}_{i k} |Ψ_{EI}⟩ = Δ_{i} * Δ_{j} / 2 E (E + ε_{b} / 2 - ε_{a} / 2)$ , $⟨Ψ_{EI}| {\hat{b}}_{i k}^{+} {\hat{b}}_{i k} |Ψ_{EI}⟩ = {(v^{0})}^{2} / 6$ , $⟨Ψ_{EI}| â_{k}^{+} â_{k} |Ψ_{EI}⟩ = {(u^{0})}^{2}$ , where we omitted the dependence of right-hand-side terms on k to ease the notation, neglected the in-plane anisotropy of the valence band, $ε_{i b} = ε_{b}$ , and put $E = {{[ε_{b} - ε_{a}]}^{2} / 4 + | Δ^{0} |^{2}}^{1 / 2}$ . This allows us to write explicitly the ground-state wave function,

|Ψ_{EI}⟩ = \prod_{k} {\hat{γ}}_{k}^{+} |vacuum⟩,

[20]

in terms of Bogoliubov–Valatin-like creation operators,

{\hat{γ}}^{+}

, which are defined as

{\hat{γ}}_{k}^{+} = u_{k}^{0} â_{k}^{+} + \frac{v_{k}^{0}}{\sqrt{6}} \sum_{i = 1}^{6} e^{- i φ_{i}} {\hat{b}}_{i k}^{+} .

[21]

As discussed in the main text, time reversal symmetry limits the number of independent condensate phases to three:

φ_{1}

φ_{3}

, and

φ_{5}

(recall that

u_{k}^{0} = u_{- k}^{0}

and

v_{k}^{0} = v_{- k}^{0}

are real positive quantities) (SI Appendix, Fig. S6C).

Inversion Symmetry Breaking.

The ground-state wave function allows us to understand the symmetry breaking associated with exciton condensation. The inversion operator, $\hat{I}$ , acts differently on $b_{i}$ and $a$ Bloch states, since the envelope function at $Γ$ is odd: $\hat{I} â_{k}^{+} = - â_{- k}^{+}$ , $\hat{I} {\hat{b}}_{1 k}^{+} = {\hat{b}}_{4 - k}^{+}$ , etc. Therefore, the inverted ground state, $\hat{I} |Ψ_{EI}⟩$ , is not proportional to the original one:

\begin{matrix} ⟨Ψ_{EI}| \hat{I} |Ψ_{EI}⟩ = \prod_{k} {- {(u_{k}^{0})}^{2} \\ + & \frac{{(v_{k}^{0})}^{2}}{3} [\cos (2 φ_{1}) + \cos (2 φ_{3}) + \cos (2 φ_{5})]} . \end{matrix}

[22]

The magnitude of the expression enclosed in curly brackets is less than one (unless

φ_{1} = φ_{3} = φ_{5} = \pm π / 2

, i.e.,

\hat{I} |Ψ_{EI}⟩ = - |Ψ_{EI}⟩

); hence, in the thermodynamic limit, the overlap between

\hat{I} |Ψ_{EI}⟩

and

|Ψ_{EI}⟩

tends to zero as the two states become orthogonal. Since the ground state has a lower symmetry than the Hamiltonian, inversion symmetry is broken.

Charge Density Wave.

The form 5 of the purely electronic charge density wave, $Δ ϱ = Δ ϱ_{1,4} + Δ ϱ_{3,6} + Δ ϱ_{5,2}$ , is derived in a straightforward manner by averaging the density operator, $\hat{ϱ} (r) = 2 {\hat{ψ}}^{†} (r) \hat{ψ} (r)$ , over $|Ψ_{EI}⟩$ , with the Fermi field operator, $\hat{ψ} (r)$ , being defined as

\hat{ψ} (r) = \sum_{k} e^{i k \cdot r} [ψ_{Γ} (r) â_{k} + \sum_{i = 1}^{6} \exp (i {\vec{Γ Λ}}_{i} \cdot r) ψ_{Λ_{i}} (r) {\hat{b}}_{i k}] .

[23]

Cross-terms proportional to

ψ *_{Λ_{i}} ψ_{Λ_{j}}

average out to zero, once summed together, as the various

ψ_{Λ_{i}}

s are obtained one from the other by either rotation by

\pm 2 π / 3

along the

z

axis or complex conjugation. Apart from the envelope functions, which have the lattice periodicity,

Δ ϱ

depends on r through a sum over three exponentials, whose imaginary arguments are respectively (times the prefactor

i

)

{\vec{Γ Λ}}_{1} \cdot r - φ_{1}

{\vec{Γ Λ}}_{3} \cdot r - φ_{3}

, and

{\vec{Γ Λ}}_{5} \cdot r - φ_{5}

, as illustrated in the main text.

We show below that, for any given two condensate phases, say $φ_{1}$ and $φ_{3}$ , there exist a lattice vector $R_{shift}$ and a phase $φ_{5} = - φ_{1} - φ_{3}$ such that a rigid translation of the density wave by $R_{shift}$ provides the density wave corresponding to $φ_{1} = φ_{3} = φ_{5} = 0$ ; i.e., ${[Δ ϱ (r - R_{shift})]}_{φ_{1}, φ_{3}, φ_{5}} = {[Δ ϱ (r)]}_{0,0,0}$ .

Let us construct explicitly $R_{shift}$ as $R_{shift} = - R_{∥} - R_{⊥}$ , where $R_{∥} = n_{∥} t_{2}$ and $R_{⊥} = n_{⊥} (2 t_{1} + t_{2})$ are respectively parallel and perpendicular to ${\vec{Γ Λ}}_{1}$ (SI Appendix, Fig. S6C); $n_{∥}$ and $n_{⊥}$ are integers to be determined; and $t_{1}$ , $t_{2}$ are the primitive vectors that generate the hexagonal lattice in Mattheiss’s (47) coordinate frame. Since ${\vec{Γ Λ}}_{1}$ is generically not commensurable with the reciprocal lattice vectors, there exists an integer $n_{∥}$ such that ${\vec{Γ Λ}}_{1} \cdot R_{∥} = φ_{1}$ with arbitrary accuracy (4), modulus an integer multiple of $2 π$ . Similarly, we may fix $n_{⊥}$ such that ${\vec{Γ Λ}}_{3} \cdot R_{⊥} = - {\vec{Γ Λ}}_{5} \cdot R_{⊥} = φ_{3} - {\vec{Γ Λ}}_{3} \cdot R_{∥}$ . Finally, we take $φ_{5} = - φ_{3} + 2 {\vec{Γ Λ}}_{3} \cdot R_{∥} = - φ_{3} - φ_{1}$ . One may verify, by direct substitution into the expression $Δ ϱ = Δ ϱ_{1,4} + Δ ϱ_{3,6} + Δ ϱ_{5,2}$ , that ${[Δ ϱ (r - R_{shift})]}_{φ_{1}, φ_{3}, - φ_{1} - φ_{3}} = {[Δ ϱ (r)]}_{0,0,0}$ , Q.E.D.

This theorem implies that the set of charge density waves ${[Δ ϱ (r)]}_{0,0, φ_{5}}$ labeled by the continuous parameter $φ_{5}$ spans all possible modulations of the electronic charge density of the EI, each realization having in turn a huge translational degeneracy, which is parameterized by the two continuous variables $φ_{1}$ and $φ_{3}$ .

Antiferroelectric Order.

The electronic charge density wave of the EI ground state (Eq. 5) induces an out-of-plane electric dipole, $P_{z} (R_{i})$ , in the $i$ th cell of the pristine 2 $H$ phase located at $R_{i}$ , with $i = 1, \dots, N$ ( $N$ is the total number of cells). This is illustrated in Fig. 4B, where the dipoles $P_{z} (R_{i})$ are depicted as red arrows. The local dipole $P_{z} (R_{i})$ is given by the coherent superposition of three density waves, whose characteristic wave vectors are $q_{i} = {\vec{Γ Λ}}_{i}$ , with $i = 1,3,5$ ,

P_{z} (R_{i}) = \frac{P_{z 0}}{Ω} \sum_{k} \frac{4}{\sqrt{6}} u_{k}^{0} v_{k}^{0} \sum_{j = 1,3,5} \cos (q_{j} \cdot R_{i}) .

[24]

The maximum value,

P_{z} (0)

, is shown in Fig. 4D. Here

P_{z} (R_{i})

is evaluated within the envelope function approximation, the factor

P_{z 0}

being derived from first principles through the overlap charge density of the periodic part of conduction and valence Bloch states at

Γ

and

Λ

, respectively, which is shown in Fig. 4C. The latter is numerically integrated over the pristine unit cell volume,

Ω_{cell}

P_{z 0} = \sum_{σ} e \int_{Ω_{cell}} d r z [ψ *_{Γ σ} (r) ψ_{Λ σ} (r) + c.c.],

[25]

the frame origin being placed at the inversion center—the midpoint between the two Mo atoms of the 2

H

cell. As the charge displacement that gives rise to the dipole is essentially localized on Mo atoms (Fig. 4C), we expect

|P_{z 0}|

to be well defined. We obtain

P_{z 0} / e =

15.1 Bohr at

P = 34

GPa.

Acknowledgements

D.V. acknowledges the joint work with Davide Sangalli to implement the finite-momentum Bethe–Salpeter calculation into the Yambo code. This work was supported in part by the “MAterials design at the eXascale” (MaX) European Center of Excellence (www.max-centre.eu) funded by the European Union H2020-INFRAEDI-2018-1 program, Grant 824143. It was also supported by the Italian national program PRIN2017 2017BZPKSZ “Excitonic insulator in two-dimensional long-range interacting systems.” We acknowledge access to the Marconi supercomputing system based at Consorzio Interuniversitario per la Gestione del Centro di Calcolo Elettronico dell’Italia Nord-Orientale (CINECA), Italy, through Partnership for Advanced Computing in Europe and the Italian SuperComputing Resource Allocation program.

The authors declare no competing interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2010110118/-/DCSupplemental.

Data Availability

Many-body perturbation theory calculations were performed by means of the codes Yambo (www.yambo-code.org/) and Quantum ESPRESSO (www.quantum-espresso.org), which are both open source software. Results for the two-band model were obtained through a custom Fortran code that is available at Zenodo, doi.org/10.5281/zenodo.4455373. The data that support the findings of this study (crystal structures) are available at Zenodo, doi.org/10.5281/zenodo.4455373 (68).

References

L. V. Keldysh, Y. V. Kopaev, Possible instability of the semimetallic state against Coulomb interaction. Sov. Phys. Sol. State 6, 2219 (1965).

J. des Cloizeaux, Excitonic instability and crystallographic anomalies in semiconductors. J. Phys. Chem. Solid. 26, 259 (1965).

D. Jèrome, T. M. Rice, W. Kohn, Excitonic insulator. Phys. Rev. 158, 462 (1967).

W. Kohn, “Metals and insulators” in Many-Body Physics, C. de Witt, R. Balian, Eds. (Gordon & Breach, New York, NY, 1967), pp. 351–411.

J. Bardeen, L. N. Cooper, J. R. Schrieffer, Theory of superconductivity. Phys. Rev. 108, 1175–1204 (1957).

B. I. Halperin, T. M. Rice, The excitonic state at the semiconductor-semimetal transition. Solid State Phys. 21, 115 (1968).

R. R. GuseÄŋnov, L. V. Keldysh, Nature of the phase transition under the condition of an “excitonic” instability in the electronic spectrum of a crystal. Sov. Phys. JETP 36, 1193 (1973).

T. Portengen, T. Östreich, L. J. Sham, Theory of electronic ferroelectricity. Phys. Rev. B 54, 17452 (1996).

L. Pitaevskii, S. Stringari, Bose-Einstein Condensation (Oxford University Press, Oxford, UK, 2003).

J. P. Eisenstein, A. H. MacDonald, Bose-Einstein condensation of excitons in bilayer electron systems. Nature 432, 691–694 (2004).

P. B. Littlewood, “Exciton coherence” in Problems of Condensed Matter Physics, A. L. Ivanov, S. G. Tikhodeev, Eds. (International Series of Monographs on Physics, Oxford University Press, Oxford, UK, 2008), vol. 139, pp. 163–181.

M. Rontani, L. J. Sham, “Coherent exciton transport in semiconductors” in Novel Superfluids Vol. 2, K. H. Bennemann, J. B. Ketterson, Eds. (International Series of Monographs on Physics, Oxford University Press, Oxford, UK, 2014), vol. 157, pp. 423–474.

V. A. Volkov, Y. V. Kopaev, Theory of phase transitions in semiconductors of the A₄B₆ group. Sov. Phys. JETP 37, 1103–1108 (1974).

D. Varsano, M. Palummo, E. Molinari, M. Rontani, A monolayer transition-metal dichalcogenide as a topological excitonic insulator. Nat. Nanotechnol. 15, 367–372 (2020).

B. Remez, N. R. Cooper, Effects of disorder on the transport of collective modes in an excitonic condensate. Phys. Rev. B 101, 235129 (2020).

A. Nandi, A. D. K. Finck, J. P. Eisenstein, L. N. Pfeiffer, K. W. West, Exciton condensation and perfect Coulomb drag. Nature 488, 481 (2012).

L. V. Butov, C. W. Lai, A. L. Ivanov, A. C. Gossard, D. S. Chemla, Towards Bose–Einstein condensation of excitons in potential traps. Nature 417, 47–52 (2002).

A. A. High, Spontaneous coherence in a cold exciton gas. Nature 483, 584–588 (2012).

R. Anankine, Quantized vortices and four-component superfluidity of semiconductor excitons. Phys. Rev. Lett. 118, 127402 (2017).

T. Rohwer, Collapse of long-range charge order tracked by time-resolved photoemission at high momenta. Nature 471, 490–494 (2011).

A. Kogar, Signatures of exciton condensation in a transition metal dichalcogenide. Science 358, 1314–1317 (2017).

Y. F. Lu, Zero-gap semiconductor to excitonic insulator transition in

{T a}_{2} {N i S e}_{5}

. Nat. Commun. 8, 14408 (2017).

D. Werdehausen, Coherent order parameter oscillations in the ground state of the excitonic insulator T

a_{2}

NiS

e_{5}

. Sci. Adv. 4, eaap8652 (2018).

F. J. D. Salvo, D. E. Moncton, J. V. Waszczak, Electronic properties and superlattice formation in the semimetal TiS

e_{2}

. Phys. Rev. B 14, 4321 (1976).

H. Hedayat, Excitonic and lattice contributions to the charge density wave in

1 T

-TiS

e_{2}

revealed by a phonon bottleneck. Phys. Rev. Res. 1, 023029 (2019).

J. S. Zhou, Anharmonicity and doping melt the charge density wave in single-layer TiS

e_{2}

. Nano Lett. 20, 4809–4815 (2020).

A. Nakano, Antiferroelectric distortion with anomalous phonon softening in the excitonic insulator T

a_{2}

NiS

e_{5}

. Phys. Rev. B 98, 045139 (2018).

J. Yan, Strong electron-phonon coupling in the excitonic insulator T

a_{2}

NiS

e_{5}

. Inorg. Chem. 58, 9036–9042 (2019).

W. Kohn, D. Sherrington, Two kinds of bosons and Bose condensates. Rev. Mod. Phys. 42, 1–11 (1970).

L. Hromadová, R. Martonák, E. Tosatti, Structure change, layer sliding, and metallization in high-pressure MoS₂. Phys. Rev. B 87, 144105 (2013).

Z. H. Chi, Pressure-induced metallization of molybdenum disulfide. Phys. Rev. Lett. 113, 036802 (2014).

A. P. Nayak, Pressure-induced semiconducting to metallic transition in multilayered molybdenum disulphide. Nat. Commun. 5, 3731 (2014).

Z. Chi, Superconductivity in pristine

2 H_{a}

-MoS₂ at ultrahigh pressure. Phys. Rev. Lett. 120, 037002 (2018).

G. Onida, L. Reining, A. Rubio, Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 74, 601–659 (2002).

D. Varsano, Carbon nanotubes as excitonic insulators. Nat. Commun. 8, 1461 (2017).

Z. Y. Cao, J. W. Hu, A. F. Goncharov, X. J. Chen, Nontrivial metallic state of MoS₂. Phys. Rev. B 97, 214519 (2018).

Y. Ge, A. Y. Liu, Phonon-mediated superconductivity in electron-doped single-layer MoS₂: A first-principles prediction. Phys. Rev. B 87, 241408 (2013).

R. Roldán, E. Cappelluti, F. Guinea, Interactions and superconductivity in heavily doped MoS₂. Phys. Rev. B 88, 054515 (2013).

M. Rösner, S. Haas, T. O. Wehling, Phase diagram of electron-doped dichalcogenides. Phys. Rev. B 90, 245105 (2014).

R. Aksoy, X-ray diffraction study of molybdenum disulfide to 38.8 GPa. J. Phys. Chem. Solid. 67, 1914–1917 (2006).

N. Bandaru, Effect of pressure and temperature on structural stability of MoS₂. J. Phys. Chem. C 118, 3230–3235 (2014).

Y. Zhuang, Pressure-induced permanent metallization with reversible structural transition in molybdenum disulfide. Appl. Phys. Lett. 110, 122103 (2017).

M. Brotons-Gisbert, Optical and electronic properties of 2H-MoS₂ under pressure: Revealing the spin-polarized nature of bulk electronic bands. Phys. Rev. Mater. 2, 054602 (2018).

A. F. Goncharov, Structure and stability of

2 H_{a}

-MoS₂ at high pressure and low temperatures. Phys. Rev. B 102, 064105 (2020).

H. Guo, T. Yang, P. Tao, Y. Wang, Z. Zhang, High pressure effect on structure, electronic structure, and thermoelectric properties of MoS₂. J. Appl. Phys. 113, 013709 (2013).

C. Monney, Spontaneous exciton condensation in 1T-TiS

e_{2}

: BCS-like approach. Phys. Rev. B 79, 045116 (2009).

L. F. Mattheiss, Band structures of transition-metal-dichalcogenide layer compounds. Phys. Rev. B 8, 3719–3740 (1973).

A. N. Kozlov, L. A. Maksimov, The metal-dielectric divalent crystal phase transition. Sov. Phys. JETP 21, 790–795 (1965).

R. S. Knox, Theory of Excitons (Solid State Physics, Academic Press, New York, NY, 1963), vol. suppl. 5.

G. Grüner, Density Waves in Solids (CRC Press, Boca Raton, FL, 2018).

A. N. Kozlov, L. A. Maksimov, Collective excitations in semimetals. Sov. Phys. JETP 22, 889–893 (1966).

P. Giannozzi, Quantum ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).

P. Giannozzi, Advanced capabilities for materials modelling with quantum espresso. J. Phys. Condens. Matter 29, 465901 (2017).

J. P. Perdew, K. Burke, M. Ernzerhof, Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).

D. Hamann, Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B 88, 085117 (2013).

S. Baroni, S. de Gironcoli, A. Dal Corso, P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory. Rev. Mod. Phys. 73, 515–562 (2001).

M. S. Hybertsen, S. G. Louie, Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 34, 5390 (1986).

G. Strinati, Application of the Green’s functions method to the study of the optical properties of semiconductors. Riv. Nuovo Cimento 11, 1–86 (1988).

A. Marini, C. Hogan, M. Grüning, D. Varsano, Yambo: An ab initio tool for excited state calculations. Comput. Phys. Commun. 180, 1392–1403 (2009).

D. Sangalli, Many-body perturbation theory calculations using the Yambo code. J. Phys. Condens. Matter 31, 325902 (2019).

R. W. Godby, R. J. Needs, Metal-insulator transition in Kohn-Sham theory and quasiparticle theory. Phys. Rev. Lett. 62, 1169–1172 (1989).

F. Bruneval, X. Gonze, Accurate GW self-energies in a plane-wave basis using only a few empty states: Towards large systems. Phys. Rev. B 78, 085125 (2008).

M. Gatti, F. Sottile, Exciton dispersion from first principles. Phys. Rev. B 88, 155113 (2013).

J. A. Soininen, E. L. Shirley, Effects of electron-hole interaction on the dynamic structure factor: Application to nonresonant inelastic x-ray scattering. Phys. Rev. B 61, 16423–16429 (2000).

G. L. Bir, G. E. Pikus, Symmetry and Strain-Induced Effects in Semiconductors (Wiley, New York, NY, 1974).

T. G. Pedersen, S. Latini, K. S. Thygesen, H. Mera, B. K. Nikolić, Exciton ionization in multilayer transition-metal dichalcogenides. New J. Phys. 18, 073043 (2016).

J. Zittartz, Anisotropy effects in the excitonic insulator. Phys. Rev. 162, 752–758 (1967).

S. Samaneh Ataei, D. Varsano, E. Molinari, M. Rontani, Source custom Fortran code and supporting data for “Evidence of ideal excitonic insulator in bulk MoS₂ under pressure.” Zenodo. https://zenodo.org/record/4455373. Deposited 4 November 2020.