Charge Order in High-$$ T_c$$ Cuprates

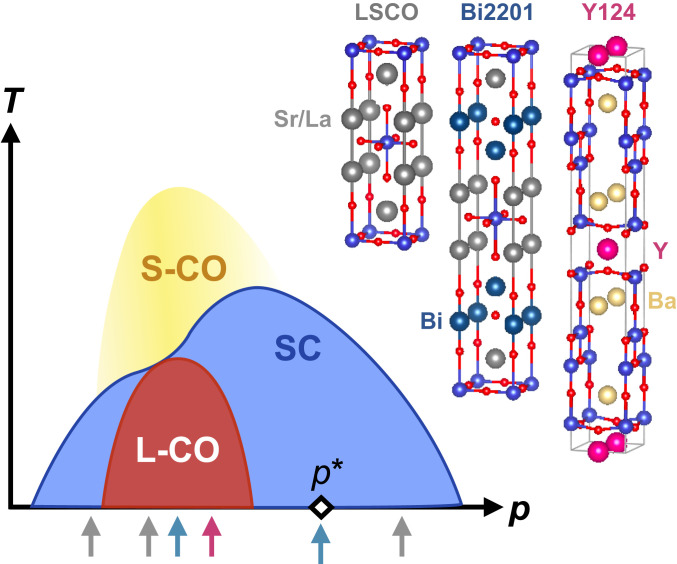
The $$ T-p$$ phase diagram of hole-doped cuprates across the superconducting dome is illustrated schematically in Fig. 1. Two forms of charge order have previously been observed in underdoped Y123, LSCO, and Bi2201 by a variety of experimental probes (345–6, 252627282930–31). The first one, found in zero applied magnetic field, has short-range correlations within the $$ {\mathrm{C}\mathrm{u}\mathrm{O}}_2$$ plane (345–6) and weak antiphase correlations along the $$ c$$ axis (26). Recent resonant X-ray scattering experiments (32, 33) report that this short-range charge order persists in overdoped LSCO and Bi2201 (up to $$ p\approx $$ 0.23). A second, related type of charge order, with a longer in-plane correlation length and in-phase $$ c$$-axis correlations, has been found in a large magnetic field (2526272829–30). There is strong evidence from NMR (29) for magnetic-field–induced long-range charger order within the underdoped regime $$ 0.09\lesssim p\lesssim 0.16$$ in the cuprate families studied here. In LSCO, stripe order$$ -$$interlocked charge and spin order$$ -$$is present in the underdoped regime $$ p\approx $$ 0.12 and found to be strongly enhanced by a moderate magnetic field (34, 35). Despite the lack of direct evidence, the presence of charge order in Y124 has been inferred from the existence of a small electron pocket (10, 11, 36) for which charge order of sufficiently long range is believed to be responsible (14).

Fig. 1.

Temperature–doping phase diagram of superconducting cuprates. Charge order with short-range in-plane correlations (S-CO) at zero magnetic field (345–6, 32, 33) and long-range three-dimensional correlations (L-CO) at high magnetic field (252627282930–31) is found to onset at temperatures indicated by the dome-shaped shades peaked at $$ p\approx 0.12$$. L-CO are found to occur for 0.09 $$ \lesssim p\lesssim 0.16$$, while recent X-ray scattering experiments (32, 33) have found signatures of S-CO in overdoped Bi2201 and LSCO up to $$ p\approx $$ 0.23. Vertical arrows underneath the dome of superconductivity (SC) mark the doping levels of the three different cuprate families studied in this work, whose crystal structures are labeled by corresponding colors.

Onset of Nonohmic Resistivity

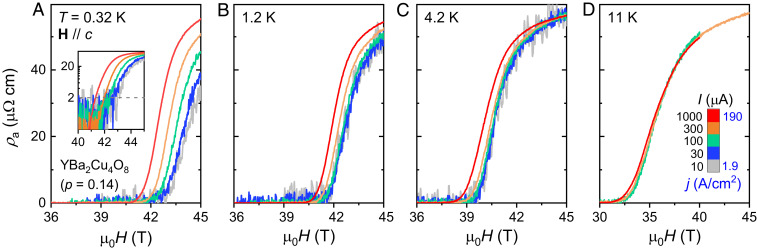
Fig. 2 shows the longitudinal resistivity $$ {\rho }_{\mathrm{a}}$$ of a Y124 crystal measured in a magnetic field up to 45 T, over the temperature range 0.32 K $$ ⩽T⩽$$ 11 K and for excitation currents 10 $$ \mathrm{\mu }$$A $$ ⩽I⩽$$ 1 mA. The resistive transition field, $$ {\mu }_0{H}_{\mathrm{r}}$$, is defined as the field strength at which the resistivity exceeds a certain value set by the noise level at the lowest excitation currents as illustrated in Fig. 2$$ A$$, Inset. Below $$ {\mu }_0{H}_r$$, vortices are assumed to be pinned and frozen into a vortex solid state, with or without long-range translational order. In a typical type-II superconductor, this field is equivalent to the irreversibility field (37). At 11 K, $$ {\rho }_{\mathrm{a}}$$ and $$ {\mu }_0{H}_{\mathrm{r}}$$ are essentially independent of $$ I$$ as expected for a normal metallic state. At $$ T⩽$$ 4.2 K, however, $$ {\rho }_{\mathrm{a}}$$ and $$ {\mu }_0{H}_{\mathrm{r}}$$ become dependent on the magnitude of $$ I$$, whose effect becomes increasingly pronounced with decreasing temperature. An increase in $$ {\mu }_0{H}_{\mathrm{r}}$$ of 2 T is observed at 0.32 K when $$ I$$ is reduced from 1 mA to 10 $$ \mathrm{\mu }$$A (Fig. 2$$ A$$). The same behavior is observed in two other Y124 crystals measured simultaneously (SI Appendix, Fig. S1). Previously, the onset of a thermal conductivity drop in Y124 below $$ {\mu }_{0}H\approx $$ 44 T at 1.6 K $$ ⩽T⩽$$ 9 K has been interpreted as the manifestation of increased electron scattering due to the emergence of vortices and therefore as a signature of $$ H_{\mathrm{c}\mathrm{2}}$$ (16). While this field scale is comparable with the magnetic field above which ohmic behavior is restored at 4.2 K (Fig. 2$$ C$$), the pronounced nonohmic behavior at $$ T⩽$$ 1.2 K, extending up to 45 T, indicates that the resistive state is not a conventional metallic ground state but rather a dissipative vortex liquid (37). The extent of the second vortex solid regime (i.e., the intervening regime in which $$ {\mu }_0{H}_r$$ increases with decreasing $$ I$$) is smaller than that observed in Y123 at $$ p$$ = 0.11 (20, 21), possibly reflecting the improved stoichiometry in Y124 and/or the weaker strength of the charge order (14, 23).

Fig. 2.

Nonohmic resistivity and superconducting transitions in Y124. (A–D) Longitudinal resistivity $$ {\rho }_{\mathrm{a}}$$ as a function of magnetic field at temperatures of ($$ A$$) 0.32 K, ($$ B$$) 1.2 K, ($$ C$$) 4.2 K, and ($$ D$$) 11 K. Excitation current $$ I$$ and corresponding current density $$ j$$ are indicated in $$ D$$. $$ {\rho }_{\mathrm{a}}$$ becomes $$ I$$ dependent at $$ T⩽$$ 4.2 K with the onset magnetic field of finite resistivity $$ {\mu }_0{H}_{\mathrm{r}}$$ shifting to higher values upon reducing $$ I$$. ($$ A$$, Inset) The same 0.32-K data plotted on a semilog scale. A resistivity threshold, defined by the noise level of the 10-$$ \mathrm{\mu }$$A sweep and marked by the horizontal dash, is used to define $$ {\mu }_0{H}_{\mathrm{r}}$$. No apparent effect of $$ I$$ on $$ {\rho }_{\mathrm{a}}$$ is observed at 11 K.

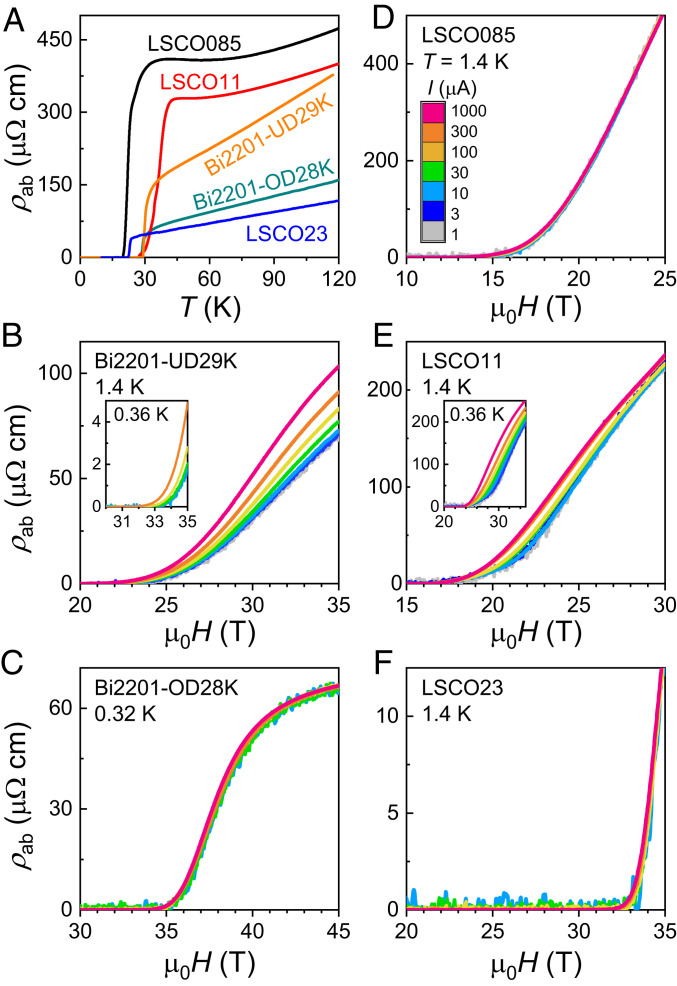
To further clarify the role of electronic disorder and charge order in the nonohmic regime, we proceed to investigate the low-$$ T$$ electronic transport in the more disordered cuprates LSCO and Bi2201 over a broader doping range. Fig. 3 shows the in-plane resistivity $$ {\rho }_{\mathrm{a}\mathrm{b}}$$ of LSCO and Bi2201 crystals with doping levels extending from the highly underdoped ($$ p$$ = 0.085) to the heavily overdoped regime ($$ p$$ = 0.23). Data at the lowest temperatures at which the resistive state could be accessed with a magnetic field of 35 T (Fig. 3 B and D– $$ F$$) or 45 T (Fig. 3$$ C$$) are shown. In the underdoped crystals where long-range charge order is believed to be present, namely Bi2201-UD29K (underdoped, $$ T_{\mathrm{c}}$$ = 29 K; $$ p\approx $$ 0.125) and LSCO11 ($$ p$$ = 0.11), nonohmic behavior onsets once again below 10 K and becomes more pronounced with decreasing temperature (Fig. 3 $$ B$$ and $$ E$$ and SI Appendix, Fig. S2). In stark contrast, in the highly underdoped LSCO085 (Fig. 3$$ D$$) and overdoped Bi2201-OD28K (overdoped, $$ T_{\mathrm{c}}$$ = 28 K; $$ p\approx $$ 0.19) and LSCO23 (Fig. 3 $$ C$$ and $$ F$$), where long-range charge order has not been observed, $$ {\rho }_{\mathrm{a}\mathrm{b}}$$ remains ohmic down to the lowest accessible temperatures. The concurrence of nonohmic behavior and long-range charge order indicates that these two phenomena are closely linked.

Fig. 3.

Confined nonohmic behavior within the long-range charge-ordered regime. ($$ A$$) In-plane resistivity $$ {\rho }_{\mathrm{a}\mathrm{b}}\left(T\right)$$ of LSCO and Bi2201 crystals studied in this work. Doping levels $$ p$$ are denoted for LSCO (i.e., $$ p$$ = 0.085 for LSCO085) and $$ T_{\mathrm{c}}$$ values are denoted for underdoped (UD) ($$ p\approx 0.125$$) and overdoped (OD) ($$ p\approx 0.19$$) Bi2201. ($$ B$$–$$ F$$) Magneto-resistivity $$ {\rho }_{\mathrm{a}\mathrm{b}}\left({\mu }_{0}H\right)$$ measured using excitation currents $$ I$$ ranging from 1 $$ \mathrm{\mu }$$A to 1 mA (color coded in $$ D$$), at constant temperatures as indicated. No effect of the magnitude of $$ I$$ on $$ {\rho }_{\mathrm{a}\mathrm{b}}$$ is observed in ($$ D$$) highly underdoped LSCO085, ($$ C$$) overdoped Bi2201-OD28K, and ($$ F$$) LSCO23, all of which are located outside the long-range charge-ordered regime; meanwhile $$ {\rho }_{\mathrm{a}\mathrm{b}}$$ is highly nonohmic in the resistive state of long-range charge-ordered ($$ B$$) Bi2201-UD29K and ($$ E$$) LSCO11.

The possibility of an extrinsic origin for the observed nonohmic behavior, such as chemical inhomogeneity and temperature instability, is carefully examined and effectively ruled out. First, the fact that $$ {\rho }_{\mathrm{a}}$$ is $$ I$$ independent at $$ T⩾$$ 10 K argues against a possible contribution from filamentary or surface superconductivity to the nonohmic behavior, for which an $$ I$$-dependent $$ {\rho }_{\mathrm{a}}$$ would be expected at all temperatures. Second, no discernible trace of temperature instability from the thermometer or from the samples is found in our measurements (except potentially at the highest excitation currents—see Materials and Methods for details). Finally, the observance of Ohm’s law in LSCO and Bi2201 crystals, outside of the charge-ordered doping regime, appears to rule out a disorder- or heating-induced origin of the low-$$ T$$ nonohmic behavior. We therefore conclude that the observed nonohmic behavior is an intrinsic property of long-range charge-ordered cuprates at low temperature and high magnetic field.

Anomalous Vortex Liquid and $$ H$$–$$ T$$ Phase Diagram

Having established the nonohmic resistivity as an intrinsic characteristic of the low-$$ T$$ electrical transport in long-range charge-ordered cuprates, we now proceed to explore its underlying mechanism. In a type-II superconductor, vortices can be depinned by thermal fluctuations at $$ T\gg 0$$ or by quantum fluctuations as $$ T\to 0$$. At $$ T\gg T_{\mathrm{m}}$$, the temperature above which vortices become mobile, the thermal energy $$ k_{\mathrm{B}}T$$ is much larger than the pinning potential $$ U_0$$ and no pinning is expected. In this regime, the resistivity due to vortex flow is ohmic and given by $$ {\rho }_{\mathrm{fl}\mathrm{o}\mathrm{w}}={\rho }_{\mathrm{n}}\left(H/H_{c2}\right)$$, where $$ {\rho }_{\mathrm{n}}$$ is the normal-state resistivity (38). At $$ T\to T_{\mathrm{m}}$$, $$ U_0$$ becomes comparable to $$ k_{\mathrm{B}}T$$, at which point vortex motion becomes activated, which can lead to an anomalous vortex liquid state with its resistivity following a thermally activated form: $$ \rho =\left({\rho }_{\mathrm{fl}\mathrm{o}\mathrm{w}}/A\right)$$ exp$$ \left(-U_0/T\right)$$ with $$ A\gg $$ 1. While the identification of $$ {\rho }_{\mathrm{n}}$$ in cuprates in the absence of superconductivity remains controversial (3940–41), a nonohmic resistivity can be regarded as the defining experimental signature of a vortex-liquid state. Fig. 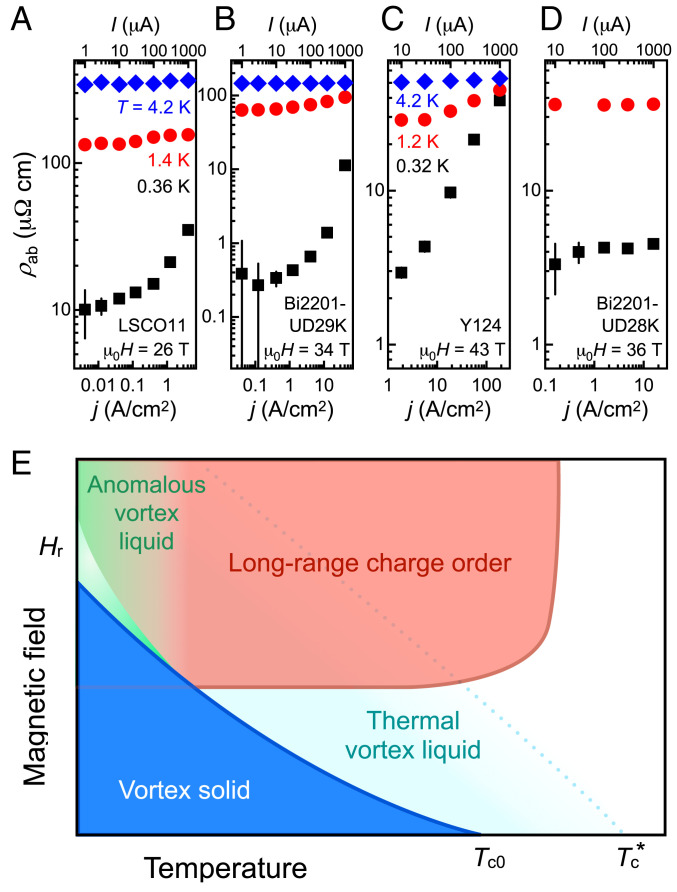4 $$ A$$–$$ C$$ shows the in-plane resistivity as a function of applied current density $$ j$$ of long-range charge-ordered cuprates at $$ T⩽$$ 4.2 K and magnetic fields near the vortex solid boundary at $$ T\to 0$$, where thermal fluctuations are minimized. At $$ T\approx $$ 0.3 K, $$ \rho $$ in all three crystals is weakly $$ j$$ dependent at low $$ j⩽$$ 1 A/$$ {\mathrm{c}\mathrm{m}}^2$$ and strongly $$ j$$ dependent at the intermediate regime 1 A/$$ {\mathrm{c}\mathrm{m}}^2⩽j⩽$$ 100 A/$$ {\mathrm{c}\mathrm{m}}^2$$, which appears to converge with $$ \rho $$ at higher temperatures. Access to the regime of $$ j⩾$$ 100 A/$$ {\mathrm{c}\mathrm{m}}^2$$ is precluded by joule heating, despite a low contact resistance $$ \approx $$1 $$ \mathrm{\Omega }$$ at room temperature in our pristine crystals. The dependence of $$ \rho $$ on $$ j$$ in the long-range charge-ordered crystals is characteristic of an anomalous vortex liquid occurring at $$ T\gtrsim T_{\mathrm{m}}$$ (37). Furthermore, the highly nonohmic resistivity shown in Fig. 4 $$ A$$–$$ C$$ follows $$ \rho \propto $$ exp$$ \left(-U_0/T\right)$$ with $$ U_0\approx $$ 1 K (SI Appendix, Fig. S4) and strongly contrasts the nearly $$ j$$-independent, ohmic resistivity observed in overdoped Bi2201-OD28K (Fig. 4$$ D$$), despite the fact that the resistive state at $$ {\mu }_{0}H=$$ 36 T is evidently within the vortex-liquid regime (Fig. 3$$ C$$). Therefore, we attribute the low-$$ T$$ nonohmic behavior to the emergence of an anomalous vortex liquid under high magnetic fields in the charged-ordered cuprates.

Fig. 4.

Signature of anomalous vortex liquid and schematic magnetic field$$ -$$temperature phase diagram. ($$ A$$–$$ D$$) In-plane resistivity as a function of applied current density $$ j$$ on a log-log scale for ($$ A$$) LSCO11, ($$ B$$) Bi2201-UD29K, ($$ C$$) Y124, and ($$ D$$) BI2201-OD28K at temperatures as indicated (same color code for $$ A,B$$ and $$ C,D$$, respectively). The magnetic fields at which resistivity is extracted, as indicated in each panel, are chosen to be slightly above $$ {\mu }_0{H}_{\mathrm{r}}$$ at $$ T\approx $$ 0.3 K, where thermal fluctuations are minimized. For all three underdoped cuprates ($$ A$$–$$ C$$), $$ \rho $$ is increasingly $$ j$$ dependent upon decreasing temperatures, the experimental signature of an anomalous vortex-liquid state at $$ T\gtrsim T_{\mathrm{m}}$$, the temperature above which vortices become mobile (37). In stark contrast, $$ \rho $$ in overdoped Bi2201-OD28K ($$ D$$, $$ p\approx 0.19$$) is independent of $$ j$$ within the experimental uncertainty. ($$ E$$) Schematic magnetic-field$$ -$$temperature phase diagram of charge-ordered cuprates. $$ T_{\mathrm{c}\mathrm{0}}$$ and $$ T_{\mathrm{c}}*$$ denote the onset temperature of zero-resistivity and fluctuating superconductivity. The dotted line encompasses a broad regime of superconducting fluctuations with mobile vortices depinned by thermal fluctuations at high temperatures and quantum fluctuations as $$ T\to 0$$. In zero magnetic field and above $$ T_{\mathrm{c}\mathrm{0}}$$, where no static vortices are expected, superconducting fluctuations can arise from the phase incoherence or spontaneous creation of vortex–antivortex pairs due to thermal fluctuations (42). The vortex solid boundary is mapped by $$ H_{\mathrm{r}}\left(T\right)$$, below which the measured resistivity descends into the noise floor (Fig. 2A). Below 10 K, the temperature at which long-range charge order and vortex solid coexist in high fields, $$ H_{\mathrm{r}}$$ is determined by the magnitude of the driving current and a regime of fragile superconductivity with an unusually low $$ j_{\mathrm{c}}$$ (marked in light green) is realized. The neighboring regime of anomalous vortex liquid, experimentally identified by the emergence of nonohmic resistivity, does not represent a distinct state of matter but rather a crossover from the thermal vortex liquid with unpinned vortices to a low-$$ T$$ regime in which the vortices become increasingly pinned. This crossover is found to onset in the range 4.2 K $$ <T<$$ 10 K, as illustrated by the gradated color shading.

Our key findings are summarized in the $$ H-T$$ phase diagram shown in Fig. 4$$ E$$, which illustrates the same qualitative behavior observed in the three long-range charge-ordered cuprates investigated here. The presence of long-range charge order (2526272829–30) within the vortex solid regime at $$ T⩽$$ 10 K appears to suppress the critical current, leading to a dynamic vortex-solid boundary with respect to the driving current, in accordance with previous magnetic torque and transport experiments (19, 20, 21). While the upper field limit to which the nonohmic behavior persists is unclear from the present study, our results reveal the existence of an anomalous vortex liquid above $$ {\mu }_0{H}_{\mathrm{r}}$$ at the lowest accessible temperatures, where thermal fluctuations are expected to be negligible and vortices are likely to be depinned by quantum fluctuations intensified by high magnetic fields. Importantly, the present study reveals a doping dependence that ties the emergence of the anomalous vortex liquid, irrespective of the level of disorder or structural details, to the regime of long-range charge order. We note that a very recent nonlinear magnetotransport study (43) on stripe-ordered Nd- and Eu-doped LSCO ($$ p\approx $$ 0.11) finds similar evidence for such a vortex liquid state, with an onset temperature of $$ \approx $$ 10 K, which exists between $$ {\mu }_0{H}_r$$ and $$ {\mu }_0{H}_{c2}$$ over a broad field range $$ \approx $$ 20 T at $$ T\approx $$ 20 mK. The common behavior now observed in five different cuprate families (including the previously studied Y123 and Nd/Eu-LSCO) suggests a general applicability of Fig. 4$$ E$$ to charge-ordered cuprates, despite the fact that field-induced long-range charge order has been only indirectly inferred for Y124 and LSCO.

Intertwined Charge Order and Superconductivity

Ordinarily, the introduction of an additional periodically modulated energy landscape would act to increase $$ U_0$$ and strengthen vortex pinning. However, considering the extremely small amplitude of the lattice displacements brought about by the charge order (on the order of $$ 5\times 10^{-3}$$ Å or 0.1% of the interatomic distances) (44), any strengthening of vortex pinning is likely to be negligible. Rather, the presence of long-range charge order is likely to have a detrimental effect on the superconductivity. In the following, therefore, we consider possible origins for the suppression of $$ j_c$$ within the regime of coexisting vortex solid and charge order. In conventional superconductors, the vortex pinning strength scales with $$ {\mathrm{\Delta }}^2$$, the square of the pairing amplitude. Hence, any suppression of $$ \mathrm{\Delta }$$ within the charge-ordered regime would have a correspondingly adverse effect on the strength of the depinning field.

In ref. 20, the suppression in $$ j_c$$ in Y123 ($$ p$$ = 0.11) was attributed to a transition of the pairing pattern of the superconducting condensate to accommodate the competing charge order when it becomes long ranged. A possible association to the pair-density-wave (4546–47) or related Fulde–Ferrel–Larkin–Ovchinnikov state (48) was suggested. The extent to which these exotic pairing states can lead to a dramatic suppression of $$ j_c$$, however, remains to be clarified. It is nevertheless worthwhile to consider the relevant length scales of the charge order and the vortex lattice and how they might affect $$ j_c$$. Assuming a two-dimensional array of vortices without disorder, the average distance between vortices is given by $$ r_{\mathrm{B}}=\sqrt{{\mathrm{\Phi }}_0/\pi {\mu }_{0}H}$$ = 70 Å, where $$ {\mathrm{\Phi }}_0$$ is the flux quantum, at the onset magnetic field (25, 26, 30) for long-range charge order of 15 T. For Y123, the charge order correlation length (26) $$ {\xi }_{\mathrm{C}\mathrm{O}}$$ increases almost fourfold from $$ \approx $$70 to 300 Å in an applied magnetic field of 25 T. Although the corresponding correlation lengths for the underdoped cuprates investigated here have not been reported, a similar enhancement, e.g., from $$ \approx $$20 to 80 Å, when the charge order evolves from being short ranged (5, 6) to long ranged, can be expected. Recent scanning–tunneling (49) and NMR studies (29) on underdoped cuprates have found compelling evidence that the emergence of charge order is associated with the vortex cores. Consequently, once $$ {\xi }_{\mathrm{C}\mathrm{O}}$$ exceeds $$ r_{\mathrm{B}}$$, the long-range correlations between the pinned charge order can have an impact on the dynamical response of the vortex liquid with respect to the external driving current. Within the framework of weak collective pinning theory proposed by Larkin and coworkers (37) and Larkin and Ovchinnikov (50) (applicable to the cuprates as the depairing current density $$ j_o$$ is much greater than the critical current density, i.e., $$ j_{\mathrm{c}}/j_o\ll 1$$),

Very recently, X-ray scattering experiments (51) on Y123 ($$ p=0.12$$) in fields up to 16.5 T have found evidence that the two forms of charge order coexist in a spatially separated manner and compete with superconductivity in different ways. The charge order with three-dimensional long-range in-phase $$ c$$-axis correlations is found to suppress superconductivity more strongly than its counterpart with short-range antiphase correlations. The locally distinct competition between superconductivity and charge order could lead to a spatially dependent pinning potential for the vortices and therefore a suppression in $$ j_{\mathrm{c}}$$. Further X-ray studies on LSCO and Bi2201 are required to determine whether the same mechanism is also at play in the underdoped regime of these materials. In Y124, the absence of X-ray or NMR evidence suggests that the charge order would occur only at higher fields, possibly around 35 T above which a negative Hall coefficient (36) and a nonohmic resistivity are observed (Fig. 2), making transport probes more suited to study the impact of charge order in this compound.

Our current work demonstrates that the intertwining of superconductivity and charge order can lead to the emergence of an unconventional vortex phase at $$ T\ll T_{\mathrm{c}}$$ and suggests a state of locally fragile superconductivity (23) and anomalous metallicity in the underdoped cuprates (43, 52). Previously, the observation of quantum oscillations in underdoped cuprates, typically appearing soon after the resistive transition (1314–15), had been interpreted in terms of a reconstructed Fermi surface of the underlying normal state in which superconductivity is completely suppressed. Such an interpretation may now need to be reexamined. In particular, quantum oscillations in Y124 that onset at $$ \approx $$45 T are seen to occur within the newly revealed anomalous vortex-liquid state. Proposals of quantum oscillations arising from a vortex state should thus be reconsidered (5354–55), while the interpretation of other high-field experiments, including thermal conductivity (16), X-ray scattering (25), specific heat (5657–58), and NMR (59), may be improved by considering the possible influence of the vortex contribution.

Materials and Methods