The Model.

In classical HIT, the finite size $$ D$$ of the turbulent box bounds the largest scale. The turbulent energy is supplied at some characteristic scale $$ M\le D$$, which might be the size of a bluff body, the mesh size of the turbulence-generating grid, or $$ D$$ itself. In a steady state, the turbulent kinetic energy, $$ K$$, and the rate of energy dissipation $$ \epsilon $$ at small scales are related by $$ \epsilon =-dK/dt$$. Nonlinearity ensures that the energy is dissipated in a different range of scales than the injection range. By the processes of advection and stretching, the energy is thought to undergo the Richardson cascade down the scales until it reaches small scales of dissipation. The characteristic scale around which the turbulent energy eventually dissipates is the Kolmogorov scale $$ \eta \equiv {({\nu }^3/\epsilon )}^{1/4}$$, where $$ \nu $$ is the fluid viscosity; the corresponding Kolmogorov wavenumber $$ k_{\eta }=2\pi /\eta $$. One can also define, taking $$ \nu $$ and $$ \epsilon $$ as the only relevant variables, a corresponding velocity scale $$ u\equiv {(\nu \epsilon )}^{1/4}$$, which characterizes the motion of the scale $$ \eta $$; the characteristic Reynolds number $$ {\mathrm{R}\mathrm{e}}_{\eta }=u\eta /\nu \equiv 1$$. From these considerations, scales smaller than $$ \eta $$ are not relevant to turbulence dynamics in a classical viscous fluid.

If the energy input at scale $$ M$$ is small enough for the Kolmogorov dissipation length $$ \eta $$ to be of the order of $$ M$$, no turbulence can be created. Upon increasing $$ \epsilon $$, $$ \eta $$ becomes smaller and crosses $$ M$$; gradually an “inertial range” of scales develops between $$ M$$ and $$ \eta $$. According to our present understanding, the part of the spectrum for $$ k<M$$ acquires a $$ k^2$$ slope by the equipartition theorem, in agreement with the Birkhoff–Saffman invariant (7, 8). By requiring the spectral energy density $$ E(k)$$ in the inertial range to depend only on the wavenumber $$ k$$ and $$ \epsilon $$ (which is transmitted across the inertial range without dissipation), one arrives at the celebrated Kolmogorov form $$ E(k)=C{\epsilon }^{2/3}{k}^{-5/3}$$, where the constant $$ C$$ is experimentally known to be about $$ 1.62\pm 0.17$$ (9).

After the cessation of energy input, the energy-containing scale grows with time and could saturate at $$ D$$ at some point. Although $$ \eta $$ also grows with time, leading to a shorter inertial range, considerable scale separation could persist and the spectrum in the decaying state could retain the same form as above. In this state of decay (10), it is possible to solve for the energy as a function of time. The result is that $$ \epsilon \propto t^{-2}$$ and the turbulent energy decays as $$ K\propto t^{-2}$$.

In pure superfluid turbulence, there is no viscosity and hence no dissipative scale $$ \eta $$. The flow exists down to the smallest scale, which is the size of the vortex core $$ {\xi }_4\approx 0.1$$ nm in He II and $$ {\xi }_3\approx 10\hspace{0.17em}to\hspace{0.17em}60$$ nm in ³He-B. One can, however, define the superfluid Reynolds number $$ {\mathrm{R}\mathrm{e}}_Q$$ by replacing the kinematic viscosity $$ \nu $$ by the quantum of circulation $$ \kappa $$ of the same dimensions, and ask for the length scale $$ {\ell }_{\text{Q}}$$ at which $$ {\mathrm{R}\mathrm{e}}_Q={\mathrm{u}}_{\text{Q}}{\ell }_{\text{Q}}/\kappa \equiv 1$$, where $$ u_{\text{Q}}\equiv {(\kappa \epsilon )}^{1/4}$$.* We call the length $$ {\ell }_{\text{Q}}$$ as the quantum length scale^† $$ {\ell }_{\text{Q}}={({\kappa }^3/\epsilon )}^{1/4}$$ and define a corresponding wavenumber as $$ k_{\text{Q}}=2\pi /{\ell }_{\text{Q}}$$. Physically, $$ {\ell }_{\text{Q}}$$ marks the transition between quasiclassical scales for which quantization of circulation plays no role (or the “granularity” of QT does not matter) and the quantum scales for which quantum restrictions are essential.

The Kolmogorov cascade cannot proceed beyond $$ k_{\text{Q}}$$ because its very existence is a purely quantum effect. The transfer of turbulent energy farther down the scales is possible by a different mechanism mediated by the Kelvin wave cascade on individual vortex lines in incompressible flow (12) [although a bottleneck, analogous to the classical case (13), might develop around $$ {\ell }_{\text{Q}}$$ (14)]. The dissipation mechanism for $$ k>k^{*}$$ is the phonon emission by Kelvin waves in He II (15) or the excitation of Caroli–Matricon states in vortex cores in ³He-B (16). For this range, L’vov and Nazarenko (17) derived (neglecting these dissipation mechanisms) the superfluid energy spectrum for $$ k>k_{\text{Q}}$$ to be of the form

Now, let us examine the evolution of the steady-state superfluid energy spectrum in a box of size $$ D$$, assuming a sustained energy input at scale $$ M$$ (e.g., by a grid of mesh size $$ M$$, $$ {\xi }_3,{\xi }_4\ll M\ll D$$) (Fig. 1). Any remnant vorticity (21) (e.g., vortex loops pinned on the grid surface, which is nearly always rough on these scales) becomes unstable by the Glaberson–Donnelly instability (22), leading to a vortex tangle when the critical flow velocity is exceeded. A steady-state superfluid energy spectrum develops after a transient, truncated at $$ k^{*}$$ by one of the mechanisms described above.

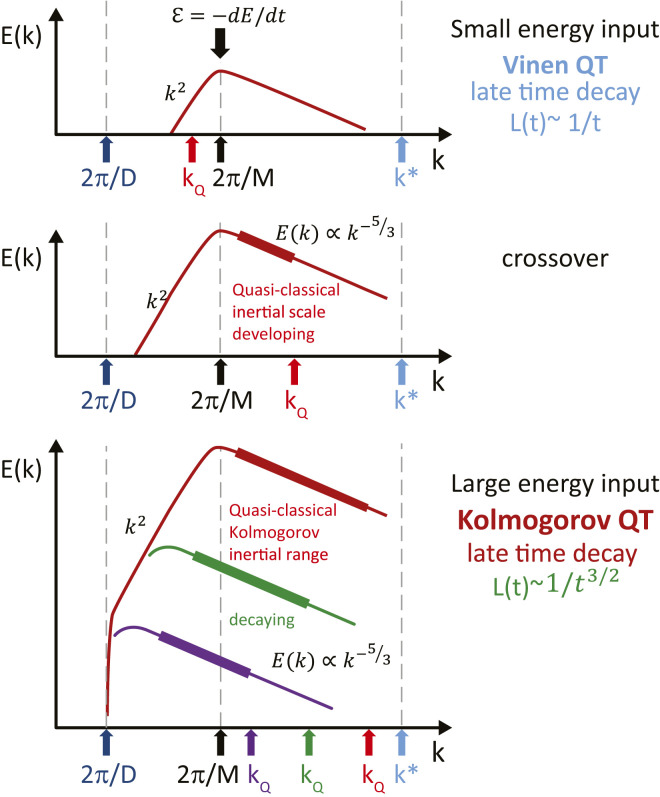
Fig. 1.

Schematic in log-log coordinates of the general shapes of 3D energy spectra $$ E(k)$$ plotted versus the wavenumber $$ k$$ of purely superfluid turbulence, assuming that it is forced at the scale $$ M$$. (Top) Vinen turbulence, where $$ {\ell }_{\text{Q}}$$ (red arrow) is larger than $$ M$$. (Middle) Crossover from Vinen to Kolmogorov turbulence. With increasing $$ \epsilon $$, $$ {\ell }_{\text{Q}}$$ crosses $$ M$$. The classical Richardson cascade begins to operate and an inertial range of scales (thick red) develops gradually. (Bottom) For large enough $$ \epsilon $$, a significant extent of the inertial range develops as in steady-state classical 3D HIT (red). After the forcing stops, the decaying spectrum is shown in green and violet for two subsequent times; $$ k_{\text{Q}}$$ values are shown explicitly for each of them. The energy-containing scale grows during decay and eventually saturates at $$ D$$ and the classical decay of the form $$ L(t)\propto t^{-3/2}$$ follows (20). Also, $$ k_{\text{Q}}$$ decreases faster than the energy-containing scale, so the inertial range shrinks with time. The spectra between $$ k_{\text{Q}}$$ and $$ k^{*}$$ have been drawn with slopes of $$ -5/3$$ to be consistent with Eq. 1.

The actual form of the steady-state energy spectrum depends on the interplay between the two important scales, $$ M$$ and $$ {\ell }_{\text{Q}}$$. For small enough $$ \epsilon $$, $$ {\ell }_{\text{Q}}>M$$, and so the Richardson cascade cannot operate. Energy is transferred down the scales via a Kelvin wave cascade or quantum stress cascade, until $$ k^{*}$$ is reached. This is the Vinen (ultraquantum) turbulence, where the vortex tangle is approximately random (Fig. 1, Top). The temporal decay of this turbulence, characterized by just one fixed length scale (quantized vortices in the tangle are assumed to be approximately evenly spaced), was first discussed by Vinen (23). On page 504, he wrote, “We shall now suppose that, if two oppositely directed vortex lines approach each other sufficiently closely, they can break up into small vortex rings in the manner suggested by Feynman (6) and eventually degenerate into thermal excitations” and argued that the vortex line density decays according to the equation

Let us now increase $$ \epsilon $$ so that $$ {\ell }_{\text{Q}}$$ becomes nominally smaller than $$ M$$ (Fig. 1, Middle). Assuming an interaction between scales á la the equipartition theorem, the spectrum to the left of $$ M$$ must acquire the $$ k^2$$ form, but the situation to the right of $$ M$$ changes by developing an inertial range between $$ M$$ and $$ {\ell }_{\text{Q}}$$, with the energy transfer from the small to the large wavenumbers occurring quasiclassically via the Richardson cascade. With increasing $$ \epsilon $$, the inertial range of scales increases and contains most of the kinetic energy of superfluid turbulence; see the red spectrum in Fig. 1, Bottom. This is the Kolmogorov (quasiclassical) turbulence, containing large vortex structures which can be thought of as composed of vortex-line bundles, achieved by partial polarization of the tangle. At scales sufficiently larger than $$ {\ell }_{\text{Q}}$$, the shape of the energy spectrum is thus Kolmogorov’s. How far in $$ k$$ this picture holds depends on the interplay between classical and quantum physics, since the latter starts to intervene when approaching $$ k_{\text{Q}}=2\pi /{\ell }_{\text{Q}}$$; thereon, the turbulent motion is discretized and governed by quantum physics, described by the dynamics of individual quantized vortices. The quasiclassical limit is very similar to 3D Navier–Stokes for HIT, where viscous dissipation acting at small scales of order $$ \eta $$ is replaced by one of the mechanisms discussed above. At scales smaller than $$ {\ell }_{\text{Q}}$$ the turbulence is always ultraquantum.

A key point is that for classical turbulence in the unbounded case, there are only two length scales to consider: $$ M$$ and $$ \eta $$. In superfluid turbulence, there is an additional important scale, $$ {\ell }_{\text{Q}}$$, which intervenes as described above. Pure superfluid turbulence therefore cannot be considered, in contrast to statements in the literature, a simple “prototype” of turbulence; despite the similarities, it is different and more complex than the classical case. Naturally, however, the quasiclassical part of the picture is the same as that of classical 3D HIT and its temporal decay follows predictions of the spectral decay model (10, 24, 25). It is applicable also for decaying vortex line density, $$ L$$, since the quasiclassical relation $$ \epsilon ={\nu }_{\text{eff}}{(\kappa L)}^2$$, following from the Navier–Stokes equations, holds (20). Here $$ \kappa L$$ is the quasiclassical vorticity and $$ {\nu }_{\text{eff}}$$ denotes the effective kinematic viscosity. We present the experimental evidence for this relationship in Cross-Over from the Vinen to Kolmogorov Forms.

We note that this close correspondence of the Kolmogorov-type QT with the classical case suggests the plausibility that the intermittency corrections may be the same for classical 3D HIT and for Kolmogorov pure superfluid turbulence at scales sufficiently larger than $$ {\ell }_{\text{Q}}$$. We will comment more on it later.

Manifestations of Vinen and Kolmogorov Forms of QT.

At present, there are no direct spectral measurements of superfluid turbulence at zero temperature (i.e., close enough to zero that the normal component is essentially nonexistent), so we cannot test the model in detail. Following Vinen (20), we introduce an effective mean-square vorticity in the superfluid component, defined by $$ {\langle {\omega }^2\rangle }_{\text{eff}}={(\kappa L)}^2$$, which allows us to make direct reference to the experimentally measured quantity $$ L$$. Using the above relation, we obtain the expression $$ L(t)\propto 1/t^{3/2}$$ at late times for Kolmogorov QT when the length-scale saturation occurs; this is the result we shall test repeatedly here. The spectral form of the Vinen turbulence is not known [it could be of the $$ k^{-5/3}$$ form as in Eq. 1 with a bottleneck or of the $$ k^{-3}$$ form of Tanogami (19)].^‡ For the purposes of Fig. 1, we take the manifestation of the Vinen turbulence to be Eq. 2, according to which (at late times) $$ L\propto 1/t$$. This is the main result we will test here. Our other important exploration concerns the cross-over between the two types of turbulence.

Cross-Over from the Vinen to Kolmogorov Forms.

We will illustrate the cross-over in both steady-state and decaying quantum turbulence in ³He-B in the measurements of the Lancaster group (27). QT was generated by oscillating grids and detected using the unique technique of Andreev reflection, which is possible because of the fermionic nature of superfluidity in ³He-B. Briefly, the equilibrium number of quasiparticles (and quasiholes) can be sensed by a vibrating wire resonator. The drag force exerted on the vibrating wire by these ballistically propagating excitations is reduced if the wire is surrounded by a vortex tangle, as some incoming quasiparticles (quasiholes) cannot reach it, being Andreev reflected by energy barriers of the velocity field near the vortex cores.^§ The fractional decrease in damping can then be converted into the vortex line density in the tangle (27).

Two complementary experiments are worthy of attention. In the first one, quantum turbulence is generated by an oscillating grid of fine copper wires spaced $$ M=50\mu $$m apart. By increasing the forcing, more and more energy is supplied to the flow at the scale $$ M$$, all of which is being dissipated in the steady state. Facing the grid are detectors of quantum turbulence—two vibrating wire resonators—detecting the transition to quantum turbulence above a certain drive level (28). Increasing the oscillation amplitude of the grid results in a higher energy decay rate, $$ \epsilon $$; consequently, the quantum wavenumber $$ k_{\text{Q}}\propto {\epsilon }^{1/4}$$ increases. Bradley et al. (29) then investigated the temporal decay of vortex line density originating from various levels of intensity of the steady state; they presented representative results in their figure 2. With increasing $$ \epsilon $$ used to reach the steady state, temporal decay changed its form from $$ L(t)\propto t^{-1}$$ (Vinen QT) to $$ L(t)\propto t^{-3/2}$$ (the Kolmogorov QT in a bounded domain).^¶

In the second experiment, Bradley et al. (31) measured directly the energy decay rate $$ \epsilon $$ of grid-generated turbulence inside a small box acting as a black body radiator of quasiparticles. The late-time decay changes in character, from $$ \epsilon \propto t^{-2}$$ to $$ \epsilon ={\nu }_{\text{eff}}{\kappa }^2{L}^2\propto t^{-3}$$—consequently the turbulent energy decays as $$ K\propto t^{-2}$$, in agreement with the late decay of turbulent energy in classical 3D HIT in a bounded domain. We emphasize that this experiment provides a direct measurement of the energy released by freely decaying quantum turbulence. It is remarkable that, leaving aside caveats such as homogeneity and isotropy of the turbulence inside the black box radiator, the decay of pure superfluid turbulence was found to be surprisingly similar to the known decay of classical 3D HIT. The results also confirm that the key phenomenological relationship, $$ \epsilon =-dK/dt={\nu }_{\text{eff}}{(\kappa L)}^2$$, first suggested by Vinen (20), is meaningful for the Kolmogorov type of pure superfluid turbulence.

We now consider another indication of the transition from Vinen to Kolmogorov turbulence in pure superfluid, following the scenario of Fig. 1, this time in He II. It is based on the observation of three critical velocities marking cross-overs between different types of flow due to the oscillating quartz tuning fork that resonates at 6.5 kHz, with prongs 3.50 mm long and a $$ 90\times 75-\mu $$m cross-section (32). The first critical velocity of about 2 cm/s is hydrodynamic in origin, related to the formation of a vortical boundary layer, and therefore not directly relevant to turbulence in the bulk liquid.^#

The second critical velocity can be linked reliably to significant production of quantized vorticity, which then propagates away from the surface of the tuning fork (or similar oscillators such as vibrating wires) and features a rapid increase in the drag force.^‖ The observed drag coefficients are typically $$ 10^{-2}\hspace{0.17em}to\hspace{0.17em}10^{-1}$$, much lower than in classical oscillatory flows, where drag coefficients of order unity are expected for cylinders or tuning forks at sufficiently high Reynolds number (or Keulegan–Carpenter number). This strongly suggests flow patterns significantly different from classical turbulence. No large flow structures resembling the classical wake exist in the superflow above the second critical velocity, which we therefore associate with the Vinen turbulence. It is only above the third critical velocity, about 1.5 m/s, that the drag coefficient starts to rise toward unity, the value typical for classical high $$ \mathrm{R}\mathrm{e}$$ flows. This is most likely related to a distinct change in the flow pattern, in which the superfluid develops larger polarized structures and starts to mimic the behavior of classical turbulent flows. We are therefore led to conclude that the third critical velocity marks the transition from Vinen- to Kolmogorov-type superfluid QT.

Pure Superfluid Turbulence in He II Driven at Small and Large Scales.

Quantitative data on steady-state and decaying pure superfluid He II turbulence have been obtained by Golov and coworkers (3435–36). They injected negative ions into the experimental cell by a sharp field-emission tip and manipulated them by an electric field. This technique can be used for both the generation and detection of quantum turbulence. We focus first on the pure superfluid turbulence generated by impulsive spin-down, in which a rotating cubic-shaped container of He II, 4.5 cm in size, is brought rapidly to rest. For all starting angular velocities ($$ 0.05\le \mathrm{\Omega }\le 1.5$$ rad/s) (34), observed decays are of the form $$ L(t)\propto t^{-3/2}$$, expected for late decay in classical 3D HIT decaying in the bounded domain—a strong signature of Kolmogorov-type QT.

Let us now consider temporal decay of pure superfluid turbulence with relatively low starting vortex line density, generated using an alternative technique of a jet of charged vortex rings of size about $$ 1\mu $$m, resulting from the injection of negative ions. At late times, two distinctly different power law decays were observed, depending on experimental conditions and the history of preparing the initial vortex tangle. Basically, instances of QT produced after short injection of ions display $$ L(t)\propto 1/t$$ decay, while those generated after sufficiently long injection follow $$ L(t)\propto t^{-3/2}$$ decay law at late times, in agreement again with Kolmogorov’s pure superfluid turbulence generated by the rapid spin-down technique.

The phenomenological explanation within our model is as follows. For short charging times, the turbulent energy is supplied to the flow at the scale given by the typical size, $$ 1\mu $$m, of small vortex rings injected to the flow. The situation is basically the same as in Fig. 1, Top, with the size of the injected rings playing the role of the mesh size of the grid, $$ M$$. The result is the Vinen turbulence with its typical signature, the $$ L(t)\propto 1/t$$ form of the late decay. On the other hand, if the tangle of the same vortex line density is prepared by long charging times, the injected vortex rings have plenty of time to interact with each other (for more details, see ref. 14 and numerical simulations therein) as well as with the already existing vortex tangle. During the reconnection processes, both smaller and larger vortex loops are created, the former quickly propagating and decaying and the latter eventually creating large energy-containing superfluid eddies. This way, a superfluid energy spectrum is formed whose large scales have a form similar to classical turbulence. This results in the $$ L(t)\propto t^{-3/2}$$ form of the late decay, a typical signature of the Kolmogorov turbulence in contained domains.

Situations intermediate to these two limiting cases are also possible, depending on the duration of charging, for which QT is neither of the Vinen nor of the Kolmogorov type. When charging is stopped, the vortex line density first roughly obeys the Vinen $$ L(t)\propto 1/t$$ type of decay (corresponding to the decay of energy contained in small eddies of the size of order $$ {\ell }_{\text{Q}}$$), displays a cross-over, and enters the $$ L(t)\propto t^{-3/2}$$ regime.

Superfluid Turbulence in Stationary Normal Fluid of ³He-B.

This case represents the next logical step in the phenomenological description of QT because of its simplicity. The simplicity arises from the relatively high kinematic viscosity of the normal fluid of ³He-B, which renders the normal fluid effectively stationary. ** Although we formally deal with two velocity fields, the velocity field of the normal fluid only determines the unique and physically significant frame of reference in which the normal fluid is at rest.

Experiments with ³He-B have to be performed at sub-milliKelvin temperatures; to keep the flow so cold, the energy input needs to be very modest, typically of the order a few nanowatts. It is this factor and the high viscosity of the normal fluid that ensure that the normal fluid remains at rest with respect to the experimental container. The vortex lines will thus not move freely but are subject to a friction force as they move; this friction is temperature dependent and becomes larger as $$ T\to T_{\text{c}}$$ (38). We should therefore expect that superfluid turbulence considered in the earlier section in the zero-temperature limit will be modified by the presence of damping: Vortex lines will appear smoother and short Kelvin waves and vortex cusps resulting from reconnections will be quickly damped out. With increasing temperature the damping becomes so strong that above $$ \approx 0.6T_{\text{c}}$$ quantum turbulence does not exist. Temperature thus plays a similar role here as the inverse Reynolds number in classical turbulence (39).

The energy spectrum of the turbulent superfluid possesses the following special features: 1) There is a maximum size of the turbulent eddy limited by mutual friction (40), and 2) dissipation due to mutual friction occurs at all length scales and 3) modifies the roll-off exponent to −3 at largest scales which, according to predictions of continuum approximation, displays a cross-over to the classical −5/3 (40, 41). Let us emphasize, however, that these results have been obtained theoretically within the continuum approximation, i.e., assuming that all relevant length scales of the problem are sufficiently larger than $$ \ell $$ and the energy input occurs at large scales. These features are yet to be investigated in detail experimentally.

Quantum Turbulence in He II above $$ \approx 1$$ K.

Here He II displays the two-fluid behavior. Isothermal incompressible flow of the normal fluid of He II can be described using the Navier–Stokes equations with density $$ {\rho }_{\text{n}}$$ and very low kinematic viscosity of order $$ \kappa $$, characterized by the analogue of the Reynolds number in classical viscous fluids: the Donnelly number, $$ \mathrm{D}\mathrm{n}$$, which is based on the kinematic viscosity of the normal fluid alone, $$ {\nu }_{\text{n}}=\mu /{\rho }_{\text{n}}$$, not on the kinematic viscosity $$ \nu =\mu /\rho $$ of the entire fluid.^†† Schmoranzer et al. (37) used this nomenclature for oscillatory flows at high Stokes numbers, but we extend its definition for any quantum flow of superfluid helium and suggest that its meaning is the same for the normal fluid flow as that of the Reynolds number in classical flows. Flow of the superfluid component of He II is potential. In isothermal flow of He II, the normal and superfluid velocity fields are independent but become coupled by the mutual friction force when quantized vortices appear in the superfluid. Additionally, any temperature gradient in He II results in a thermal counterflow of the normal and superfluid components against each other which we shall consider in detail later.

From the fluid-dynamical point of view, the situation in He II differs from that in ³He-B because the normal fluid is much less viscous. Additionally, the mutual friction force (characterized by the dissipative mutual friction parameter $$ \alpha $$) (42) at temperatures far enough away from $$ T_{\lambda }$$ is typically weaker by one to two orders of magnitude than in ³He-B above $$ \approx 0.3T_{\text{c}}$$, considered above. It therefore seems sensible to check whether the physical picture of two nearly independent velocity fields agrees with some experimental observations. We first focus on the isothermal and mechanically driven flows of He II.

It is often stated in the literature that the mechanically driven He II, with both components forced in the same way, results in the so-called coflow and represents Kolmogorov-type QT. This, however, is generally not the case. Experimental evidence on this point comes from a recent Prague experiment. QT is driven mechanically by a small quartz tuning fork with prongs of small $$ (75\times 90)\mu {\mathrm{m}}^2$$ cross-section. Fig. 2, Right shows that $$ L(t)\propto 1/t$$, the late temporal decay of the Vinen type, in accordance with Fig. 1, Top, where the flow is driven at a scale smaller than or comparable to $$ {\ell }_{\text{Q}}$$.^‡‡ The normal fluid is therefore driven by the fork at scale smaller than $$ {\eta }_{\text{n}}$$, for which the classical phenomenology is hardly applicable. The situation is somewhat as in ³He-B, but without the unique quiescent normal fluid frame; the normal fluid flow is characterized by $$ \mathrm{D}\mathrm{n}=17$$, which is slightly past the classical instability (37). Mutual friction is weak and does not significantly affect the decay.

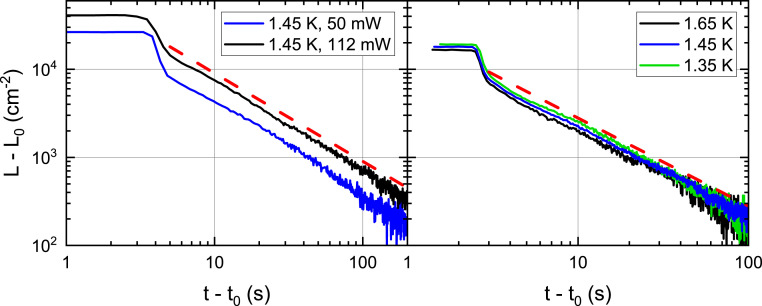
Fig. 2.

Temporal decay of vortex line density (Left) in spherical counterflow generated by a steady-state central heater and (Right) generated mechanically by a vibrating fork. In both panels, $$ t_0$$ is a virtual origin of time and $$ L_0$$ denotes the remnant vorticity. Red dashed lines have the slope $$ 1/t$$ to guide the eye.

It is fair to note that QT generated by an oscillating fork is far from HIT, so the experimental results should be interpreted with care. The nonhomogeneous tangle is expected to undergo a decay process accompanied by vortex diffusion. However, convincing experimental evidence was provided by Milliken et al. (43), who used the technique based on pulses of negative ions propagating through the steady state and decaying vortex tangles generated by ultrasound. The pulses were shaped by gate grids and manipulated by electric field, so that they could be stopped at a chosen position to provide spatial as well as temporal information on the decay. An overall inverse time decay of $$ L$$ was observed, which seemed to preserve its spatial profile, indicating that local decay dominates over diffusive phenomena. Under such an assumption, the nonlinear decay rate $$ \propto L^2$$ would first lead to a rapid homogenization of the tangle, which would further decay as $$ L(t)\propto t^{-1}$$.^§§

Kolmogorov Quantum Turbulence in Coflowing He II.

Consider now QT in coflowing He II at $$ T>1$$ K. Perhaps surprisingly, it has properties closely similar to those of 3D HIT in classical fluids. In contrast with ³He-B, the normal fluid of He II becomes readily turbulent: There are not one but two turbulent velocity fields, coupled by the mutual friction force, acting at all relevant length scales. We are dealing here with the situation of double turbulence and have to examine both the superfluid and the normal fluid energy spectra.

Let us consider the example of turbulent He II flow driven by a grid at mesh scale $$ M\gg {\ell }_{\text{Q}}$$. To simplify the problem, let us artificially switch off the mutual friction and assume that the temperature is just below $$ 1.5\mathrm{K}$$, where $$ {\nu }_{\text{n}}\approx \kappa $$ (42)—in other words, the Donnelly number is equal to the superfluid Reynolds number. It follows that $$ {\ell }_Q$$ in the superfluid is equal to the Kolmogorov dissipation scale $$ {\eta }_{\text{n}}$$ in the normal fluid and that the turbulent spectra in the normal fluid and in the superfluid are naturally matched at scales considerably larger than $$ {\ell }_Q$$ or $$ {\eta }_{\text{n}}$$. The difference is that while in the normal fluid the Richardson cascade is terminated at this scale, it continues in the superfluid in the form of a Kelvin wave or quantum stress cascade, and the dissipation occurs beyond $$ k^{*}$$ introduced above. Upon decreasing (increasing) the temperature, due to the steep temperature dependence of $$ {\nu }_{\text{n}}(T)$$, $$ {\eta }_{\text{n}}$$ becomes larger (smaller) than $$ {\ell }_Q$$. By turning on the mutual friction, not much happens at large scales (significantly exceeding $$ {\eta }_{\text{n}}$$ or $$ {\ell }_Q$$, whichever is larger), as large eddies of normal and superfluid components are closely matched. Upon approaching smaller and smaller scales, however, the matching cannot be complete, dissipation due to mutual friction starts to operate (the roll-off exponent becomes gradually steeper), and one component starts to act as a source or drain for the other. This results in an increase of intermittency corrections, as predicted by Boue et al. (44) and experimentally confirmed by Varga et al. (45).

Both the superfluid and normal energy spectra in steady-state and decaying Kolmogorov turbulence of He II contain an inertial range of scales. This has been observed in a number of coflow experiments, first by Maurer and Tabeling (46) in the von Kármán flow and by Roche and coworkers (47) in superfluid wind tunnels (48). In these experiments, velocity fluctuations were determined using a Pitot tube, and the characteristic $$ f^{-5/3}$$ frequency dependence of the spectrum was observed; this scaling corresponds to $$ E(k)\sim k^{-5/3}$$, if one uses Taylor’s frozen flow hypothesis, and confirms the presence of a Richardson energy cascade as in classical turbulence. Geometrically it means that the turbulence contains, within a tangle of random vortex lines, partially polarized vortex lines, or bundles, with relatively large coarse-grained superfluid vorticity. We also note that the inertial range in the turbulent normal fluid was observed by Guo and coworkers (45) by visualizing grid-generated turbulence using neutral He$$ 2*$$ molecules, allowing one to measure transverse velocity structure functions selectively in the normal fluid. This is possible due to the small size of He$$ 2*$$ triplet molecules that are effectively part of the normal fluid and do not trap vortex lines above $$ \approx 1$$ K (49).

Grid-generated QT in He II, driven at the large-scale $$ M$$, when both components are turbulent on scales appreciably larger than $$ {\ell }_Q$$, represents a typical example of Kolmogorov QT. Large normal and superfluid scales are closely coupled by mutual friction, which does not cause any appreciable energy loss and, in accordance with Richardson’s picture, there is an inertial range characterized by the −5/3 exponent (neglecting intermittency). Matching is not possible once the quantum or Kolmogorov length scale is reached. Mutual friction partly dissipates and partly transfers the turbulent energy from superfluid eddies to normal ones and vice versa, with either fluid serving as the drain or source of energy for the other. Viscous dissipation, together with the coupling by dissipative mutual friction, terminates both normal and superfluid cascades. The Kelvin wave or quantum stress cascades, so important in the zero-temperature limit, do not play a significant role here. Turbulent coflowing He II above about 1 K can thus be treated, at least approximately, as a single-component quasiclassical fluid, characterized by the temperature-dependent effective kinematic viscosity $$ {\nu }_{\text{eff}}$$. Its value can be extracted from the temporal decay, when $$ L(t)$$ displays the universal form of the decay [as observed in many experiments (10, 24, 25, 5051–52) and reviewed in ref. 25]:

Thermal Counterflow of He II.

The flow of He II can take various forms because of the existence of two fluid components. One can push the normal fluid and the superfluid components to flow with different average velocities, a situation generally called counterflow. A special case of counterflow is the thermal counterflow, easily achieved in a channel closed at one end and open to the He II bath at the other. Heat flux $$ \dot{q}$$ supplied at the closed end is carried away by the normal fluid, with the superfluid flowing in the opposite direction so that the net mass flux is zero. The counterflow velocity $$ u_{\text{ns}}=\dot{q}/({\rho }_{\text{s}}\sigma T)$$ is established, where $$ \sigma $$ is the entropy of He II. QT appears in the channel when $$ \dot{q}$$ exceeds a critical value.

It has been known since early experiments, notably those performed by Tough’s group (56), that counterflow turbulence can exist in two forms, referred to as T I and T II. Recently Guo and coworkers (49, 57), using helium excimer molecules as tracers of the normal fluid, revealed that the normal fluid in the T II state is turbulent. In the T I state, where the flow of the normal component is laminar beyond reasonable doubt, the turbulent energy is injected around $$ {\ell }_{\text{Q}}$$ by the reconnection-based mechanism first identified by Schwarz (54, 55). The superfluid energy spectrum therefore has the shape as sketched in Fig. 3, Top. The shape is the same as in Fig. 1, Top. For small enough $$ \epsilon $$ we deal with Vinen turbulence, the decay of which was experimentally confirmed (58) to obey $$ L(t)\propto t^{-1}$$ at late times.

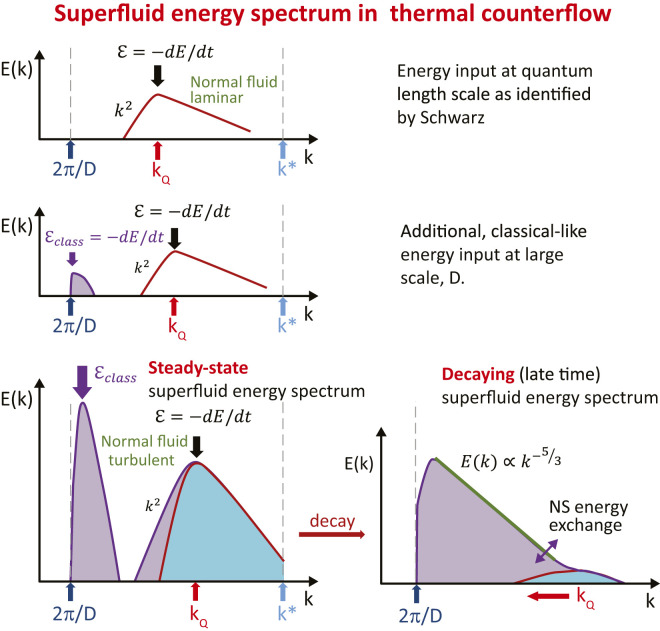
Fig. 3.

Schematic view in log-log coordinates of the general shapes of 3D superfluid energy spectra of thermal counterflow turbulence in He II. (Top) Vinen turbulence, where the energy input identified by Schwarz (54, 55) occurs at $$ {\ell }_{\text{Q}}=2\pi /k_{\text{Q}}$$ (red arrow). The temporal decay is of the form $$ L(t)\propto 1/t$$. (Middle) Upon increasing the heat flux, there is additional quasiclassical energy input in the normal component at large scale which, because of mutual friction, occurs in the superfluid component as well. (Bottom Left) With increasing heat input, there is energy input at large scale akin to classical turbulence, but the inertial range of the Kolmogorov-type QT, characterized by the −5/3 roll-off exponent, cannot develop, as mutual friction acts on all scales making the roll-off in this range much steeper. There is still a quantum peak because of the energy input at quantum length-scale $$ {\ell }_{\text{Q}}$$, which itself shifts to the right with increasing heat input. (Bottom Right) Once the heat flux ceases, the quantum energy peak quickly decays and the energy content at large scales gradually cascades down the scales, forming an inertial range that acquires classical Kolmogorov form. It results in a classical decay of the form $$ L(t)\propto 1/t^{3/2}$$, with growing quantum length-scale $$ {\ell }_{\text{Q}}$$.

The two forms of QT in He II—Vinen and Kolmogorov—display two distinctly different forms of decay which subsequently allow the definition of two effective kinematic viscosities of turbulent He II. In addition to $$ {\nu }_{\text{eff}}(T)$$ introduced above for Kolmogorov QT, we now follow refs. 36 and 52 and note that the energy per unit mass associated with a random tangle of vortex lines in Vinen QT (i.e., superflow circulating with velocity $$ \kappa /(2\pi r)$$ around vortex lines) is given by $$ ({\rho }_{\text{s}}{\kappa }^2)/(4\pi \rho )L\ln (\ell /{\xi }_4)$$, where $$ \ell =1/\sqrt{L}$$ denotes the mean intervortex distance in the tangle. By differentiating with respect of time and using Eq. 2, we see that the turbulent energy would then decay as $$ \epsilon ={\nu }^{\prime }{\kappa }^2{L}^2$$, where the quantity

We thus have two definitions for two effective kinematic viscosities $$ {\nu }^{\prime }$$ and $$ {\nu }_{\text{eff}}$$, which can be extracted from decaying turbulent He II flow of the Vinen and Kolmogorov forms. Their existence is not a consequence of the two-fluid behavior, since they readily exist in the $$ T\to 0$$ limit as well. And they need not be the same, either. Indeed, while $$ {\nu }_{\text{eff}}$$ is a property of turbulent flow of the entire He II, i.e., of both fluids whose turbulent motions are coupled at large enough scales, $$ {\nu }^{\prime }$$ is the property of a single fluid flow, namely of the turbulent superfluid component, coupled by the mutual friction force to the normal fluid. This difference—coupling to the normal fluid as well as the factor $$ {\rho }_{\text{s}}/\rho $$—should disappear with dropping temperature, as $$ {\rho }_{\text{s}}$$ approaches $$ \rho $$ and the mutual friction gradually ceases to operate. For reasons such as ill-defined boundary conditions in He II below 1 K, the values of $$ {\nu }^{\prime }$$ and $$ {\nu }_{\text{eff}}$$ are so far not determined with sufficient accuracy to unequivocally confirm that $$ {\nu }^{\prime }$$ equals $$ {\nu }_{\text{eff}}$$ at low temperature; however, they both have been found to be of order $$ 0.1\kappa $$ (51).^¶¶

At this point, we need to discuss the relation between the quantum length scale, defined as before quasiclassically as $$ {\ell }_{\text{Q}}={({\kappa }^3/\epsilon )}^{1/4}$$, and the mean intervortex distance $$ \ell =1/\sqrt{L}$$, as this quantity is also often referred to in the literature as quantum length scale. It is easy to show that for Kolmogorov turbulence in He II they are roughly equal. Indeed, assuming the validity of the above quasiclassical relationship $$ \epsilon ={\nu }_{\text{eff}}{(\kappa L)}^2$$ (20), we obtain their ratio to be

Let us now return to counterflow turbulence. Upon increasing the heat load, there develops an instability of laminar flow that carries the heat away from the heater, and the transition to turbulence occurs in the normal fluid (as in any channel or pipe flow of classical viscous fluid) to which the energy is injected quasiclassically, at the outer scale of order the size of the counterflow channel, $$ D$$. An inertial range of scales with the classical roll-off exponent of −5/3 cannot be established in the normal fluid. The reason is that mutual friction creates superfluid eddies and couples them with normal eddies and also dissipates the turbulent energy at all scales. This mutual friction mechanism serves as an additional source of energy injection to the superfluid component, at large scales, resulting in the gradual growth of a classical-like peak, as sketched in Fig. 3, Middle; the situation for increasing heat input is shown in Fig. 3, Bottom. The sketch takes into account that eddies larger than $$ D$$ cannot exist and that steady-state measurements of the structure functions (49, 57) suggest a steeper roll-off exponent of its right-hand side. Of course, the steady energy input into the superfluid component identified by Schwarz (54, 55) operates and results in a quantum peak in the superfluid energy spectrum around $$ {\ell }_{\text{Q}}$$. Its low wavenumber end is again of the $$ k^2$$ form because of the equipartition theorem (62).

This steady-state, two-peak shape of the superfluid energy spectrum drastically changes during the temporal decay that occurs when heating is switched off. For a short transition time, counterflow is still driven by the excess entropy contained in the channel; for details, see refs. 63 and 64. The quantum peak quickly decays, displaying a decay of the $$ L\propto 1/t$$ type. Simultaneously, over times of the order of the turnover time of large eddies, the energy contained at large scales of both fluids proceeds through the inertial range of scales. From now on, the inertial range is characterized by the classical −5/3 roll-off exponent, as superfluid and normal eddies are coupled at these scales; thus, hardly any significant dissipation occurs, with the situation being similar to that in the coflow (Kolmogorov) QT. As the energy reaches smaller and smaller scales, a larger number of vortex lines are needed for carrying nearly the same energy content. This is displayed as a “bump” in recorded decay curves of $$ L(t)$$. The quasiclassical decay occurs beyond this point, displaying $$ L(t)\propto t^{-3/2}$$ (58, 62).

The dynamics of vortex tangles in thermal counterflow are not fully understood by any means. Their complexity can be illustrated by an experimental study of thermal counterflow in a channel when the turbulence was not allowed to settle to a statistical steady state (64). This was achieved by modulating by a square-wave $$ \dot{q}$$ and a similarly varying counterflow velocity $$ u_{\text{ns}}$$. The turbulent transients thus obtained allowed one to study, by using the phase portrait, the time evolution of both the growth and decay of $$ L$$. In particular, while the growth of $$ L$$ always followed the same form, independent of the length of the heat pulse, the temporal decay of vortex line density was strongly affected by the history of the turbulent sample (figure 7 in ref. 64). The bump in decaying $$ L(t)$$ was displayed only in decays of dense original tangles, prepared using long heat pulses sufficient for generating large eddies and, with the aid of mutual friction, the classical-like part of the superfluid energy spectrum. The situation is similar to that discussed earlier, when the tangle was generated in the $$ T\to 0$$ limit by the injection pulses of ions (immediately creating small vortex rings) of variable duration (36). In both these cases the decay of $$ L(t)$$ depends on the shape of the superfluid energy spectrum (also on the shape of the energy spectrum in the normal fluid in the case of thermal counterflow, due to coupling by the mutual friction force); these shapes depend on how intensely and on which length scales QT is driven.

Let us add that this phenomenological scenario of thermal counterflow and its decay, complex though it is, derives indirect support from complementary experiments. First, the Prague group investigated in detail the steady-state (65) and temporal decay (66) of pure superflow in square channels, with ends covered by sintered silver superleaks, allowing a net throughflow of the superfluid component only (the normal fluid throughflow was suppressed by submicrometer pores of the sintered silver plugs). While the measurements of $$ L$$ in the steady states of counterflow and pure superflow display the same value for the same mean counterflow velocity, the temporal decays are distinctly different. The experimentally recorded bump on $$ L(t)$$ decay curves originating from pure superflow is suppressed, either fully or at least significantly. The reason is easily understood: In pure superflow the classical energy input at large scale of order $$ D$$ is inefficient, as there is no net flow of the normal component through the channel.

In the second example, the Prague group utilized an experimental cell of the outside form of a regular dodecahedron containing a spherical sample of He II. The heat, supplied by a small spherical heater in the center, generates a nearly spherical counterflow. Upon exceeding some critical heating level, an inhomogeneous vortex tangle is formed and surrounds the spherical heater. A full account of this experiment will be published elsewhere, but preliminary second sound data display temporal decay of the form $$ L(t)\propto 1/t$$, where $$ L(t)$$ now stands for the spatially averaged vortex line density, detected by a chosen spherical resonant harmonic of second sound, as shown in Fig. 2, Left. Assuming local decay, this is a typical signature of Vinen type of quantum turbulence. It is important to emphasize that this decay form follows the steady-state vortex line density values which, in conventional 1D thermal counterflow, would have displayed a complex decay containing a bump and subsequent quasiclassical late decay $$ \propto t^{-3/2}$$. The reason for this distinctive difference is the lack of classical large-scale energy input that in the “conventional” 1D counterflow occurs due to the friction between the normal fluid and solid channel wall. Such an energy input does not exist in spherical counterflow with radial normal fluid flow.