
Edited by György Buzsáki, New York University Langone Medical Center, New York, NY, and approved December 24, 2020 (received for review April 7, 2020)
Author contributions: B.H.S. and D.S.B. designed research; B.H.S. performed research; B.H.S., A.A., K.A.D., F.M., B.L., and D.S.B. analyzed data; and B.H.S., A.A., J.S., F.P., B.L., and D.S.B. wrote the paper.
- Altmetric
Responsive neurostimulation is an increasingly accessible treatment for medication-resistant epilepsy that aims to suppress seizures using electrical stimulation from implanted intracranial electrodes. However, the optimal cortical location and time point for intervening once a seizure begins are not well understood. Here we represent a seizure as a series of effective connectivity networks over time and compute metrics of network controllability and optimal control energy. Our results allow us to characterize when and where the brain network may be the most responsive to an external stimulus.
Over one third of the estimated 3 million people with epilepsy in the United States are medication resistant. Responsive neurostimulation from chronically implanted electrodes provides a promising treatment alternative to resective surgery. However, determining optimal personalized stimulation parameters, including when and where to intervene to guarantee a positive patient outcome, is a major open challenge. Network neuroscience and control theory offer useful tools that may guide improvements in parameter selection for control of anomalous neural activity. Here we use a method to characterize dynamic controllability across consecutive effective connectivity (EC) networks based on regularized partial correlations between implanted electrodes during the onset, propagation, and termination regimes of 34 seizures. We estimate regularized partial correlation adjacency matrices from 1-s time windows of intracranial electrocorticography recordings using the Graphical Least Absolute Shrinkage and Selection Operator (GLASSO). Average and modal controllability metrics calculated from each resulting EC network track the time-varying controllability of the brain on an evolving landscape of conditionally dependent network interactions. We show that average controllability increases throughout a seizure and is negatively correlated with modal controllability throughout. Our results support the hypothesis that the energy required to drive the brain to a seizure-free state from an ictal state is smallest during seizure onset, yet we find that applying control energy at electrodes in the seizure onset zone may not always be energetically favorable. Our work suggests that a low-complexity model of time-evolving controllability may offer insights for developing and improving control strategies targeting seizure suppression.
Responsive neurostimulation (RNS) is a nonresective treatment for medication-resistant epilepsy that aims to suppress seizures by delivering an electrical stimulus through intracranial electrodes in response to abnormal electrographic activity. Despite the fact that the first implantable RNS device was approved in 2013, the mechanism of action and optimal patient-specific stimulation settings remain unknown (1, 2). A better understanding of the cortical locations and patterns of brain activity that are most responsive to stimulation would improve treatment efficacy and efficiency. By modeling the brain as a network, with distinct brain regions representing nodes and with statistical dependencies representing measures of influence between regions as edges, the challenge of finding the best strategy for seizure suppression can be recast as a problem of network control (3, 4).
Evidence from prior empirical and computational studies suggests that a linear network control framework can be used to predict how neural activity will respond to an external stimulus, where the dynamics are constrained by a static, structural brain network built from the pattern of white matter tract connections between large-scale cortical and subcortical anatomical regions (567–8). The theory also provides predictions of the optimal stimulation parameters required to drive the brain state, a time-dependent measure of activity at each brain region in the network, from an initial state to a desired target state through a series of state transitions along an optimal trajectory (9, 10). These predictions have been quantified for direct electrical stimulation targeted at improving memory (7) but have not yet been defined or tested for stimulation applied to controlling seizures for two main reasons. First, seizures are characterized by rapid state transitions that violate the assumption of linearity over the course of the whole seizure (11, 12). Second, it is theorized and observed that information propagation through the brain may depend on the underlying state of coherence between brain regions and that exogenous inputs to brain regions may bias the direction of information flow (13, 14). In light of these data, it is clear that informing linear estimates of controllability with static white matter networks fails to capture dynamic corticocortical influences over changing patterns of network coherence (15).
A number of nonlinear models exist that faithfully describe the intricacies of seizure progression and stimulation (16, 17). A linear control framework can approximate such models over short time horizons and can offer a greater repertoire of accessible tools for full network control (18). Therefore, we address the above limitations in an extension to the linear control framework; instead of assuming that a single, structural connectivity network governs the transitions between brain states, we estimate a sequence of effective connectivity (EC) networks from intracranial electroencephalography (iEEG) seizure recordings to capture the evolving constraints on neural dynamics throughout a seizure. Our networks are constructed such that nodes represent iEEG electrodes and edges represent a measure of EC derived from the electrographic time series. Unlike functional connectivity measures, which describe only how activity between network nodes is correlated, EC implies underlying causality between nodes in a network (19). A number of data-driven methods including Granger causality, directed transfer function, and partial directed coherence have been used to create EC brain networks (2021–22). In the context of this paper, EC describes the undirected conditional dependence of nodes in a network, given the activity of all other nodes, and is therefore a powerful approach for understanding the impact of an external stimulus on seizure dynamics (20) (Fig. 1). We define brain state at each second to be high- band power (30 to 150 Hz) at each electrode; this measure of brain activity is sensitive to frequency and amplitude changes accompanying ictal transitions in neural recordings (7, 23, 24). Our model supports the assumption that structural connectivity only partially dictates our ability to control rapidly evolving neural processes via external stimulation and that the transient coupling between brain regions also impacts neural controllability.

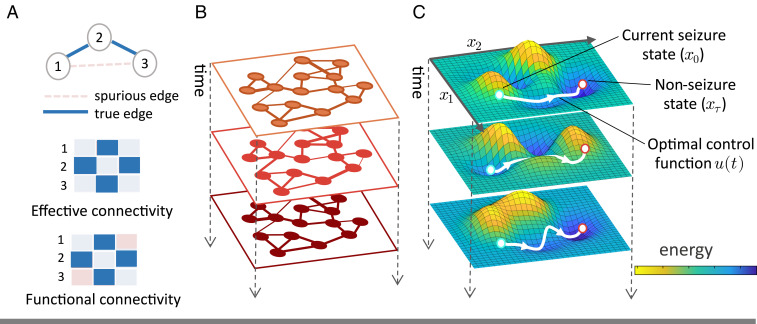
Time-evolving EC as a tool in seizure control strategies. (A) In a toy network with two empirical functional connections across three nodes, correlative functional connectivity may estimate a spurious edge between nodes that interact indirectly. Conversely, EC reflects the direct influence between nodes in a network, setting the edge weight of conditionally independent nodes to zero, and thus provides a scaffold to model control strategies over time. Throughout a seizure, we can build EC networks to represent distinct regimes of neural connectivity (B) and infer a dynamic control energy landscape from those networks, shown superimposed on the principal axes of the system’s state space (C). We can then use tools from control theory to determine the optimal control input required to drive neural activity to seizure freedom given the state of the control energy landscape.
We use our model to build on prior work in network control theory to address several specific hypotheses regarding seizure dynamics in humans. We focus on two measures of controllability that characterize the ease of driving the brain into new states as time evolves (3, 25). Average controllability reflects the average input energy required at a node to transition the activity from some initial brain state to all nearby states (brain state vectors with a unit magnitude) (9, 26). The EC networks used in our model can be decomposed into sets of eigenmodes, representing invariant axes in state space upon which neural activity can be measured over time, and eigenvalues dictating the rate of activity decay along each mode. Modal controllability reflects the ease of moving a system to states dominated by small eigenmodes that are intuitively difficult to reach because they contribute less to the dynamics of the system and are far from the dominant energy minimum (6, 9, 27). Specifically, the metric quantifies the extent to which input at a given node controls activity along all eigenmodes of the system, weighted toward smaller modes, thus summarizing how the underlying network will respond to control inputs. Modal controllability can be separated into the measures of persistent modal controllability and transient modal controllability, which describe the extent to which control input at a node perturbs the slow- or fast-decaying modes of the system, respectively (4, 7, 25). Collectively, these metrics allow a broad assessment of a system’s accessible control strategies. We hypothesize that seizure propagation will be accompanied by a heightened average controllability and decremented modal controllability with respect to values at seizure onset, consistent with an enhanced strengthening of the epileptic network (9, 27). We extend this evaluation by using a model of seizure-regime-dependent linear control to find the optimal control function required to drive the brain to a seizure-free state from a subset of control nodes. We predict that controlling the nodes that define the observed seizure onset zone (SOZ) as epileptiform activity emerges will be the most effective. Although the true epileptogenic zone, defined as the brain region supporting seizure generation, may extend beyond the SOZ (28), our prediction is built upon prior observations that SOZ nodes precede the rest of the nodes in the constructed network in showing increased functional connectivity (29). We reason that this may facilitate local control before the seizure spreads. Broadly, our study builds on the principles of network control theory to study time-evolving coherence-mediated control, which has the potential to inform practical efforts to improve neurostimulation-based therapies.
Results
Characterizing Seizure Regimes.
Prior studies of functional connectivity networks built with electrocorticography (ECoG) data suggest that seizures can be segmented into three main regimes—onset, propagation, and termination (12, 30, 31)—and that linear modeling is applicable within 1-s time windows in each regime given the stationarity of the time series (22, 32). We sought to determine whether such a regime separation existed in EC; if so, dynamic controllability could be meaningfully compared in seizure regimes. To address this question, we began by constructing EC networks from consecutive 1-s time windows of preictal and ictal ECoG recordings from 34 partial or secondarily generalized seizures across 14 subjects undergoing EEG monitoring prior to surgical treatment for medication-resistant epilepsy. EC networks were obtained using the Graphical Least Absolute Shrinkage and Selection Operator (GLASSO) method to estimate the regularized partial correlation between pairs of recorded time series in each time window as this method has been shown to estimate the presence of true network connections with high sensitivity compared to other EC methods (see Materials and Methods for more details) (11, 3334–35). For each seizure of variable length

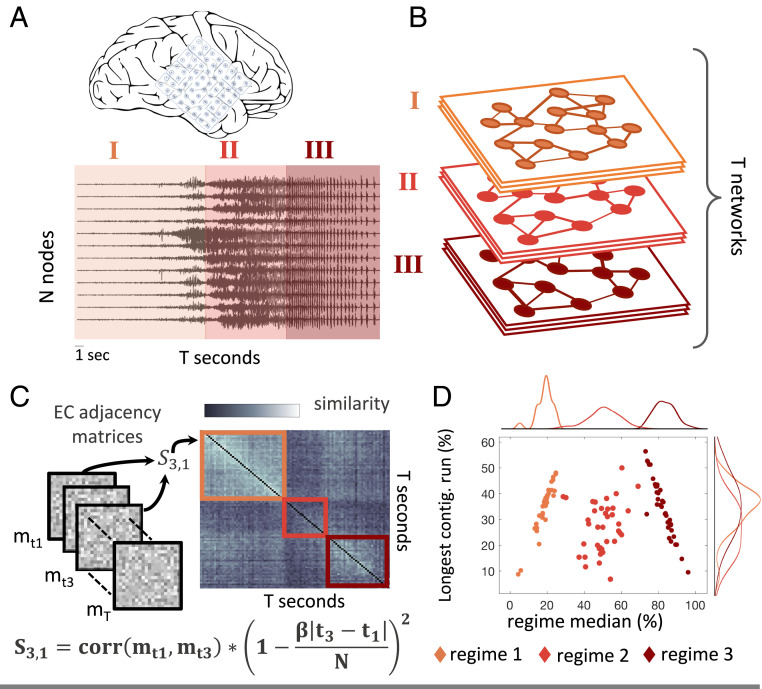
Time evolving controllability through EC. (A) For each seizure, we extracted consecutive 1-s time windows of cortical ECoG recordings from
For the purposes of our analysis, we next used a retrospective community detection method to detect seizure regimes; real-time seizure regime classification remains an interesting challenge that lies outside the scope of this study. We calculated what has previously been termed a functional connectivity dynamics matrix (36) or a configuration similarity matrix (30). This
Dynamic Controllability of Epileptic Networks.
We now turn to an investigation of how the EC network representing each seizure regime impacts regime-dependent controllability. In the context of our model, analysis of the average and modal controllability metrics can answer the question of whether energy input during a given regime will be characterized by diffuse propagation throughout the network, pushing the brain state into other nearby states (high average controllability), or whether control input is able to drive the brain to states that are hard to reach by maintaining influence over the small modes of the system (high modal controllability). Additional analysis of persistent modal and transient modal controllability metrics can describe the extent to which input energy into the brain network is either sustained while controlling slowly decaying modes or attenuated while controlling quickly decaying modes, respectively. We investigate metrics in each seizure regime under the assumption that the seizure progressed naturally (without prior stimulation) up to the seizure regime of interest.
For all four controllability metrics, we observed a significant regime dependence at the group level. We obtained 12 metric values for each seizure—four single values to summarize the average, modal, persistent modal, and transient modal controllability metrics in three regimes—and then compared the values in each regime across the 34 seizures. Within a regime, a given metric was calculated for each node in each EC network assigned to the regime. Then the median value for each node was obtained across networks, and the average of the resulting N × 1 vector was used to summarize the regime. Across 34 seizures in 14 epilepsy patients, we observed a significant effect of seizure regime on average controllability

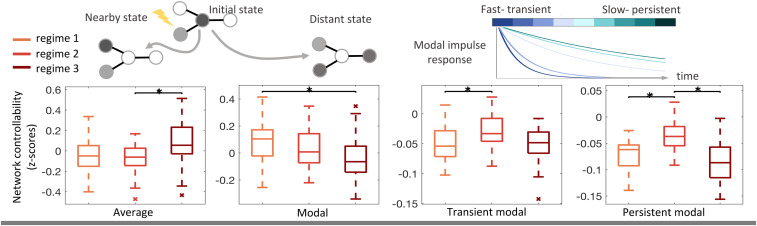
Group-level controllability dynamics throughout early, middle, and late seizure regimes. A single controllability metric value was obtained for each regime in a seizure, and the distribution of regime metric values across all seizures (
Regime-Dependent Optimal Control Energy.
The linear dynamical model used to understand state-invariant controllability in brain networks can also reveal the optimal control energy necessary to drive the brain from an initial brain state
We began by obtaining a representative EC network for each regime in each seizure as the network with the highest average similarity to other networks in the given regime. Per seizure, we quantified an N × 1 initial brain state vector

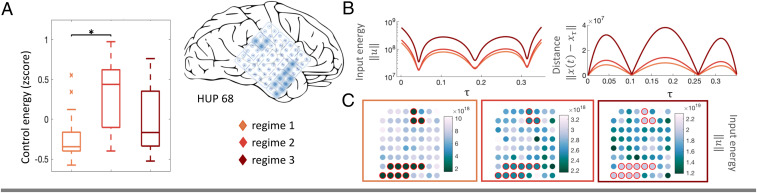
State-dependent optimal control energy. (A) A significant effect of optimal control energy on seizure regime was found at the group level
Control Localization in Onset Regime.
The optimal control energy results demonstrated that the seizure onset regime is preferred for its low energy requirements. In an effort to find the best control location, we next asked whether controlling nodes at the SOZ required less energy than controlling any other subset of nodes, given that RNS treatments are typically localized to the SOZ (1, 37). Seizures in all but four subjects exhibited focal onsets, for a total of 22 seizures localized within the area of the cortical grid electrodes and used in this analysis. We again measured the control energy required to drive the brain state along an optimal trajectory from the initial states
Robustness of Results to Selected Parameters.
Our analysis relies on a number of assumptions, as well as parameterized methods for EC network generation and regime delineation, and a parameterized optimal control energy model. We sought to evaluate the reliability of our findings by assessing the sensitivity of our results to our assumptions and parameter values. First, given that spatiotemporal patterns of seizures propagating from the same SOZ may be diverse within a subject (38), we chose to treat each seizure as an independent data point. We completed an alternative analysis after grouping seizures within subjects and found that the group-level trends of our main findings were preserved, with persistent and transient modal controllability maintaining significant differences across regimes despite the reduction in number of data points (SI Appendix, Fig. S3). We also varied the sparsity tuning hyperparameter,
Discussion
For patients with medication-resistant epilepsy, RNS as a means of seizure suppression is a relatively new option that provides an alternative to more permanent and invasive choices such as cortical resection or laser ablation. While the majority of patients improve over the course of months to years with treatment, the current trial and error routine for selecting stimulation parameters is far from ideal, and only rarely do patients achieve seizure freedom (1, 2, 37). We completed this study to introduce a control-theory framework for dynamic controllability that could provide support for clinical treatment decisions and highlight the regions and time points for stimulation that require the least input.
Emergence of Quasi-Static Seizure Regimes.
In a challenge to a static brain controllability perspective, a number of studies find that multiple patterns of corticocortical coupling may appear on the same structural foundation and that time-evolving EC networks may provide a more accurate view of the connectivity landscape (14, 15, 35, 39). By estimating edges in our EC networks as regularized partial correlations between brain regions, we strive to remove contributions of common latent inputs from subcortical structures and describe only direct corticocortical influences. Using this framework as a linear approximation of the region-to-region dependencies in each seizure regime, we demonstrated superiority to a static structural model (SI Appendix, Results) and uncovered a dynamic profile of controllability with implications for the input energy distribution across brain regions in a given regime. Our results demonstrate increasing average controllability and decreasing modal controllability throughout the majority of seizures. Low average controllability at onset implies that a widespread, diffuse distribution of input energy is hindered at seizure initiation, complementing findings in functional connectivity that show marked decoupling between brain regions at onset due to loss of inhibitory restraint (12, 31). Later throughout propagation and into termination regimes where coupling between brain regions has been shown to increase (12, 29, 31), our results suggest that it will become harder to direct the brain into energetically unfavorable states (low modal controllability).
Interestingly, the temporal trend of persistent and transient modal controllability differs from overall modal control in the onset regime. The relatively low metric values at onset reflect the combination of two factors—first, that input attenuation governed by the extreme eigenmodes could be relatively slower in general at seizure onset than during propagation, and second, that external perturbations may be less aligned with the extreme eigenmodes at onset. Our findings are consistent with a prior investigation of ictal eigenmode stability in a dynamical linear framework showing that relatively faster decay in the slowest eigenmodes occurred during midseizure, perhaps reflecting greater synchrony with compensatory inhibition during the propagation period (32). Our results indicate that decoupling between brain regions at onset could make it particularly difficult to control the very fast or very slow dynamics associated with the extreme eigenmodes of the brain’s activity in that regime.
Spatiotemporal Control as a Tool for RNS Intervention.
From the perspective of clinical RNS treatment, our model supports the current practice of intervening at seizure onset (37), with group-level results indicating that the amount of control energy required for a transition to a seizure-free state is smallest at onset. We note that increased energy requirements for propagation and termination regimes may be driven by our effort to counteract the natural ictal progression, by fully controlling brain state along a direct trajectory to seizure freedom, at an energetic cost. Our analysis on locally differentiated optimal control energy between SOZ and non-SOZ nodes found that the SOZ required significantly less energy for seizure suppression in seizures in only half of the subjects. This finding does not support the SOZ as a universally energetically favorable stimulation target and begs the question of whether energetically favorable points outside the SOZ could still be clinically relevant stimulation targets. There are a number of possible explanations and factors that drive this result. Epilepsy is theorized to be a network disorder (30, 40, 41); thus, it is likely that multiple cortical locations may be targeted to modulate the same pathologic network. Additionally, in resective surgery, removal of the SOZ alone is often insufficient, indicating that additional brain regions within the broader epileptogenic zone contribute to support seizures (28). These facts combined with evidence suggesting that seizure precursors may appear outside of the SOZ (40), that tissue damage at the SOZ may have remote effects on the functionality of other brain regions (42), and that the vicinity of stimulus location to the SOZ is not always significant for patient outcomes (43) indicate that energetically favorable control points selected by our model may still be effective even if outside the SOZ. Among other factors, our results may also be constrained by the linear control framework, which may capture shorter time horizons for control but could oversimplify the true trajectory back to a seizure free state (SI Appendix, Results).
Although current RNS technology is limited by a restricted number of seizure detection criteria and stimulation response patterns (2), our methodology could enrich a number of model-based control approaches that could be adapted to improve seizure suppression in future implantable devices. For example, model predictive control (MPC) is a multivariable control algorithm that periodically reassesses the control function every few time steps along the planned trajectory (44). MPC relies on an internal representation of the dynamical environment, and our partial correlation EC model may improve upon prior estimates by reflecting direct corticocortical influences. Other recent work has theoretically demonstrated that seizures may be controlled via static output feedback of a linear dynamical system, wherein the underlying model is derived using multivariate autoregression (MVAR) (45). This work could be extended by removing spurious links in an MVAR model using a partial correlation constraint that assesses the correlation between a pair of nodes after removing the linear effects of other variables in the same and previous time points (46). Exciting future directions include testing the hypotheses generated from these models using intracranial data from patients with RNS implants and prospectively in new stimulation paradigms.
Methodological Considerations.
Our model of dynamic controllability has a number of limitations. First, we chose to operationalize brain state here as high-
In conclusion, we employed a method of measuring controllability of effective networks and optimal seizure control energy across three temporal seizure stages. Our results present preliminary work in building theoretically informed hypotheses for future empirical validation.
Materials and Methods
Subject Data.
The ECoG data used for this study were recorded from subdural electrodes implanted in 14 epilepsy patients undergoing EEG monitoring prior to surgical treatment for medically refractory epilepsy at the Hospital of the University of Pennsylvania (HUP) (512 Hz sample rate) or at the Mayo Clinic in Rochester, MN (500 Hz sampling rate). All subjects included in this study gave written informed consent. This study was approved by the University of Pennsylvania Institutional Review Board and Mayo Clinic Institutional Review Board. The implanted surface electrodes (ad Tech Medical Instruments) were composed of both grid and strip arrays with 2.3-mm-diameter contacts at 10 mm intercontact spacing. Electrode placement was planned according to clinical protocol by a team of epileptologists with a separate reference electrode placed distant to the site of seizure onset, as in prior studies (30, 39). The following characterizations were determined by an epileptologist and reviewed in a clinical conference at HUP: seizure categorization as complex partial and/or secondarily generalized, the earliest electrographic onset, unequivocal electrographic onset, and focal SOZ or lack of seizure focus. The deidentified patient data were retrieved from the online International Epilepsy Electrophysiology Portal (IEEG Portal) (50).
EC Networks.
For each epileptic event, EC networks were constructed from 1-s time windows of both ictal and preictal data. All time series data from ECoG channel recordings were rereferenced to the common average reference to avoid broad field effects (30, 35, 38). Each channel was digitally filtered with 60 Hz notch, 120 Hz low-pass, and 1 Hz high-pass filters using a fourth-order Butterworth design to remove line noise, drift, and high-frequency noise, respectively (38). The preprocessed data were partitioned into consecutive 1-s time windows spanning the length of the seizure and preictal period. For each window, the GLASSO method was used to find a regularized partial correlation EC matrix (33). See SI Appendix, Methods, for details.
Community Detection to Identify Seizure Regimes.
A similarity matrix was computed using the Pearson correlation coefficient between all pairwise combinations of the
Controllability Metrics and Optimal Control Calculations.
Average, modal, persistent modal, and transient modal controllability metrics were calculated in MATLAB with custom scripts and code from ref. 7. Before calculating a given controllability metric, each function first ensures that the network is stable by enforcing Schur stability and then subtracting the identity matrix to normalize the eigenvalues (25). Optimal control energy was also calculated in MATLAB using functions referenced in ref. 7. Optimal control energy requires the selection of the value for
Statistical Methods.
Friedman’s ANOVA,
Diversity Statement.
Recent work in several fields of science has identified a bias in citation practices such that papers from women and other minorities are undercited relative to the number of such papers in the field (53545556–57). Here we sought to proactively consider choosing references that reflect the diversity of the field in thought, form of contribution, gender, and other factors. We obtained predicted gender of the first and last author of each reference by using databases that store the probability of a name being carried by a woman (57, 58). By this measure (and excluding self-citations to the first and last authors of our current paper), our references contain 22.92% woman(first)/woman(last), 26.05% man/woman, 6.67% woman/man, and 44.36% man/man. This method is limited in that 1) names, pronouns, and social media profiles used to construct the databases may not, in every case, be indicative of gender identity and 2) it cannot account for intersex, nonbinary, or transgender people. Second, we obtained predicted racial/ethnic category of the first and last author of each reference by databases that store the probability of a first and last name being carried by an author of color (59, 60). By this measure (and excluding self-citations), our references contain 9.29% author of color (first)/author of color(last), 12.25% white author/author of color, 23.54% author of color/white author, and 54.92% white author/white author. This method is limited in that 1) names, Census entries, and Wikipedia profiles used to make the predictions may not be indicative of racial/ethnic identity and 2) it cannot account for Indigenous and mixed-race authors or those who may face differential biases due to the ambiguous racialization or ethnicization of their names. We look forward to future work that could help us to better understand how to support equitable practices in science.
Acknowledgements
We thank both Jason Z. Kim for helpful discussions regarding control theory and Dr. Xiaosong He for helpful discussions regarding structural and EC model comparison. This work was primarily funded by NSF award BCS-1631550 (to D.S.B.) and National Institute of Neurological Disorders and Stroke award R01 NS099348 (to B.L. and D.S.B.). D.S.B. acknowledges additional support from the John D. and Catherine T. MacArthur Foundation, the Alfred P. Sloan Foundation, the Institute for Scientific Interchange Foundation, the Paul Allen Foundation, the Army Research Laboratory (W911NF-10-2-0022), and the Army Research Office (Bassett-W911NF-14-1-0679 and Grafton-W911NF-16-1-0474). B.L. acknowledges additional support from the Mirowski Family Foundation, the Pennsylvania Health Research Formula Fund, Johnathan and Bonnie Rothberg, and Neil and Barbara Smit. The content is solely the responsibility of the authors and does not necessarily represent the official views of any of the funding agencies.
Data Availability.
Anonymized iEEG were retrieved from the publicly accessible database hosted on the International Epilepsy Electrophysiology Portal (www.ieeg.org) (50).
References
1
2
3
4
5
6
7
8
9
10
12
13
14
15
16
17
18
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
 Time-evolving controllability of effective connectivity networks during seizure progression
Time-evolving controllability of effective connectivity networks during seizure progression
