The Velocity of MDA-MB-231 Cells on Microlanes Shows Biphasic Dependence on Fibronectin Density.

We developed a microcontact printing protocol for Fibronectin-coated microlanes with varying density that is based on two stamping steps (SI Appendix, Fig. S1). It created 15-$$ \mathrm{\mu }$$m-wide lanes with alternating fields of specific Fibronectin densities. The area between the microlanes was coated with cell-repellent polyethylene glycol (PEG) (Fig. 1A). The Fibronectin absolute surface density was estimated by the fluorescence intensity of the labeled Fibronectin for each segment individually (SI Appendix, Fig. S2). MDA-MB-231 breast cancer cells were seeded on the lanes (Fig. 1 B and C; Movie S2). The width of the lanes of 15 $$ \mathrm{\mu }$$m is still broad enough for the morphology of the cells being close to the morphology in two dimensions (40), but major protrusions can only form along the direction of the lane (Movie S1). The cell nuclei were fluorescently labeled to allow automated cell tracking (Fig. 1A). We used scanning time-lapse microscopy and were able to observe about 2,000 single cells in about 100 view fields per measurement. Images were taken every 10 min for 48 h.

Fig. 1.

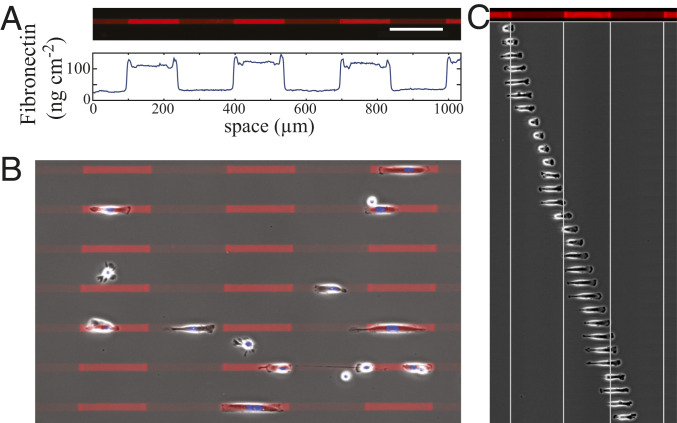
Fibronectin lanes and cell motion. (A) Fluorescence image of a Fibronectin-coated lane with fields of different Fibronectin density shown below. (Scale bar: 150 $$ \mathrm{\mu }$$m.) (For a discussion of absolute Fibronectin densities, see SI Appendix, section S1B.) (B) MDA-MB-231 cells seeded on Fibronectin lanes. Overlay of phase-contrast and fluorescence images of patterns (red) and nuclei labeled with Hoechst (blue). Cells are restricted to one-dimensional motion on the microlanes and frequently traverse to fields with different Fibronectin densities. They sometimes also spontaneously reverse direction or stay at one position for some time. (C) Time course of the position of a single cell migrating on the lane shown on top. Phase-contrast images were taken every 10 min.

We used lanes with different combinations of Fibronectin densities and analyzed more than 15,000 single-cell tracks. The velocity averaged over the cell population shows the biphasic behavior with maximal velocity for intermediate Fibronectin densities (Fig. 2B) that was reported by several studies for different cell types (678–9, 31, 33, 35). Published data did not permit a clear distinction between a monotonous decrease of the cell velocity with increasing adhesion strength beyond the velocity maximum and saturating effects of adhesion on the velocity. We have chosen a sufficiently small step size in coating densities and a sufficiently large number of measurements per data point to clearly identify saturation.

Fig. 2.

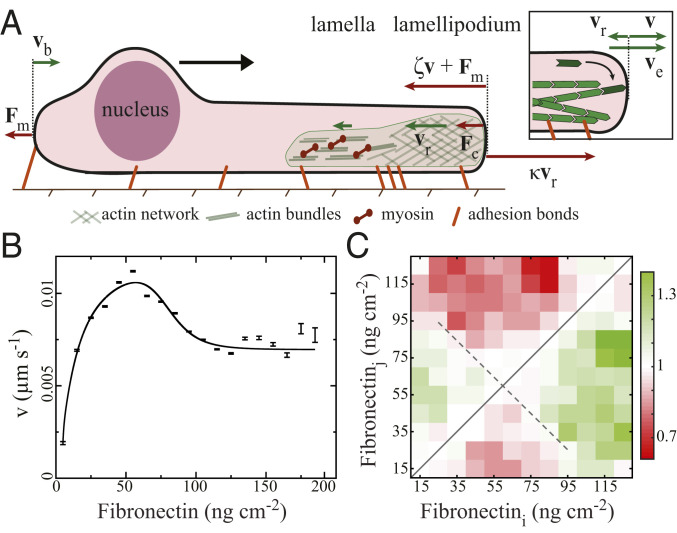
The adhesion–velocity relation. (A) Sketch of a cell with velocities of the leading edge $$ v$$, the retrograde flow $$ v_r$$, the network-extension rate $$ v_e$$, the back velocity $$ v_b$$, and the related elements of the force balance of steady motion $$ \zeta v$$ and $$ \kappa v_r$$. $$ F_c$$ and $$ F_m$$ are forces acting on the cell membrane. $$ F_m$$ could be the force from an obstacle to motion or pulling the rear, for example. (B) Measured adhesion–velocity relation of MDA-MB-231 cells (symbols). The full line shows the fit to Eqs. 4 and 5 with the parameters listed in Table 1; bars show SEM. Each data point contains, on average, 1,000 cell tracks, but with decreasing numbers for very large and very small Fibronectin densities (SI Appendix, Table S6). (C) Relative velocities for all combinations of different Fibronectin densities. Distribution of relative velocities before and after transitions from $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$ to $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$ have been measured for each pair of densities. The color coding compares the relation between the medians: green for $$ v_j>v_i$$, white for $$ v_j=v_i$$, and red for $$ v_j<v_i$$. Lines indicate combinations of Fibronectin densities where the velocities on both of them are equal.

We also analyzed the velocity changes at transitions between different Fibronectin densities with regard to the biphasic relation at the single-cell level (Fig. 2C and Movie S3). Cells move from fields with coating Fibronectin density, $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$, to fields with density $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$. Both densities are equal on the diagonal ($$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$ = $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$) of Fig. 2C. We have transitions from low to high density above the diagonal. Fig. 2C presents increases (green), decreases (red), and no change (white) of the median relative velocity of single cells during transitions. Evidently, the velocities on both densities are approximately equal on the diagonal with $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$ = $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$ (full line in Fig. 2C). Interestingly, there are distinct pairs of Fibronectin concentrations around the density with maximal velocity $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_{max}$$, where, despite a sharp step in Fibronectin density, the cell velocities do not change. This consequence of the biphasic relation manifests itself as a second weakly white diagonal line $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$ = $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_{max}$$ − $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$ (dashed line in Fig. 2C). This line separates two regimes: below the line $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$ = $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_{max}$$ − $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$, we observe the rising phase of the adhesion–velocity relation with increasing velocities. Above this line, we enter the falling phase of this relation and see decreasing velocities during the transition from $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$ to $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$. Below the diagonal $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_i$$ = $$ {\mathrm{F}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{n}}_j$$, we see transitions from high to low density.

Force Balance at the Leading Edge, Force-Dependent Polymerization, and Cooperative Adhesion Determine the Adhesion–Velocity Relation.

In this section, we formulate a force balance at the leading edge in order to describe cell motion. Forces act on the cell across the whole area of contact with the substrate. They are coupled across the whole cell to the leading edge by tension (36, 484950–51) or by the F-actin network for those parts of the network which are mechanically continuous with the lamellipodium (52). On that basis, we can place our force balance at the leading edge without neglecting forces acting on different parts of the cell, including the lamella.

We focus on the steady motion, when average front and rear velocity of the cell are equal on areas with homogeneous Fibronectin density in this section. Fig. 2A shows the forces acting at the leading edge of the cell. Each individual filament pushes with its force $$ f$$, which increases the activation energy for the polymerization reaction, since the addition of length to the filament has to work against $$ f$$. That entails the Arrhenius factor $$ e^{-\frac{fd\cos \theta }{k_{B}T}}$$ in the polymerization rate with $$ \theta $$ denoting the tilt angle of the filament, $$ k_B$$ the Boltzmann constant, and $$ T$$ the temperature (5354–55). We approximate the average single-filament force by the total force per leading-edge contour length $$ F$$ divided by the number of filaments per leading-edge contour length $$ N$$. Since the extension velocity of the network is mainly determined by the polymerization rate, it obeys

The extension velocity $$ v_e$$ is the vectorial difference of the protrusion velocity $$ v$$ and retrograde-flow velocity $$ v_r$$ (Fig. 2A). Their absolute values obey

$$ F_c$$ is a force acting on the network at the leading edge like, for example, from contraction by myosin. Contractile forces are positive with our choice of sign in Eq. 3. $$ F_m$$ is a velocity-independent force acting on the leading-edge membrane, e.g., myosin activity pulling the rear or an obstacle to cell motion.

The basic thermodynamic relation Eq. 1 and the force balance Eq. 3 determine the cell velocity $$ v$$ uniquely. The solution uses the Lambert function $$ W_0$$ (56):

Binding of a ligand to integrin is one of the most important ways how cells sense their environment. The binding event is input to a complex signaling network (27, 34, 57, 58). The signaling state of related pathways—e.g., Rho signaling to stress fibers (27, 57, 5960–61) or Rac signaling to FAs (25, 59, 6263–64) and other systems (656667–68)—and force-, flow-, and myosin-mediated feedbacks affect the density of adhesion structures (8, 20, 23, 31, 60, 69707172–73), interact with integrin signaling, and thus shape the relations between $$ \kappa $$, $$ \zeta $$, and the ligand density $$ B$$. In the different experimental settings, $$ B$$ represents the Fibronectin density, Fibrinogen concentration, or Arg-Gly-Asp (RGD) functionalized poly-l-lysine-graft-PEG copolymer (PLL-PEG-RGD) density (see below). Catch bonds between integrin and Fibronectin (74) or actin and vinculin (75) will contribute to the positive feedback in this relation. We will explore the relations $$ \kappa \left(B\right)$$ and $$ \zeta \left(B\right)$$ by fitting the velocity Eq. 4 to experimental results. The complexity of adhesion-related pathways (see refs. 9, 10, 27, 34, 57, 58, 66, and 76 for reviews) entails most likely a more complicated relation between $$ \kappa $$, $$ \zeta $$, and ligand density than the type we will choose, but we cannot expect to learn all of the details of this relation from our experimental data and, therefore, have to choose a sufficiently simple ansatz.

According to the basic ideas on the biphasic adhesion–velocity relation, $$ \kappa \left(B\right)$$ and $$ \zeta \left(B\right)$$ should increase with $$ B$$. The observation that velocities saturate for large Fibronectin densities in Fig. 2B requires that $$ \kappa \left(B\right)$$ and $$ \zeta \left(B\right)$$ are also saturating functions. Therefore, we choose the ansatzes

Analysis of the Adhesion–Velocity Relation.

We analyze the adhesion–velocity relation by fitting Eqs. 4 and 5 to the measured data in Fig. 2B of the MDA-MB-231 dataset. The fit reproduces the relation, including the velocity maximum and the saturating behavior. The resulting parameters are listed in Table 1. We also include data from literature for keratocytes (33), PtK1 cells (31), and CHO cells (7) into the analysis (Figs. 3 and 4 and Table 1). We calculate the force $$ F$$, retrograde-flow velocity $$ v_r$$, and network-extension rate $$ v_e$$ with the parameters from the fits and Eqs. 2–5.

Table 1.

Parameter values resulting from the fits of Eqs. 4 and 5 to experimental data shown in Figs. 2B and 3

Parameter	MDA-MB-231	CHO	Keratocytes	PtK1	Units
F-actin network extension Eq. 1
Force-free network-extension rate $$ V_e^0$$	0.0156	0.057	0.197	0.030	$$ \mathrm{\mu }$$m$$ \cdot $$$$ {\mathrm{s}}^{-1}$$
Network depolymerization rate $$ k^{-}$$	0.0027	0.010	0.0017	0.0016	$$ \mathrm{\mu }$$m$$ \cdot $$$$ {\mathrm{s}}^{-1}$$
Retrograde-flow friction coeff. $$ \kappa \left(B\right)$$ Eq. 5
Hill coefficient $$ n_{\kappa }$$	8.77	7.71	1.94	2.11
Half-max. value $$ K_{\kappa }$$	73.6	4.63	66.1	22.3	$$ \mathrm{\mu }$$g$$ \cdot $$m$$ {\mathrm{L}}^{-1}$$, ng$$ \cdot $$c$$ {\mathrm{m}}^{-2}$$
Max. value $$ {\kappa }_{max}$$	70.1	13.8	6.12	2.60	nN$$ \cdot $$s$$ \cdot \mathrm{\mu }$$$$ {\mathrm{m}}^{-2}$$
Membrane drag coefficient $$ \zeta \left(B\right)$$ Eq. 5
Hill coefficient $$ n_{\zeta }$$	7.59	7.53	1.36	1.53
Half-max. value $$ K_{\zeta }$$	85.7	5.33	218.6	382	$$ \mathrm{\mu }$$g$$ \cdot $$m$$ {\mathrm{L}}^{-1}$$, ng$$ \cdot $$c$$ {\mathrm{m}}^{-2}$$
Max. value $$ {\zeta }_{max}$$	30.8	296.0	2.86	117	nN$$ \cdot $$s$$ \cdot \mathrm{\mu }$$$$ {\mathrm{m}}^{-2}$$
Forces Eq.3 and SI Appendix, Eq. S8
$$ F_c$$	0	0	0	0	nN$$ \cdot \mathrm{\mu }$$$$ {\mathrm{m}}^{-1}$$
$$ F_m$$	0	0	0	0	nN$$ \cdot \mathrm{\mu }$$$$ {\mathrm{m}}^{-1}$$
$$ \frac{F_{max}^{pol}}{N}$$	0.007	0.007	0.019	0.012	nN

The values g = 0.37579, gd/k_BT = 248 nN⁻¹, andN = 248 μm⁻¹ (1777)SI Appendix, section S4 relates some parameter values to available published results. Coeff., coefficient; max., maximum.

Fig. 3.

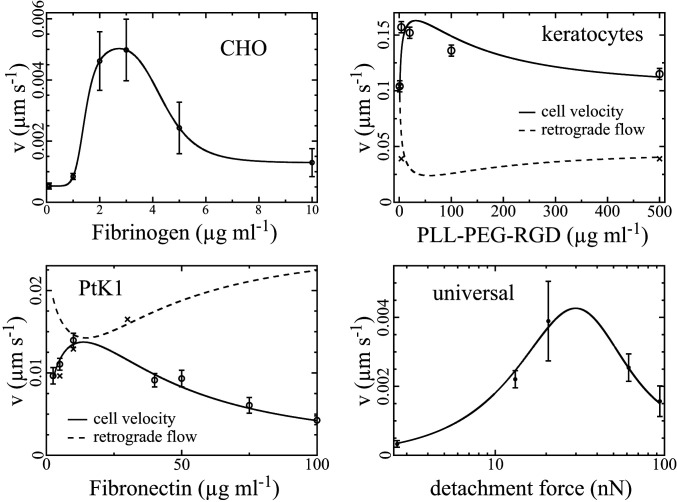
The dependency of the cell velocity on the substrate ligand density in terms of the concentration of Fibrinogen in the coating solution for CHO cells (data from the $$ {\alpha }_{iib}{\beta }_3$$ resting cells in ref. 7), the concentration of Fibronectin for PtK1 cells (data from ref. 31), the concentration of PLL-PEG-RGD for keratocytes (data from ref. 33). The sets of experimental data (symbols) were fitted to Eqs. 4 and 5. The parameter value results are listed in Table 1. There are also retrograde-flow data (x) available for keratocytes and PtK1 cells, which we included in the fit. The fit for PtK1 cells deviates in the data point of retrograde flow at 5 $$ \mathrm{\mu }$$g$$ \cdot $$m$$ {\mathrm{L}}^{-1}$$ from the experimental values. We discuss that deviation in SI Appendix, section S4A. Palecek et al. (7) could collapse several experimental sets to a single universal curve by relating the velocity to the detachment force, which is proportional to the adhesion bond density. We fit this universal relation data to Eqs. 4 and 5 in the universal graph (Lower Right). However, the fit is not unique with five data points only, and, therefore, we did not continue the analysis with this dataset (results in SI Appendix, Table S1). We found the introduction of (small) coating density-independent terms $$ {\kappa }_0$$ = 8 × $$ {\mathrm{10}}^{-5}$$ nN$$ \cdot $$s$$ \cdot \mathrm{\mu }$$$$ {\mathrm{m}}^{-2}$$ and $$ {\zeta }_0$$ = 7 × $$ {\mathrm{10}}^{-4}$$ nN$$ \cdot $$s$$ \cdot \mathrm{\mu }$$$$ {\mathrm{m}}^{-2}$$ in Eq. 5 to be necessary to obtain the inflection point the velocity dependency of the CHO cells exhibits left of the maximum. They may indicate the relevance of physical interactions between cell and substrate or coating-independent surface bonds. Bars indicate SEM for PtK1 cells and keratocytes and 95% CI for CHO cells and the universal dataset.

Fig. 4.

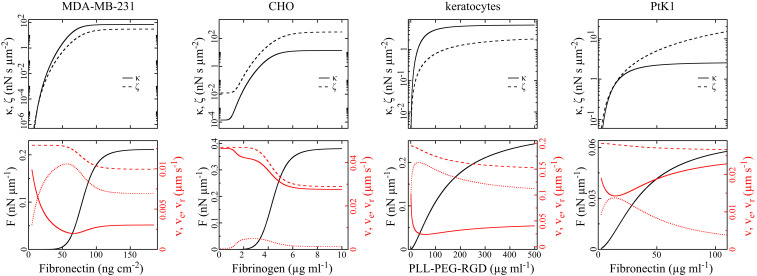
Predictions of Eqs. 2–5 with the parameters for the different cell types listed in Table 1 resulting from the fits of Eqs. 4 and 5 to experimental data shown in Figs. 2B and 3. (Upper) Retrograde-flow velocity friction coefficient $$ \kappa $$ and membrane drag coefficient $$ \zeta $$ (Eq. 5). (Lower) Network-extension rate $$ v_e$$ (red dashed line; Eq. 2), retrograde-flow velocity $$ v_r$$ (red full line; Eq. 3), cell velocity $$ v$$ (red dotted line; Eq. 4), and the force $$ F$$ (black full line; Eq. 3) acting on the leading-edge membrane.

Keratocytes offer the best opportunity for relating our results to prior knowledge, since they are the best-studied cell type among our examples. The forces occurring in keratocyte migration on coating densities covered by the experiments are in the same range (Fig. 4) as the forces of the dynamic (1415–16) and predicted stationary force–velocity relation (SI Appendix, Fig. S4), and are in agreement with experimental and theoretical analyses of membrane tension in moving keratocytes (80). Keratocytes exhibit $$ \kappa \gg \zeta $$ (Fig. 4) in agreement with observations by Anderson and Cross (81) and Möhl et al. (82) for fish and human epidermal keratinocytes, respectively (resp.), showing vanishing adhesion density toward the trailing edge of the cell. The maximum of the cell velocity is at intermediate $$ \kappa $$ values, in agreement with experimental results on adhesion-site density for different Fibronectin-coating densities (31). SI Appendix, Table S3 provides additional information. The high quality of the fits to the experimental results in Figs. 2 and 3 and the quantitative agreement with prior knowledge on keratocytes strongly suggests that we included all relevant processes in the formulation of the velocity equation (Eq. 4).

Forces.

Interestingly, fitting reveals that both velocity-independent forces vanish, $$ F_m$$ = 0 and $$ F_c$$ = 0, for all experiments but the universal set, and, there, $$ F_m$$ = 0 and $$ F_c$$ is tiny (SI Appendix, Table S1). Hence, velocity-independent forces do not contribute to the leading-edge force balance in a noticeable way (see also Discussion). This finding also entails $$ v/v_r=\kappa /\zeta $$ (Eq. 3). Hence, we can measure the ratio $$ \kappa /\zeta $$ by measuring $$ v/v_r$$.

The force $$ F$$ increases, and the network-extension rate $$ v_e$$ decreases with increasing substrate-coating density for all four cell types in Fig. 4, in line with Eq. 1. If we see a substantial decrease of $$ v_e$$ as with MDA-MB-231 and CHO cells, it starts at coating densities close to the velocity maximum. The extension velocity decreases typically by less than 30%, but this amount is the larger part of the cell-velocity decrease beyond the maximum in MDA-MB-231 cells, keratocytes, and CHO cells.

PtK1 and CHO cells with $$ \zeta \ge \kappa $$ turn a large fraction of the network-extension rate into retrograde flow. This correlates to the force regime in which these cells operate. We can assess the force regime by inspecting the stall forces (83), i.e., the strength of a force $$ F_m$$ required to stall leading-edge motion:

$F_m^{stall}=\frac{N}{a}{W}_0\left(\frac{a{V}_e^0\kappa }{N}{e}^{\frac{a}{N}\left(F_c+k^{-}\kappa \right)}\right)-\kappa k^{-}-F_c.$ [6]

The force $$ F$$ acting on the leading-edge membrane is very close to $$ F_m^{stall}$$ if $$ \zeta /\left(\kappa +\zeta \right)\approx $$ 1 or $$ \kappa \ll \zeta $$ holds (see also Eq. 4), i.e., if resistance to motion is large. Indeed, the force in PtK1 and CHO cells is close to $$ F_m^{stall}$$ (SI Appendix, Fig. S5), and $$ \kappa $$ is much smaller than $$ \zeta $$ (Fig. 4). The CHO cells exhibit even $$ F\approx F_m^{stall}$$ (SI Appendix, Fig. S5) and, consequently, move with tiny cell velocities. Forces in all four cell types are one order of magnitude below the maximally possible force $$ F_{max}^{pol}$$ (SI Appendix, Eq. S8), where polymerization stops, and which is reached with very large $$ \kappa $$ only (SI Appendix, Figs. S5 and S6).

We find both stronger effects of adhesion on protrusion force at the front $$ \kappa \ge \zeta $$ (MDA-MB-231 and keratocytes) and stronger effects of adhesion on resisting force $$ \zeta \ge \kappa $$ (CHO cells and PtK1 cells). Pushing ($$ \kappa v_r$$) and resisting ($$ \zeta v$$) forces are not only determined by $$ \kappa $$ and $$ \zeta $$, but also by retrograde flow and cell velocity. Pushing may be strong due to fast retrograde flow, despite small $$ \kappa $$ (PtK1 cells), and resistance may be small due to slow cell velocity, despite large $$ \zeta $$ (CHO cells). Hence, motion is possible in both cases, when adhesion effects on pushing forces (large $$ \kappa $$) or on resisting forces (large $$ \zeta $$) dominate.

The relations between the ligand density $$ B$$ and the friction coefficient ($$ \kappa \left(B\right)$$) and drag coefficient ($$ \zeta \left(B\right)$$), respectively, hold information on the signaling pathway from integrin to adhesion structures.

The values of $$ \kappa $$ and $$ \zeta $$ increase with increasing Fibronectin, Fibrinogen, or PLL-PEG-RGD density, in accordance with the idea that higher ligand density causes more adhesion structures, entailing larger friction and drag. We illustrate adhesion structures by staining of Paxillin, an adhesion-site protein, and F-actin in Fig. 5A and SI Appendix, Fig. S13. The MDA-MB-231 cell in Fig. 5A exhibits high adhesion-site density a few micrometers behind the leading edge, where also stress fibers are anchored (F-actin image). F-actin density is the highest in the lamellipodium. SI Appendix, Fig. S13 shows larger regions with high adhesion-site density on high Fibronectin (SI Appendix, Fig. S13A) than on low Fibronectin (SI Appendix, Fig. S13B) and, thus, corroborates the relation between ligand density and adhesion structures.

Fig. 5.

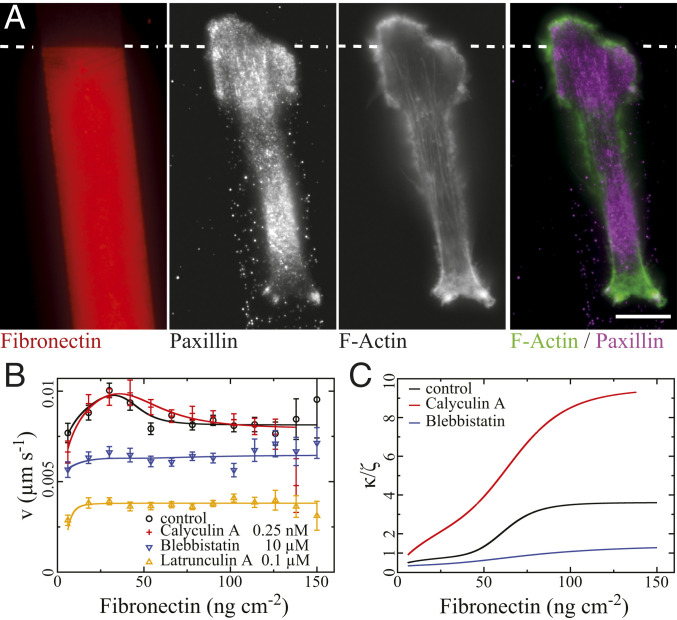
F-actin, adhesion sites, and effects of inhibitors in MDA-MB-231 cells. (A) Fixed cell on a Fibronectin step (moving up, 8 to 40 ng$$ \cdot $$c$$ {\mathrm{m}}^{-2}$$). Images of labeled Fibronectin and Phalloidin-stained F-actin are acquired with epifluorescence, and antibody-stained Paxillin with total internal reflection fluorescence microscopy. (Scale bar: 10 $$ \mathrm{\mu }$$m.) (B) Velocity– adhesion relation of MDA-MB-231 H2B mCherry control cells and cells treated with 10 $$ \mathrm{\mu }$$M ($$ \pm $$)-Blebbistatin, 0.1 $$ \mathrm{\mu }$$M Latrunculin A, or 0.25 nM Calyculin A. (C) Ratios of friction coefficients $$ \kappa $$ and $$ \zeta $$ resulting from the fits in B. A different batch of labeled Fibronectin was used compared to Fig. 2. (For a discussion of absolute Fibronectin densities, see SI Appendix, section S1B.)

Our fitting results show rather strong positive feedback in the pathway from integrin to adhesion structures in MDA-MB-231 and CHO cells (values of $$ n_{\kappa }\gg 1$$ and $$ n_{\zeta }\gg 1$$; Table 1). These cells exhibit a fast rise of the cell velocity by about a factor of six at low coating density (Figs. 2 and 3) and a steep rise of the force $$ F$$ (Fig. 4). This likely reflects the feedbacks on adhesion strengthening mediated by myosin (31, 33, 72, 84) and other pathway components (8), by F-actin flow (20), the effect of force on adhesion strength, and possibly catch bonds (9, 60, 69, 70, 7374–75, 85). PtK1 cells and keratocytes show values of $$ n_{\kappa }$$ and $$ n_{\zeta }$$ between 1.4 and 2.1; the initial rise of velocities is by a factor of about 1.5 only; and the force rises much slower and does not even saturate within the investigated range of substrate coating-density values (Figs. 3 and 4). The small values of $$ n_{\kappa }$$ and $$ n_{\zeta }$$ in keratocytes might be related to the spatial distribution and direction of myosin-related stress in these cells. The wings and lateral extensions show the strongest response to ligand-density increase (33), and stress orthogonal to the direction of motion is about five times stronger than in the direction of motion (22, 86). Hence, a large part of the response may not contribute to propulsion.

We learn more about the positive feedback by applying Blebbistatin, Calyculin A, or Latrunculin A. Blebbistatin inhibits myosin II activity. Its application (10 $$ \mathrm{\mu }$$M) reduces the cell velocity by about 40% (Fig. 5C). The maximum of the velocity in dependence on Fibronectin density vanished. The curve is much closer to a monotonously increasing relation than a biphasic relation. The values of both $$ n_{\kappa }$$ and $$ n_{\zeta }$$ are substantially reduced to about 2.8 in comparison to about 6.5 of the control data and about 4.5 of the Calyculin A data (SI Appendix, Table S2), indicating that myosin suppression removes an essential element of the positive feedback from Fibronectin to adhesion structures. The ratio of the coefficients $$ \kappa $$—entailing protrusive forces—and $$ \zeta $$—entailing resisting forces—illustrates the action of the drugs on the positive feedback. The ratio grows with increasing Fibronectin density in control cells. Blebbistatin abolishes large $$ \kappa $$ to $$ \zeta $$ ratios.

Calyculin A amplifies myosin II activity. Its application (0.25 nM) caused a broader maximum of the velocity (Fig. 5C). This shape of the relation entails a decrease of $$ n_{\kappa }$$ and $$ n_{\zeta }$$ from control values of about 6.5 to 4.7 and 4.1, resp., since the slope from the maximum toward the saturation value is less steep (Fig. 5C and SI Appendix, Table S2). Application of Calyculin A entails the largest ratio $$ \kappa $$/$$ \zeta $$, indicating a strong increase of the density of adhesion structures in areas with retrograde flow.

Latrunculin A inhibits F-actin polymerization. Its application (0.1 $$ \mathrm{\mu }$$M) entails much smaller velocity than control and also a monotonously increasing relation. In line with the effect of the drug, the value of the parameter quantifying the force-free polymerization $$ V_e^0$$ was determined as about one-fifth of the control value by the fit (SI Appendix, Table S2). Latrunculin A also substantially increased the half-maximum values $$ K_{\kappa }$$ and $$ K_{\zeta }$$, rendering precise fit results for $$ n_{\kappa }$$, $$ {\kappa }_{max}$$, $$ n_{\zeta }$$, and $$ {\zeta }_{max}$$ difficult (SI Appendix). In the end, the large values of $$ K_{\kappa }$$ and $$ K_{\zeta }$$ also abolish positive feedback and entail a monotonous dependency of $$ v$$ on Fibronectin.

Fibronectin Density Steps Reveal Spring-Like Interaction of Front and Rear.

We have considered steady motion of cells on homogeneous Fibronectin density so far. Characterizing the mechanical properties of the front–rear interaction requires perturbations of the motion on homogeneous coating, as given by the transitions between different Fibronectin densities (Fig. 6 A and B). Cell front and rear see different ligand densities during transitions between density fields (Fig. 6A). The velocity of the cell in Fig. 6B increases when its front part enters a region with high adhesion density and slightly decreases when its rear part also reaches the high-Fibronectin region (Fig. 6 A and B). When the cell enters a region with low Fibronectin density, it shows the opposite behavior with decreased velocity during the transition and an increase when the transition is completed (Fig. 6 A and B). This directly confirms the idea that strong adhesion at the front supports motion, and strong adhesion at the back resists motion.

Fig. 6.

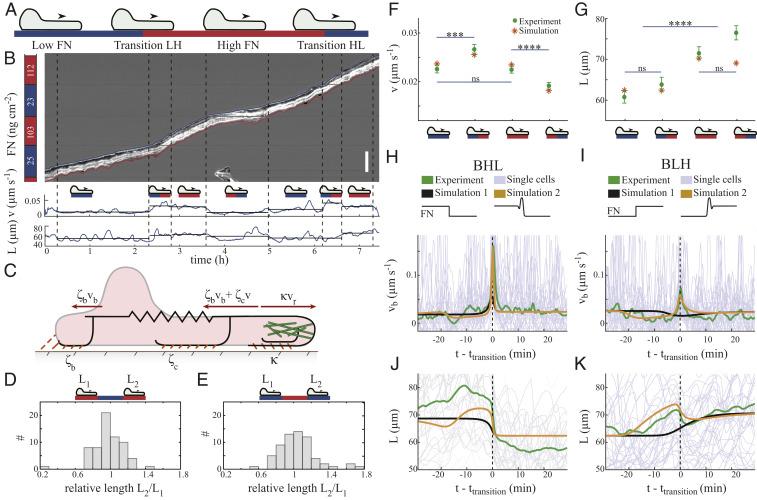
Perturbation of steady motion at Fibronectin density steps. (A) We distinguish phases where cells are completely on one density segment, and transition phases where cell front and back are on different densities. FN, Fibronectin. (B) Kymograph of a cell running through areas of different Fibronectin densities (given on the left). We trace front (blue) and back (red) and provide the time course of front velocity (v) and cell length (L). Mean velocities and mean lengths are indicated by horizontal lines for each phase. (Scale bar: 100 $$ \mathrm{\mu }$$m.) (C) Sketch of the cell model with spring-like front–rear interaction force. (D and E) The ratio of the mean lengths of individual cells after to before crossing a density region. (F) Front velocity averaged over individual phases measured from 99 kymographs set in relation to simulation results. Error bars show SEM. (G) Length averaged for individual phases from the same kymographs as in E and compared to simulation results. Results of two-sided t test are indicated. ***P < 0.001; ****P < 0.0001. ns, not significant. (H and I) Back velocity during a transition of the back (B) from high (H) to low (L) Fibronectin (BHL) and low to high (BLH). (J and K) Cell length for BHL and BLH transitions. (H–K) Thin gray lines are individual measured trajectories; the green line shows their average values. The black lines show the simulated time courses for a simple step profile of the Fibronectin density. Simulation results with the detailed Fibronectin profile with additional bumps as in Fig. 1 are shown by the yellow lines.

Kymographs of another set of measurements with 20-s time resolution show that the front is moving rather smoothly and changes its velocity at the Fibronectin density steps (Fig. 6B and Movie S4). The rear motion exhibits larger fluctuations and can even form a transient protrusion extending backward. We consider the front velocity $$ v$$ as the cell velocity and, additionally, introduce the velocity of the back $$ v_b$$. Although $$ v_b$$ fluctuates, it is, on average, equal to $$ v$$ during steady-state motion.

We need to look closer at the force-resisting motion to understand the differential behavior of $$ v$$ and $$ v_b$$. We will see below that the cell length $$ L$$ is mainly determined by the Fibronectin density at the rear of the cell, while the velocity is affected by both front and rear density. Based on that observation, we split the resisting force up into the drag force required to pull the front part and cell body on the substrate, $$ {\zeta }_{c}v$$, and the force required to pull the cell rear, $$ {\zeta }_b{v}_b$$ (Fig. 6C). The force balance also includes the length dynamics $$ \dot{L}$$ now, and is given by (taking $$ F_c=F_m=0$$ into account)

We start our experimental investigations on the nature of the front–rear coupling with the question for an intrinsic Fibronectin-related cell length. If it exists, the cell length should mainly be set by the Fibronectin density $$ B$$, and not by the history of the cell motion. We measure the length of a cell on one density and the length after transitions to the other density and back. The distribution of the ratio of these two lengths peaks around one (Fig. 6 D and E); hence, cells have an intrinsic Fibronectin-density-dependent length $$ L_0\left(B\right)$$. This motivates our choice for the force resisting cell stretching $$ F_S$$ to be an elastic one $$ F_S=E\left(L-L_0\right)$$. This elastic force–length relation is a phenomenological description. We cannot conclude from our data how cells realize this spring-like behavior. It might be the one-dimensional analogon to a preferred shape in two dimensions (33, 87, 88) or might be realized by the fast front–rear interaction reported by Maiuri et al. (89) or by other means.

The elastic force $$ F_S$$ mediates front–rear interaction and, thus, the dependency of the cell velocity on the coating densities at both ends. The force $$ \kappa v_r$$ pushing at the front drags the cell ($$ {\zeta }_{c}v$$) and stretches it by the force pulling on the rear $$ {\zeta }_b{v}_b=E\left(L-L_0\right)$$ (Fig. 6C). Fig. 6F summarizes this effect for the four different density combinations by averages across all measured data points in the different regimes. The adhesion–velocity relation Eq. 4 accounts not only for homogeneous Fibronectin density, but also for the situations with differential densities at front and back (see also SI Appendix, Eqs. S13–S16). We use it to fix the $$ \zeta $$ values for these situations based on the measured velocities. Our analysis shows $$ \zeta $$ to be small when the front of the cell is on low density and large when the front is on high density (SI Appendix, section S7, Figs. S9 and S10, and Table S5). We can also quantify $$ {\zeta }_b$$ on the basis of the transitions between densities. The rear part $$ {\zeta }_{b}v$$ of the force resisting motion stays small across the whole ligand-density range. Hence, if we see substantial resistance to motion, most of it is offered by the front part resisting force $$ {\zeta }_{c}v$$ (Eq. 7; SI Appendix, Eqs. S17–S20).

The behavior of the cell length $$ L$$ reflects the contributions of the cell parts to resistance. $$ L$$ is the shortest when the rear of the cell is on low Fibronectin, and the force $$ {\zeta }_b{v}_b$$ stretching the spring is small. It is the longest when the rear is on high Fibronectin, and stretching forces are larger (Fig. 6G; SI Appendix, Figs. S9 and S10), in agreement with results of Hennig et al. (90).

The biphasic character of the adhesion–velocity relation and cell variability entail a qualitative difference between two groups of cells with respect to the velocity behavior. Some cells moving across the density regions in a given experiment are in the rising phase of the adhesion–velocity relation and exhibit a smaller velocity $$ v$$ on low Fibronectin than on high Fibronectin ($$ v_{LL}<v_{HH}$$), and some are in the falling phase and show $$ v_{LL}>v_{HH}$$ (see also SI Appendix, Fig. S12). Cells in the phase $$ v_{LL}<v_{HH}$$ of the adhesion–velocity relation show the higher velocities when the cell front is on high density, since increasing Fibronectin density also increases $$ \kappa $$ and, therefore, the force generated by the front region (SI Appendix, Fig. S9). With cells in phase $$ v_{LL}>v_{HH}$$, $$ \kappa $$ is close to saturation on both high and low Fibronectin density (SI Appendix, Fig. S10). Increasing adhesion at the front increases force generation not via $$ \kappa $$ in this phase, but by increasing retrograde flow on the expense of the cell velocity $$ v$$. Therefore, velocities are the highest when resistance to motion is the lowest, i.e., when the cell rear is on low density. These observations nicely illustrate that the biphasic character of the adhesion–velocity relation results from competing forces.

The dynamic behavior during transitions between density regions shows qualitative differences of front versus back of the cell. The mean velocity of the front adapts quickly to the values set by the adhesion–velocity relation (SI Appendix, Fig. S11). During transitions of the front, the back velocity does not change dramatically, but follows the trend of the front velocity (SI Appendix, Fig. S11). In contrast, $$ v_b$$ exhibits a pronounced peak when the cell back-traverses from high to low (BHL transition; Fig. 6H). This peak is reproduced by simulations (Fig. 6H). Surprisingly, we also find a peak of the back velocity during a transition of the back from low to high density (BLH), but smaller than for BHL transitions. If we use a simple step for the Fibronectin profile at the transition points, the BLH simulation does not show a peak in difference to the experiments (Fig. 6I). It turned out that details of the profile are relevant for this transition (Fig. 1A). The profile exhibits small density maxima bordering the high-density range and neighboring small minima next to them toward the interior of this range. When implementing this detailed Fibronectin profile, the results of simulations exhibit a positive peak of back velocity at the BLH transition, which is consistent with experimental data (Fig. 6 H and I).

During BHL transitions, the average length of the cell shows a sudden drop (Fig. 6J), which corresponds to the peak of $$ v_b$$. Additionally, we find an increase of the cell length prior to the transition. Simulations capture this behavior, if we use the detailed Fibronectin-density profile. Only the absolute changes of the cell length are slightly underestimated by the model. The length during BLH transitions increases before the transition, drops slightly during the transition, and subsequently increases again. Maybe the most remarkable result of the analysis of velocity and cell length during transitions is that also small Fibronectin-density variations, like the little bumps on the boundary of the density ranges, affect migration dynamics.

We quantify the elastic modulus $$ E$$ of the force $$ F_S=E\left(L-L_0\right)$$ by an analysis of the trailing-edge dynamics. It provides $$ E/{\zeta }_b\approx $$ 0.011 $$ {\mathrm{s}}^{-1}$$ (SI Appendix, Fig. S8). With the estimate for $$ {\zeta }_b$$, we obtain $$ E$$ = 0.001 to 0.0015 nN$$ \cdot \mathrm{\mu }{\text{m}}^{-2}$$ (SI Appendix, Table S5). Considering $$ L_0\approx $$ 50 $$ \mathrm{\mu }$$m and an average cell height of $$ \approx $$ 0.5 $$ \mathrm{\mu }$$m, we find a mean Young modulus of the cell of $$ \approx $$0.10 to 0.15 kPa (SI Appendix, Eq. S1), which is in the range of Young moduli of adherent cells measured experimentally, $$ \approx $$0.25 kPa (91). We could reproduce the measured stationary and dynamic length behavior only by choosing a length-dependent force between front and rear. The time scale during which this force acts is in the range of a few minutes, which is longer than the visco-elastic relaxation time of cells (92). Therefore, a visco-elastic front–rear interaction force would not have been applicable. This confirms our choice of an elastic force for cell stretching in addition to the intrinsic length.