Monovalent Cation Permeation.

Our starting structure for MD simulations was the AMPAR channel in its activated conformation (Protein Data Bank [PDB] ID: 5WEO) (1), which we embedded into a palmitoyloleoyl phosphatidylcholine (POPC) lipid bilayer (Fig. 1D). To reduce the number of atoms in the simulations, we removed the extracellular ATD and LBD and the four Stargazin molecules decorating the periphery of the channel. To retain the open channel conformation, we held the transmembrane domain (TMD) of AMPAR open by physically restraining the end of the truncated linkers (Fig. 1B and see Methods for details). This approach, while facile, was highly reproducible, and the channel did not lose its overall stability (SI Appendix, Fig. S1) or close spontaneously during any simulation run (Fig. 2A). Simulations of ion conduction were performed with the computational electrophysiology method (23, 24). In this setup, the simulation box contains two membranes that define two compartments, and a voltage difference across each membrane is created by an ion gradient that is maintained alchemically during the simulations (Fig. 1D). From an analysis of the temporal evolution of the root mean square deviation (rmsd) (SI Appendix, Fig. S2), the different transmembrane voltages (up to 550 mV) induced by these ion gradients caused no systematic distortions to the receptor structure during each simulation run.

Fig. 2.

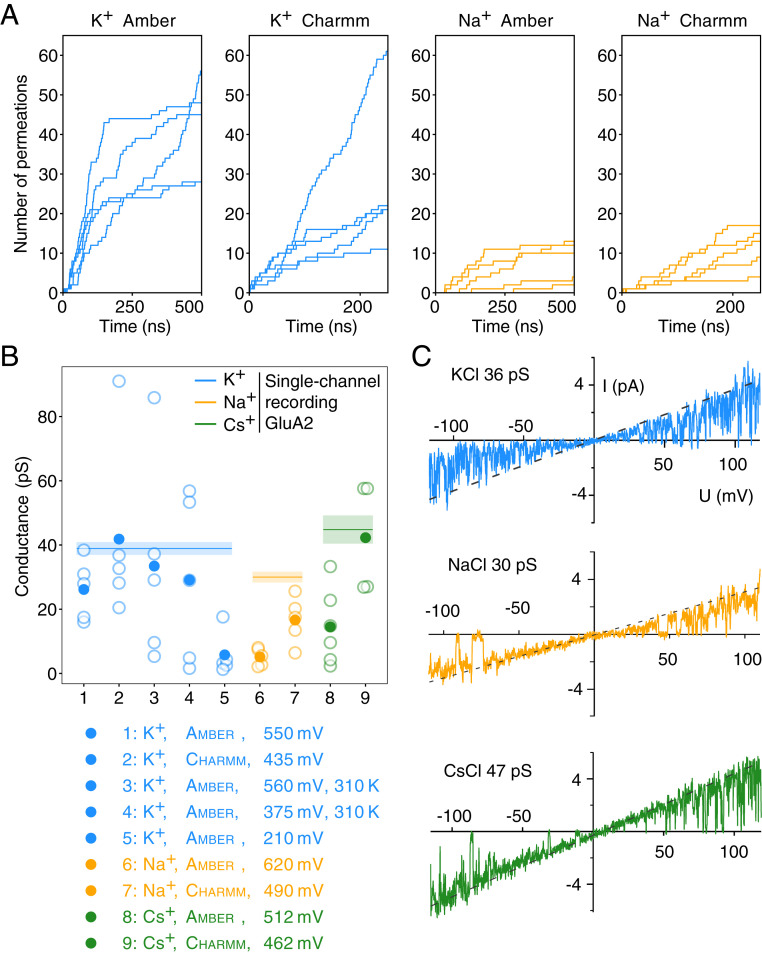
Ion conductances in GluA2. (A) Cumulative ion permeation events in the GluA2 pore for individual trajectories of K⁺ and Na⁺ simulations with the respective force fields. The simulations were performed at 303 K using an ion imbalance of 6e⁻ between two compartments $$ \alpha $$ and $$ \beta $$. (B) Conductances derived from the K⁺ (blue), Na⁺ (orange), and Cs⁺ (green) simulations performed with amber99sb and charmm36 force fields. Simulations were carried out at different temperatures at the nominal transmembrane voltages indicated. Filled and empty circles mark mean and individual conductances determined from MD simulations. The mean conductances from single-channel recordings for Na⁺, K⁺, and Cs⁺ (30 ± 2, 39 ± 2, and 45 ± 4 pS, respectively) are displayed as lines (shading are SDs of the means) with the same color code as the wet experiments. (C) Outside-out patch clamp electrophysiology of a single GluA2 (Q) channel in symmetrical Na⁺, K⁺, and Cs⁺. The voltage ramp (200 ms in duration) was made in the presence of 10 mM glutamate and 100 µM CTZ. The dashed lines are the fitted chord conductances, and the conductances for the individual recordings are shown.

Classical electrophysiology experiments suggest AMPARs are broadly nonselective over different alkali metal cations, although most measurements were not made on GluA2 (7, 25). We began by performing a series of ion permeation simulations with the principal biological ion species, Na⁺ and K⁺. To ensure the robustness of our observations, we undertook simulations at different temperatures, with different force fields and different driving forces on the ions (see Discussion and Methods). The conductances of the AMPA channel pore were directly calculated from the ion permeations observed in these simulations. We counted cations that traversed the entire narrow region of the pore domain delineated by the ⁵⁸⁶QQGCDI⁵⁹¹ sequence, summarized in Table 1 and Fig. 2B. Outside of this region, ion movements lacked order and made only rare interactions with the channel, leading to a largely flat energy landscape (SI Appendix, Fig. S3). In all trajectories, the channel pore remained conductive for Na⁺ or K⁺ during the entire 500-ns run, as exemplified by the ion track plots in Fig. 2A and SI Appendix, Fig. S4. In a typical 500-ns trajectory with a transmembrane potential of 450 mV, we recorded over 40 K⁺ permeation events, corresponding to a conductance of 32 pS.

Table 1.

Summary of computational electrophysiology simulations

Cation	Force field	∆q (e–)	[C] (mM)	Vm (mV)	T (K)	Replicates	Ion permeations	γ (pS)
K+	Amber	6	273.8	550	303	5	220	26 ± 8
K+	Amber	2	273.8	210	303	5	18	6 ± 6
Na+	Amber	6	273.8	620	303	5	50	5 ± 2
K+	Charmm	6	212.1	435	303	5	144	41 ± 25
Na+	Charmm	6	212.1	490	303	5	63	17 ± 6
Cs+	Amber	6	273.8	512	303	6	133	15 ± 11
Cs+	Charmm	6	212.1	462	303	4	121	42 ± 15
K+	Amber	6	273.8	560	310	5	300	33 ± 29
K+	Amber	4	273.8	375	310	5	163	29 ± 23
K+	Amber	0	121.5	77	303	5	0	0
K+, closed	Amber	6	284	433	303	3	0	0
K+	Single-channel recording	—	150	−120 to +120	296	3 patches	—	39 ± 2
Na+	Single-channel recording	—	150	−120 to +120	296	3 patches	—	30 ± 2
Cs+	Single-channel recording	—	150	−120 to +120	296	3 patches	—	45 ± 4

Simulations of the GluA2 TMD for Na⁺, K⁺, and Cs⁺ permeation are shown. In addition to changing cations, we also varied temperature (T), charge imbalance (∆q), and the force field employed. C is the salt concentration. Each simulation replicate was 500 ns, except for charmm runs, in which the duration was 250 ns. These simulations represent an aggregate time of 20.5 µs. amber refers to amber99sb and charmm to charmm36. The single-channel conductance of GluA2 (Q) in Na⁺, K⁺, and Cs⁺ each determined from three recordings is also included.

Although K⁺ permeated readily in the simulations with amber99sb force field (26), we observed substantially fewer permeations of Na⁺ under the same simulation condition. The simulated conductances of both K⁺ and Na⁺ were higher in the charmm36 force field (27), allowing direct observation of Na⁺ permeation at close to physiological rates (Table 1 and Fig. 2B). Higher conductance using charmm36 compared to amber99sb was previously reported in simulations of K⁺-selective and nonselective NaK-CNG channels (14). We also performed five unbiased K⁺ simulation runs without ion gradient. Within each 500-ns run, several K⁺ ions spontaneously entered the SF from both intracellular and extracellular sides and found stable binding sites (SI Appendix, Fig. S5). Nevertheless, no complete permeation through the filter could be observed in 2.5 µs of simulation time. A comparison of ion occupancy showed that the major ion binding site within the SF (see below, S_I) was rarely occupied during these simulations at nominal zero transmembrane voltage (SI Appendix, Fig. S6).

Binding Sites for Permeant Ions.

SF architectures differ widely among tetrameric ion channels. While K⁺ channels generally have long, straight filters, nonselective cation channels tend to have shorter filters that display more plastic or eccentric geometries (28, 29). To understand how the AMPAR SF supports cation-selective ion conduction, we determined one- and two-dimensional ion occupancies in the AMPA channel, which were sampled from cumulative simulations of K⁺ and Na⁺ with the respective force fields (Figs. 3B and 4A and SI Appendix, Fig. S7). For each ion species, these plots reveal only one principal binding site (which we call S_I) in the SF, which is located around 15 Å along the pore axis (Fig. 3). At this site, the primary coordination of permeant ions is by backbone carbonyls of Q586 that replace some but not all of waters of hydration (SI Appendix, Fig. S8). Secondary, less frequent interactions occur with the mobile side chain of Q586 and the backbone carbonyls of Q587 (Fig. 1C). In some trajectories using amber99sb force field, solvated Na⁺ ions stayed at the S_I longer than 100 ns (Fig. 4B), which may explain the slower permeation. During outward permeation, ions leaving the S_I site frequently paused above the tip of the SF (25 Å at the pore axis in Fig. 4A) and then rapidly entered bulk water as they traversed the upper reaches of the channel. Before reaching the major binding site S_I, multiple ions simultaneously entered the inner mouth of the channel, classically expected to be part of the SF (2, 30) and composed by the residues G588, C589, and D590 (Fig. 1C). K⁺ and Na⁺ paused frequently but briefly at several secondary sites in the lower SF region (for example, the S_II site around 10 Å into the pore, cytoplasmic to the S_I site, Fig. 3B). Compared to the primary site, the secondary sites were weakly populated (SI Appendix, Fig. S4) with shorter residence times (Fig. 4B). Therefore, we conclude that the true SF region of the AMPA is the shortest seen in any tetrameric channel to date, comprising essentially only Q586 and Q587 that form the S_I site.

Fig. 3.

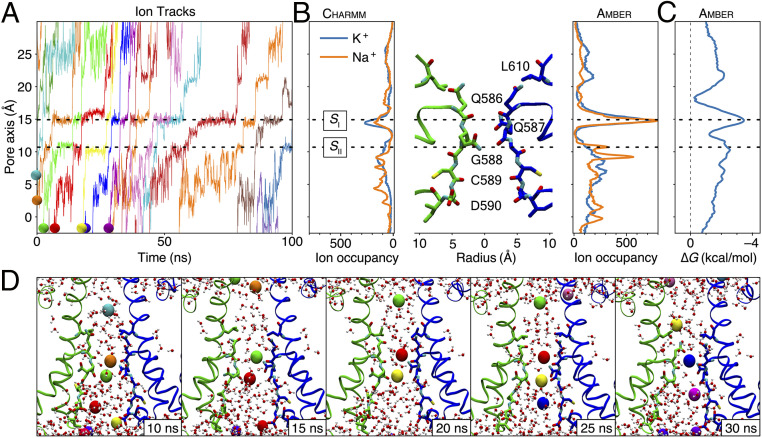
Simulated Na⁺ and K⁺ permeation of GluA2. Simulations were performed at 303 K using an ion imbalance of 6 e⁻ between two compartments $$ \alpha $$ and $$ \beta $$. (A) Representative traces of K⁺ passing through the SF of the AMPA channel pore. Ions drawn in D are indicated by balls. The center of mass of the SF backbone atoms corresponds to the 10 Å point along the pore axis. The major ion binding site S_I and the immediately adjacent minor site S_II are indicated by dashed lines in A, B, and C. (B) One-dimensional ion occupancy of cations within the SF of the AMPA channel pore. Occupancy from simulations with (Left) the charmm36 force field and (Right) the amber99sb force field. (C) Free-energy profile for K⁺ permeation constructed from amber99sb force field. (D) Representative snapshots of a simulation (from Movie S1) showing multiple K⁺ ions passing the SF during ion conduction. The color code of ions is identical with the ion track plot in A.

Fig. 4.

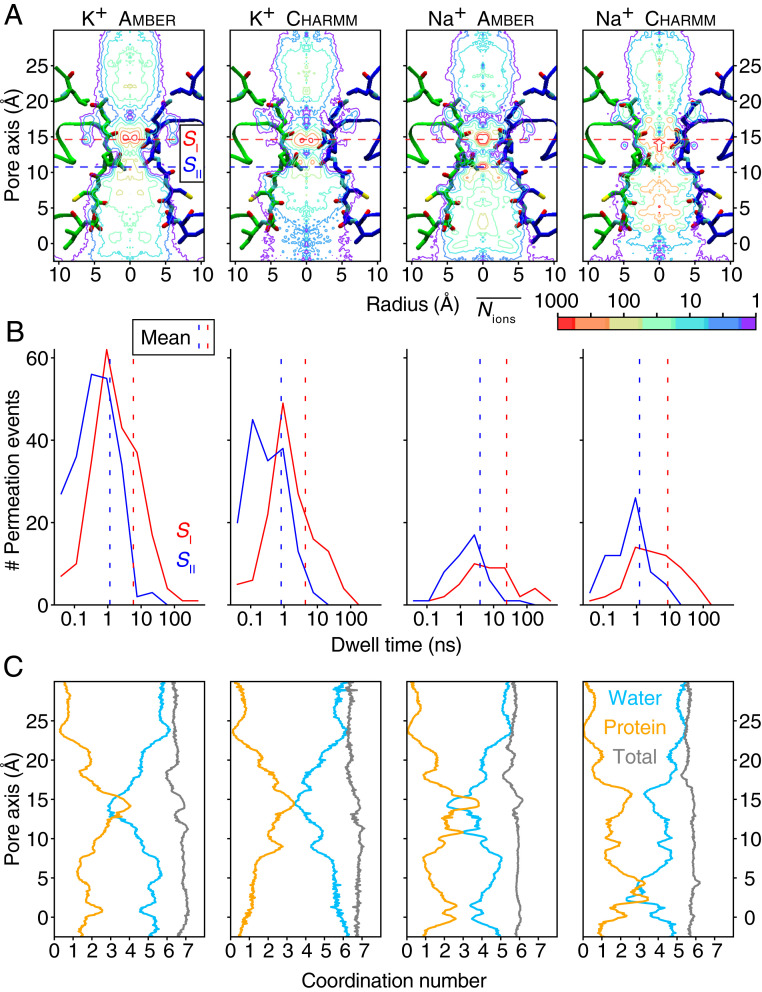
Ion occupancy, dwell time distribution, and hydration states. (A) Two-dimensional ion occupancy within the SF resolved radially and along the pore axis (z-axis) as a contour plot calculated from MD simulations of GluA2 with different ion types (K⁺ and Na⁺) and force fields (amber99sb and charmm36). The simulations were performed at 303 K using an imbalance of six cations between the two compartments, α and β. The ion occupancy in number of ions per 0.001 ų per 500 ns was normalized according to the volume change along the radius. The center of mass of the SF backbone atoms corresponds to the 10 Å point along the pore axis. Approximate centers of the binding sites are drawn as dashed lines (S_I, red and S_II, blue). (B) Dwell time histograms for S_I and S_II binding sites. Vertical dotted lines are means of the respective dwell times. (C) The number of oxygens within the first hydration shell of the according ion type along the pore axis. The number of coordinating water oxygens is in blue, the number of coordinating protein oxygens is in orange, and their sum is in gray.

Cation Conduction Mechanism and Selectivity.

During ion conduction, we observed multiple ions in the canonical SF region of ⁵⁸⁶QQGCDI⁵⁹¹ (Fig. 3D and Movies S1 and S2), with an average occupancy of 2.4 ± 0.6 and 2.3 ± 0.7 for K⁺ and Na⁺, respectively, in amber simulation runs (SI Appendix, Fig. S9). Ions followed a loosely coupled knock-on mechanism, where in most cases, the exit of an ion to the upper cavity was closely followed by the entry of an ion to the S_I site (Fig. 3D and Movies S1 and S2). From the free-energy profiles (Fig. 3C and SI Appendix, Fig. S7), we conclude that the energy barriers bracketing S_I (at around 13 Å and 18 Å along the pore axis) are the major obstacles for ion conduction in the SF. The ion entering the S_I site was normally supplied from the adjacent secondary sites, presumably aiding permeant ions to overcome the main energy barriers before and after the S_I site (10).

To understand better where cation selection occurs, we examined the paths of chloride (Cl⁻) ions during our simulations. Consistent with a very short selective region, Cl⁻ ions occasionally entered the cone-shaped space below the SF and readily approached the QQ filter from the bundle crossing side. Surprisingly, Cl⁻ ions found stable binding sites immediately above the QQ filter (SI Appendix, Fig. S10) in all simulations. We also observed one Cl⁻ permeation event during the K⁺ simulations (Movie S3) but not in the Na⁺ simulations, providing a crude estimate of the Cl⁻:K⁺ permeability ratio at around 1:220. In practical terms, this relative selectivity would correspond to an ∼15 µV shift in the reversal potential (Goldman-Hodgkin-Katz [GHK] equation, see Methods) compared to no Cl⁻ permeation at all. In other words, at this level of selection between cations and chloride, any reversal potential shifts are too small to be measured experimentally. Further context comes from the observation that R-edited homomeric GluA2 channels are anion permeable (5). The observation of an infrequent yet stable anion approach to the face of the QQ filter favored for anions by the electric field provides a simple explanation as to how this point mutation can switch selectivity simply by changing local electrostatics.

Ion Hydration States during Permeation.

To determine the ion hydration states during permeation, we calculated the number of ion-coordinating oxygens from both water molecules and protein residues within each ion’s first solvation shell. Hydration shells are dynamic; here, we defined the waters of hydration using the radii corresponding to the minimum in the radius of gyration profiles: 3.1 Å for Na⁺, 3.4 Å for K⁺, and 3.8 Å for Cs⁺ (31, 32). All monovalent ions were principally coordinated by waters in the lower SF region (Fig. 4C), while the contribution of protein oxygens (backbone oxygens of Q586 and backbone and side-chain oxygens of Q586 and Q587, Fig. 1C and SI Appendix, Fig. S8) increased substantially at the major ion binding site and surpassed the water oxygens for K⁺ and Cs⁺. The average number of ion-coordinating oxygens in the first hydration shell (gray line) remained remarkably stable along the pore axis, being six, seven, and eight for Na⁺, K⁺, and Cs⁺, respectively (Figs. 4C and 5C). This total number of ion-coordinating oxygens was in very good agreement with the coordination number for hydrated ions determined experimentally (33). The simulations indicate a qualitatively similar mechanism for each ion species. Cations were never fully dehydrated, but we also observed permeation by water that was independent of ion conduction (SI Appendix, Table S1). The retention of water is probably a strong factor in determining the lack of selectivity across the alkali metal series.

Fig. 5.

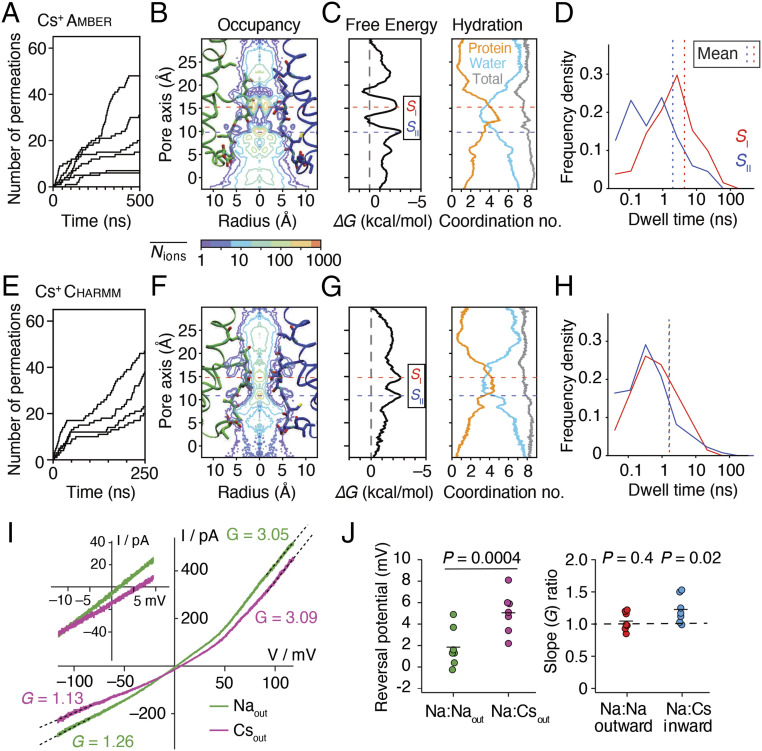
Cs⁺ permeation of GluA2. (A) Permeation events for Cs⁺ in the amber99sb force field. (B) Two-dimensional ion occupancy plots. The center of mass of the SF backbone atoms corresponds to the 10 Å point along the pore axis. Approximate centers of the binding sites are drawn as dashed lines (S_I, red and S_II, blue) that extend to C. (C) Free energy and hydration profiles for Cs⁺ along the pore axis. (D) Dwell time histograms for Cs⁺ in the S_I and S_II sites, with mean dwell time for each site indicated with a dashed line. (E–H) Same as for A–D but for the charmm36 force field. (I) Outward rectifying responses to voltage ramps in Na⁺ (green) and Cs⁺ (purple) measured with patch clamp electrophysiology. The outward rectification (ratio of chord conductances at +100/−100 mV) was 2.7 ± 0.3 for Na⁺ and 3.1 ± 0.3 for Cs⁺ (n = 7 patches). The inset shows the typical shift in reversal potential on exchange of external Cs^+- and Na⁺. The pipette solution contained Na⁺. (J) Reversal potential of AMPAR currents in external NaCl and CsCl solution and conductance ratios of Na⁺ versus Cs⁺ for inward and outward permeation. Probability of no difference in the slope ratio was versus a ratio of 1 with paired Student’s t test.

Cesium Permeation.

Cs⁺ is impermeant or a blocker of most potassium channels (34) and also blocks nonselective HCN channels (35). In this context, it is somewhat surprising that classical electrophysiological measurements of reversal potentials for cloned AMPA receptors show, at most, minor differences in the permeation of Cs⁺ (van der Waals radius 343 pm) from that of Na⁺ and K⁺ (radii 227 pm and 280 pm, respectively) (7). The hydrated radius of Cs⁺ in bulk water (at least 3.1 Å) is expected to be substantially greater than that of Na⁺ and K⁺ (2.4 Å and 2.8 Å, respectively) (36). We reasoned that to achieve similar permeation statistics despite its greater size, Cs⁺ should either alter SF geometry, occupy distinct binding sites, or have a different hydration state during permeation. To resolve this point, we simulated Cs⁺ permeation in the same conditions as for K⁺ and Na⁺. From both amber and charmm simulations, we observed similar conductances for Cs⁺ and K⁺ (Fig. 2B and Table 1) that were higher than for Na⁺. However, the geometry at the tip of the pore loop did not change. The hydration profile of Cs⁺ as it passes through the pore is more similar to K⁺ than Na⁺, with protein oxygens outnumbering the water oxygens at the S_I and S_II sites in the QQ SF. However, in amber simulations, the major binding site (S_I) for Cs⁺ is axially displaced by about 0.5 Å toward the bundle crossing gate compared to those of K⁺ and Na⁺ (Fig. 5B and SI Appendix, Fig. S7), with a concomitant longer distance to the S_II site. Most critically, in both amber and charmm simulations, the mean residence time for Cs⁺ at the S_I site was much less (∼1 ns) than for Na⁺ or K⁺ and matched that at the S_II site (Figs. 4B and 5 D and H). Based on observations that NaK could be converted into a potassium-selective channel by introducing consecutive K⁺ binding sites (37), serial binding to two effectively equivalent sites suggested that Cs⁺ may be selected over Na⁺ and K⁺. In other words, the simulations suggest that Cs⁺ might be more permeant than Na⁺ or K⁺ and have a higher conductance than Na⁺, with the caveat that permeability and conductance are not related in a simple way (38).

Extensive studies of GluA1 (7) suggest a small shift in reversal potential between Cs⁺ and Na⁺, corresponding to selection, but the permeation of cations in GluA2 (Q) might be different. We performed patch clamp electrophysiology experiments on unedited GluA2 channels expressed in HEK293 cells to reexamine the reversal potentials and slope conductances for Na⁺ and Cs⁺ in the same recording. We readily detected a small but consistent shift in the reversal potential in external Cs⁺ of 3.7 ± 0.5 mV (n = 7 patches, Fig. 5 I and J), meaning Cs⁺ was slightly more permeant than Na⁺ (P_Cs:P_Na = 1.16 ± 0.02), like in GluA1. The slope conductance for the inward arm of the current–voltage (I–V) relation in Cs⁺ was similar to that of Na⁺ (82 ± 6%; n = 7 patches). Taken together with our single-channel recordings (Fig. 2), these observations are consistent with the AMPAR pore being mildly selective for Cs⁺ over Na⁺ and Cs⁺ permeating with a higher conductance despite using a subtly different permeation mechanism on the same overall scaffold.

Conformational Dynamics in the Vicinity of the SF.

To identify the major conformational states of the SF during ion permeation, we performed a conformational clustering analysis on Na⁺, K⁺, and Cs⁺ simulations, respectively. Interestingly, only one mainly populated state was found for the respective simulations across different cations (SI Appendix, Table S2), which in each case was highly similar (Fig. 6A). A comparison of these representative structures from clustering analysis with the original Cryo-EM structure revealed no large structural differences, but the top part of the SF (Q586 and Q587) is slightly more open in the Cryo-EM structure (Fig. 6A).

Fig. 6.

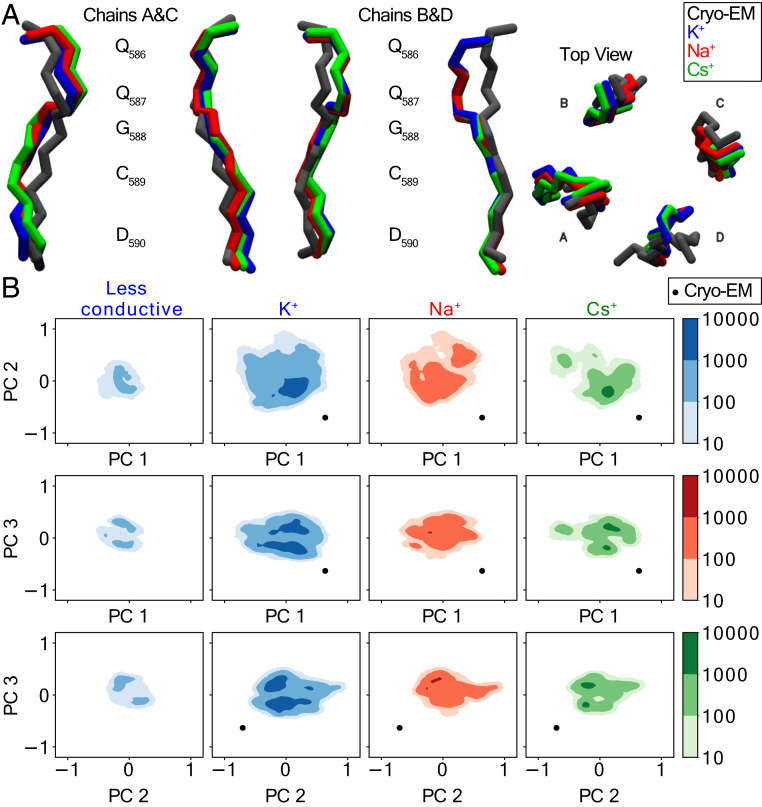
PCA and clustering analysis. (A) Comparison of the SF in Cryo-EM structure and the representative structures of the K⁺, Na⁺, and Cs⁺ simulations using amber99sb force field. The representative structure is the middle structure of the most populated cluster from clustering analysis (SI Appendix, Table S1). An rmsd cutoff of 0.05 nm was used for cluster determination. A total simulation time of 2.5 μs was obtained for K⁺ and Na⁺ simulations, respectively, while for Cs⁺, the total simulation time is 3.0 μs. (B) Results of the PCA analysis on the SF part, where trajectories of K⁺, Na⁺, and Cs⁺ simulations were combined for the determination of the principal components. Conformational dynamics of the SF in K⁺, Na⁺, and Cs⁺ simulations were projected individually onto the first three principal modes. Less conductive states were combined from K⁺ simulation run 1 (300 to 450 ns), run 3 (200 to 300 ns), and run 5 (200 to 350 ns) of the lower channel (SI Appendix, Fig. S4), where only one permeation event was observed during the entire simulation period.

To further understand the conformational dynamics of the SF during ion permeation, we performed a principal component analysis (PCA), in which the most pronounced motion of the SF can be described by a few eigenvectors with large eigenvalues (39). For the PCA analysis, we used the combined trajectories of Na⁺, K⁺, and Cs⁺ simulations (with the amber forcefield) that were initially aligned on the SF (⁵⁸⁶QQGCD⁵⁹⁰). The first three eigenvectors (with the largest eigenvalues) account for >45% of all the motion in the combined trajectories (SI Appendix, Fig. S11). We have visualized the motion of these first three eigenvectors, which correspond to asymmetric deformation or distortion of one to two subunits in the SF (SI Appendix, Fig. S12). Conformational asymmetry is also reflected in the major states determined from clustering analysis (Fig. 6A). Furthermore, we projected the first three eigenvectors onto the individual Na⁺, K⁺, and Cs⁺ simulations, respectively. States of the SF sampled from the K⁺, Na⁺, and Cs⁺ simulations are highly similar (Fig. 6B), suggesting no significant difference in conformational dynamics during ion permeations with different ion types. Finally, we combined three parts of less-conductive trajectories from K⁺ simulations (SI Appendix, Fig. S4, lower channel, run 1: 300 to 450 ns, run 3: 200 to 300 ns, and run 5: 200 to 350 ns). Projection of the first three eigenvectors on the less-conductive simulations showed that they sampled the same conformational landscape as the rest of the simulations, ruling out structural changes for the variations in the instantaneous conduction rate observed during the simulations.

Examining the root mean square fluctuations (rmsf) of heavy atoms in residues in the traditional SF and its neighboring regions (⁵⁸⁵MQQGCDI⁵⁹¹) reveals a clear split in dynamics (SI Appendix, Fig. S13). The backbone atoms at the pore loop (⁵⁸⁵MQQG⁵⁸⁸) are comparatively immobile, similar to the M3 backbone adjacent at L610. In the lower filter region, the backbone and side chains of CDI residues are comparatively unrestrained. The side chain of Q586 is more flexible than the Q587, as it points toward the cavity and thus has more freedom for movement. Similar to the results of PCA analysis, the dynamics of the SF were indistinguishable across the different ionic conditions, with the rmsf profiles of both backbone and side-chain atoms in the Na⁺, K⁺, and Cs⁺ simulations being highly similar (SI Appendix, Fig. S13). These observations further underline that the stable structure of the QQ filter is sufficient for selecting cations.

Computational Electrophysiology.

To prepare the Cryo-EM structure of the AMPAR in an open state (PDB ID: 5WEO) (1) for MD simulations, we removed the four copies of the auxiliary protein Stargazin. We truncated the receptor linkers before I504 and G774 and after I633 and A820 and added N-methyl amide and acetyl caps at the newly created C and N termini. We used MODELER (55) to build missing loops (residues 550 to 564 of the intracellular loops of each subunit) as well as missing side chains (sidechains of S818 and R819 of subunits B and D and K505 of subunit D). To hold the truncated structure together and in an open state, we restrained protein at the heavy atoms of all four peptide chain termini with a harmonic potential of 10,000 kJ/mol for each subunit.

We performed MD simulations with both charmm36 (27) and amber99sb (26) force fields. In the amber setup, insertion of the AMPAR TMD into a POPC lipid bilayer was performed with the Gromacs internal embedding function, whereas in the charmm setup, this process was carried out in charmm–GUI (56). The concentration of KCl, NaCl, and CsCl was 274 mM in simulations with amber, except for one simulation setup of the closed channel in which the amber force field was 284 mM KCl. For charmm simulations, we used a salt concentration of 212 mM. Improved lipid parameters (57) and ion parameters (36) were used in the amber simulations. We used the TIP3P (transferable intermolecular potential with three points) water model (58) in all simulations.

All the MD simulations were carried out with the gromacs software package (versions 2016.1 and 2019.5) (59). Short-range electrostatic interactions were calculated with a cutoff of 1.7 nm, whereas long-range electrostatic interactions were treated by the particle mesh Ewald method (60). The cutoffs for van der Waals interactions were set to 1.7 nm. The simulations were performed at 303 K or 310 K with an enhanced Berendsen thermostat (gromacs v-rescale thermostat) (61). A surface-tension Berendsen barostat was employed to keep the pressure within the membrane plane (xy-axis) at 250 bar per nm per lipid surfaces and at 1 bar in z-axis direction (62). All bonds were constrained with the Linear Constraint Solver (LINCS) algorithm (63). Interatomic forces (van der Waals and Coloumb) were calculated with a 1.5-nm cutoff. Long-range electrostatic forces were computed with the Particle-Mesh-Ewald method. To decrease computational cost, we employed virtual sites for hydrogens in all amber simulations. amber simulations were calculated with an integration time step of 4 fs. All charmm-based simulations used an integration time step of 2 fs.

Before starting the simulation of the AMPAR with an ion gradient, the system was first energy minimized and equilibrated. After the systems energy was minimized to below 1,000 kJ/mol with gromacs “steepest descent” implementation, a 10-ns free equilibration without any restraints (except those for the linkers) was performed. For charmm-based simulations, the recommended energy minimization and equilibration steps from charmm-GUI were performed.

For the computational electrophysiology study (23), two copies of the equilibrated system of the AMPAR TMD in the lipid bilayer were included in a simulation box of typically 10 × 10 × 20 nm (Fig. 1D). A charge gradient and therefore transmembrane potential was generated by introducing an ion difference of 2, 4, or 6 cations between the two compartments separated by the two lipid bilayers. Since the instantaneous introduction of a charge gradient into the system can produce large perturbations in the system, we omitted the first 20 ns of every simulation. During MD simulations, the number of ions in each chamber was kept constant alchemically by an additional algorithm (23). The resulting membrane potential can be calculated by double integration of the charge distribution using the Poisson equation as implemented in the gromacs tool gmx potential (64). During the simulations, a permeation event was counted when an ion traversed the entire filter region. Individual simulation runs were 500 ns in the amber setups and 250 ns in the charmm setups (Table 1).

The majority of the production runs were conducted at 303 K using an imbalance of six cations (∆q of six elementary charges, e^–) between the two compartments $$ \alpha $$ and $$ \beta $$ (Fig. 1D), resulting in a transmembrane potential of around 500 mV (Table 1). Although ion channel recordings are possible at these voltages, they lay well outside the physiological range. We additionally simulated K⁺ permeation using ∆q of 4 and 2 e^– with amber99sb, respectively, corresponding to a voltage difference of 275 mV and 100 mV. The simulation at 275 mV shows a similar conductance to the one at 450 mV. At 100 mV, the conductance is less but still substantial (Table 1 and Fig. 2B), indicating that similar conduction mechanisms are at play. The principal consequence of high membrane voltage is merely statistical—it allows us to record more permeation events. Furthermore, compared to the simulations conducted at 303 K, we noted that simulations at 310 K revealed only slightly larger currents but with much greater variations in the ion permeation rate within a given simulation run (Fig. 2B). Finally, to buttress our observations and validate the relevance of the starting structure, we performed equivalent MD simulations of a closed AMPA structure (PDB ID: 5WEM; GluA2-GSG1L-apo-1) with the ATD, LBD, and GSG1L removed and peptide termini restrained. We observed no ion permeation events over the same time scale as the open structure simulations, and the structure did not spontaneously open on this time scale.

To align results over different setups, we used the center of mass of the backbone atoms of the classical SF residues (⁵⁸⁶QQGCD⁵⁹⁰) as a reference point. All trajectories were analyzed with gromacs tools and python using mdanalysis (65). Molecular visualizations were made with Visual Molecular Dynamics (VMD) (66).

For clustering analysis, five runs, each comprising a 500 ns trajectory, were combined for the simulations of K⁺ and Na⁺, while six runs of 500 ns were concatenated for Cs⁺ simulations. All simulations were performed with amber99sb force fields. Clustering analysis was performed with gromacs clustering tool. To decrease the computational effort, we calculated the clusters based on the backbone heavy atoms of the SF (Q₅₈₆-D₅₉₀) only. The SF atoms were fitted for all frames of the trajectories. A clustering cutoff of 0.05 nm in rmsd was used to decide cluster affinity. Simulations involving K⁺, Na⁺, or Cs⁺ each yielded one dominant cluster and a number of minor ones (SI Appendix, Table S2). PCA was performed on the same selected atoms as the clustering analysis, where trajectories of K⁺, Na⁺, and Cs⁺ simulations were combined for the determination of the principal components. Proportion of variance for the derived principal modes from PCA analysis is shown in SI Appendix, Fig. S11. Conformational dynamics of the SF in K⁺, Na⁺, and Cs⁺ simulations were projected individually onto the first nine principal modes (SI Appendix, Fig. S15).

Patch Clamp Electrophysiology.

HEK293 cells were plated on glass coverslips in dishes and incubated for 20 to 44 h before calcium phosphate transfection with 3 µg cDNA. For macroscopic current recordings, the cDNA transfection was done with the Rat GluA2 (Q) pRK5 vector encoding enhanced green fluorescent protein after an internal ribosome entry site. Single-channel recordings from outside-out patches were performed 24 h after transfection. For single-channel recordings, we used a plasmid ratio approach to obtain sparse expression (67), whereby the rat GluA2 (Q) vector was cotransfected with enhanced green fluorescent protein and empty vector (pCDNA3.1+) in a ratio of 1:63:313. Standard extracellular solution contained 150 mM NaCl, 0.1 mM MgCl₂, 0.1 mM CaCl₂, 5 mM HEPES, and 10 µM EDTA and was titrated with NaOH to a pH of 7.3. We included EDTA to chelate trace contamination by divalent ions. The internal solution contained 115 mM NaCl, 1 mM MgCl₂, 0.5 mM CaCl₂, 10 mM NaF, 5 mM Na₄BAPTA, 10 mM Na₂ATP, and 5 mM HEPES, titrated to a pH of 7.3 with NaOH. Pipettes were mounted in an ISO holder (G23 Instruments) and had a resistance of 3 MΩ for macroscopic current recordings. For single-channel recording, pipettes were fire polished to a resistance of 10 to 25 MΩ and were coated with Sylgard. The junction potential between the pipette and Na⁺-bath solution (E_bath-E_pip, considering Na⁺, Cl⁻, and F⁻ mobilities) was 3.7 mV (68). For reversal potential experiments with Cs, we substituted NaCl in the extracellular solution with CsCl and titrated the pH to 7.3 with CsOH. For single-channel recordings in near-symmetrical K⁺ or Cs⁺, in external solutions, we substituted NaCl with KCl or CsCl, respectively, and titrated to pH 7.3 with KOH or CsOH, respectively. The Cs internal solution contained 115 mM CsCl, 1 mM MgCl₂, 0.5 mM CaCl₂, 10 mM CsF, 5 mM Cs₄BAPTA, 10 mM K₂ATP, and 5 mM HEPES, titrated to a pH of 7.3 with CsOH. The potassium internal solution contained 115 mM KCl, 1 mM MgCl₂, 0.5 mM CaCl₂, 10 mM CsF, 5 mM Cs₄BAPTA, 10 mM K₂ATP, and 5 mM HEPES, titrated to a pH of 7.3 with KOH. Cyclothiazide (Hello Bio) was prepared as a 100-mM stock solution in DMSO and used at 100 µM (giving a final concentration of 0.1% DMSO). EDTA stock solution was prepared in NaOH. Reagents were obtained from Carl Roth GmbH, Sigma Aldrich, or Toronto Research Chemicals, unless otherwise noted. For fast perfusion of outside-out patches, the perfusion tools were made with custom-designed four-barrel square profile glass (Vitrocom) mounted on a piezo electric stack (Physik Instrument). Currents were filtered at 10 kHz (−3 dB cutoff, 8-pole Bessel) with an Axopatch 200B amplifier (Molecular Devices). For analog–digital conversion, an InstruTECH ITC-18 digitizer (HEKA Elektronik Dr. Schulze GmbH) was used at 40-kHz sampling rate. Data were recorded and analyzed with AxoGraph X (AxoGraph Scientific).

For single-channel conductance measurements, in each record, we ran a ramp protocol (−120 to +120 mV, 1.2 V ⋅ s⁻¹) both before and during glutamate application (10 mM) to the outside-out patch. The leak current recorded during the no-glutamate ramp was subtracted from the current recorded during glutamate application. Stretches of the recording corresponding to one open channel were selected and the open levels were fit with a linear relation to obtain the chord conductance.

For macroscopic measurements of reversal potential and conductance, we alternated washing each patch with Cs⁺ and Na⁺ external solution. Slope conductances were fit to the traces over the 30-mV ranges at the extreme positive and negative ends of the ramp. For the slope conductance, we compared the conductance ratios (Cs versus Na inward and Na versus Na outward) from the same patch against the null (ratio = 1) using a paired t test. We assumed that there was a similar junction potential (within 0.5 mV) in both cases because the junction potential from the pipette to the Cs⁺ solution (−1.7 mV) is cancelled by a second junction potential from Cs⁺ solution back to the bath electrode in Na⁺ (4.9 mV) (69). We added this junction potential to the measured mean reversal potential. The flow rate through the local perfusion tool was low (<200 µL/min), meaning the overall bath Cs⁺ concentration remained low.

We used the GHK equation (70) to calculate permeability ratios based on shifts in reversal potentials:

where X was Na⁺ or Cs⁺.

Likewise, to calculate the putative shift in E_rev because of a minor chloride permeability, we took internal [X]_i and external [X]_O ion concentrations, where X was Na⁺, Cs⁺, or Cl⁻ permeability ratios of P_Cs:Na of 1.16:1, as measured, and assumed P_Cl:Na of either 1:220 (an upper estimate based on the observation of a single anion permeation in our potassium simulations) or zero (no chloride permeability). Cesium terms were only used for the bi-ionic condition of [Na⁺]_i to [Cs+]_o:

Statistical analysis and data plotting was done in IGOR Pro (Wavemetrics).