
Contributed by Nils Chr. Stenseth, November 24, 2020 (sent for review August 18, 2020; reviewed by Robert D. Holt and Karl Sigmund)
Author contributions: K.G., H.H., E.R.J., and N.C.S. designed research; K.G., H.H., E.R.J., and N.C.S. performed research; and K.G., H.H., E.R.J., and N.C.S. wrote the paper.
Reviewers: R.D.H., University of Florida; and K.S., University of Vienna.
1K.G., H.H., and E.R.J. contributed equally to this work.
- Altmetric
Many evolutionary studies of ecological systems assume, explicitly or implicitly, ecologically stable population dynamics. Ecological analyses typically assume, on the other hand, no evolution. We study a model (using predator–prey dynamics as an example) combining ecology and evolution within the same framework. For this purpose, we use the evolutionarily stable strategies (ESSs) framework, emphasizing that evolutionary change, in general, will occur as a result of mutant strategies being able to invade a population. The significance of our contribution is to derive mathematical conditions for the existence of an ESS in a periodically limit-cycle ecological system.
An evolutionarily stable strategy (ESS) is an evolutionary strategy that, if adapted by a population, cannot be invaded by any deviating (mutant) strategy. The concept of ESS has been extensively studied and widely applied in ecology and evolutionary biology [M. Smith, On Evolution (1972)] but typically on the assumption that the system is ecologically stable. With reference to a Rosenzweig–MacArthur predator–prey model [M. Rosenzweig, R. MacArthur, Am. Nat. 97, 209–223 (1963)], we derive the mathematical conditions for the existence of an ESS when the ecological dynamics have asymptotically stable limit points as well as limit cycles. By extending the framework of Reed and Stenseth [J. Reed, N. C. Stenseth, J. Theoret. Biol. 108, 491–508 (1984)], we find that ESSs occur at values of the evolutionary strategies that are local optima of certain functions of the model parameters. These functions are identified and shown to have a similar form for both stable and fluctuating populations. We illustrate these results with a concrete example.
1. Introduction
Natural systems exhibit both ecological and evolutionary dynamics. Nevertheless, many studies focus only on either the ecological or the evolutionary dynamics, assuming the other nonchanging and fixed. There are many excellent exceptions (see, e.g., refs. 1 and 2). Here, we study the ecological and evolutionary dynamics in both ecologically stable as well as periodically fluctuating populations of predator and prey, using the Rosenzweig–MacArthur predator–prey model (3) (see also refs. 45678–9). Our overall aim is to understand under what conditions evolutionarily stable strategies (ESSs) will exist. Specifically, we focus on evolutionary stability in stable as well as periodically fluctuating ecological systems.
The concept ESS was originally coined by Maynard Smith (10) (see also Smith and Price) (11), as an extension of Hamilton’s (12) “unbeatable strategy.” Maynard Smith (10) defined it as a strategy that, once adopted by a majority of the members of a population, cannot be overturned by any alternative strategy that is initially rare. It is essentially a Nash equilibrium that is evolutionary stable (13). The concept of ESS was used initially in behavioral ecology and sociobiology but Lawlor and Smith (14)—see also Roughgarden (15) and Nowak (16)—extended its use to ecological dynamics of competing populations.
Many ecological systems are characterized by fluctuating dynamics, some of which have periodic fluctuations: the famous lemming and small rodent cycles (see, e.g., refs. 1718–19) and the North American hare–lynx cycle (see, e.g., ref. 20). The predator–prey models of the kind presented by Rosenzweig and MacArthur (17) are therefore of broad ecological interest. Several studies have analyzed these—and related—models from an ecoevolutionary perspective (5, 2122232425–26). However, no one has addressed this from an ESS perspective, particularly for the limit-cycle case. This we do in the present contribution.
Models for predatory–prey interactions have played a major role within the field of ecology since the pioneering contribution by Lotka (27, 28) and Volterra (29) (see, e.g., ref. 30). Depending on the choice of parameters, such models are known to accommodate equilibrium populations that are constant or fluctuating (including limit-cycle dynamics).
The biological contribution of this paper will be the theoretical question regarding the existence of ESS in periodically fluctuating populations exemplified by Rosenzweig–MacArthur predator–prey systems. Specifically, we establish sufficient conditions for the existence of ESSs in such models. We consider populations that become stable (constant) over time and periodically fluctuating populations or systems exhibiting stable limit-cycle dynamics. Extending the approach of Reed and Stenseth in ref. 31, we show that ESSs occur at values of the evolutionary strategies that are local optima of certain functions of the model parameters. We identify these functions and show that they have a similar form for both stable and fluctuating populations. These results are illustrated with a concrete example.
The main mathematical contribution is that we prove Lyapunov stability through an adaptation of classical linearization arguments, variation of parameter formulas, and Floquet-type analysis. The main finding is the case of limit cycles, where we establish stability of two-dimensional limit cycles in a four-dimensional system of ordinary differential equations. Within the approach of Reed and Stenseth (31) to evolutionary games and ESS, we then show that these stability results lead to sufficient conditions for ESSs for both types of equilibrium solutions. These sufficient conditions could be of independent interest in game theory.
In section 2, we state the model and results about equilibrium solutions. Then, in section 3, we combine ecology and evolution: evolutionary strategies, an extended ecological model, and the concept of ESS are introduced. The strategies are model parameters that can be changed over time by the populations to ensure a more beneficial evolution, and the extended model includes mutant populations for predators and prey satisfying the same model equations at different (i.e., mutant) values of the strategies. An ESS is introduced as an extension of the definition of Reed and Stenseth (31) to include periodically fluctuating populations—it is a choice of evolutionary strategies for which mutant populations cannot survive in the long run. Evolution can be seen as a competition between different species and be modeled as a game (13). An ESS is then a Nash equilibrium (32), in the sense that no population can improve their own survivability acting alone. A game can only move away from an ESS when the original populations change their strategies. An ESS is therefore a type of locally optimal evolutionary strategy for the original populations.
When time becomes large, the populations will approach limit populations, a (stable) equilibrium solution of the model. Examples of equilibrium solutions are constants (limit points) and periodic solutions (limit cycles). In sections 4 and 5, we study such solutions for the extended ecological model. We first observe that equilibrium solutions of the two-population model remain equilibrium solutions in the extended model when the mutant populations are zero. Then, we establish conditions to guarantee the (Lyapunov) stability of these solutions. Stability here means that solutions starting near an equilibrium solution will over time converge to the equilibrium solution. These results extend earlier results for models with two populations. By taking into account the dependence on the strategies in our extended model, we use the stability results and our definition of ESS to give conditions that guarantee ESS. In section 4, we give the results for equilibrium points (constant populations in the limit), and in section 5, we give the results for limit cycles (periodic limit populations). ESSs are shown to occur at values of the evolutionary strategies that are local optima of certain functions of the model parameters. These results are the main contribution of our paper. In section 4, we also discuss examples of functional dependencies that lead to an ESS: loosely speaking, if we take the predation rate to be an increasing bilinear function of the evolutionary strategies, then we find that the rate constants of prey growth and predator mortality have to be decreasing convex functions. We give a concrete example where the latter two rate constants are quadratic functions of the evolutionary strategies.
2. The Ecology of Predator–Prey Models
Let and
This model goes into a long tradition of predator–prey models of the form
For this system, the first quadrant is an invariant region (i.e., the populations can never become negative). Under some reasonable assumptions, the system has three limit points and up to one limit cycle. These results along with stability results are given in the next theorem (also see Fig. 1).

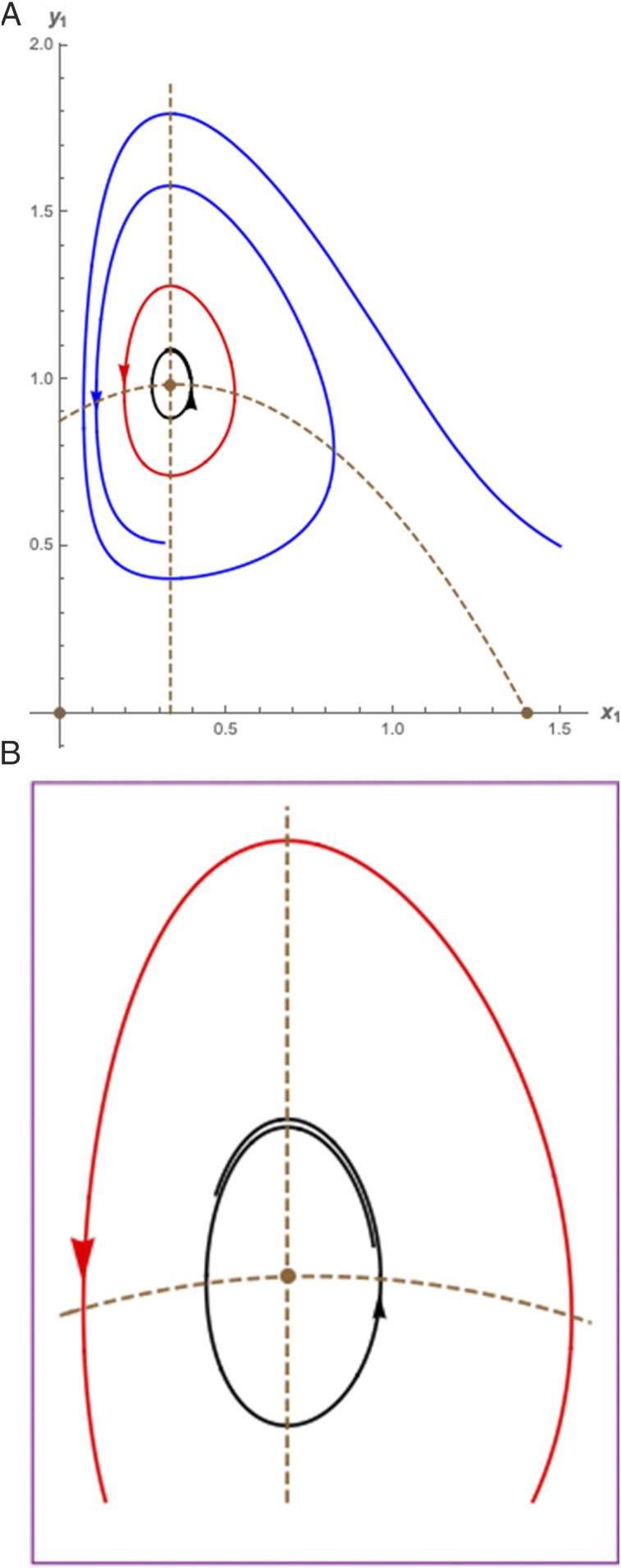
The phase diagram of Eq. 1 with
Theorem 2.1 (37)
Assume that
(a)Solutions
(b)Define
(i)If
(ii)If
(iii)If
Further properties can be found in SI Appendix.
3. Evolution: The Extended Ecological Model
Evolutionarily, there is a “conflict” or “arms race” between the predator and the prey regarding predation: the prey “wants” to evolve to avoid being caught by the predator, whereas the predator “wants” to be able to catch prey as efficiently as possible, even when the prey is at low abundance. However, this will come at some costs: we assume that for the prey, a decreased predation rate will lead to a reduced growth rate, whereas for the predator, an increased predation rate may lead to an increased mortality rate. A natural way to analyze this situation is through (differential) game theory and concepts like Nash equilibriums and ESS; we refer to refs. 13, 14, 40, and 41 for more information. We will follow the simplified approach of Reed and Stenseth (31), an approach explicitly emphasizing that a new mutant will have to establish itself through competition, even though rare initially.
Let
We now make some assumptions about how the different model parameters depend on
In the next step, we extend the model to include mutants. Let
We now introduce evolutionary strategies
Remark 3.1:
(i)If
(ii)If
(iii)If
An ESS corresponds to the situation where the original population
Definition 3.2:
Assume we are given an asymptotically stable equilibrium point (limit cycle)
An ESS has the Nash equilibrium-like property that if
Remark 3.3:
The ESS, as defined in Definition 3.2, is stable against mutations in one or both populations at the same time. Single population mutations are realized simply by letting the other mutant population be zero over time.
The issue of time scales for the ecological and evolutionary processes is important here (see, e.g., Carroll et al.) (43). The approach of Reed and Stenseth (31) emphasizes the ecological interaction between the common wild-type strategy (with its corresponding phenotype) and the rare mutant strategy (with its corresponding phenotype). If the mutant strategy cannot (ecologically) invade the wild-type ecological system, there will be evolutionary stability (here in the form of ESS). If the mutant strategy can invade the wild-type ecological system, it will eventually change into a new one. The result will depend upon many features of the different populations—issues that are beyond our current discussion but are essentially addressed by Dercole et al. (44), Dercole and Rinaldi (45), Doebeli (46), and Cortez and Weitz (26). This all refers to ecological processes and time scales. The overall question being addressed in this contribution is under which conditions will we have evolutionary stability in ecologically varying (periodically fluctuating) systems.
The evolutionary processes and time scales enter in relation to how frequent new mutant strategies appear in the two populations (through the process of mutation and/or invasions)—issues outside of our current discussion. The discussion by Khibnik and Kondrashov (47) are relevant here.
4. Equilibrium Points, Stability, and ESS
SI Appendix, Eq. 1 has three equilibrium points:
We show in SI Appendix that the eigenvalues
Lemma 4.1
The equilibrium point
Theorem 4.2 (Conditions for ESS—Equilibrium Point Case)
Assume
Eq. 12. A constant evolutionary strategy
(i)
(ii)
(iii)the function
(iv)the function
Proof:
Note that by the definition of
Now, we consider an example where
Example 4.3:
Assume

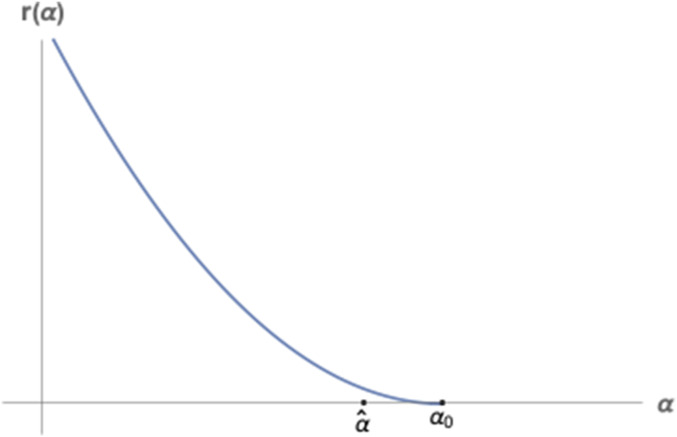
The function

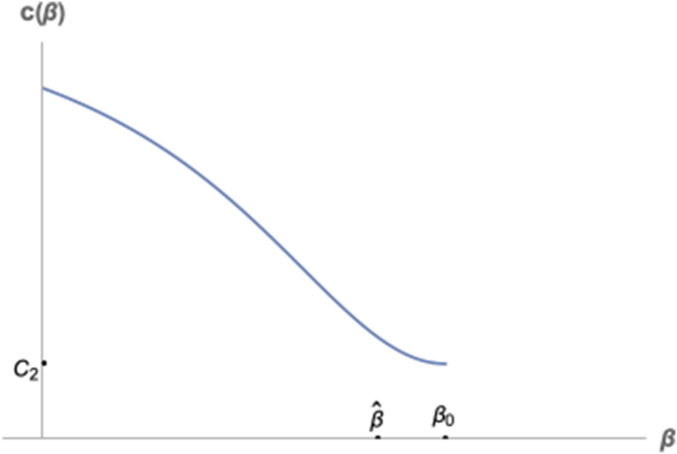
The function
Note that we need
Biologically, this example may be interpreted as follows. An ESS will exist when the evolutionary strategies
5. Limit Cycles, Stability, and ESS
We now find conditions for when there exist (asymptotically) stable limit-cycle solutions of Eq. 9 with the two last components
In ref. 37, it has been shown that every limit cycle surrounding
Theorem 5.1
Let
Remark 5.2:
The condition in Eq. 17 in Theorem 5.1 plays a similar role for limit cycles in
In our case, this condition, which has been checked in ref. 37, reads,
Based on the discussion in this section for Eq. 1, we are going to identify conditions under which the solution
We have the following result.
Lemma 5.3
Assume
Theorem 5.4 (Conditions for ESS—The Limit-Cycle Case)
Assume
Eq. 12. A constant strategy
(i)
(ii)
(iii)the function
(iv)the function
Proof:
The proof follows from Lemma 5.3 and the fact that
With this result, we have given conditions that will ensure the existence of an ESS in a periodically fluctuating population (exhibiting a limit cycle). This is an important contribution of this paper. With empirically derived functions
6. Red Queen Type of Continued Evolution or Stasis
Our analysis is related to the issue of Red Queen type of continued evolutionary evolution of stasis (cf. Van Valen) (49); see also Schaffer and Rosenzweig (50) and Rosenzweig et al. (51). In Example 4.3, we have assumed that both the predator and the prey have equal influence on the determination of the overall half-saturation parameter
7. Discussion
We establish conditions that guarantee stability of equilibrium solutions of the extended ecological model. This model has four equations, and, for periodic solutions, such a result appears to be previously undescribed. We prove full Lyapunov stability of the periodic solutions. The proof relies on an adaptation of classical linearization arguments, variation of parameter formulas, as well as Floquet-type analysis. The approach of Reed and Stenseth in ref. 31 to evolutionary games and ESS is extended to include fluctuating populations. ESSs are then shown to occur at values of the evolutionary strategies that are local optima of certain functions of the model parameters. We identify these functions and express them in a similar way for both stable and fluctuating populations. A concrete example to illustrate our results is given. Mathematically, these results are obtained from the abovementioned stability results, and our characterizations of ESSs seem to be previously undescribed and could be of independent interest in game theory.
The concept of ESSs was developed with a stable ecological setting in mind. However, typically ecological systems vary in time, often with more or less periodic fluctuations. Predator–prey systems are such examples. If we are to link ecology and evolution, we must allow for varying ecological population fluctuations. With this contribution, we have extended the ESS concept to be applicable for periodically fluctuating ecological systems.
The application of ESS to ecology is similar to the “adaptive dynamics” approach in that it models the time evolution of populations. See Dieckmann et al. (53); see also Kang and Fewell (54). The “adaptive dynamics” approach focuses on how strategies evolved under changing ecological conditions. The ESS approach, on the other hand, focuses on finding the unbeatable fixed strategy within a population. To our knowledge, it has not been shown before that such unbeatable ESS strategies do exist when the ecological system exhibits a periodically fluctuating dynamics. With this contribution, we derive the mathematical conditions for such fixed ESSs to exist when the ecological system exhibits limit cycle-type dynamics.
By extending the approach presented by Reed and Stenseth (31), it furthermore becomes clear that evolution occurs through the ecological process of a variant type being able to invade an ecological system (or population) when it is at its stable state—be this a stable equilibrium or a limit cycle. Whenever such ecological invasion occurs (i.e., the wild type is not an ESS), evolution will occur—and the ecology of the system changes. This emphasizes the interlinkages between ecology and evolution: it is a matter of realizing both that “nothing in biology makes sense except in the light of evolution” (55) as well as “very little in evolution makes sense except in the light of ecology” (56).
Acknowledgements
K.G., H.H., and E.R.J. were supported by the grant “Waves and Nonlinear Phenomena (WaNP),” and K.G. was supported by “Wave Phenomena and Stability—A Shocking Combination (WaPheS),” both grants from the Research Council of Norway. N.C.S. was supported by the project “Drivers of Evolutionary Change: Understanding Stasis and Non-stasis through Integration of Micro- and Macroevolution” (Project 263149 funded by the Research Council of Norway) and the Centre for Ecological and Evolutionary Synthesis of the University of Oslo and by NTNU through the Centre for Biodiversity Dynamics. We thank Peter A. Abrams, Juan A. Bonachela, Folmer Bokma, Jostein Starrfelt, and Jason D. Whittington for providing valuable comments on an earlier version.
Data Availability.
There are no data underlying this work.
Change History
November 18, 2021: The SI Appendix has been updated to coincide with a formal Correction.
References
1
2
3
5
6
7
8
9
10
11
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
 Evolutionarily stable strategies in stable and periodically fluctuating populations: The Rosenzweig–MacArthur predator–prey model
Evolutionarily stable strategies in stable and periodically fluctuating populations: The Rosenzweig–MacArthur predator–prey model
