
Edited by Harry L. Swinney, University of Texas at Austin, Austin, TX, and approved November 11, 2020 (received for review June 19, 2020)
Author contributions: P.A.G. and S.B. designed research, performed research, analyzed data, and wrote the paper.
1P.A.G. and S.B. contributed equally to this work.
- Altmetric
We explore the compaction dynamics of a granular pile after a hard quench from a liquid into the glassy regime. First, we establish that the otherwise athermal granular pile during tapping exhibits annealing behavior comparable to glassy polymer or colloidal systems. Like those other systems, the pile undergoes a glass transition and “freezes” into different nonequilibrium glassy states at low agitation for different annealing speeds, starting from the same initial equilibrium state at high agitation. Then, we quench the system instantaneously from the highly agitated state to below the glass transition regime to study the ensuing aging dynamics. In this classic aging protocol, the density increases (i.e., the potential energy of the pile decreases) logarithmically over several decades in time. Instead of system-wide, thermodynamic measures, here we identify the intermittent, irreversible events (“quakes”) that actually drive the glassy relaxation process. We find that the event rate decelerates hyperbolically, which explains the observed increase in density when the integrated contribution to the downward displacements is evaluated. We argue that such a hyperbolically decelerating event rate is consistent with a log-Poisson process, also found as a universal feature of aging in many thermal glasses.
This paper links the nonequilibrium glassy relaxation behavior of otherwise athermal granular materials to those of thermally activated glasses. Thus, it demonstrates a much wider universality among complex glassy materials out of equilibrium. Our three-dimensional molecular dynamics simulations, fully incorporating friction and inelastic collisions, are designed to reproduce experimental behavior of tapped granular piles. A simple theory based on a dynamics of records explains why the typical phenomenology of annealing and aging after a quench should extend to such granular matter, activated by taps, beyond the more familiar realm of polymers, colloids, and magnetic materials that all exhibit thermal fluctuations.
In thermodynamic systems, physical aging arises when disordered systems fall out of equilibrium after a sudden quench through the glass transition into a glassy regime where relaxation timescales begin to exceed experimental timescales at low temperature, high density, low shear, and so on (1). The experimental observation of “anomalous” nonequilibrium events (234567–8) has established intermittency as key property of the relaxation dynamics commonly referred to as “aging” (9) in a wide variety of glassy materials. Spin-glass thermoremanent magnetic data (10), magnetic flux creep in type-II high- superconductors (11), and particle motion data in dense colloids (12, 13) have all been interpreted using the statistics of “quakes,” that is, rare, localized events which lead the system from one of its metastable states to the next.
The classic experiments on the “Chicago pile” (14, 15) have established the slow dynamic nature of the relaxation in tapped granular piles. Unlike for fluctuating thermodynamic systems (15), a tap is needed for a cycle of momentary acceleration of the grains, followed by complete dissipation. By measuring the density evolution of a tapped column of grains, ref. 14 reported that, for low-intensity taps, changes in density are logarithmic in time (measured in taps). Remarkably, such logarithmic behavior is also characteristic of relaxation in thermal systems (1617–18). For the pile, this logarithmic density evolution has been successfully modeled using the parking-lot model for compaction (14, 19), which has been noted as an example of event-driven dynamics (20). The events driving the long-time relaxation behavior in granular experiments are unclear. Such granular piles have been shown to fall out of equilibrium when the energy infused by tapping is insufficient to break all contacts between grains during each tap (21). How changes within the pile, for example in its contact network, relax the free energy and increase its density remains largely unexplored.
Here, we study the relaxation of the Chicago pile in molecular dynamics (MD) simulations and show that the ensuing nonequilibrium aging phenomenology is surprisingly similar to other glassy systems. Density fluctuations are induced athermally through a cycle of taps imposed externally to briefly accelerate the grains upward. Kinetic energy is completely dissipated through friction before the application of a new tap. First, we establish that the granular pile exhibits annealing behavior comparable to glassy polymer or colloidal systems, shown in Fig. 1. To that end, we anneal the pile repeatedly from an equilibrated, highly agitated regime into a completely jammed state over a wide range of fixed speeds by which the acceleration amplitude is gradually reduced. The system falls apparently out of equilibrium below a certain level of agitation, akin to a glass transition (16, 18, 2223–24), by attaining densities that systematically vary with the speed. Then, we study the aging dynamics following the conventional protocol of quenching instantly, at infinite speed, from the equilibrated into the nearly jammed regime of agitation, well below the observed glass transition but still sufficiently agitated to discern its relaxation. The evolution of density on average reproduces the logarithmic rise found in the Chicago experiment. We can attribute this slow rise to a hyperbolic deceleration in the rate of irreversible events by which grains progressively solidify in their neighborhood matrix. These events are signaled by a geometric rearrangement of a grain reaching a new record in its number of contacts.

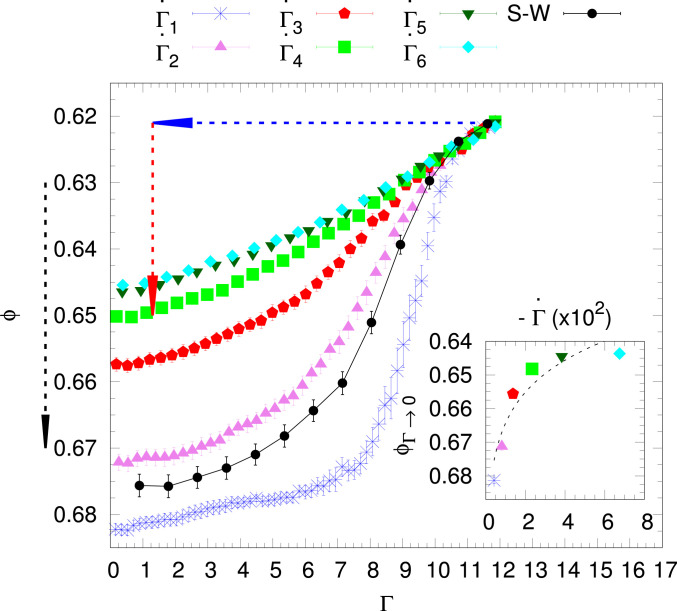
Average packing fraction
Materials and Methods
Methods.
We employ a numerical implementation inspired by the experimental setup used for the Chicago experiment. Our pile consists of 60,000 bidisperse spheres 1 to 1.02 mm in diameter contained in a vertical cylinder of 2.4-cm diameter. The resulting column height is about 11.5 cm. A minute bidispersity, in equal proportion, was introduced in order to prevent crystallization and the grain diameter ratio was chosen to avoid segregation.
We use MD, in particular the implementation of the soft spheres (25) model provided by the LIGGGHTS (LAMMPS improved for general granular and granular heat transfer simulations) (26) open source software. Within LIGGGHTS, we apply a Hertz model for the grain–grain and grain–wall contact forces (with Young’s modulus
Taps consist of moving the whole container along a semisinusoidal wave pulse of amplitude
Because of gravity, density is not uniform along the height of the system (14, 30, 31). For this reason, the analysis is performed for three narrow horizontal slices at different heights of the silo, at z = 3 to 4 cm, z = 4.5 to 5.5 cm, and z = 6 to 7 cm. To avoid wall effects, only the 2-cm-diameter inner region is considered. Then, each slice contains of the order of 3,500 particles. Apart from the quantitative differences imposed by gravity, all regions behave consistently, and, for simplicity, results corresponding only to the central slice (z = 4.5 to 5.5 cm) are shown here. Analysis corresponding to the remaining slices can be found in SI Appendix.
Local “grain densities” are obtained by dividing grain volume by their corresponding Voronoi volume, obtained using Voro++ (32) open source software. The reported density (or packing fraction)
Results
Annealing Simulations.
Using a stepwise protocol inspired by the Chicago experiments, we obtain a “reversible branch” (14) that will serve as a reference for the annealing simulations. It follows a stepwise ramp-down of the tap acceleration
Our annealing simulations, also shown in Fig. 1, employ instead a protocol of gradual changes after each tap, reducing
The densities during gradual annealing as well as during the stepped Chicago protocol track each other closely for high accelerations
Aging Simulations.
For the remainder of this paper we focus on the aging protocol indicated by dashed arrows in Fig. 1. The aging dynamics is induced by a hard quench (
In Fig. 2, we plot the evolution of the average density

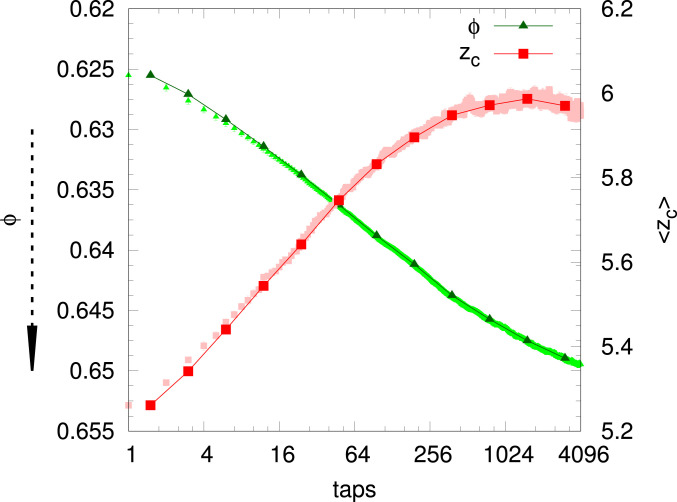
Average density
Identifying and counting events that facilitate such irreversible changes is far from straightforward. We define as such an event the moment at which a given grain for the first time increases its coordination number from

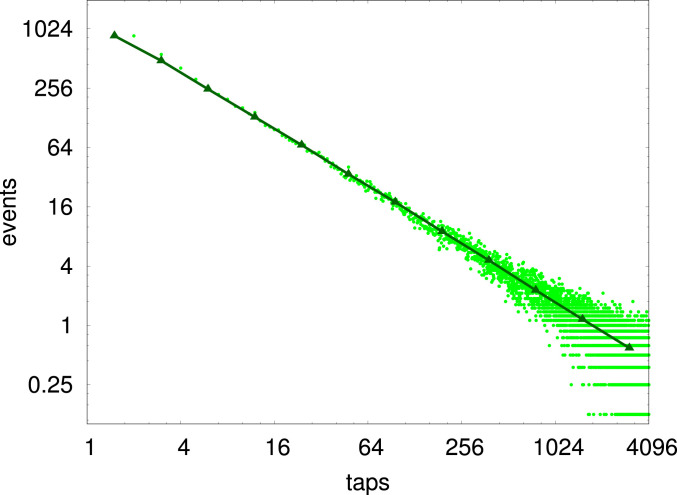
Number of new record events per unit time (tap), where an event is accounted when a particle increases its coordination number from
It proves prohibitive to relate such a topological change in the contact network to an immediate, adjacent increase in density. Due to gravity, discrete topological changes in one place may often lead to a net increase in local density spread widely and much farther upstream. However, the accumulative effect of these events reveals itself microscopically in the net downward drift of all grains individually, as Fig. 4 shows. Unlike for colloidal systems in the absence of gravity, where diffusion drives relaxation and dissipation of free energy (5, 13), no discernible mean-square displacement within the horizontal plane is present in the granular pile. Instead, particles predominantly drift downward in intermittent steps, ever more slowly, as those tracks in Fig. 4 indicate. Such downward displacements signify the loss of free energy, the main mechanism by which this system relaxes and density increases.

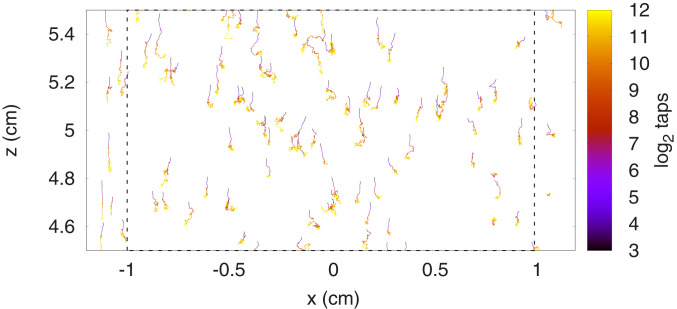
Tracking of the displacement for a few randomly selected particles in the observed region (dashed box) inside the pile. The color coding is logarithmic in time (taps) and indicates a decelerating downward drift along increasingly rugged (intermittent) trajectories.
To examine the history of particle trajectories in more detail, we study the downward drift as a function of two times, namely the displacement achieved at

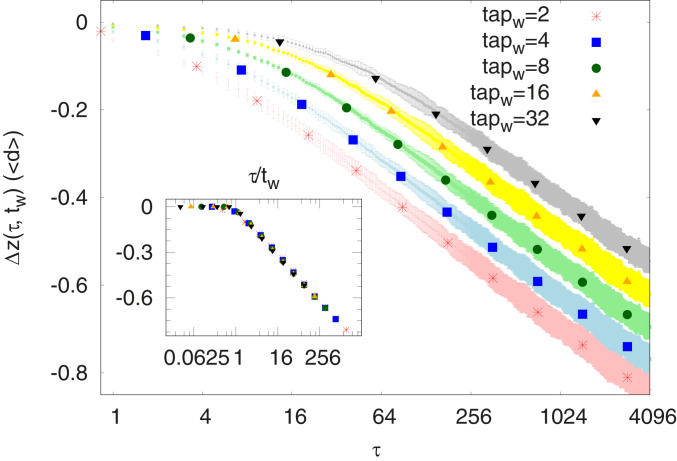
Plot of the downward displacement averaged over all grains within the observation region as a function of lag time
Discussion
Remarkably, we thus find that a tapped granular pile exhibits an aging phenomenology, after being driven out of equilibrium by a hard quench, akin to many other thermal systems, not only macroscopically (14) but also in the statistics of local events facilitating relaxation. The statistics of these events closely resemble a log-Poisson process, which is at the heart of a universal description—essential for explaining the ubiquity of this phenomenology across so many materials—in terms of record dynamics (12, 373839–40). These events are enabled, in fact, by statistically independent, record-sized fluctuations that evolve the dynamics irreversibly and in ever more rare increments. Hence, the instantaneous rate
Indeed, we find that the rate of meaningful events in stiffening a grain’s contact network follows such a statistics of records, as shown in Fig. 3. Then, according to Eq. 1, any two-time functions, such as the displacements in Fig. 5, become subordinate (34, 39) to this process,
In conclusion, we have found that a granular pile has similar relaxation behavior after a quench compared with other glassy materials. While there has been much discussion concerning the possibility of describing athermal granular systems in terms of an equilibrium thermodynamics (424344–45), our study shows that, with regard to the aging phenomenology, granular piles belong in a wide class of glassy materials that exhibit universal behavior out of equilibrium. Our data are consistent with predictions based on a log-Poisson process, in which increasingly rare, record-sized fluctuations provide the activation to move a glassy system from one metastable state to the next, marginally more stable state and irreversibly expel free energy. As the origin of such fluctuations, either from thermal or from athermal driving, is irrelevant for the existence of records, such a theory is well-suited to account for the ubiquity of this phenomenology across many materials.
In the process, we also found that during the annealing of a granular pile, at finite but very slow, fixed damping, the observed relaxation trajectories undergo a glass transition similar to polymer glasses, as shown in Fig. 1. Beyond that transition, the system falls out of equilibrium and settles into an ensemble of metastable states whose average energy (i.e., its density) varies systematically with the annealing speed. The variable dependence of macroscopic observables on annealing speed has not been noted previously and contradicts established assumptions about granular piles and, thus, warrants future investigation.
Acknowledgements
We thank P. Sibani for fruitful discussions about this project. These simulation were performed at the Imperial College Research Computing Service (see DOI: 10.14469/hpc/2232).
Data Availability.
All study data are included in the paper and SI Appendix.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
33
34
35
36
37
38
39
40
41
42
43
44
 Universal features of annealing and aging in compaction of granular piles
Universal features of annealing and aging in compaction of granular piles
