
The authors have declared that no competing interests exist.
- Altmetric
There is increasing evidence that pleiotropy, the association of multiple traits with the same genetic variants/loci, is a very common phenomenon. Cross-phenotype association tests are often used to jointly analyze multiple traits from a genome-wide association study (GWAS). The underlying methods, however, are often designed to test the global null hypothesis that there is no association of a genetic variant with any of the traits, the rejection of which does not implicate pleiotropy. In this article, we propose a new statistical approach, PLACO, for specifically detecting pleiotropic loci between two traits by considering an underlying composite null hypothesis that a variant is associated with none or only one of the traits. We propose testing the null hypothesis based on the product of the Z-statistics of the genetic variants across two studies and derive a null distribution of the test statistic in the form of a mixture distribution that allows for fractions of variants to be associated with none or only one of the traits. We borrow approaches from the statistical literature on mediation analysis that allow asymptotic approximation of the null distribution avoiding estimation of nuisance parameters related to mixture proportions and variance components. Simulation studies demonstrate that the proposed method can maintain type I error and can achieve major power gain over alternative simpler methods that are typically used for testing pleiotropy. PLACO allows correlation in summary statistics between studies that may arise due to sharing of controls between disease traits. Application of PLACO to publicly available summary data from two large case-control GWAS of Type 2 Diabetes and of Prostate Cancer implicated a number of novel shared genetic regions: 3q23 (ZBTB38), 6q25.3 (RGS17), 9p22.1 (HAUS6), 9p13.3 (UBAP2), 11p11.2 (RAPSN), 14q12 (AKAP6), 15q15 (KNL1) and 18q23 (ZNF236).
We propose a new approach PLACO that uses aggregate-level genotype-phenotype association statistics—commonly referred to as GWAS summary statistics—to identify genetic variants that influence risk of two traits or diseases. It allows correlation in summary statistics between studies that may arise due to sharing of controls between disease traits. We demonstrate that PLACO can achieve major power gain over alternative methods that are typically used. We applied PLACO to Type 2 Diabetes and Prostate Cancer summary data from two large case-control studies. Many previous studies have reported an inverse association of these two chronic diseases suggesting shared risk factors; however, shared genetic mechanisms underlying this association is poorly understood. PLACO identified a number of novel shared genetic regions that are not detected by individual trait analysis. Many of the loci implicated by PLACO increase risk for one disease while decreasing risk for the other. PLACO can similarly be used on other traits to shed light on shared genetic risk factors.
Introduction
Years of genetic research on various complex human traits have implicated numerous genetic variants as risk factors for two or more traits. Pleiotropy, the phenomenon where a genetic region or locus confers risk to more than one trait [1], is widely observed for many diseases and traits [2], especially cancers [3], autoimmune [4] and psychiatric [5, 6] disorders. It has also been observed in seemingly unrelated traits; for instance, early-onset androgenetic alopecia and Parkinson’s disease [7], Crohn’s disease and Parkinson’s disease [8], and coronary artery disease and tonsillectomy [9]. Pleiotropy provides new opportunities, as well as challenges, for diagnosis, therapeutics, and intervention on diseases [1, 2, 10, 11]. Consequently, it is important to identify and study shared genetic basis of complex traits.
To detect potential pleiotropic effects of genetic variants, many statistical methods for jointly analyzing multiple traits in genome-wide association studies (GWAS) have been proposed [1, 12, 13]. Use of these methods—commonly referred to as “cross-phenotype association tests”—has been gaining traction over the past few years, and has led to successful discovery and replication of genetic overlap among different human disorders and traits [5, 14–21]. Typical cross-phenotype association methods test the global null hypothesis that no trait is associated with a given genetic variant against the alternative hypothesis that at least one of the traits is associated. Thus, rejection of the null hypothesis could just be due to one trait being associated with the genetic variant, and not necessarily due to pleiotropy.
A number of Bayesian approaches exist that allow evaluation of pleiotropy on a genome-wide scale based on posterior probability of simultaneous association of a variant with two or more traits given GWAS summary data for each trait [12]. However, the power of these methods for detecting variant-level pleiotropy at specified family-wise error rate (FWER) or type I error rate are not well understood. For instance, conditional false discovery rate (FDR) approach [22], GPA [23] and their generalizations [24, 25] provide association mapping for a fixed FDR, which, unlike FWER, is more liberal and is not the standard GWAS error measure. Additionally, due to the higher level of complexity of Bayesian approaches and the well-established standard interpretations of frequentist approaches in GWAS, frequentist approaches are sometimes more appealing to researchers for association mapping.
In the frequentist realm, recently a few methods have been proposed to specifically test for pleiotropy, where the rejection of the null hypothesis of no pleiotropy is driven by the significant association of a genetic variant with more than one trait [26–29]. All of these methods require individual-level phenotype and genotype data on the same set of randomly sampled individuals, and cannot be readily extended to diseases on which case-control samples are available. While one may compare the significant variants of one trait with those of another, it is worth noting that the discovery of the variants in the first place may be under-powered in individual GWAS. Two other common strategies for examining genetic overlap between traits involve estimating genetic correlation, and testing how well polygenic risk score of one disease explains variation of the other. Both these approaches describe an overall genetic sharing, and do not indicate genetic sharing at a locus level or implicate novel shared variants/loci. To our knowledge, there is currently no summary statistics based frequentist approach to specifically test for pleiotropy between any two traits. Furthermore, there is no frequentist method for identifying pleiotropic loci between case-control traits that may or may not share controls.
In this article, we propose a formal statistical test of pleiotropy of two traits borrowing ideas from statistical mediation analysis literature. The proposed method, PLACO (pleiotropic analysis under composite null hypothesis), can be applied to summary-level data available from GWAS of two traits and can account for potential correlation across traits, such as that arising due to shared controls in case-control studies. We conduct extensive simulation experiments to study type I error and power of PLACO at stringent significance levels. We apply PLACO to summary data on common variants from two large case-control GWAS of European ancestry on Type 2 Diabetes (T2D) and on Prostate Cancer (PrCa). Many previous studies have reported an inverse association of these two chronic diseases suggesting shared risk factors; however, shared genetic mechanisms underlying this T2D-PrCa association is poorly understood. We replicate some candidate and known shared genes, and identify a number of novel shared genetic regions.
Material and methods
Model and notation
Consider two genome-wide studies of traits Y1 and Y2 on n1 and n2 individuals respectively who were genotyped and/or imputed or sequenced at p genetic variants. Assume n1 individuals are independent of n2 individuals, with no overlapping samples between the studies. Let Yk and Xk be the vectors of k-th trait values and genotypes at a given genetic variant respectively on all nk individuals (k = 1, 2). For the ease of explanation, we will assume the two traits are binary (e.g., case-control traits); however, our approach, being based on summary statistics, is applicable to two qualitative and/or quantitative traits. An individual’s outcome or trait can take value 0 for controls or 1 for cases. If the genetic variant under consideration is a bi-allelic single nucleotide polymorphism (SNP), an individual’s genotype can take values 0, 1 or 2 depending on the number of copies of minor alleles at the SNP. If the variant is imputed, the genotypic value will range between 0 and 2. For simplicity, we assume there is no covariate. Note, this assumption can be easily relaxed by considering trait residuals (obtained from regressing the covariates on the trait) instead of the raw trait values. Although residualizing outcome data is not standard, previous studies have shown that it does not affect validity of genetic association tests [30–32].
The typical approach in a GWAS is to test for association of each genetic variant with the trait, and report the estimated genetic effect sizes, their standard errors and the corresponding p-values for all genetic variants (often referred to as ‘summary statistics’). For a given genetic variant, the marginal model for outcome data is
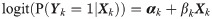
Statistical framework for a formal testing of pleiotropy
Defining the null hypothesis
The conventional cross-phenotype association methods test the global null hypothesis that none of the traits is associated with the given genetic variant (i.e., β1 = β2 = 0). Rejection of this global null can be due to one associated trait (β1 ≠ 0, β2 = 0 or β1 = 0, β2 ≠ 0) or both (β1 ≠ 0, β2 ≠ 0). Here, we are interested in identifying the genetic variants that are associated with both the traits or outcomes (i.e., pleiotropy). The effects of such a genetic variant on the traits may or may not be equal. Formally, our null hypothesis of no pleiotropy is H0: at most 1 trait is associated with the genetic variant while the alternative hypothesis is Ha: both traits are associated.
A simple approach for testing pleiotropy
Mathematically, our null hypothesis of no pleiotropy is a composite null hypothesis H0: H00 ∪ H01 ∪ H02 while the alternative hypothesis is
Other suitable approaches for testing pleiotropy
Observe that our null hypothesis of no pleiotropy can simply be written as H0: β1
β2 = 0 vs. the alternative hypothesis Ha: β1
β2 ≠ 0. This immediately reminds us of the product of coefficients hypothesis tests for the significance of mediation effects in epidemiology [34]. It involves constructing test statistics by dividing
In the context of genome-wide mediation analysis, the normal approximation of Sobel’s method depends on a condition that only holds if at least one of the mediation coefficients is non-zero [36]. In the context of our pleiotropy test in GWAS, we expect most genetic variants to be not associated with either of the traits (i.e., we expect the global null H00 to be true for most genetic variants). As a consequence of sparse signals and hence the breakdown of condition for asymptotic normality of Sobel’s method, testing pleiotropy using Sobel’s method fails to control type I error and lacks power to detect pleiotropic effects of a genetic variant. In the mediation literature, as an alternative to Sobel’s method, [36] proposed a modified p-value calculation for the test of estimated mediation effect that maintains appropriate type I error under the assumption that most of the significance tests of mediation are conducted under the global null that both coefficients are zero. In this article, we borrow Huang’s approach [36] from mediation analysis to propose a new single-variant test of pleiotropy of two traits in GWAS. Our approach for identifying pleiotropic variants is particularly useful for characterizing genetic overlap between two disease traits from case-control GWAS at a variant level.
Our proposed test of pleiotropy: PLACO
Two independent traits
Suppose the global null H00 holds with probability π00 under which the single-trait test statistics Z1 and Z2 have asymptotic standard normal distributions. Further assume that the sub-null hypothesis H01 holds with probability π01 under which Z1 has a standard normal distribution and Z2 has a conditional N(μ2, 1) distribution given the mean parameter μ2. We assume a
In other words, we are assuming (a) Z1 and Z2 are independent N(0, 1) variables under H00; (b) Z1 and Z2 are independent N(0, 1) and
The p-value (two-tailed) for testing H0: β1 β2 = 0 (no pleiotropy) against Ha: β1 β2 ≠ 0 using the product of Z-scores as our test statistic is given by
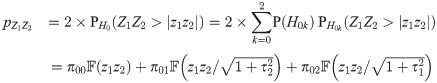
Asymptotic approximation of PLACO p-value
The PLACO p-value in Eq 2 can be approximated as
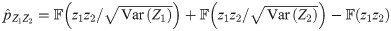
Adjusting PLACO for correlation across GWAS
The above formulation of PLACO assumes that the Z-scores for the two traits are independent. While the independence of the effects
For two outcomes from two case-control studies, the correlation between the Z-scores is
The number of overlapping samples between studies/traits may not be known when only GWAS summary data are available. In such a situation, one can estimate the correlation parameter ρ by the Pearson correlation of the Z-scores for the genetic variants with “no effect” on any trait. For a real dataset, the truth about which genetic variants have “no effect” is unknown. We choose the genetic variants that do not exceed a pre-defined significance threshold (say, genetic variants with single-trait p-value > 10−4) for any trait to estimate the correlation ρ between Z-scores [43]. One may also use cross-trait LD-score regression [44] to estimate ρ; however we did not find appreciable differences between GWAS results obtained using estimates from these two approaches [13]. Irrespective of the approach, this estimation is done only once, as implemented in PLACO software, before applying PLACO genome-wide. If Z = (Z1, Z2)′ be the vector of Z-scores for a given genetic variant and
Simulation experiments
To evaluate operating characteristics of PLACO as a test for pleiotropy, we conduct simulation experiments in R [38]. We consider three broad simulation settings: one where we have traits from independent case-control studies, another with traits from case-control studies with shared controls, and the other with correlated traits from quantitative studies. For simplicity, we do not simulate any covariate or confounder. We simulate unrelated individuals and 10 million independent bi-allelic genetic variants in Hardy-Weinberg equilibrium with a fixed population-level minor allele frequency (MAF) 5%. We assume the commonly used additive genetic model in our simulations. Since we need multiple independent replicates to assess type I error control and power at stringent error thresholds, we generate the genetic variants independently. Subsequently, we calculate estimated type I error (power) by averaging over the number of independent null (non-null) variants identified as having significant pleiotropic effect on both traits at a fixed significance level α.
Out of the 10 million genetic variants, we assume 99% of variants to be under the global null of no association H00 (i.e., none of the two traits is associated with these genetic variants), 0.5% variants under the sub-null H01 (i.e., only the second trait is associated with these genetic variants), 0.4% variants under the sub-null H02 (i.e., only the first trait is associated with these genetic variants), and 0.1% variants under the alternative Ha (i.e., these genetic variants have pleiotropic effects on both traits). Thus, our simulated dataset has 9.99 million null variants to estimate type I error and 10, 000 non-null variants to estimate statistical power. Note, we have explored additional simulation settings such as those with higher proportion of variants associated with at least one trait or with larger MAF of variants; the details and results of which are provided in Section C of S1 Appendix.
Scenario I: Traits from two independent case-control studies
We simulate the two case-control studies such that the individuals in one study are independent of the other. We consider situations where the two studies have either comparable (1:1) or unbalanced (4:1) sample sizes. In other words, either the two studies have equal sample sizes (n1 = n2 = 2000) or the first study on the first trait is 4 times larger than the second study on the second trait (n1 = 8000, n2 = 2000). We assume a case-control ratio of 1:1 in each study, and a baseline disease prevalence of 15% and 10% for the first and the second disease trait respectively. Our generative model, described in Section C of S1 Appendix, has been widely used before [45–47] and is distinct from the hierarchical model assumed by PLACO. In this scenario, we compare type I error and power of Sobel’s approach, maxP, and PLACO to detect pleiotropy of the two independent case-control outcomes. Among the existing variant-level Bayesian pleiotropy methods applicable on a genome-wide scale, while both GPA and conditional FDR approaches are the most similar to PLACO in terms of the research question, we choose to compare PLACO with only GPA since GPA was previously shown to be superior to conditional FDR approach in most scenarios [23]. We keep this comparison separate from the main results because frequentist and Bayesian approaches are not directly comparable; moreover, PLACO aims to control FWER while GPA uses FDR control. The null genetic variants with non-zero effect on one trait only are assumed to have an odds ratio (OR) of 1.15 for the associated trait. For the non-null variants used to estimate power, we consider different choices of the two ORs to incorporate traits with genetic effects of varying directions and/or magnitudes.
Scenario II: Traits from two case-control studies with overlapping controls
We assume either 20%, 40%, 80% or 100% of the controls are shared, assuming equal number of controls in the two studies. Our generative model is the same as used in Scenario I. Here, we compare type I error of Sobel’s approach, maxP, and PLACO with and without correction for sample overlap. Evaluating power in this scenario is redundant since the power will depend on the total number of independent samples, which we explore in Scenario I. For implementing PLACO that accounts for the overlap, we assume the number of overlapping samples is not available to calculate correlation through the Lin-Sullivan approach [42], and instead estimate the Pearson correlation of the Z-scores.
Scenario III: Two correlated traits from a study of quantitative traits
We simulate a single study with measurements on two correlated quantitative traits measured either on the same individuals (n1 = n2 = 2000) or the first trait is measured on many additional individuals (n1 = 8000, n2 = 2000). We vary both the strength and the direction of pairwise trait correlation: ρtrait = {−0.9, −0.4, 0, 0.4, 0.9}. The null genetic variants with non-zero effect on one trait only are assumed to explain 0.1% of the variance of the associated trait. The generative model is the same as before except that a bivariate normal model with means 0, variances 1, and pairwise correlation ρtrait is used to simulate the quantitative traits. In this scenario too, we only compare type I error of Sobel’s approach, maxP, and PLACO (with and without correction for correlation), and do not evaluate power.
Application to T2D and PrCa GWAS summary data
Many epidemiologic studies [48–52] of T2D and PrCa have reported association between these two diseases, suggesting shared risk factors. A few studies [53–56] have been undertaken to identify shared genetic risk factors underlying this T2D-PrCa association. To elucidate shared genetic mechanisms between these two diseases, which is still poorly understood, we use our statistical approach PLACO on summary data from two of the largest and most recent GWAS of T2D and of PrCa in individuals of European ancestry.
Xue et al. [57] meta-analyzed 62,892 T2D cases and 596,424 controls from three large GWAS datasets of European ancestry (DIAGRAM [58], GERA [59] and UK Biobank [60]). The authors reported summary statistics on 5,053,015 genotyped (from GWAS chip and Metabochip) and imputed autosomal SNPs (GRCh37/hg19) with MAF ≥1% that were common to the three datasets. All imputed SNPs have imputation info score ≥0.3. The reported summary statistics were obtained by fixed effects inverse-variance meta-analysis of GWAS summary statistics from each dataset after adjusting for study-specific covariates such as age, sex and principal components (PCs).
Schumacher et al. [61] meta-analyzed 79,194 PrCa cases and 61,112 controls from eight GWAS or high-density SNP panels of European ancestry imputed to 1000 Genomes Phase 3. All imputed SNPs have imputation r2 ≥ 0.3. The authors combined the per-allele odds ratios and standard errors, adjusted for PCs and study-relevant covariates, for the SNPs from the Illumina OncoArray and each GWAS by fixed effects inverse-variance meta-analysis. The summary statistics file contained information on 20,370,947 SNPs (GRCh37/hg19) across the autosomes and the X chromosome.
In this paper, we use the two sets of meta-analysis summary statistics of genetic association with T2D and with PrCa to detect shared common SNPs. Sources of these summary statistics are provided under Web resources. We remove any SNP with allele mismatch between the two datasets, and focus on the remaining 5, 041, 948 autosomal SNPs with MAF ≥1% that are available in both the studies. For a given SNP, we harmonize the same effect allele across the two studies so that Z-scores from the two datasets can be jointly analyzed appropriately using PLACO. From the effect estimates and the standard errors, we calculate the Z-scores, and remove SNPs with Z2>80 [62, 63] since extremely large effect sizes can disproportionately influence our analysis. The component studies underlying the T2D and the PrCa GWAS do not appear to overlap. The estimated correlation between the Z-scores from T2D and those from PrCa is approximately 0 as well.
To characterize the findings from PLACO, we clump all the significantly associated SNPs (pPLACO<5 × 10-8) in ±500 Kb radius and linkage disequilibrium (LD) threshold of r2>0.2 into a single genetic locus using FUMA [64] (SNP2GENE function, v1.3.5e). The gene annotations for all loci are based on proximity to the most significant/lead SNPs as mapped by FUMA. We perform different gene-set enrichment analyses using the GENE2FUNC function, where the genes were prioritized by FUMA based on the loci identified by PLACO. To provide additional evidence of sharing at these loci, we perform Bayesian colocalization test [65] of the PrCa and the T2D summary data using R package coloc (v3.2.1). This test computes 5 different overall posterior probabilities of the chosen region:
Results
Simulation experiments: Type I error
Scenario I: Traits from two independent case-control studies
Irrespective of whether the sample sizes of the two studies are same or widely different, PLACO has well-calibrated type I error at stringent significance levels (Fig 1). In comparison, the Sobel’s and maxP approaches are extremely conservative.

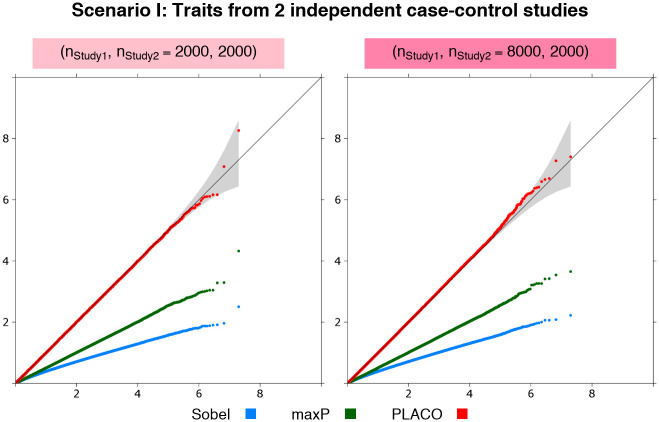
Scenario I: QQ plots for pleiotropic analysis of null data on traits from 2 independent case-control studies.
Observed(−log10p-values) are plotted on the y-axis and Expected(−log10p-values) on the x-axis. Either each study has 1, 000 unrelated cases and 1, 000 unrelated controls, or Study 1 is 4 times that of Study 2, where Study 2 has 1, 000 unrelated cases and 1, 000 unrelated controls. Type I error performance of tests of pleiotropic effect of a genetic variant on the 2 traits is based on 9.99 million null variants with genetic effects that are either {β1 = 0 = β2} or {β1 = 0, β2 = log(1.15)} or {β1 = log(1.15), β2 = 0}. The gray shaded region represents a conservative 95% confidence interval for the expected distribution of p-values. P-values ≥10-10 are shown here.
Scenario II: Traits from two case-control studies with overlapping controls
Regardless of the extent of control overlap in the two studies, PLACO exhibits appropriate type I error when correlation is accounted for in the analysis (Fig 2 and S1 Fig). We also note that if Z-scores are not decorrelated for studies with overlapping samples, pleiotropy analysis will likely show spurious association signals as indicated by the inflated ‘PLACO (no overlap correction)’ curve. The other approaches are still very conservative across all scenarios of overlap.

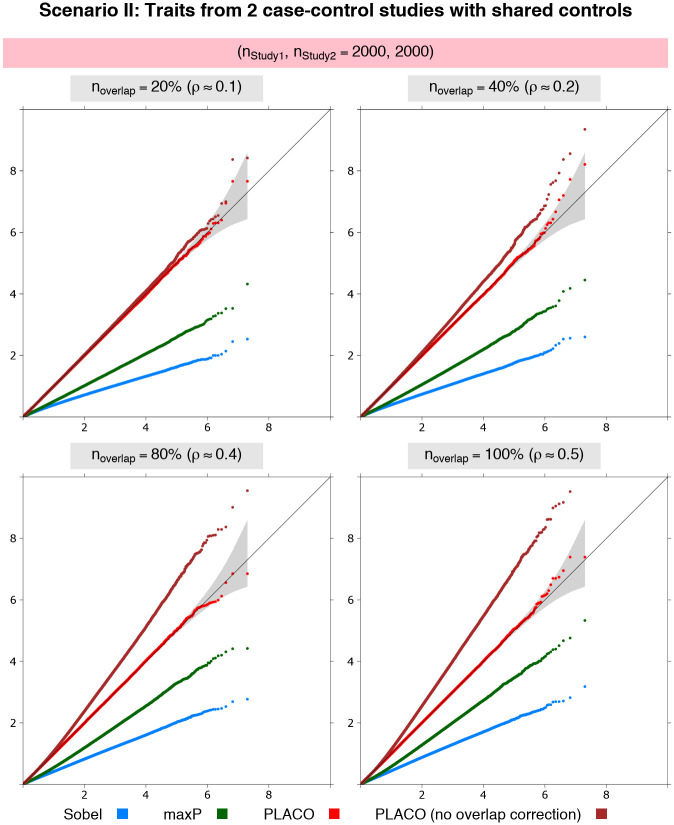
Scenario II: QQ plots for pleiotropic analysis of null data on traits from 2 case-control studies with different proportions of overlapping controls.
Observed(−log10p-values) are plotted on the y-axis and Expected(−log10p-values) on the x-axis. Equal study sample size, and equal case-control size assumed in each study. Each study has 1, 000 unrelated cases and 1, 000 unrelated controls, of which either 20%, 40%, 80% or 100% of the controls are shared between the two studies. Type I error performance of tests of pleiotropic effect of a genetic variant on the 2 traits is based on 9.99 million null variants with genetic effects that are either {β1 = 0 = β2} or {β1 = 0, β2 = log(1.15)} or {β1 = log(1.15), β2 = 0}. The gray shaded region represents a conservative 95% confidence interval for the expected distribution of p-values. P-values ≥10-10 are shown here.
Scenario III: Two correlated traits from a study of quantitative traits
We find PLACO has well-calibrated type I error for moderately correlated traits irrespective of the direction of correlation between the traits, and has inflated type I error for strongly correlated traits (S2 Fig). Application of PLACO ignoring correlation will show spurious association signals. As before, the other approaches exhibit conservative behavior across all scenarios of pairwise trait correlation. The ‘maxP’ approach can, however, be less conservative for strongly correlated traits.
Simulation experiments: Power
For benchmarking, we compare power of PLACO against Sobel’s and maxP, along with the naive approach of declaring pleiotropy when a variant reaches genome-wide significance for the first trait with the larger sample size and reaches a more liberal significance threshold for the second trait. We use two such naive approaches: one using criterion pTrait1<5 × 10-8, pTrait2<5 × 10-5 and the other pTrait1<5 × 10-8, pTrait2<5 × 10-3 (‘Naive-1’ and ‘Naive-2’ respectively in our figures). As reasoned before, comparing power under Scenario I is sufficient. Regardless of the magnitude and directions of pleiotropic association and the sample size differences between studies, PLACO has dramatically improved statistical power to detect pleiotropy compared to the naive approaches (Fig 3). The Sobel’s and maxP approaches especially lack power due to their very conservative type I error control.

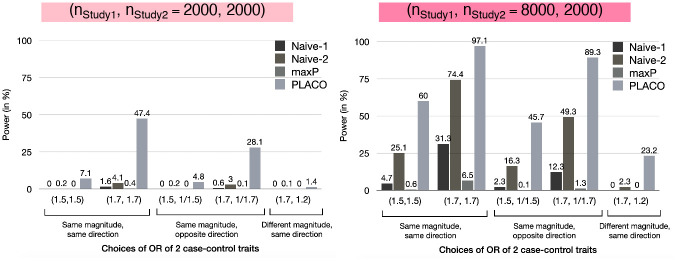
Scenario I: Power of PLACO, maxP and naive approaches at genome-wide significance level (5 × 10−8) for varying genetic effects of traits from 2 independent case-control studies.
Sobel’s approch is excluded from this figure since it has <1% power across all scenarios. The first naive approach (‘Naive-1’) declares pleiotropic association when pTrait1<5 × 10−8 and pTrait2<5 × 10−5, while the second naive approach (‘Naive-2’) uses a more liberal criterion pTrait1<5 × 10−8 and pTrait2<5 × 10−3. Each study either has 1, 000 unrelated cases and 1, 000 unrelated controls, or Study 1 has 4 times sample size as Study 2, where Study 2 has 1, 000 unrelated cases and 1, 000 unrelated controls.
Simulation experiments: Comparison with an existing Bayesian approach
To make PLACO and GPA comparable to the extent possible, we use the Benjamini-Hochberg FDR [72] corrected PLACO p-values and 5% FDR threshold to declare significant pleiotropic association instead of using the FWER genome-wide threshold. For GPA, we use the association mapping results at global FDR threshold of 5% as provided by the R package GPA. It appears that PLACO is superior to GPA in terms of the number of discoveries made when fewer true pleiotropic variants are present genome-wide, especially if the pleiotropic effects are not very strong (S1 Table). This observation holds even for skewed sample sizes of the two traits (S2 Table).
Application to T2D and PrCa GWAS summary data
Overview of joint T2D-PrCa locus level associations
PLACO identified 1, 329 genome-wide significant SNPs that mapped to 44 distinct loci (Fig 4). The lead SNPs of 24 loci (55%) increase risk for one outcome while decreasing risk for the other. This observation is consistent with what observational studies [49, 73, 74] and genetic risk-score studies [54, 55] have reported before: an inverse association between T2D and PrCa. We define a locus as novel if there is no ‘previously associated SNP’ from GWAS catalog [75] (as of December 16, 2019) within ±500 Kb radius or in LD (r2>0.2) with our index SNP, the GWAS peak, from that locus. To define ‘previously associated SNP’ in our context of pleiotropy of T2D and PrCa, we looked for any SNP within each locus that is associated with both T2D-related trait (either of T2D, 2-hour glucose challenge, glucose level, glycated albumin, HbA1c, insulin level, pro-insulin level, insulin resistance, insulin response, or glycemic traits) and PrCa-related trait (either of PrCa or prostate-specific antigen levels). Since GWAS catalog includes exome-wide studies, we chose a slightly liberal exome-wide significance threshold of p<5 × 10−7 to define previously reported associations. We discovered 38 potentially novel loci, after liftover of GRCh38 genomic coordinates in GWAS catalog to hg19 using R package liftOver [76].

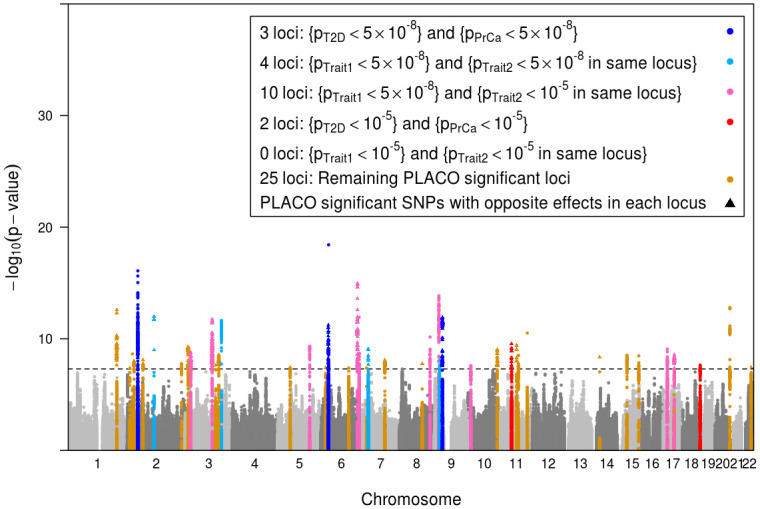
Manhattan plot of the PLACO p-values of pleiotropic association of common genetic variants with outcomes (traits) T2D and PrCa.
The black horizontal dashed line corresponds to genome-wide significance level α = 5 × 10−8. The 44 loci with genome-wide significant pleiotropic lead SNP have been highlighted. A locus is defined by clumping SNPs in ±500 Kb radius around the lead SNP and with LD r2>0.2. Within each locus, if a PLACO significant SNP has genetic effects in opposite directions for T2D and PrCa, it is plotted as a solid triangle (24 such loci), else as a solid circle. Each identified pleiotropic locus is categorized (color-coded) as follows. Three loci harbor SNPs that are marginally genome-wide significant for both T2D and PrCa (single-trait p<5 × 10−8). Four loci contain SNPs that are marginally genome-wide significant for one disease, and in close proximity (i.e., in the same locus) with another SNP marginally genome-wide significant for the other disease. There are 10 loci where SNPs are marginally genome-wide significant for one disease and in close proximity with another SNP marginally suggestively significant (single-trait p<10−5) for the other disease. Two loci harbor SNPs that are marginally suggestively significant (but not genome-wide significant) for both T2D and PrCa. There is no locus that contains SNPs that are marginally suggestively significant (but not genome-wide significant) for one disease, and in close proximity with another SNP marginally suggestively significant (but not genome-wide significant) for the other disease. The rest of the 25 loci identified by PLACO contain SNPs that are not even marginally suggestively significant for either T2D or PrCa.
PLACO points to known and candidate shared genetic regions
GWAS catalog search reveals that 6 out of 44 loci near genes THADA, BCL2L11, AC005355.2, PBX2 (in the major histo-compatibility complex or MHC region of 6p21), JAZF1 and CDKN2A/B have been previously implicated in studies of both T2D and PrCa. In particular, THADA [51] (S3 Fig) and JAZF1 [53] (S4 Fig) represent well-recognized shared genetic regions between T2D and PrCa. HNF1B, also known as TCF2, is another recognized shared gene [53, 77], which we fail to detect possibly because we excluded SNPs with extremely large effect sizes [62, 63] (
Gene-set enrichment analysis
For further analysis, we exclude the 1 locus that lay in the MHC region of chromosome 6p21 because of strong SNP associations in this long-range and complex LD block that complicates fine-mapping efforts [70]. The 310 genes to which the 43 pleiotropic loci were mapped by FUMA are significantly enriched in GWAS catalog reported genes for PrCa, T2D and other T2D related traits (S9 Fig). When tested for tissue specificity against differentially expressed genes from GTEx v8 data across 53 tissue types, these genes are significantly enriched in pancreas (a T2D-relevant tissue) and whole-blood (S10 Fig). Analyses in other annotated gene sets from Molecular Signatures Database (MSigDB v7.0) [78] and in curated biological pathways from WikiPathways [79], and functional enrichment analyses are described in Section D of S1 Appendix.
Colocalization analysis
Bayesian colocalization tests of ±200 Kb region around the lead SNPs of the 43 loci reveal 26 lead SNPs as having the highest posterior probability of being associated with both PrCa and T2D (Table 1). Eight loci show convincing evidence of containing SNPs that are likely causal for both T2D and PrCa, 7 of which have the highest posterior probabilities of being causal SNPs and exhibit stronger signals of pleiotropic association compared to the single trait associations (Table 2). The lead SNP for the eighth locus, near RGS17, is 54 Kb away from the SNP with the highest causal probability (rs6932847), and both have similar PLACO p-value of pleiotropic association.

| Sl. no. | Lead SNP from PLACO analysis | coloc analysis of ±200kb around lead SNP | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| overall probabilities | SNP with highest causal probability | |||||||||||||
| locus | position (hg19) | rsID | nearest gene | pPLACO | effect† direction |
 | nSNP |
 |
 | rsID | position | pPLACO |
 | |
| 1 | 1q32.1 | 204560677 | rs6679717 | AL512306.3 | 2.6 × 10−13 | + − | 0.375 | 482 | 0.267 | 8 | Same as lead SNP | |||
| 2 | 2p25.1 | 10094526 | rs73913932 | GRHL1 | 4.2 × 10−8 | −+ | 0.394 | 909 | 0.33 | 40 | Same as lead SNP | |||
| 3 | 2p24.1 | 20881840 | rs2289081 | C2orf43 | 2.3 × 10−9 | + + | 1 | 690 | 0.192 | 14 | Same as lead SNP | |||
| 4 | 2p23.3 | 27827092 | rs12464616 | ZNF512 | 9.9 × 10−9 | −+ | 2 × 10−6 | 331 | 0.203 | 0.1 | rs1260334 | 27748597 | 2.2 × 10−6 | 1 |
| 5 | 2p21 | 43797710 | rs11904510 | THADA | 8.2 × 10−17 | −− | 0.168 | 809 | 1 | 0 | rs10179648 | 43808065 | 9.0 × 10−14 | 0.434 |
| 6 | 2p14 | 65276452 | rs1009358 | CEP68 | 7.9 × 10−9 | −+ | 0.75 | 792 | 0.407 | 15 | Same as lead SNP | |||
| 7 | 2q13 | 111896243 | rs17041869 | BCL2L11 | 1.0 × 10−12 | −+ | 0.446 | 626 | 0.994 | 1.2 | Same as lead SNP | |||
| 8 | 2q36.3 | 227174983 | rs2673148 | AC068138.1 | 1.7 × 10−8 | + + | 0.057 | 680 | 0.057 | 4.2 | rs2673129 | 227139572 | 1.9 × 10−8 | 0.285 |
| 9 | 3p25.2 | 12276493 | rs11709119 | PPARG | 5.3 × 10−10 | −+ | 6 × 10−4 | 709 | 0.154 | 0.1 | rs35000407 | 12351521 | 1.9 × 10−4 | 0.653 |
| 10 | 3p24.3 | 23284303 | rs114460169 | UBE2E2 | 1.7 × 10−9 | −+ | 7 × 10−6 | 1179 | 0.672 | 0.0 | rs1496653 | 23454790 | 8.7 × 10−6 | 1 |
| 11 | 3q13.2 | 113309149 | rs6808932 | SIDT1 | 1.8 × 10−12 | + − | 0.394 | 728 | 0.879 | 0.4 | rs12635148 | 113284208 | 2.6 × 10−12 | 0.605 |
| 12 | 3q21.3 | 128039895 | rs11708733 | EEFSEC | 2.4 × 10−8 | −+ | 9 × 10−6 | 488 | 0.023 | 0.6 | rs2811478 | 127899624 | 7.2 × 10−4 | 0.071 |
| 13 | 3q23 | 141140366 | rs6763927 | ZBTB38 | 2.8 × 10−9 | −+ | 0.174 | 504 | 0.923 | 5.3 | Same as lead SNP | |||
| 14 | 3q25.1 | 152010142 | rs76360965 | MBNL1 | 2.3 × 10−12 | −− | 0.058 | 558 | 1 | 0.1 | Same as lead SNP | |||
| 15 | 5q11.2 | 52058673 | rs4530726 | ITGA1 | 3.6 × 10−8 | + − | 0.099 | 1026 | 0.826 | 7.1 | Same as lead SNP | |||
| 16 | 5q31.1 | 133848917 | rs10900829 | AC005355.2 | 4.7 × 10−10 | −− | 0.109 | 358 | 0.877 | 1.9 | Same as lead SNP | |||
| 17 | 6p22.3 | 20844151 | rs9356756 | CDKAL1 | 3.9 × 10−8 | −+ | 0.064 | 849 | 0.043 | 0.3 | rs9465883 | 20761335 | 1.3 × 10−5 | 0.189 |
| 18 | 6q22.1 | 117264990 | rs1741652 | RFX6 | 4.1 × 10−8 | −− | 10−4 | 716 | 0.1 | 0.1 | rs682726 | 117104975 | 1.3 × 10−3 | 0.175 |
| 19 | 6q25.2 | 153394728 | rs4385321 | RGS17 | 1.1 × 10−15 | + − | 0.17 | 1094 | 0.986 | 67 | rs6932847 | 153448307 | 1.4 × 10−15 | 0.58 |
| 20 | 6q25.3 | 160683381 | rs316025 | SLC22A2 | 1.2 × 10−12 | + + | 0.997 | 655 | 0.709 | 1.1 | Same as lead SNP | |||
| 21 | 7p15.3 | 21012144 | rs6944344 | LINC01162 | 4.2 × 10−8 | + + | 0.697 | 772 | 0.055 | 3.3 | Same as lead SNP | |||
| 22 | 7p15.1 | 28028432 | rs38514 | JAZF1 | 8.3 × 10−10 | + − | 0.366 | 626 | 1 | 0 | Same as lead SNP | |||
| 23 | 7q21.3 | 97754074 | rs73404162 | LMTK2 | 8.4 × 10−9 | −+ | 7 × 10−8 | 577 | 0.215 | 0.1 | rs12667763 | 97668012 | 7.0 × 10−8 | 0.704 |
| 24 | 8q22.1 | 95739642 | rs67763258 | DPY19L4 | 1.7 × 10−8 | −+ | 0.507 | 1019 | 0.368 | 7.8 | Same as lead SNP | |||
| 25 | 8q24.21 | 128391412 | rs62516032 | CASC8 | 6.9 × 10−11 | −− | 0.093 | 550 | 0.518 | 0.0 | rs1962471 | 128281708 | 1.6 × 10−6 | 0.197 |
| 26 | 9p22.1 | 19064129 | rs13287517 | HAUS6 | 1.4 × 10−14 | + + | 0.379 | 1322 | 0.999 | 30 | Same as lead SNP | |||
| 27 | 9p21.3 | 22003223 | rs3217992 | CDKN2A/B | 7.5 × 10−9 | + − | 10−4 | 482 | 1 | 0 | rs1063192 | 22003367 | 1.7 × 10−6 | 0.739 |
| 28 | 9p13.3 | 34025640 | rs1758632 | UBAP2 | 1.2 × 10−12 | −+ | 0.065 | 511 | 1 | 15 | Same as lead SNP | |||
| 29 | 10p13 | 12208307 | rs1053403 | NUDT5 | 2.6 × 10−8 | + + | 10−8 | 646 | 0.744 | 0.0 | rs11257655 | 12307894 | 3.8 × 10−7 | 0.869 |
| 30 | 10q26.12 | 123038897 | rs12413648 | LINC01153 | 9.2 × 10−10 | + − | 0.15 | 714 | 0.651 | 3.4 | Same as lead SNP | |||
| 31 | 11p11.2 | 47461693 | rs7103835 | RAPSN | 2.8 × 10−10 | −+ | 0.503 | 467 | 0.992 | 11 | Same as lead SNP | |||
| 32 | 11q13.3 | 68894753 | rs12284087 | RP11-554A11.7 | 3.9 × 10−10 | + + | 0.67 | 547 | 0.179 | 1.4 | Same as lead SNP | |||
| 33 | 11q13.5 | 76257215 | rs3753051 | C11orf30 | 3.0 × 10−9 | −− | 0.123 | 714 | 0.262 | 2 | rs17749618 | 76251818 | 3.2 × 10−9 | 0.129 |
| 34 | 11q23.2 | 113807181 | rs11214775 | HTR3A/B | 3.1 × 10−11 | −− | 1 | 640 | 0.723 | 97 | Same as lead SNP | |||
| 35 | 14q13.1 | 33302882 | rs17522122 | AKAP6 | 4.4 × 10−9 | + − | 0.973 | 787 | 0.94 | 980 | Same as lead SNP | |||
| 36 | 15q15.1 | 40881116 | rs10400825 | KNL1 | 3.0 × 10−9 | −− | 0.058 | 625 | 0.908 | 11 | Same as lead SNP | |||
| 37 | 15q26.1 | 90429148 | rs12912009 | AP3S2 | 3.3 × 10−9 | + + | 0.222 | 520 | 0.382 | 2.8 | Same as lead SNP | |||
| 38 | 17p11.2 | 17724789 | rs11656665 | SREBF1 | 8.4 × 10−10 | + + | 0.289 | 412 | 0.951 | 0.4 | Same as lead SNP | |||
| 39 | 17q21.32 | 45885756 | rs9911983 | OSBPL7 | 4.8 × 10−8 | −+ | 0.939 | 683 | 0.707 | 13 | Same as lead SNP | |||
| 40 | 17q21.32 | 47037024 | rs11079847 | GIP | 2.7 × 10−9 | −+ | 0.016 | 667 | 0.843 | 0.1 | rs9894220 | 46989154 | 7.4 × 10−9 | 0.172 |
| 41 | 18q23 | 74562251 | rs7236466 | ZNF236 | 2.3 × 10−8 | + + | 0.1 | 880 | 0.949 | 14 | Same as lead SNP | |||
| 42 | 20q13.33 | 62337406 | rs6011040 | ARFRP1 | 1.6 × 10−13 | −− | 0.367 | 281 | 0.724 | 22 | Same as lead SNP | |||
| 43 | 22q13.1 | 40479811 | rs9607685 | TNRC6B | 3.7 × 10−8 | −+ | 0.035 | 393 | 0.114 | 5.7 | rs34419824 | 40499103 | 1.6 × 10−7 | 0.267 |
† The effect direction duplet reports the effect direction of T2D first, and then of PrCa for the chosen effect allele at the lead SNP.
A high

| Locus no. | Lead SNP from PLACO analysis | Summary statistics for lead SNP | pPLACO | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| locus | position hg19) | rsID | nearest gene | effect allele | other allele | effect allele freq. | CADD score |
 | pT2D |
 | pPrCa | ||
| 13 | 3q23 | 141140366 | rs6763927 | ZBTB38 | T | A | 0.44 | 3.18 | -0.0316 | 6.8 × 10−5 | 0.0459 | 8.5 × 10−9 | 2.8 × 10−9 |
| 19 | 6q25.2 | 153394728 | rs4385321 | RGS17 | A | G | 0.35 | 4.05 | 0.0352 | 2.8 × 10−6 | -0.0724 | 2.7 × 10−18 | 1.1 × 10−15 |
| 26 | 9p22.1 | 19064129 | rs13287517 | HAUS6 | C | G | 0.39 | 0.44 | 0.0402 | 5.3 × 10−7 | 0.0609 | 7.1 × 10−14 | 1.4 × 10−14 |
| 28 | 9p13.3 | 34025640 | rs1758632 | UBAP2 | C | G | 0.38 | 1.24 | -0.0491 | 1.4 × 10−9 | 0.0432 | 1.1 × 10−7 | 1.2 × 10−12 |
| 31 | 11p11.2 | 47461693 | rs7103835 | RAPSN | A | G | 0.31 | 7.53 | -0.0384 | 1.2 × 10−6 | 0.046 | 1.4 × 10−7 | 2.9 × 10−10 |
| 35 | 14q13.1 | 33302882 | rs17522122 | AKAP6 | T | G | 0.48 | 2.19 | 0.0403 | 5.2 × 10−8 | -0.0337 | 4.0 × 10−5 | 4.4 × 10−9 |
| 36 | 15q15.1 | 40881116 | rs10400825 | KNL1 | G | A | 0.15 | 2.66 | -0.0452 | 4.0 × 10−5 | -0.0612 | 2.4 × 10−8 | 3.0 × 10−9 |
| 41 | 18q23 | 74562251 | rs7236466 | ZNF236 | G | T | 0.38 | 4.03 | 0.0368 | 3.8 × 10−6 | 0.0364 | 8.2 × 10−6 | 2.3 × 10−8 |
Characterizing the 8 most interesting potentially novel pleiotropic loci
The lead SNPs of 6 of the 8 potentially novel pleiotropic loci with convincing evidence from the colocalization analyses have effect alleles that increase risk for one disease while protecting from the other (Table 2). While the 8 loci contain cis-eQTLs in multiple T2D-relevant tissues (S11–S16 Figs), SNPs in the loci near RGS17 (Fig 5) and UBAP2 (Fig 6) show significant cis-eQTL associations in both T2D-relevant and PrCa-relevant tissues. In Open Targets Genetics, genes near the ZBTB38, UBAP2 and ZNF236 loci show associations with various cancers, diabetes and obesity (no relevant mouse data available for these genes). The RGS17 locus show associations with various cancers, including PrCa and prostate neoplasm, and body mass index (BMI) but has no known associations with any T2D-related trait (no relevant mouse data available). Of particular interest are the HAUS6 and the RAPSN loci. While HAUS6 and its nearby genes RRAGA and PLIN2 have various cancers (including PrCa) as associated diseases in Open Targets Genetics, one or more of them are related to metabolism phenotype, abnormal gluconeogenesis and hypoglycemia in mice. GWAS catalog search of these genes did not yield any known association result with any T2D-related trait. Similarly, the nearby gene MADD for the RAPSN locus has various cancers, neoplasms and glucose-related phenotypes as associated diseases in Open Targets Genetics; and is a recognized T2D gene, which when knocked out in mice, show impaired glucose tolerance, hyperglycemia and abnormal pancreatic beta cell morphology.

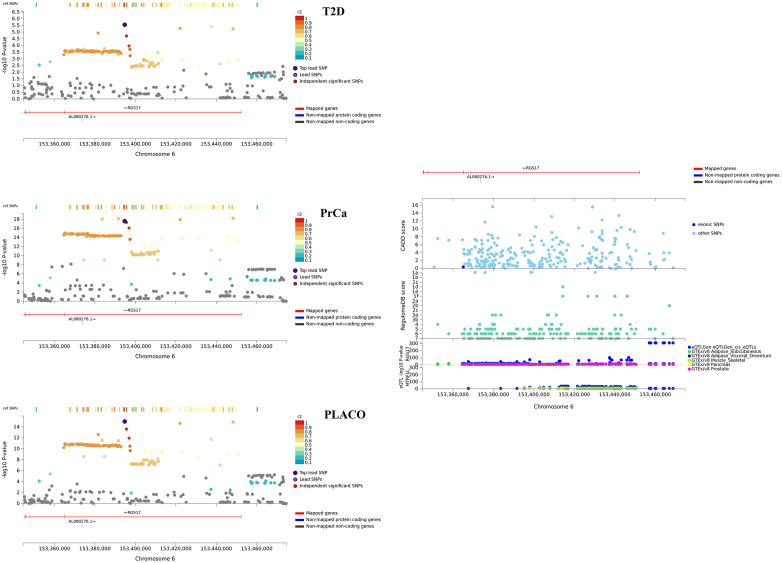
Regional association plot of significant pleiotropic locus near RGS17 with annotations such as CADD scores, RegulomeDB scores, and cis eQTL association p-values from 6 tissues.
Tissues considered are whole blood from eQTLGen Consortium; and adipose, liver, muscle-skeletal, pancreas, and prostate tissues from GTEx v8.

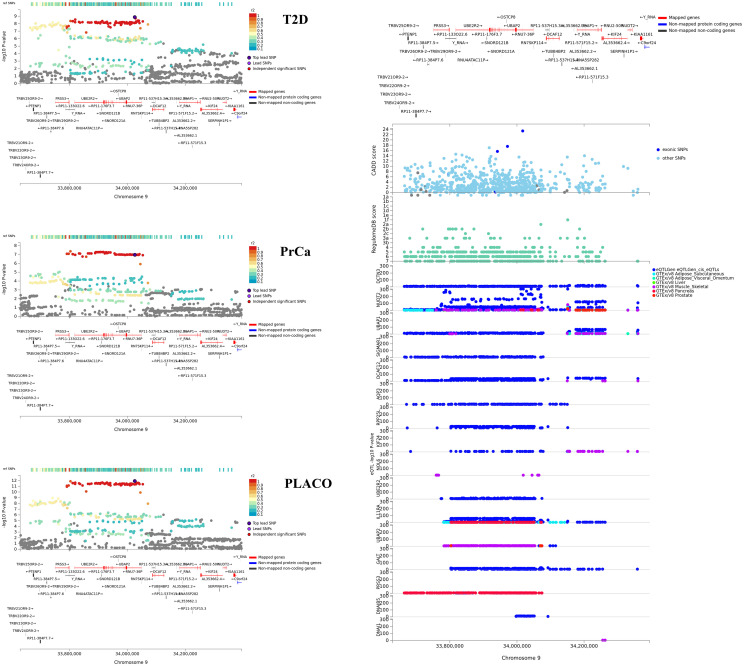
Regional association plot of significant pleiotropic locus near UBAP2 with annotations such as CADD scores, RegulomeDB scores, and cis eQTL association p-values from 6 tissues.
Tissues considered are whole blood from eQTLGen Consortium; and adipose, liver, muscle-skeletal, pancreas, and prostate tissues from GTEx v8.
Discussion
In this paper, we propose a formal statistical hypothesis test and a novel method, PLACO, to determine common pleiotropic or shared variants of two independent traits and show how it may well be applied to correlated traits or traits from studies with sample overlap. In our simulations involving qualitative and quantitative traits with unequal prevalences, unequal genetic effect sizes, unequal sample sizes—ranging from modest to large—and with/without overlapping samples, PLACO exhibits well-calibrated type I error. We find PLACO is powerful in detecting subtle genetic effects of pleiotropic variants that may or may not be in the same direction and that may be missed when each disease trait is analyzed separately (see some additional simulations in Section C of S1 Appendix). Statistical power is significantly improved when PLACO is used, compared to the naive approach that identifies pleiotropy when a genetic variant reaches genome-wide significance for the trait with larger sample size and reaches a more liberal threshold for the other. We also observe improved power over other existing approaches, both Bayesian and frequentist, in most scenarios. Based on our simulations, we advocate using PLACO on independent traits, or moderately correlated traits after decorrelating the Z-scores as described before.
We use the most recent publicly available case-control GWAS summary data on T2D and on PrCa in individuals of European ancestry to determine variants that influence risk to both these diseases. We identify several known and candidate shared genes, and detect a number of novel shared genetic regions near ZBTB38 (3q23), RGS17 (6q25.3), HAUS6 (9p22.1), UBAP2 (9p13.3), RAPSN (11p11.2), AKAP6 (14q12), KNL1 (15q15) and ZNF236 (18q23). A recent study [80] showed a weak positive genetic correlation between T2D and PrCa. It is worth noting that the concept of genetic correlation is different from pleiotropy. For genetic correlation to be non-zero, the directions of effect of non-null variants must be consistently aligned [44]. Effect alleles of at least half of the significant SNPs identified by PLACO have opposite genetic effects on the two diseases, which supports many previous studies reporting inverse relationship between T2D and PrCa, and likely explains the weak genetic correlation in the previous study.
The key advantage of PLACO among existing frequentist approaches is not requiring individual-level data which makes it easily applicable to datasets for which only GWAS summary data are available. It does not require compute intensive permutations or Monte Carlo simulations to calculate p-value of simultaneous association of two traits with one genetic variant. We are conveniently using the asymptotic normality of MLE of genetic effects to get at the null distribution of the PLACO test statistic. The existence of an analytical form for PLACO p-value (Eq 2) and its approximation (Eq 3) makes it suitable for application on a genome-wide scale. While we have applied PLACO to summary statistics from population-based case-control GWAS, it may also be applied to two traits from family-based designs (e.g., disease traits from case-parent trio studies). For instance, family-based GWAS data from several study cohorts will soon be available under the cohort collaboration study, Environmental influences on Child Health Outcomes (ECHO, https://www.nih.gov/research-training/environmental-influences-child-health-outcomes-echo-program), to understand genetic underpinnings of pediatric outcomes. One important scientific question will be to identify genetic overlap of such outcomes (e.g., neurodevelopmental disorders, respiratory disorders), which PLACO can conveniently address, that too without having to pool individual-level data.
Our study and our statistical approach are not without limitations. PLACO requires genome-wide summary data to infer pleiotropic association of each variant, and cannot be used when summary data on only a handful of candidate genetic variants are available. Calculation of PLACO p-value requires parameter estimation using variants across the genome, and hence cannot be used to test pleiotropy of a set of variants known to be significantly associated with one trait. PLACO shows inflated type I error when the traits are strongly correlated even after using our decorrelation approach. The approximate PLACO p-value (
Acknowledgements
This research was carried out in part using computing cluster—the Joint High Performance Computing Exchange (JHPCE)—at the Department of Biostatistics, Johns Hopkins Bloomberg School of Public Health. Part of this research project was conducted using computational resources at the Maryland Advanced Research Computing Center (MARCC). DR is thankful to Dr. Terri H Beaty (Johns Hopkins University) for conversations that motivated this work, and helpful discussions thereafter.
Web resources
PLACO, https://github.com/RayDebashree/PLACO
Type 2 diabetes summary data, http://cnsgenomics.com/data/t2d
Prostate cancer summary data, ftp://ftp.ebi.ac.uk/pub/databases/gwas/summary_statistics/SchumacherFR_29892016_GCST006085
Bayesian colocalization analysis, https://cran.r-project.org/web/packages/coloc
FUMA, https://fuma.ctglab.nl/
Open Targets Genetics platform, https://genetics.opentargets.org/
QQ plot code,https://genome.sph.umich.edu/wiki/Code_Sample:_Generating_QQ_Plots_in_R
Manhattan plot code, https://genome.sph.umich.edu/wiki/Code_Sample:_Generating_Manhattan_Plots_in_R
Locuszoom plot, http://locuszoom.org/
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
 A powerful method for pleiotropic analysis under composite null hypothesis identifies novel shared loci between Type 2 Diabetes and Prostate Cancer
A powerful method for pleiotropic analysis under composite null hypothesis identifies novel shared loci between Type 2 Diabetes and Prostate Cancer
