CF Splitting and Superexchange Hamiltonian.

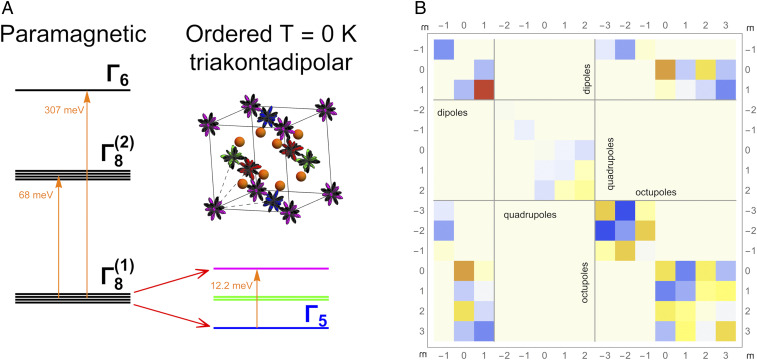
We start with evaluating the Np CF splitting in paramagnetic NpO₂; as discussed above, this splitting determines the space of low-energy states forming the MMO. The CF splitting of the Np $$ 5f^3$$ ground-state multiplet $$ J$$ = 9/2 calculated by DFT + HI is shown in Fig. 1A. The ground-state $$ {\mathrm{\Gamma }}_8$$ quartet is separated from another excited $$ {\mathrm{\Gamma }}_8$$ quartet by 68 meV, in agreement with the experimental range for this splitting, 30 to 80 meV, inferred from INS measurements (19, 32, 40). The broad experimental range for the excited $$ {\mathrm{\Gamma }}_8$$ energy is due to the presence of a dispersive phonon branch in the same range [this overlap has been a major source of difficulties for the phenomenological analysis of NpO₂ in the framework of effective CF model model (8)]. The third exited level, $$ {\mathrm{\Gamma }}_6$$ doublet, is located at much higher energy above 300 meV (see Fig. 1A).

Fig. 1.

Np 5$$ f$$ on-site splitting and Np–Np intersite interactions in NpO₂. (A) Calculated CF spiting of Np $$ 5f^3$$ J = 9/2 multiplet in paramagnetic state (Left) and exchange splitting of the ground-state quartet in the predicted ordered phase at zero temperature (Right). Note the energy rescaling for the $$ {\mathrm{\Gamma }}_6$$ level on the CF splitting plot. (Inset) The crystal structure of the NpO₂. Positions of the Np atoms are surrounded by the polar plot of the calculated primary order parameter (triakontadipoles) in the ground state. Different colors indicate four nonequivalent Np positions in the ordered state. The orange spheres are oxygen atoms. (B) SEI matrix between NN Np in NpO₂. These SEIs couple multipolar operators $$ {Ô}_{lm}$$ in the $$ J_{e\mathit{ff}}$$ = 3/2 space of the $$ {\mathrm{\Gamma }}_8$$ CF ground state. Their values in the local coordinate system (with z axis directed along the given bond direction and y axis along the edge of the face-centered cubic lattice) are presented as a temperature map, with the warm and cool colors representing antiferromagnetic and ferromagnetic coupling of the corresponding multipoles, respectively.

Our calculated CF corresponds to $$ x$$ = −0.54 parameterizing the relative magnitude of the four- and six-order contributions to the cubic CF (41). Our values are in good agreement with $$ x$$ = −0.48 inferred from INS measurements (19) and analysis of CF excitation energies along the actinide dioxide series (31). The CF-level energies calculated within DFT + HI are also in good agreement with previous DFT + DMFT calculations by Kolorenč et al. (42) employing an exact diagonalization approach to Np 5$$ f$$. The calculated wave functions (WFs) of the CF ground-state $$ {\mathrm{\Gamma }}_8$$ quartet (SI Appendix, Table S1) feature a small admixture of the excited $$ J$$ = 11/2 and 13/2 multiplets.

The space of CF GS $$ {\mathrm{\Gamma }}_8$$ quadruplet is conveniently represented by the effective angular momentum quantum number $$ J_{eff}$$ = 3/2, with the $$ {\mathrm{\Gamma }}_8$$ WFs labeled by the corresponding projection $$ M=-3/2\dots +3/2$$ and the phases of WFs chosen to satisfy the time-reversal symmetry (SI Appendix, Table S1). The on-site degrees of freedom within the GS quadruplet are (pseudo-)dipole, quadrupole, and octupole moments defined for $$ J_{e\mathit{ff}}$$ = 3/2 in the standard way (8). Hence, the most general form for a superexchange coupling between $$ {\mathrm{\Gamma }}_8$$ quadruplets on two Np sites reads

We employed the FT-HI approach (38) to evaluate all interactions $$ V_{K{K}^{\prime }}^{Q{Q}^{\prime }}\left(R\right)$$ from the converged DFT + HI NpO₂ electronic structure for the several first Np coordination shells. Only NN SEIs are significant, with longer-distance ones being more than an order of magnitude smaller. All SEIs $$ V_{K{K}^{\prime }}^{Q{Q}^{\prime }}\left(R\right)$$ for a given bond $$ R$$ form a matrix, designated below as the SEI matrix, with the rows and columns labeled by the moments $$ KQ$$ and $$ K^{\prime }{Q}^{\prime }$$ on the sites $$ R_0$$ and $$ R_0+R$$, respectively. The NN SEI matrix $$ \widehat{V}\left(R\right)$$ is graphically represented in Fig. 1B (SI Appendix, Table S2) using a local coordinate system with the quantization axis $$ z\Vert R$$. This $$ 15\times 15$$ matrix is of a block-diagonal form since the interactions between time-even and time-odd moments are zero by symmetry. It can thus be separated into the dipole–dipole (DD), quadrupole–quadrupole (QQ), octupole–octupole (OO), and dipole–octupole (DO) blocks. Despite this simplification, the SEI matrix $$ \widehat{V}$$ can in principle contain 70 distinct elements. The number of distinct nonzero matrix elements in $$ \widehat{V}$$, while reduced by the cubic symmetry to 38, remains rather large.

Our calculations predict the largest values for the diagonal DD $$ x-x$$ (AF, 1.6 meV) SEI. However, the off-diagonal OO $$ xyz$$ to $$ y\left(x^2-3y^3\right)$$ (ferro, −1.5 meV) and DO $$ z$$ to $$ z^3$$ (AF, 0.95 meV) couplings are of about the same magnitude as the DD $$ x-x$$ one. Overall, the calculated $$ \widehat{V}$$ matrix shown in Fig. 1B features many nonnegligible DD, OO, and DO interactions of a comparable magnitude. The QQ interactions are weaker, reflecting the secondary nature of the quadrupole order. Our calculations thus predict a complex and frustrated superexchange in NpO₂, which may give rise to multiple competing time-odd orders. Therefore, as has been previously noted (8, 25), extracting a full superexchange Hamiltonian of NpO₂ from experimental (e.g., INS) data is virtually impossible due to a large number of parameters entering into the fit of an excitation spectra. The same difficulty is encountered by ab initio approaches based on total energy calculations for symmetry broken phases (15, 33, 43), which require a large number of very precises calculations to extract multiple nonnegligible matrix elements of $$ \widehat{V}$$, with the magnitude of 0.5 meV and above. Within the present framework, all interactions are extracted from a single ab initio calculation for paramagnetic NpO₂.

Ordered State of NpO₂.

The calculated superexchange Hamiltonian for NpO₂ reads

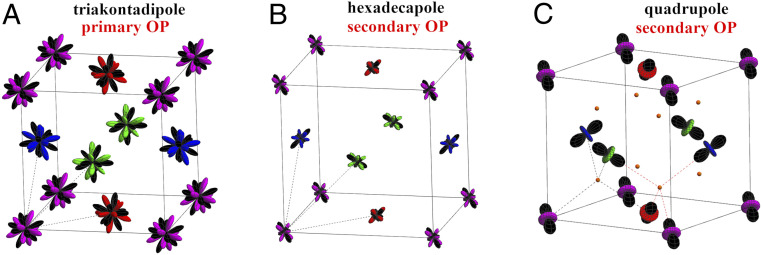
The resulting GS order of NpO₂ in the $$ J_{e\mathit{ff}}$$ space consists of a primary (pseudo-)DO order combined with secondary (pseudo-)quadrupole one (SI Appendix, Table S3 lists the values of all $$ J_{e\mathit{ff}}$$ order parameters; see also SI Appendix, Fig. S1). The pseudodipole order is a complex 3$$ \mathit{k}$$ planar AF structure, with four inequivalent simple-cubic sublattices forming two pairs with different moment magnitude; the moments of those two pairs are aligned along the $$ ⟨\mathrm{1,1,0}⟩$$ and $$ ⟨\mathrm{3,1,0}⟩$$ directions in the fcc lattice, respectively. The origin of this inclined AF structure of pseudodipoles is in the DO SEI, similar to physical AF magnetic orders found in some materials with large spin-orbit coupling that are likely induced by higher-order magnetic multipolar interactions. The pseudoctupoles order is also oriented in nonsymmetrical directions. The secondary pseudoquadrupole order is of a 3$$ \mathit{k}$$ type, which we analyze in detail below.

We subsequently mapped the moments calculated in the $$ J_{e\mathit{ff}}=3/2$$ space into the observable multipolar moments that are defined in the physical $$ J=9/2$$ space of Np 5$$ f^3$$ GS multiplet (Methods). The calculated physical multipole order of NpO₂ is displayed in Fig. 2. Notice that observable moments up to $$ K$$ = 7 can exist on an $$ f$$-electron shell (8); we show the largest primary (odd) and secondary (even) order parameters as well as the physically important quadrupole order. All nonzero multipole moments are listed in SI Appendix, Table S4. The physical dipole magnetic moments are found to completely vanish since their contribution into the $$ ⟨O_x⟩$$ and $$ ⟨O_y⟩$$ pseudodipole $$ J_{e\mathit{ff}}=3/2$$ moments is exactly canceled by that due to the $$ ⟨T_x⟩$$ and $$ ⟨T_y⟩$$ pseudoctupoles. The primary order parameter is of rank 5 (triakontadipole); the physical octupole moment is an order of magnitude smaller, and the magnitude of rank 7 moments is about 1/3 of that for triakontadipoles, in agreement with previous estimates for the relative contribution of those multipoles into the MMO order in NpO₂ (24). The magnetic triakontadipoles on different sublattices are oriented in four different directions (forming mutual angles corresponding to the angles between the cube’s main diagonals), thus structured similarly to the 3$$ \mathit{k}$$-AFM dipole order in UO₂ (Fig. 2A). The secondary order is dominated by hexadecapole (rank 4) (Fig. 2B). The ordered quadrupole moments (Fig. 2C) are roughly twice smaller. The quadrupole order is directly related to the pseudoquadrupole one since the $$ {\mathrm{\Gamma }}_5$$ (or $$ t_{2g}$$) pseudoquadrupoles directly map into the physical ones, apart from swapping $$ xy\leftrightarrow yz$$ and $$ x^2-y^2\leftrightarrow xz$$. The resulting physical quadrupole order can be represented, in the space of $$ {\mathrm{\Gamma }}_5$$ quadrupoles [$$ O_{yz}$$,$$ O_{xz}$$,$$ O_{xy}$$] by four directions [$$ \overline{1}$$11], [1$$ \overline{1}$$1], [11$$ \overline{1}$$], and [111] for four inequivalent Np sublattices [0,0,0], [1/2,1/2,0], [1/2,0,1/2], and [0,1/2,1/2], respectively. These quadrupoles can be depicted as $$ ⟨O_{z^2}⟩$$ moments with the principal axes $$ z$$ along the corresponding direction at each given site (Fig. 2C). One sees that the ordered quadrupoles on the four Np sites forming the tetrahedron around each oxygen can either have their principal axes directed along the Np–O bonds toward the central O or form the same angle of $$ 70.5^{○}$$ with respect to those bonds. In both cases, the tetrahedron symmetry is preserved. The first case is realized for two O along one of the principal cubic diagonals, while the second one is found for six others, resulting in the lowering of NpO₂ symmetry to $$ Pn\overline{3}m$$ from $$ Fm\overline{3}m$$ without any distortion of the cubic structure. This longitudinal 3$$ \mathit{k}$$ quadrupole order, previously proposed on the basis of resonant X-ray scattering (30) and subsequently confirmed by the splitting of ¹⁷O-NMR spectra in ordered NpO₂ (21), is thus predicted by our ab initio superexchange Hamiltonian (2).

Fig. 2.

Calculated multipolar order in NpO₂. This order of the physical multipoles in NpO₂ is derived by mapping of the $$ J_{e\mathit{ff}}$$ = 3/2 space to the full $$ J$$ = 9/2 space. The physical magnetic dipoles (magnetic moments) are exactly canceled on all Np sites, resulting in a purely multipolar order. (A) The primary physical order parameter (OP), $$ K$$ = 5 triakontadipole. (B) The largest secondary “slave” OP, $$ K$$ = 4 hexadecapole. The displayed isovalue for the primary and secondary OPs is normalized with respect to the maximum possible value of a given moment in the $$ {\mathrm{\Gamma }}_8$$ CF ground-state quartet. Hence, the relative size of plotted moments indicates their relative magnitude. Black dashed lines are the primitive lattice translations of the original Np cubic face-centered sublattice, which, in the ordered phase, connects inequivalent Np sublattices. (C) Longitudinal 3$$ \mathit{k}$$ order of slave quadrupole moments, which are scaled on the plot by a factor of four. Np–O bonds for two inequivalent O sites (small orange balls) in ordered NpO₂ are indicated by dashed lines. One sees that in the Np tetrahedron around each O, all ordered Np quadrupoles either are directed along the Np–O bonds or form the same angle with those bonds. This longitudinal 3$$ \mathit{k}$$ quadrupolar order preserves the cubic positions of oxygen sites in the ordered phase of NpO₂, in contrast to the transverse 3$$ \mathit{k}$$ quadrupole order in UO₂.

Exchange Splitting and Magnetic Excitations.

Having obtained the MMO of NpO₂, we subsequently calculated its excitation spectra, which have been previously measured, in particular, by INS (19, 25).

The MMO lifts the degeneracy of CF GS $$ {\mathrm{\Gamma }}_8$$ quartet; the resulting exchange splitting calculated from the ab initio superexchange Hamiltonian (2) is depicted in Fig. 1 A, Right. The ground state is a $$ {\mathrm{\Gamma }}_5$$ singlet with the first excited doublet found at 6.1 meV above the GS $$ {\mathrm{\Gamma }}_5$$ singlet and the second excited level, singlet, located at 12.2 meV. The calculated position of first excited doublet is in excellent agreement with the location of a prominent peak in INS spectra at about 6.4 meV (19) in the ordered phase; another broad excitation was observed in the range of 11 to 18 meV (25) (see below).

Previously, an exchange splitting of the $$ {\mathrm{\Gamma }}_8$$ was obtained in ref. 24 assuming a diagonal uniform SEI between $$ {\mathrm{\Gamma }}_5$$ triakontadipoles. The value of this SEI was tuned to reproduce the experimental position of the excited doublet; the energy for the excited singlet calculated in ref. 24 is in agreement with our ab initio result.

We also calculated the theoretical INS cross-section, $$ \frac{d^2\sigma \left(q,E\right)}{dEd\mathrm{\Omega }}=S\left(q,E\right)\propto {\sum }_{\alpha ,\beta }\left({\delta }_{\alpha \beta }-\frac{q_{\alpha }{q}_{\beta }}{q^2}\right)\mathrm{I}\mathrm{m}{\chi }_{\alpha \beta }\left(q,E\right)$$, where $$ E$$ ($$ q$$) is the energy (momentum) transfer; $$ \alpha \left(\beta \right)=x,y,z$$; and $$ {\chi }_{\alpha \beta }\left(q,E\right)$$ is the dynamical magnetic susceptibility. The latter was evaluated within the random-phase approximation (RPA) from the full calculated ab initio superexchange Hamiltonian (2) (Methods). The resulting INS spectrum $$ S\left(q,E\right)$$ for $$ q$$ along high-symmetry directions of the fcc lattice is displayed in Fig. 3A. Along the $$ \mathrm{\Gamma }-X$$ path, it is similar to that previously calculated from the simplified empirical superexchange Hamiltonian of ref. 24. The $$ S\left(q,E\right)$$ structure is richer along other directions showing multiple branches in the $$ E$$ range from 4 to 8 meV. The experimental INS spectrum $$ S\left(q,E\right)$$ has not been measured so far due to lack of large single-crystal samples (8); hence, our result represents a prediction for future experiments. The calculated spherically averaged INS cross-section $$ \int S\left(q,E\right)d\widehat{q}$$ is compared in Fig. 3B with that measured (25) on powder samples at the same $$ \left|q\right|$$ = 2.5 Å⁻¹. The theoretical INS spectrum exhibits prominent peaks at around 6 meV and at about 12.5 meV, corresponding to the transition from the $$ {\mathrm{\Gamma }}_5$$ GS to the excited doublet and singlet, respectively.

Fig. 3.

INS spectra in ordered NpO₂. (A) INS cross-section $$ S\left(q,E\right)$$ with the momentum transfer $$ q$$ along a high-symmetry path in the fcc BZ. The special points are $$ \mathrm{\Gamma }$$ = [0,0,0], X = [1,0,0], W = $$ \left[1,\frac{1}{2},0\right]$$, and L = $$ \left[\frac{1}{2},\frac{1}{2},\frac{1}{2}\right]$$, in units of $$ 2\pi $$/a. (B) Powder (spherically averaged) INS cross-section vs. energy transfer $$ E$$ for $$ \left|q\right|$$ = 2.5 Å⁻¹. The theoretical spectra were broadened with the Gaussian resolution function of 1.5 meV. The experimental points are from Magnani et al. (25). (C) Ratio of the spectral weights of the low-energy (around 6-meV) and high-energy (10- to 20-meV) features vs. momentum transfer in the powder INS spectra (B). The experimental points are from Magnani et al. (25). Theoretical points from the same work are calculated with a semiempirical superexchange Hamiltonian (in the text).

The theoretical low-energy feature agrees very well with the measured INS spectra, after experimental broadening is taken into account (Fig. 3B). The high-energy feature, however, is clearly split in experiment into two broad peaks centered at about 12 and 16 meV. In order to understand whether the relative weights of the low- and high-energy features are captured in the theory, we employed the same analysis as Magnani et al. (25). Namely, we evaluated, as a function of the momentum transfer, the ratio of high-energy feature spectral weight to that of the low-energy one. The calculated ratio is in excellent agreement with experiment up to $$ \left|q\right|$$ = 2.5 Å⁻¹. As noticed in ref. 25, a phonon contribution to INS appears below 18 meV for large $$ \left|q\right|$$, thus rendering the separation of magnetic and phonon scattering less reliable for $$ \left|q\right|>$$ 2 Å⁻¹. The splitting of high-energy peak was clearly observed at all measured $$ \left|q\right|$$; it was not reproduced by the simplified semiempirical SEI employed by Magnani et al. (25). They speculated that this splitting might stem from complex realistic Np–Np SEIs, which they could not determine from experiment. In the present work, we determined the full superexchange Hamiltonian for the GS CF $$ {\mathrm{\Gamma }}_8$$ quadruplet. Hence, the fact that the splitting of INS high-energy feature is still not reproduced points out to its origin likely being a superexchange coupling between the ground-state and first excited $$ {\mathrm{\Gamma }}_8$$ quadruplets (a significant contribution of the very high-energy $$ {\mathrm{\Gamma }}_6$$ CF doublet is unlikely). This interquadruplet coupling can be in principle derived using the present framework; we have not attempted to do this in the present work.

Alternatively, lattice-mediated interactions might be also considered as the origin of the high-peak splitting. Those interactions couple time-even moments (i.e., the quadrupoles within the $$ J_{e\mathit{ff}}$$ space). However, the QQ coupling is rather expected to impact the shape of the low-energy peak in Fig. 3B because the corresponding lowest on-site excitation in the ordered phase (Fig. 1 A, Inset) is due to reverting of the on-site quadrupole moment (24). Indeed, we recalculated the theoretical INS spectrum (Fig. 3B) with the magnitude of QQ block in the SEI (Fig. 1B) scaled by a factor from zero to five. These variations of the QQ coupling strength do modify the shape of the low-energy peak but have no impact on the high-energy one. Since the lattice-mediated coupling is expected to modify exclusively the QQ block, it is thus quite unlikely to be the origin of the splitting.

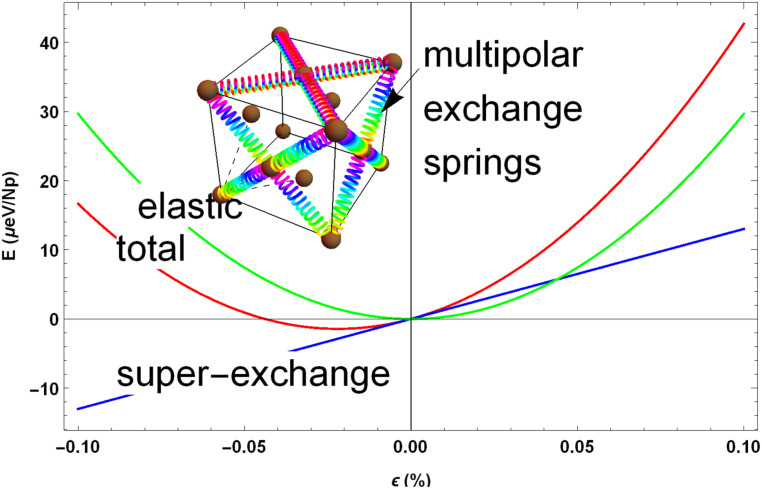
Multipolar Exchange Striction.

The onset of the HO phase NpO₂ is marked by an anomalous volume contraction vs. decreasing temperature (anti-Invar anomaly). The estimated total volume contraction in the ordered state as compared with the paramagnetic phase is 0.018% at zero temperature (20). This effect cannot be attributed to the conventional volume magnetostriction since ordered magnetic moments are absent in NpO₂. Hence, this anomaly was speculated (39) to be induced by a (secondary) quadrupole order coupling to the lattice. As we show below, this is not the case, and the volume contraction in NpO₂ rather stems from the volume-dependent SEI coupling high-rank magnetic multipoles.

In order to make a quantitative estimation for this anomaly, we evaluated the volume dependence of NpO₂ ordering and elastic energies. To that end, we adopted the elastic constants calculated for NpO₂ in the framework of the DFT + U approach (45): $$ C_{11}$$ = 404 GPa, $$ C_{12}$$ = 143 GPa. The corresponding parabolic volume dependence of elastic energy $$ E_{elast}=1/3\left(C_{11}/2+C_{12}\right){ϵ}^2\equiv K_{el}{ϵ}^2$$, where $$ ϵ=\left(V-V_0\right)/V_0$$ is the volume contraction and $$ V_0$$ is the NpO₂ equilibrium volume (45), is depicted in Fig. 4. The dependence of MMO energy vs. volume was obtained by calculating the SEIs at a few different volumes and then evaluating the MF order and ordering energy vs. volume expansion or contraction. The superexchange ordering energy remains linear vs. $$ ϵ$$ in a rather large range ($$ ϵ=\pm $$1%); its dependence upon $$ ϵ$$ for the relevant range of small $$ ϵ$$ is thus easily obtained.

Fig. 4.

Multipolar exchange striction in NpO₂. The curves represent the DFT + U elastic energy (green) and the ordering energy of the multipolar ground state vs. volume (blue); the latter is calculated from the volume-dependent ab initio SEIs. The multipolar order is seen to induce the contraction of the equilibrium volume (total energy; red curve) due to the two-site multipolar striction effect, analogously to the two-site volume magnetostriction in conventional magnetically ordered materials. The “springs” in Inset schematically illustrate the action of the intersite superexchange energy upon the onset of NpO₂ multipolar order.

As is seen in Fig. 4, the superexchange contribution shifts the equilibrium volume in the ordered state toward smaller volumes. The negative slope for the ordering energy vs. volume is expected as the SEIs become larger with decreasing Np–Np distance. Thus, the multipolar SEIs act as springs (scheme in Fig. 4, Inset) pulling Np atoms closer as the order parameters increase below $$ T_0$$. Our approach is thus able to qualitatively capture this very small in magnitude subtle effect: The calculated spontaneous multipolar exchange striction is 0.023% (Fig. 4) at zero $$ T$$ as compared with the experimental estimate of 0.018% (20, 39).

We also performed the same calculations suppressing the QQ superexchange, obtaining only a very minor change, by about 0.5%, in the slope of MMO energy vs. volume. Hence, the secondary quadrupole order plays virtually no role in the anomalous volume contraction. The physical origin of this effect is the volume dependence of leading, time-odd SEIs.

To analyze the temperature dependence of the anomalous contraction, one may recast the linear in volume MMO energy (Fig. 4) into a general form of $$ K_{SEI}^{pr}ϵ{\xi }_{pr}^2\left(T\right)+K_{SEI}^{sec}ϵ{\xi }_{sec}^2\left(T\right)$$, where $$ {\xi }_{pr}\left(T\right)$$ and $$ {\xi }_{sec}\left(T\right)$$ are primary and secondary order parameters, respectively, and $$ K_{SEI}^{pr}$$ and $$ K_{SEI}^{sec}$$ are the slopes of volume dependence for the corresponding contributions to MMO energy. The temperature dependence of the anomalous volume contraction is thus given by that of squares of the order parameters, $$ {\xi }_{pr}^2\left(T\right)$$ and $$ {\xi }_{sec}^2\left(T\right)$$. As shown in SI Appendix, Fig. S2, secondary quadrupole $$ {\xi }_{sec}^2\left(T\right)$$ exhibits a smooth evolution across $$ T_0$$ and rather slowly increases vs. decreasing $$ T$$, while primary time-odd $$ {\xi }_{pr}^2\left(T\right)$$ features a discontinuity in the slope at $$ T_0$$, as expected, with a rapid growth for $$ T<T_0$$, reaching about 60% of total magnitude at $$ 3/4T_0$$. This behavior of $$ {\xi }_{pr}^2\left(T\right)$$ is in a perfect agreement with the shape of temperature dependence of the volume anomaly (20), thus confirming that it is induced directly by the time-odd primary order.

DFT + HI First-Principles Calculations.

Our charge self-consistent DFT + DMFT calculations using the HI approximation for Np 5$$ f$$, abbreviated as DFT + HI, were carried out for the CaF₂-type cubic structure of NpO₂ with the experimental lattice parameter $$ a=5.434$$ Å. We employed the Wien-2k full-potential code (47) in conjunction with “TRIQS” library implementations for the DMFT cycle (36, 48) and HI. The spin-orbit coupling was included in Wien2k within the standard second-variation treatment. The Brillouin zone (BZ) integration was carried out using 1,000 k points in the full BZ, and the local density approximation (LDA) was employed as DFT exchange correlation potential.

The Wannier orbitals representing Np 5$$ f$$ states were constructed by the projective technique of refs. 49 and 50 using the Kohn–Sham bands enclosed by the energy window $$ \left[-2.04:2.18\right]$$ eV around the Kohn–Sham Fermi energy; this window thus encloses all Np 5$$ f$$-like bands. The use of a narrow window enclosing only the target (5$$ f$$-like) band for the construction of local orbitals results in a so-called “extended” Wannier basis. By employing such a basis within DFT + HI, one may effectively include the contribution of hybridization to the CF splitting on localized shells, as discussed in ref. 51. The same choice for the local 5$$ f$$ basis was employed in our previous DFT + HI study (52) of UO₂, resulting in a good quantitative agreement of the calculated CF splitting with experiment.

The on-site Coulomb interaction between Np 5$$ f$$ was specified by the Slater parameter $$ F_0$$ = 4.5 eV and the Hund’s rule coupling $$ J_H$$ = 0.6 eV; the same values were previously employed for UO₂ (52). The double-counting correction was computed using the fully localized limit (53) with the atomic occupancy of Np $$ f^3$$ shell (54). The DFT + DMFT charge self-consistency was implemented as described in ref. 55. In our self-consistent DFT + HI calculations, we employed the spherical averaging of the Np 5$$ f$$ charge density, following the approach of Delange et al. (56), in order to suppress the contribution of LDA self-interaction error to the CF. The DFT + HI calculations were converged to 5 $$ \mu $$Ry in the total energy.

CF and SEIs.

The self-consistent DFT + HI calculations predict a CF split ⁴I_9/2 atomic multiplet to have the lowest energy, in agreement with Hund’s rules for an $$ f^3$$ shell; the calculated spin-orbit coupling $$ \lambda $$ = 0.27 eV. The CF splitting of the ⁴I_9/2 multiplet predicted by these calculations is shown in Fig. 1A, and the corresponding CF WFs are listed in SI Appendix, Table S1. The cubic CF parameters—$$ A_4^0⟨r^4⟩$$ = −152 meV, $$ A_4^4⟨r^4⟩=5A_4^0⟨r^4⟩$$, $$ A_6^0⟨r^6⟩$$ = 32.6 meV, and $$ A_6^4⟨r^6⟩=21A_6^0⟨r^6⟩$$—were extracted by fitting the converged DFT + HI one-electron 5$$ f$$-level positions (56).

The states of the CF ground-state quadruplet $$ {\mathrm{\Gamma }}_8$$ were labeled by projection $$ M$$ of the pseudoangular quantum number $$ J_{e\mathit{ff}}$$ = 3/2 as specified in SI Appendix, Table S1. We subsequently employed the FT-HI method (38) to evaluate all SEIs between the $$ J_{e\mathit{ff}}=3/2$$ quadruplet for several first Np–Np coordination shells. Previously, the FT-HI method was applied to systems with conventional magnetic primary order (52, 57). Within this method, matrix elements of intersite coupling $$ V^R$$ for the Np–Np bond $$ R$$ read

MF Calculations and Analysis of Order Parameters.

We solved the obtained superexchange Hamiltonian (2) using the numerical MF package MCPHASE (44) including all 1$$ k$$ structures up to 4 $$ \times $$ 4 $$ \times $$ 4 unit cells. We have also verified the numerical solution by an analytical approach. Namely, the MF equations read

This order in the $$ J_{e\mathit{ff}}=3/2$$ space was subsequently mapped into the physical $$ J=9/2$$ space. The $$ J_{e\mathit{ff}}$$ density matrix on the inequivalent site $$ a$$ reads $$ {\rho }_a\left(J_{e\mathit{ff}}\right)=Ô\cdot {⟨Ô⟩}_a$$, where $$ {⟨Ô⟩}_a$$ are the corresponding (pseudo-)moments. This density matrix is upfolded into the one in the $$ J=9/2$$ space, neglecting small contributions of the excited $$ J=11/2$$ and $$ 13/2$$ multiplets and renormalizing the $$ {\mathrm{\Gamma }}_8$$ CF states accordingly, as $$ {\rho }_a\left(J\right)=\left|{\mathrm{\Gamma }}_8\right.⟩{\rho }_a\left(J_{e\mathit{ff}}\right)\left.⟨{\mathrm{\Gamma }}_8\right|$$, where $$ \left|{\mathrm{\Gamma }}_8\right.⟩$$ is the CF GS $$ {\mathrm{\Gamma }}_8$$ basis, with WFs written as columns in the order of $$ M=-J_{e\mathit{ff}}\dots J_{e\mathit{ff}}$$. The physical $$ J=9/2$$ moments are then calculated in the standard way, $$ {⟨O{\left(J\right)}_K^Q⟩}_a=\mathrm{T}\mathrm{r}\left[{\rho }_a\left(J\right)O{\left(J\right)}_K^Q\right]$$.

Calculations of Dynamical Susceptibility.

In order to calculate the dynamical magnetic susceptibility $$ {\chi }_{\alpha \beta }\left(q,E\right)$$, we implemented a general RPA approach (59). Namely, the general susceptibility matrix in the $$ J_{e\mathit{ff}}$$ space reads

The local susceptibility $$ {\widehat{\chi }}_{0a}\left(E\right)$$ for the inequivalent site $$ a$$ is calculated from the MF eigenvalues $$ E^a$$ and eigenstates $$ {\mathrm{\Psi }}^a$$:

After the $$ J_{e\mathit{ff}}$$ susceptibility matrix $$ \overline{\chi }\left(q,E\right)$$ is calculated, it is “upfolded” to the physical $$ J=9/2$$ space similarly to the $$ {\rho }_a\left(J_{e\mathit{ff}}\right)$$ density matrix as described above. The magnetic susceptibility $$ {\chi }_{\alpha \beta }\left(q,E\right)$$ is given by the DD blocks of the upfolded $$ \overline{\chi }\left(q,E\right)$$ summed over the sublattice indices.