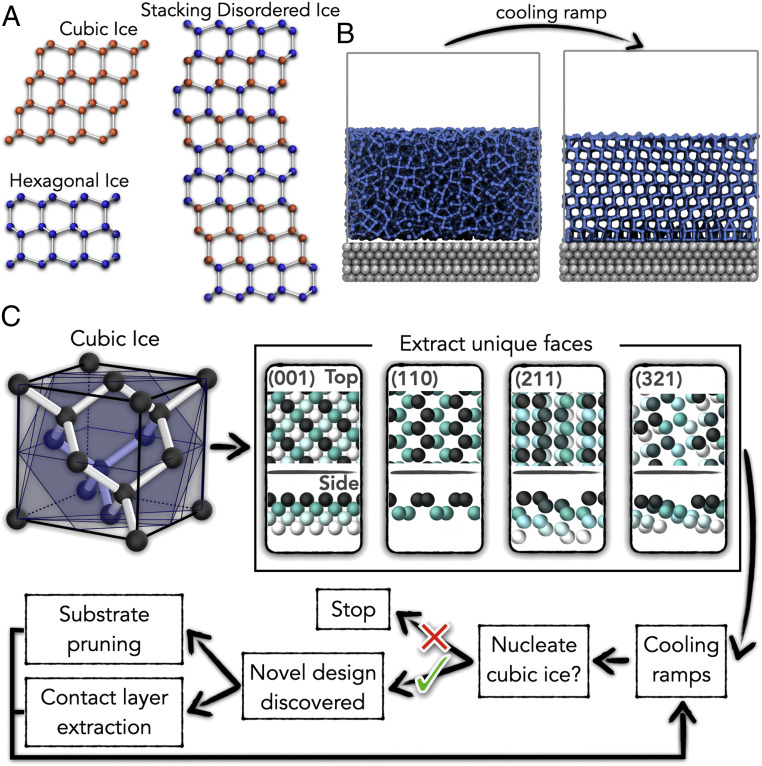
Ice I has two distinct polytypes: stable hexagonal ice () and metastable cubic ice (Ic). Under conditions ordinary on Earth, the free energy difference between these polytypes has been experimentally determined to be just ∼30 to 50 J mol−1 in favor of Ih (2–). Pristine Ic has not directly and unambiguously been observed in nature, yet there is much indirect evidence of its existence. For example, observations of a rare halo of the sun, called Scheiner’s halo, have provided evidence of Ic in the Earth’s atmosphere (). Similarly, studies of the topology of snowflakes provide evidence of growth from an initial nucleus of Ic (, ), and crystals sampled from the polar stratosphere appear to have Ic characteristics (). In addition, cirrus clouds have been observed to have a relatively high water vapor supersaturation, possibly due to the presence of Ic ().
These observations have led to a large body of experimental work related to Ic. Metastable forms of ice with cubic diffraction patterns have been made in various ways, such as water vapor deposition on cold substrates (10–), freezing confined water in mesopores (), or heating low-density amorphous ice (). However, it has only become clear in the last few years that what was widely referred to as Ic is actually stacking disordered ice (Isd), an ice I structure composed of interlaced cubic and hexagonal sequences (). An example of an Isd stacking sequence is shown in Fig. 1A, as well as images of the Ic and Ih polytypes.
Fig. 1.
(A) The three polytypes of ice I: cubic ice (Ic), hexagonal ice (Ih), and an example of stacking disordered (Isd). Isd consists of interlaced layers of Ic and Ih, which stack along the (111) and basal plane of the respective polytypes. Different stacking sequences are possible; the image shown is just a single example. For simplicity, Isd is referred to as its own polytype in this article. (B) Example of a simulation before and after nucleation. Water molecules (blue) and substrate (gray) are shown. (C) Workflow for creating novel systems that nucleate a desired polytype, illustrated on Ic. Different Miller indices for faces unique to the polytype are taken from the unit cell to make slab substrates (atoms are colored by height). Water is placed on the substrates, and cooling ramps are performed. From this, substrates that nucleate Ic are identified. Successful substrates can then be pruned, or the ice contact layer that forms on them can be used to make additional substrate designs (as discussed in the text).
The realization that pristine Ic had not been directly observed sparked renewed interest in Ic and attempts to make it without stacking faults (i.e., with 100% “cubicity”). Significantly, in 2020, del Rosso et al. () and Komatsu et al. () reported the formation of pure Ic in the laboratory (). del Rosso et al. () made it by heating a powder of D2O ice XVII to 160 K under vacuum, and Komatsu et al. () made it by decompression of a C2 hydrogen hydrate at 100 K. There can be little doubt that these studies represent important milestones in the field. However, the approaches taken to obtain pristine Ic are rather complex, involving very well-defined experimental conditions that will not readily be encountered in nature. With this in mind, it is interesting to ask: “Are there other routes to pristine Ic?” In particular, given that in nature, Ih or Isd invariably forms through a heterogeneous nucleation process at the interface with foreign materials, the question arises if Ic (completely lacking in stacking faults) can form through a heterogeneous nucleation process. Previous studies lend support to this possibility. For instance, Ic was formed in simulations of supercooled water confined within graphene-based nanostructures () and between two slabs of “ice 0” (), which shows that desired polytypes of ice I can be achieved through heterogeneous nucleation. Ic has also been observed in simulation studies upon the application of external static electric fields (). More broadly, in pharmaceuticals foreign substrates are used as an experimental means of controlling polymorphism and crystal structure (212223–). Another example is elemental silicon where conversely, the cubic polytype is stable over the hexagonal; hexagonal silicon was first achieved experimentally via epitaxial growth upon a foreign substrate in 2015 ().
Understanding the formation of ice Ic is important not just from a fundamental desire to understand one of the two polytypes of ice I but because the existence of different polytypes and stacking fractions affects important physiochemical properties of ice including crystal shape (), light scattering (), vapor pressure (), and surface chemistry (). In addition, unlike Ih, Ic is believed to be benign to biological tissue, yielding potential in cryopreservation (, ). Considering this, the aim of the current study is to explore routes to pristine Ic through heterogeneous nucleation. This requires developing the understanding of the interplay of ice polytypism and heterogeneous ice nucleation and answering a more general question: “To what extent can templating achieve heterogeneous nucleation of desired polytypes?” To tackle this, we use molecular dynamics on model slab substrate plus water systems using the coarse-grained monoatomic water (mW) water model (). Since effective ice nucleating agents (INAs) are many and varied in nature [e.g., AgI (), feldspar (33–), kaolinite (36–), organic crystals (), and biological materials (40414243–)], we simulate a broad range of model substrates (over 1,100) to minimize overreliance upon a single case study and to boost the chances of extracting general insights. From these simulations, we find that 1) many different substrates can promote the formation of pristine ice I polytypes, including the elusive Ic; 2) pristine Ic can be selectively nucleated for even the most mild supercooling; 3) the water contact layer’s resemblance to a face of ice is the key factor determining the polytype selectivity and nucleation temperature (Tn), independent of which polytype is promoted; and 4) substrate lattice match to ice is not indicative of the polytype obtained. In addition, the substrate design methodology presented here and the insights obtained can be used to control polymorphism and stacking disorder in materials beyond water–ice.
Designing Substrates to Control Ice I Polytypism
Substrate designs with polytype selectivity were discovered for Isd, Ih, and Ic using the general workflow illustrated in Fig. 1C. Starting with the bulk unit cell of the desired polytype, slabs of substrate are generated by taking different Miller index cuts of the faces unique to the polytype (templating shared faces will lead to stacking disorder—which can also be done if this is the desired outcome). The substrate is modeled as either a Lennard–Jones (LJ) system (over a range of interaction parameters) or as an arrangement of OH groups. Water is then placed upon the substrate, and cooling ramps are performed, as illustrated in Fig. 1B. Successful systems, where the desired polytype forms, are then identified and used to generate new substrate designs through two routes: 1) substrate pruning via manually deleting atoms and 2) extraction of the ice contact layer with the substrate, which is subsequently used as a new substrate. The former was done with the aim of making the substrate simpler and/or flatter since if successful, candidates would be easier to engineer experimentally. The latter was done to utilise the deformations present in ice contact-layers to widen the variety of substrate designs considered. Through these approaches, substrates with different surface densities, structures, and symmetries from the original ice lattice can be identified. Cooling ramps are then performed on these new designs, and the process is repeated for systems that are successful. In total, 219 systems were generated this way, which combined with the 900 taken from prior work (Materials and Methods), gives a total of 1,119 systems in the database.
Ice I Polytypism: Prevalent but Controllable
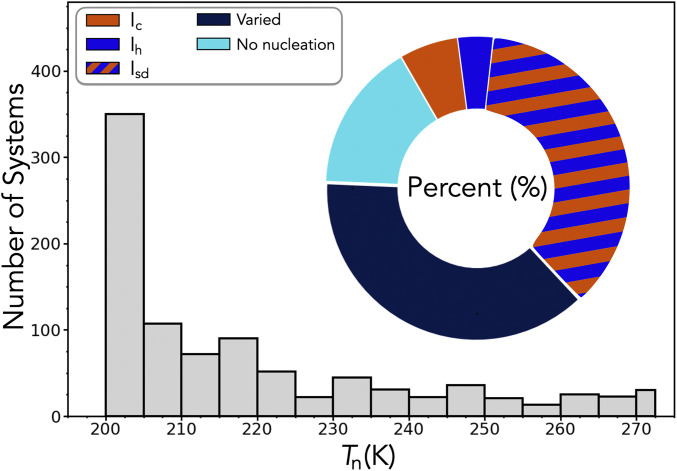
Fig. 2 summarizes the results of the cooling ramps performed on the database of over 1,100 slab substrate and water systems. Tn provides a quantitative measure of the nucleation ability of a substrate, with higher Tn for more potent INAs. A substrate’s polymorph/type selectivity is given by its ability to consistently nucleate a polymorph/type. The full range of nucleating abilities is present, from systems where nucleation is not observed at all to potent ice nucleation ability requiring only very mild supercooling. The nucleation of all three polytypes is also seen for many different systems, with the relative proportions of the different polytypes found shown in Fig. 2, Inset.
Fig. 2.
Histogram of nucleation temperature (Tn) for all systems in the database where nucleation was observed. For each system, five cooling ramps are performed, and Tn is the average temperature at which nucleation is observed. Systems where nucleation is not observed are omitted from the histogram. Inset is a donut plot showing the proportion of systems in the database for which a polytype (or no nucleation) was observed. A system’s polytype is labeled “varied” when no single polytype is obtained 100% of the time.
In SI Appendix, Fig. S1, we explore the polytype distribution with Tn and find the nucleation of Ic, Ih, and Isd for even very mild supercooling (temperatures up to ∼272.5 K). The presence of not only Isd, which contains individual layers of the metastable Ic, but also, pristine Ic crystals at relatively high temperatures is a surprising result. Due to its metastability, the existence of cubic layers of ice has been believed to be only prominent at strong supercooling. In heterogeneously formed ice, it has only been observed up to 257 K in experiment (), and samples of Isd will eventually transform to pristine Ih upon heating above ∼240 K (46–). However, our results suggest ice polytypism could be prevalent in nucleation not only for highly supercooled conditions, but for all levels of supercooling. Before explaining this observation and the general insights obtained into polytype selectivity, we now focus on the nucleation of Ic given its previously elusive nature.
Nucleation of Ic: Highly Robust and Promoted by Numerous Diverse Substrates
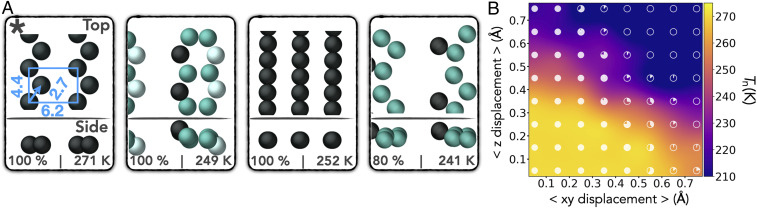
The workflow illustrated in Fig. 1C produced many substrates that nucleated Ic. In total, 70 substrate setups, 56 of which are unique structures (where the difference is not just a varied water–substrate interaction), were found to nucleate Ic 100% of the time. Most effective substrates are composed of OH groups, and several active substrates lack any strong similarity to the Ic lattice. Some examples of effective and structurally simple substrates are shown in Fig. 3A. Structure files for a selection of the most promising substrates are provided in SI Appendix.
Fig. 3.
Hydroxyl group substrate designs to nucleate Ic. (A) Top and side views of some promising designs discovered that nucleate Ic, labeled with percentage chance Ic nucleates and Tn. OH groups are colored by height, with distances for one unit cell given. (B) Heat map exploring the adaptability of a substrate’s nucleation characteristics to atomic displacements within the substrate. Specifically, Tn is plotted against mean absolute displacement of substrate atoms in the xy plane and z axis for the substrate indicated by the asterisk in A. Atoms are randomly displaced by vectors derived from a Gaussian distribution centered at 0.5 and with SD of 0.2. The axes show the mean displacement, and the maximum displacements present will be approximately twice this. Each marker is a pie chart, whose filled area indicates the percentage chance of obtaining Ic—calculated from 6 cooling ramps over five different substrates, giving 30 cooling ramps per pie chart.
The example substrates shown in Fig. 3A have specific arrangements of OH groups and surface unit cells, as is indicated for one of the substrates. If precisely this specific arrangement of OH groups is required to nucleate Ic, then the chances of finding such a structure in nature or creating it in a laboratory would be extremely slim, and even thermal vibrations might render it ineffective in exclusively nucleating Ic. To explore how robust to change a substrate is, we took the two-dimensional (2D) hydroxyl group design marked with an asterisk in Fig. 3A, made random displacements of the substrate atoms, and examined ice nucleation upon it. The results of this analysis are shown in Fig. 3B, from which it can be seen that the nucleation ability of this substrate is indeed highly adaptable and robust to random displacement. Pristine Ic is achieved for 100% of simulations with mean absolute displacements of up to 0.45 Å in the xy plane and for at least 0.75 Å in z (maximum displacements present will be approximately twice this). Therefore, there is a high degree of resilience in this system. Ic is also obtained for a large range of Tn, from ∼272 to 210 K.
Considering the possible introduction of stacking faults leading to Isd, it is natural to think of system size effects. Larger systems will have a greater chance for the introduction of stacking faults and will involve ice growth farther away from the substrate. It has been suggested in prior work that the resulting ice will always be Isd despite any initial nucleation of a particular polytype (). To address this, we simulated nucleation of a computationally very large system of 600,000-mW molecules (which is at the limit of affordability) upon a perturbed 2D substrate from Fig. 3B (i.e., a more realistic substrate than a pristine one), at constant temperature (above the system’s Tn to ensure the nucleation event is not spinodal decomposition). More details of this simulation are given in SI Appendix. The system fully crystallized to pristine Ic. The present-day mismatch between available scales in computational and experimental work means it is not possible to fully understand the scale limit here, but this result is very encouraging and shows this 2D design has a remarkable ability to impose a specific crystal orientation over significant length scales.
To further guide the search for appropriate materials to nucleate pristine Ic, we suggest the following approximate structural-based guidelines.
1)OH–OH separation: The symmetry of the substrate can differ from that of ice; however, generally, the substrate’s radial distribution function (rdf) contains a peak in the region of ∼2.5 to 2.7 Å and/or ∼4.3 to 4.6 Å. This corresponds to the first and second peaks of the rdf of bulk water, respectively.
2)Water–substrate interaction: Most substrates that are effective in promoting Ic have a minimum water–substrate bond length of ∼2.6 to 3.0 Å. None had a minimum bond beyond 3.5 Å. The first coordination shell of the water–substrate rdf also has a well-defined peak, indicating a well-defined local structure.
3)Water contact layer: The structure of the water contact layer is not required to match that of the substrate.
In addition to these structure-based guidelines, we also show later that a high Tn is a good indicator that a strong crystal orientation is being imposed upon the water.
Structure of Water Contact Layer Determines Polytype Selectivity
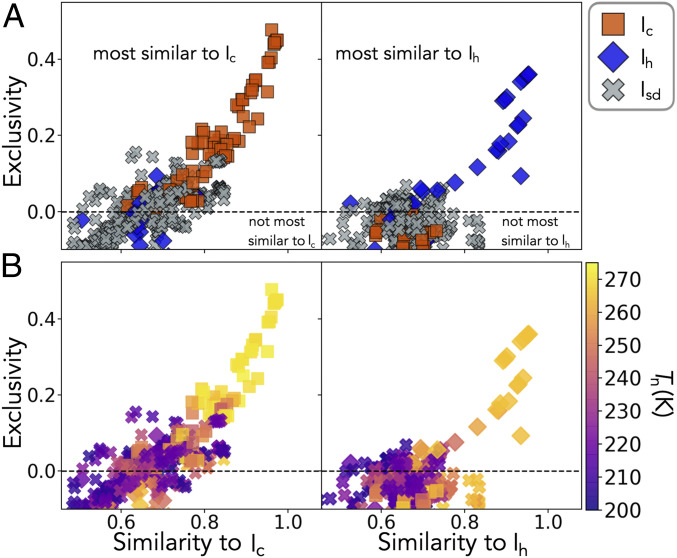
To get further insight into the connection between substrate structure and polytype selectivity, we look again at the full database of systems. Analyzing the water contact-layer structure on each substrate shows a strong connection between its similarity to an ice face and the polytype obtained. The similarity measurement is defined in and returns a value between zero and one for the match between 2D patterns. The contact layers were computed using the same simulation setup as described in Materials and Methods but run at a constant temperature of 285 K for 2 ns. The water contact-layer structure is extracted every 0.5 ps, giving independent snapshots that are used to extract the average structure. Fig. 4 shows the maximum similarity to Ic and Ih and the “exclusivity” of the structure to that polytype (equal to maximum similarity to polytype minus maximum similarity to a different polytype). Positive values of exclusivity correspond to templates that look most similar to the polytype, and negative values indicate templates that look more similar to a different polytype.
Fig. 4.
Resemblance of the water contact layer of systems to polytypes of ice. The similarity in the xy plane to each polytype is calculated (details are in SI Appendix). (Left) Maximum result obtained for similarity to Ic. (Right) Maximum result obtained for similarity to Ih. Points plotted against exclusivity, which is equal to the maximum similarity to the polytype minus the maximum similarity to a different polytype. (A) Points labeled as a polytype if it was obtained for 100% of simulations of that system. (B) The same data as in A but with the points colored by Tn.
From Fig. 4A, it is clear that both the water contact layer’s similarity to an ice face and its exclusivity to a polytype are related to polytype selectivity. A strong connection between this and nucleation ability can be seen in Fig. 4B. Physically, strong similarity and exclusivity can be understood as an effective geometric bias of the system toward forming a particular ice face. Stronger similarity of the water contact layer to an ice face increases the chances of ice clusters forming, which in turn, increases the chance a cluster reaches the size of the critical nucleus. This determines the systems nucleation ability/temperature. Polytype selectivity can be seen as a level of detail greater than nucleation ability alone, where the geometric bias is strong enough to ensure that only one polytype forms.
Similar trends are seen for Ic and Ih (Fig. 4, Left and Right, respectively). As the water contact layer template becomes less exclusively similar to an ice face of the respective polytype, Isd is obtained. This should not be confused for some global preference for the Isd faces [basal and (111) of Ih and Ic, respectively]. Isd is obtained for systems that still have a reasonably strong resemblance to unique Ic or Ih faces due to the introduction of stacking faults. It is known that ice forming homogeneously lacks any imposed crystal orientation, resulting in Isd with 50:50 randomly arranged hexagonal/cubic stacking (49–). It has also been shown that the homogeneous critical nucleus (at 230 K) with stacking faults has a lower free energy than that of pure Ih (). Thus, the promotion of ice without stacking faults requires a strong crystal orientation to be imposed. Bi et al. () achieved this by using a concave wedge to give a multidimensional structural match to the water that reduced the ability of stacking faults to enter. Here, we see that individual substrates can promote ice without stacking faults by imposing a strong orientation upon the water contact layer. Specifically, the water contact layer needs to 1) be similar to a face of the desired polytype (similarity measurement) and 2) not be similar to a face of a different polytype (exclusivity measurement). The requirement of exclusivity is in agreement with the idea that a substrate that does not promote the basal face can lead to ice without stacking disorder. (, 53–) As the quality of the template weakens (similarity and exclusivity drop), the water contact layer imposes a weaker orientation upon the crystal, resulting in the greater likelihood of stacking faults entering and thus, yielding the formation of Isd. This yields the intermixing of polytypes promoted and poorer nucleation ability that can be seen in Fig. 4. Furthermore, both the metastable Ic and the stable Ih show a very similar behavior in Fig. 4. This shows that for heterogeneous ice nucleation, it may not be the very small free energy difference between these two polytypes, and that of Isd, but instead the geometric biasing of the water contact-layer that determines both Tn and the ability of a polytype to form. Consequently, no significant difference in nucleation ability nor polytype selectivity is seen between substrates that promote Ih and those that promote Ic.
We note that when the water contact layer strongly resembles Isd [basal and (111) face of Ih and Ic, respectively], nucleation upon the Isd faces is also seen in the exact same manner. The systems have high Tn and result in ice with that crystal orientation. Although we do not focus on Isd in this study, we note that it could be possible to use the techniques presented here to design potent INAs for Isd or achieve “higher-order polytypes” with desired stacking sequences [e.g., the (hc)x polytype, which consists of perfectly alternating layers of cubic and hexagonal ice].
Weak Correlation between the Substrate and Water Contact Layer Template
Predicting the nucleation characteristics of substrates a priori is highly desirable and still not currently possible. Given our finding that the water contact layer’s similarity to ice is key, one might think the requirement is simply a high substrate lattice match with ice. Lattice match of substrates has been discussed widely since the discovery of the nucleation ability of AgI (). However, much recent work has shown lattice match alone is not enough to predict a substrates nucleation ability (5758–). Less work has investigated the connection to polytype selectivity, but a similar (if not stronger) requirement would be natural to infer. This apparent contradiction in the understanding of the water contact layer leads to an interesting question: What is the connection between the similarity of the substrate to ice and the similarity of the resulting water contact layer to ice?
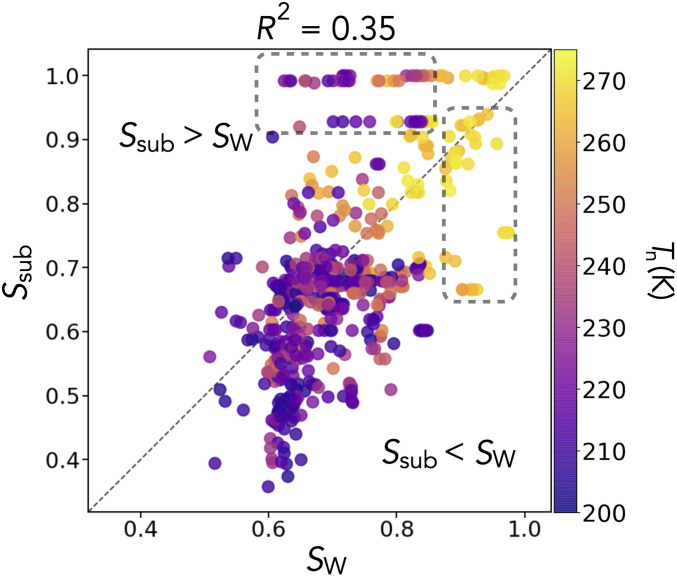
The connection between the similarity of the substrate to ice and the similarity of the resulting water contact layer to ice is reported in Fig. 5. The maximum similarity of water to any polytype is extracted, and the polytype is noted, which we call SW. The similarity of the substrate to this polytype is then extracted to give Ssub. We see that SW and Ssub do not correlate well, with an R2 value of only 0.35. As discussed earlier, the structure of the water contact layer determines much of a substrate’s nucleation ability and polytype selectivity. The substrate lattice match is thought to imply the structure of the water contact layer; however, we show here that it does not. It is therefore necessary to separate these two ideas in the understanding of heterogeneous ice nucleation. Substrates with a poor lattice match to ice can give water contact layers very similar to ice, yielding potent ice nucleation ability. Conversely, substrates with high lattice match can give water contact layers very dissimilar to ice, yielding poor ice nucleation ability. Therefore, for the systems studied here, the water contact layer structure is a better descriptor of ice nucleating ability than the substrate structure. Observing Fig. 5, the descriptive improvement this gives can be understood by comparing the regions (dashed outlines in Fig. 5) of large SW but low Ssub, where Tn is large, and of large Ssub but low SW, where Tn is small.
Fig. 5.
Substrate’s and water contact layer’s similarity to ice, colored by Tn. Maximum similarity of water to any polytype is extracted, and the polytype is noted, giving SW. The similarity of the substrate to this polytype is then extracted to give Ssub. The correlation between SW and Ssub is weak, with an R2 value of 0.35. Comparing the dashed outlined regions of large SW but low Ssub, where Tn is large, and large Ssub but low SW, where Tn is small, illustrates the difference in these metrics’ ability to describe Tn.
Discussion
Further Insight and Future Perspectives.
By direct simulation of heterogeneous ice nucleation, we have revealed the detailed interplay between ice I polytypism and heterogeneous ice nucleation. Our results explicitly show, for flat smooth substrates, that both the temperature at which nucleation is induced and the polytype promoted by a substrate is determined by the water contact layer’s resemblance to a face of ice. The two metrics introduced here, similarity and exclusivity, capture the geometric bias underlying this. In addition, the structure within the contact layer is shown to be more informative than the substrate lattice match. A liquid structure mechanism for polytype/morph selectivity has also been suggested for homogeneous nucleation of other systems such as hard spheres (, ), soft spheres (), carbon (), and molybdenum (). Thus, the insight gained here for heterogeneous nucleation could extend beyond ice.
The results of this study reinforce the point that future nucleation studies should take into account the possibility of Ih, Ic, and Isd, instead of just the thermodynamically stable Ih. Evidence of this is provided by the prevalence of all of the ice I polytypes seen here, combined with both the fact that the stable Ih and metastable Ic are achieved in the same manner and the surprising ease in which Ic is promoted. We therefore highlight the suggestion of prior work (), which formulated heterogeneous classical nucleation theory taking into account the polytype selectivity of the substrate. We will now place our results in a broader context and discuss their implications and links to experiment.
Connections to Experiment.
In this study, we propose that polytypism is prevalent at even the most mild supercooling (in initial ice nuclei). Our evidence is that 1) we see the formation of not only Isd but also, pristine Ic for temperatures up to ∼272.5 K on many systems; 2) promotion of Ic at this temperature is shown to be extremely reliable via many simulations on one of our most promising designs; and 3) analysis of the water contact layer shows the nature of the INA’s templating effect and not the temperature of the system is the determining factor for polytype selection.
However, this is in conflict with the view that ice polytypism is important only at strong supercooling. del Rosso et al. () and Komatsu et al. () found Ic to Ih transition temperatures of 215 and 250 K, respectively. The difference between these results leaves the relative stability of Ic unclear, but it appears to be more stable at strong supercooling. With regard to Isd, experimental studies have shown it is energetically unfavorable to have stacking disorder in ice, and above 240 K, it will eventually anneal to form pristine Ih (, 46–). Thus, Isd could be expected to be more prevalent at lower temperatures. Yet, as noted by Murray et al. (), while this is true for, for example, crystals at −80°C sampled from the tropical tropopause where 50% of crystals had the trigonal structure indicative of Isd, the trend is less clear for warmer temperatures. For instance, studies by Yamashita () showed for crystals grown at around −15°C, no trigonal crystals formed, whereas at −7°C, 69% were trigonal. Other experimental studies have also seen evidence of Isd for very mild supercooling (, ), yielding the conclusion that initial presence of cubic layers in ice could be relevant over a very wide range of temperatures ().
Our results support this conclusion and help resolve this debate by showing that in fact the promotion of any of the ice I polytypes is possible for even the most mild supercooling. Moreover, we see that unless a unique face of Ih is strongly templated in the nucleation event, then cubic layers of ice will be present in the initial ice nuclei. It therefore appears that both hexagonal and cubic layers of ice are ubiquitous in heterogeneous ice nucleation. Even as cubic layers anneal at such temperatures, their presence in the initial nuclei can affect the properties of the resulting macroscopic crystals (, ). Ice polytypism could therefore be more important than previously thought for many fields, a prime example being atmospheric science. Thus, weight is added to the claims of Ic’s potential importance in phenomena such as the topology of snowflakes (, ), cryopreservation (, ), and the high water vapor supersaturation of cirrus clouds () as well as its general existence in the atmosphere ().
Routes to Polymorphs/Types.
We aimed to understand if heterogeneous nucleation of pristine Ic could be a valid route to its formation and found much evidence indicating it is. A methodology to design substrates with desired polytype selectivity leads to the discovery of many promising designs that promote Ic. No dependence in a substrate’s nucleation capacity upon the polytype being promoted is observed, and the nucleation of pristine Ic is shown to have a high degree of adaptability and robustness to both substrate deformations and system size. This shows the small free energy difference between Ih, Ic, and that of Isd can be overcome via substrate design. Thus, we suggest that heterogeneous nucleation could be a valid route to the formation of pristine Ic.
Synthesizing in the laboratory one of the substrate designs proposed here, or discovering them in nature, yields the possibility of achieving pristine Ic from supercooled water. This possibility is further enhanced by the observation of Ic forming at its “most metastable temperature” (most mild supercooling), and the fact that many hydroxyl patterns were discovered (as this gives a great number of candidate materials). We note that experiments with the aim of achieving Ic should be carried out at strong supercooling where Ic is more stable. This will help avoid annealing to Ih after the initial nucleation. If a suitable material is discovered, utilizing, for example, the techniques of water vapor deposition could be used to control the growth of crystals to larger sizes, analogous to the widespread use of chemical vapor deposition to make, for example, laboratory-grown diamonds. Experiments should consider the front propagation speed of different ice faces, as anisotropy in ice crystal growth has been seen (, ), and a faster front propagation speed could encompass defects, resulting in stacking disorder. The effects of confinement on water can also be utilized. First, in, for example, the case of 2D confinement, two material surfaces could impose a stronger orientation upon the resulting crystal. Second, confinement can affect the relative stabilities of polytypes; for example, this was reported to result in Isd with high cubicity being observed in alumina pores (). With regard to candidate materials, the approximate structural-based guideline presented earlier can help their discovery. Interesting avenues would be groups of materials with hydroxylated surfaces, where examples of effective INAs are already known. These include the myriad of clays and minerals (33343536–), organic crystals [such as alcohols (), amino acids, and steroids (, )], and biological matter (4243–). The latter is particularly interesting as there exists the possibility of utilizing the technique of sequence-controlled polymerization to make biomaterials with desired hydroxyl group structures (, ). Furthermore, synthesis of the 2D designs of Fig. 3A could be achieved by designing self-assembled monolayers. A design with a hexamer chair-like configuration is shown in Fig. 3A. This templating could be mimicked via adsorption of molecules with such structures upon flat substrates. In addition, materials with a close lattice match to ice that possess the cubic structure could be promising, such as the cubic forms of AgI and CuI ().
Finally, the substrate design methodology presented here can easily be extended to the plethora of materials that show polymorphism and stacking disorder in materials science, ranging from pharmaceuticals to close-packed metals and alloys. As shown in Fig. 1, the key steps of the approach are to take unique faces from the desired polymorph/type, simulate nucleation of the liquid/gas form upon this, and generate new designs by pruning and/or the extraction of contact layers. This can be utilized to discover substrate designs for nucleating pristine polymorphs/types or even for desired levels of stacking faults to give higher-order polytypes with desired stacking sequences. This would enable the fine tuning of physiochemical properties (e.g., solubilities, mechanical, band gaps, dielectric properties) by giving access to the full range of possible structures (76–). This is highly desirable as stacking disorder can affect things such as the solubility of pharmaceuticals and even the band gap and dielectric constant of diamond (). Ritonavir is a well-known example of the former, a drug that has found use in treating HIV and was part of the World Health Organization’s “SOLIDARITY” global trial to treat COVID-19 (79–). For carbon, the metastable hexagonal polymorph, Lonsdaleite, has been calculated to have superior mechanical properties to diamond but is yet to be synthesized without stacking faults (, ). Systems that can nucleate desired crystal structures can be used to grow to macroscopic scales via, for example, vapor deposition. Moreover, the connection between polytype selectivity and nucleation ability seen in this study means that the substrate design methodology could instead be used to discover potent nucleating agents, even in situations where controlling the polymorph/type obtained is not required.
We provide additional material in SI Appendix about 1) the polytype distribution with Tn for the substrate database, 2) a selection of promising substrate designs to nucleate pristine Ic, 3) the large-scale simulation of the nucleation of Ic, and 4) the 2D similarity calculation methodology.
A selection of 15 substrates is provided that are promising in both their ability to nucleate Ic and their potential for discovery/synthesis. The coordinates are in a single “txt” file, which gives the OH-group (x, y, z) coordinates for each substrate (units are angstroms).
Materials and Methods
Molecular Dynamics Setup.
To model heterogeneous nucleation, water molecules are placed above a frozen slab of crystalline surface, periodic in (x, y). An example of this before and after nucleation can be seen in Fig. 1B. In total, 1,119 different substrate–water systems were used in this study. This database consists of the LJ systems from ref. ; graphitic and graphite oxide surfaces modeled in a manner similar to those in refs. and , respectively; and the OH-group patterns from ref. plus over 200 systems generated for this work using the methodology presented in Fig. 1C. The simulation boxes are ∼45 to 60 Å in (x, y); 4,000 to 6,000 water molecules are used giving layers of 35- to 60-Å thickness, thick enough to yield a region of water within the film in which the bulk water density is recovered. For the water–substrate interaction, various Stillinger–Weber or LJ (12/6) parameters are used, depending on the nature of the substrate.
All simulations are performed with the large-scale atomic/molecular massively parallel simulator (LAMMPS) code (); and sampled the constant number of particles, constant volume, and constant temperature (NVT) canonical ensemble, using chains of 10 Nosé–Hoover thermostats with a relaxation times of 0.5 ps; and integrated the equations of motion with a time step of 10 fs. Simulations are initially equilibrated for at least 50 ps with a time step of 5 fs, prior to the production run. To observe nucleation, cooling ramps are used following the procedures in, for example, refs. , , and , with the temperature reduced from 275 K at 1 K ns−1. For each system, five cooling ramps are performed, and Tn is extracted by the drop in the systems potential energy. Nucleation events were checked by hand, and there is no indication that any were homogeneous. The polytype formed upon nucleation is identified using the local q3 order parameter of Li et al. (), in combination with the CHILL+ algorithm of Nguyen and Molinero (). These are computed using the plugin for metadynamics 2 (PLUMED2) (, ) and the open visualization tool (OVITO) () software, respectively. Ice structures are labeled as Ih or Ic only if they are completely lacking the other polytype.
This study employed the coarse-grained mW model. This model has inherent limitations; for example, no distinction is made between acceptors and donors of hydrogen bonds, atomic-scale resolution is lost, and water dissociation is not accounted for. It also does not have charge, meaning the effects of surface charge on water in contact with substrates are not included. However, the mW model is an appropriate choice for our study for several reasons. First, it has been widely and successfully used in studying water, especially the nucleation of ice (, , , , , , , , 919293949495969798–). Second, it accurately describes important properties of water such as the density, structure, and melting temperature (). Third, it captures the small metastability of Ic compared with Ih (, ) as well as the thermodynamics of stacking faults. Both the calculated free energy cost of a growth fault in Ih and the cost to grow a pair of cubic layers have been shown to be in very close agreement with experiment, with comparative calculation and experimental values from 15.3±2.3 to 16.5±1.7J mol−1 and from 9.7±1.9 to 8.0J mol−1, respectively (, , ). Last, but not least, the low computational cost of the model—compared with atomistic models—allows for nucleation simulations to be performed on an extensive database of substrates, as is done here. Extending this study of polytype selection to atomistic models would be interesting, as it is foreseeable that effects such as the hydrogen ordering induced by a substrate could be important and potentially even increase the polytype selectivity. The effect of the faster kinetics of coarse-grained models could also then be investigated (we note that this could be small, as the faster kinetics of mW should be present for all polytypes; thus, the relative trends observed here should hold). However, capturing the energetics between polytypes is a fundamental requirement for the model, and we are not aware of any atomistic model that does this and is affordable for nucleation studies.
Similarity Calculations.
In this study, similarities between 2D images of the water contact layers (and also the substrates) and faces of ice (from the three ice I polytypes) are calculated. These structures are represented as 2D histograms on a fine grid with spacing 0.1 Å, upon which a rotationally symmetric normalized 2D Gaussian is placed at the position of each atom. Here, the general concepts of the similarity calculations are explained. More details are given in SI Appendix.
The similarity between an extracted, f, and reference, g, pattern was calculated as
The first term on the right-hand side determines whether the pattern
g is present in
f regardless of additional noise and whether
g is a weaker signal than
f (giving 0.5 if so), whereas the second term on the right-hand side determines whether
f is present in
g, regardless of additional noise and whether
f is a weaker signal than
g (giving 0.5 if so). By combining the two, one can determine if
f is the same as
g, as a value of one will be obtained only if
f is exactly
g, both in pattern and intensity [i.e.,
f(
x,
y) =
g(
x,
y)]. Effectively, this is a calculation of the similarity between two images, a topic of much work with numerous methods (). Here, this method is chosen for its simplicity, which maintains a strong physical connection and avoids obscuring interpretation.
Acknowledgements
We thank C. G. Salzmann, I. J. Ford, and B. Slater for stimulating discussions and suggestions. We are grateful for the use of the University College London Grace, Myriad, and Legion facilities and associated support services; the London Center for Nanotechnology Salviati and Centurion facilities and associated support services; the ARCHER UK National Supercomputing Service through the Materials Chemistry Consortium through Engineering & Physical Sciences Research Council (EPSRC; United Kingdom) Grant EP/L000202; and the UK Materials and Molecular Modeling Hub, which is partially funded by EPSRC Grants EP/P020194/1 and EP/T022213/1.
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data Availability
Input files to generate all of the trajectories, along with all data and code to generate the figures, and analysis code for the water contact-layer and substrate similarity calculations are openly available at the University of Cambridge Data Repository (Apollo; https://doi.org/10.17863/CAM.65175). All other data are included in the article and/or supporting information.
References
Y. P.
Handa, D. D.
Klug, E.
Whalley,
Difference in energy between cubic and hexagonal ice.
J. Chem. Phys.
84,
7009–
7010 (
1986).
Y. P.
Handa, D. D.
Klug, E.
Whalley,
Energies of the phases of ice at low temperature and pressure relative to ice Ih.
Can. J. Chem.
66,
919–
924 (
1988).
O.
Yamamuro, M.
Oguni, T.
Matsuo, H.
Suga,
Heat capacity and glass transition of pure and doped cubic ices.
J. Phys. Chem. Solid.
48,
935–
942 (
1987).
M.
Riikonen,
Halo observations provide evidence of airborne cubic ice in the Earth’s atmosphere.
Appl. Optic.
39,
6080–
6085 (
2000).
T.
Kobayashi, Y.
Furukawa, T.
Takahashi, H.
Uyeda,
Cubic structure models at the junctions in polycrystalline snow crystals.
J. Cryst. Growth
35,
262–
268 (
1976).
T.
Takahashi,
On the role of cubic structure in ice nucleation.
J. Cryst. Growth
59,
441–
449 (
1982).
J.
Goodman, O. B.
Toon, R. F.
Pueschel, K. G.
Snetsinger, S.
Verma,
Antarctic stratospheric ice crystals.
J. Geophys. Res. Atmos.
94,
16449–
16457 (
1989).
J. E.
Shilling,
Measurements of the vapor pressure of cubic ice and their implications for atmospheric ice clouds.
Geophys. Res. Lett.
33,
1–
5 (
2006).
H.
Konig,
Eine kubische eismodifikation.
Z. Kristallogr.
105,
279–
286 (
1943).
W. F.
Kuhs, C.
Sippel, A.
Falenty, T. C.
Hansen,
Extent and relevance of stacking disorder in “ice Ic.”Proc. Natl. Acad. Sci. U.S.A.
109,
21259–
21264 (
2012).
K.
Thürmer, S.
Nie,
Formation of hexagonal and cubic ice during low-temperature growth.
Proc. Natl. Acad. Sci. U.S.A.
110,
11757–
11762 (
2013).
K.
Morishige, H.
Yasunaga, H.
Uematsu,
Stability of cubic ice in mesopores.
J. Phys. Chem. C
113,
3056–
3061 (
2009).
T. L.
Malkin,
Stacking disorder in ice I.
Phys. Chem. Chem. Phys.
17,
60–
76 (
2015).
L.
del Rosso,
Cubic ice Ic without stacking defects obtained from ice XVII.
Nat. Mater.
19,
663–
668 (
2020).
K.
Komatsu,
Ice Ic without stacking disorder by evacuating hydrogen from hydrogen hydrate.
Nat. Commun.
11,
464 (
2020).
C. G.
Salzmann, B. J.
Murray,
Ice goes fully cubic.
Nat. Mater.
19,
586–
587 (
2020).
Y.
Bi, B.
Cao, T.
Li,
Enhanced heterogeneous ice nucleation by special surface geometry.
Nat. Commun.
8,
15372 (
2017).
J.
Russo, F.
Romano, H.
Tanaka,
New metastable form of ice and its role in the homogeneous crystallization of water.
Nat. Mater.
13,
733–
739 (
2014).
P. K.
Nandi, C. J.
Burnham, N. J.
English,
Electro-nucleation of water nano-droplets in No Man’s Land to fault-free ice Ic.
Phys. Chem. Chem. Phys.
20,
8042–
8053 (
2018).
C. A.
Mitchell, L.
Yu, M. D.
Ward,
Selective nucleation and discovery of organic polymorphs through epitaxy with single crystal substrates.
J. Am. Chem. Soc.
123,
10830–
10839 (
2001).
J. F.
Kang, J.
Zaccaro, A.
Ulman, A.
Myerson,
Nucleation and growth of Glycine crystals on self-assembled monolayers on gold.
Langmuir
16,
3791–
3796 (
2000).
A. Y.
Lee, A.
Ulman, A. S.
Myerson,
Crystallization of amino acids on self-assembled monolayers of rigid thiols on gold.
Langmuir
18,
5886–
5898 (
2002).
C. P.
Price, A. L.
Grzesiak, A. J.
Matzger,
Crystalline polymorph selection and discovery with polymer heteronuclei.
J. Am. Chem. Soc.
127,
5512–
5517 (
2005).
V.
López-Mejías, J. W.
Kampf, A. J.
Matzger,
Nonamorphism in flufenamic acid and a new record for a polymorphic compound with solved structures.
J. Am. Chem. Soc.
134,
9872–
9875 (
2012).
H. I. T.
Hauge,
Hexagonal silicon realized.
Nano Lett.
15,
5855–
5860 (
2015).
B. J.
Murray,
Trigonal ice crystals in Earth’s atmosphere.
Bull. Am. Meteorol. Soc.
96,
1519–
1531 (
2014).
P.
Behr, A.
Terziyski, R.
Zellner,
Acetone adsorption on ice surfaces in the temperature range T = 190-220 K: Evidence for aging effects due to crystallographic changes of the adsorption sites.
J. Phys. Chem. A
110,
8098–
8107 (
2006).
J.
Dubochet,
Cryo-electron microscopy of vitrified specimens.
Q. Rev. Biophys.
21,
129–
228 (
1988).
P.
Mehl, P.
Boutron,
Cryoprotection of red blood cells by 1,3-butanediol and 2,3-butanediol.
Cryobiology
25,
44–
54 (
1988).
V.
Molinero, E. B.
Moore,
Water modeled as an intermediate element between carbon and silicon.
J. Phys. Chem. B
113,
4008–
4016 (
2009).
C.
Marcolli, B.
Nagare, A.
Welti, U.
Lohmann,
Ice nucleation efficiency of AgI: Review and new insights.
Atmos. Chem. Phys.
16,
8915–
8937 (
2016).
J. D.
Atkinson,
The importance of feldspar for ice nucleation by mineral dust in mixed-phase clouds.
Nature
498,
355 (
2013).
A.
Harrison,
Not all feldspars are equal: A survey of ice nucleating properties across the feldspar group of minerals.
Atmos. Chem. Phys.
16,
10927–
10940 (
2016).
A.
Kiselev,
Active sites in heterogeneous ice nucleation—the example of K-rich feldspars.
Science
355,
367–
371 (
2017).
G. C.
Sosso, G. A.
Tribello, A.
Zen, P.
Pedevilla, A.
Michaelides,
Ice formation on kaolinite: Insights from molecular dynamics simulations.
J. Chem. Phys.
145,
211927 (
2016).
G. C.
Sosso, T.
Li, D.
Donadio, G. A.
Tribello, A.
Michaelides,
Microscopic mechanism and kinetics of ice formation at complex interfaces: Zooming in on kaolinite.
J. Phys. Chem. Lett.
7,
2350–
2355 (
2016).
X. L.
Hu, A.
Michaelides,
Water on the hydroxylated (001) surface of kaolinite: From monomer adsorption to a flat 2D wetting layer.
Surf. Sci.
602,
960–
974 (
2008).
E.
Ochshorn, W.
Cantrell,
Towards understanding ice nucleation by long chain alcohols.
J. Chem. Phys.
124,
54714 (
2006).
N.
Fukuta, B. J.
Mason,
Epitaxial growth of ice on organic crystals.
J. Phys. Chem. Solid.
24,
715–
718 (
1963).
N.
Fukuta,
Experimental studies of organic ice nuclei.
J. Atmos. Sci.
23,
191–
196 (
1966).
L. R.
Maki, E. L.
Galyan, M. M.
Chang-Chien, D. R.
Caldwell,
Ice nucleation induced by pseudomonas syringae.
Appl. Microbiol.
28,
456–
459 (
1974).
J.
Lindemann, G. J.
Warren, T. V.
Suslow,
Ice-nucleating bacteria.
Science
231,
536 (
1986).
R.
Pandey,
Ice-nucleating bacteria control the order and dynamics of interfacial water.
Sci. Adv.
2,
e1501630 (
2016).
B. G.
Pummer, H.
Bauer, J.
Bernardi, S.
Bleicher, H.
Grothe,
Suspendable macromolecules are responsible for ice nucleation activity of birch and conifer pollen.
Atmos. Chem. Phys.
12,
2541–
2550 (
2012).
W. F.
Kuhs, G.
Genov, D. K.
Staykova, T.
Hansen,
Ice perfection and onset of anomalous preservation of gas hydrates.
Phys. Chem. Chem. Phys.
6,
4917–
4920 (
2004).
B. J.
Murray, A. K.
Bertram,
Formation and stability of cubic ice in water droplets.
Phys. Chem. Chem. Phys.
8,
186–
192 (
2006).
T. C.
Hansen, M. M.
Koza, P.
Lindner, W. F.
Kuhs,
Formation and annealing of cubic ice. II. Kinetic study.
J. Phys. Condens. Matter
20,
285105 (
2008).
T. L.
Malkin, B. J.
Murray, A. V.
Brukhno, J.
Anwar, C. G.
Salzmann,
Structure of ice crystallized from supercooled water.
Proc. Natl. Acad. Sci. U.S.A.
109,
1041–
1045 (
2012).
E. B.
Moore, V.
Molinero,
Is it cubic? Ice crystallization from deeply supercooled water.
Phys. Chem. Chem. Phys.
13,
20008 (
2011).
A.
Haji-Akbari, P. G.
Debenedetti,
Direct calculation of ice homogeneous nucleation rate for a molecular model of water.
Proc. Natl. Acad. Sci. U.S.A.
112,
10582–
10588 (
2015).
L.
Lupi,
Role of stacking disorder in ice nucleation.
Nature
551,
218–
222 (
2017).
B.
Cao, E.
Xu, T.
Li,
Anomalous stability of two-dimensional ice confined in hydrophobic nanopores.
ACS Nano
13,
4712–
4719 (
2019).
M.
Fitzner, G. C.
Sosso, S. J.
Cox, A.
Michaelides,
The many faces of heterogeneous ice nucleation: Interplay between surface morphology and hydrophobicity.
J. Am. Chem. Soc.
137,
13658–
13669 (
2015).
S. J.
Cox, Z.
Raza, S. M.
Kathmann, B.
Slater, A.
Michaelides,
The microscopic features of heterogeneous ice nucleation may affect the macroscopic morphology of atmospheric ice crystals.
Faraday Discuss
167,
389–
403 (
2013).
D.
Turnbull, B.
Vonnegut,
Nucleation catalysis.
Ind. Eng. Chem.
44,
1292–
1298 (
1952).
G. C.
Sosso,
Crystal nucleation in liquids: Open questions and future challenges in molecular dynamics simulations.
Chem. Rev.
116,
7078–
7116 (
2016).
P.
Pedevilla, M.
Fitzner, A.
Michaelides,
What makes a good descriptor for heterogeneous ice nucleation on OH-patterned surfaces.
Phys. Rev. B
96,
115441 (
2017).
P.
Pedevilla, S. J.
Cox, B.
Slater, A.
Michaelides,
Can ice-like structures form on non-ice-like substrates? The example of the K-feldspar microcline.
J. Phys. Chem. C
120,
6704–
6713 (
2016).
M.
Fitzner, P.
Pedevilla, A.
Michaelides,
Predicting heterogeneous ice nucleation with a data-driven approach.
Nat. Commun.
11,
4777 (
2020).
T.
Kawasaki, H.
Tanaka,
Formation of a crystal nucleus from liquid.
Proc. Natl. Acad. Sci. U.S.A.
107,
14036–
14041 (
2010).
J.
Russo, H.
Tanaka,
The microscopic pathway to crystallization in supercooled liquids.
Sci. Rep.
2,
505 (
2012).
J.
Russo, H.
Tanaka,
Selection mechanism of polymorphs in the crystal nucleation of the Gaussian core model.
Soft Matter
8,
4206–
4215 (
2012).
L. M.
Ghiringhelli, C.
Valeriani, E. J.
Meijer, D.
Frenkel,
Local structure of liquid carbon controls diamond nucleation.
Phys. Rev. Lett.
99,
55702 (
2007).
S.
Menon, G.
Díaz Leines, R.
Drautz, J.
Rogal,
Role of pre-ordered liquid in the selection mechanism of crystal polymorphs during nucleation.
J. Chem. Phys.
153,
104508 (
2020).
M.
Fitzner, G. C.
Sosso, F.
Pietrucci, S.
Pipolo, A.
Michaelides,
Pre-critical fluctuations and what they disclose about heterogeneous crystal nucleation.
Nat. Commun.
8,
2257 (
2017).
A.
Yamashita,
On the trigonal growth of ice crystals.
J. Meteorol. Soc. Japan. Ser. II
51,
307–
317 (
1973).
A.
Yamashita,
Uncommon ice crystals observed in a large cold room.
J. Meteorol. Soc. Japan. Ser. II
47,
57–
58 (
1969).
K. G.
Libbrecht, H. M.
Arnold,
Aerodynamic stability and the growth of triangular snow crystals.
arXiv [Preprint] (2009) https://arxiv.org/abs/0911.4267 (Accessed 8 December 2020).
D.
Rozmanov, P. G.
Kusalik,
Anisotropy in the crystal growth of hexagonal ice, I(h).
J. Chem. Phys.
137,
94702 (
2012).
S.
Choi, E.
Jang, J. S.
Kim,
In-layer stacking competition during ice growth.
J. Chem. Phys.
140,
14701 (
2014).
Y.
Suzuki,
Homogeneous nucleation of predominantly cubic ice confined in nanoporous alumina.
Nano Lett.
15,
1987–
1992 (
2015).
J. F.
Lutz,
Sequence-controlled polymerizations: The next holy grail in polymer science?
Polym. Chem.
1,
55–
62 (
2010).
M. J.
Austin, A. M.
Rosales,
Tunable biomaterials from synthetic, sequence-controlled polymers.
Biomater. Sci.
7,
490–
505 (
2019).
R. L.
Smith, M.
Vickers, M.
Rosillo-Lopez, C. G.
Salzmann,
Stacking disorder by design: Factors governing the polytypism of silver iodide upon precipitation and formation from the superionic phase.
Cryst. Growth Des.
19,
2131–
2138 (
2019).
S. P.
Gao,
Band gaps and dielectric functions of cubic and hexagonal diamond polytypes calculated by many-body perturbation theory.
Phys. status solidi
252,
235–
242 (
2015).
Z.
Pan, H.
Sun, Y.
Zhang, C.
Chen,
Harder than diamond: Superior indentation strength of wurtzite BN and lonsdaleite.
Phys. Rev. Lett.
102,
55503 (
2009).
L.
Qingkun, S.
Yi, L.
Zhiyuan, Z.
Yu,
Lonsdaleite—a material stronger and stiffer than diamond.
Scr. Mater.
65,
229–
232 (
2011).
J.
Bauer,
Ritonavir: An extraordinary example of conformational polymorphism.
Pharm. Res.
18,
859–
866 (
2001).
S. L.
Morissette, S.
Soukasene, D.
Levinson, M. J.
Cima, Ö.
Almarsson,
Elucidation of crystal form diversity of the HIV protease inhibitor ritonavir by high-throughput crystallization.
Proc. Natl. Acad. Sci. U.S.A.
100,
2180–
2184 (
2003).
B.
Cao,
A trial of lopinavir–ritonavir in adults hospitalized with severe covid-19.
N. Engl. J. Med.
382,
787–
1799 (
2020).
S. J.
Cox, S. M.
Kathmann, B.
Slater, A.
Michaelides,
Molecular simulations of heterogeneous ice nucleation. II. Peeling back the layers.
J. Chem. Phys.
142,
184705 (
2015).
L.
Lupi, V.
Molinero,
Does hydrophilicity of carbon particles improve their ice nucleation ability?
J. Phys. Chem. A
118,
7330–
7337 (
2014).
S.
Plimpton,
Fast parallel algorithms for short-range molecular dynamics.
J. Comput. Phys.
117,
1–
19 (
1995).
L.
Lupi, A.
Hudait, V.
Molinero,
Heterogeneous nucleation of ice on carbon surfaces.
J. Am. Chem. Soc.
136,
3156–
3164 (
2014).
T.
Li, D.
Donadio, G.
Russo, G.
Galli,
Homogeneous ice nucleation from supercooled water.
Phys. Chem. Chem. Phys.
13,
19807–
19813 (
2011).
A. H.
Nguyen, V.
Molinero,
Identification of clathrate hydrates, hexagonal ice, cubic ice, and liquid water in simulations: The CHILL+ algorithm.
J. Phys. Chem. B
119,
9369–
9376 (
2015).
M.
Bonomi,
PLUMED: A portable plugin for free-energy calculations with molecular dynamics.
Comput. Phys. Commun.
180,
1961–
1972 (
2009).
G. A.
Tribello, M.
Bonomi, D.
Branduardi, C.
Camilloni, G.
Bussi,
PLUMED 2: New feathers for an old bird.
Comput. Phys. Commun.
185,
604–
613 (
2014).
A.
Stukowski,
Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool.
Model. Simulat. Mater. Sci. Eng.
18,
15012 (
2009).
E. B.
Moore, E.
de la Llave, K.
Welke, D. A.
Scherlis, V.
Molinero,
Freezing, melting and structure of ice in a hydrophilic nanopore.
Phys. Chem. Chem. Phys.
12,
4124–
4134 (
2010).
A.
Hudait, S.
Qiu, L.
Lupi, V.
Molinero,
Free energy contributions and structural characterization of stacking disordered ices.
Phys. Chem. Chem. Phys.
18,
9544–
9553 (
2016).
J. R.
Espinosa, E.
Sanz, C.
Valeriani, C.
Vega,
Homogeneous ice nucleation evaluated for several water models.
J. Chem. Phys.
141,
18C529 (
2014).
T.
Li, D.
Donadio, G.
Galli,
Ice nucleation at the nanoscale probes no man’s land of water.
Nat. Commun.
4,
1887 (
2013).
Y.
Bi, R.
Cabriolu, T.
Li,
Heterogeneous ice nucleation controlled by the coupling of surface crystallinity and surface hydrophilicity.
J. Phys. Chem. C
120,
1507–
1514 (
2016).
R.
Cabriolu, T.
Li,
Ice nucleation on carbon surface supports the classical theory for heterogeneous nucleation.
Phys. Rev. E
91,
52402 (
2015).
S. J.
Cox, S. M.
Kathmann, B.
Slater, A.
Michaelides,
Molecular simulations of heterogeneous ice nucleation. I. Controlling ice nucleation through surface hydrophilicity.
J. Chem. Phys.
142,
184704 (
2015).
A.
Haji-Akbari, R. S.
DeFever, S.
Sarupria, P. G.
Debenedetti,
Suppression of sub-surface freezing in free-standing thin films of a coarse-grained model of water.
Phys. Chem. Chem. Phys.
16,
25916–
25927 (
2014).
M. M.
Gianetti, A.
Haji-Akbari, M.
Paula Longinotti, P. G.
Debenedetti,
Computational investigation of structure, dynamics and nucleation kinetics of a family of modified Stillinger–Weber model fluids in bulk and free-standing thin films.
Phys. Chem. Chem. Phys.
18,
4102–
4111 (
2016).
S.
Hussain, A.
Haji-Akbari,
The role of interfacial synergy and structural modulation in contact freezing in water.
arXiv [Preprint] (2020) https://arxiv.org/abs/2009.02395 (Accessed 8 December 2020).
D.
Quigley,
Communication: Thermodynamics of stacking disorder in ice nuclei.
J. Chem. Phys.
141,
121101 (
2014).
T.
Hondoh, T.
Itoh, S.
Amakai, K.
Goto, A.
Higashi,
Formation and annihilation of stacking faults in pure ice.
J. Phys. Chem.
87,
4040–
4044 (
1983).
H. B.
Mitchell,
Image Similarity Measures BT—Image Fusion: Theories, Techniques and Applications (
Springer,
Berlin, Germany,
2010), pp.
167–
185.