Robust identification of investor beliefs

Xiaohong Chen, Lars Peter Hansen, Peter G. Hansen

Contributed by Lars Peter Hansen, October 26, 2020 (sent for review September 24, 2020; reviewed by Anmol Bhandari and Monika Piazzesi)

Author contributions: X.C., L.P.H., and P.G.H. designed research and wrote the paper.

Reviewers: A.B., University of Minnesota; and M.P., Stanford University.

¹X.C., L.P.H., and P.G.H. contributed equally to this work.

https://doi.org/10.1073/pnas.2019910117, Volume: 117, Issue: 52, Pages: 1-11

Article Type: research-article Article History

Publisher: National Academy of Sciences

- Facebook
- Twitter
- Linkedin
- Whatsapp
Altmetric

Table of Contents

Literature Review.
Outline of the Paper.
1. Asset Pricing with Distorted Beliefs
2. Data Generation and Probability Divergence
3. Moment Bounds
4. Illustration
5. Bounding Other Probabilities
6. Conclusions
Supplementary Material
Data Availability.

Abstract

Prices in asset markets reflect a combination of investor beliefs and their risk preferences. Researchers, as well as policymakers, look to asset market data as a barometer of public beliefs. Such data are informative because investors must be compensated for exposure to macroeconomic shocks, and thus beliefs about future macroeconomic performance are encoded in asset prices. This paper develops a method informed by data and models to recover information about investor beliefs. Our approach uses information embedded in forward-looking asset prices in conjunction with asset pricing models. We entertain families of potential belief distortions bounded by a statistical measure of divergence. Additionally, our method allows for the direct use of sparse survey evidence to make these bounds more informative.

This paper develops a method informed by data and models to recover information about investor beliefs. Our approach uses information embedded in forward-looking asset prices in conjunction with asset pricing models. We step back from presuming rational expectations and entertain potential belief distortions bounded by a statistical measure of discrepancy. Additionally, our method allows for the direct use of sparse survey evidence to make these bounds more informative. Within our framework, market-implied beliefs may differ from those implied by rational expectations due to behavioral/psychological biases of investors, ambiguity aversion, or omitted permanent components to valuation. Formally, we represent evidence about investor beliefs using a nonlinear expectation function deduced using model-implied moment conditions and bounds on statistical divergence. We illustrate our method with a prototypical example from macrofinance using asset market data to infer belief restrictions for macroeconomic growth rates.

Keywords

subjective beliefs, asset pricing, intertemporal divergence, bounded rationality, large deviation theory

License: CC BY

Chen,Hansen,and Hansen: Robust identification of investor beliefs

Prices in asset markets reflect a combination of investor beliefs and their risk preferences. Researchers, as well as policymakers, look to asset market data as a barometer of public beliefs. Derivative claims prices potentially enrich what we can infer about conditional probability distributions of future events, but events of interest often entail components of macroeconomic uncertainty for which there will be a paucity of information along some dimensions. Moreover, since a central tenet of asset pricing is that investors must be compensated for exposure to macroeconomic shocks that are not diversifiable, beliefs about future macroeconomic performance are of paramount importance to understanding asset prices.

To disentangle the contributions of risk aversion from beliefs, many empirical approaches in the last few decades have focused on models of investor preferences by assuming rational expectations. Using the implied moment conditions of the investor’s portfolio choice problem in conjunction with this restriction gives a directly applicable and tractable approach for estimating and testing alternative model specifications. This approach, however, often leads to risk prices in some time periods that are attributed to an arguably extreme level of investor risk aversion or a rejection of the model. Risk aversion and belief formulation are intertwined. Rational expectation as a model of belief formation is meant to be a simplifying approximation. It can serve as an elegant and powerful modeling choice when appropriate. In a complex environment, however, it can be challenging to make statistical inferences pertinent to forward-looking decision making. In such settings, we find the presumption that model-dwelling investors and entrepreneurs know the true data-generating process to be tenuous and worthy of relaxation. We are not alone in this view.

Some researchers have explored mechanisms that could account for this evidence via a different channel, namely beliefs which differ from rational expectations. It is sometimes argued, but typically not justified formally, that these alternatives are small departures from rational expectations. These “belief distortions” relative to rational expectations alternatively could reflect the lack of investor confidence about the assignment of probabilities to future events. This has been modeled and captured formally as ambiguity aversion or concerns about model misspecification.

This paper proposes a formal methodology for analyzing models that imply conditional moment restrictions where the restrictions are presumed to hold under a distorted probability measure. It extends a previous econometrics literature that represents the statistical implications of asset pricing implications as conditional moment restrictions under rational expectations. Rational expectations on the part of individuals or enterprises can be motivated by a law of large numbers approximation used to pin down the beliefs of these economic agents “inside the model.” Once we relax the rational expectations, there are typically many choices of investor beliefs that satisfy the conditional moment restrictions. Rather than imposing a specific alternative to rational expectations, we restrict the family of investor probabilities to satisfy discrepancy bounds, which gives us a way of relaxing the rational expectations hypothesis based on pushing back from a law of large numbers approximation. We then use the conditional moment restrictions along with statistical discrepancy bounds, to characterize families of probabilities that satisfy the conditional moment restrictions.

Our approach provides a version of “bounded rationality” when assessing empirical evidence. Not only are the bounds we deduce of direct interest; they also can be used as diagnostics for specific models of belief distortions. Additionally, we show how to include survey data on subjective beliefs. Such data are typically sparse and not sufficient to pin down full probabilistic characterizations of beliefs. Given these data limitations, we bound probabilities even when certain features of the data may be known through direct evidence.

A common way to represent a probability distribution of a random vector is through how it assigns expectations to functions of that random vector. Since we have multiple probability distributions in play, we represent our bounds by building what is called a “nonlinear expectation” that minimizes expectations over members of the family of probability distortions that we identify. This gives us a formal way to characterize properties of probability distributions that are consistent with model-implied conditional moment restrictions. The choice of minimization is essentially a normalization as we bound expectations of functions of observable variables as well as the negative of such functions. Given the flexibility in our choice of what functions of observables we use when forming expectation bounds, our analysis provides a rich characterization of implications for the belief distortions.

While we use asset pricing applications for motivation, our analysis is more generally applicable to economic models with forward-looking agents. These agents may be groups of individuals making investment or portfolio choices when facing production or financial opportunities that are exposed to uncertainty in different ways. Alternatively, they may be forward-looking enterprises, making decisions today that have important consequences for the future.

In summary, our methodology gives a way to extract information on investor beliefs from asset market and survey data pertinent for both external analysts and policymakers who are looking for evidence to gauge private sector sentiments. In addition, our computations provide revealing diagnostics for model builders that embrace specific formulations of belief distortions as is common in the behavioral economics and finance literatures.

Literature Review.

There is a long intellectual history exploring the impact of expectations on investment decisions. As was well appreciated by economists such as in refs. (1 2–3), investment decisions are in part based on people’s views of the future. Alternative approaches for modeling expectations of economic actors were suggested including static expectations, ref. 4’s extrapolative expectations, ref. 5’s adaptive expectations, or appeals to data on beliefs; but these approaches leave open how to proceed when using dynamic economic models to assess hypothetical policy interventions. A productive approach to this modeling challenge has been to add the hypothesis of rational expectations. Motivated by long histories of data, this hypothesis pins down beliefs by equating the expectations of agents inside the model to those implied by the data-generating distribution. This approach to completing the specification of a stochastic equilibrium model was initiated by ref. 6 and developed fully in ref. 7.

Recently there has been a renewed interest in alternative belief distortions within the asset pricing literature. See, for example, refs. 8 9 10 11–12. Relatedly, since survey evidence on investor beliefs is typically rather sparse and not able to produce entire predictive distributions, refs. 13 and 14 fitted time series models to the observed beliefs that can be distinct from the actual data evolution. Our approach is different from these literatures, but complementary to them. We focus on the construction of the implied bounds for expectations for functions of the stochastic process of interest that could provide empirical targets of tests of parametric models of subjective beliefs fitted to time series.

There is similarity in motivation and overlaps in the methods we use to the study of robust optimization (see, for instance, refs. 15 and 16) and robust Markov chain modeling (see, for instance, ref. 17). But our is aim different. While the robust optimization research features decision makers that confront multiple probabilities, our perspective is that of analyst seeking information about the beliefs of economic decision makers from observed financial market data or survey data through the lens of a dynamic economic model.

Refs. 18 and 19 describe and implement econometric methods for confronting conditioning information under correct model specification under rational expectations, within a generalized method of moments framework. Refs. 20 and 21 give extensions of the measure of model misspecification proposed by ref. 22 to accommodate conditioning information. Similarly, the models we consider are misspecified under rational expectations. This misspecification is induced as it is in precursors (23, 24) by investor belief distortions (these two papers abstract from the role of conditioning information). Our innovation is to propose and justify a dynamic formulation with belief uncertainty that 1) accommodates conditioning and 2) uses the recursive structure of multiperiod likelihoods to characterize families of beliefs that are consistent with alternative divergence thresholds.

Outline of the Paper.

1. Asset Pricing with Distorted Beliefs introduces the framework we use for moment restrictions implied by an asset pricing model. 2. Data Generation and Probability Divergence specifies the probabilistic environment that underlies our computations and gives a dynamic version of the divergence with a built-in recursive structure. 3. Moment Bounds presents and justifies our recursive formulation of the functional equation used to compute the bounds along with some special cases that are of particular interest. This section provides a more complete characterization of the solution for the familiar relative entropy divergence and discusses the relation to results from large deviation theory. Finally, 3. Moment Bounds characterizes a nonlinear expectation as a way to represent the bounds on the subjective probabilities. 4. Illustration presents an empirical illustration of our methodology. 5. Bounding Other Probabilities shows how to apply our approach to extract information about the one-period, risk neutral measure and the long-term counterpart without assuming the existence of data on a complete set of Arrow–Debreu securities. Both of these probability measures are of interest in their own right. 6. Conclusions concludes.

1. Asset Pricing with Distorted Beliefs

In standard economic applications, moment conditions are justified via an assumption of rational expectations. This assumption equates population expectations with those used by economic agents inside the model. These expectations are therefore presumed to be revealed by the law of large numbers applied to time series data.

Let $(Ω, G, P)$ denote the underlying probability space and $I \subset G$ represent information available to investors. The original moment equations under rational expectations are of the form

E [f (X, θ) ∣ I] = 0,

[1]

where the function,

f

, captures the parameter dependence,

θ

, of either the payoff or the stochastic discount factor along with a random vector,

X

, of variables observed by the econometrician and used to construct the payoffs, prices, and the stochastic discount factor.

A typical asset pricing example is as follows: Let $R$ denote an $n$ -dimensional vector of gross returns corresponding to payoffs on financial or physical assets over some investment horizon, let $S$ denote the corresponding stochastic discount factor for this horizon, and let $I$ denote the investor information set. The stochastic nature of the stochastic discount factor captures the market compensations for exposure to uncertainty.

The underlying asset pricing equation is

E [S R - 1_{n} | I] = 0,

where

1_{n}

is an

n

-dimensional vector of ones. Both the stochastic discount factor and the return vector

R

may depend on unknown parameters, giving rise to . The vector of returns can be parameter dependent when the investment is in a physical asset with an unobserved return. While we posed this as an asset-pricing relation, restrictions of the same form can be derived from investment or asset demand equations with potentially differential exposures to uncertainty. Even in such models, there is a counterpart to stochastic discount factors that are perhaps different across agent types. More generally, these equations feature the forward-looking behavior of individuals or enterprises as they depend on the perceptions of the future.

A. Market Beliefs.

We allow for the beliefs that are revealed by the market to differ from the rational expectations beliefs implied by (infinite) histories of data. We represent what we call “market beliefs” by introducing a positive random variable $N$ with a unit conditional expectation. Thus, we consider moment restrictions of the form

E [N f (X, θ) ∣ I] = 0 .

[2]

The random variable

N

provides a flexible change in the probability measure and is sometimes referred to as a Radon–Nikodym derivative or a likelihood ratio. The dependence of

N

on random variables not in the information captured by

I

defines a relative density that informs how rational expectations are altered by market beliefs.

By using $N$ to represent a potential market belief, we require that any event that depends on the realization of $X$ and has conditional probability measure zero under the rational expectation distribution will continue to have conditional probability zero under this change in distribution. We will, however, sometimes allow for $N$ to be zero on events that have positive conditional probability under the original measure, at least as a possible limiting case. Such events would be a complete surprise to market participants.

The introduction of $N$ into the analysis is seemingly an innocuous change in formulating the observable implications. But it has rather dramatic consequences for econometric analyses. Specifically, we consider estimation environments in which a researcher uses data only on a limited set of asset returns. With observations on a complete set of asset returns and a prespecified stochastic discount factor, we could identify uniquely the belief distortion, $N$ . Given our interest in macroeconomic risk compensation, we presume a more modest set of data is available to use as empirical inputs. As a consequence, even with a known stochastic discount factor, there may be an extensive family of beliefs that is consistent with the underlying pricing restrictions expressed as conditional moments. To elaborate, we suppose that Eq. 1 may not have solutions for any $θ$ under rational expectations. Once we relax rational expectations by introducing $N$ , Eq. 2 will in general be satisfied for an infinite-dimensional set of possible $N$ s for each value of $θ$ . Thus, the parameter vector $θ$ and the corresponding $N$ fail to be point identified in a rather spectacular way. The set of $N$ s associated with a given value of $θ$ will be of particular interest to us.

Given our interest in the set of $N$ s, we are led to deduce implied bounds on moments. Consider, for instance, the relation

E (N S R ∣ I) - 1_{n} = 0 .

[3]

Then the proportional risk premia from the perspective of the altered probability are

\log E (N R ∣ I) + 1_{n} \log E (N S ∣ I) .

The first term is the logarithm altered expectation of

R

and the second term is the negative of the logarithm of the risk-free return. Our methods allow us to compare the rational expectations version of the risk compensations to bounds on these proportional compensations as implied by market data.

Two classes of asset pricing models that have received considerable attention provide motivation for our analysis. One class allows for subjective beliefs to differ from those implied by rational expectations because of “market psychology.” Alternative models of expectations from behavioral finance imply alternative specifications of $N$ . Another class includes models with investors that are ambiguity averse. Associated with many such models are belief specifications that emerge as altered probabilities encoded in asset prices. These distortions reflect some form of caution, depending on modeling details. While both literatures derive counterparts to $N$ , our methods put very modest structure on the beliefs beyond potentially small statistical departures from rational expectations and can provide revealing diagnostics for assessing models that impose specific distortions in expectations.

Since the form of our pricing equation applies to investment or asset demand equations, there is a direct extension of our analysis to the case in which there are distinct classes of economic agents with potentially different subjective beliefs or concerns about ambiguity aversion.

B. Incorporating Survey Evidence.

When constructing our moment conditions, we could also include direct data on investor expectations to help inform the direction and magnitude of the subjective belief distortion from historical evidence. This would entail augmenting the moment conditions used to constrain beliefs to include the variable being forecasted minus the observed forecast all scaled by $N$ .

Suppose we have data $D$ on beliefs that reflect subjective expectations of $\tilde{X}$ . These data could include survey responses or analyst forecasts. We may include this in our analysis by imposing the conditional moment condition:

E (N \tilde{X} ∣ I) = D .

[4]

In words, this restriction says that

D

is the best forecast of

\tilde{X}

under the subjective belief measure. Note that we can incorporate probabilistic forecasts into our framework by letting

\tilde{X}

be an indicator function.

Remark 1.1:

Time series of survey data are often shorter relative to data on returns or macroeconomic variables. This can be accommodated in our framework provided that there is sufficient time series variation for these data to add nontrivial incremental information to the analysis.

2. Data Generation and Probability Divergence

In this section we construct and use the dynamic counterpart to the statistical divergence measure. We focus initially on relative entropy as a measure of statistical divergence, a measure which frequently arises in the analysis of large deviations of stochastic processes with temporal dependence (see, for instance, refs. 27 or 28). While we use relative entropy as a starting point, we go much farther by extending the so-called $ϕ$ divergence measures in ways that have a recursive structure that is very similar to that of relative entropy.

While the applications that interest us use Markov formulations, we relax this assumption to entertain non-Markov distortions. For this reason, we initially consider a stationary and ergodic formulation that nests stationary, ergodic Markov processes. This is the same environment used by ref. 29 to study bounds on statistical efficiency and ref. 30 to study testable implications of asset pricing models, both in the presence of conditional moment restrictions. The ref. 30 analysis imposes rational expectations in contrast to the analysis in this paper.

We start with a baseline probability triple $(Ω, G, P)$ and a measurable one-to-one transformation $U$ which is measure preserving and ergodic under $P$ . We use $U$ to construct stochastic processes and filtrations.^†

Let $I_{0} \subset G$ depict information available at date zero. We use the transformation $U$ to capture the information available at future dates via the recursion

I_{t} = \{Λ \in G : U^{- 1} Λ \in I_{t - 1}\} = \{Λ \in G : U^{- t} Λ \in I_{0}\} .

We presume that information accumulates,

I_{t} \subset I_{t + 1},

which in turn implies that

\{I_{t} : - \infty < t < + \infty\}

is a filtration. Similarly, for any random variable

B_{0}

that is

I_{0}

measurable, we form

B_{t}

recursively:

B_{t} (ω) = B_{t - 1} [U (ω)] = B_{0} [U^{t} (ω)] .

Thus for each initial random vector

B_{0}

, there is a corresponding stochastic process

{B_{t} : t \geq 0}

that is adapted to the filtration

{I_{t} : t \geq 0}

. Since

U

is measure preserving, the process

{B_{t} : t \geq 0}

is stationary.

A. Alternative Probabilities.

In what follows, we hold fixed the transformation $U$ while considering alternative probability measures. Let $Q$ denote an alternative probability distribution on $(Ω, G)$ that is measure preserving and ergodic, and let $Q_{t}$ be the restriction of $Q$ to $I_{t}$ . We consider only $Q$ s for which there exists an $N_{1} \geq 0$ that is $I_{1}$ measurable and satisfies

\int B_{1} d Q_{1} = \int E (N_{1} B_{1} ∣ I_{0}) d Q_{0}

[5]

for all bounded

I_{1}

measurable random variables

B_{1}

. This

N_{1}

necessarily satisfies

E (N_{1} ∣ I_{0}) = 1

. When

Q

is distinct from

P

, there is a bounded random variable for which the

Q

and

P

distributions differ. Because both are ergodic, the law of large numbers is applicable to both with distinct almost sure limit points. For the purposes of this analysis, the probability measure

Q

encodes the limits implied by the law of large numbers.

Form the product

M_{T} = \prod_{t = 1}^{T} N_{t} .

[6]

Then under

Q

, the date-

T

conditional expectation of a bounded,

I_{T}

random variable

B_{T}

E (M_{T} B_{T} ∣ I_{0}) .

We think of

M_{T}

as a relative likelihood between two models over horizon

T

constructed recursively through the familiar likelihood factorization. We further restrict

Q

to imply stochastic stability:

Definition 2.1:

We say that $Q$ induces stochastic stability if for any $B_{0}$ that is $I_{0}$ measurable and satisfies $\int | B_{0} | d Q_{0} < \infty$ ,

lim_{T \to \infty} E (M_{T} B_{T} ∣ I_{0}) = \int B_{0} d Q_{0} .

Definition 2.2:

The set $N$ contains all $N_{1}$ s for which there is a corresponding probability $Q$ satisfying Eq. 5 and is stochastically stable.

We presume that $N_{1} = 1$ is in this set and hence $P$ is stochastically stable.

B. Intertemporal Divergences

First consider the Kublack–Leibler divergence. Represent the expected log-likelihood ratio as a sum of contributions for each date by using the recursive structure of a relative likelihood:

E (M_{T} \log M_{T} ∣ I_{0}) = E (M_{T} \sum_{t = 1}^{T} \log N_{t} | I_{0}) \geq 0 .

Dividing by

T

and taking limits gives

\begin{array}{l} R (N_{1}) & = lim_{T \to \infty} \frac{1}{T} E (M_{T} \log M_{T} ∣ I_{0}) \\ = lim_{T \to \infty} \frac{1}{T} E (M_{T} \sum_{t = 1}^{T} \log N_{t} | I_{0}) \\ = \int E (N_{1} \log N_{1} ∣ I_{0}) d Q_{0}, \end{array}

which is the measure of relative entropy that we will use in our analysis. Note that there is an explicit connection between

N_{1}

and

Q_{0}

, which gives rise to a restriction that we impose when computing bounds.

Remark 2.3:

The relative entropy measure $R (N_{1})$ is the discrete-time analog to the relative entropy measure that is used in the Donsker–Varahadan large deviation theory applied to Markov processes [see refs. 28, 32, and 33 (chap. 3)].

Finite relative entropy restricts substantially the tail behavior of the probability distributions. For this reason we consider other divergences, but modified to exploit the recursive structure implied by the likelihood factorization. We use the conditional version of what is commonly called a $ϕ$ divergence as an important building block:

E [ϕ (N_{t}) ∣ I_{t - 1}]

for a strictly convex function

ϕ

defined on

(0, \infty)

with

ϕ (1) = 0

. There is an equivalent way to represent this divergence that we use. Construct a function

ψ

such that

n ψ (\frac{1}{n}) = ϕ (n) .

It may be shown that

ψ

is also strictly convex with

ψ (1) = 0

. By design,

E [ϕ (N_{t}) ∣ I_{t - 1}] = E [N_{t} ψ (\frac{1}{N_{t}}) | I_{t - 1}] .

[7]

On the right-hand side, we use the conditional probability associated with

N_{t}

to compute expectations. The random variable

\frac{1}{N_{t}}

is the Radon–Nikodym derivative of the baseline conditional probability with respect to the

N_{t}

conditional probability distribution. The function

ψ

in plays a role analogous to

ϕ

once we change the probability we use in the expectation.

We use $ψ$ to represent an intertemporal divergence measure:

\begin{align} R (N_{1}) & = lim_{T \to \infty} \frac{1}{T} \sum_{t = 1}^{T} E (M_{t - 1} E [ϕ (N_{t}) ∣ I_{t - 1}] ∣ I_{0}) \\ = lim_{T \to \infty} \frac{1}{T} \sum_{t = 1}^{T} E [M_{t} ψ (\frac{1}{N_{t}}) | I_{0}] \\ = lim_{T \to \infty} \frac{1}{T} E [M_{T} \sum_{t = 1}^{T} ψ (\frac{1}{N_{t}}) | I_{0}] . \end{align}

[8]

The limiting version of this measure as implied by the law of large numbers for stationary, ergodic processes is

\int E [N_{1} ψ (\frac{1}{N_{1}}) | I_{0}] d Q_{0} = \int E [ϕ (N_{1}) ∣ I_{0}] d Q_{0} .

Note that we use the conditional version of what is commonly called a

ϕ

divergence measure averaged using the altered stationary probability

Q

. This coincides with the relative entropy divergence when

ϕ (n) = n \log n

. SI Appendix, section A shows that this intertemporal divergence extension of

ϕ

divergence is convex.

Alternatively, there has been considerable interest in members of the Wasserstein class of divergences, including in the study of robust Markov chains and machine learning. Wasserstein divergences could also be used as conditional divergences that are averaged using the altered stationary probability $Q$ .^#

Remark 2.4:

Empirical likelihood methods (35, 36) use a divergence measure $ϕ (n) = - \log n$ for independent and identically distributed data. The corresponding intertemporal divergence measure is

E (- \log N_{1}) .

[9]

Note that this measure uses the original baseline probability measure implied by

P_{0}

and not

Q_{0}

to average over the conditioning information. Were we to average using

Q_{0}

in the divergence, then our analysis would apply. Elsewhere, we and others have argued that this strictly decreasing

ϕ

is not well suited for detecting departures from baseline probabilities restricted by moment conditions.

Remark 2.5:

Using positive random variables, $M_{T}$ , to depict alternative probabilities for date- $T$ events imposes absolute continuity (conditioned on date-zero information). As we already noted, this same absolute continuity will not be true over the infinite future, however. Our division by $T$ when constructing intertemporal divergence Eq. 8 allows for the altered probability to have different limits under the law of large numbers.

Remark 2.6:

Our analysis assumes that the underlying processes are stationary under the alternative $Q$ s. However, the results we obtain will still apply under certain classes of nonstationarity processes. While we restrict $Q$ to be measure preserving and ergodic, any probability measure that is absolutely continuous with respect to $Q$ will obey the same laws of large numbers even though it may not be measure preserving. Such measures may also imply the same intertemporal divergence measure Eq. 8. Moreover, specific examples that could be of interest are probabilities associated with Markov processes that eventually “escape” from their dependence on the initialization. While we do not explore such cases formally, these observations suggest that the bounds that we compute could be justified under an even broader set of probability measures.

3. Moment Bounds

We next present the recursive approach we use for computing probability bounds. To represent these bounds, we entertain a rich family of functions $g$ and compute sharp lower bounds on the expectation $g (X_{1})$ . As a special case, $g (X_{1})$ could be an indicator of an event with its expectation being the probability of that event. We will be interested in other choices of $g$ in our empirical illustration. We compute an upper bound on $g (X_{1})$ by finding the negative of the lower bound on the expectation $- g (X_{1})$ . Formally, we are interested in solving

inf_{N_{1} \in N} \int E (N_{1} g (X_{1}) | I_{0}) d Q_{0}

subject to the constraints

\begin{array}{l} R (N_{1}) & \leq κ \\ E [N_{1} f (X_{1}) ∣ I_{0}] & = 0 . \end{array}

To compute a bound for a given choice of

g

, we will borrow an idea from the robust control literature. See, for instance, refs. and . We will initially solve a problem with a discrepancy penalty indexed by a parameter

ξ > 0

and show how to solve a problem given

ξ

. We will then treat

ξ

as a Lagrange multiplier and trace out the implied discrepancies for each such

ξ

. In this way,

ξ

may be chosen to enforce the constraint

R (N_{1}) \leq κ

. For notational simplicity we suppress the parameter dependence in the moments of

f (X_{t})

and

g (X_{t})

In much of what follows, we aim to solve the following:

Problem 3.1.

\begin{array}{l} μ^{*} & = inf_{N_{1} \in N} lim_{T \to \infty} \frac{1}{T} E (M_{T} \sum_{t = 1}^{T} [g (X_{t}) + ξ ψ (\frac{1}{N_{t}})] | I_{0}) \\ = inf_{N_{1} \in N} \int E (N_{1} [g (X_{1}) + ξ ψ (\frac{1}{N_{1}})] | I_{0}) d Q_{0} \end{array}

subject to

E [N_{1} f (X_{1}) ∣ I_{0}] = 0

It suffices to optimize over $N_{1}$ because this choice determines the $N_{t}$ for all $t \geq 1$ through the transformation $U^{t - 1}$ and $M_{T}$ as constructed in Eq. 6.

A. Martingale Construction.

While we solve Problem 3.1 via recursive methods, as a precursor to this, we use a convenient martingale construction used in connection with the objective function. Suppose that for $N_{1} \in N$ , we find a random variable $v_{0}$ such that

E (N_{1} [g (X_{1}) + ξ ψ (\frac{1}{N_{1}}) - μ + v_{1}] | I_{0}) - v_{0} = 0,

[10]

where

μ = \int E (N_{1} [g (X_{1}) + ξ ψ (\frac{1}{N_{1}})] | I_{0}) d Q_{0},

and where

v_{1} (ω) = v_{0} [U (ω)]

and

v_{0}

I_{0}

measurable. Then iterating on , it follows that

\begin{array}{l} E (M_{T} \sum_{t = 1}^{T} [g (X_{t}) + ξ ψ (\frac{1}{N_{t}}) - μ] | I_{0}) \\ + E (M_{T} v_{T} ∣ I_{0}) - v_{0} = 0 . \end{array}

In fact,

\sum_{t = 1}^{T} [g (X_{t}) + ξ ψ (\frac{1}{N_{t}})] - T μ + v_{T} - v_{0}

is a martingale under the probability measure

Q

with expectation zero. Moreover,

\begin{align} v_{0} & - \int v_{0} d Q_{0} \\ = lim_{T \to \infty} E (M_{T} \sum_{t = 1}^{T} [g (X_{t}) + ξ ψ (\frac{1}{N_{t}}) - μ] | I_{0}) \end{align}

[11]

provided that the almost sure limit on the right-hand side is finite. The random variable

v_{o}

is in fact well defined only up to a constant translation. Our recursive approach will simultaneously solve for

v_{0}

used in the martingale construction and

μ

computed at the minimizing solution for

N_{1}

B. Recursive Formulation

We use a rearranged version of Eq. 10 when posing the recursive formulation of the optimization problem.

Problem 3.2.

Find a pair $(μ, v)$ that satisfies

μ = inf_{N_{1} \in N} E (N_{1} [g (X_{1}) + ξ ψ (\frac{1}{N_{1}}) + v_{1}] | I_{0}) - v_{0}

subject to the constraint

E [N_{1} f (X_{1}) ∣ I_{0}] = 0,

where

v_{1} (ω) = v_{0} [U (ω)]

and

v_{0}

I_{0}

measurable and

μ

is a finite number. This optimization problem determines the constant

μ

and the random variable

v_{0}

up to a translation by a constant.

This problem is recognizable as a fixed point problem in $(μ, v_{0})$ captured by the relation between $v_{1}$ and $v_{0}$ . While we posed this problem in terms of date zero and date one, given our presumed stationary data generation the problem could equivalently be stated in terms of date $t$ and date $t + 1$ for $t > 0$ . The minimization over $N_{1}$ can be solved using convex duality methods familiar from the analysis of $ϕ$ divergence measures. We let $(μ^{*}, v_{0}^{*})$ denote the solution to Problem 3.2 and $N_{1}^{*}$ be the corresponding minimizer. The following objects are of interest from this problem:

•the moment bound, $\int E [N_{1}^{*} g (X_{1}) | I_{0}] d Q_{0}^{*};$

•the corresponding conditional moment, $E [N_{1}^{*} g (X_{1}) | I_{0}]$ ;

•the implied divergence,

\int E [ϕ (N_{1}^{*}) ∣ I_{0}] d Q_{0}^{*} = \int E [N_{1}^{*} ψ (\frac{1}{N_{1}^{*}}) | I_{0}] d Q_{0}^{*},

where

N_{1}^{*}

solves Problem 3.2 and

Q_{0}^{*}

is an implied stationary distribution.

There are three features of Problem 3.2 that require further comment. First, the minimization problem includes “continuation-value” adjustments depicted by $v_{0}$ and its next period counterpart $v_{1}$ along with the numerical value $μ$ . We include these adjustments to account for the fact that the choice of $N_{1}$ has implications for future time periods. Second, limit Eq. 11 is not finite for all measure-preserving and ergodic probabilities measures $Q$ . For the minimum to be attained, we presume that this limit is finite at the minimizing solution. Third, $ξ E (N_{1} ψ (\frac{1}{N_{1}}) ∣ I_{0})$ acts as a per-period divergence penalty, but we may equivalently think of $ξ$ as a Lagrange multiplier and subsequently maximize over $ξ$ . Thus, we use $ξ$ to index alternative problems that penalize the increment to the intertemporal divergence. The value $μ^{*}$ of this objective depends on $ξ$ , leading us to write $μ^{*} (ξ)$ . To impose a specific divergence constraint $κ$ , we solve

\begin{align} sup_{ξ > 0} & μ^{*} (ξ) - ξ κ \\ = sup_{ξ > 0} \int E (N_{1}^{*} [g (X_{1}) + ξ ψ (\frac{1}{N_{1}^{*}}) - ξ κ] | I_{0}) d Q_{0}^{*} . \end{align}

[12]

Alternatively, we can back out the implied

κ

for each

ξ

by computing the derivative

\frac{d μ^{*}}{d ξ}

or by computing directly the divergence associated with

N_{1}^{*}

. To determine the

ξ

sensitivity, many versions of the optimization problem could be solved in parallel using convex duality and dynamic programming methods. The computed bound

μ^{*} (ξ^{*})

is for the unconditional expectation of

g (X_{1})

, although we find the conditional expectation,

E [N_{1}^{*} g (X_{1}) ∣ I_{0}]

that is a central part of the calculation, to be of interest in its own right. Finally,

lim_{ξ \to \infty} μ^{*} (ξ) / ξ

reveals the minimum possible divergence subject to the conditional moment restrictions. This limit gives a lower bound on magnitude of

κ

used in our analysis. It can be computed directly by solving a counterpart to Problem 3.2.

C. Nonlinear Expectation

Consider now the set $B$ of bounded Borel measurable functions $g$ to be evaluated at alternative realizations of the random vector $X_{1}$ . Given a divergence bound $κ$ , we construct a mapping $K$ from functions $g$ in $B$ into the real line that assigns the computed bound. Formally, define

K (g) = \int E [N_{1}^{*} g (X_{1}) | I_{0}] d Q_{0}^{*},

where the right-hand side is computed using the value of

ξ

that solves . This mapping can be thought of as a nonlinear expectation, as formalized in the following proposition:

Proposition 3.3.

The mapping $K : B \to R$ given by $\int E [N_{1}^{*} g (X_{1}) | I_{0}] d Q_{0}^{*}$ implied by Problem 3.2 for each $g \in B$ has the following properties** :

1)If $g_{2} \geq g_{1}$ , then $K (g_{2}) \geq K (g_{1})$ ;

2)if $g$ is constant, then $K (g) = g$ ;

3) $K (r g) = r K (g), f o r a s c a l a r r \geq 0$ ;

4) $K (g_{1}) + K (g_{2}) \leq K (g_{1} + g_{2})$ .

All four properties follow from the definition of $K$ . Property 4 includes an inequality instead of an equality because we compute by solving a minimization problem, and the $N_{1}$ s that solve this problem can differ depending on $g$ .

Remark 3.4:

While $K (g)$ gives a lower bound on the expectation of $g (X)$ , by replacing $g$ with $- g$ , we construct an upper bound on the expectation of $g (X)$ . The upper bound will be given by $- K (- g)$ . The interval

[K (g), - K (- g)]

captures the set of possible values for the distorted expectation of

g (X)

consistent with divergence less than or equal to

κ

Remark 3.5:

In our statement of Problem 3.2, we suppressed the dependence of the function $f$ on an unknown parameter vector $θ$ in a parameter space $Θ$ . But many applications will necessarily include parameter uncertainty. Provided that we can compute the solution to this problem quickly using duality, we can assess parameter sensitivity by perhaps solving this problem many times in parallel. Bounds that are robust to parameter sensitivity could be obtained by minimizing over the set $Θ$ or over a family of probability distributions over $Θ$ .

Remark 3.6:

For some applications, it is of interest to bound ratios of expectations of functions $g_{1}$ and $g_{2}$ of $X_{1}$ . Expectations conditioned on discrete events are such ratios and proportional risk compensations are logarithms of such ratios. As we elaborate in SI Appendix, section E, bounds of ratios can be computed by first bounding expectations of $g_{1} (X_{1}) - ζ g_{2} (X_{1})$ for alternative choices of the real number $ζ$ and then searching over $ζ$ for the smallest ratio.

D. Dual Problem

We show that the dual problem for the relative entropy divergence is equivalent to a principal eigenvalue problem. This gives a representation of the distorted measures that underlies the bounds and a revealing link to large deviation theory.

By a direct application of duality for $ϕ (n) = n \log n$ ,

\begin{array}{l} μ & + v_{0} \\ = max_{λ_{0}} - ξ \log E (\exp [- \frac{1}{ξ} g (X_{1}) + λ_{0} \cdot f (X_{1}) - \frac{1}{ξ} v_{1}] | I_{0}), \end{array}

where the random vector

λ_{0}

is restricted to be

I_{0}

measurable and is the vector of Lagrange multipliers for the conditional moment restriction. See SI Appendix, section C for a more complete development of the primal and the dual problems. Let

ϵ = \exp (- \frac{μ}{ξ})

and

e_{0} = \exp (- \frac{v_{0}}{ξ})

. Then an equivalent statement of the dual problem is

ϵ = min_{λ_{0}} E (\exp [- \frac{1}{ξ} g (X_{1}) + λ_{0} \cdot f (X_{1})] (\frac{e_{1}}{e_{0}}) | I_{0}) .

In this optimization problem

λ_{0}

is again restricted to be a

I_{0}

measurable random vector and

e_{0}

is restricted to be positive as is the real number

ϵ

When the state space is not discrete, this eigenvalue problem can have multiple solutions. While there could be multiple solutions to this eigenvalue problem, the next result identifies the eigenvalue of interest.

Lemma 3.7.

When there are multiple positive eigenvalue solutions for a given $λ_{0}$ , at most one of them induces a probability measure that is stochastically stable.

See SI Appendix, section B for a proof.^††

Proposition 3.8.

Problem 3.2 with $ϕ (n) = n \log n$ can be solved by finding the answer to

ϵ = min_{λ_{0}} E (\exp [- \frac{1}{ξ} g (X_{1}) + λ_{0} \cdot f (X_{1})] (\frac{e_{1}}{e_{0}}) | I_{0}),

where

\begin{array}{l} μ & = - ξ \log ϵ \\ v_{0} & = - ξ \log e_{0} . \end{array}

In this optimization problem, the random vector

λ_{0}

is restricted to be a

I_{0}

measurable random vector, the random variable

e_{0}

is restricted to be

I_{0}

measurable and positive, and

e_{1} (ω) = e_{0} [U (ω)]

with probability one. The real number

ϵ

is positive. The implied solution for the probability distortion is

N_{1}^{*} = \frac{\exp [- \frac{1}{ξ} g (X_{1}) + λ_{0}^{*} \cdot f (X_{1})] e_{1}^{*}}{ϵ^{*} e_{0}^{*}},

where

λ_{0}^{*}

is the optimizing choice for

λ_{0}

and

(ϵ^{*}, e_{0}^{*})

are selected so that the resulting

Q^{*}

induces stochastically stability. The conditional expectation implied by the bound is

E [N_{1}^{*} g (X_{1}) ∣ I_{0}],

which in turn implies a bound on the unconditional expectation equal to

\int E [N_{1}^{*} g (X_{1}) ∣ I_{0}] d Q_{0}^{*} .

The implied relative entropy is

\int E (N_{1}^{*} \log N_{1}^{*} ∣ I_{0}) d Q_{0}^{*} .

Remark 3.9:

Our characterization is reminiscent of the results from large deviation theory for Markov processes. As in our analysis, large deviation theory studies an undiscounted limiting problem. See, for instance, refs. 28 and 32 for valuable treatises on large deviation theory.^‡‡

A more substantive link to large deviations helps us interpret the relative entropy bounds that we input into our analysis. When using the empirical probability to detect potential departures from the baseline model, there is typically a positive probability that the empirical distribution mistakenly detects a departure. For a fixed criterion, the probability of this mistake becomes increasingly small as the sample size gets large with a well-defined rate characterized by large deviation theory. Under some additional regularity conditions, remarkably, the decay rate can be made to be arbitrarily close to the minimum relative entropy bound that we compute. Moreover, this theory computes excursions, represented probabilistically, that make the decay rate as small as possible. See SI Appendix, section D for an elaboration.

While we draw on insights from large deviation theory, our ultimate aim is quite different from that theory. Nevertheless, we find it revealing to compute both relative entropies and related Chernoff entropy as described, for instance, in refs. 42 and 43 as part of a sensitivity analysis.

E. Markov Specification

To proceed in a tractable way, we impose Markovian restrictions on the underlying data-generating processes. Specifically we presume that ${X_{t} : t \geq 0}$ is a time-invariant function of Markov process, appropriately restricted.

Assumption 3.10.

${(X_{t}, Z_{t}) : t = 0,1, \dots .}$ is a first-order Markov process for which the joint distribution of $(X_{t + 1}, Z_{t + 1})$ conditioned on $(X_{t}, Z_{t})$ depends only on $Z_{t}$ .

Given this assumption, the ${Z_{t}}$ process by itself is a first-order Markov process. We view both $X_{t}$ and $Z_{t}$ as observable. The triangular structure for the dynamic evolution allows us to use a more sparse representation of the conditioning information. The alternative probabilities that we explore are not restricted to be Markov, but the solution to the minimization problem will be, for reasons that are familiar from dynamic programming. With the Markov specification, we solve the recursion.

Problem 3.11.

Find a pair $(μ, v)$ that solves

\begin{array}{l} μ & + υ (z) \\ = min_{N_{1} \in N} E (N_{1} [g (X_{1}) + ξ ψ (\frac{1}{N_{1}}) + υ (Z_{1})] | Z_{0} = z) \end{array}

subject to the constraint

E [N_{1} f (X_{1}) ∣ Z_{0} = z] = 0 .

This optimization problem determines the constant

μ

and the random variable

υ

up to a translation by a constant.

While the primal problem “imposed” stochastic stability, it suffices to verify the stability of the process that we obtain as our candidate solution. Since it is Markovian, this restriction is satisfied when the process ${Z_{t}}$ is aperiodic and Harris recurrent.

4. Illustration

We illustrate these methods using a familiar asset pricing model with recursive utility investors as in refs. 44 and 45. While much of the asset pricing literature appeals to an arguably large risk aversion in conjunction with rational expectations when confronting data, we constrain risk aversion and instead explore belief distortions as an alternative expectation. We follow ref. 46 by allowing for market segmentation and avoid the direct use of consumption data. We then ask what implications asset market data have for predicted consumption growth rates.

Much of the macroasset pricing literature imposes risk aversion that is arguably large at least for some states of the macroeconomy. Refs. 47 and 48 give alternative rationales for substantially restricting the risk aversion coefficient. While we do not view as a settled issue what precise bounds should be imposed on risk aversion, we assume a unit risk aversion to feature the role of belief distortions when confronting asset pricing evidence. Our choice of unity is admittedly for convenience. As we will see, this choice leads to some particularly simple asset pricing implications.

Let $R_{t}^{w}$ denote a presumed observable return on wealth. As noted by ref. 45, the one-period stochastic discount factor under rational expectations is the reciprocal of the gross return on wealth when risk aversion is unity. Thus, under distorted beliefs represented by $N_{t}$ ,

S_{t} = N_{t} {(R_{t}^{w})}^{- 1},

where

S_{t}

is the one-period stochastic discount factor under rational expectations. We use this setup for our illustration.

As ref. 45 notes, the consumption Euler equation for an investor implies

E [N_{t} \log R_{t}^{w} ∣ I_{t - 1}] = - \log β + (1 - ρ) E [N_{t} \log G_{t} ∣ I_{t - 1}]

where

G_{t}

is the ratio of consumption growth over two adjacent time periods. The parameter

β

is the subjective discount factor, and

ρ

is the reciprocal of the intertemporal elasticity of substitution. By deducing bounds on the left-hand side, we may infer bounds on

ρ

times the market expectation of consumption growth of equity market participants expressed in logarithms. Recursive utility preferences are specified in terms of continuation values that determine the rankings of prospective consumption processes. As a rough approximation, when

ρ < 1

, the wealth is positively related to the continuation value, where both are relative to current consumption. Conversely, they are negatively related when

ρ > 1

. Thus, for this model of investor preferences, whether

ρ

is larger or smaller than one impacts how we interpret the evidence based on conditioning information.

In our illustration, we draw on the literature that suggests returns can be predicted from dividend–price ratios. While there have been debates on how fragile this evidence is, we step aside from that discourse and take the predictability evidence at face value to illustrate our method. Given our direct use of dividend–price measures, we purposefully choose a very coarse conditioning of information and split the dividend–price ratios into three bins using the three empirical terciles. We take the dividend–price terciles to be a three-state Markov process. Dividend–price ratios are known to be persistent, and this will be evident in our calculations.^¶¶

We implement our approach using quarterly data from 1954 to 2016. We use the return on the CRSP (Center for the Research on Security Prices) value-weighted index to proxy for the return on wealth. For asset returns, we use the return on a 3-mo treasury bill and the three Fama–French factor excess returns. We impose moment conditions for each return implied by Eq. 3, each scaled by three indicator functions for the terciles of the dividend–price ratio, giving a total of 12 moment conditions. All returns are converted from nominal to real returns using the deflator for nondurables consumption obtained from the Bureau of Labor Statistics. We then apply the methods described in 3. Moment Bounds to bound functions of the return on wealth as measured by the value-weighted return.

In Fig. 1, we report the bounds on the beliefs about the expected log return, which under the assumption of the unitary risk aversion coefficient are approximately proportional to the consumption growth rate belief when the subjective discount factor $β$ is very close to one. The conditional expectation of log returns and the unconditional counterpart are all lower than their empirical counterparts. This observation follows by comparing the $•$ s with the boxes in Fig. 1, where the top and bottom of the boxes are the upper and lower bounds with a relative entropy constraint imposed at a magnitude that is 20% higher than the minimum. The minimum relative entropy rate implies a half-life of about 24 quarters for reducing the probability by 50% of mistakenly rejecting the rational expectations. Increasing this by 20% reduces the half-life by the same percentage to about 20 quarters.^## While our choice of a 20% increase is a bit arbitrary and used for illustration purposes, it is straightforward to compute bounds with other choices of divergence thresholds. Across alternative applications, a choice of 20%, independent of magnitude of the minimal possible divergence, would be hard to defend. One nice aspect of relative entropy is that there is an explicit statistical interpretation that we find to be revealing, and thus the magnitude of the divergence has meaning.

Fig. 1.

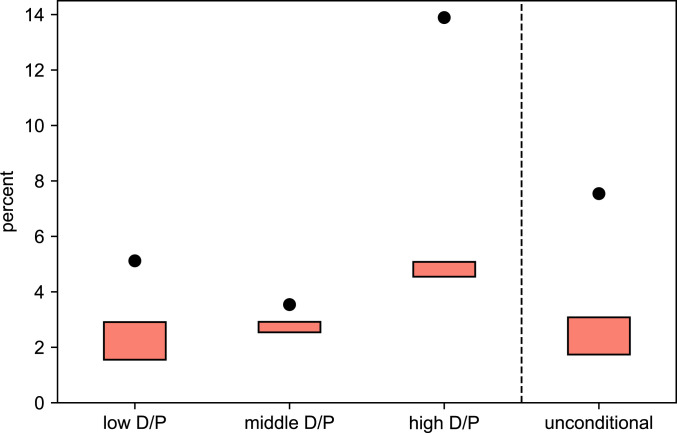
Expected log market return. The $•$ s are empirical averages and the boxes give the imputed bounds when we inflated the minimum relative entropy by $20 %$ . The minimum relative entropy is 0.0284 with a half-life of 24.4 quarters.

Interestingly, it is when we condition on the low value of the dividend–price ratio that we find the box with the largest height (biggest difference between the upper and lower bounds). Also, the bounds on the unconditional distorted expectations are very similar to those we found for the low dividend–price ratio. As a robustness check, we repeated these calculations for a quadratic conditional divergence and found only very modest differences (SI Appendix, section F).

Not only are conditional means distorted, but so are the transition probabilities as reported in Table 1. While the implied stationary probabilities are fairly evenly distributed over the three dividend states, essentially by construction, the minimal entropy probabilities down-weight substantially the high dividend–price ratio state and up-weight the low dividend–price state. The high dividend–price state, in particular, has a very small stationary probability under the minimum distorted stationary distribution. Consistent with this, the transition probabilities into this state are lower under the distortion and they are higher for exiting this state. The opposite happens for transitions in and out of the low dividend–price state. Thus, a hypothetical process that behaves in accordance with the minimum entropy distorted Markov transition matrix is likely to spend substantially more time in the low expected log-return state and much less time in the high expected log-return state. When we increase the relative entropy bound by 20%, the implied distorted transition matrices are quite similar to the implied transition matrix recovered by the minimizing relative entropy and depart from the empirical transition matrix in comparable ways.

Table 1.

Empirical and distorted transition probabilities

	Empirical	Minimum entropy
Transition matrix	$(\begin{matrix} 0.96 & 0.04 & 0 \\ 0.05 & 0.88 & 0.07 \\ 0 & 0.08 & 0.92 \end{matrix})$	$(\begin{matrix} 0.98 & 0.02 & 0 \\ 0.08 & 0.88 & 0.04 \\ 0 & 0.17 & 0.83 \end{matrix})$
Stationary probabilities	$[\begin{matrix} 0.42 & 0.31 & 0.27 \end{matrix}]$	$[\begin{matrix} 0.76 & 0.20 & 0.04 \end{matrix}]$

An alternative approach would be to solve static versions of our analysis for each of the three different specifications of the conditioning information. Under this approach, there would be no reason for distorting the transition probabilities as the dynamical evolution of the conditioning information is ignored. Not surprisingly, this approach does lead to notable differences in bounds. The minimized entropy over the alternative configurations of the conditioning information using the undistorted transition probabilities is 0.047 in comparison to the much smaller 0.028 that we found using our method. We view belief distortions in the transition probabilities are of particular interest in behavioral models and in models with ambiguity aversion and see this as a virtue over methods that analyze the conditional problems separately.

As we mentioned at the outset of this section, there is a substantial asset pricing literature that studies time-varying risk compensation, often appealing to high values of risk aversion. We illustrate how belief distortions can imitate large risk compensations. Thus, consider the bounds on the implied risk compensations when we restrict the risk aversion parameter to be one. We report proportional risk premium using the ex post real return on treasury bills, $R^{f}$ , as our riskless benchmark in Fig. 2. To construct these results, we compute bounds on $\log E R^{w} - \log E R^{f}$ by extending the approach of 3. Moment Bounds as described in SI Appendix, section E. Restricting investor risk aversion allows for belief distortions to capture the fluctuating empirical compensations for exposure to uncertainty.

Fig. 2.

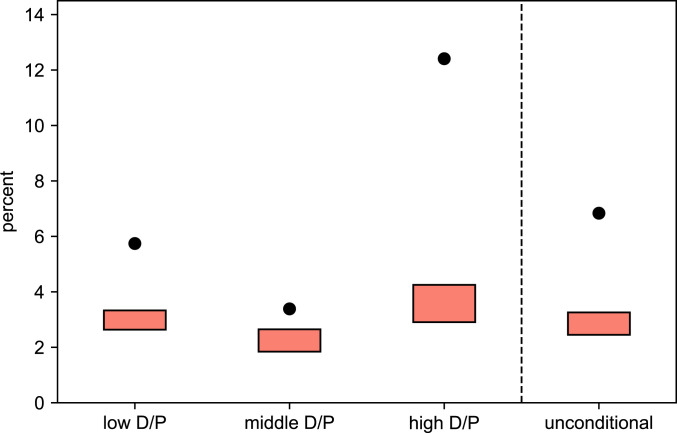
Proportional risk compensations computed as $\log E R^{w} - \log E R^{f}$ scaled to an annualized percentage. The $•$ s are the empirical averages and the boxes give the imputed bounds when we inflated the minimum relative entropy by $20 %$ .

Finally, since our empirical method looks at other information from two other Fama–French excess returns, we also report bounds on other risk compensations that we included in our analysis. We convert the excess returns into returns by adding the gross returns on bonds. We report these findings in SI Appendix, section E. Again, the risk compensations are greatly reduced relative to the empirical counterpart, and in most instances they are less sensitive to conditioning information.

Putting aside the empirical debate on return predictability, we see two possible conclusions from these results. One possibility is that the statistical divergence (measured as relative entropy) for the distortions is high enough to challenge a bounded rationality view of the recursive utility model with a unitary risk aversion. The other possibility is that this divergence is defensible, in which case our dynamic implementation reveals the most statistically plausible distortions on the evolution of the dividend–price ratios. It remains a judgment call as to when the resulting statistical bounds we find here are implausible. Researchers that embrace rational expectations do not consider belief distortions, while behavioral finance researchers seldom consider the implied statistical divergence of their modeled beliefs. Neither practice uses tools for assessing statistical approximation as we have done in this paper. We view these computations as providing a valuable empirical complement to the assessment of specific models of belief distortions or ambiguity aversion. Moreover, we have noted how survey evidence can be included within our framework, and we view this as a potentially valuable extension of the illustration presented here.

5. Bounding Other Probabilities

We have motivated our analysis as a method for extracting expectation bounds for subjective beliefs or restricted “worst-case” beliefs that support valuation under ambiguity aversion. These same methods provide expectation bounds for two other probability measures that are of interest in asset valuation. These measures are the one-period risk-neutral probabilities and the long-term forward probabilities. While surveys cease to provide information about these probabilities, even sparsely observed asset values, as we assume here, are revealing. We now comment on how to apply our method for both of these applications.

A. Risk-Neutral Measure

Under risk-neutral pricing, the reciprocal of the gross one-period riskless return acts as a stochastic discount factor. Thus, in this case,

N_{t} S_{t} = N_{t} {(R_{t}^{f})}^{- 1} .

Refs. 51– target the

N_{t}

s with the smallest relative entropy divergence to use in pricing derivative claims. We map this type of problem into our analysis by viewing the empirically relevant distribution as the “correct distribution” and the risk-neutral transformation as a way to correct for model misspecification. As in refs. and , the measures of particular interest to us are the ones with a small divergence, although we explore more probabilities than just the

N_{t}

with the minimal divergence. While not our primary motivation, the methods we develop in this paper allow the user to obtain robust bounds on risk-neutral expectations of macroeconomic variables that incorporate information embedded in asset prices.

B. Long-Term Forward Measure

A substantively distinct, but mathematically related, literature studies the martingale decomposition of the stochastic discount factor. This decomposition expresses the stochastic discount factor as the product of a martingale component and a transitory component. The martingale component can be interpreted as a change of probability measures that imposes risk neutrality in valuation over long investment horizons. Refs. 53 and 54 show that the reciprocal of the gross holding-period return on a long-term bond is the stochastic discount factor net of a martingale component.

Since the work of ref. 54, the martingale component is referred to as the permanent component to the cumulative stochastic discount factor process. In providing a more formal mathematical characterization, refs. 40 and 41 find it more revealing to appeal to probabilistic characterization of this component. As emphasized by ref. 55, the probability measure associated with the martingale absorbs long-term risk adjustments for stochastically growing cash flows. This probability measure is the risk-neutral, forward measure that captures long-term risk–return tradeoffs.

Many structural models of asset pricing have stochastic discount factor processes with martingale components that dominate risk prices over long investment horizons. These components can reflect permanent shocks to the macroeconomy or forward-looking components to valuation. These components are present when investors have recursive utility preferences in which the intertemporal composition of risk matters or when they are averse to ambiguity in assigning probabilities to future events.

To relate this to our analysis, suppose that this martingale component is missing from the model specification. In such circumstances, ref. 53 justifies the use of the reciprocal of the gross holding-period return on a long-term bond, $R_{t}^{h}$ , as the stochastic discount factor: $S_{t} = {(R_{t}^{h})}^{- 1}$ . When there is a martingale component, ref. 54 advocated bounding its magnitude by, in effect, using this return reciprocal as a misspecified stochastic discount factor. For this application, we use

S_{t} = N_{t} {(R_{t}^{h})}^{- 1}

as the stochastic discount factor where

N_{t} \geq 0

has conditional expectation equal to one and thus induces a change of a probability measure that absorbs long-term risk adjustments. Our method applied to this problem complements and extends those of refs. and by providing bounds on expectations implied by this measure.

Remark 5.1:

Ref. 57 gives conditions under which investor beliefs can be uniquely identified from asset prices. This identification hinges on a complete panel of state prices being available to the econometrician, as well as an implicit restriction that the stochastic discount factor process does not contain a martingale component. This latter restriction is violated in many standard asset pricing models (see ref. 55 for a discussion). More generally this identification reveals a forward probability measure that absorbs long-term growth rate risk. Our approach avoids the requirement of a complete set of state prices and can be used to identify sets of long-term forward probabilities that are consistent with asset pricing model restrictions and within a small deviation of rational expectations.

6. Conclusions

In this paper, we developed methods designed to extract information on investor beliefs from data on asset prices and investor surveys. Our approach presumes an econometric model of investors or enterprises that could be misspecified under rational expectations. We illustrated how limiting the statistical discrepancy between investor beliefs and rational expectations implies bounds on investors’ expectations. Formally, we represented this relationship through a nonlinear expectation function and derived its dual representation.

Going forward, we see two types of applications of our methods. Deducing market expectations about the future from forward-looking asset prices is a common practice in both the public and private sectors. But this is typically done either informally or by targeting so-called risk-neutral probabilities that confound beliefs and risk preferences. Our method provides a formal way to compute and represent information on investor beliefs constrained by a model of risk aversion along with a measure of statistical divergence.

Alternatively, we could use our approach to provide diagnostics for model misspecification under rational expectations. The bounds we deduce will help assess alternative models of subjective beliefs or ambiguity aversion. Implied belief bounds for small or moderate restrictions on the statistical divergence can give suggestive results for model builders as to how to repair potentially misspecified models. By comparing models of subjective beliefs or ambiguity aversion supported by belief distortions to the implied bounds, applied researchers could assess whether such departures from rational expectations could be easily discerned from limited data.

Future applications of our methodology could incorporate information from survey data on investor beliefs. One approach would be to include survey data directly as additional moment conditions when constructing expectation bounds. Another approach would be to compare survey-implied expectations to expectation bounds on the corresponding variables formed without using the survey data as information. The latter approach would provide a check on how plausible the survey data are as a representation of investor beliefs used in decision making.

While we focused on constraining probabilities based on intertemporal measures of divergence, these bounds could be used formally in the design of economic policy. For instance, refs. 58 and 59 pose dynamic policy problems in which a government policymaker fails to have precise knowledge of the beliefs of the private sector when designing a prudent course of action. While these papers explore what impact this imprecision could have on policy, our work looks more systematically at how to extract credible information about the beliefs.

Acknowledgements

We thank Fernando Alvarez, Orazio Attanasio, Anmol Bhandari, Stéphane Bonhomme, Tim Christensen, Jim Heckman, Leo De Aparisi Lannoy, Winston Dou, Ralph Koijen, Marco Loseto, Yueran Ma, Andrey Malenko, Stefan Nagel, Diana Petrova, Monika Piazzesi, Eric Renault, Jose Scheinkman, Azeem Shaikh, Ken Singleton, Grace Tsiang, Harald Uhlig, and Xiangyu Zhang for helpful comments and suggestions. We gratefully acknowledge the research assistance of Han Xu and Zhenhuan Xie. We thank the Alfred P. Sloan Foundation (Grant G-2018-11113) for financial support.

The authors declare no competing interest.

*See ref. and the published comments for an overview and discussion of the use of survey data in macroeconomics and ref. for a probe into the impact of heterogeneity in the study of overreaction.

^†A common specification of

U

is the shift transformation applied to the space of infinite sequences of vectors of real numbers.

^‡From a measure-theoretic perspective,

Q

and

P

cannot be equivalent. There exist events based on limits for which

Q

assigns probability one and

P

assigns probability zero and conversely.

^§Stochastic stability as defined here is satisfied when the process is beta mixing (or absolutely regular); see, e.g., theorem 3.29 in ref. .

^¶For some

ϕ

divergences the domain can be extended to include zero.

^#For example, see ref. . Ref. deduces a Laplace principle for large deviation theory and other approximations with an overlapping class of intertemporal divergences. While ref. poses a problem that is mathematically related, the formulation does not nest ours.

^∥In contrast to our analysis, ref. incorporates conditioning information to identify a subjective belief by minimizing the divergence given in under

P

**The first two of these properties are taken to be the definition of a nonlinear expectation by ref. . Properties (3) and (4) are referred to as “positive homogeneity” and “superadditivity.”

^††Relatedly, ref. proves a counterpart to this result for continuous-time specifications in a Markovian environment. Moreover, ref. extends the ref. analysis by, among other things, relaxing the Markov assumption.

^‡‡In particular, the analysis in ref. , chaps. 7 and 8 features discrete-time Markov specifications and large sample approximation in the formulation of a Laplace principle.

^§§See equations 17 and 18 of ref. except that we allow for more general expectations.

^¶¶As an alternative starting point, we could use the regime probabilities from Markov switching models of ref. as possible states along with the implied return distributions.

^##The Chernoff entropy at the minimum is 0.0096 with a half-life of 72 quarters. The Chernoff measure is motivated by a common decay rate imposed on type I and type II errors of testing one model against another and is expected to be considerably smaller. We computed it using the approach described in ref. for Markov processes. While symmetric, this measure is less tractable to implement and not included in the family of recursive divergences that we describe. We use it merely to provide, ex post, additional information about the magnitude of the bound.

This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2019910117/-/DCSupplemental.

Data Availability.

Computer code and computations with standard data sources have been deposited in Github at https://github.com/lphansen/Beliefs with computational details on the implementation. All study data are included in this article and SI Appendix.

References

Pigou

, Industrial Fluctuations (Macmillan and Co. Limited, London, UK, 1927).

Keynes

J. M.

, The General Theory of Employment, Interest, and Money (Macmillan, London, UK, 1936).

Hicks

, Value and Capital (Oxford, 1939).

Metzler

L. A.

, The nature and stability of inventory cycles. Rev. Econ. Stat. 23, 113–129 (1941).

Nerlove

, Adaptive expectations and cobweb phenomena. Q. J. Econ. 72, 227–240 (1958).

Muth

J. F.

, Rational expectations and the theory of price movements. Econometrica 29, 315–335 (1961).

Lucas

R. E.

, Expectations and the neutrality of money. J. Econ. Theor. 4, 103–124 (1972).

Fuster

, Laibson

, Mendel

, Natural expectations and macroeconomic fluctuations. J. Econ. Perspect. 24, 67–84 (2010).

Hirshleifer

, Li

, Yu

, Asset pricing in production economies with extrapolative expectations. J. Monet. Econ. 76, 87–106 (2015).

Barberis

, Greenwood

, Jin

, Shleifer

, X-CAPM: An extrapolative capital asset pricing model. J. Financ. Econ. 115, 1–24 (2015).

Adam

, Marcet

, Nicolini

J. P.

, Stock market volatility and learning. J. Finance 71, 33–82 (2016).

Bordalo

, Gennaioli

, Porta

R. L.

, Shleifer

, Diagnostic expectations and stock returns. J. Finance 74, 2839–2874 (2019).

Piazzesi

, Salomao

, Schneider

, Trend and cycle in bond premia. https://web.stanford.edu/∼piazzesi/trendcycle.pdf Accessed 8 December 2020.

Bhandari

, Borovicka

, Ho

, Survey data and subjective beliefs in business cycle models. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3473120 (22 October 2019).

Petersen

I. R.

, James

M. R.

, Dupuis

, Minimax optimal control of stochastic uncertain systems with relative entropy constraints. IEEE Trans. Automat. Contr. 45, 398–412 (2000).

Duchi

, Glynn

, Namkoong

, Statistics of robust optimization: A generalized empirical likelihood approach. Math. Oper. Res., in press.

Škulj

, Discrete time Markov chains with interval probabilities. Int. J. Approx. Reason. 50, 1314–1329 (2009).

Hansen

L. P.

, Singleton

K. J.

, Efficient estimation of linear asset-pricing models with moving average errors. J. Bus. Econ. Stat. 14, 53–68 (1996).

Nagel

, Singleton

K. J.

, Estimation and evaluation of conditional asset pricing models. J. Finance 66, 873–909 (2011).

Gagliardini

, Ronchetti

, Comparing asset pricing models by the conditional Hansen-Jagannathan distance. J. Financ. Econom. 18, 333–394 (2020).

Antoine

, Proulx

, Renault

, Pseudo-true SDFs in conditional asset pricing models. J. Financ. Econ., 10.1093/jjfinec/nby017 (2018).

Hansen

L. P.

, Jagannathan

, Assessing specification errors in stochastic discount factor models. J. Finance 52, 557–590 (1997).

Hansen

L. P.

, Nobel lecture: Uncertainty outside and inside economic models. J. Polit. Econ. 122, 945–987 (2014).

Ghosh

, Julliard

, Taylor

A. P.

, What is the consumption-CAPM missing? An information-theoretic framework for the analysis of asset pricing models. Rev. Financ. Stud. 30, 442–504 (2017).

Manski

C. F.

, Survey measurement of probabilistic macroeconomic expectations: Progress and promise. NBER Macroecon. Annu. 32, 411–471 (2018).

Bordalo

, Gennaioli

, Ma

, Shleifer

, Over-reaction in macroeconomic expectations. Am. Econ. Rev. 110, 2748–2782 (2020).

Donsker

M. D.

, Varadhan

S. S.

, Asymptotic evaluation of certain Markov process expectations for large time, I-IV. Commun. Pure Appl. Math. 28, 1–47 (1975).

Dupuis

, Ellis

, A Weak Convergence Approach to the Theory of Large Deviations (John Wiley and Sons, Inc., New York, NY, 1997).

Hansen

L. P.

, A method for calculating bounds on the asymptotic covariance matrices of generalized method of moments estimators. J. Econom. 30, 203–238 (1985).

Hansen

L. P.

, Richard

S. F.

, The role of conditioning information in deducing testable restrictions implied by dynamic asset pricing models. Econometrica 55, 587–613 (1987).

Bradley

, Introduction to Strong Mixing Conditions (Kendrick Press, Heber City, UT, 2007), vol. I.

Varadhan

S. R.

, Special invited paper: Large deviations. Ann. Probab. 36, 397–419 (2008).

Dembo

, Zeitouni

, Large Deviations Techniques and Applications (Springer Science & Business Media, 2009), vol. 38.

Eckstein

, Extended Laplace principle for empirical measures of a Markov chain. Adv. Appl. Probab. 51, 136–167 (2019).

Qin

, Lawless

, Empirical likelihood and general estimating equations. Ann. Stat. 22, 300–325 (1994).

Owen

A. B.

, Empirical Likelihood (CRC Press, 2001).

Hansen

L. P.

, Sargent

T. J.

, Robust control and model uncertainty. Am. Econ. Rev. 91, 60–66 (2001).

Ghosh

, Roussellet

, Identifying beliefs from asset prices. 10.2139/ssrn.3400005 (17 June 2019).

Peng

, “Nonlinear expectations, nonlinear evaluations and risk measures” in Stochastic Methods in Finance: Lecture Notes in Mathematics, Frittelli

, Runggaldier

, Eds. (Springer Berlin Heidelberg, Berlin, Heidelberg, Germany, 2004), pp. 165–253.

Hansen

L. P.

, Scheinkman

J. A.

, Long-term risk: An operator approach. Econometrica 77, 177–234 (2009).

Qin

, Linetsky

, Long-term risk: A martingale approach. Econometrica 85, 299–312 (2020).

Newman

C. M.

, Stuck

B. W.

, Chernoff bounds for discriminating between two Markov processes. Stochastics 2, 139–153 (1979).

Anderson

E. W.

, Hansen

L. P.

, Sargent

T. J.

, A quartet of semigroups for model specification, robustness, prices of risk, and model detection. J. Eur. Econ. Assoc. 1, 68–123 (2003).

Kreps

D. M.

, Porteus

E. L.

, Temporal resolution of uncertainty and dynamic choice. Econometrica 46, 185–200 (1978).

Epstein

L. G.

, Zin

S. E.

, Substitution, risk aversion, and the temporal behavior of consumption and asset returns: An empirical analysis. J. Polit. Econ. 99, 263–286 (1991).

Campbell

, Intertemporal asset pricing without consumption data. Am. Econ. Rev. 83, 487–512 (1993).

Epstein

L. G.

, Farhi

, Strzalecki

, How much would you pay to resolve long-run risk?. Am. Econ. Rev. 104, 2680–2697 (2014).

Dillenberger

, Gottlieb

, Ortoleva

, Stochastic impatience and the separation of time and risk preferences. 10.2139/ssrn.3645071 (8 July 2020).

Maheu

J. M.

, McCurdy

T. H.

, Identifying bull and bear markets in stock returns. J. Bus. Econ. Stat. 18, 100–112 (2000).

Stutzer

, A Bayesian approach to diagnosis of asset pricing models. J. Econom. 68, 367–397 (1995).

Stutzer

, A simple nonparametric approach to derivative security valuation. J. Finance 51, 1633–1652 (1996).

Avellaneda

, Minimum-relative-entropy calibration of asset-pricing models. Int. J. Theor. Appl. Finance 1, 447–472 (1998).

Kazemi

H. B.

, An intertemporal model of asset prices in a Markov economy with a limiting stationary distribution. Rev. Financ. Stud. 5, 85–104 (1992).

Alvarez

, Jermann

U. J.

, Using asset prices to measure the persistence of the marginal utility of wealth. Econometrica 73, 1977–2016 (2005).

Borovička

, Hansen

L. P.

, Scheinkman

J. A.

, Misspecified recovery. J. Finance 71, 2493–2544 (2016).

Bakshi

, Chabi-Yo

, Variance bounds on the permanent and transitory components of stochastic discount factors. J. Financ. Econ. 105, 191–208 (2012).

Ross

, The recovery theorem. J. Finance 70, 615–648 (2015).

Woodford

, Robustly optimal monetary policy with near-rational expectations. Am. Econ. Rev. 100, 274–303 (2010).

Hansen

L. P.

, Sargent

T. J.

, Three types of ambiguity. J. Monet. Econ. 59, 422–445 (2012).