Microbes and Hosts Cooccur in a Patchy Environment.

We consider a microbial population and a population of hosts in a landscape of $$ M$$ patches that decay over time. The microbial population consists of two different types, a fast-growing type and a slow-growing type whose growth rate is reduced by $$ c$$ with $$ 0\le c\le 1$$ relative to the fast type. Starting from an initially small founder population of $$ N_0$$ cells, both microbial types grow within a patch until the carrying capacity $$ K$$ of the patch is reached. We model this microbial growth within a patch as a stochastic process. Specifically, at each time step, a random microbial individual from the local population is chosen for reproduction with a probability proportional to its growth rate. If the population size within the patch is below the maximum size $$ K$$, its offspring is added to the same patch. As soon as the maximal population size is reached, microbial growth stops, thus the microorganisms stop dividing, and the final population composition of that patch is reached. Note that choosing a stochastic equivalent of logistic growth for the within-patch microbial dynamics does not change the results (SI Appendix, section 2). Once the carrying capacity of a patch is reached, the microbial population can only increase by dispersing to new patches. We assume that the microbes have only a very limited potential for independent dispersal, such that spread to new patches is mainly mediated by hitchhiking on multicellular, mobile organisms. In the following, we use Drosophila fruit flies as an example for a dispersing host, but our model applies to all host animals with similar ecologies.

The hosts develop within a patch alongside the microbes. Once they reach adulthood, the hosts leave the patch and act as dispersal vectors by inadvertently taking a sample of the local microbial population with them. The size $$ b$$ of this sample is assumed to be much smaller than the patch capacity $$ K$$, which is likely realistic for many host taxa, such as our focus example of insects on rotting fruit patches, where a much larger number of microbes grow on the substrate than are able to be taken up by the host. We assume that this uptake of microbes is completely random, meaning that hosts will indiscriminately take up both microbial types as a by-product of developing and feeding in a microbe-rich environment (i.e., there is no active selection by the host for the slow or fast microbial type). Similarly, for both microbial types, the host animals are simply dispersal vectors, and neither of them is inherently better at surviving the host-associated dispersal stage. Consequently, the microbial population within any specific host is, on average, a direct reflection of the microbial community structure of its source patch. Thus, the relative abundances of the two microbial types in hosts from the same patch are, on average, identical to their relative abundances within the original patch.

From the population of all adult hosts on all patches, a maximum of $$ D$$ randomly picked hosts eventually enter a common dispersal pool. From the dispersal pool, the hosts are randomly assigned to $$ M$$ new patches, where each host lays $$ H_0$$ eggs which found a new generation of hosts. Thus, each patch receives between zero and $$ n\hspace{0.17em}{H}_0$$ eggs, where $$ n$$ is the number of hosts assigned to this patch. Note that this allows for multiple host animals to simultaneously colonize the same patch and for patches to remain uncolonized. Along with the eggs, the hosts bring in the hitchhiking microbes they have picked up at their source patches to start a new within-patch cycle of microbial population increase. The microbes introduced to the new patch increase according to the stochastic population dynamics described above. A sketch of the full model alternating between a within-patch growth cycle and a dispersal phase is shown in Fig. 1. For details of the model, see Methods.

Fig. 1.

The stochastic dynamics of the slow (green dots) and fast (blue triangles) microbial types growing in a patchy landscape, illustrated by the patch-specific growth curves. Patches with a higher relative abundance of the slow type decay more slowly, allowing more hosts to develop to maturity. A random sample of the surviving mature hosts enters the dispersal pool, and each host takes a small random sample of the local microbial population with it. These hosts then lay their eggs in randomly assigned new patches, while the hitchhiking microbes provide the founding microbial population. This starts a new cycle of within-patch growth of microbes and development of hosts. The hosts in the dispersal pool are generally enriched in the slow type, because of prolonged survival of developing hosts in slower-decaying patches, setting the stage for a more specific association between the hosts and the slow type. It also allows for the survival or even gradual increase of the slow microbial type across all patches. The timeline at the bottom illustrates the consecutive phases of the dynamics and shows how, on average, the relative abundance of the slow type is higher within hosts in the dispersal pool than in the patches. The table on the right provides an overview of the model parameters and their definitions. The values given are the ones used for all simulations, unless otherwise stated. See Model and Results for further details.

Entanglement of Host Development and Microbial Growth within Patches.

We now introduce two factors which, together, have the potential to lead to an overrepresentation of one of the microbial types within the host animals, that is, a tipping of scale toward a more specific interaction with one of the types. The first factor is that patches decay in quality over time, and this decay is detrimental to the development of hosts. There are several not mutually exclusive reasons for this patch decay. For example, patch quality for the hosts may be directly linked to the availability of resources, which decline over time as the growing microbial populations consume these resources. In this scenario, the microbes act as competitors to the developing hosts. In a related scenario, other microbes or animals may tap into the resources a patch provides, thereby leading to a gradual decline of resources up to the complete destruction of a patch. Whatever the reasons for patch decay, the survival probabilities of developing hosts decline with deteriorating patch quality. The second factor is that the slowly replicating microbial type delays the decay of a patch. This could be due to either a reduced uptake of resources as a consequence of slower growth or an active role in protecting the patch against other competitors, for example, through the costly production and release of a metabolite toxic to competitors (11, 15).

The survival of hosts depends, at least in part, on how fast the patch is decaying, which, in turn, is influenced by the abundances of the two microbial types. Here we assume that a patch decays faster with increasing absolute abundances of the fast type ($$ N_f$$) and of the slow type ($$ N_s$$) within the patch. Specifically, assuming that the relationship between patch decay and host survival is proportional to the sum of the microbial abundances, we write the decay probability of a host at each time step as

The ability of the microbes and hosts to colonize new patches now depends on two opposing processes with distinct timescales. The first one is the time it takes for the hosts to fully develop. Here we assume that each host takes $$ \tau $$ time steps to maturation. The second timescale is determined by the survival time of developing hosts, that is, the average number of time steps until all hosts within a patch are dead. We derive analytical formulas for the survival of hosts in important special cases in SI Appendix, section 1, showing that hosts indeed, on average, survive longer in patches with higher abundances of the slow type (see SI Appendix, Fig. S1). The entanglement of these two timescales leads to an indirect interaction between the microbial population and the developing hosts within a single patch. If the development time $$ \tau $$ of the hosts is longer than their survival time, on average, no host animal reaches maturation, and the hosts eventually die out. If, on the other hand, hosts mature very quickly, they are not affected by patch decay, and most hosts reach maturity regardless of the composition of the microbial population. Between these two extremes, however, the number of surviving hosts from a specific patch depends on the composition of the microbial population within that patch.

The composition of the microbial populations will generally vary between different patches, since population growth is a stochastic process. If the initial abundance of the fast type is low compared to the carrying capacity $$ K$$, and if then a single slow type is introduced, the fast type will typically reach much higher abundances than the slow type (Fig. 2). However, despite the clear local advantage of the fast type, its relative abundance across patches can vary considerably due to stochastic effects, which are especially pronounced when population size is small. This variation then entails random differences in the survival rate of developing hosts between patches, ultimately resulting in considerable variation in the number of hosts leaving a patch (Fig. 2).

Fig. 2.

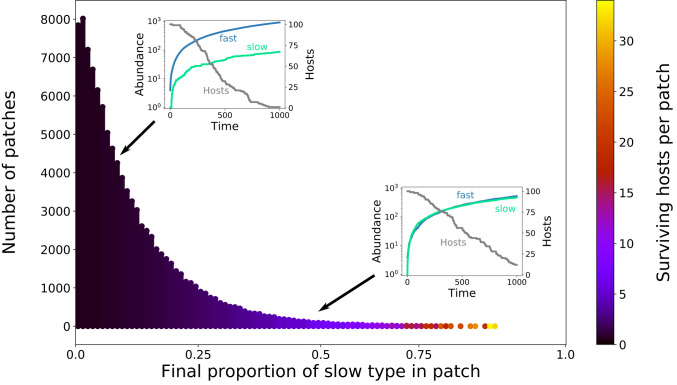
Histogram of the final proportions of the slow microbial type in 100,000 patches, each starting with an initial microbial population of one slow and four fast types, and the corresponding expected number of surviving hosts per patch (color coded). As expected, the fast type dominates in almost all patches, with the slow type mostly reaching relative abundances of less than 20%. A typical example of the corresponding within-patch population growth is shown in Top Left Inset. However, due to the stochastic population dynamics, in particular during the low abundances at the start of the growth cycle, in some patches, the slow type reaches relative abundances comparable to the fast type. An example of this is shown in the Bottom Right Inset. The coloring of the bars indicates the average number of hosts surviving in the corresponding patches. Each patch initially receives 100 developing hosts, and, in patches with a higher abundance of the slow type, which slows down patch decay, on average, a higher number of those hosts survive. Parameter values: $$ M=50,\hspace{0.17em}K=10^4,\hspace{0.17em}D=100,\hspace{0.17em}c=0.15,\hspace{0.17em}{H}_0=100,\hspace{0.17em}b=5,\hspace{0.17em}\tau =10^3,\hspace{0.17em}{\delta }_K=0.1,\hspace{0.17em}{\delta }_s=0.1$$.

Multiple Patches and Dispersal Can Favor the Slowly Growing Microbial Type.

Even though, locally, the slow microbial type is outcompeted by the fast type, and the microbiota of hosts directly reflect the community compositions of their respective source patches, the hosts in the dispersal pool are, on average, enriched in the slow type. This is because patches with a higher abundance of the slow type decay more slowly and thus allow more hosts to mature. Thus, patches in which the slow type is more abundant, on average, contribute more hosts to the dispersal pool, which necessarily carry a higher abundance of the slow type, reflecting the population structure of their source patch. This enrichment of the slow type within dispersing hosts is a central, dynamic effect in our model, which increases the chances of a new patch being colonized by a host enriched in the slow type. This counteracts the within-patch advantage of the fast-growing microbial type and can allow the slow and fast types to coexist over many growth and dispersal cycles (Fig. 3), until, eventually, one of the two goes to fixation. This process is illustrated in Fig. 4 across a few exemplary patches and growth cycles.

Fig. 3.

Example of the average relative abundance of the slow microbial type within patches and within hosts. The relative abundance $$ f$$ of the slow type during the host-associated phase is generally higher than in the patches themselves; that is, the hosts are enriched in the slow type. Parameters: $$ M=50,\hspace{0.17em}K=10^4,\hspace{0.17em}D=100,\hspace{0.17em}c=0.15,\hspace{0.17em}{H}_0=100,\hspace{0.17em}b=2,\hspace{0.17em}\tau =10^3,{\delta }_K=0.1,\hspace{0.17em}{\delta }_s=0.1$$.

Fig. 4.

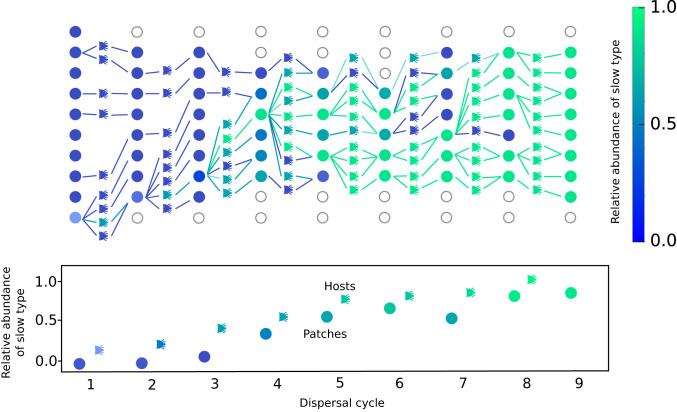
Illustration of a simulation showing the gradual increase and eventual fixation of the slow microbial type across a maximum of 10 patches after several growth cycles, despite growing slower in all patches. We start from a single slow type in one patch. Patches are colored according to the relative abundance of the slow type at the end of a growth cycle, with empty circles denoting noncolonized patches. Each patch contributes a specific number of hosts to the dispersal pool, which are also color-coded according to the relative abundance of the slow type within each individual host. The hosts are then randomly assigned to a new patch, where the growth cycle restarts. Clearly, patches with a higher abundance of the slow type contribute, on average, more hosts to the dispersal pool, which colonize more patches, thus leading to a gradual increase and eventual fixation of the slow type across all patches. The graph at the bottom illustrates both this increase of the relative abundance of the slow type across patches and its higher abundance within hosts compared to the patch environments. Parameters: $$ M=10,K=10^4,\hspace{0.17em}c=0.15,\hspace{0.17em}{H}_0=100,\hspace{0.17em}b=5,\hspace{0.17em}D=10,\hspace{0.17em}\tau =10^3,\hspace{0.17em}{\delta }_K=0.1,\hspace{0.17em}{\delta }_s=0.1$$.

Since each host picks up only a very few microbes compared to the total local population, that is, $$ b\ll K$$, the dispersal stage poses a bottleneck for the microbes. The fixation of the slow type becomes more likely when this dispersal-induced bottleneck becomes more severe (Fig. 5A). This is because, by chance, some hosts will pick up only slow-growing cells and initiate, after dispersal, pure slow-type patches. Such pure slow-type patches allow a disproportionate number of hosts to mature, all of which then again carry only slow microbial types to new patches. As a consequence, a pure slow-type lineage can rapidly expand and cause displacement of less advantageous, in terms of host survival, fast-type or mixed patches. If the bottleneck is small enough, this can then lead to the extinction of the fast microbial type and the fixation of the slow type in all patches (Fig. 5A). The size of the dispersal pool, that is, how many hosts disperse compared to the number of available patches, has a relatively small effect on the slow type’s fixation probability (Fig. 5B). The fixation probability initially increases slightly, but, as soon as each new patch receives, on average, at least one host, it remains largely unaffected by a further increase in the number of host animals in the dispersal pool.

Fig. 5.

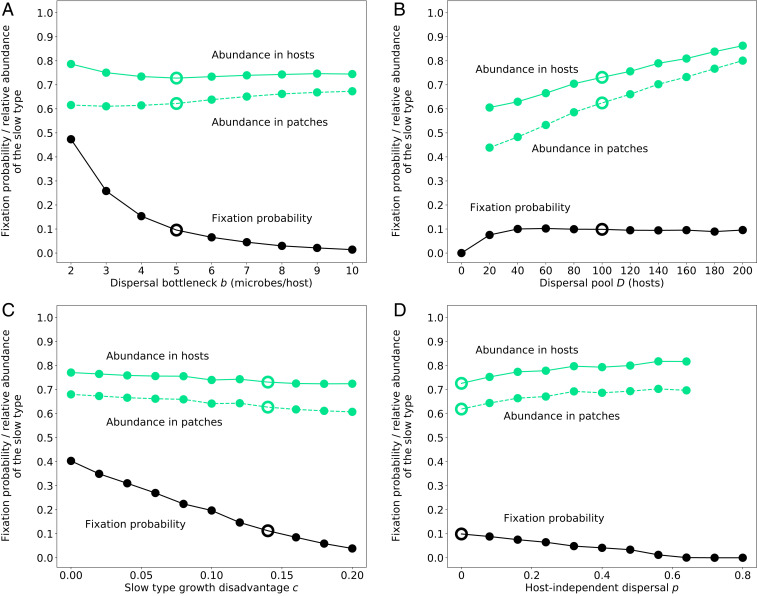
Fixation probability of a single invader of the slow microbial type and corresponding average abundance of the slow type in patches and in hosts as a function of (A) the size of the dispersal bottleneck imposed by hosts, (B) the size of the host dispersal pool, (C) the fitness disadvantage of the slow type, and (D) the number of microbes dispersing independent of hosts relative to the maximally possible number of microbes dispersing within hosts ($$ p=m/\left(b\hspace{0.17em}D\right)$$). Importantly, the average relative abundance of the slow type is always higher in the hosts than in the patches. In all cases, each data point represents the average of 10,000 stochastic simulations. The open circles denote the parameter values used in the other panels, and the remaining fixed parameters are $$ M=50,\hspace{0.17em}K=10^4,\hspace{0.17em}\hspace{0.17em}{H}_0=100,\hspace{0.17em}\tau =10^3,\hspace{0.17em}{\delta }_K=0.1,\hspace{0.17em}{\delta }_s=0.1$$.

As expected, fixation of the slow type becomes less likely the greater its fitness disadvantage relative to the fast type (Fig. 5C). In general, the impact of the slow type on patch decay is independent of its fitness, and, for a fixed growth rate of the slow type, its fixation is most likely when it does not contribute to patch decay at all (see SI Appendix, Fig. S3A). The more the slow type contributes to patch decay, the fewer hosts survive in the patch and the less likely becomes the slow type’s survival and fixation. When it has essentially the same impact as the fast type (i.e., $$ {\delta }_s$$ close to one), survival of the slow type becomes virtually impossible (see SI Appendix, Fig. S3A). An interesting scenario arises when the slowly growing type reduces patch decay through reduced uptake of resources. In this case, the fitness of the slow type and its contribution to patch decay are coupled. If the slow type’s contribution to patch decay decreases with increasingly disadvantageous fitness relative to the fast type, there is an optimal growth rate of the slow type at which survival and fixation are most likely (see SI Appendix, Fig. S3B). This optimal growth rate emerges at an intermediate value, where the slow type’s fitness is still high enough to allow it to occasionally reach high abundances within a patch, but not so high that it leads to rapid patch decay. This represents a balance between within-patch competition (high growth rate) and dispersal (low impact on host development).

This analysis reveals the crucial role of microbial growth rate and patch decay in shaping microbial abundance in the host. To further test whether the results depend on the specific within-patch growth dynamics as described above, we replaced the corresponding stochastic process with a stochastic equivalent of logistic growth (SI Appendix, section 2). This yields almost identical results (SI Appendix, Figs. S5 and S6), showing that the effect of enrichment of the slow type does not critically depend on the specific form of microbial growth.

In all these scenarios, we have assumed that host-mediated dispersal is the only route by which microbes can reach new patches. It is, however, possible to relax this assumption and allow for host-independent microbial dispersal between patches. We include such host-independent dispersal by sampling $$ m$$ microbes from across all patches at the time of host dispersal, and assigning them randomly to new patches. This process is similar to assuming that patches already contain small resident populations of microbes. Because the sampling from the source patches is random, the compositions of these initial populations, on average, directly reflect the composition of the metapopulation of microbes in the source patches. This type of global dispersal thus leads to increased nonassortative mixing of the microbial populations on the patchy landscape, which generally favors fast growth. But, over a large range of the relative sizes of the host-independent microbial dispersal pool, the previous results still hold (Fig. 5D). Only when host-independent dispersal between patches approaches levels similar to host-mediated dispersal will the fast-growing type be almost universally favored. This shows that a patchy environment and dispersal limitation is indeed crucial for the observed results.

Enrichment of the Slow Type in the Host.

The observed survival and fixation of the slow type is possible, despite its fitness disadvantage, because the relative abundances of the slow microbial type are always higher in the dispersing hosts than in the patches (Fig. 5). This is a key result of our model, which does not depend on the slow type being specifically beneficial to the host or being actively picked up by it. We explicitly assumed that, just like the fast microbial type, the slow type impairs development of hosts within a patch. But, crucially, it does so to a lesser extent than the fast type. The enrichment of the slow type is thus a consequence of patches with higher abundances of the slow type disproportionately contributing to the host dispersal pool, rather than a specific beneficial effect of the slow type.

This association between the slow type and the hosts is not only a general pattern; the host metapopulation is also very stable against reinvasion of the fast microbial type. This is because, if a patch is invaded by a fast-growing type, this particular patch will not allow many hosts to mature, while the remaining pure slow-type patches contribute a very high number of hosts to the dispersal pool. So, even if a few hosts survive in the invaded patch, the resulting mature hosts carrying fast-growing types are diluted out in the dispersal pool and only rarely colonize new patches. This makes dispersal from an invaded/contaminated patch to new patches less likely, thus effectively containing invading fast types in a self-imposed quarantine.

Sterile Patches.

So far, we have assumed that, initially, all patches are occupied by microbes. Under these conditions, hosts can never develop in a completely microbe-free (or sterile) patch, since they will always bring a founding microbial population from their nonsterile source patch. But Eq. 1 implies that hosts would, in fact, perform best on sterile patches, as hosts do not decay at all under those conditions (i.e., $$ \delta =0$$). To investigate whether our results still hold when hosts can develop in sterile patches, we repeated our simulations with only 10% of the patches initially being colonized by microbes. In this case, the sterile patches initially contribute the vast majority of hosts to the dispersal pool, since there is no decay of hosts in these patches. In the absence of host-independent dispersal, this means that the microbes die out within the first few dispersal cycles, resulting in almost all patches and all hosts remaining sterile afterward (see SI Appendix, Fig. S4). However, with increasing host-independent dispersal, complete sterility of patches, and hosts, becomes harder and harder to maintain. Then, as in our previous results, patches with a higher proportion of the slow type contribute more hosts to the dispersal pool, making the spread of the slow type and its fixation more likely (see SI Appendix, Fig. S4). In contrast to the case when all patches were initially occupied by microbes (Fig. 5D), increasing host-independent dispersal thus increases the fixation probability of the slow type when the majority of patches are initially sterile. In fact, in this scenario, small to intermediate amounts of dispersal independent of hosts make it even more likely for the slow type to go to fixation, as it encounters reduced competition from the fast type within the metapopulation across all patches. But, as before, when host-independent dispersal becomes the dominant mode of dispersal, its mixing effect favors fast growth and leads to a decline of the fixation probability of the slow type (see SI Appendix, Fig. S4). When many patches are initially microbe free, an intermediate level of host-independent dispersal is thus optimal for the slow-growing type and its association with the host. In general, sterile patches, and thus microbe-free hosts, can only be maintained under the restrictive assumption that sterile patches exist initially and that there is only very little host-independent dispersal. In more realistic scenarios, microbial populations will occupy the majority of patches, making it unlikely for the hosts to avoid codevelopment with microbes.

Timing of Host Dispersal.

In our model, we have assumed that all surviving hosts across all patches disperse synchronously in evenly spaced intervals determined by the host development time $$ \tau $$. At the same time, a completely new set of patches is available for the dispersing hosts to colonize. Our analysis of the survival of hosts within patches over time (SI Appendix, section 1 and Fig. S1) indicates that this assumption can be relaxed, as there is, in fact, a time window for host dispersal which is optimal with respect to enrichment of the slow type. If hosts develop quickly and disperse early, they are not affected by patch decay and enrichment, and fixation of the slow type is unlikely (SI Appendix, Fig. S2). Conversely, if the development time is too long, the hosts do not survive until dispersal and fixation of the slow type is again unlikely (SI Appendix, Fig. S2). This shows that enrichment of the slow type is most likely if hosts disperse in a time window that is mainly determined by the decay rate given in Eq. 1.

But this effect of host dispersal timing does not require that all hosts disperse synchronously at the same time, as we will now show. We consider a generalized version of the model where each individual host has a random development time drawn from a uniform distribution on the interval $$ \left[\tau -{\tau }_d,\tau +{\tau }_d\right]$$ around a mean development time $$ \tau $$. We further generalize the model by relaxing the assumption that there is a complete turnover of patches coinciding with host dispersal. We do this by replacing a randomly sampled number $$ M_0\le M$$ of patches with empty patches at random times $$ t_i$$. The synchronous model we have discussed above then corresponds to the special case $$ {\tau }_d=0$$ and $$ t_i=\tau $$ for all $$ i$$ with complete patch renewal (i.e., $$ M_0=M$$).

We illustrate the dynamics of this more general model by letting the development times of individual hosts vary by $$ {\tau }_d=200$$ around a mean value of $$ \tau =10^3$$. These hosts now migrate on a landscape of $$ M=100$$ patches, of which a single patch ($$ M_0=1$$) is renewed at, on average, every 100 time steps. As a consequence, the synchronized cycles of dispersal and within-patch microbial growth across all patches are broken, and the majority of patches are occupied by growing microbial populations at all times (SI Appendix, Fig. S7A). The corresponding dynamics in the host metapopulation show fluctuations around long-term averages, with marked differences depending on whether the slow type can spread across the patches or not (SI Appendix, Fig. S7B). While the hosts can survive on pure fast-type patches, the average number of live hosts per patch is much higher when the slow type is able to spread (SI Appendix, Fig. S7B). In line with our above results for synchronous host dispersal, when the slow type spreads across the patches, its average relative abundance is always higher in dispersing hosts compared to its relative abundance within the patches (SI Appendix, Fig. S7C).

Microbial Within-Patch Dynamics.

We consider a population of $$ N_f$$ fast types and $$ N_s$$ slow types in a patch of maximal size $$ K$$. At each time step, the probabilities for the abundance of the fast ($$ N_f$$) or the slow ($$ N_s$$) type to increase by one are given by

Host Decay and Dispersal.

Denote by $$ H$$ the number of live hosts at a certain time within a patch with microbial abundances of $$ N_f$$ fast types and $$ N_s$$ slow types. The probability of each host to die is given by Eq. 1, and the total number $$ H_{\delta }$$ of hosts to die at this time step is then drawn from a binomial distribution $$ H_{\delta }\approx B\left(H,\delta \right)$$ with mean $$ H\hspace{0.17em}\delta $$.

After $$ \tau $$ time steps for each surviving host, a sample of size $$ b$$ is randomly drawn without replacement from the local microbial population. Since $$ b$$ is constant and independent of the current size of the microbial population, uptake is modeled in terms of the proportions of the microbial types, not their absolute abundances. This is reasonable because the numbers taken up by an individual host are orders of magnitude lower than the total pool available in the patch. Moreover, we assume that the number of hosts will only ever decrease in a patch, so that, even if microbes grow extremely slowly, the number of microbes dispersing with hosts is still small compared to the total number of microbes within a patch. The microbial samples are then randomly assigned to $$ M$$ new patches as the initial microbial populations.