
Competing Interests: The authors have declared that no competing interests exist.
- Altmetric
Prisoner’s dilemma game is the most commonly used model of spatial evolutionary game which is considered as a paradigm to portray competition among selfish individuals. In recent years, Win-Stay-Lose-Learn, a strategy updating rule base on aspiration, has been proved to be an effective model to promote cooperation in spatial prisoner’s dilemma game, which leads aspiration to receive lots of attention. In this paper, according to Expected Value Theory and Achievement Motivation Theory, we propose a dynamic aspiration model based on Win-Stay-Lose-Learn rule in which individual’s aspiration is inspired by its payoff. It is found that dynamic aspiration has a significant impact on the evolution process, and different initial aspirations lead to different results, which are called Stable Coexistence under Low Aspiration, Dependent Coexistence under Moderate aspiration and Defection Explosion under High Aspiration respectively. Furthermore, a deep analysis is performed on the local structures which cause defectors’ re-expansion, the concept of END- and EXP-periods are used to justify the mechanism of network reciprocity in view of time-evolution, typical feature nodes for defectors’ re-expansion called Infectors, Infected nodes and High-risk cooperators respectively are found. Compared to fixed aspiration model, dynamic aspiration introduces a more satisfactory explanation on population evolution laws and can promote deeper comprehension for the principle of prisoner’s dilemma.
Introduction
The emergence and stability of cooperative behavior among selfish individuals is a challenging problem in biology, sociology and economics [1]. The prisoner’s dilemma(PD) game is considered as a paradigm to portray competition among selfish individuals [2–6]. For general parameter settings, defection is favoured by evolutionary selection, but we can easily observe numerous cooperation phenomenon in various scenarios, e.g., animals will cooperate to obtain food instead of preying alone [7]; companies will set appropriate commodity prices instead of maliciously cutting prices [8]; humans will choose to obey the order instead of jumping in line, etc [9]. Evolutionary game theory provides a practical framework to explain how the cooperation forms [10–14]. Besides, five representative mechanisms considered as promoting cooperation have been investigated: kin selection, direct and indirect reciprocity, network reciprocity and group selection [15].
Since the pioneering work of Nowak and May [16], spatial games were proposed and have attracted ample attention of researchers, in which players are located on the spatially structured network and only interact with their neighbors. Since then, numerous studies have emerged to propose various mechanisms which explain the emergence and stability of cooperative behavior, such as punishment [17–20], migration [21–23], game organizers [24, 25], teaching ability [26–28], and so on. In recent years, aspiration, a parameter representing individual’s expectation, has attracted many researchers’ attention [29–32]. Win-Stay-Lose-Learn is a representative model based on aspiration, in which one will try to change its strategy only when its payoff is lower than aspiration [33–35]. Liu and Chen investigated the Win-Stay-Lose-Learn rules in spatial prisoner’s dilemma game [33]; Chu and Liu added the voluntary participation into the Win-Stay-Lose-Learn rules [34]; Fu studied the stochastic Win-Stay-Lose-Learn rules in the spatial public goods game [35].
These research held the assumption that an individual player’s aspiration is fixed. However, according to Expected Value Theory and Achievement Motivation Theory proposed by Atkinson [36], one’s aspiration will be influenced by its previous payoff, and individuals tend to lower their aspirations in interactions in a crisis [37]. If one’s payoff is higher than its aspiration, the aspiration tends to be increased, otherwise decreased, some researchers also paid attention to this and had some related researches. [37–39]. In this paper, a dynamic aspiration model is introduced based on Win-Stay-Lose-Learn rules, and the principle of defection’s expansion or cooperation’s survival under the dynamic aspiration model is investigated. The rest of our paper is organized as follows. First the detailed model of the dynamic aspiration based on Win-Stay-Lose-Learn rules is shown. Then the main results under our model is provided by four parts: Overview, Stable Coexistence under Low Aspiration, Dependent Coexistence under Moderate aspiration and Defection Explosion under High Aspiration. The concept of enduring (END) and expanding (EXP) periods [40–42] are also used to justify the mechanism of network reciprocity in view of time evolution and find typical feature nodes called Infectors, Infected nodes and High-risk cooperators respectively. Finally the wider implications of our work and the direction of the future research are discussed.
Model
Our model is described as follows. We use the L × L square lattice with periodic boundary conditions. Each node represents a player who has one of the following two strategies: cooperation(), or defection(
(a)Rule of game: Each node i plays the prison’s dilemma game with its four neighbors and gets the payoff

 |
 | |
 | R | S |
 | T | P |
Without loss of generality, we set R = 1 and P = 0. And to ensure single parameter, there are some typical representative sub-classes of PD game, e.g., Donor & Recipient (D & R) game which assumes T + S = 1 [43–49] and boundary game which assumes t = b and S = 0 [16, 33]. In this paper, the boundary game is used as what we mainly study is the impact of T on evolution process. Thought it has S < 0 in PD games, our experiment shows that the Monte Carlo simulation result is almost the same as S = 0 when S is close to 0(for instance, S = −0.01), so it is assumed that S = 0 in boundary games.
(b)Rule of strategy’s update: Each node i chooses one of its four neighbors j randomly with equal probability. If i’s payoff is lower than its aspiration Ai, i will be dissatisfied and choose to adopt j’s strategy with the probability:
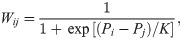
(c)Rule of aspiration’s update: Each node i updates its aspiration by the formula:
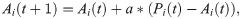
The step (a)-(c) will repeat 100,000 times in one simulation. The fraction of cooperators and defectors at step t are denoted as
Results
0.1 Overview
Our experiment is performed on the 100 × 100 square lattice with periodic boundary conditions. In initial, cooperators and defectors are distributed uniformly at random occupying half of the square lattice respectively, and all the nodes are given the same initial aspiration A. As the main parameters, we consider the initial aspiration level A and the temptation to defect b. Fig 1 presents the fraction

Average fractions of cooperation when stable as a function of b for different values of the initial aspiration A, as obtained by means of simulations on square lattices.
0.2 Stable Coexistence under low aspiration (A ≤ 1.0)
For small values of A, individual’s aspiration is easy to be satisfied so cooperators and defectors can coexist. For A = 0, all the nodes are satisfied and never change their strategies, so
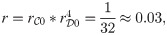
0.3 Dependent Coexistence under moderate aspiration (1.0 < A ≤ 2.0)
For moderate values of A, cooperators can’t survive for small values of b. Fig 2 shows the spatial distributions of strategies and aspirations at different time steps t for A = 1.6 and b = 1.2. The evolution process can be divided into the following stages:
At first, every node with strictly less than two
When t = 10, some cooperators still survive by forming some clusters in the END period. The defectors neighboring with the clusters are dissatisfied and have lower payoffs than their
When t = 100, cooperators have expanded fully during the EXP period and
When t = 200, defectors gradually penetrated into the cooperators’ clusters. These cooperators’ aspirations are now close to 4.0 so once they neighbor with a defector, they will be dissatisfied and also change into defectors gradually. As a result, chain phenomenon happens that defectors almost occupy the entire network and the cooperators almost disappear rapidly.

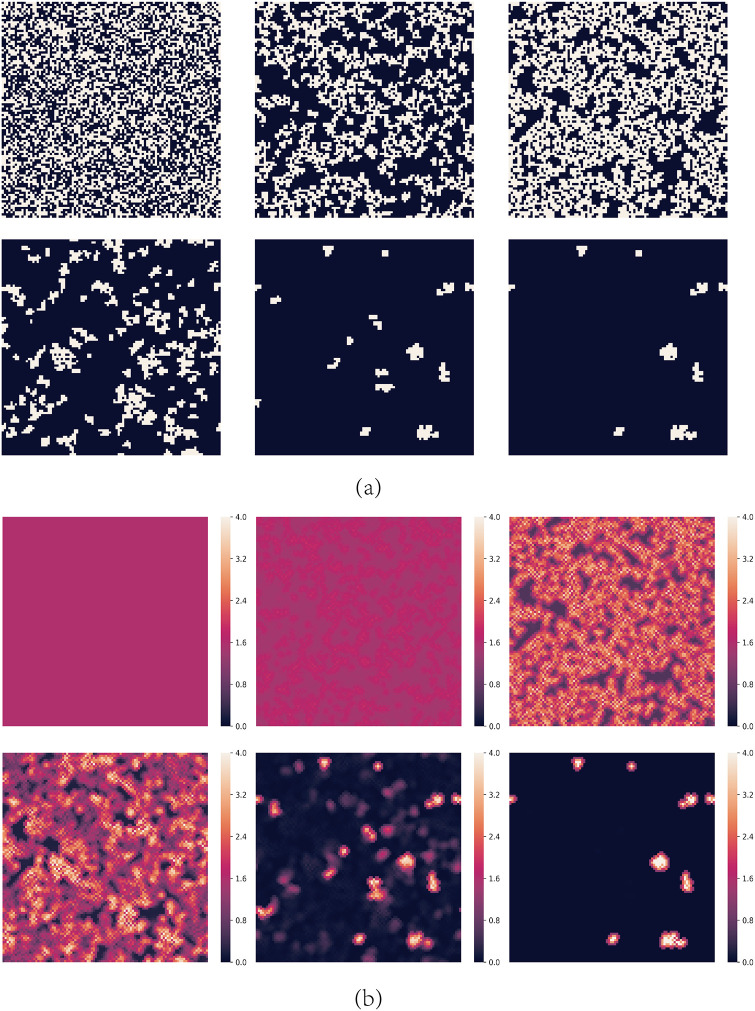
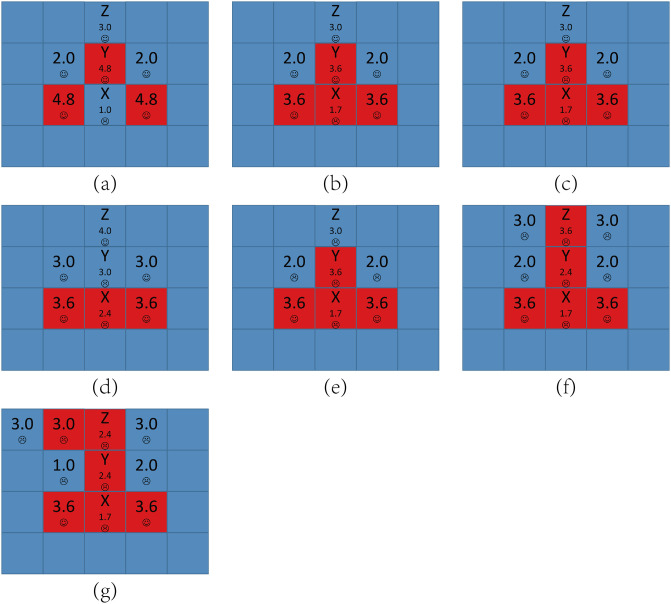
Snapshots of typical distributions of strategies and aspirations at different time steps t for A = 1.6 and b = 1.2.
(a) represents strategies, where cooperators are depicted white and defectors are depicted black. (b) represents aspirations. The steps of them are t = 0, 10, 100, 200, 500 and 1000 respectively.
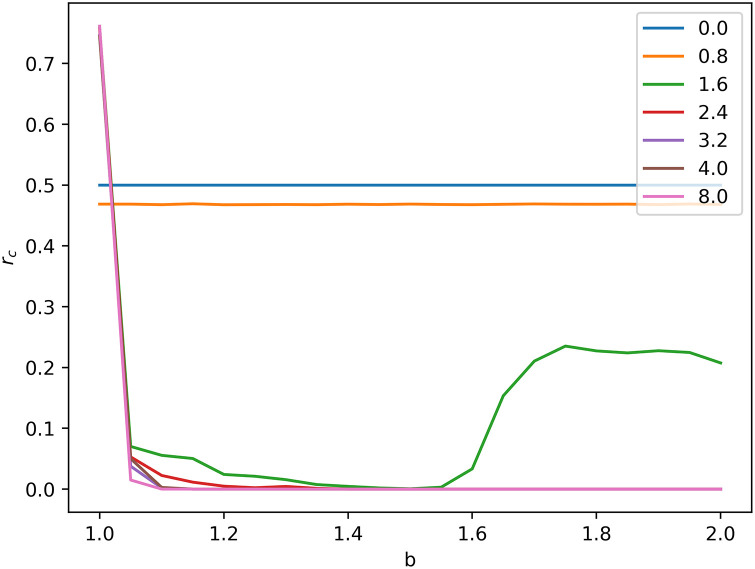
One can see that although cooperators can survive in the END period and expand in the EXP period by forming clusters, defectors finally occupy the network when it is stable. The network reciprocity is undermined by dynamic aspirations. In dynamic aspiration models, cooperators’ aspirations will become too high to endure defectors’ re-expansion because of the long-term satisfaction. which is different from the fixed aspiration model. Fig 3 shows the probability that cooperators could survive as a function of the cooperators’ initial proportion

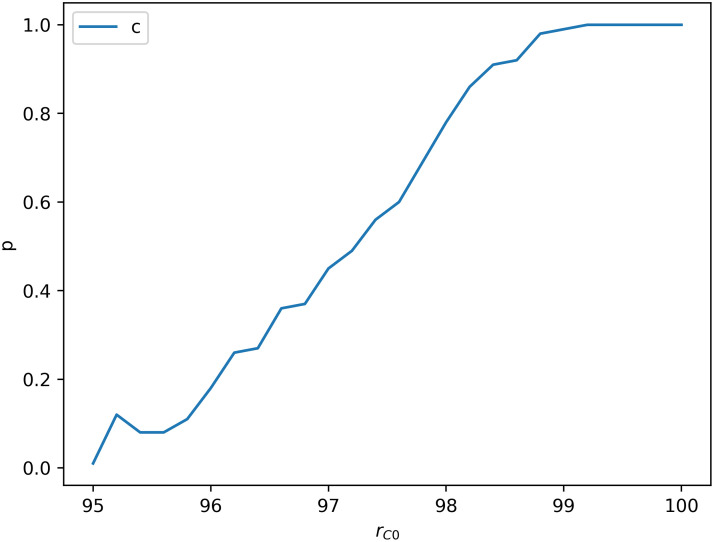
The probability that cooperators can survive as a function of the cooperators’ initial proportion
Cooperators are easier to survive when
Fig 4 shows all possible local structures in the network for A = 1.6 and b = 1.2. When a node has two or less

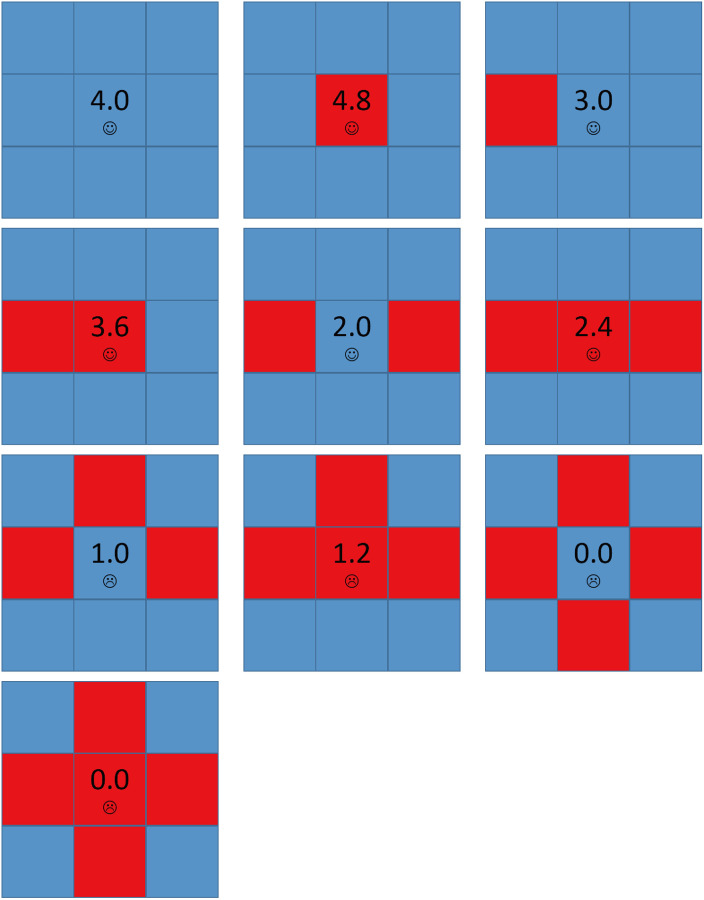
The local structures of strategies for A = 1.6 and b = 1.2.
Each square corresponds to a single player, where cooperators are depicted blue and defectors are depicted red. Value denoted in the center square is the individual’s payoff. Smiling face represents satisfaction while crying face represents dissatisfaction.
Now we consider the structure that a node has three
When t = 0, the only one node dissatisfied is node X because its aspiration is 1.0. Since it has three D neighbors and one 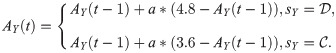
With t growing, we can easily prove that AY will be higher than 3.6. Next time when X evolves into a defector, PY = 3.6 < AY, so Y is dissatisfied. Y has three 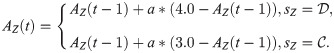
With t further growing, we can easily prove that AZ will be higher than 3.0. Next time when Y evolves into a defector, PZ = 3.0 < AZ, so Z is dissatisfied and may evolve into a defector in a few steps. Now Z’s other neighbors’ aspirations are all near to 4.0, which we call High-risk cooperator. Once Z evolves into a defector, their payoffs decrease to 3.0 so they are dissatisfied and may evolve into defectors, too.
Furthermore, almost every node’s aspiration in the network is near to 4.0 because their payoffs have been keeping 4.0 for a long time. In other word, all the cooperators in the network have became High-risk cooperators. As a result, for each cooperator i, once one of i’s neighbors evolves into a defector, i may evolve into a defector soon, which is a chain phenomenon and causes defectors’ expanding.

The detailed principle for defectors’ expanding for A = 1.6 and b = 1.2.
A node is surrounded by three defectors and one cooperator initially. Smiling face represents satisfaction while crying face represents dissatisfaction.
Fig 6 shows the spatial distributions of strategies and aspirations at different time steps t for A = 1.6, b = 1.2 with the above initial structure, from which we can also get the expansion trajectory by the aspiration distribution.

Snapshots of typical distributions of strategies and aspirations at different time steps t under the initial structure shown in Fig 4 for A = 1.6 and b = 1.2.
(a) represents strategies, where cooperators are depicted white and defectors are depicted black. (b) represents aspirations. The steps of them are t = 0, 10, 100, 200, 500 and 1000 respectively.
In the network with random setup, during the END and EXP period, cooperators will survive and expand by the mechanism of network reciprocity. But once there is at least one Infector who has three
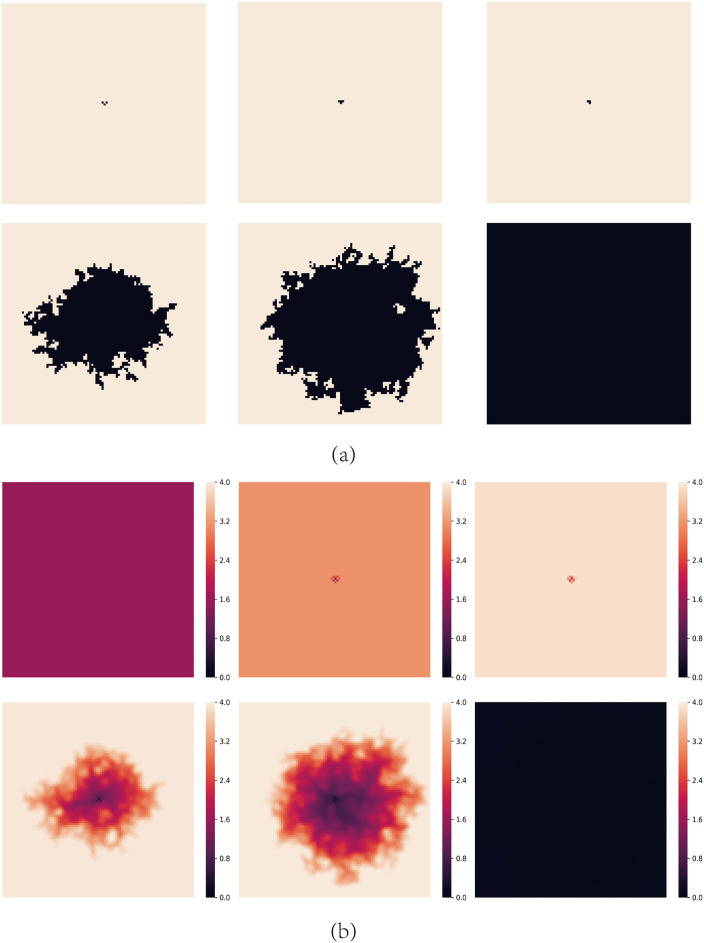
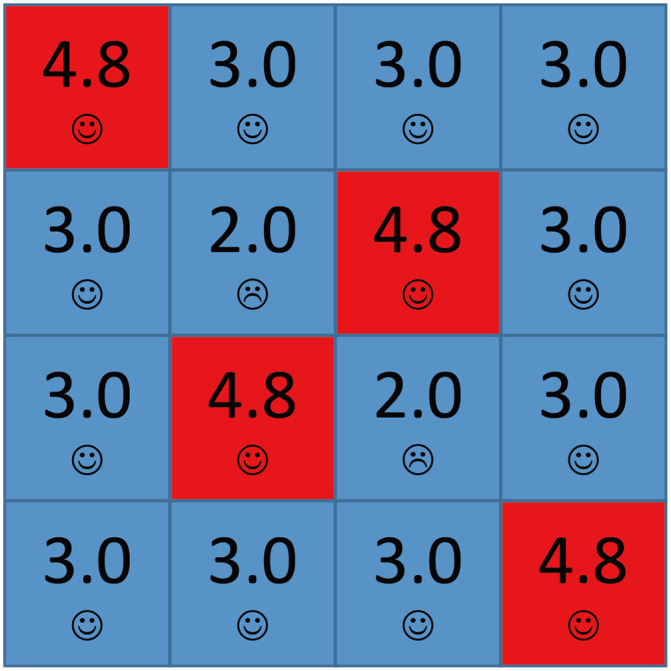
However, for large values of b, cooperators can partially survive. Fig 7 shows all possible local structures in the network for A = 1.6 and b = 1.7. Compared to Fig 4, if a cooperator has three

The local structures of strategies for A = 1.6 and b = 1.7.
Each square corresponds to a single player, where cooperators are depicted blue and defectors are depicted red. Value denoted in the center square is the individual’s payoff. Smiling face represents satisfaction while crying face represents dissatisfaction.


Snapshots of typical distributions of strategies and aspirations at different time steps t for A = 1.6 and b = 1.7.
(a) represents strategies, where cooperators are depicted white and defectors are depicted black. (b) represents aspirations. The steps of them are t = 0, 10, 100, 200, 500 and 1000 respectively.
From the above we know the main difference between b < 1.6 and b ≥ 1.6 for A = 1.6 is whether a defector who has three
To conclude, for moderate values of A, cooperators will survive and expand in the early stages of evolution when b is lower than A, which are END and EXP periods respectively. But according to our results, the existence of Infectors may lead to defectors’ re-expansion. The core reason for this phenomenon is that the cooperators increase their aspirations excessively and become the so-called High-risk cooperators, which needs to be vigilant in the evolution process of cooperation.
0.4 Defection Explosion under High Aspiration (A > 2.0)
For A = 2.4, cooperators can survive only when
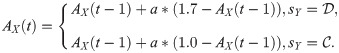

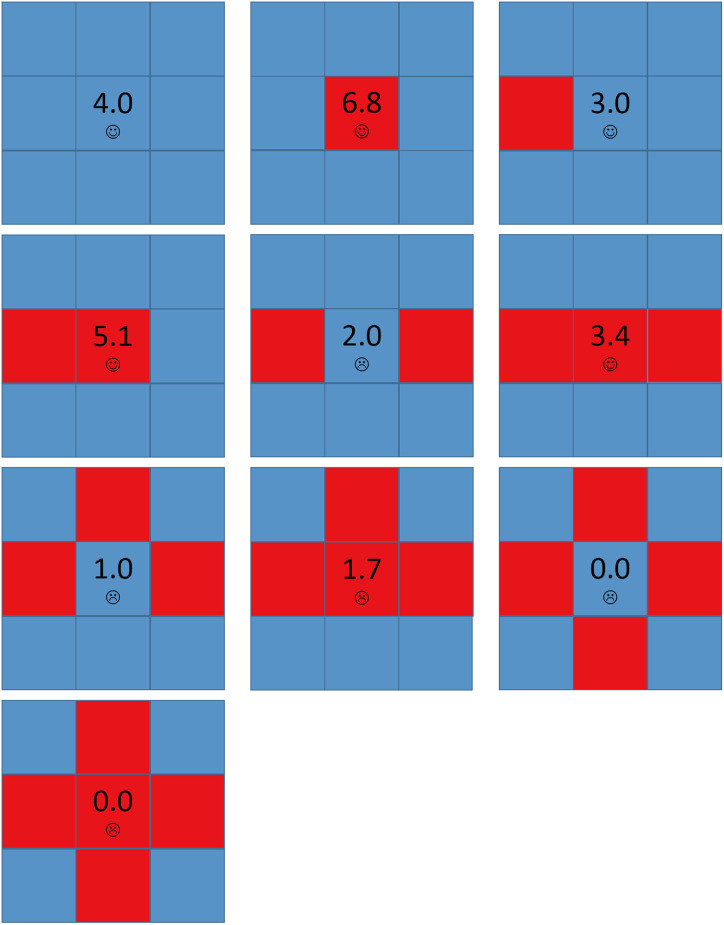
The local structures of strategies for A = 2.4 and b = 1.7.
Each square corresponds to a single player, where cooperators are depicted blue and defectors are depicted red. Value denoted in the center square is the individual’s payoff. Smiling face represents satisfaction while crying face represents dissatisfaction.
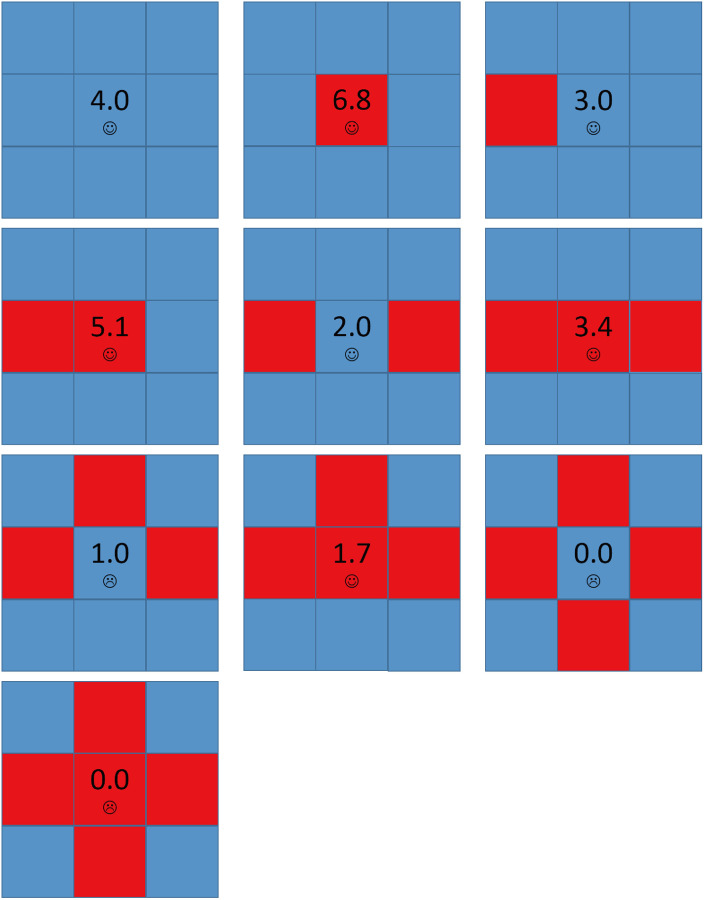
Fig 10 shows the structure which causes the defectors’ expansion. In initial, nodes X1 and X2 are dissatisfied and may evolve into defectors. Once X1 evolves into a defector, nodes Y1 and Y2 become dissatisfied and may also evolve into defectors, so do the other five nodes. All the nine nodes are dissatisfied and evolve into cooperators and defectors repeatedly. In other word, they are all Infectors. As a result, colored cooperators’ aspiration will be higher than 3.0 as time goes so they are High-risk cooperators. Next time when one of the nodes evolves into a defector, the cooperator will be dissatisfied and evolve into a defector. Since the other nodes’ aspirations are close to 4.0 and have became High-risk cooperators, chain phenomenon occurs and defectors will occupy the whole network.

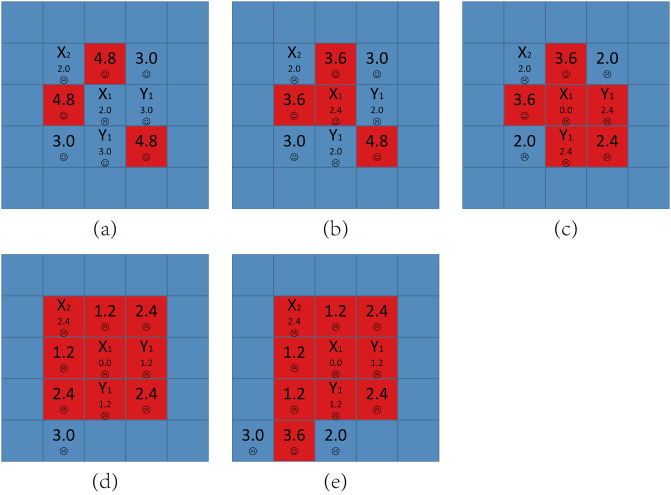
The detailed principle for defectors’ expanding for A = 2.4, b = 1.7.
The initial local structure is shown in (a). Smiling face represents satisfaction while crying face represents dissatisfaction.
When b is lower, defectors’ expansion requires more strict requirement. When b = 1.2, for the same structure shown in Fig 10, defectors can’t expand. We find that before cooperators’ aspirations are higher than 3.0, the nine nodes will be all satisfied in a step so that the network becomes stable with high probability. The lower b makes the network stable soon if there are only nine nodes participating in the evolution. Fig 11 shows the initial structure which causes the defectors’ expansion, and similar to Fig 10, sixteen nodes participate in the evolution. More Infectors make the evolutionary process last longer, so the colored nodes have enough time to increase their aspirations to higher than 3.0 and all of them will become High-risk cooperators. Fig 12 shows the spatial distributions of strategies and aspirations at different time steps t for A = 2.4, b = 1.7 with the initial structure shown in Fig 10. The situation of A = 2.4, b = 1.2 with the initial structure shown in Fig 11 is almost the same. In fact, the above conclusion is suitable for all the 2.0 < A ≤ 3.0. Defectors’ expansion requires more defectors’ gathering when b is lower or A is higher, vice versa.

The initial structure that causes defectors’ expansion for A = 2.4, b = 1.2.
Smiling face represents satisfaction while crying face represents dissatisfaction.

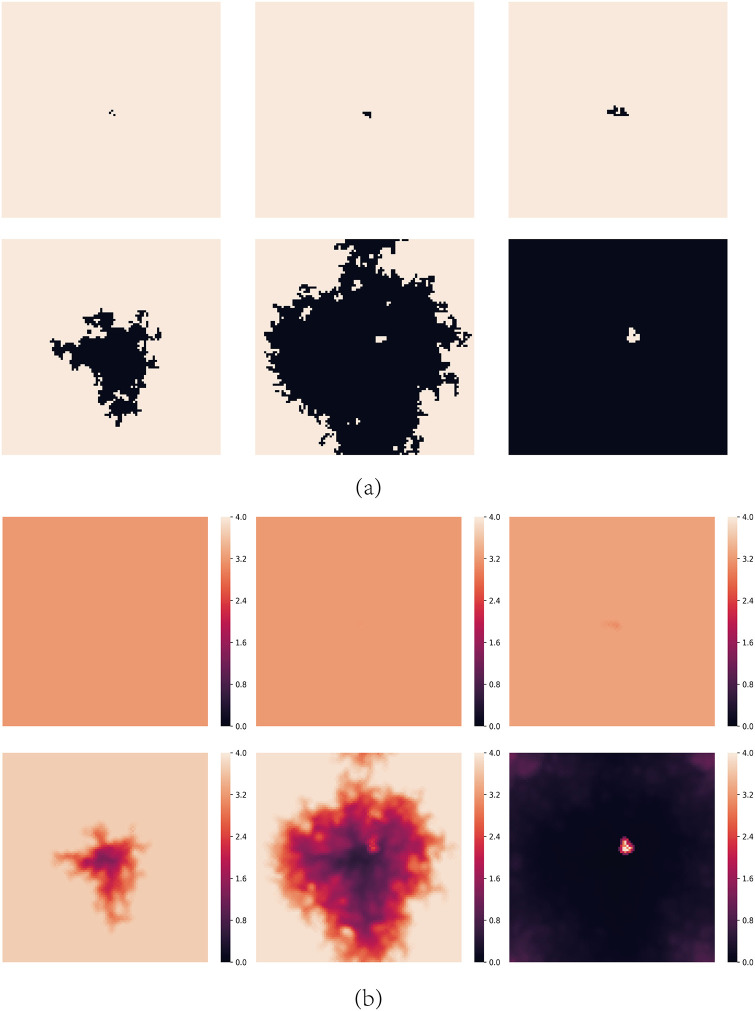
Snapshots of typical distributions of strategies and aspirations at different time steps t for A = 2.4 and b = 1.7 with the initial structure shown in Fig 10.
(a) represents strategies, where cooperators are depicted white and defectors are depicted black. (b) represents aspirations. The steps of them are t = 0, 10, 100, 200, 500 and 1000 respectively.
For A > 3.0, the nodes which have at least one

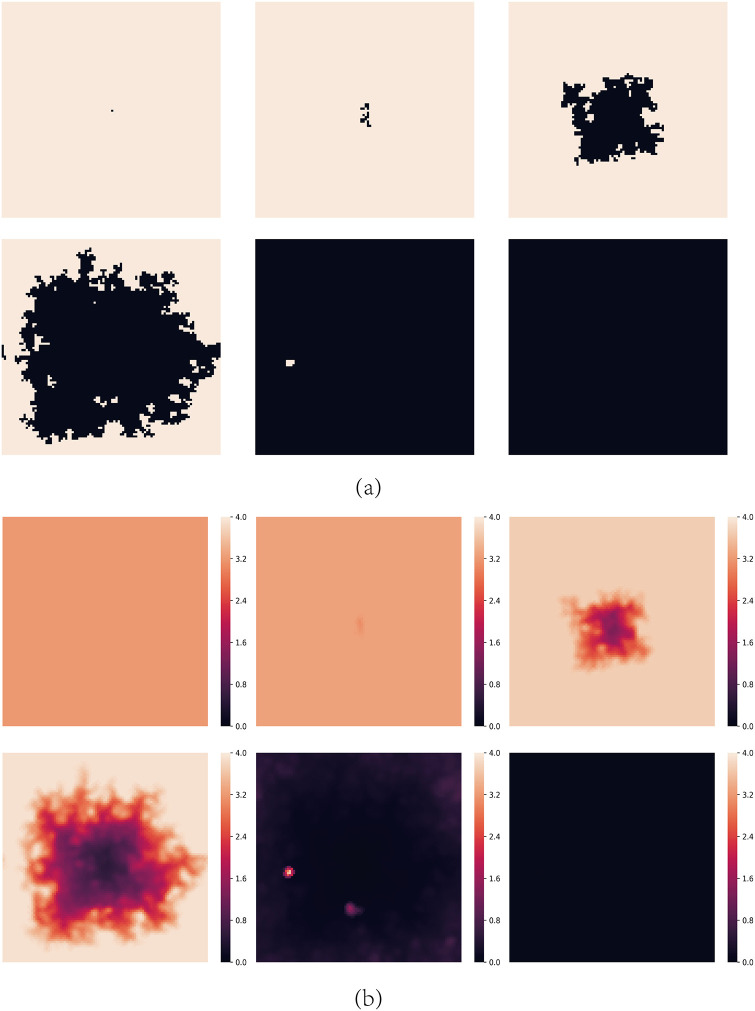
Snapshots of typical distributions of strategies and aspirations at different time steps t for A = 3.2 and b = 1.2 with only one defector initially.
(a) represents strategies, where cooperators are depicted white and defectors are depicted black. (b) represents aspirations. The steps of them are t = 0, 10, 100, 200, 500 and 1000 respectively.
In dynamic aspiration model, three different phases could be observed. The phase under low aspiration is similar to the fixed aspiration model because most nodes are always satisfied and their aspirations are changed in a small range. However, dynamic aspiration model plays a critical role under moderate aspiration and high aspiration, where some nodes called Infector are dissatisfied no matter they are cooperators or defectors and their strategies are changed repeatedly. As a result, their neighbors’ payoff are changed and aspirations will be influenced by the evolution process, and these neighbors act as Infected nodes. Their aspirations become higher gradually but their payoffs changed repeatedly, which results in their dissatisfaction and Infected nodes will become Infectors. Once a High-risk cooperator node becomes dissatisfied, chain phenomenon happens in High-risk cooperators and defectors will expand fast.
Conclusion
To conclude, the evolution process of the Win-Stay-Lose-Learn strategy updating rule on the prisoner’s dilemma game is studied in this paper. Based on the previous work, a dynamic aspiration model is proposed, in which players will not only change their strategies based on aspirations, but also change their aspirations due to their payoffs.
Three different phases are found. Cooperators and defectors can coexist for small values of A, which is called Stable Coexistence under Low Aspiration. Only a few cooperators will evolve into defectors then and the network will be stable immediately, which is not affected by the value of b. As a comparison, defectors will easily expand to the whole network for large values of A, which is called Defection Explosion under High Aspiration respectively. Two kinds of local structures which can lead to defectors’ expansion are found, depending on the values of b. The most interesting phenomenon is cooperators can survive for higher b(b ≥ A) and die out for lower b(b < A) when 1.0 < A ≤ 2.0, which is abnormal because higher b should have meant that it is harder for the cooperators to survive, and it is called Dependent Coexistence under Moderate aspiration. The local structure leading to the defectors’ expansion is that a cooperator is surrounded by one cooperator and three defectors. Dynamic aspiration plays an important role for the above results because a constantly changing individual(Infectors) may make its neighbors’ (Infected nodes) aspirations gradually rise up and they will become Infectors. At the same time, all the other cooperators’ aspirations gradually rise up and they become High-risk cooperators. When a High-risk cooperator neighbors with an Infector, it will become a defector soon and chain phenomenon happens.
Our work provides a new enlightening opinion for the Win-Stay-Lose-Learn strategy updating rule. Dynamic aspiration introduces a more satisfactory explanation on population evolution laws. Under the mechanism of network reciprocity, the defectors’ re-expansion is got attentions. How to avoid such unfavorable phenomenon under moderate aspirations is still a challenging problem. It is hoped that our work offers a valuable method that can help explore the principle behind prisoner’s dilemma better, especially when combining with other rules which use aspiration level for personal decision making such as myopic, other-regarding preference or Pavlov-rule [52–57].
Acknowledgements
We thank Marco Antonio Amaral, Xin Wang and Yuanchen Guo for discussions and suggestions.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
 Dynamic aspiration based on Win-Stay-Lose-Learn rule in spatial prisoner’s dilemma game
Dynamic aspiration based on Win-Stay-Lose-Learn rule in spatial prisoner’s dilemma game
