
Competing Interests: The authors have declared that no competing interests exist.
- Altmetric
Satellite communication has played an important part in many different industries because of its advantages of wide coverage, strong disaster tolerance and high flexibility. The security of satellite communication systems has always been the concern of many scholars. Without authentication, user should not obtain his/her required services. Beyond that, the anonymity also needs to be protected during communications. In this study, we design an efficient and provably secure key agreement scheme for satellite communication systems. In each session, we replace user’s true identity by a temporary identity, which will be updated for each session, to guarantee the anonymity. Because the only use of lightweight algorithms, our proposed scheme has high performance. Furthermore, the security of the proposed scheme is proved in the real-or-random model and the performance analysis shows that the proposed scheme is more efficient than some other schemes for satellite communication systems.
Introduction
With the development of communication technology, satellite communication has played an important part in many industries, such as economy, politics, culture, military affairs, etc [1–3]. Compared with traditional satellite communication systems, the low-earth-orbit(LEO) satellite communication systems have the advantages of shorter transmission delay, higher efficiency, higher availability and higher cost performance. As shown in Fig 1, an LEO communication system is made up of mobile devices/users (U), gateways, LEO and the network control center (NCC). The most of entities in this LEO satellite communication system are connected wirelessly, the natural defects of the wireless communication bring great security risks, which will cause the system to be easily attacked by attackers.


A LEO satellite communication system.
In order to solve these problems, some low-Earth-orbit satellite communication protocols [4–7] have been proposed. In 1996, the first security satellite communication scheme was proposed by Cruickshank [8], but it cost too much computation. In 2003, Hwang et al. proposed an authentication scheme for mobile satellite communication system [9]. However, Chang et al. pointed out that their scheme couldn’t proved perfect forward secrecy [10]. In 2009, Chen et al. proposed a self-verification scheme and claimed there was no sensitive information stored in the verification [11]. But Lee et al. pointed out the user’s secret key is not secure in Chen et al.’s scheme when the hash value of user identity and another parameters are coprime numbers in 2011 [12]. In 2014, Zhang et al. proposed an improved authentication scheme [13]. But soon after, Qi et al. pointed out that Zhang et al.’s scheme was vulnerable to stolen-verifier attack and denial of service attack [14]. In 2017, Qi et al. proposed an enhanced authentication with key agreement scheme based on ECC(Elliptic Curves Cryptography), but the scheme has poor performance and some security defects. In this paper, we propose an enhanced scheme and prove that our scheme is secure under the real-or-random model.
In this context, an effective satellite communication scheme must possess the following characteristics to ensure the secrecy of normal operations in mobile satellite communication systems:
Mutual authentication: NCC and user U can authenticate each other and generate a session key without being illegally obtained by the attacker.
Perfect forward secrecy: if a session key or sensitive data is leaked to an attacker, he/she cannot obtain previous session keys from the preceding interception.
Anonymity: the user’s identity is securely hidden and an attacker cannot derive user identity in any way.
Resistance to stolen-verifier attacks: an attacker may break into servers and steal verification table from trusted servers. However, he or she cannot use the data in the verification table to launch any attack.
Resistance to smart card loss attacks: if an attacker gets a legal user’s smart card in some way, he or she cannot derive sensitive data from it.
Resistance to denial of service attacks: prevent attackers from occupying server resources illegally to ensure that the legal users can access the authentication server normally.
Resistance to impersonation attacks: an attacker cannot attempt to communicate with a trusted server as a legitimate user and also cannot attempt to communicate with a legitimate user as a server.
The rest of this paper is organized as follows: We describe the detail of our proposed scheme in Section 2 and section 3 shows the security analysis of our scheme. Section 4 compares the security and the performance of our scheme with other related schemes. Finally, section 5 presents our conclusion.
Our proposed scheme
In this section, we propose an efficient and provably secure key agreement scheme for satellite communication systems. Some notions in our scheme are shown in Table 1. In the proposed scheme, we abandon the traditional temporary identity verification table, and adopt a dynamic temporary identity table [15]. Usually, the traditional temporary identity table only stores temporary identity of this time. However, when an attacker intercepts messages returned from NCC, the data in NCC’s database has been updated and the data in the smart card has not been updated, so data inconsistency occurs between database and smart card. To solve this problem, we adopt a dynamic temporary identity table which consists of hash value of user’s identity, shared hash value, dynamic temporary identity of last time and dynamic temporary identity of this time(shown in Table 2).

| x | Private key of NCC |
| IDu | Identity of user U |
| Tid | Temporary identity |
| PW | Password of user U |
| LEOid | Identity of LEO |
| h(⋅) | A one-way hash function |
| ⊕ | XOR operation |
| || | Concatenation operation |

| Hash value of user’s identity(hID) | Shared hash value (hPW) | Dynamic identity of last time(Tido) | Dynamic identity of this time(Tid) |
|---|---|---|---|
| 110101…101100 | 011011…101111 | NULL | 111001…000011 |
| 110101…101101 | 101110…010001 | 010110…110110 | 010101…110110 |
| … … | … … | … … | … … |
| … … | … … | … … | … … |
| 011011…010101 | 100010…110001 | 011101…000101 | 011101…110010 |
Our scheme contains the following phases: initialization phase, registration phase, login and authentication phase and password update phase. The details of our scheme are as follows.
Initialization phase
NCC chooses a large prime x as long-term private key randomly and specifies a secure hash algorithm h(⋅). In the meantime, NCC creates a table in the databases. The table stores four data for each legitimate user. Two of these data are the hash values which used to authenticate the identity. The remaining two are used to store user’s dynamic ID. One ID is for last time, the other one is for this time. If a user fails to authenticate with the this time ID, he will try to re-authenticate with the last time ID.
Registration phase
To be a legal user, he/she must submit his/her registration request to NCC (see in Fig 2).

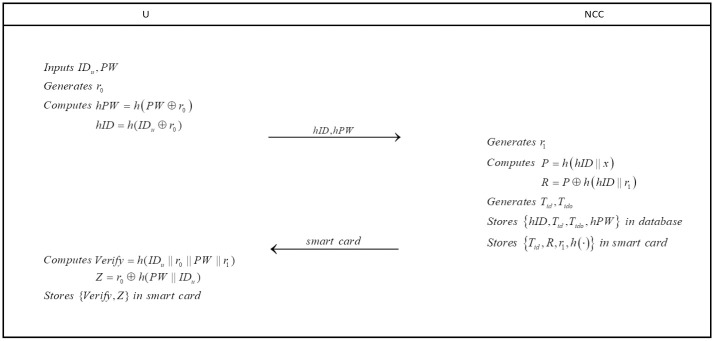
Registration phase.
step 1: With the permission of NCC, user U inputs IDu and PW chosen by himself/herself. After that, user U generates a random number r0 and computes

step 2: After receiving registration message, NCC generates a random number r1 and computes
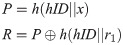
step 3: NCC delivers the smart card to user U in a secure channel.
step 4: User U computes
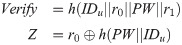
Login and authentication phase
Login and authentication phase are indispensable steps for user to get services from server. The following operations are intended to achieve the goal (see in Fig 3).


Login and authentication phase.
step 1: User U inserts his/her smart card into card reader and inputs IDu and PW. Then, U computes
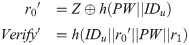

step 2: LEO receives the login request from U and forwards the login request {Q, S, Tid, LEOid} to NCC.
step 3: After receiving the login request from LEO, NCC begins to match Tid in the dynamic verification table(Table 2). Firstly, NCC searches the column of Dynamic identity of this time(Tid). If there is a value equals to Tid, NCC extracts the corresponding hID, hPW and chooses a new temporary identity Tidnew. Then NCC replaces (Tido, Tid) with (Tid, Tidnew). Else, NCC keeps searching the column of Dynamic identity of last time(Tido) in the verification table to see if there is a value equals to Tid. If so, NCC extracts the corresponding hID, hPW, chooses a new temporary identity Tidnew and replaces (Tido, Tid) with (Tido, Tidnew). If NCC cannot match Tid in the dynamic verification table, it will reject the login request.
step 4: After completion of matching, NCC computes
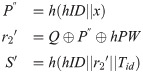

step 5: LEO forwards the message {v1, v2, v3} from NCC to user U.
step 6: After receiving {v1, v2, v3} from LEO, user U computes
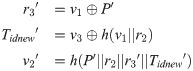
Password update phase
To enhance security, users are advised to update their passwords at set intervals. To complete the process, user U will perform the following steps(see in Fig 4).


Password update phase.
step 1: User U inserts the smart card and inputs IDu,PW,PWnew where PWnew is the new password chosen by himself/herself. Then user U computes

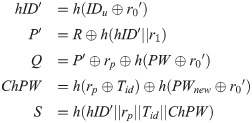
step 2: LEO forwards the message received form user with LEOid to NCC.
step 3: Upon receiving the message, NCC executes the step 3 in Login and authentication phase to obtain hID and hPW. Then NCC computes

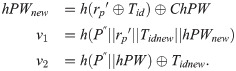
Next, NCC replaces (Tido, Tid, hPW) with (Tid, Tidnew, hPWnew) or (Tido, Tidnew, hPWnew). Then, NCC sends message {v1, v2, LEOid} to the LEO.
step 4: Upon receiving the message {v1, v2, LEOid}, LEO forwards {v1, v2} to U.
step 5: After receiving the message, user U computes
Security analysis
In this section, we will show that our scheme is provably secure in the real-or-random model.
Security model
In 2005, Abdalla et al. introduced a new security model for two-party password-based authenticated key exchange scheme [16]. Based on their real-or-random model, we can prove the security of our scheme. In the model, there are two types of participants, user U and network control center NCC, respectively. Ui denotes the ith instance of U. The adversary A, which is abstracted as a probabilistic polynomial time Turing Machine, interacts with other participants through a bounded number of queries which model the capabilities of the adversary in an actual attack. The ability of adversary A is defined by the following queries.
Excute(Ui, NCC): Return the messages transmitted between Ui and NCC in their last key agreement conversation. This query models the eavesdropping attack.
Send(Ui/NCC, m): After receiving message m sent by A, Ui/NCC generates a corresponding message for m and outputs it as the result of this query. This query models the active attacks such as replay attack, impersonation attack and so on.
CorruptSC(Ui): Return the current data stored in Ui’s smart card. This query models the smart card lost attack.
CorruptDB(NCC): Return the current data stored in NCC’s database. This query models the insider attack and the stolen verifier attack.
Test(Ui/NCC): The semantic security of the session key is simulated by flipping an unbiased coin. The query returns a random binary of the same size of session key if b = 0 or the session key between Ui and NCC if b = 1. The adversary can ask only one time of Test query.
H(x): This is a hash query. If a record (x, h) exists in the hash list, h is returned. Otherwise, return a uniformly random string h and store (x, h) in the table.
Semantic security: Providing the above-mentioned queries, the adversary A may interact with the participants to help him/her verify the value of b. If he/she can guess correctly, the scheme fails to provide semantic security. Let Succ denotes the event that A wins. A has an advantage

Security proof
Theorem 1: Let SID and SPW be uniformly distributed dictionary of user identity and password, respectively. |SID| and |SPW| denoted the size of SID and SPW. |H| denotes the range space of the hash function. Beyond that, we denote qh and qs to represent the number of H(x) oracle queries and the total number of queries executed by A. Then, we have
Game Gm0: This game models the real attack by the adversary. We have
Game Gm1: To increase the advantage of success, A launches an eavesdropping attack by querying the Excute(Ui, NCC) oracle. Since the session key SK is computed by hID, r2,r3 and P, A tries to obtain these values from the messages transmitted in the public channel. We know that r2 = Q ⊕ P ⊕ hPW, r3 = v1 ⊕ P and P = h(hID||x) = R ⊕ h(hID||r1). The hID is concealed in the hash function. Thus, A cannot get the values of hID, r2, r3 and P. In this game, the Excute(Ui, NCC) query dose not provide any advantage compared to game Gm0 and we have
Game Gm2: In this game, we add the send query to simulate an active attack. In order to pass the authentication, A must use H(x) query to fabricate messages. No collisions will be found in the input while querying H(x) oracle, because every message contains some different random numbers. By the birthday paradox, we can get
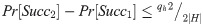
Game Gm3: We transfer game Gm2 to this game by adding the CorruptSC(Ui) query or the CorruptDB(Ui) query.
Case 1: The adversary asks the CorruptSC(Ui) query. Then he/she can extract {Tid, R, r1, Verify, Z} stored in the user Ui’s smart card. For the adversary, hID = h(IDu ⊕ r0) = h(IDu ⊕ Z ⊕ h(PW||IDu)), r2 = Q ⊕ P ⊕ hPW = Q ⊕ R ⊕ h(hID||r1) ⊕ h(PW ⊕ Z ⊕ h(PW||IDu)), r3 = v1 ⊕ P = v1 ⊕ R ⊕ h(hID||r1) and P = h(hID||x) = R ⊕ h(hID||r1). So A tries a dictionary attack with the possible identity and password of the user in SID and SPW. Since the scale of the dictionary is |SID| and |SPW|, the adversary need to guess the correct values of U’s identity and password simultaneously. In this case, the probability of a successful dictionary attack is negligible. So, we have

Case 2: The adversary A asks the CorruptDB(NCC) query. Then he/she can extract {hID, Tid, Tido, hPW} stored in NCC’s database. For the adversary, r2 = Q ⊕ P ⊕ hPW = Q ⊕ h(hID||x) ⊕ hPW, r3 = v1 ⊕ P = v1 ⊕ h(hID||x) and P = h(hID||x). So A tries a dictionary attack with the possible private key of NCC. So, we have

The adversary A can choose case 1 or case 2 as the last game Gm3. From game Gm0 to game Gm3, all the oracles are simulated and A has no choice but querying the Test query and guessing the bit b in the last game. Therefore,
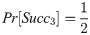

The advantage for an adversary to guess the correct session key is negligible since |H|,|SID| ⋅ |SPW| and 2k are beyond the polynomial time. So our scheme can provide semantic security in the real-or-random model.
Other security features
In this section, we will analyze the security and practicability of our scheme [17–20].
Provide credible mutual authentication: In login and authentication phase, NCC can authenticate user U only when user U submits correct identity IDu, password PW which can satisfy the equation S′ = h(hID||r2′||Tid) = S. An attacker cannot falsify valid S and Q to pass NCC’s authentication without the correct identity and password. User U can authenticate NCC only when the user receives the correct message {v1, v2, v3} which can satisfy the equation v2′ = h(P′||r2||r3′||Tidnew′) = v2. But an attacker cannot counterfeit the correct message {v1, v2, v3} without P. Thus, our scheme provides credible mutual authentication.
Provide perfect forward secrecy: Forward secrecy means an attacker cannot obtain the past session keys even he/she has got NCC’s private key, users’ password and users’ identity. In our scheme, the session key SK = h(hID||r2||r3′||P′) is established with the user’s identity, the random number r2, r3 and the hash value P = h(hID||x). Even if an attacker obtains those sensitive data, he/she cannot obtain other session keys because he/she cannot derive r2 = P ⊕ hPW ⊕ Q without user U’s corresponding hPW. Therefore, our scheme can provide forward secrecy.
Provide anonymity: Some traditional schemes often transmitted users identity IDu in the public channel, which may lead to leakage of identity information, obviously those schemes can not provide anonymity. There are also some schemes claim that they can provide anonymity. But their identities usually can be guessed by attackers. In our scheme, we transmit temporary identity Tid instead of user’s identity IDu, and the temporary identity will be updated after each session. And the attacker cannot guess IDu from R = P ⊕ h(hID||r1), Verify = h(IDu||r0||PW||r1), Z = r0 ⊕ h(PW||IDu) or other equations. So our scheme can provide anonymity.
Resist stolen-verifier attack: Stolen-verifier attack means an insider attacker may steal the data in the database, and he can derive users’ password or impersonate legal users to send legitimate login requests. In our scheme, the database stores {hID, Tido, Tid, hPW}, if the insider attacker steals these data, he/she cannot derive users’ password PW without the random number r0. In addition to this, the insider attacker cannot impersonate legal users to send legitimate login requests Q = P′ ⊕ r2 ⊕ h(PW ⊕ r0′) and S = h(hID||r2||Tid) to NCC without the password PW, the secret data P and the random number r0. Therefore, our scheme can resist the stolen-verifier attack.
Resist smart card loss attack: Assume an attacker gets user U’s smart card and extracts the parameters {Tid, R, r1, h(⋅), Verify, Z} from it and the attacker also intercepts the communication message between user U and NCC. But these parameters do not help him/her perform any attacks without the user’s password PW and identity IDu. Thus, our scheme can resist smart loss attack.
Resist denial-of-service attack: In login and authentication phase, after NCC authenticating user U, an attacker may intercept and modify the message {v1, v2, v3} which is forwarded from NCC to U. Obviously, the modified message cannot pass the authentication of user U and the updating of temporary identity will be inconsistent between NCC and user U which must lead to the denial-of-service attack. To avoid that, our scheme adopts dynamic temporary identity(see in Table 2), and NCC stores the temporary identity both of this time and last time. Even the update is inconsistent, the legal user also can login successfully next time with the old temporary identity. Thus, our scheme can resist denial-of-service attack.
Resist impersonation attack: Impersonation attack means that an attacker impersonates a legal user to login NCC or impersonates NCC to communicate with a legal user. In our scheme, if the attacker intends to impersonate a legal user U, he/she must computes Q = P′ ⊕ r2 ⊕ h(PW ⊕ r0′) and S = h(hID||r2||Tid). However, Q and S are established with the secret data P, the temporary identity Tid, the password PW and the identity IDu. All of those data are secret, so the attacker cannot impersonate a legal user. On the other hand, even if the attacker obtains the temporary identity of the user, he/she cannot know P′ = h(hID||x) without NCC’s private key x. So the attacker cannot masquerade as NCC without P to compute the correct message {v1, v2, v3}. Therefore, our scheme can resist impersonation attack.
Security and performance comparison
In this section, we evaluate the performance of our proposed scheme with other three related schemes [14, 21, 22]. The computational cost in the login and authentication phase is compared in detail and the security features of these schemes are also analyzed.
In the proposed scheme, the traditional verification table is improved to form a dynamic one which can resist the denial-of-service attack. In addition, the value stored in the smart card is useless for the attacker to launch any attack. Even if the smart card is lost, user information will not be leaked out. As for the transmitting messages, we transmit user’s temporary identity Tid replace user’s true identity IDu. Thus, anonymity has been achieved.
As shown in Table 3, the related schemes [14, 21, 22] have some design flaws and cannot satisfy all the security features. Qi et al.′s scheme [14] suffers from smart card loss attack, denial-of-service attack, off-line guessing attack, replay attack. In addition to this, their scheme also cannot provide forward secrecy and anonymity. Lin et al.′s scheme [21] satisfies most of the security requirements, where as they ignore the smart card loss attack. In Mo et al.′s scheme [22], they cannot resist stolen-verifier attack, smart card loss attack, impersonation attack and cannot provide forward secrecy. Compared with the related works, our scheme can resist most of the known attacks and provide password update service for users to choose.

| Ours | Qi et al.’s [14] | Lin et al.’s [21] | Mo et al.’s [22] | |
|---|---|---|---|---|
| Provide credible mutual authentication | Y | Y | Y | Y |
| Provide anonymity | Y | N | Y | Y |
| Provide forward secrecy | Y | N | Y | N |
| Provide password update | Y | Y | N | N |
| Resist stolen-verifier attack | Y | - | Y | N |
| Resist smart card loss attack | Y | N | N | N |
| Resist denial-of-service attack | Y | Y | Y | Y |
| Resist impersonation attack | Y | N | Y | N |
| Resist off-line guessing attack | Y | N | Y | Y |
| Resist replay attack | Y | N | Y | Y |
Since the registration phase just needs to be executed only once for a certain user, the password update phase isn’t always executed and the login and authentication phase is executed each time, we focus on the performance of login and authentication phase.
The running time of a hash function is Th, the running time of a large number addition is TLA, the running time of an elliptic curve scalar point multiplication is TPM and the running time of a XOR operation is Tx. Table 4 shows theoretical computational costs comparisons between the proposed scheme and other related schemes in the login and authentication phases. As we know, point multiplication based on elliptic curves is quite time-consuming operation [23–26], our proposed scheme and Lin et al.′s scheme have a great advantage on computational costs, because only hash, XOR and string connection operations are adopted in our scheme and Lin et al.′s scheme.

We carried out a simulation of these schemes with Miracl Library. The hardware platform for user and sever is given an Inter(R) Core(TM) i7-6700 HQ CPU @ 2.60GHz and 8.00GB memory. The length of the random number we used in our simulation is 1000 bits, each simulation was performed for 100 times and the logarithm of average execute time(ms) in the login and authentication phase are shown in Fig 5. The bottom part of the Fig 5 shows real average execute time(ms) of the login and authentication phase. Because the value of time is too small, in the vertical axis of the histogram, we use lg(t) to represent the result, where t is real average execute time(ms). The computational costs in Qi et al.′s [14] and Mo et al.′s [22] schemes are much higher than our proposed scheme and Lin et al.′s [21] scheme. The reason is that those schemes involve point operations of an elliptic curve [27–30]. Thus, they are not suitable for satellite communication systems due to the limited computational capability of the devices. Compared with our scheme, the computational overhead of Lin et al.′s scheme costs a little more and we offer more security features such as anonymity, which is not provided in Lin et al.′s scheme. Therefore, our proposed scheme provides an efficient and secure authentication for satellite communication systems.

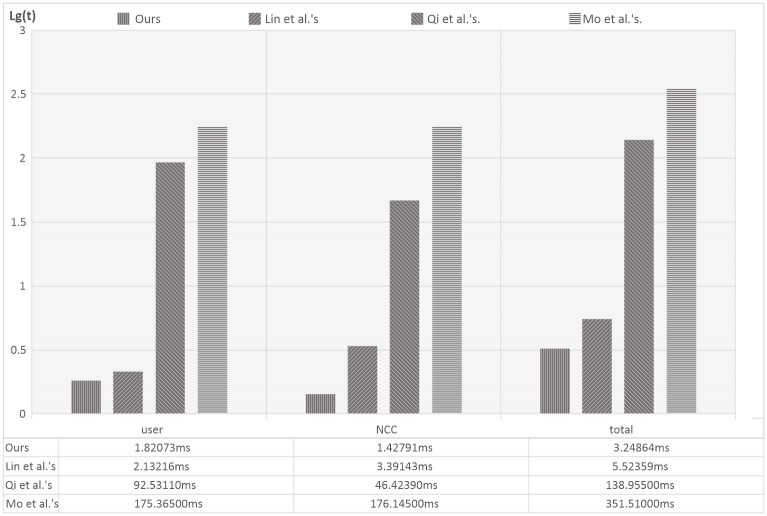
Computation cost comparisons of the login and authentication phase(the vertical axis is lg(t)).
Conclusions
In this paper, we proposed an efficient and provably secure key agreement scheme for satellite communication systems to provide credible mutual authentication. A dynamic temporary identity mechanism was adopted to ensure users’ anonymity. Besides, the traditional verification table was replaced by a dynamic verification table to resist denial-of-service attack caused by inconsistent data updating between NCC and user U. In addition, our scheme only adopted lightweight hash and string operations, which reduced the computational cost in comparison with other related works. We also proved the proposed scheme is provably secure in the real-or-random model. Therefore, the proposed scheme can meet the efficiency demands and security needs of communication satellite systems successfully.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
 An efficient and provably secure key agreement scheme for satellite communication systems
An efficient and provably secure key agreement scheme for satellite communication systems
