$$ {\widehat{\mathit{C}}}_2$$ rotation anomaly in SrPb

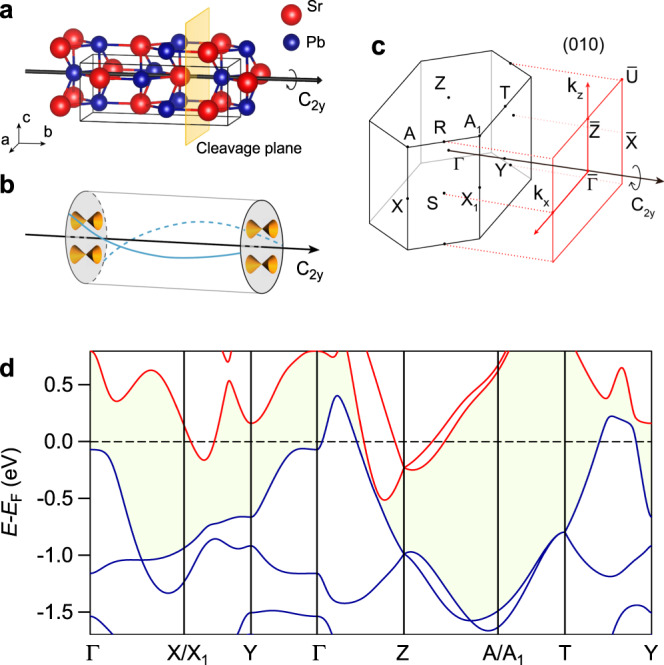
SrPb crystallizes in a centrosymmetric orthorhombic unit cell (a = 5.018 Å, b = 12.23 Å, and c = 4.648 Å) with space group Cmcm (SG #63)³³, as shown in Fig. 1a. Both Sr and Pb atoms occupy the 4c (0, y, 1/4) Wyckoff position with the internal parameter y = 0.132 and 0.422 for Sr and Pb, respectively. The lattice is formed by a stacking of slightly buckled SrPb layers along the [010] direction. The point group of the structure is D_2h generated by inversion $$ \widehat{I}$$, twofold rotational symmetries ($$ {\widehat{C}}_{2x}$$ and $$ \left\{{\widehat{C}}_{2y}\mid 00\frac{1}{2}\right\}$$), screw rotational symmetry $$ \left\{{\widehat{C}}_{2z}\mid 00\frac{1}{2}\right\}$$, mirror symmetries ($$ {\widehat{M}}_x$$ and $$ \left\{{\widehat{M}}_z\mid 00\frac{1}{2}\right\}$$), and glide-mirror symmetry $$ \left\{{\widehat{g}}_y\mid 00\frac{1}{2}\right\}$$. $$ \left\{{\widehat{C}}_{2\mathit{n}}\mid ijk\right\}$$ is the twofold rotational symmetry with respect to the vector n followed by a fractional lattice translation $$ i\mathit{a}+j\mathit{b}+k\mathit{c}$$, and $$ \left\{{\widehat{M}}_{\mathit{n}}\mid ijk\right\}$$ is the mirror reflection with respect to the plane with the normal vector n followed by a fractional lattice translation $$ i\mathit{a}+j\mathit{b}+k\mathit{c}$$, where a, b, and c are three unit cell vectors.

Fig. 1

Crystal structure and band structure of SrPb.

a Crystal structure of SrPb with the rotation axis $$ {\widehat{C}}_{2y}$$ along the b axis. The yellow plane indicates the cleavage position at the (010) surface. b Schematic of topological surface states with $$ {\widehat{C}}_2$$ rotation anomaly, showing two Dirac cones on each surface perpendicular to the $$ {\widehat{C}}_2$$ rotation axis, which are connected by two helical edge modes on the side surface. c Bulk BZ and (010) surface BZ of SrPb with high-symmetry points indicated. d Calculated bulk bands of SrPb along high-symmetry lines with SOC. The blue and red curves represent valence and conduction bands, respectively. The shadow region indicates the continuous gap between the valence and conduction bands.

The full-potential linearized augmented-plane-waves method as implemented in the WIEN2K code is employed to calculate the band structure of SrPb (see Methods for the calculation details), which is shown in Fig. 1d. It is clear that the band-gap opening due to spin-orbit coupling (SOC) occurs around the Fermi level (E_F), leading to the existence of a continuous direct gap between the conduction and valence bands at each k point in the full Brillouin zone (BZ). Therefore, the Fu-Kane topological invariants $$ {\mathbb{Z}}_2$$ ($$ {\nu }_0;{\nu }_1{\nu }_2{\nu }_3$$)³⁴ and symmetry-based indicators $$ \mathcal{Z}$$_{2, 2, 2, 4} ($$ z_{2,i=1,2,3};z_4$$)^18,19 for band insulators are well defined for SrPb in SG #63 (note that $$ {\nu }_i=z_{2,i}$$ with i = 1, 2, 3). Because of the existence of inversion symmetry in SrPb, the Fu-Kane parity criterion³⁴ can be used to easily calculate the topological invariants $$ {\mathbb{Z}}_2$$ = ($$ {\nu }_0;{\nu }_1{\nu }_2{\nu }_3$$), where $$ {\nu }_0$$ ($$ {\nu }_{i=1,2,3}$$) is the strong (weak) topological index. Based on the parities of occupied bands at eight time-reversal-invariant momenta (TRIM) listed in Table 1, the Fu-Kane topological invariants $$ {\mathbb{Z}}_2$$ are computed to be (0;110), which are consistent with the previous calculations^22,23. The symmetry-based indicators $$ {\mathcal{Z}}_{2,2,2,4}$$ are computed to be (1102)^22,35, with $$ {\mathcal{Z}}_4=2$$ indicating the existence of higher-order topology in the TCI SrPb.

Table 1

Parities of four pairs of occupied bands at eight TRIM.

TRIMs	Position	Parities order	Parity product
1Γ	(0, 0, 0)	++−−	+
1Y	(0, 2π, 0)	++−−	+
2S	(−π, π, 0) (π, π, 0)	+−−−	−
1Z	(0, 0, π)	++−−	+
1T	(0, 2π, 0)	++−−	+
2R	(−π, π, π) (π, π, π)	++−−	+

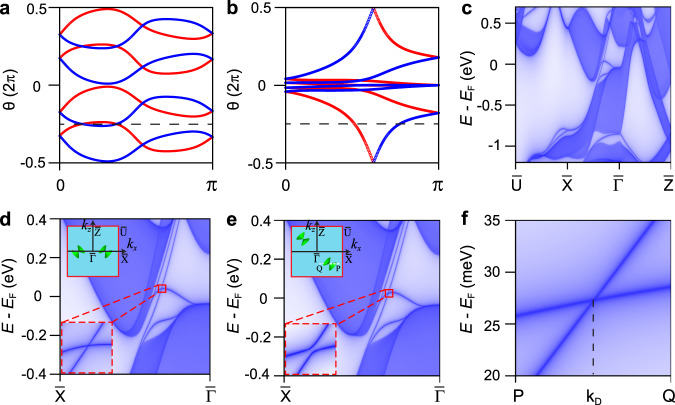
Given that the mapping from symmetry-based indicators to topological invariants is one-to-many mapping (it is a one-to-four mapping for SrPb), the mirror Chern numbers ($$ n_{{\widehat{M}}_x}$$ and $$ n_{{\widehat{M}}_z}$$) are calculated in order to confirm the exact topological phase in SrPb. In the presence of time-reversal symmetry, the Chern number ($$ n_{\widehat{M}}$$) can be identified in half of the plane by the 1D Wilson loops of the two mirror eigenvalues ($$ +i$$ and $$ -i$$) subspaces³⁶. The Wannier charge centers of the k_z-directed and k_x-directed Wilson loops as a function of k_y for the k_x = 0 and k_z = 0 planes are shown in Fig. 2a, b, respectively. The results show that $$ n_{{\widehat{M}}_x}$$ of the k_x = 0 plane and $$ n_{{\widehat{M}}_z}$$ of the k_z = 0 plane are 0 and −2, respectively, signaling the existence of topologically protected surface states on the surfaces preserving the mirror symmetry $$ {\widehat{M}}_z$$. According to ref. ¹⁹, we conclude that SrPb, with the indicators (1102) and invariants $$ n_{{\widehat{M}}_x}=0$$, $$ n_{{\widehat{M}}_z}=2$$, belong to the TCI phase in Table 2, which has nontrivial values of the $$ {\widehat{C}}_2$$ anomaly indices. The invariant $$ {\nu }_{{\widehat{C}}_{2y}}=1$$ guarantees the $$ {\widehat{C}}_{2y}$$ rotation anomaly in the (010) surface of SrPb. Two Dirac-cone surface states can be stabilized by $$ {\left(\widehat{T}\cdot {\widehat{C}}_{2y}\right)}^2=1$$ and protected from annihilation by the coexistence of $$ \widehat{T}$$ and $$ {\widehat{C}}_{2y}$$.

Fig. 2

WCCs and Dirac surface states of SrPb.

a, b WCCs of the k_z-directed and k_x-directed Wilson loops as a function of k_y in the $$ k_x=0$$ and $$ k_z=0$$ planes, respectively. The red and blue curves represent the flow of the WCCs for the bands with mirror $$ +i$$ and $$ -i$$ eigenvalues, respectively. The horizontal dashed lines are reference lines. c, d Surface band structures of SrPb on the (010) surface. e Surface Dirac cone on the line $$ \overline{X}-\overline{\mathrm{\Gamma }}$$ is gapped out when the $$ {\widehat{M}}_z$$ is broken. The upper insets in (d, e) schematically show the positions of the type-II Dirac surface cones in the (010) surface BZ. The lower inset in (e) clearly shows the gapped Dirac cone. f Dispersions of the $$ {\widehat{C}}_{2y}$$ rotational symmetry-protected surface Dirac cone along the line $$ P-Q$$ on the (010) surface. The positions of P, $$ k_D$$, and Q are (0.2077, −0.0022), (0.2052, −0.0022), and (0.2027, −0.0022), respectively. The positions are given in unit of Å⁻¹.

Table 2

Symmetry-based indicators and topological invariants of SrPb.

$$ Z_{2,2,2,4}$$	$$ \left({\nu }_1{\nu }_2{\nu }_3\right)$$	$$ \left\{{\widehat{M}}_z\mid 00\frac{1}{2}\right\}$$	$$ {\widehat{M}}_x$$	$$ \left\{{\widehat{g}}_y\mid 00\frac{1}{2}\right\}$$	$$ \left\{{\widehat{C}}_{2y}\mid 00\frac{1}{2}\right\}$$	$$ \left\{{\widehat{C}}_{2x}\right\}$$	$$ \widehat{I}$$	$$ \left\{{\widehat{C}}_{2z}\mid 00\frac{1}{2}\right\}$$
1102	110	−2	0	0	1	1	1	0

Surface band calculation

The nonzero topological invariants suggest the existence of topologically nontrivial surface states, which are calculated with the Green’s function methodology, as shown in Fig. 2c, d. We find two type-II surface Dirac cones on the (010) surface, which are consistent with the nontrivial topological invariant $$ {\nu }_{{\widehat{C}}_{2y}}=1$$. Interestingly, the Dirac cones are constrained on the high-symmetry line $$ \overline{X}-\overline{\mathrm{\Gamma }}$$ on account of the nonzero $$ n_{{\widehat{M}}_z}$$ Chern number. Next, we study the influence of the breaking of mirror symmetry $$ {\widehat{M}}_z$$ on the two surface Dirac cones. After applying a tiny shear strain (about 2%), the third primitive lattice vector $$ \overrightarrow{c}$$ becomes (0.1, 0, $$ c$$) in unit of Å, while the other primitive lattice vectors and the internal parameters of Sr and Pb atoms remain unchanged, resulting in a crystal without $$ {\widehat{M}}_z$$ but preserving $$ {\widehat{C}}_{2y}$$. The results of surface state calculations are shown in Fig. 2e, f, which show that the two surface Dirac cones cannot be gapped out but move away from the high-symmetry line $$ \overline{X}-\overline{\mathrm{\Gamma }}$$ to generic k points due to $$ {\left(\widehat{T}\cdot {\widehat{C}}_{2y}\right)}^2=1$$. In view of the higher-order bulk-boundary correspondence, the higher-order TI with two helical hinge states is expected on the hinges parallel to the y axis, as shown in Fig. 1b.

Bulk electronic structures of SrPb

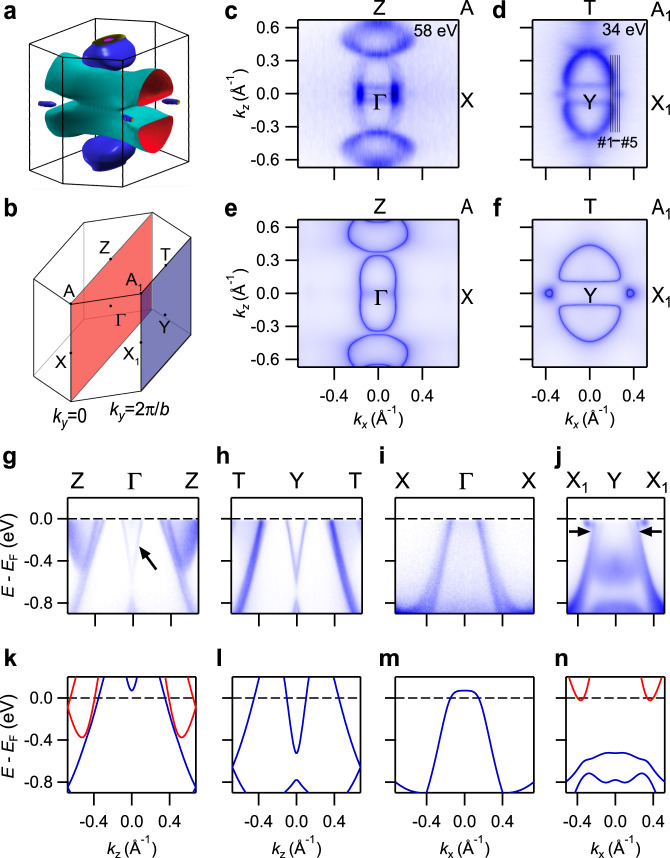
To examine our theoretical prediction of the nontrivial topological phase, we have carried out systematical ARPES measurements on the (010) cleavage surface of SrPb single crystals. We determine momentum locations perpendicular to the sample surface by photon energy (hv) dependent ARPES measurements (see Supplementary Fig. 1 in Supplementary Information). Figure 3c, d shows the in-plane Fermi surfaces (FSs) measured with hv = 58 and 34 eV, which are consistent with the calculated FSs in the $$ k_y=0$$ (Fig. 3e) and $$ k_y=2\pi /b$$ (Fig. 3f) planes, respectively. As seen in Fig. 3a, the calculations exhibit quasi-2D FSs extending along the $$ k_y$$ direction and three-dimensional (3D) FSs located around the $$ k_y=0$$ and $$ k_y=2\pi /b$$ planes in the 3D BZ. The quasi-2D FSs have two semicircular contours in the $$ k_y=2\pi /b$$ plane (Fig. 3d, f) and they merge to form a nearly elliptical contour enclosing the Γ point in the $$ k_y=0$$ plane (Fig. 3c, e). In addition, Fig. 3c shows two faint semicircular contours near the Γ point, which are ascribed to momentum broadening of the FSs near the Y point because of short mean free path of the photoelectrons. On the other hand, the 3D FSs are observed near the Z point in the $$ k_y=0$$ plane (Fig. 3c, e) and on the $$ Y-X_1$$ line in the $$ k_y=2\pi /b$$ plane (Fig. 3d, f).

Fig. 3

Bulk electronic structures of SrPb.

a Calculated FSs of bulk states in the 3D BZ. b 3D bulk BZ with the $$ k_y=0$$ and $$ k_y=2\pi /b$$ planes marked with red and blue colors, respectively. c, d ARPES intensity plots at E_F recorded on the (010) surface with $$ h\nu =$$ 58 and 34 eV, respectively. The data in (c, d) are symmetrized with respect to $$ \mathrm{\Gamma }-X$$ and $$ Y-X_1$$, respectively. The black lines in (d) indicate momentum locations of the cuts in Fig. 4i, j. e, f Calculated FSs in the $$ k_y=0$$ and $$ k_y=2\pi /b$$ planes, respectively. g–j ARPES intensity plots showing band dispersions along $$ \mathrm{\Gamma }-Z$$, $$ Y-T$$, $$ \mathrm{\Gamma }-X$$, and $$ Y-X_1$$, respectively. The arrows in (g) and (j) indicate extra bands compared with the calculated bulk bands. k–n Calculated bulk bands along $$ \mathrm{\Gamma }-Z$$, $$ Y-T$$, $$ \mathrm{\Gamma }-X$$, and $$ Y-X_1$$, respectively. We note that the Fermi level in the calculations is shifted down by 0.14 eV to match the experimental results because the samples are slightly hole-doped.

Dirac surface states protected by $$ {\widehat{\mathit{C}}}_2$$ rotational symmetry

In Fig. 3g–n, we compare the experimental bands with the calculated bulk bands along the high-symmetry lines $$ \mathrm{\Gamma }-Z$$, $$ Y-T$$, $$ \mathrm{\Gamma }-X$$, and $$ Y-X_1$$. As shown in Fig. 1c, both $$ \mathrm{\Gamma }-Z$$ and $$ Y-T$$ are projected onto $$ \overline{\mathrm{\Gamma }}-\overline{Z}$$ while both $$ \mathrm{\Gamma }-X$$ and $$ Y-X_1$$ are projected onto $$ \overline{\mathrm{\Gamma }}-\overline{X}$$ on the (010) surface. The experimental bands are generally consistent with the calculated bulk bands. In addition, we identify some extra bands, as indicated with arrows in Fig. 3g, j. The extra band dispersion at the Γ point in Fig. 3g is identical with the one at the Y point in Fig. 3h. As the extra band is very sharp, we attribute it to 2D surface states rather than the momentum broadening of 3D bulk states, the latter usually smears the band dispersions. The surface band is located at the lower boundary of the valence band continuum and has nothing to do with the topology of the band gap between the valence and conduction states. On the other hand, we observe two hole-like bands across E_F along $$ \mathrm{\Gamma }-X$$ and $$ Y-X_1$$ (Fig. 3i, j), whereas the calculations (Fig. 3m, n) indicate only one hole-like bulk band. Our ARPES measurements show that the inner band dispersion exhibits obvious variation while the outer one remains unchanged with varying photon energy (see Supplementary Fig. 2 in Supplementary Information). The inner band is identified as the valence band of bulk states, while the outer one is attributed to the surface band, which is located in the band gap between the valence and conduction bulk states.

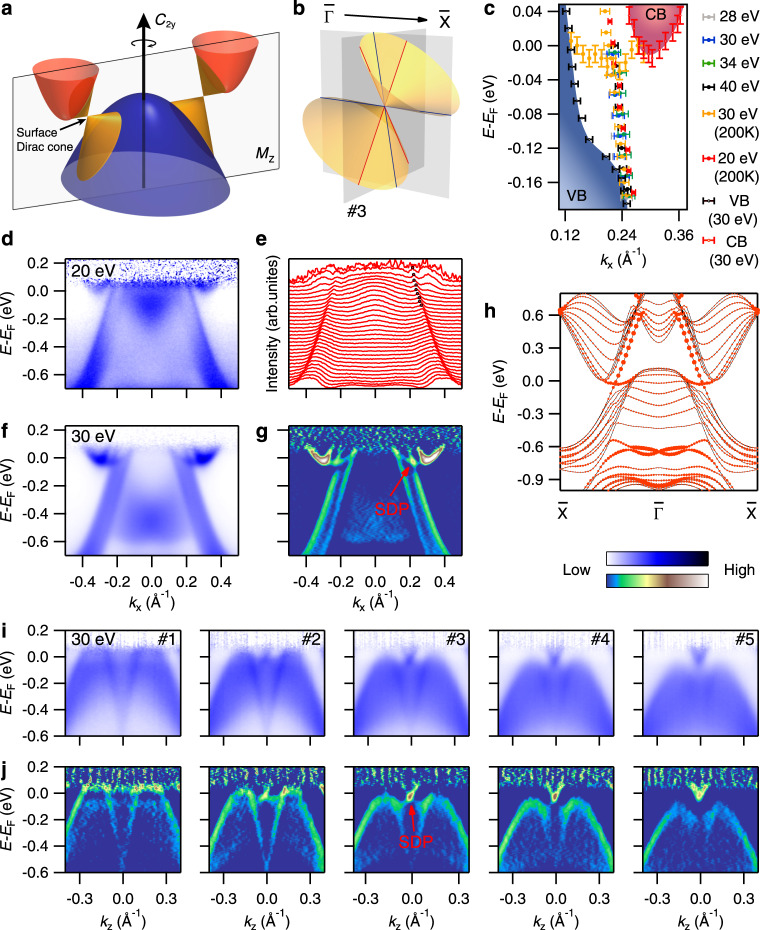
We also discern the sign of a nearly flat band at E_F in the bulk band gap from the ARPES data collected at 30 K (see Supplementary Fig. 2 in Supplementary Information). In order to exhibit the near-E_F band more clearly, we have carried out ARPES measurements at 200 K, which reduce the influence of the Fermi cutoff effect so that the bands above E_F can be observed. The ARPES data collected at 200 K in Fig. 4f, g reveal a relatively flat band near E_F, which emanates from the bottom of the conduction band and extends to the valence band. Remarkably, the two bands in the bulk band gap forming a crossing at ~20 meV below E_F. In Fig. 4c, we plot the band dispersions extracted from the experimental data collected along $$ \overline{\mathrm{\Gamma }}-\overline{X}$$. The observation of Dirac-like band crossing in the bulk band gap is in accord with our theoretical expectation, whereas the experimental surface band dispersions in Fig. 4c are obviously different from the tight-binding calculations in Fig. 2d, which do not consider the real situation of cleavage surface. We thus performed slab calculations considering two kinds of terminations (see Supplementary Fig. 4 in Supplementary Information). While the calculations for both terminations show Dirac-like surface states along $$ \overline{\mathrm{\Gamma }}-\overline{X}$$, the calculated surface bands for termination A in Fig. 4h well reproduce the experimental results. The excellent consistency between experiment and calculation provides compelling evidence for the nontrivial topology of the bulk band gap.

Fig. 4

Dirac surface states on the (010) surface.

a Schematic band structures of SrPb showing two surface Dirac cones protected by $$ {\widehat{C}}_{2y}$$ rotational symmetry. b Schematic of tilted surface Dirac cones, showing dispersions of Dirac-like band crossings along and perpendicular to the tilt direction. c Near-E_F band dispersions along $$ \overline{\mathrm{\Gamma }}-\overline{X}$$ extracted from the ARPES data collected at different photon energies and temperatures. d ARPES intensity plot along $$ \overline{\mathrm{\Gamma }}-\overline{X}$$ measured with $$ h\nu =$$ 20 eV at 200 K. e Momentum distribution curves of the data in (d). f ARPES intensity plot along $$ \overline{\mathrm{\Gamma }}-\overline{X}$$ measured with $$ h\nu =$$ 30 eV at 200 K. g 2D curvature intensity plot of the data in (f), showing two surface bands cross each other forming a surface Dirac point (SDP). The method of 2D curvature was developed in⁴⁵. h Calculated band structures along $$ \overline{\mathrm{\Gamma }}-\overline{X}$$ of a slab with a thickness of five unit cells along the [010] direction for termination A, whose cleavage position is indicated as a yellow plane in Fig. 1a. The size of red dots scales the contribution from the outmost two SrPb layers. The Fermi level of the calculated bands is shifted down by 0.14 eV. i, j ARPES intensity plots and corresponding 2D curvature intensity plots along the cuts perpendicular to $$ \overline{\mathrm{\Gamma }}-\overline{X}$$, whose momentum locations are indicated in Fig. 3d. The data in (i) were collected with hν = 30 eV at 200 K. The ARPES data in Fig. 4 are divided by the Fermi–Dirac distribution function.

We further investigate band dispersions of the Dirac surface states perpendicular to $$ \overline{\mathrm{\Gamma }}-\overline{X}$$. Figure 4i, j shows band dispersions measured along a series of cuts perpendicular to $$ \overline{\mathrm{\Gamma }}-\overline{X}$$, whose momentum locations are indicated in Fig. 3d. A Dirac-like band crossing is clearly resolved at ~20 meV below E_F along cut #3. These experimental data demonstrate that the Dirac-cone surface states are strongly tilted along the $$ \overline{\mathrm{\Gamma }}-\overline{X}$$ direction as the schematic drawing in Fig. 4b. As seen in Fig. 3d, the equal-energy contour of the Dirac-cone surface states is not a closed FS but an open arc connecting to the FSs of bulk states. The tilted Dirac-cone surface states are reminiscent of the type-II Weyl and Dirac semimetals^37,38.

Sample synthesis

Single crystals of SrPb are grown using self-flux methods. The starting materials Sr (distilled dendritic pieces, 99.8%) and Pb (shot, 99.999%) are mixed with a molar stoichiometric ratio of 1:1.32 in a glove box filled with high-purity Ar gas. The mixture is placed in an alumina crucible and sealed in an evacuated quartz tube. The tube is heated to 1000 °C and kept for 10 h. The sample is quickly cooled down to 830 °C and then slowly cooled down to 730 °C at a rate of 2 °C/h followed by centrifuging to remove the excess of Pb. Finally, the shiny crystals SrPb are obtained on the bottom of the crucible. Because the crystals are extremely sensitive to air and water, it is important to store the crystals in an Argon atmosphere.

Angle-resolved photoemission spectroscopy

All the ARPES data shown are recorded at the “Dreamline” beamline of the Shanghai Synchrotron Radiation Facility. We conducted complementary experiments at the Surface and Interface Spectroscopy beamline at the Swiss Light Source, the CASSIOPEE beamline of Soleil Synchrotron, and beamline 13U of National Synchrotron Radiation Laboratory. The energy and angular resolutions are set to 15–30 meV and 0.2°, respectively. All the samples for ARPES measurements are mounted in a BIP Argon (>99.9999%)—filled glove box, cleaved in situ, and measured at 25 K and 200 K in a vacuum better than 5 × 10⁻¹¹ torr.

Calculation method

The calculations are performed using the full-potential linearized augmented-plane-waves method as implemented in the WIEN2K code⁴⁰. The exchange and correlation potential is treated within generalized gradient approximation of Perdew, Burke and Ernzerhof type⁴¹. SOC is included in the calculation as a perturbative step. The atomic radii of the muffin-tin sphere RMT are 2.5 bohrs for Sr and Pb. The 9 × 9 × 10 kmesh is used in the BZ. The s orbitals of Sr and p orbitals of Pb are used to construct the maximally localized Wannier functions⁴², which are then used to calculate the boundary states by an iterative method^43,44.