
Competing Interests: The authors have declared that no competing interests exist.
- Altmetric
Material decomposition (MD) is an important application of computer tomography (CT). For phase contrast imaging, conventional MD methods are categorized into two types with respect to different operation sequences, i.e., “before” or “after” image reconstruction. Both categories come down to two-step methods, which have the problem of noise amplification. In this study, we incorporate both phase and absorption (PA) information into MD process, and correspondingly develop a simultaneous algebraic reconstruction technique (SART). The proposed method is referred to as phase & absorption material decomposition-SART (PAMD-SART). By iteratively solving an optimization problem, material composition and substance quantification are reconstructed directly from absorption and differential phase projections. Comparing with two-step MD, the proposed one-step method is superior in noise suppression and accurate decomposition. Numerical simulations and synchrotron radiation based experiments show that PAMD-SART outperforms the classical MD method (image-based and dual-energy CT iterative method), especially for the quantitative accuracy of material equivalent atomic number.
Introduction
Conventional polychromatic X-ray CT aims at reconstructing the linear absorption coefficient, which depends on material composition and energy-related attenuation performance. This imaging modality relies on its X-ray spectrum, which leads to a weak ability to identify substances. For example, in medical diagnosis, traditional CT often fails to distinguish iodine contrast agents and bone tissue [1]. To overcome the shortcoming, dual-energy CT is developed, which collects projections with two different X-ray spectra and is able to perform selective reconstruction for equivalent atomic number and atomic density, basic-material based concentration distributions, and so on. The commercialized dual-energy CT, like by SIEMENS and GE, can distinguish iodine contrast agents and bone tissue, tendons and ligaments, blood vessels and bone tissue, and so on [2]. The decomposition rationale for dual-energy CT depends on the fact that the energy attenuation behavior of matter varies with different X-ray spectra. However, this assumption is challenged in the real application with low-Z compounds, which have weak absorption and poor discrimination.
Different from traditional absorption-based X-ray CT, phase-based X-ray CT imaging employs both the absorption feature and the phase shift manifestation to reveal the anatomic characteristics. For low-Z material, although the absorption behavior is very similar, the performance on phase shift is quite different [3]. Therefore, theoretically, phase CT has a superior material distinguishability than absorption CT. Methodologically, the phase-contrast CT can be implemented by a grating interferometer based differential phase imaging method, which obtains three perspective images in terms of absorption, differential phase (refraction angle) and scattering. Technically, by employing CT reconstruction technique, the spatial distribution of linear absorption coefficient (μ), the real part of refractive index (δ) and the scattering coefficient can be obtained simultaneously. Assuming the X-ray is monochromatic, these physical indexes can be calculated with traditional analytical algorithms, such as filtered backprojection (FBP). Specifically, the μ and scattering coefficient can be reconstructed by the Shepp-Logan filter based FBP algorithm, while the δ can be reconstructed by the Hilbert filter based FBP [4] or BPF algorithm [5]. Moreover, they can be reconstructed from algebraic iterative reconstruction algorithm [6, 7].
Wang et al. employed absorption and small-angle scattering information to quantitatively measure the material composition and concentration [8], which works for the measurement of volumetric breast density (VBD) and the classification of breast micro-calcification. However, the small-angle scattering information originates from the unevenness inside a resolution unit, which is inappropriate for the substance with uniform composition inside the resolution unit but gradual variation between neighbor resolution units. To overcome this limitation and to improve the reliability of quantitative analysis, considering the high sensitivity of the phase signal, both phase and absorption information are combined for matter decomposition. In 2010, Qi et al. reconstructed μ and δ, and meanwhile calculated the three-dimensional spatial distribution of the material electron density and the effective atomic number [9]. In 2017, Han et al. employed a grating interferometer to acquire absorption and differential phase information, established a two-component absorption and differential phase equation, and performed two-substrate based decomposition in projection domain [10, 11]. In 2018, Braig et al. proposed a two-substrate equation for material decomposition, and investigated material electron density and effective atomic number [12].
The aforementioned methods belong to a two-step strategy, which separately perform decomposition and reconstruction. One strategy is decomposing in projection domain, such as Han’s work [10, 11]. The other is in image domain, such as Qi [9] and Braig [12]. However, whatever the sequence is, noise amplification exists all the time. For projection-domain decomposition, both phase and absorption projections need to be known at the same time. When obtaining the phase projection by integrating the differential phase shift data along the X-ray refraction direction, strip artifacts are introduced and low-frequency noise are amplified in the phase projection [13, 14]. For image-domain decomposition, it is necessary to know the reconstructed μ and δ. When reconstructing the δ, the Hilbert filter based method lacks a noise-suppression mechanism and suffers serious noise influence. All these two approaches are presented in the Methods section.
In order to overcome the inevitable noise amplification of the two-step methods, we propose an optimization-based one-step decomposition method (PAMD-SART, phase & absorption material decomposition-SART), which directly reconstructs substrate images from the differential phase and absorption projections. Noticeably, the optimization model contains a noise-suppression mechanism and can be effectively solved by an iterative scheme.
Theory and method
Imaging theory
The interaction between X-rays with matter can be described by the following complex refractive index
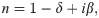
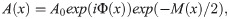
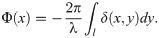
Let M describe the absorption of X-rays, which can be formularized as
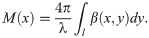
After penetrating the object, the intensity of X-ray decays to
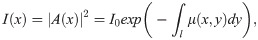
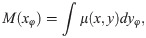
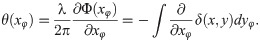
According to the material decomposition method, μ of the measured object can be expressed as a linear combination of μ of two basic materials. Under the condition of monochromatic X-ray exposure, δ can also be linearly expressed by δ of two basic materials [11] as follows,
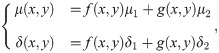
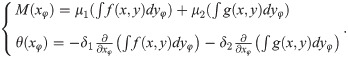
To demonstrate the superiority of the phase and absorption based substrate decomposition than the conventional dual-energy based one, we illustrate a simple example in Fig 1. As shown in Fig 1A, assuming two X-ray beams with energy of 20 keV and 30 keV successively pass through water and PMMA with the same thickness of 1 mm, the corresponding absorption equations read,
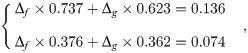
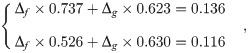


Schematic diagram.
(A) Schematic diagram of ray and matter interaction and (B) the decomposition equation line.
Reconstruction algorithm
In this section, we introduce the discrete mathematical model of the phase-based basic material decomposition, investigate the derivation process, and present the implementation steps of the proposed PAMD-SART method.
Imaging model
Let f = (f1, f2, …fJ)τ and g = (g1, g2, …gJ)τ denote the discretized images of f(x, y) and g(x, y), where fj and gj are the sampled values of f(x, y) and g(x, y) at the jth pixel, J the total pixel number, and τ the vector transpose operation. Let
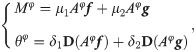
Solution algorithm
The projection-domain based material decomposition is a traditional method [11]. This method uses the inverse of the differential operator D−1 and the boundary condition to solve D−1θφ. Applying D−1 directly spreads the signal error, and leads to stripe artifacts. In order to effectively suppress these artifacts, optimization based methods are taken into consideration [13, 14]. First, (12) need to be converted as,
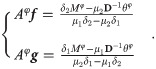
Then the traditional reconstruction method is employed to recover f and g. The other kind of methods can be viewed as image-domain based material decomposition, which converts (12) to
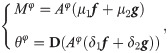
PAMD-SART algorithm
The algorithm proposed in this paper is to obtain the final decomposition image by solving the following optimization model:
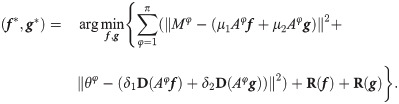
The definition of each symbol is consistent with section Imaging model and R(⋅) is a regularization operator such as total variation (TV) [16, 17], gradient L0 [18], Mumford-Shah [19] or an image filter. In the following, inspired by the SART reconstruction strategy [20], an iterative algorithm to directly reconstruct f and g from the absorption projection Mφ and the differential phase projection θφ is given.
Assuming the current estimate images are (f(m), g(m)), then the projection estimations of absorption and differential phase can be calculated by
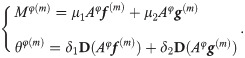
Furthermore, the residual can be expressed as
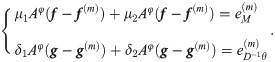
After solving the above equations, we obtain
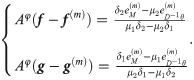
Finally, by using SART algorithm, we get the iterative form
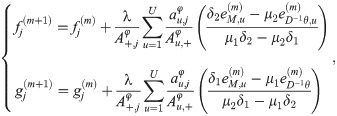
In the iterative scheme, the calculation of phase residual
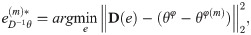
Algorithm 1 The PAMD-SART Method
1: Initialization: f(0) = 0, g(0) = 0, m = 0
2: Calculate the estimate of absorption projection Mφ(m) and its residuals
3: Iteratively solve f(m+ 1), g(m+1) according to (19).
4: Do a regularization operator to f(m+1), g(m+1).
5: Set m = m + 1 and turn to step (2) until the stop condition is met.
6: Return f(m), g(m)
Verification
In this section, we performed numerical simulations and real experiments to verify the proposed method, including visual comparison of material decomposition results and quantitative analysis of acquired equivalent atomic number.
The image quality was measured with peak signal-tonoise ratio (PSNR)
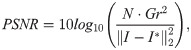
Numerical simulations
The numerical phantom was derived from the FORBILD head phantom [21]. As shown in Fig 2A, the size is 9.8mm*7.8mm, including bone and water. In order to enhance the comparison performance, we added multiple water-like objects to the original image. The specific density is shown in Fig 2C. In the simulated experiment, for the sake of simplicity, we used 20 keV monochromatic X-ray. The μ and δ of water and bone were from the X-ray optics software toolkit(XOP) [22]. First, the projection data of the sample was obtained using the forward projection method, and then Poisson noise was added, where the number of original photons was 106 per ray. The differential phase projection was obtained by performing center-difference to the phase projection, and the δ values of water and bone were multiplied by the same ratio so that they were similar to the absorption value μ. In the simulation, a parallel-beam setting was used to acquire 540 projections equally spaced in 180 degrees. The detector contained 512 cells with a size of 20 um. The diameter of the covered field of view was 10.24 mm.

Phantom in numerical experiments.
(A) Numerical phantom, (B) The Bone material of the phantom, and (C) The Water material of the phantom.
In image reconstruction, bone and water were selected as the basic materials, and the reconstructed image size was 512 × 512. The PAMD-SART method was implemented by C++ and CUDA with GPU acceleration. For better comparison, we implemented regularized iterative method to reconstruct μ [6] and δ [7] in the first step of the image based method. TV was employed as a regularization term and the solution algorithm was from the Chambolle’s method [17]. This method is very efficient and easy to be implemented, of which only one regularization parameter (λTV) is used to adjust the image fidelity and TV. According to our experimental results, λTV = 0.1*mean(image) was a good beginning for Chambolle’s method. Specifically, ray-casting method was used for forward projection process, and pixel-driven method for backward projection.
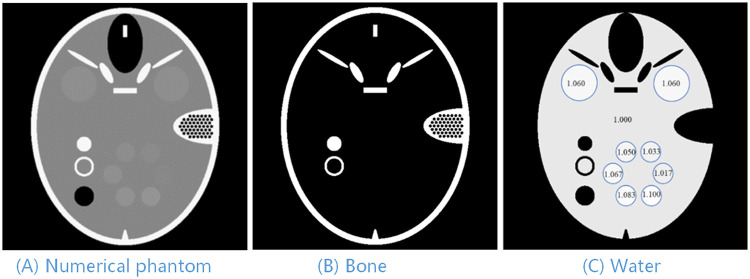
The decomposed results under noise-free and noisy cases are shown in Fig 3. For each case, both image-based method and PAMD-SART were performed. We zoomed in the local region of water-like objects and illustrated in the third column to improve the visual comparison. The profile of water-based image in noisy case and the convergence curve of the PAMD-SART method are shown in Fig 4. The PSNR values for both methods in the noise-free and noise cases are shown in Table 1.


Reconstruction result of phantom study.
Comparison of image-based and PAMD-SART results in noise free and noisy case. All the bone fraction images are displayed in gray window [0, 1], and water in [0.8, 1.2].

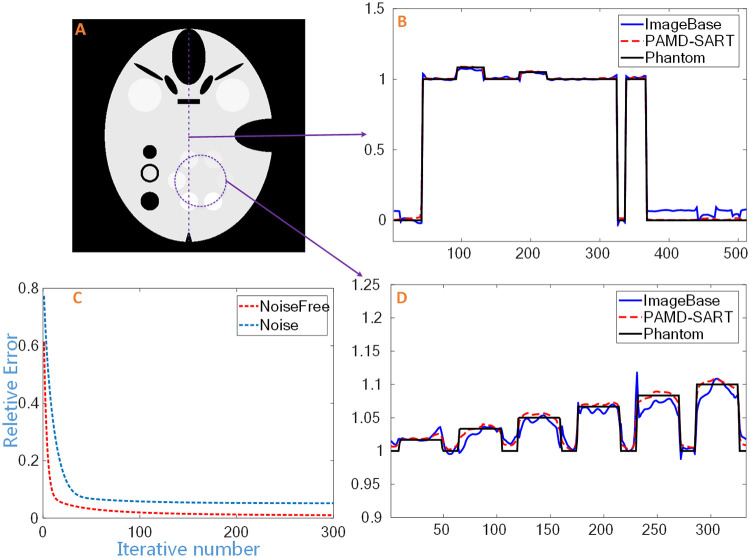
Profile of water-based reconstruction image in noisy case.
The vertical (B) and circular (D) profile in the water-based image (A), and (C) the convergence curve of the PAMD-SART method.

| Noise free | Noise | |||
|---|---|---|---|---|
| Image-Based | PAMD-SART | Image-Based | PAMD-SART | |
| bone | 51.47 | 55.06 | 32.31 | 36.01 |
| water | 40.66 | 43.70 | 26.69 | 32.02 |
From the results in Figs 3 and 4 and Table 1, we can see that the PAMD-SART method is superior to the image-based method. In the noise-free case, looking at the first and second lines of Fig 3, both methods can reconstruct the result without artifacts, but when comparing the circle structure with the lowest contrast in the third column, the boundary of the structure in image-based method is a little blurry, while the result of PAMD-SART is very sharp. In the noisy case, PAMD-SART performs much better than image-based method. From Table 1, the PSNR value of the image-based method is smaller than PAMD-SART, which indicates that the former keeps a larger error. From the circular water-like material region in the third column of Fig 3, the two materials with the lowest density can hardly be distinguished from the image-based method, but are clear in PAMD-SART. From the profile in Fig 4, we can see that there is a large oscillation in the image-based result, and the material with smallest density is too close to the water to be separated. However, PAMD-SART can well identify the small contrast change. The curve of relative error indicates the convergence of PMAD-SART in numerical.
The reason for this result is that the original image has a large dynamic range, it is difficult to balance the fidelity term and the regularization term when directly regularizing the original image. When suppressing noise artifacts, the border of low contrast objects will inevitably be blurred. The proposed PAMD-SART method uses projection information of μ and δ simultaneously in the reconstruction process, which reduces the noise interference. Moreover, PAMD-SART performs the regularization on substrate images which has smaller dynamic range than the original images, so has less effect on low-contrast objects. Because PAMD-SART has the advantages in these two aspects, it is much superior to the image-based method.
Real experiment
Real experiments were performed using the X-ray grating interferometer on the BL13W experimental station by Shanghai Synchrotron Radiation Facility. The grating interferometer consisted of a π/2 phase grating with a period of 2.396 um and an absorption grating with a period of 2.4 um. The distance between the two gratings was 46.38 mm and the photon energy used in the experiment was 20 keV. The sCMOS X-ray detector with effective pixel array of 2048 × 600 was applied, and the pixel size was 6.5 × 6.5 um2. In order to obtain the phase and absorption projection, the step method was used for data acquisition. The number of steps was 8, which meant the phase grating moved 8 steps in a period to take samples separately, then completed the data acquisition from one angle. Finally, the data of 540 angles were collected at equal intervals within 180 degrees. The average digital value of 8 referenced acquired image in a period was about 25000, and the fringe visibility about 50%. The absorption and differential phase projections were calculated from the data collected at each angle by the phase step formula in [23]. The reconstructed image size was 1024 × 1024, and the maximum iterations was set as 200 which was the stop condition of PAMD-SART.
Phantom experiment
As shown in Fig 5A, the phantom consists of four components, Low Density Polyethylene (LDPE), Polymethyl Methacrylate (PMMA), Polytetrafluoroethylene (PTFE), and water. The PTFE, LDPE and PMMA cylinders with diameters of 2.0 mm, 4.0 mm and 5.6 mm, respectively, were placed in a polyethylene plastic tube with an external diameter of 10.7 mm and injected with pure water to form the whole sample.

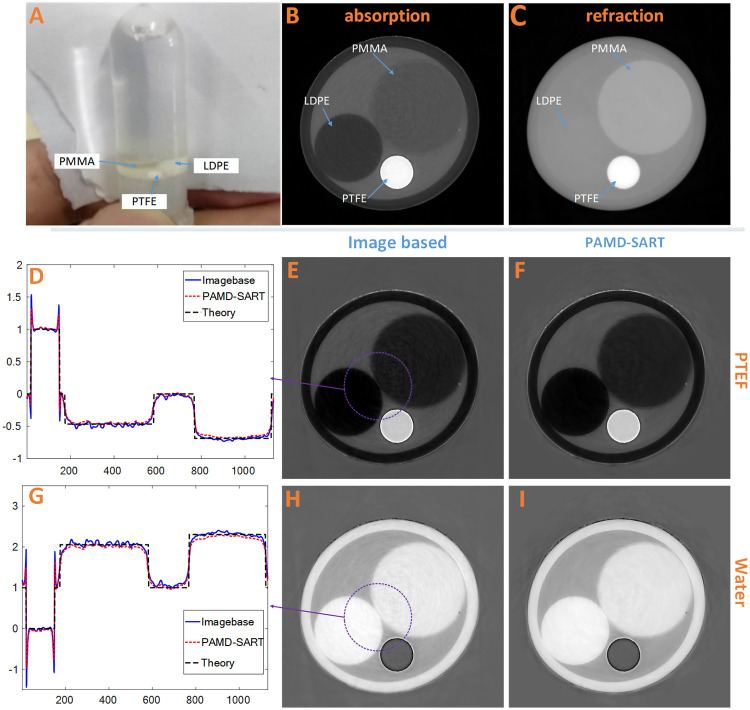
Experimental results of phantoms.
(A) The physical photo, (B) the reconstructed tomogram of the μ and (C) the δ; the second and third lines are the PTFE-based and water-based results decomposed by the image-base method and the PAMD-SART method, including the line Comparison chart and tomogram. (D) is the profile line of PTFE-based result, while (G) the water-based result; (E) and (F) are PTFE-based decomposed result of method image based and PAMD-SART; (H) and (i) are water-based decomposed result of method image based and PAMD-SART. The display window for B is [0, 0.2], C [0, 8.2], E and F [-0.7, 1.4], H and I [-1, 2.5].
In this experiment, we used water and PTFE as substrates to perform PAMD-SART and image-based decomposition. Then based on the substrate images, μ and δ images and equivalent atomic number were calculated. This result was compared with the dual energy CT method.
Fig 5 shows the decomposition results of different methods. Fig 5B is the absorption coefficient tomography. The outer ring in the image represents the polyethylene plastic container, and there are three different components in the inner ring, namely, three circles with different gray levels in the middle of the ring, LDPE phantom with the lowest gray level on the left, PTFE phantom with the highest gray level at the bottom, PMMA phantom at the upper right and water at the rest. In Fig 5C, it can be seen that LDPE and water are difficult to be distinguished. This phenomenon shows that the contrast of phase information is not necessarily higher than the absorption. Comparing the decomposition results of image-based and PAMD-SART methods, i.e., Fig 5D–5I, it is obvious that PAMD-SART method has better noise removal performance.
Both works of Qi [9] and Braig [12], refer to the calculation of electron density ρe and equivalent atomic number Z from absorption μ and phase δ, by employing the following relationship
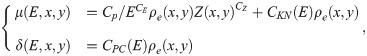
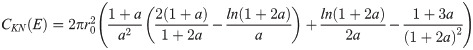
In the proposed method, by using the obtained substrate images, the refraction and absorption images can be calculated by (8), and then introduced to (22) to get ρe and Z. The theoretical equivalent atomic number Z for a compound was calculated by the following equation [24]
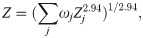
Using the μ in formula (22) with two different energies, the atomic number can also be calculated, which is employed in dual-energy CT [25]. Hence, we acquired two CT datasets by using 20keV and 12keV on the synchrotron radiation station, and the number of views was the same as the grating based scanning. The integration time of detector was adjusted, so that the digital value of acquired image under direct exposure was around 50000. Compared to the data acquired with grating, from the view of detector, the total dose of two monochromatic CT was about half of the grating.
As shown in Table 2, the fitted results are very close to the theoretical values. Fig 6 and Table 2 show that the accuracy of the atomic tomographic image reconstructed by the substrate image is close to the theoretical value, while the result by the dual-energy method contains a large error for PTFE and LDPE. Theoretically, the equivalent atomic number of PTFE should be greater than water. However, when using the dual-energy method with 12 keV and 20 keV X-ray beams, the calculated atomic number of PTFE is smaller than water. Once ρe(x, y) and Z(x, y) were obtained, μ(x, y) at any energy can be calculated by formula 22, which generated a virtual image. In the 12 keV virtual image, it can be found that the μ ratio of PTFE to water is 2.78, while is 2.41 in the 12 keV actual absorption image. These results demonstrate that the empirical formula of atomic number calculated by dual energy (ZC(μ1, μ2)) has a large error in the low energy case. Furthermore, by comparing and analyzing the absorption coefficients of various substances, it can be found that the empirical formula (ZC(μ1, μ2)) is no longer valid when the X-ray energy is less than 20 keV. This is mainly because the linear attenuation coefficient in (22) ignores the coherent scattering term (Rayleigh cross section). However, Table 3 shows that in the energy below 30 keV this term is non-negligible. In Table 3, the cross section of photon interaction are from xraylib [26], these data can also be found in Evaluated Nuclear Data Library(ENDL) [27].

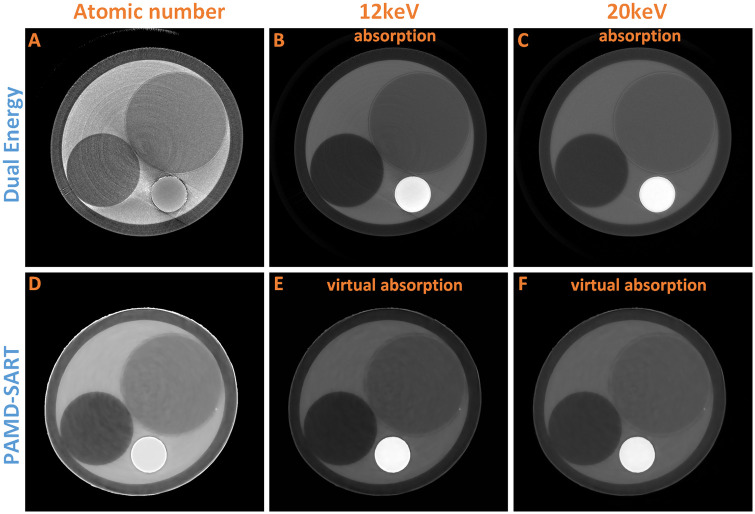
Phantom results of atomic number.
(A) is the equivalent atomic number by dual energy method using absorption of 12keV (B) and 20keV (C). (D) is the equivalent atomic number by PAMD-SART method. (E) and (F) are the virtual absorption at 12keV and 20keV respectively. The display window for A and D are [5,9], B [0,0.7], C and F [0,0.2], and E [0,0.8].

| Water | PTFE | PMMA | LDPE | |
|---|---|---|---|---|
| δ(20keV) | 5.653e-7 | 1.039e-6 | 6.777e-7 | 5.863e-7 |
| μ1(20keV) | 7.369e-1 | 1.907 | 6.280e-1 | 3.905e-1 |
| μ2(12keV) | 2.729 | 6.776 | 2.111 | 1.195 |
| ZT | 7.417 | 8.433 | 6.467 | 5.444 |
| ZC(δ, μ1) | 7.416±0.10 | 8.398±0.04 | 6.433±0.11 | 5.409±0.12 |
| ZC(μ1, μ2) | 7.410±0.24 | 6.881±0.15 | 6.612±0.15 | 6.002±0.18 |
(ZT is the theoretical value by (24), ZC is the calculated value).

| cm2/g | Water | PTFE | ||||
|---|---|---|---|---|---|---|
| 12 keV | 20 keV | 30 keV | 12 keV | 20 keV | 30 keV | |
| Photoionzation | 2.7828 | 0.5438 | 0.1457 | 3.6262 | 0.7170 | 0.1938 |
| Compton | 0.1625 | 0.1774 | 0.1829 | 0.1305 | 0.1473 | 0.1544 |
| Rayleigh | 0.1805 | 0.0885 | 0.0469 | 0.2117 | 0.1025 | 0.0544 |
Biological sample experiment
Taking into account the blooming applications in biological sample imaging, we employed a chicken paw bought from supermarket as the specimen. The results are shown in Fig 7. In the second row of Fig 7(D)–7(F) are the result of image-based method. In the third row, (G)-(I) are the result of PAMD-SART. Since the sample is complex, in order to keep the image fidelity, the regularization term at all reconstruction was small.


Biological sample result.
(A) Chicken paw. The tomogram of μ (B) and δ (C). (D) and (G) Equivalent atomic number. (E)(H) Decomposed image of water. (F)(I) Decomposed image of bone. (D-F) are the result of image-based method, (G-I) are result of PAMD-SART. The display window for B is [-0.2, 0.8], C [-0.1, 5.3], D and G [3.3, 16.5], E and H [-0.4, 1.1], F and I [-0.4, 1].
In this experiment, the refraction image contained more artifacts than the absorption image. The reason lied in the dry chicken paw included a lot of air regions, which caused a sharp change in the refractive index and further led to these artifacts. It was noticeable that the noise of the water-based and bone-based tomographic images was not amplified by the PAMD-SART method, but almost the same as the image-based method. In the equivalent atomic number image, the ZC of water in PAMD-SART method was more close to theoretical value than the image-based method. As is shown at the dotted frame part of bone in Fig 7D and 7G, the image-based method suffers an error at some part. It is because δ is less than zero, but μ larger than zero. However, the PAMD-SART method avoids this error, since it adopts the projection information of both μ and δ in the reconstruction process. Thus, it indicates that the proposed PAMD-SART method is also better than image-based method at complex biological applications.
Discussion and conclusion
In this paper, we propose an iterative method, PAMD-SART, for phase and absorption based substrate decomposition. This method directly reconstructs basic images with desirable noise suppression and boundary maintenance. Numerical simulations and real experiments validate the superiority of the proposed method than the traditional image-based method. In addition, the obtained absorption and phase images are further quantitatively analyzed in terms of equivalent atomic number. The corresponding results are close to the theoretical values, and are more precise than the dual-energy method for low X-ray energies. The proposed PAMD-SART method works well for the synchrotron monochromatic projection data, and will be further extended to the laboratory light source CT system according to the equivalent monochromatic method.
The phase contract CT has not yet been applied to clinical practical applications, and is mainly limited by the manufacture of gratings [28–30]. The method proposed in this paper is a primary research. We verify the effectiveness of PAMD-SART with the data acquired by grating interferometer at synchrotron radiation station. And the size of phantom is just about 10mm due to the limitation of low energy and the limited size of grating and detector.
When calculating the equivalent atomic number (Z), there is actually no obvious comparability between phase CT and dual energy CT. It is because the principles of these two imaging patterns are not the same. However, the comparison experiments show that dual energy has more clear conditions for Z calculation. In the case of low energy (less than 30 keV), using two absorption coefficient equations which ignore the coherent scattering (Rayleigh scattering) term to solve Z will have a large error. While in conventional applications of medical or industrial CT, the photon energy is relatively high (more than 40 keV), so it is feasible to ignore the coherent scattering term. Validation and comparison in polychromatic and high energy X-ray are beyond the scope of this study, and will be investigated in future.
Acknowledgements
This work was carried out with the support of Shanghai Synchrotron Radiation Facility. The authors thank Pof. Dr. Biao Deng for the help and support during the experiments at SSRF.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
 A method for material decomposition and quantification with grating based phase CT
A method for material decomposition and quantification with grating based phase CT
