2.1 Oxygen diffusion in tissue

The oxygen-consuming tissue is a mixture of cells, extracellular matrix and extracellular fluid. Oxygen transport in tissue depends mostly on diffusion. The diffusion constant and solubility of oxygen may vary slightly in different tissue. Here we assume a uniform oxygen diffusivity D and uniform solubility α. Oxygen diffusion in tissue at steady state satisfies the reaction-diffusion equation

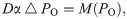
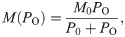
2.2 Blood flow and blood pressure

The blood flow and blood pressure can be computed with Ohm’s law and Kirchhoff’s circuit law that form a system of linear equations. For a small blood vessel, which can be regarded as a cylinder, the blood flow in the vessel can be well approximated by the Poiseuille flow. The conductance of the vessel is

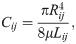
The blood pressure and blood flow rate from node i to node j, Q_ij, satisfies the Ohm’s law

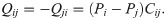
The Kirchhoff’s circuit law describes the conservation of mass

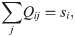
2.3 Oxygen flux in vessels

Oxygen carried by blood includes two parts, the minor of which is directly dissolved in the plasma while the major of which is associated with hemoglobin. The relation between oxygen saturation S_a and blood oxygen partial pressure P_b satisfies the Oxygen-hemoglobin dissociation relation

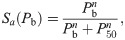
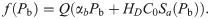
2.4 Oxygen exchange on vessel walls

Let s be the arc-length parameter along the centerline of a vessel and x(s) be the coordinate of the centerline. Assume the cross-section of the blood vessel is a circle with radius R, then the total oxygen flux q(s) through the blood vessel wall per unit length is

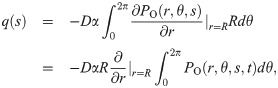
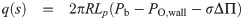
Ignoring the oxygen consumption in blood, we obtain the conservation of oxygen

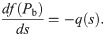
Given the oxygen flux q(s), the above equation becomes a first-order ordinary differential equation (ODE). A boundary condition is required to solve the equation for each vessel. In real applications, we may have P_b at the inlet of each vessel: (1) At the inlets of the vessel system, P_b is given; (2) At the bifurcation points, P_b at the inlet of the downstream vessels is inherited from the parent vessel; (3) At collecting junctions, P_b at the inlet of the downstream vessel is obtained from its parent vessels as the mixed value by conservation of oxygen.

2.5 Model simplification

Since the oxygen partial pressure should be continuous in the whole domain, i.e., the tissue domain and the vessel domain, P_b provides a Dirichlet boundary condition on vessel walls for P_O in Eq (1). However, the disordered structure of blood vessel walls brings great difficulties in meshing and numerical simulations to solve the above coupled system. In previous studies [37], the oxygen flux is represented by oxygen sources on the centerlines of vessels. Under this simplification, the governing equation for oxygen supply is defined in the whole domain. In this case, the governing equation becomes

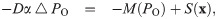
Note that the vessel radius is relatively small (2 ∼ 3μm) compared to the distance between capillaries (∼100μm). Therefore, this simplification can be a good approximation at least for far field. The oxygen partial pressure may be overestimated near the vessels, which can lead to a slight overestimate of the oxygen source M(P_O). Further improvement on such an approximation has been discussed in the work of Ref. [26, 38]. Instead of concentrated oxygen sources on the centerlines of blood vessels, distributed sources using smooth kernel functions are also used in a recent study [39]. This can be effectively used to avoid the weak singularities of the oxygen field.

Now we have obtained a coupled system for oxygen delivery, which includes a PDE (10) on the whole domain, a set of nonlinear ODEs (9) on the vessel centerlines, and a system of linear equations for blood pressures and blood flows in all vessels.

3.1 Nonlinear iteration

Mainly due to the nonlinearity of the ODEs (9) and the unusual form of coupling, general iteration methods, such as the full Newton-like iterative methods, are both hard in code implementation and lack of convergence guarantee for the coupled system. Here we propose an iterative method by decoupling the system and alternatively updating P_O and P_b. In particular, we introduce pseudo time step in order to reach the steady state solution. The rest of the section then explains how each (pseudo) time step is solved, namely with a semi-implicit Euler method.

Given $$ P_{\text{O}}^n$$ and $$ P_{\text{b}}^n$$ at step n, by assuming that the blood oxygen partial pressure P_O = P_b on vessel walls, Eq (7) allows us to evaluate the flux qⁿ(s) numerically. In the 3-D case, we expand the Laplacian operator in series near the vessel first, and then use particular fitting to evaluate the derivative in Eq (7). In the 2-D case, linear fitting on both sides of the vessel can be directly utilized to evaluate the flux qⁿ(s). Detailed discussion on the fitting method is included in Appendix A. Similar treatment can also be used to evaluate the oxygen flux utilizing the Kedem-Katalchsky’s law. In general, we denote the evaluation of qⁿ as

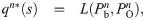
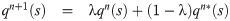
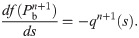
The fourth-order Runge-Kutta method is used to solve the ODE (13) to obtain $$ P_{\text{b}}^{n+1}$$ in each vessel segment. In practice, q^n* can also be updated in a Gauss-Seidel fashion. Namely, the values of $$ P_{\text{b}}^{n+1}$$ on the updated nodes can be used in Eq (11) to evaluate the flux.

The flux qⁿ⁺¹ is also used to calculate the oxygen source Sⁿ⁺¹, which is required in computing $$ P_{\text{O}}^{n+1}$$. It is possible to update P_O by fully solving the PDE (10) with given oxygen source Sⁿ⁺¹. However, since we still need the nonlinear iteration, it is neither necessary nor efficient to find the accurate solution at each iteration step. Instead, we use the following scheme to update P_O

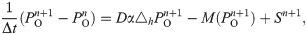
Note that an increase of the oxygen partial pressure $$ P_{\text{O}}^n$$ in tissue can lead to a decrease of the oxygen flux qⁿ⁺¹ (thus the oxygen source Sⁿ⁺¹). This implies at least one negative eigenvalue of the coupled system in the sense of linearization. As a result, it may even be not stable to update P_O by fully solving the steady state PDE (10) for each iteration step (namely, Δt = ∞). The instability has been observed in our numerical test. From this point of view, a suitable time step size Δt should be selected so that it is both good for iteration stability (Δt is not too big) and good for fast convergence (Δt is sufficiently big).

3.2 PDE solver

Based on the iteration framework above, our remaining task is to numerically solve the PDE (10) efficiently. For the simplified coupled system, we do not consider the detailed geometry of vessel walls. Thus, a square mesh can be easily used in our simulation. We simply use the central difference as the numerical Laplacian △_h, where h is the mesh size. This brings great convenience in developing a fast solver. The system in this paper contains no fluid convection and maintains a uniform diffusion coefficient. Under this situation, the central differential scheme is equivalent to the finite volume method, which ensures the local mass conservation. When convection becomes significant, we can use the mass-conservative finite volume method instead.

There are two problems left for us to solve: First, the oxygen sources are located on vessel centerlines, we need to distribute the sources onto the square mesh points; Second, in order to conduct a large scale simulation, we need to use a relatively large spatial mesh size while maintaining sufficient numerical accuracy.

In order to distribute the oxygen sources onto the square mesh points, first we discretize the sources to be point sources $$ S_k^n\left(\mathbf{x}\right)=q^n\left({\mathbf{x}}_k\right)h_k\delta (\mathbf{x}-{\mathbf{x}}_k)$$ on the center lines, where k is the index of the point source at x_k = (x_k,1, x_k,2, …, x_k,d) (d is the space dimension) and h_k is the step size on the centerline; Then, we use Peskin’s numerical δ-function $$ \overline{\delta }(·)$$ (see Appendix B) to distribute all point sources onto their neighboring mesh points [40]. Namely, we have

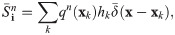
Due to the nonlinearity in the consumption function M(⋅), we use the standard multigrid algorithm combined with the Newton’s method to solve Eq (14). According to our numerical tests, only a few steps of Newton-iteration are sufficient to make the numerical error small enough.

Notably, the above redistribution of oxygen-sources can lead to numerical error in the solution. As a result of using Peskin’s numerical δ-function, the numerical error induced by source redistribution is local—mainly on the local mesh points to which the oxygen sources are distributed (see Appendix C). Nevertheless, the local oxygen field around the blood vessels must be sufficiently accurate for evaluating the oxygen flux using Eq (11). Therefore, without further improvement, we can only use a small spatial mesh size h to perform simulations.

Next, we introduce a post-processing technique to reduce the local error induced by the redistribution of oxygen-sources. With this post-processing step, we are able to use a relatively large mesh size h (e.g., be comparable to or even larger than vessel diameters) while maintaining a sufficiently small numerical error.

3.3 Post-processing

The post-processing is designed to reduce the error introduced by oxygen-source redistribution. This error can be defined as the difference $$ \delta P=P_{\text{O}}^{n+1}-{\overline{P}}_O^{n+1}$$, where $$ P_{\text{O}}^{n+1}$$ and $$ {\overline{P}}_{\text{O}}^{n+1}$$ satisfy the following equations

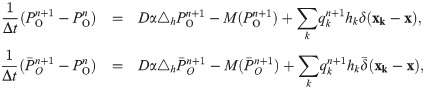
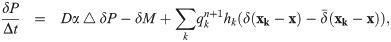
Eq (16) appears to be nonlinear due to the nonlinearity in δM. However, in real applications, this term is always very small and we can neglect it. The reason that δM is small is double fold: For mesh points near a vessel, the oxygen partial pressure is relatively high (much bigger than P₀), thus $$ M^{\prime }\left(P_{\text{O}}^{n+1}\right)$$ is very small; whereas for mesh points away from all vessels, δP becomes very small thanks to the good property of the numerical δ-function. Therefore, we can evaluate δP by neglecting the nonlinear term

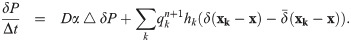
Due to the linearity of Eq (17), δP can be regarded as the linear combination $$ \delta P={\sum }_k{q}_k^{n+1}{h}_k\delta P_k$$, where δP_k satisfies

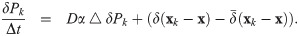
The boundary condition for Eq (18) is that δP_k vanishes when x → ∞. In fact, as shown in Appendix C, only a few mesh-sizes away from x_k, the error δP_k is already negligible. This observation allows us to solve δP_k only on local mesh near to x_k (e.g., an 8 × 8 mesh in the 2-D case).

The error δP_k can be further decomposed into two parts $$ \delta P_k=P_k-{\overline{P}}_k$$, where the first part $$ P_k={\int }_0^{\Delta t}\frac{1}{\sqrt{{\left(4\pi D\alpha s\right)}^d}}exp(-\frac{|{\mathbf{x}}_{\mathbf{k}}{-\mathbf{x}|}^2}{4D\alpha s})ds$$ is the fundamental solution corresponding to the point source δ(x_k − x) and the second part $$ {\overline{P}}_k$$ is corresponding to the distributed sources

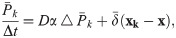
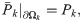
In summary, for each source point x_k, δP_k is evaluated on a local mesh at the beginning. At each iteration step, the linear combination $$ \delta P={\sum }_k{q}_k^{n+1}{h}_k\delta P_k$$ is used to evaluate the error on mesh points close to vessels introduced by oxygen-source redistribution. This error is then removed from $$ {\overline{P}}_{\text{O}}^{n+1}$$.

5.1 Blood vessel network structures

Four model structures of blood vessel networks are used in our simulation (see Fig 1). The simple cobweb structure (Fig 1(a)) in 2D and the single vessel (Fig 1(c)) in 3D are used for model validation and numerical convergence analysis. The 2D and 3D refined structures (Fig 1(b) and 1(d)) are adapted from real experimental measurements on a mouse retina. They are further used for analyzing the efficiency of oxygen supply. In this study, the no-flux boundary condition is used in solving the oxygen field with Eq (1).

Fig 1

Model vessel structures.

(a) A cobweb vessel structure mimicking the main branches of retinal vessel networks. There are six inlets and six outlets for blood flow near the center of the network. The inlets and outlets are in a spaced arrangement. The arrows show the direction of blood flow. (b) A refined vessel network with 4306 blood vessels. The network structure is adapted from a real retinal vessel network measured in experiment by stretching and symmetrical extensions. There are four flow inlets and flow outlets near the center. (c)A single vessel embedded in a tissue cube. (d) A refined 3D vessel network with 7815 blood vessels. The intermediate and deep capillary plexi layers in retina are reconstructed by projecting the above 2D network onto two spherical shells. The diameter of the two spheres for the deep capillary plexi layer, the intermediate layer, and the choroid layer is 2 mm, 2.1 mm, and 2.2 mm, respectively. The widths of the lines in each figure show the radii of blood vessels. The unit for the axes is micrometer for (c), and millimeter for others.

5.2 Numerical solution for the cobweb vessel network

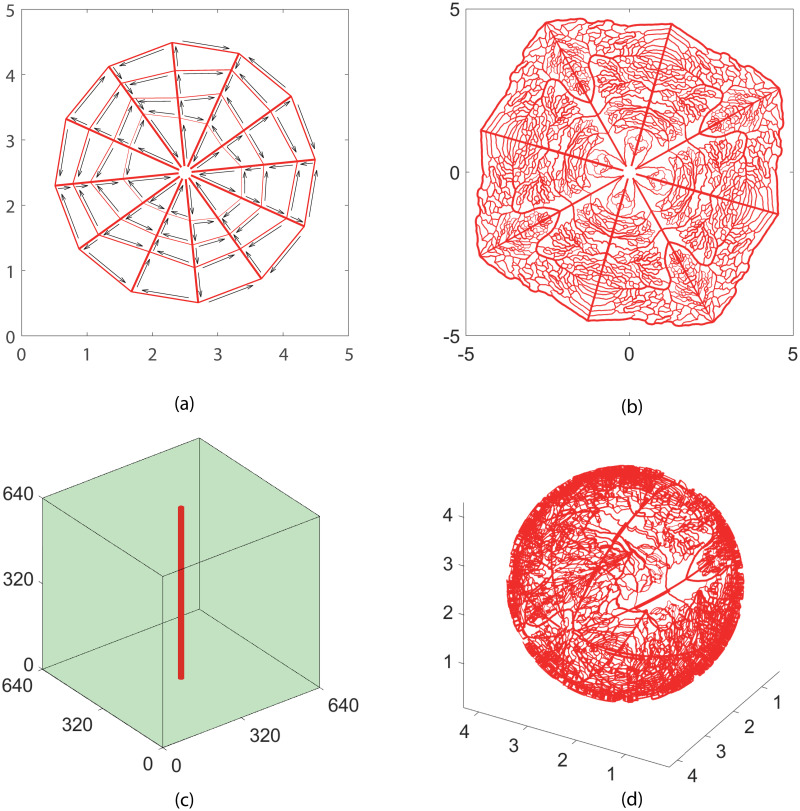
In Fig 2(a), we show the numerical solution of the oxygen partial pressure obtained with a 1024 × 1024 square mesh for the cobweb vessel structure. Since the distance between neighboring vessels is much bigger than that of real microvasculature, tissue away from the vessels is in a hypoxic state, i.e., the oxygen partial pressure is very low. The width of the well irrigated region for each vessel depends on the blood flow in it, being roughly on the scale of 100 μm. Note that the gap between neighboring capillaries in normal tissue is also roughly on the scale of 100 μm, which is much smaller than that in the cobweb structure. With such a high capillary density, normal tissue can be well irrigated.

Fig 2

Oxygen partial pressure and its numerical error.

(a) Numerical solution of the oxygen partial pressure obtained with a 1024 × 1024 square mesh. (b) Numerical error of the oxygen partial pressure calculated by the difference between the solution obtained with a 1024 × 1024 mesh and a 2048 × 2048 mesh. The unit for oxygen partial pressure is mmHg.

The numerical error of the oxygen partial pressure is shown in Fig 2(b). The error is calculated by comparing the solution obtained with a 1024 × 1024 mesh and a 2048 × 2048 mesh. The error is smaller than 1 mmHg. This suggests that with a mesh size of about 5 μm, the numerical error can be smaller than one percent.

In Fig 3, we show the blood oxygen partial pressure P_b and oxygen flux q on all vessels. Because the blood vessels of the most inner loop are very small, they have a big resistance to blood flow. As a result, the blood flow in these vessels is very small, which leads to a fast decay in blood oxygen partial pressure along the flow direction (see Fig 3(a)). From Fig 3(c), we can see that the blood oxygen partial pressure P_b decreases along each vessel segment as the oxygen diffuses from vessel to tissue. Similarly, in Fig 3(b) and 3(d), we show the oxygen flux q. From Fig 3(b), we can see that the flux q reaches minimums at most cross-links of the vessel segments. This is because that more than one vessels share the oxygen supply to the local tissue at the cross-links. On the contrary, from Fig 3(d), we can see that the oxygen flux in vessel a and d reaches the maximums at their one or two ends. This is due to the vacancy of vessels at the center and the outer domain. At the end of the vessel segment b, the blood oxygen partial pressure becomes a constant and the flux becomes zero, because the oxygen partial pressure is higher in the surrounding tissue than the blood inside the vessel. Note that this unphysiological behavior is a consequence of the cobweb vessel structure. Here we set the negative flux to be zero. This setting does not significantly change the tissue oxygen level and blood oxygen concentration in downstream vessels since this piece of vessel is always short.

Fig 3

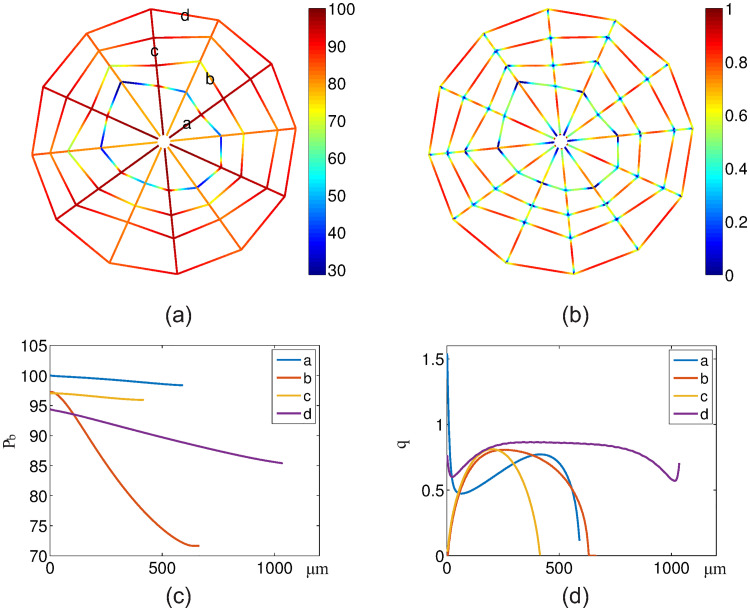
Blood oxygen partial pressure and oxygen fluxes from the vessels.

(a) Blood oxygen partial pressure P_b on the vessels. (b) Oxygen fluxes q from the vessels to tissue. (c-d) P_b and q on four marked vessel segments in (a). The x-axis denotes the distance from the inlet for each vessel (i.e., arc-length coordinate). The unit of P_b is mmHg. The unit of q is 10⁻⁹cm³O₂/cm/s.

5.3 Numerical solution for the 2D refined vessel network

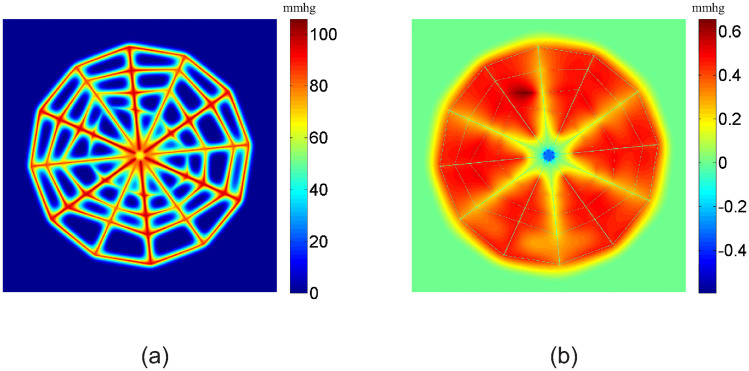
The numerical solutions of the oxygen partial pressure P_O obtained with the refined vessel network with a 1024 × 1024 mesh are shown in Fig 4. The oxygen partial pressure field is obtained with a normal tissue consumption (M₀ = 1.7 × 10⁻⁴cm³O₂/cm³/s) (see Fig 4(a)), whereas the partial pressure field is obtained with a reduced tissue consumption (M₀ = 2.89 × 10⁻⁵cm³O₂/cm³/s) (see Fig 4(c)). In both cases, we can see that the oxygen partial pressure directly reflects the refined vessel structure. In Fig 4(b) and 4(d), we statistically analyze the oxygen fields inside the circles shown in Fig 4(a) and 4(c), respectively. The distance between the circle and the outer vessels is greater than 200 μm. Hence the boundary effects is insignificant. For the normal consumption case as shown in Fig 4(a) and 4(b), tissue in the outer domain has a very low oxygen supply. This is due to the large stretch in the outer domain when we generate the refined vessel network, which significantly affects the oxygen supply in two folds: First, it increases the irrigated area of the corresponding blood vessels in the outer domain; Second, it increases the resistance of these vessels, thus decreases the blood flow in these vessels. For the reduced consumption case as shown in Fig 4(c) and 4(d), all tissue inside the circle is well irrigated. This statistical results of oxygen field under various tissue consumption are consistent with that reported in previous works [21, 46].

Fig 4

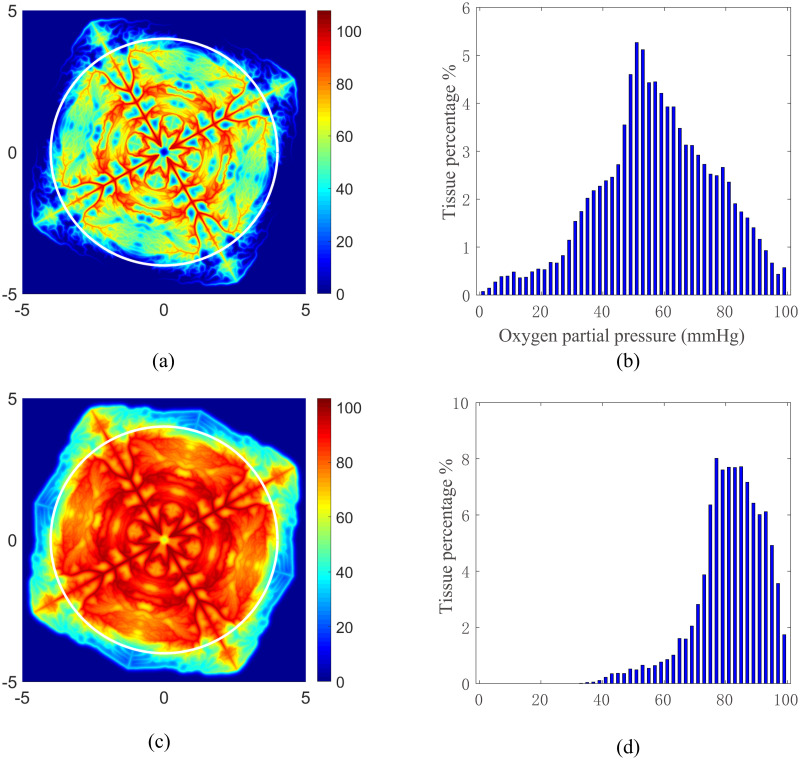
Oxygen partial pressure obtained with the refined vessel network.

The partial pressure for normal tissue consumption and reduced tissue consumption are shown in (a) and (c), respectively. The tissue inside the white circles shown in (a) and (c) are used to statistically evaluate the area percentages of tissue with particular partial pressure of oxygen. The statistical results are shown in Figure (b) and (c), respectively. The unit of the x− and y− axes in (a) and (c) is mm. The unit of oxygen partial pressure is mmHg.

5.4 Numerical solution for the 3D refined vessel network

The 3D refined structure with 7815 vessels is adapted from the intermediate and deep capillary plexi of a mouse retina and used for simulation of the oxygen field with a 512 × 512 × 512 mesh. The tissue consumption rate M₀ = 2 × 10⁻³cm³O₂/cm³/s and total blood flow Q = 10nl/s are adapted from experimental data to simulate the real situation [47, 48]. The simulated oxygen field at different layers is displayed in Fig 5. While low oxygen partial pressure can be observed in the layers away from the capillary plexus, the capillary-rich areas are well irrigated, which agrees well with the experimental data. Note that the irrigation efficiency depends on the total blood flow rate Q and the vessel density.

Fig 5

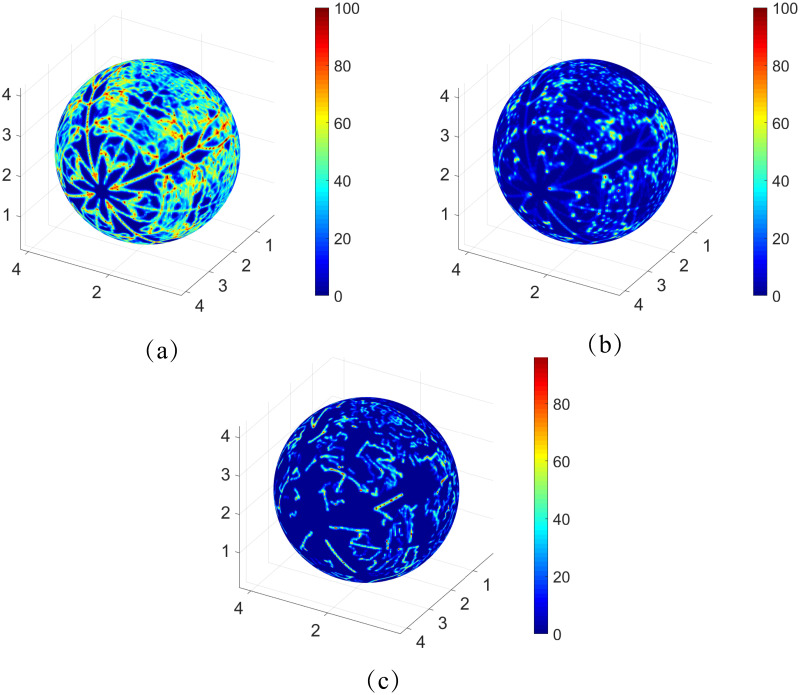
The oxygen partial pressure at different layers of the retina.

The oxygen profiles on the layers corresponding to 0, 25, and 50 percent of the retina depth are shown in the Figure (a), (b), and (c), respectively. The unit of the axes is mm and the unit of oxygen partial pressure is mmHg.

5.5 Model validation

The comparison between our results and previous experimental and simulation results are shown in Fig 6. The horizontal axis represents the normalized retinal depth and the vertical axis represents the oxygen partial pressure. Despite the large differences in the independent experimental profiles, the profiles indeed share similar features, e.g., relatively high oxygen partial pressure is observed near the choroid surface and the deep capillary plexi, which is attributed to the high local vessel density. Meanwhile, a ‘peak’ can be observed in the middle, which corresponds to the intermediate capillary plexi layer. Despite the differences induced by particular parameter settings and experimental conditions, the simulation results are relatively consistent with the experimental data.

Fig 6

Comparison between retina oxygen partial pressure profiles simulated by our model for the mouse retina and those experimentally measured in mice by [47], in macaques by [41], in rats by [48] and in a human retina model [31].

DCP: deep capillary plexi, ICP: intermediate capillary plexi.

The comparison between our simulation results and that obtained with the numerical method developed in Ref. [26] are shown in Fig 7. Both simulations are performed on the same single-vessel domain as shown in Fig 1(C). The edge length of the cube is 640 μm and the vessel radius is 10 μm. The oxygen profile in Fig 7(a) was obtained from a line through the cube center perpendicular to the vessel. All curves exhibit a similar diffusion distance that agrees well with the data under physiological conditions. Our results show good consistency with that obtained with the method developed in Ref. [26]. The blood oxygen partial pressure P_b obtained with different mesh size is shown in Fig 7(b). A more detailed illustration of the error in oxygen field is shown in Fig 12. According to these results, a mesh size of 10μm is sufficient to achieve a relatively low numerical error (1%).

Fig 7

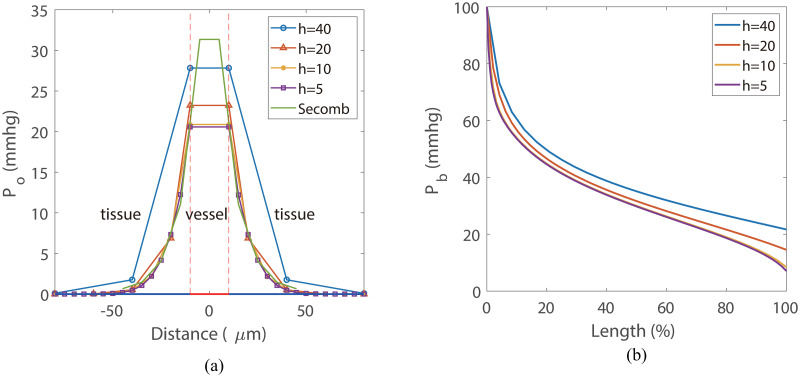
Model validation and convergence analysis.

(a) The profiles of oxygen partial pressure on a line perpendicular to the vessel, where x = 0 represents cube center. The oxygen partial pressure inside the vessel (−10, 10) are set to be equal to the blood oxygen partial pressure P_b. The line “Secomb” is obtained from the method developed in Ref. [26] with a mesh size of 10μm. All simulations are performed with tissue consumption M₀ = 2.0 × 10⁻³cm³O₂/cm³/s and total blood inflow Q₀ = 0.05nl/s. (b) The blood oxygen partial pressure P_b along the blood vessel.

5.6 Convergence analysis and efficiency analysis

We use the cobweb vessel network in 2D and the simple single-vessel network in 3D to numerically study the convergence of our new method. The results for mesh refinement test are shown in Fig 8(a). The relative error E_n is computed by the normalized L²-norm of the difference between the solutions obtained with an N^k mesh and a 2N^k mesh, where k is the dimension of the model. The numerical convergence order is about 1.7 for both the 2-D and 3-D cases. For the 3-D case, the relative error reaches at about 1% with a mesh size of 10μm, which is consistent with the result shown in and Fig 7.

Fig 8

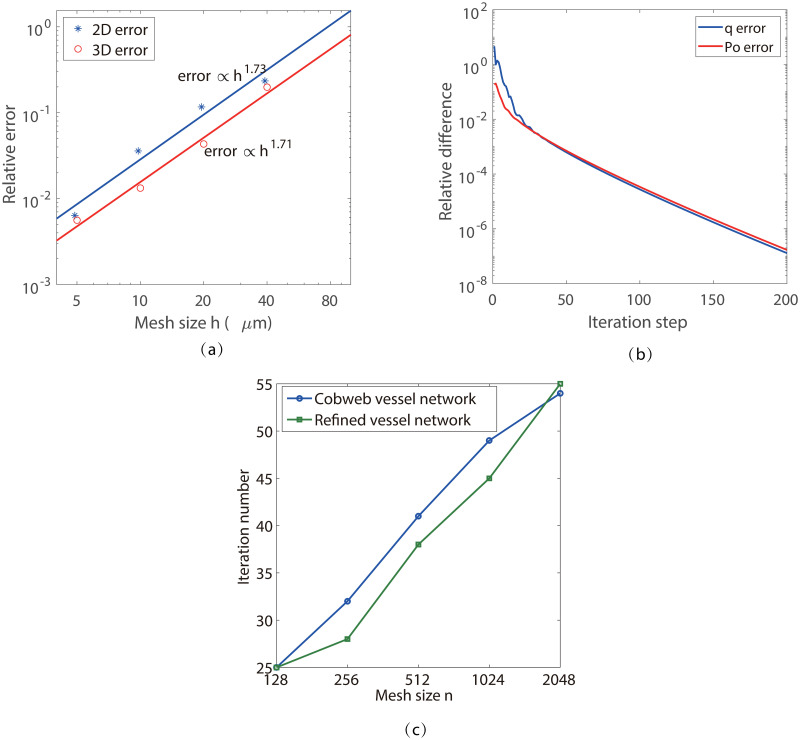
Numerical convergence analysis.

(a)Mesh refinement test. The stars show the numerical error. The fitted lines show a convergence order of 1.73 for the 2D case and 1.71 for the 3D case with respect to mesh size. The relative error is computed by the normalized L²-norm of P_O. (b) The decay of the relative difference between two iteration steps. The relative difference is computed by the normalized L²-norm of q. (c) Iteration numbers for different mesh size.

The iteration convergence is shown in Fig 8(b), where the relative difference is shown by the normalized L²-norm of the difference of the corresponding functions, q and P_O, between two iteration steps. We can see that the relative differences have a fast decay at the beginning, followed by a relatively slower linear convergence. In Fig 8(c), we show the iteration numbers required to make the relative difference smaller than 1 × 10⁻³. We can see that the iteration numbers are comparable for the simple and refined vessel network structures, while both of them increase slightly with the mesh size N. The increase in iteration numbers is mainly due to the choice of the temporal step size Δt in Eq (14). As we have discussed above, a large Δt is helpful for convergence while a too large Δt can induce instability in the iteration. According to our numerical test, the optimal Δt decreases with N. For example, Δt ≈ 5000 is used for N = 1024 in our simulation, while Δt ≈ 3500 is used for N = 2048. The behavior in the 3-D case is similar.

The average number of Newton iterations required for each full iteration step is about 5 ∼ 6. Therefore, the time cost is about 40 seconds to find the solution with a relative error smaller than 1% on a 1024 × 1024 mesh with a standard 3.7 GHz personal computer, whereas about 170 seconds on a 2048 × 2048 mesh. The iteration process for the 3-D simulation shares the similar convergence rate to that for the 2-D case. In our simulation, the complete 3-D simulation requires about 726 seconds on a 256 × 256 × 256 mesh and about 8200 seconds on a 512 × 512 × 512 mesh. This time increase from 2-D to 3-D comes mainly from the increase in solving the PDE.

The average time cost for each Newton iteration is analyzed in Fig 9. At the beginning of each iteration, three to six Newton iterations are required for each full iteration step. In each Newton iteration step, two to three V-cycles of multigrid iterations are required to solve the oxygen partial pressure field. After a few full iteration steps, only two to three Newton iteration steps, each with only one V-cycle, are sufficient to make the error small enough for each iteration step. In Fig 9(a) and 9(b), we show the average time cost for solving the oxygen field in tissue (PDE-time), solving the blood oxygen partial pressure (ODE-time), and post-processing (P-time) in each Newton iteration step, tested on a standard 3.7 GHz personal computer.

Fig 9

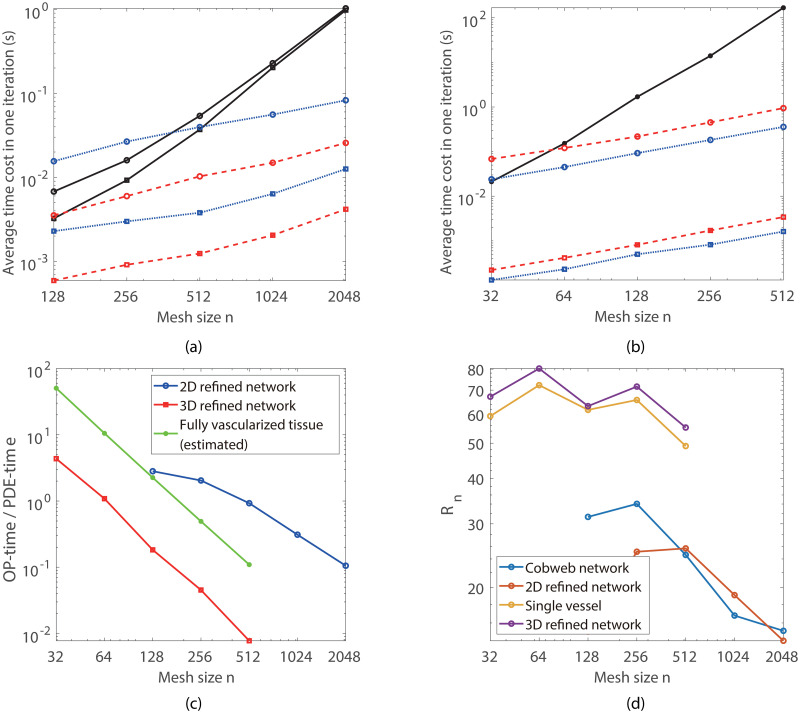
Numerical efficiency analysis.

(a) and (b) Average time cost for each iteration step in the 2-D and 3-D cases, respectively. The black solid lines, the blue dotted lines, and the red dashed lines show the average time cost for solving the PDE, the ODEs, and the post-processing in each Newton iteration step, respectively. For the 2-D case, the circled and squared lines show the time cost for the refined vessel network and the simple cobweb network, respectively; whereas for the 3-D case, the circled and squared lines show the time cost for the refined retina network and the single vessel system, respectively. (c) The time ratio between the OP-time and PDE-time for the 2-D and 3-D cases. (d) The normalized time ratio for different systems.

In our simulations, the step size along the blood vessels is set to be $$ h_k=\frac{h}{3}=\frac{L}{3n}$$, where L is the domain size and n is the mesh size on one direction. For a given vessel network structure, the total number of discrete nodes on the blood vessels is proportional to n. Hence the sum of the ODE-time and P-time (OP-time) is also proportional to n. Note that for the standard multigrid method, the computation complexity and the PDE-time are O(n²logn) for 2-D cases and O(n³logn) for 3-D cases, which increase much faster than the OP-time (see Fig 9(a) and 9(b)). As shown in Fig 9(c), for large mesh size n, the OP-time is only a small fraction of the PDE-time for the refined retina vessel networks.

In many real applications, simulations are required to perform in fully-vascularized 3-D tissue domains. Thus it is of interest to estimate the OP-time required in such cases. Obviously, the OP-time increases linearly with the total length of blood vessels. In principle, the OP-time is proportional to the total number of discrete grids on the blood vessels $$ N_v=\frac{L_v}{h_k}$$, where L_v is the total length of blood vessels. In order for a fair comparison for different simulations, we define the normalized time ration by

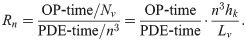
As shown in Fig 9(d), R_n is relatively invariant with the mesh size n and the total vessel length L_v. This suggests that the OP-time is really proportional to the total vessel length for given mesh size n.

For a fully vascularized tissue with fixed vessel density, the total vessel length is proportional to the volume V of the tissue domain. As a result, for given mesh step size h, the ratio between the OP-time and the PDE-time is almost invariant with the domain size. Using the vessel density suggested in Ref. [33], the total vessel length in a cube with the edge length of 5.12 mm is about 13422 mm, which is 13.3 times of that of the 3-D retina network (about 1012 mm) in this work. Therefore, for h ≤ 20μm, the ratio between the OP-time and PDE-time is about smaller than 1 for fully vascularized tissue (see Fig 9(c)). In particular, for a fully vascularized (5.12mm)³ cube, the OP-time is about 789 seconds for h = 10μm, and the total time cost is about 8000 seconds; For a fully vascularized (10.24mm)³ cube, which contains about 10⁶ vessel segments, the estimated total time is about 70390 seconds for h = 10μm.

A Oxygen flux through blood vessel walls

For the two-dimensional case, oxygen flux is evaluated on both side of the vessel walls separately. The oxygen partial pressure P_O is assumed to be equal to P_b on vessel walls. In order to evaluate the oxygen flux at a discrete node x = (x, y) on the vessel center line, we first numerically calculate the unit normal direction n by central difference. Then, we define two corresponding points x^± = x±r n on the vessel wall (see Fig 10), where r is the vessel radius. Next, the oxygen partial pressures P_O on four nearest mesh points to x⁺ outside the vessel are used to fit a linear function P_O(x, y)≈P_b + G ⋅ (x − x⁺) in the sense of least squares, where G is the gradient to be fitted. Finally, the oxygen flux is given by q = Dα G ⋅ n.

Fig 10

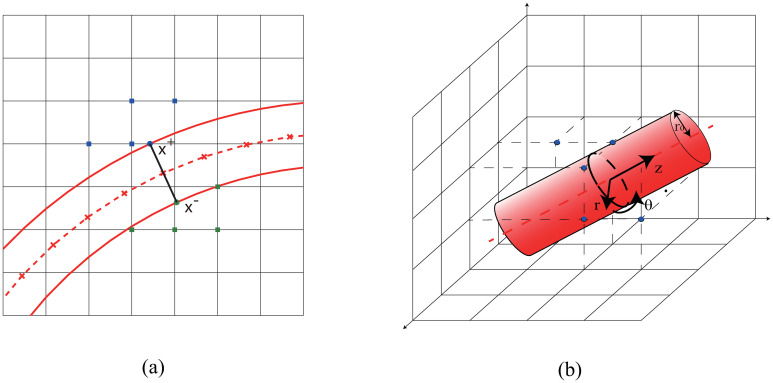
(a) Evaluation of oxygen flux in 2D. The red solid lines represent the vessel wall. The red dashed line shows the center line of the blood vessel, the crosses on which show the discrete nodes. The blue (green) solid circle shows x⁺ (x⁻), whereas the blue (green) solid squares show the nearest mesh points used to fit the linear function and evaluate the flux. (b) Evaluation of oxygen flux in 3D. The red dashed line shows the center line of the blood vessel. The black circle shows the cross-section of blood vessel, whereas the blue (green) solid squares show the nearest mesh points used to fit the solution and evaluate the flux.

For the three-dimensional case, the oxygen field near the blood vessel can be described by the Laplace equation under cylindrical coordinate system.

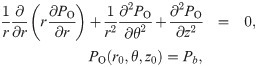
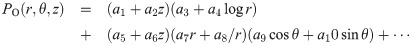
By keeping the first term and applying the boundary condition, the solution can be written as

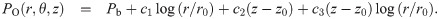
In our numerical tests, a few nearest mesh points are used fit the function in the sense of least squares. The distance between the fitting point and the point on center line is less than r₀ + h. Finally, the oxygen flux is obtained by q = 2πDαc₁.

B Peskin’s numerical δ-function

Peskin’s numerical δ-function is defined as

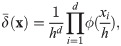
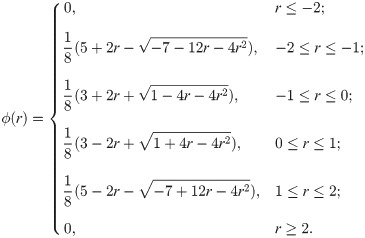
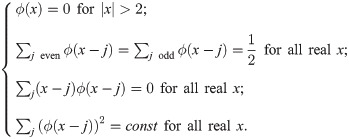
C Localization of δP_k

An example of δP_k defined in Eq (18) on the local mesh is illustrated in Fig 11, where the mesh size is h = 0.002, x_k = (0.5 + h/2, 0.5 + h/2) is set at the center of the local mesh. It can be clearly seen that δP_k decays very rapidly. When |x − x_k|>2h, the error is already negligible.

Fig 11

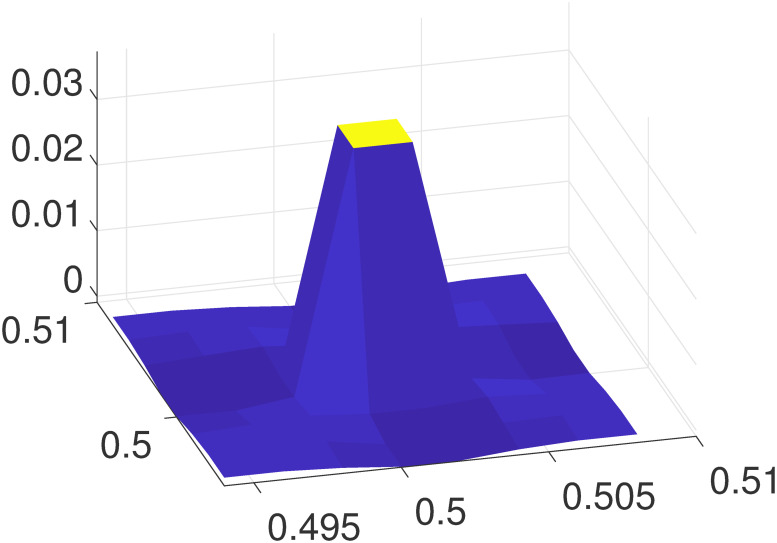
The relative error δP_k on a local mesh.

D Detail error analysis for single vessel

A detailed error analysis for this classical Krogh model is shown in Fig 12. In order to estimate the numerical error induced by the spatial discretization, we performed simulations with mesh sizes of 5,10,20 and 40 μm, respectively. The result of 5-μm mesh was used as a reference to determine the errors of those obtained with other mesh sizes. It can be observed that the errors are mainly distributed in the vessel and surrounding tissue. A space step of 40 μm will bring about 10% numerical error in the blood vessel, where the case of 10 μm only has an error less than 1%.

Fig 12

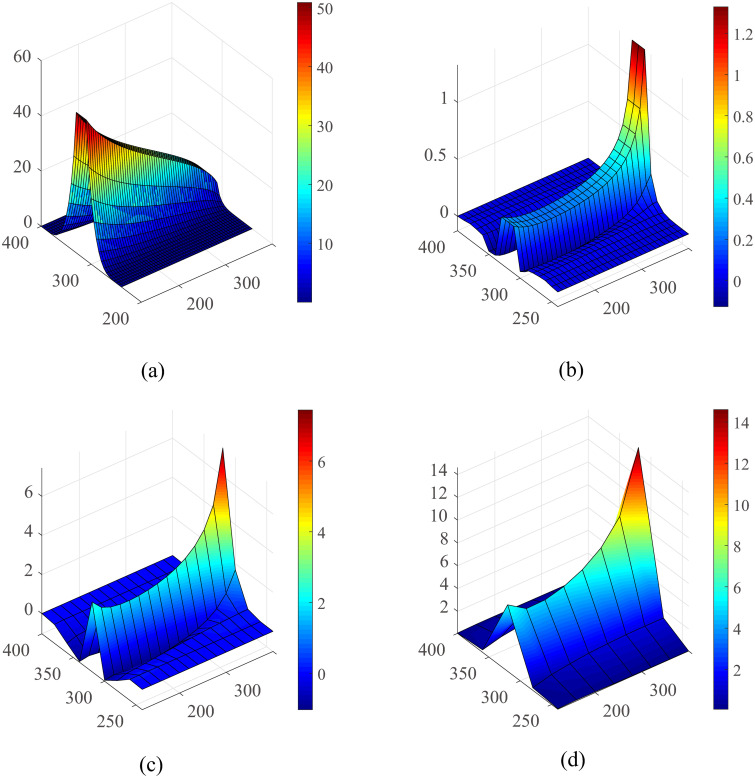
Detailed oxygen field error analysis for the single vessel model.

(a) The oxygen profile on the plane of the vessel under the fine grid (h = 5μm). The numerical error for the h = 10, h = 20 and h = 40 are shown in (b-d), respectively, while the result of 5-μm mesh were used as a standard. The unit of the axes is μm and the unit of oxygen partial pressure is mmHg.

E Inflow and outflow conditions

The inflow and outflow conditions of the four vascular systems used in in this work are listed in Table 2. When there are multiple inlets and outlets, they share the same blood flow rate.

Table 2

vascular system	Number of inlets	inlet flow	Number of outlets	outlet flow
2D cobweb network	6	0.6 nl/s	6	0.6 nl/s
2D refined network	4	1 nl/s	4	1 nl/s
3D single vessel	1	0.05 nl/s	1	0.05 nl/s
3D refined network	4	2.5 nl/s	4	2.5 nl/s