Competition and structural model

We modeled intra- and inter-species interactions using a canonical spatial Lotka-Volterra (LV) framework, with simplifying assumptions motivated by attributes of microbial ecosystems. For all species, times, and locations we assume that the carrying capacity per unit area of the environment is the same, that the basal growth rate r is the same, and that organismal migration can be described by random walks with the same diffusion coefficient D. Using those assumptions, the system of partial differential equations (PDEs) that describe an N-species spatial LV model can be non-dimensionalized and, without loss of generality, written as

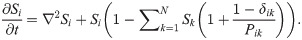
Each focal species S_i has a local concentration from zero to one in units of the carrying capacity, time is measured in units of inverse growth rate r^-1 and the natural length scale $$ \lambda =\sqrt{D/r}$$ is proportional to the root mean squared distance an organism will move over a single doubling time. Thus, the results do not depend on choice of r, D, or carrying capacity, rather those parameters set the scales of the simulation. Self-interactions and simple competition for space are accounted for by the constrained carrying capacity and the corresponding sum over S_k, and thus the diagonal elements of the interaction matrix, P_ii, are removed by the Kronecker delta, δ_ik. Pairwise interactions between species are described by the off-diagonal matrix elements P_ik which are the local concentrations of species S_k above which S_k actively reduces the local concentration of S_i. For a given pair of species that form a competitive interface, if P_ik > 1 then the local concentration of S_k needed to reduce the local concentration of S_i is greater than the carrying capacity, and hence S_k at most reduces the effective local growth rate of S_i, not its local abundance. As P_ik increases, the strength of interaction decreases. If 0 < P_ik < 1 then there is some concentration of S_k below the carrying capacity (P_ik < S_k < 1)that reduces the abundance of S_i, which we refer to here as ‘active’ competition. For any two species i and k that are adjacent in space with 0 < P_ik < 1 and 0 < P_ki < 1, a (potentially) mobile competitive interface will form between those species, regardless of steric structure. In this work, we focus on situations with 0 < P_ik < 1 for all i and k, as that is the parameter sub-space (in this model) that tends to result in competitive exclusion and reduced species coexistence in the long-time limit–we refer to this subset of models as ‘all-to-all’ (ATA) competition. This subset of models admits stationary, long-time solutions that correspond to competitive exclusion, where the number of final species is less than that number of initial species. It also admits competitive hierarchies and alliances–like the three-species rock-paper-scissors game and its variants (which we do not explicitly explore here) whose solutions can, for instance, adopt limit-cycle or chaotic dynamics [64] that maintain coexistence for long periods of time without steric structure.

Neglecting intrinsic permutation symmetries, the N(N − 1) pairwise interaction parameters for each in silico ecosystem can be thought of as a directed graph whose edges connect each pair of species. As N increases, the dimensionality of the parameter space grows quadratically, precluding exhaustive computational characterization of this model. Thus, we restricted our simulations and analysis to a single decade in species number 2 ≤ N ≤ 12, primarily focusing on N = 8 (just above the mean of that range). Previous work [64] more extensively examined the same model for N = 2. For each in silico ecosystem (i.e. over all replicates) we sampled a uniform random distribution of values for the off-diagonal elements P_ik whose mean was ⟨P⟩ = 0.25 and whose width was specified by the parameter ΔP, subject to ΔP/2 < ⟨P⟩ so that all interaction parameters remained competitive. In total, we sparsely sampled a small fraction of the 0 < P_ik < 1 parameter space (that fraction being proportional to ΔP^N(N−1)). The value ⟨P⟩ = 0.25 indicates that on average when the local concentration of a given species reaches one-quarter of the carrying capacity, active reduction of neighboring competitors will occur. Distribution width ΔP sets the maximum magnitude of competitive asymmetry between any two species. We explored ΔP over a limited range corresponding to 0.175 ≤ P_ik ≤ 0.325, or, in terms of concentration, where active competition could (depending on sampling) set-in between ~1/6 and ~1/3 of the carry capacity. These parameters were chosen because the attendant simulations displayed the full range of possible number of coexisting species in the long-time limit, for N = 8). For each value of ΔP and structural parameters, we performed 30 to 50 simulations with a unique random sampling of the interaction parameters P_ik. All simulations had initial conditions in which every grid position had a low (0.2%) probability of being populated by any one of the available species, such that each species could grow and claim territory before locally competing.

Our in silico environments were square 2D planes with steric pillars distributed in the simulation space. Both the pillars and the bounding box were modeled with reflecting boundary conditions, thus, like a grain in soil or tissue in a gut, these pillars do not allow free transport through them, nor microbes to occupy them. In a structured environment, the shape and movement of interspecies boundaries are primarily impacted by steric spacing [64], and thus for simplicity the radii of the pillars were held fixed at R = 3 in dimensionless units for all simulations. We varied the mean distance between steric objects relative to pillar radius (Δx/R), which we refer to as the ‘structural scale’, and we varied the degree of disorder in the arrangement of those steric objects. Disorder was introduced by translating each pillar in a random direction by an amount drawn from a uniform random distribution whose width is reported relative to the structural scale. Thus, disorder is characterized by a continuous dimensionless variable δ, which when equal to zero means the pillars are arranged in an ordered triangular lattice, and as δ increases the pillars approach a random arrangement in the simulation space (including the possibility of overlap) (see S1 Fig).

This model is appropriate for describing locally competitive interactions in which the movement of organisms is described by a random walk and where the mechanisms underlying competition occur between nearby cells/species. Examples of such ecosystems include situations where microbial species compete for the same constant and isotropically distributed pool of resources, and actively reduce competitor abundances through (e.g.) Type VI secretion system mediated killing [65,66], secretion of toxins [67,68] or antibiotic antagonism [69,70]. Analysis of bacterial genomes indicates that (at least) a quarter of all sequenced species contain loci encoding for mechanisms of active competition toward other species [71] (though not necessarily for the purposes of consuming them as prey). Additional PDEs would be required to describe: (i) highly motile cells whose movements are (e.g.) super-diffusive, (ii) chemotaxis in exogenous chemical gradients, (iii) flow/advection, or (iv) the production, potency, transport and decay of secreted toxins that diffuse faster than organismal diffusion. This system of PDEs (which is not new [72,73]) represents a baseline set of assumptions and corresponding phenomena from which to build more complex models [74] of structured and locally competitive population dynamics. In particular, it is part of a larger class of boundary-forming models that localize competitive interactions to zones between competitors, and thus it is a reasonable starting point for understanding the effects of steric structure in such contexts.

Finally, inherent in this modeling framework it is worth noting additional limitations and simplifications. These systems of PDEs are deterministic, that is, with the same interaction parameters, structural parameters, simulation size and initial conditions they produce the exact same dynamics. Stochasticity enters our simulations through the random initial conditions, disorder, and random samplings of the interaction parameters. A number of excellent studies have examined low-N systems using fully stochastic dynamics [75–79], revealing quantitative differences between deterministic and stochastic models, as well as qualitative differences over long time scales where stochastic fluctuations can drive a system into new parts of phase space, for example, into extinction cascades [80,81] or mobility-dependent coexistence [75,77,82]. Similarly, recent work [83] examined how non-diffusive mobility (i.e. power-law jump distributions that produce random long-range dispersal) spatially structures genotypes in an environment, finding that certain parameter regimes produce domain structures similar to those seen in this work, while other regimes produce more complex dynamics. Such non-local dispersal mechanisms would, almost certainly, alter the qualitative conclusions presented here because non-local jumps ‘bypass’ the limitations in organismal mobility imposed by structured interfaces and local diffusion.

Environmental structure stabilizes local all-to-all competition

As a computational proof of principle–that steric structure can impact coexistence of locally competing species–we compared the spatial population dynamics of an 8-species system with and without the inclusion of steric structure. In both cases, each pair of species that shared an interface engaged in active (population reducing) competition, each characterized by a pair of off-diagonal matrix elements (56 parameters in total). In Fig 1 we show the simplest version of this comparison, where the strength of the competitive interaction is equal between all pairs of species (i.e. all off-diagonal elements have the same value, ΔP = 0).

Fig 1

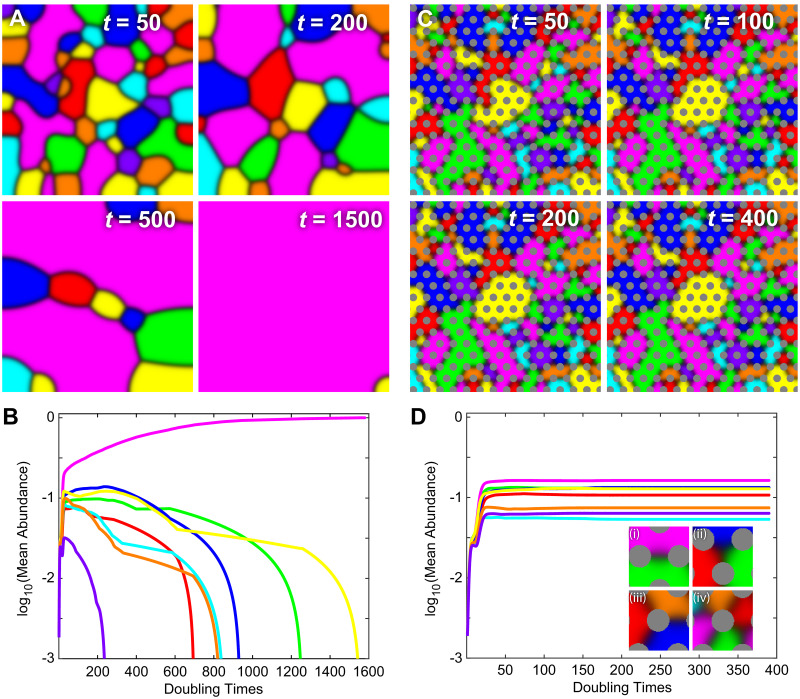
Steric structures stabilize an in silico multi-species ecosystem.

Shown here are two 8-species in silico ecosystems in which all species are actively competing with all other species and the competition parameters are equal for all pairwise interactions. (A & B) Simulation of competition in an isotropic environment. If initial species representation is statistically equal, each species has equal probability of dominating the environment in the long-time limit. However, in any single simulation the dynamics of interspecies boundaries lead to a single dominant competitor in the long-time limit. (C & D) When species compete in an environment with ordered steric structures (R = 3, Δx/R = 3.5, and δ = 0), interspecies boundaries that are mobile under isotropic conditions quickly ‘pin’ between steric objects and arrest the genetic-phase coarsening that leads to a single dominant competitor, thereby robustly producing stable representation of all species. Steric structures also permit situations where 3 or more species form a ‘junction’ around a steric object (Diii and Div). In both simulations L = 150, ⟨P⟩ = 0.25, and ΔP = 0.

Even in this state of balanced competition, if a system lacks steric structure, and is otherwise isotropic, a single dominant competitor will emerge to the exclusion of all other species given enough time [84] (Fig 1A and 1B). Other salient dynamics emerge from these PDEs and assumptions as well. Spatial domains of each species are determined by an interplay between the curvature of the interface between any two species and the relative values of the competition parameters for the species that meet at that interface [64]. Neglecting, for the moment, spatial junctions between three or more species, all competition interfaces in this model are, by geometric necessity, two species interfaces–thus analysis of two-species interfaces generally informs analysis for systems with N > 2. These model-specific observations are similar to dynamics seen in Potts models [85–87] (a generalized version of the Ising model) that can display multiple, mutually coarsening phases. If competition at a particular two-species interface is balanced (i.e. P_ik = P_ki) then interfacial curvature (linear curvature in 2D space) is the only determinant of interface movement; straight interfaces do not translate and curved interfaces translate in directions that minimize the interface length (akin to a ‘surface tension’ between competing species, whose dimensionality depends on the spatial dimensions of the system). Notably, these interfacial dynamics lead to competitive exclusion; domains of any competitor that are enclosed by equal or stronger competitors will, in open space, decrease in size until local extinction (thereby reducing interface length). System dynamics become more complex in the case that interactions at a two-species interface are unbalanced (i.e. P_ik ≠ P_ki). Straight interfaces translate in the direction of the weaker competitor, and below a critical interfacial curvature

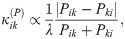
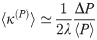
In contrast to robust competitive exclusion in isotropic space, the inclusion of physical structure leads to long-term, stable representation of multiple (and often all) species across a range of structural scales and interaction parameters. In Fig 1C and 1D we show the evolution of balanced competitive interactions between 8 species with the same initial conditions and interaction parameters as Fig 1A and 1B, but in the presence of a triangular lattice of steric pillars. In this system, the abundances of all 8 species rapidly equilibrated leading to stable coexistence. In this stable state, each species established spatial domains with boundaries primarily composed of two-species interfaces whose movement has the same relationship to interaction parameters and interfacial curvature as described above (Fig 1Di). However, inclusion of steric structure adds additional boundary conditions that locally slow or potentially halt interface dynamics, thus fostering coexistence. The steric pillars also stabilized a number of distinct ‘junctions’ between species, including three-way junctions in open space (Fig 1Dii), three-way junctions centered on a pillar (Fig 1Diii), and four-way junctions centered on a pillar (Fig 1Div). Isotropic systems without steric structure can transiently support two-species interfaces and free three-way junctions (Fig 1A), but stable three- and four-way junctions must be associated with steric objects in the local environment. Junctions centered on pillars can support more than four species if pillars are large in comparison to the thickness (w) of the competition interface (i.e. if 2πR/N > w). Though, such junctions did not occur in our simulations with random initial conditions–we only observed these higher-species junctions under contrived conditions (see S2 Fig).

Stable coexistence is robust to fluctuations in steric structure and competition asymmetries

Next we held the degree of structural disorder fixed at zero (δ = 0) and explored how changes in the structural scale (Δx/R) affected the number of stably coexisting species. Along one dimension, we held ⟨P⟩ = 0.25 and varied the interaction parameter ΔP, subject to the constraint that ΔP/2 < ⟨P⟩. Along a second parametric dimension, we varied the structural scale while holding pillar radii fixed. In Fig 2 we measured the mean number of species coexisting in the long-time limit as a function of both the width of the interaction-parameter distribution and the structural scale, with 30 replicates per parameter set for a total ~11,000 simulations. Consistent with previous work on two-species systems [64], the average number of coexisting species declined sharply both as competition asymmetry increased (i.e. as ΔP/⟨P⟩ increased) and as the structural scale increased. Conversely, systems with smaller structural scales and/or smaller competitive asymmetries robustly retained all eight species in the long-time limit (solid yellow region in Fig 2).

Fig 2

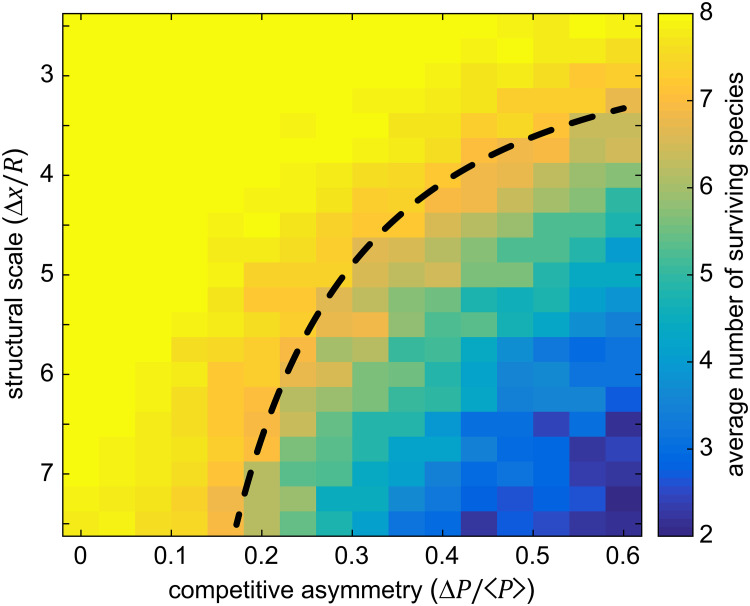
The number of species an environment can stably support depends on the degree of competition asymmetry and the structural scale.

Simulations were performed across a range of competitive asymmetries characterized by the dimensionless parameter ΔP/⟨P⟩ and across a range of structural scales characterized by the dimensionless parameter Δx/R. Each pixel corresponds to the mean of 30 simulations each with a unique random sampling of initial conditions (as described in Methods), a unique random sampling of the interaction matrix elements using ΔP and ⟨P⟩, and a fixed structural scale. Structural scale and competitive asymmetry were both potent modulators of species coexistence, with smaller structural scale and lower competitive asymmetries leading to stable representation of all species (yellow region). The black dashed line is a zero fit-parameter model relating the competitive asymmetry to the maximum curvature possible for a given structural scale, showing that relatively simple geometric considerations capture the onset of species loss. In all simulations L = 150, ⟨P⟩ = 0.25, R = 3, and δ = 0.

Assuming that competition interfaces meet reflecting boundaries at right angles and form circular arcs, a straightforward geometric calculation [64] shows that the maximum interface curvature between two pillars with radius R and center-to-center separation Δx is given by

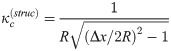
Thus, setting the two critical curvatures equal to each other ($$ \langle {\kappa }_c^{\left(\mathrm{P}\right)}\rangle ={\kappa }_c^{\left(\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{c}\right)}$$), we find a relationship that approximates the boundary between the regime of possible stable coexistence of all species and a regime with necessarily reduced species coexistence

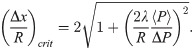
This regime boundary is shown overlaid on Fig 2, and applies to the specific statistical and structural context used here, though likely similar relationships exist for other distributions of interaction parameters and steric shapes. The equation indicates that for specified length scales, a given ensemble of interaction parameters defined by ΔP/⟨P⟩, and regardless of the carrying capacity, there is a critical structural scale (in a pillared environment) below which all species can coexist. Said differently, the equation indicates that smaller structural scales can support a wider range of interaction parameters among coexisting species, or conversely that larger structural scales select for stronger competitors. The accuracy of this approximation improves as the pillar radius becomes large compared to the width of the competitive interface.

While these results are supportive of the stabilizing effect of steric structure on long-term species coexistence, rarely do natural environments contain highly ordered (δ = 0) steric structures, thus we explored how disorder affects species abundance at a fixed structural scale. First, we simulated the simpler case where all eight species had balanced competitive interactions (like Fig 1) and examined the population dynamics in the presence of disordered steric structures (δ = 1). Like the ordered case, disordered systems with balanced competitive interactions displayed stable representation of all eight species (Fig 3A). We then compared the probability distribution for the number of coexisting species in the long-time limit across four conditions (1,000 simulations for each): with and without competitive asymmetry, and with and without structural disorder, as shown in Fig 3B. When ΔP/⟨P⟩ = 0 the number of species remained at the maximum value across all 1,000 simulations whether or not the steric structures were disordered. When competitive asymmetry was introduced the probability distribution for the number of stably coexisting species expanded across all possible values (1 to 8) and peaked between 6 and 7 species, regardless of whether the system was ordered or disordered. Those distributions were quantitatively similar, indicating that disorder was not a strong determinant of stable species coexistence.

Fig 3

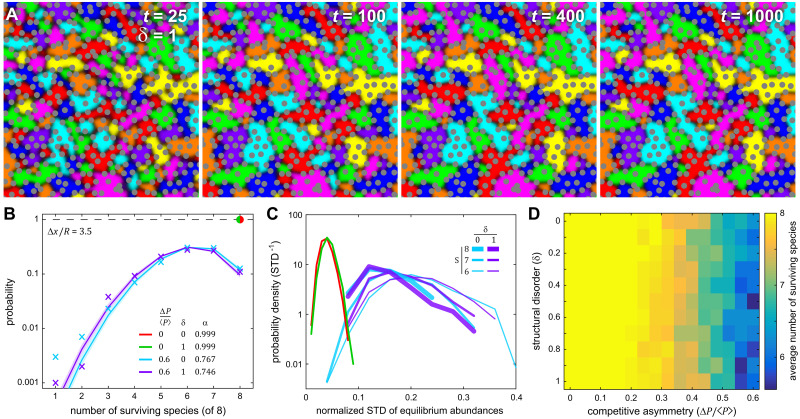
Species coexistence is robust in the presence of structural disorder.

(A) Similar to Fig 1C, these panes show the time evolution of an 8-species system where steric pillars were randomly perturbed from a triangular lattice (δ = 1). From random initial conditions the system rapidly equilibrated to a stable configuration that supported all 8 species. (B) Simulations were performed to measure the probability distribution for the number of long-term coexisting species under four conditions (1,000 each): high and low competitive asymmetry and high and low structural disorder. The structural scale was held fixed. Without competitive asymmetry all species survived in all simulations, with or without disorder (red/green dot). With high competitive asymmetry, the probability distributions spread across all possible numbers of species with relatively little distinction between ordered and disordered systems (colored X’s). Those distributions were well-described by a modified binomial distribution (solid lines) with an ensemble-average single-species survival probability of α ~ 0.75. The distributions exhibit larger variation where there are less data (i.e. lower probabilities, from one to three surviving species). (C) For each simulation, the normalized standard deviation (NSD) in equilibrium abundances was measured, and those values are shown here as a histogram for each of the four conditions. In the absence of competitive asymmetry (green, red), the mean NSD was low (~0.05 on maximum scale of 1). When competitive asymmetry was high, we examined the NSD for all simulations that had 6, 7, or 8 surviving species (cyan, purple). All of those distributions were significantly wider and had significantly higher mean NSD’s, meaning that competitive asymmetry increases the variation in species abundance at equilibrium, regardless of how many species stably coexist. (D) We compared the average number of surviving species across a range of competitive asymmetry and disorder (0 ≤ δ ≤ 1). Those distributions showed little variation with disorder and, as a function of competitive asymmetry, had a mean pairwise correlation of 0.97 (see S4 Fig). Thus our data suggest that structural scale has a stronger effect than disorder (at least in this portion of parameter space). In all simulations L = 150, ⟨P⟩ = 0.25, and R = 3.

Across each of those same four conditions, we examined the probability distributions that describe the number of coexisting species in the long-time limit and applied the simplest rule that emerges from the statistical ensemble of initial conditions, competitive asymmetries, and disorder. For a given set of conditions we assumed that there is some probability α that a species randomly selected from the full ensemble of simulations will survive in the long-term. This corresponds to a binomial distribution whose normalization is modified to account for the fact that there is no chance that all N species will die

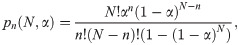
We used those same 4,000 simulations to assess the variability in species abundances resulting from the four conditions. At equilibrium, each coexisting species occupied a fraction (between 0 and 1) of the available simulation area. For each replicate we measured the standard deviation of that fraction across all coexisting species. We then repeated that for all replicates under each of the four conditions, to generate a distribution of normalized standard deviations (NSD) in species abundance for each condition. NSD values closer to zero indicate that all coexisting species within a replicate have roughly the same abundance, whereas values approaching one indicate that abundance variations between species are comparable to the size of the system itself. In the case of balanced competitive interactions, the probability distributions for abundance variations were nearly identical for the ordered and disordered systems, and the mean NSD was low (~0.05, see Fig 3C), meaning that if competitive interactions are balanced all species are have roughly the same abundance. However, introducing moderate competitive asymmetry meant that some species intrude into the territory of other species, leading both to lower species diversity and to larger variations in the abundance of surviving species. As such, we report the distribution of NSDs for all simulations that had equilibrium species numbers of either S = 6, 7 or 8 (Fig 3C). Again, disorder had little effect on those probability distributions. Systems that experienced extinctions of zero (S = 8), one (S = 7) or two (S = 6) species had higher mean NSDs (by a factor of 3 to 5) and wider distributions of NSDs as compared to balanced competition, with lower equilibrium values of S corresponding to larger mean variations in abundance. Additionally, we performed a wider sampling of the degree of disorder and the competitive asymmetry, and found that the average number of stably coexisting species showed little dependence on the degree of structural disorder (Fig 3D). When we correlated the mean number of stably coexisting species as a function of the competitive asymmetry across all values of δ, the average correlation coefficient was 0.97 (see S4 Fig), meaning that the relationship between average number of coexisting species and competitive asymmetry showed little dependence on disorder in the range 0 ≤ δ ≤ 1.

As a final characterization of spatial structure, we examined the density with which interspecies boundaries connected steric objects. Ignoring pillars at the edge of the simulation space, every steric object has a set of Voronoi nearest neighbors, typically 5 to 7 in disordered systems and exactly 6 in a triangular lattice (see S5 Fig). Across our simulations, the vast majority (~ 98%) of all interspecies boundaries connected pillars that were Voronoi nearest neighbors, which is expected given geometric constraints. The number of those connections per unit area relative to the total number of possible Voronoi connections per unit area is a dimensionless measure of the amount of localized competition in a physically structured system–below we refer to this as the ‘connection density’, whose values lie between 0 and 1. When examined through that lens, disorder, at least for balanced interactions, had a significant effect on the distribution of connection densities across the ensemble of simulations, with ordered systems exhibiting higher connection densities (see S5 Fig). However, when examined under moderate levels of competitive asymmetry connection density significantly decreased (consistent with abundance variation increasing) and the difference between ordered and disordered systems again became small. These data suggest that in sterically structured systems higher levels of competitive asymmetry, somewhat counterintuitively, correlate with less competition as measured by the density of competitive interfaces in the system, because boundaries between mismatched competitors are less stable.

Structure stabilizes larger numbers of competitors with system-size dependence

All of the simulations discussed up to this point were performed within the same size grid L = 150 (with the exception of S3 Fig, L = 75). Under any set of parametric conditions that lie within the assumptions of our model, the absolute minimum domain size for a given species is set by the area of a triangle formed by three pillars that are all mutual Voronoi neighbors (so-called ‘Delaunay triangles’[88]). Thus a system that is not large enough to contain domains of at least that size for each of N unique species cannot support all N species–this establishes a minimum system size for a particular number of species that scales as N(Δx)²; all of our simulations were well above this strict limit. However, disordered systems have an additional system-size dependence. All else being equal, as the system size grows the probability distribution for the equilibrium number of species (e.g. Fig 3B) shifts toward the maximum number of species (i.e. α → 1). The mechanism behind this shift is that as the system increases in size, there are more opportunities for randomly positioned steric objects to create a zone in which a weaker competitor is enclosed by an effectively smaller structural scale. We confirmed this by measuring the system-size independent distribution of local structural scale (S6 Fig). In an ordered system, the distribution of local structural scale is a delta-function centered on the lattice constant–all nearest-neighbors pillars are the same distance from each other. As disorder increased we found that Voronoi zones (i.e. potential species domains) emerged whose maximum convex edge-length was smaller than the mean spacing between pillars. Thus, the maximum interface curvature that can exist between two species in such domains is greater than in ordered systems with the same mean spacing. In such zones a species whose interaction parameters render it too weak to compete in an ordered system, could potentially survive. The average number of these zones per unit area is system-size independent, thus increasing system size linearly increases the average number of those zones, and thus the per-capita survival probability α increases (e.g. compare Fig 3B and S3 Fig), as does the survival probability of weaker competitors.

Finally, in an ordered system we explored how the ensemble survival probability depended on the initial number of species, across the range 2 ≤ N ≤ 12, for two system sizes and multiple competitive asymmetries. First, we measured the ensemble survival probability (α) as a function of both competitive asymmetry and the initial number of species, with 50 replicates for each parameter set (Fig 4A). For low competitive asymmetry across all values of N, the ensemble survival probability was approximately 1, meaning all species coexisted. However, similar to Fig 2, as competitive asymmetry increased species loss increased (α decreased), and the decrease in α was more dramatic the larger the initial number of species. One potential mechanism behind this species-number dependent change in α is that larger values of N offer a wider sampling of the matrix elements P_ik, and thus increase the likelihood that a single competitor dominates over many other weaker competitors and/or that ‘ultra weak’ competitors emerge.

Fig 4

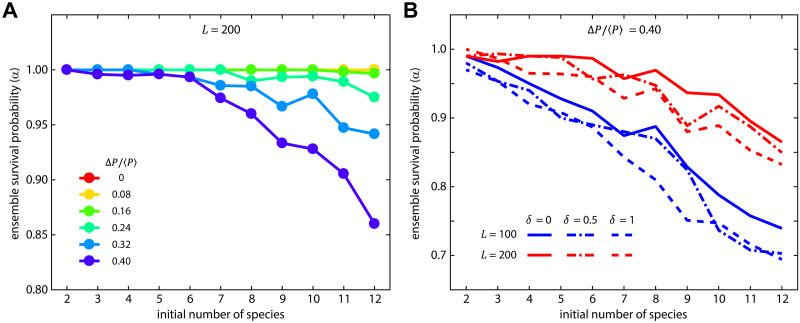
Structure stabilizes larger numbers of species, but increasing competitive asymmetry increases species loss.

(A) Holding the structural scale fixed with no disorder, we measured the survival probability as a function of the initial number of species, between 2 and 12, across multiple values of competitive asymmetry. For lower values of competitive asymmetries, the final and initial numbers of species were essentially equal (α ~ 1). Higher levels of competitive asymmetry resulted in increasing degrees of species loss as the number of initial species increased. This amplification of species loss is related, at least in part, to the same interplay between structural scale and maximum interface curvature that caused species loss in Fig 2. (B) Comparing identical conditions between two different system sizes (L = 100 and L = 200), the effects of disorder are relatively small in comparison to the effects of system size, with smaller system sizes (blue lines) showing a significant amplification of reduction in survival probability as compared to the larger system. In all simulations ⟨P⟩ = 0.25 and R = 3.

Another potential link between the initial species number and the ensemble survival probability was system-size. To test this, we ran simulations across the same range of species number at the highest value of competitive asymmetry for two different system sizes (L = 100 and L = 200). For both system sizes, survival probability dropped as the initial number of species increased (Fig 4B), but the smaller system experienced a significantly faster drop, indicating that within this limited range of conditions and all else being equal smaller structured systems statistically retain fewer species in the long-time limit. We also examined the role of disorder in this context; consistent with our previous results disorder had a relatively minor effect as determined by 95% confidence intervals of MLE for the values of α (see S7 Fig for confidence intervals). Together, these results add support to the finding that disorder at a fixed structural scale is not a strong determinant of stable coexistence under localized competition, but that system size and the number of initially competing species each modulate survival probability and hence equilibrium biodiversity in this model.