Environment

We implemented this exactly like a typical news site similar to Fig 1 below. Usually the front page consists of a section called Breaking News, which displays a pre-determined number of articles chronologically. Other important sections are: the chronological display of articles corresponding to each of the different categories, and the “most-popular” list. Commonly used news categories across different news websites are: Local News, World, Weather, Sports, Health, Business, Technology and Politics. The displayed articles in different categories are updated on arrival of a new article, whereas the most popular list of articles is updated as the reading activity progresses with arrival of readers.

Fig 1

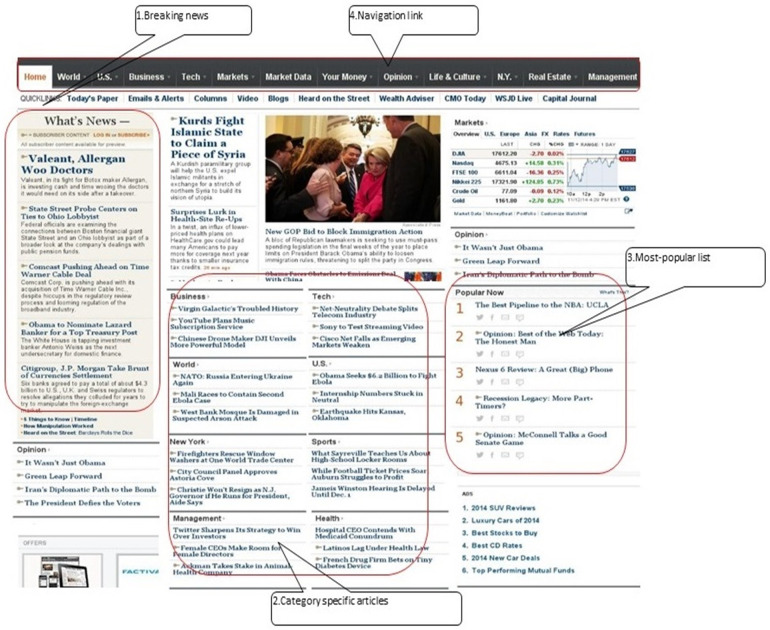
Common features available on the front page of a news website.

The links to navigate through different categories are available on the top of a page (except at the front page). When the reader clicks on one of the links corresponding to a category, then ten most recent articles corresponding to the category are displayed. When a reader clicks any of the articles, the link takes her to the page which also displays a list of 10 most-popular articles. As a common practice, the most-popular or top-N list is usually displayed prominently on each Web page of most of the news sites.

Before the simulation starts, we generate several hundred news articles with an even distribution across categories with unique ids (UID) for the articles. Each article was assigned a random initial count, drawn from a random variable that follows Zipf’s distribution [27]. The Zipf distribution is a discrete distribution defined over a finite set k ∈ (1…n) with probability mass function,

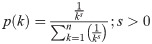
One of the weaknesses shown previously [2] in top-N systems is the disproportional drop in recognition to the (N+1)th article in a list, unknowingly penalized for “not making the cutoff”. To analyze this in a greater detail, we keep the initial reader count difference between 10^th and 11^th articles to be just one to resemble “tiny initiating events” [28] in CAS.

Agents

Individual agents may exhibit heterogenous behavior in real life. But even a simple representation of their behavior in model can help us generate the phenomena observed at the aggregate level. For example, consider the Schelling’s segregation model [29]–although not related to recommendation, it does help us illustrate the useful insights offered by a simple model. It is well known that the preference for neighborhood of an individual may depend on variety of factors such as, income, language, religion, race, age etc. Instead of considering all these factors in model, Schelling [29] posits that societal segregation may result from an individual being aware of her neighborhood and exhibiting slight preference for her group. To demonstrate this, he developed an agent based model of societal segregation. In this simplified model the behavior of an agent is governed by the proportion of agents like her in her neighborhood, and the same threshold for tolerance is used for each agent. However, in real life everyone might have different threshold and many other factors may govern an individual’s neighborhood selection. Despite its simplicity, using this model Schelling [29] was able to generate the pattern of segregation that is empirically observed in urban areas [30]. We take similar approach to develop a typical model of reader behavior in our agent based model. Our reader representation is simple, but we are able to capture the salient features of article popularity evolution.

The arrival of readers is modeled sequentially, and they start their reading activity from the front page. The number of links a reader follows before she stops reading is modeled in the standard way as a random variable L drawn from an inverse Gaussian distribution [31]. Mathematically, the distribution L is given by,

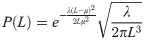
The system representing the Media Manager maintains a database of the comprehensive list of articles. Let CL_i denote the comprehensive list of articles corresponding to i^th news category. Then (CL = U_iCL_i), denotes the set of all articles. From CL, the algorithm selects N articles for display as “recommendations” at each time index ’t’. Generally, recommendations are offered in personalized or non-personalized way [33]. We focus on non-personalized top-N news recommendations. Articles are sorted and those with the highest counts are selected for the Display List (DL), which is the “top-N” recommendations.

Unlike the typical top-N recommender, in FNRS articles are selected according to probability:

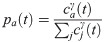
The media manager also oversees the Adaptation of the news Web site, in response to arrival of new articles. Upon arrival of a new article, CL is updated with the necessary details. Three hyperlinks for the newly arrived article are created, and they are inserted in three different lists in the system. On the front page, the hyperlinks appear at the top position of Breaking News and article-specific category sections and at the other Web pages (except front) it appears at the top position of the chronological listing accessible through category links provided on the top of that particular web page. The copies of the oldest article from each of these lists is removed and the article’s status is updated in CL_i.

Interaction

We use a "read-index" in the reader model (S1 Algorithm in S1 Appendix) to assign a higher weight of reading probability for the most recent articles in all lists that follow the chronological order of display (i.e. except the most-popular list). Although there can be various ways to assign higher reading probability to the top position in the display list [34], we implement it using the probability function $$ r_i=\frac{N+1-i}{{\sum }_{i=1}^{N}i}$$ for a particular article with rank i,i ∈ {1,2,…N} in a given list.

The interaction of a focal agent (reader) with other agents primarily takes place indirectly through the top-N (or trending) list (because this list displays the articles which are also being prominently read by other readers in the system). Other possible form of interaction among readers is also possible through parallel activities and sharing of articles through social media platform. For the ease of exposition, these complexities are excluded from the current model.

Algorithm 1. Selection of articles for recommendation using feedback function

1. pick ← 0; P ← K

2. i. $$ \Omega =\left\{\begin{array}{ccc}{c}_1,& c_2,& c_3,\cdots c_P\end{array}\right\}={\left\{c_i\right\}}_{i=1}^P$$

 ii. $$ {\mathrm{\Omega }}_{\mathrm{\gamma }}=\left\{\begin{array}{ccc}{c}_1^{\gamma },& c_2^{\gamma },& c_3^{\gamma },\cdots c_P^{\gamma }\end{array}\right\}={\left\{c_i^{\gamma }\right\}}_{i=1}^P$$

 iii. $$ {\mathrm{\Omega }}_{\mathrm{\gamma }}^{\mathrm{’}}=\left\{\begin{array}{ccc}{c}_1^{\gamma },& {c_1^{\gamma }+c}_2^{\gamma },& {c_1^{\gamma }+c}_2^{\gamma }+c_3^{\gamma },\cdots {\sum }_{k=1}^P{c}_k^{\gamma }\end{array}\right\}={\left\{{\sum }_{k=1}^i{c}_k^{\gamma }\right\}}_{i=1}^P;1\le k\le i$$

 iv. $$ {\mathrm{\Omega }}_{\mathrm{\gamma }}^0=\left\{\begin{array}{cc}0,& {\left\{{\sum }_{k=1}^i{c}_k^{\gamma }\right\}}_{i=1}^P\end{array}\right\}={\left\{{\mathrm{S}}_{\mathrm{\gamma }}^0\left(i\right)\right\}}_{i=0}^P$$

 v. Generate a random integer R, such that $$ \mathrm{R}\in \left[\begin{array}{cc}1,& {\mathrm{S}}_{\mathrm{\gamma }}^0\left(P\right)\end{array}\right]$$

 vi. Find index i, such that $$ \mathrm{R}\in \left(\left.\begin{array}{cc}{\mathrm{S}}_{\mathrm{\gamma }}^0\left(i-1\right),& {\mathrm{S}}_{\mathrm{\gamma }}^0\left(i\right)\end{array}\right]\right.$$

 vii. Select article i, for recommendation in FNRS

3. pick ← pick + 1

4. Remove article i from sorted set Ω

5. Continue from Step 2(i) until: pick <N

Illustration of update process

The key task in the design of FNRS is the selection of N articles as recommendation using the feedback probability function (i.e., the specific implementation of Eq 3 where article selection probabilities are based on the proportions). Suppose there are K recent articles in the system that have a chance to appear in the recommended list, and Ω denotes the sorted set of these articles. At a given time index j, c_i denotes the click counts that an article i has received. Using these notations Algorithm 1 presents the steps involved in selection of N articles in FNRS.

Measures

The first measure focuses on how minor differences get amplified at the boundary due to feedback and is based on examining the count evolution of the N^th article versus the (N+1)^st article in a top-N list. The second measure focuses more generally on how the top-N list is reinforced due to feedback. Finally, the third measure is Gini which captures how feedback increases clicks for all popular articles at the potential expense of increasing click-count inequality among articles. The definitions are below.

Measure 2 (top-N reinforcement)

We introduce this metric and it is measured in the following way. For any given recommender we measure the percentage of new clicks (i.e., after j = 0), received by the articles outside the initial top-10 list—determined through sorted click-counts. This measure is denoted by M2 and is defined as,

This is a measure that is interesting particularly when viewed over time. In systems where there is reinforcement in the top-N list, we would expect to see this measure decrease over time towards its value in a hard-cutoff scenario (because more of the new clicks into DL go to the top-N articles). The slope of this can also provide information on the speed at which this effect materializes. This measure therefore helps us examine the reinforcement behavior of FNRS for the different choice of the feedback value γ. As an extreme case when there is a high likelihood of only reading articles in the recommended list (probability of reading an article from DL~1), then under the top-N (hard cut-off) selection we would expect M2 to be zero since all new clicks will go to the same articles in the top-N list.

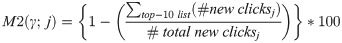
Gini

It is one of the popular measures for quantifying inequality in a system [37]. To assess the impact of news recommendation on overall popularity inequality we also track this metric during the simulation. Gini index is defined as absolute mean difference divided by mean of the click counts of articles. Mathematically, Gini coefficient is defined in the following way,

In the above expression (4), P represents the number of articles in the system at any given time, and $$ \stackrel{-}{C}=\frac{1}{P}{\sum }_{i=1}^P{C}_i$$. Note that the minimum value of G is 0 and it happens in an egalitarian system where all articles receive same number of clicks. An in the most unequal system, one article receives all clicks and other articles receive none. In this extreme case $$ G=\left(1-\frac{1}{P}\right)$$, that is G ~1 displays high inequality.

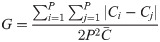
The update rule

At each time step, one reader arrives, and the arrival of a new article is determined by the rate parameter of exponential distribution. Upon arrival of a reader, apriori, the number of articles to be read by the reader is determined. The reader proceeds reading articles from front page, per her behavior described in S1 Algorithm in S1 Appendix. The probabilities for the selection of different articles from a reader are controlled in the simulation. If the reader selects an article, then the count of the selected article is increased by 1. The order of display of articles (both chronologically and based on popularity) are updated at each time index.

For two different NRS, top-N and FNRS, the selection of N articles is made for the recommended display list (DL), and DL is updated at each time index. To the extent possible, we selected realistic values of simulation parameters, and for this purpose we gathered information from various sources. We provide a detailed discussion on the choice of different simulation parameters in S1 Appendix.

Simulation parameters

Usually the popularity of items online follows the power-law (Zipf) distribution [38], therefore before the simulation starts we generated 400 articles (50 articles corresponding to each category), and choose the interval of (1, 1000) to assign them initial popularity. We take average of the number of desktop visitors on different news websites in the sample to determine μ (see S1 Table in S1 Appendix for details).

We study the behavior of FNRS for different choices of the feedback exponent γ. In the simulation, it has been varied with different integer values between 1,2,….10. For each of the cases, in the beginning of the simulation we use the same seed values for the generation of random numbers as well for more accurate comparisons across runs.

To account for the prominence of most-popular articles, the higher values of the reading probabilities are of interest. Also, empirically it has been observed that recommendation engines usually exhibit strong influence on users [39, 40]. Though different combinations of p,q,r were used in the simulation as given in Table 2, we develop our discussion on a particular choice of (p,q,r) = (0.7,0.2,0.1). This particular combination helps us examine the case where, FNRS has mild influence on reading behavior, for the other cases, in which, FNRS displays even stronger influence on reading behavior will easily follow from the discussion in present research. Additional simulation results for few selected cases are reported in S1 Appendix. To the extent readers exhibit moderate to high preference for the recommended and recent articles, the findings discussed below do not change.

Table 2

Simulation parameters.

Zipf exponent (s)	1.4
Initial seed interval for 400 articles	(1,1000)
Number of articles in DL	10
μ	3.2
λ	3
Number of readers	50,000
Arrival rate of News articles (ρ)	0.003
(p,q,r)	(0.3, 0.4, 0.3), (0.3, 0.5, 0.2), (0.4, 0.3, 0.3), (0.4, 0.4, 0.2)
	(0.5, 0.3, 0.2), (0.6, 0.2, 0.2), (0.7, 0.2, 0.1), (0.8, 0.1, 0.1)

We choose number of readers to be 50,000 in the simulation to ensure that this number is a reasonable estimate to: (a) demonstrate the emergent aspects of news recommendation, (b) on average dynamic update of the feedback exponent is performed at an interval of 20–30 minutes in a real system, and (c) the reported number is well within the daily visitors to a typical news website.

Properties of FNRS

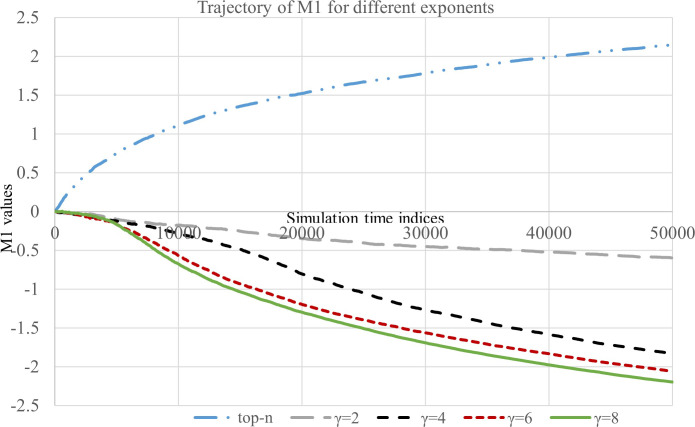
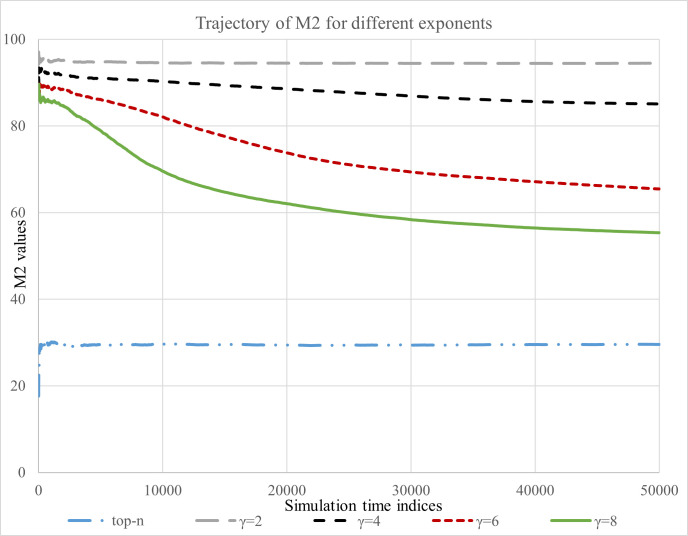
The trajectories of M1, M2 and Gini is presented in Figs 2–4, respectively. First, we summarize our findings based on the measure M1.

Fig 2

Boundary amplification of articles.

Fig 3

Reinforcement behavior of FNRS.

Fig 4

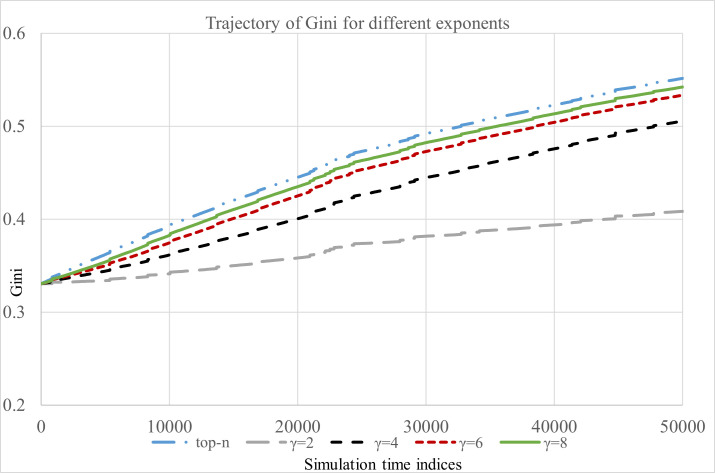
Inequality in popularity measured using Gini index.

It can be observed from the path followed by M1 (Fig 2) that for an influential top-N NRS the initial difference between the counts of N^th and (N + 1)^th article gets amplified heavily and quickly. As expected, for γ = 2, 4, 6, 8 the measure M1 takes values significantly lesser than the top-N recommendation that uses hard cutoff (see Fig 2 and additional results in S1 Appendix). It is also noteworthy that in the case of FNRSs, the popularity amplification trend between Nth and (N+1)th article does not follow a deterministic trend because their initial click count is almost same. Therefore, Nth and (N+1)th articles compete for the recommendation spot over the initial period of simulation. In the presence of positive feedback one among them eventually attains a significant lead over the other and gets selected for recommendation deterministically. The extent of popularity amplification between the Nth and (N+1)th article is controlled by the feedback exponent. These findings suggest that the phenomenon of artificial amplification due to top-N selection can be significantly mitigated using FNRS, and hence recommendation using feedback is more suitable to maintain individual fairness [36].

Fig 3 presents the findings based on M2. In the figure, the bottom line corresponds to the top-N NRS (hard-cutoff). We observe that as the value of γ increases, the performance of FNRS becomes closer to the top-N NRS. Further, the FNRS with positive feedback eventually may behave as top-N after sufficient number of time steps (for example see the path of γ = 8). Hence, using feedback selection mechanism we can generate behavior similar to traditional top-N recommendation, while maintaining reasonable level of diversity in the selection of articles.

We also observed that the share of new click counts received by the articles which were not in the initial (t = 0) recommendation list also depends on the preference a reader exhibits for the recommended articles. For example, after sufficient time steps in S7 Fig in S1 Appendix approx. 70% of new Web traffic is received by the non-recommended articles, whereas in S9 Fig in S1 Appendix it is approx. 50%. In the case of FNRS for a given feedback exponent, as recommendation evolves over time a higher level of reinforcement is observed if readers exhibit higher preference for the recommended articles.

Finally, Gini measures the extent of inequality in popularity of articles induced by the recommendation process. We observe (Fig 4) that the recommendation that uses sorting of articles based their click counts (hard cutoff) induces highest level of inequality in the popularity of articles as the simulation progresses. When readers exhibit moderate to high preference for the recommended articles the Gini coefficient exhibits increasing trend with respect to: (a) simulation time steps, (b) extent of positive feedback, and (c) the preference for the recommended articles by readers (see Fig 4, and S1–S3 Figs in S1 Appendix).

For the robustness check of the findings related to Gini coefficient we replicated the whole simulation process 50 times with different initial seed values and recorded the Gini coefficient corresponding to each feedback exponent (γ) at the end of each simulation replication.

We performed two sample t-test for independent samples for the following cases (γ_a, γ_b) = (2, 4), (4, 6), (6, 8) and (8, ∞) with γ_a < γ_b. Here γ_b = ∞ corresponds to the implementation of top-n recommendation. As stated earlier, we expect that a higher value of feedback exponent will cause more inequality in popularity of articles, therefore a higher Gini coefficient will be observed. Following hypothesis was tested corresponding to each of the cases mentioned above.

In other words, we are interested in examining if a higher value of feedback exponent results in a higher level of inequality in click counts of articles. To conduct the two sample t-test, we first examined the equality of variances for all cases of two independent samples using F-test. We failed to reject the null hypothesis of equal population variances (at 0.05 significance) in all cases (see Table 3). Therefore, we conducted the two-sample t-test for independent samples with equal variances. In all cases we reject the null hypothesis (H₀). Therefore, we conclude that a higher value of exponent leads to a higher level of inequality in the click counts of articles.

Table 3

Summary of hypotheses tests two-independent samples (sample size = 50).

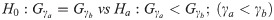
(γa,γb)	(2, 4)	(4, 6)	(6, 8)	(8, ∞)
F-test for equality of variance (p-value)	0.134	0.051	0.409	0.446
t-static (p-value) for independent sample test with equal variances	94.11 (0.00)	34.93 (0.00)	12.65 (0.00)	13.13 (0.00)

Extending M1 & M2 as design principles of FNRS

Thus far we have shown how a simple feedback parameter in FNRS can be elegantly used to mitigate some potentially harmful impacts of NRS. While this is an important contribution of our work, it does not provide a media manager sufficient flexibility to continuously guide the adaptation of system in a changing news readership landscape. This is the issue we turn to here.

As a case in point, if we retain a feedback exponent (γ; such that γ > 1) over an extended period of time, the NRS will drift towards an “equilibrium” state, where only few articles will receive majority of clicks (akin to top-N). From the complexity perspective, these states are considered “dead” or uninteresting [12]. From a practical perspective, media managers would rarely want their extensive news ecosystem to focus on a handful of news articles that most users read to the detriment of much of the other important news curated by their team of journalists and editors. To enable FNRS to adapt to the changing environment, in this section we develop a framework for updating the feedback exponent at selected discrete points in time, albeit with some form of augmentation or human intervention. In the complex systems perspective, the exponent is used as the prescription (or strategy) for the collective behavior of the system, while the sampling points act as lever points (or corrective policy intervention) at the critical stages of emergence that allow the system to co-evolve with environment and to respond based on extant capabilities [12]. The environment is not a constant, but changing and often co-evolving with time [41] as well.

An adaptive FNRS would balance two major challenges encountered in recommendations [12]: exploration (acquisition of new information and capabilities), and exploitation (the efficient use of information and capabilities already available). To perform the task of exploitation, we need to determine the extent to which we want to: (a) generate less distortion in recommendation by giving some chance to less popular articles in the recommended list, (b) capitalize on popularity of articles corresponding to highest click by recommending them (top-N reinforcement), and (c) the stopping point until we want FNRS to exhibit same behavior. We illustrate the path followed by the first two phenomena in simulation (their trajectory) through metrics M1 & M2. We examined the performance of FNRS for different values of γ, over a fixed number of readers (or horizon; t = 50,000) for these metrics. Further, for M1 we only focus on boundary articles: N^th and (N+1)^st. To extend these concepts for all articles in the system, we need to modify the functional form of M1 & M2.

Articles getting a position in the top-N list receive substantially higher visibility than the other articles. M1 captures this notion well for the boundary articles. By the inherent design of top-N recommendations, the extent of clicks for other recommended articles will at least be same if not higher than the N^th article (see the empirical evidences reported in [42, 43]). Promoting the most-read articles directs more attention to them, and hence create click-share distortion in the underlying distribution of article clicks over time. This can have its longer-term consequences for the news site, where only few selected articles receive majority of the new clicks. In an environment, where news industries are struggling to resurface or repackage their huge archives of news to readers [44], introduce diversity in recommendation [10], and trying to engineer serendipity in their recommendation engines [45], the display of articles based on hard-cutoff can be potentially troublesome due to susceptibility of the top-N recommender in creating distortion in the popularity of articles. Here distortion is defined as increase in the click-count share of the popular articles and decrease in the click-count share of the less popular articles over time due to recommendation. Hence, one objective for the dynamic adaption of FNRS is to have low distortion (defined formally later in this section), which generalizes the M1 measure.

M2 measures the extent of top-N reinforcement. The higher the feedback exponent, the higher the chance that popular articles will appear as recommendation. The more the trajectory of M2 is closer to the trajectory of hard-cutoff recommendation (Fig 3), the more FNRS exhibits recommendation akin to hard-cutoff. If clicks (or views) of articles are considered as a quality surrogate for recommendation, then the hard-cutoff top-N recommender has high accuracy since it only picks articles with highest counts. Managers wishing to optimize near-term revenue goals may find this attractive since prominently highlighting popular articles in a top-N list can drive even more traffic to these articles from newer viewers. On the other hand, the probabilistic recommender that recommends articles proportional to their popularity (γ = 1), is true towards the "natural share" of articles but often recommends articles that are not the ones with highest counts, and hence sacrifices “accuracy”. Hence, a second objective for the dynamic adaption of FNRS is to have high accuracy, which generalizes the M2 measure.

Conflicting objectives in design of FNRS

We formalize these two trade-offs (accuracy and distortion) in a formal setup. Since the FNRS can operate in a broader continuum compared to the other recommendation methods, it is particularly effective as a method to make a choice between these two trade-offs. The choice between the level of accuracy and distortion in a FNRS has the notion of subjectivity based on a media manager’s preference for these two metrics.

We record the clicks received from the initial set of readers that arrive in the system over a pre-determined time interval say (t₀,t₁). Observation during this initial period, helps us to stabilize the initial randomness in click evolution process of articles. At t₁, we select another time interval (t₁, t₂) with discrete indices j’s (t₀ < t₁ ≤ j ≤ t₂) to discuss the following novel constructs.

Accuracy-loss (generalization of M2)

At any given time for FNRS we define accuracy-loss based on comparison to a benchmark of distribution of counts of articles that appear as recommendations in a top-N NRS at the exact same time index. To quantify accuracy-loss due to recommendations, we assume that the count distribution of articles, when they are selected corresponding to highest count in top-N recommendation at each time index represents the "ground truth". We measure accuracy-loss for an FNRS with a given exponent γ, by implementing two parallel universes (systems) from the same initial conditions—FNRS with the specific level of a feedback exponent, and the other based on a traditional top-N list. In this manner, we define accuracy-loss metric in the following way at time index j:

In Eq 5, N represents, the number of articles appearing in top-N (or probabilistic) “recommended” list. $$ C_{ij}^H$$ represents the clicks of i^th article, appearing in the top-N (hard-cutoff) NRS, at the j^th time index. Whereas, $$ C_{ij}^{\gamma }$$ represents the clicks of i^th article appearing in the FNRS with exponent γ, at the j^th time index. Hence, $$ {\sum }_{i=1}^N{C}_{ij}^H$$ and $$ {\sum }_{i=1}^N{C}_{ij}^{\gamma }$$ represent the sum of clicks of all articles that appear in traditional top-N NRS and FNRS with exponent γ, respectively, at the j^th time index as recommendation.

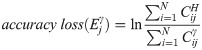
As the simulation progresses, we average the accuracy loss over the number of simulation time steps at which the recommended lists are updated to simplify the expression without introducing significant error. Hence, the average accuracy loss is:

Where ℓ is a time-index between (t₁, t₂), and we use it as a subscript for the average value of a metric over the interval (t₁, ℓ).

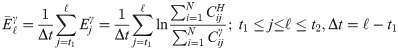
Distortion

M1 illustrates the extent of amplification due to recommendation, albeit only for the boundary articles. We extend this notion for overall count amplification due to recommendation, measured by the metric distortion. To measure share distortion, we assume that the initial share of articles at t₁, before recommendation starts, is the "ground truth".

To quantify distortion, we measure the distance between the probability distribution of initial share of articles in the system at t₁, and the modified share of articles after the recommendation, using Jensen-Shannon Divergence (JSD) [46]. Distortion created in the natural share of articles due to FNRS with exponent γ, is averaged over the number of simulation time steps at which accuracy-loss metric are updated (Eq 6). Note that the definition of JSD metric to measure the distance between two distributions remains valid even in the presence of retiring of old articles and arrival of new articles.

Let us denote the probability distribution of articles in the system in the presence of FNRS with exponent γ, at the time index j as $$ q_j^{\gamma }$$ and the initial share (j = t₁) of articles as probability distribution p. Then mean JSD is,

Both objectives (Eqs 6 and 7) depend on highly complex and random mechanism of readership, arrival of new articles, recommendation, and update of the system. Also, the trade-off between minimizing accuracy-loss and distortion would require a manager’s subjective decision. Hence, the classical optimization techniques of “tame” problems will fail to offer policy choices [19].

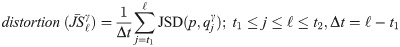
These kind of planning problems which are result of the complex interaction of various components, constantly changing environment, and has presence of multiple stakeholders and perspective, can be categorized as a “wicked” problem [20, 21]. The objectives of wicked problems are incomplete, contradictory, changing over time, and they are evaluated based on subjective preferences. Due to the conflicting nature of multiple objectives, wicked problems can be assisted through a set of Pareto-optimal solutions [47].

To generate Pareto-optimal solutions we present a framework for the evolutionary multi-objective optimization that offers sufficient flexibility and reasonably encompasses the complex search spaces and ill-behaved objective functions [48]. Evolutionary algorithms inspired by natural selection have been used to generate high-quality solutions to difficult problems with highly complex search spaces and multiple conflicting objectives [48]. In our context, we use the evolutionary algorithm NSGAII [49], to explore the search space of accuracy-distortion trade-off.

Multiobjective Pareto-optimal solutions

Consider a multi-objective optimization problem with two conflicting objectives (f₁(z),f₂(z)), z being a vector of decision variables. For each of the two conflicting objectives (f₁(z),f₂(z)), there exists one optimal objective value and the corresponding different optimal solution(s). Because, the minimum solution of objective functions f₁(z) and f₂(z), need not be the same solution, in general, we encounter non-existent solutions in multi-objective optimization [49]. To overcome this issue, in the presence of multiple conflicting objectives we use Pareto-optimal (non-dominated) solutions. In our context, the solution z is a vector of two decision variables, namely, γ and ℓ and the objective vector F(z) is defined as,

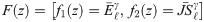
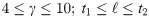
For illustration, consider the non-dominated solutions depicted in Fig 5(i). For a given solution say ‘a’ in the objective space, its corresponding solution is shown in decision space with same character (i.e. ‘a’) at a given time t₁. In this example, if manager chooses the non-dominated solution ‘a’ at t₁, then the corresponding feedback parameter is γ = 1, and the stopping point is 3 units of time (say, 3x) beyond t₁. Hence, she uses γ = 1 in the interval [t₁,t₁ + 3x].

Fig 5

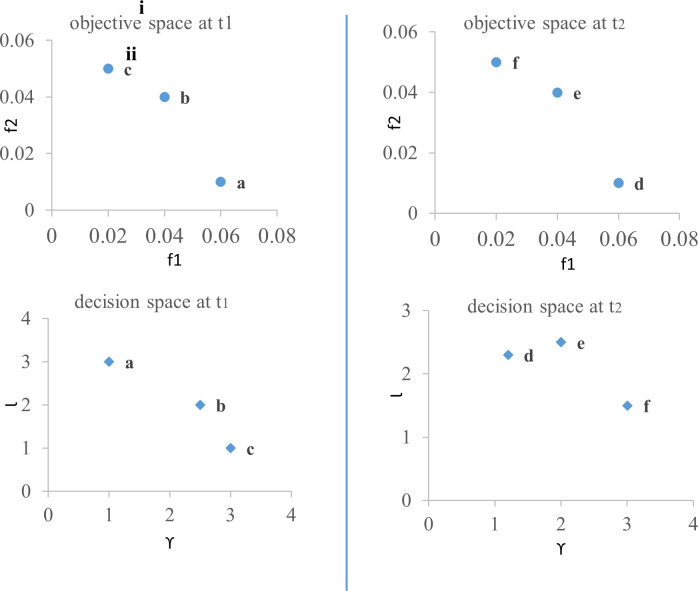
Illustration of non-dominated solutions.

(i) Set of non-dominated solutions (upper panel) and the value of their corresponding decision variables (lower panel) at t1. (ii) Set of non-dominated solutions (upper panel) and the value of their corresponding decision variables (lower panel) at t2.

Dynamic adaptation of FNRS

As mentioned earlier the use of a feedback exponent (γ > 1), over the same set of articles with high clicks over an extended period will render FNRS to emulate top-N recommendation and hence does not offer much flexibility to adapt the system with changing environment. On a typical news website, there will be arrival and retiring of articles, random and often turbulent reading patterns–partly driven by social media traffic. An FNRS should be flexible enough to adapt and co-evolve with the changing environment [12].

To model FNRS as an intelligently adapting system, we consider two decision variables—(a) the feedback exponent γ_t, and (b) the time-interval (or stopping point; Δt) corresponding to the current exponent value. The adaptation of FNRS can be represented as a search for relative optima over a “rugged landscape” of these two decision variables. For any combination of (γ_t, Δt), γ_t will be used for the time interval (t,t + Δt). At t’ = t + Δt, a new combination of (γ_t’,Δt’) are chosen from the Pareto-optimal solutions (exploration) to update the feedback exponent and the stopping point. For illustration see Fig 5(ii), in which a manager may prefer to choose non-dominated solution ‘e’. Corresponding to solution ‘e’, the feedback parameter is γ = 2, and the stopping point is 2.5 units of time beyond t₁ +3x. Hence, she uses γ = 2 in the interval [t₁ + 3x, t₁ + 5.5x].

Algorithm 2: Pseudo code to dynamically update the exponent γ

a. At t₀ = 0, choose time interval [t₀, t₁] over which the clicks received by the articles will be observed without recommendation

b. Let t = t₂(t₂>t₁)

c. Perform following steps at each t, to update the exponent values γ

 i. Update the simulation parameters using most recent observations corresponding to the moving time window [t– δt,t]

 ii. Determine the Pareto optimal front for accuracy-loss and distortion values using NSGAII

 iii. Choose the desired value of the control exponent (γ_t) and the corresponding time interval say, $$ \widehat{\Delta }t$$ from the Pareto front

 iv. $$ t=t+\widehat{\Delta }t$$

 v Use γt in FNRS until t

The update process for (γ_t, Δt), gives system the characteristic of “evolving structure” with changing environment, and serves as a credit assignment procedure [12] at intermittent time points over a desired interval. Selection of articles using updated system parameters and the feedback exponent reward those articles that seem to be causing better performance, and can be seen as corrective action [12]–subject to manager’s preference. The update process enables FNRS to make a balance between exploration (update of (γ_t, Δt) based on newly acquired information, and exploitation (the efficient use of Pareto-optimal solutions for recommendation). For the generation of Pareto-optimal solutions we do not have a definitive stopping rule, and due to constant update process the objective functions have the property of “moving target” [12].

To determine the Pareto optimal front for accuracy-loss and distortion we use NSGAII. NSGAII is an Elitist Non-Dominated Sorting Genetic Algorithm that generates various Pareto-optimal solutions in a single run of the algorithm. The selection operator of NSGAII selects a population of solutions in such a way that it preserves both diversity and elitism of non-dominated parent and offspring solutions. The general update process of exponents is detailed in Algorithm 2. In the pseudo-code, steps c(i-iv) can be considered as exploration and the step c(v) as the exploitation step of the adaptation process.

Simulation results using NSGAII

In the simulation, we choose t₀ = 0, t₁ = 20,000 and t₂ = 50,000, with unit increase in indices to obtain the values of j’s. For simplicity, a unit increase in time coincides with the arrival of a reader. The media manager chooses the interval [t₀, t₁] over which the clicks received by the articles will be observed, and the observation corresponding to interval [t₁, t₂] is used to generate Pareto-optimal fronts. At t₂, the simulation parameters, such as arrival rate of readers and average number articles read by them are updated using most recent previous observations corresponding to moving time-window of length δt. For the time interval [t₁, t₂] we present a selected set of 32 exemplar true optimal solutions, and solutions obtained through NSGAII [49] in Fig 6. The true Pareto-optimal solutions were generated using non-dominated sorting over the complete decision space.

Fig 6

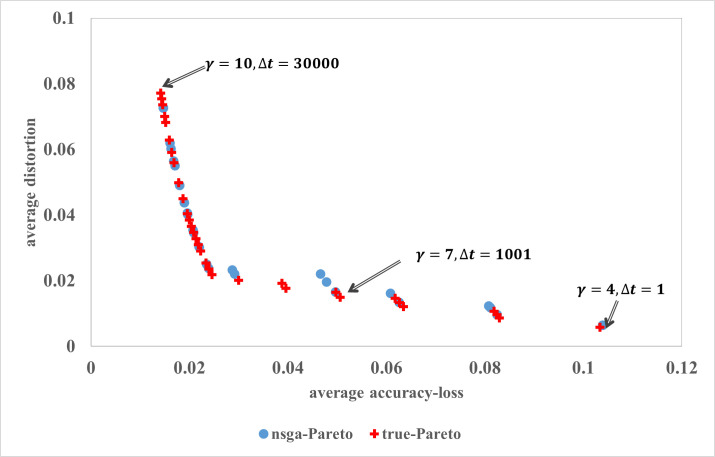
Pareto optimal front for optimization.

In live implementation of Algorithm 2, for the selection of non-dominated solutions, an implementer may prefer to set a threshold for accuracy-loss and distortion metric to eliminate trivial solutions. For example, if threshold for accuracy-loss is 0.04 then all Pareto-front solutions having accuracy-loss less than 0.04 would be in the consideration set. Similarly, a threshold can also be set for the distortion metric. The pareto front allows media manager to examine all alternatives, and removal of bad alternatives before implementing any selected tuple (γ_t, Δt).

Importantly, the framework and mechanism presented in this section provides managers with the pareto front periodically as the news ecosystem dynamically evolves. In practice the manager will then have to periodically review the pareto front and choose the option (γ_t, Δt) that best represents the firm’s current interest in balancing conflicting objectives. It may be possible to treat this as an autonomous agent as well, constantly learning and adapting and automatically choosing a point on the pareto front, if the firm’s specific goals can be captured in greater detail. We note that the update process can also be implemented using multi-objective multi-armed bandits (MOMAB) [50]. However, we do not pursue MOMAB motivated dynamic adaption of FNRS in this research.