- Altmetric
Structurally characterizing new materials is tremendously challenging, especially when single crystal structures are hardly available which is often the case for covalent organic frameworks. Yet, knowledge of the atomic structure is key to establish structure‐function relations and enable functional material design. Herein, a new protocol is proposed to unambiguously predict the structure of poorly crystalline materials through a likelihood ordering based on the X‐ray diffraction (XRD) pattern. Key of the procedure is the broad set of structures generated from a limited number of building blocks and topologies, which is submitted to operando structural characterization. The dynamic averaging in the latter accounts for the operando conditions and inherent temporal character of experimental measurements, yielding unparalleled agreement with experimental powder XRD patterns. The proposed concept can hence unquestionably identify the structure of experimentally synthesized materials, a crucial step to design next generation functional materials.
Structurally characterizing new and poorly crystalline materials such as covalent organic frameworks is highly challenging. The dynamic protocol of this work overcomes this challenge through a systematic likelihood ordering based on intuitive heuristics and X‐ray diffraction patterns. It succeeds in unambiguously identifying a material's atomic‐level structure, accounting for the operando conditions and inherent temporal character of experiments.
Introduction
The design of functional materials is instrumental for advancing technological solutions to tackle pressing societal problems,[ 1 , 2 , 3 , 4 , 5 , 6 , 7 ] such as combating climate change and creating clean energy pathways. In the last few years, new materials with particular functionalities have been proposed at a very high pace, due to an in‐depth microscopic understanding of their functionality and the growing toolbox of synthetic chemists. Within this toolbox lies the concept of reticular design, [8] where judiciously chosen building blocks are assembled in a predesigned topology, giving rise to materials such as metal‐organic frameworks (MOFs) [9] and covalent organic frameworks (COFs). [10] Due to their extensive tailorability and attractiveness for a vast range of applications, the structural design of MOFs and COFs has formed a very active field of research.[ 11 , 12 , 13 , 14 , 15 ] Thanks to a meticulous control over synthesis conditions and an ever‐expanding versatile set of experimentally available building blocks, it has even become possible to synthesize combinations of building blocks in different structures. To fully explore the functionalities of the enormous amount of potential structures that can be formed from a given set of building blocks, an accurate protocol is needed to systematically derive structural models for these materials at realistic working conditions of temperature and pressure.[ 16 , 17 ] Such structural characterization is a conditio sine qua non for the atomically guided design of functional applications in the fields of catalysis, sorption, light harvesting and more.
Reticular synthesis states that the atomic‐level structure of any framework material is defined by a structural model containing three elements: [18] (i) the material's building blocks, (ii) its topology, and (iii) the embedding of the building blocks in this topology. When designing new experimental materials, X‐ray crystallography is typically adopted to construct such a structural model. While single‐crystal X‐ray diffraction (SCXRD) measurements allow for the direct atomic‐level determination of a material's bulk structure, [19] it is notoriously difficult to obtain large single crystals for most porous materials such as MOFs and COFs and one usually resorts to powder X‐ray diffraction (PXRD) measurements [20] or electron crystallography.[ 21 , 22 ] During a PXRD measurement, however, the 3D reciprocal space is non‐injectively projected onto a 1D Bragg angle, making the determination of the true structural model impossible without prior information about the structural model. Given the need for such an ad hoc model—which is absent in SCXRD—PXRD measurements require a method to verify the validity of these proposed structural models. Therefore, as discussed in more detail in Section S1.1, whole powder pattern fitting (WPPF) methods are used to either reject or accept a possible model based on a visual analysis of the experimental and modeled PXRD patterns, and on error measures such as the weighted profile residual. [23] However, when noisy PXRD patterns are obtained, such as for structures that lack long‐range order, extracting any structural information becomes increasingly difficult. As a result, classical methods that rely on the diffraction data to refine initial structural parameters, such as the WPPF methods or other popular top‐down methods, fail to accurately discern between multiple possible structural models.[ 24 , 25 , 26 , 27 , 28 ]
To circumvent this ambiguity and ensure that no structural models are overlooked when characterizing challenging functional materials, we here present an automated protocol that fully accounts for the dynamic averaging of structures taking place at operating conditions. The procedure, schematically illustrated in Figure 1, reverses the aforementioned experimental PXRD approach by exhaustively exploring all potential structures starting from the building blocks and all possible topologies, and identifying the most likely structural model upon comparing with an experimental PXRD pattern. To that end, a large set of possible structural models is generated from the provided building blocks, which are assembled in various topologies in the first step of our protocol. In the second step, PXRD patterns are derived, using either a static or a dynamic approach in which the inherent dynamic character of an experimental measurement is introduced. In the third and final step, a heuristic is derived and applied to order the proposed structural models as a function of their likelihood to reproduce the experimental diffraction pattern. Such a systematic computational protocol has the added benefit of replacing the ad hoc visual analysis by a well defined metric, allowing quantitative statements on how well the model performs.

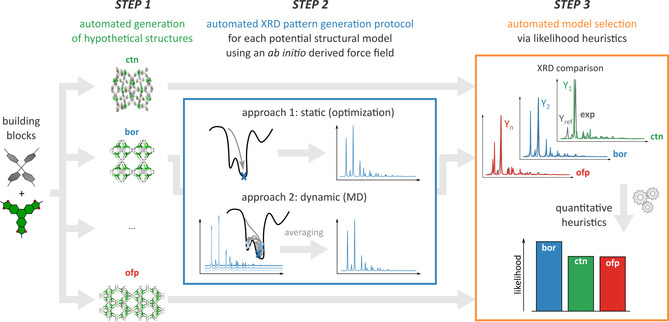
The proposed three‐step structural characterization workflow. For each of the hypothetical structural models (generated in step 1), representative PXRD patterns are derived via either a static or a dynamic approach (step 2), which are then ranked according to their likelihood to reproduce the experimental reference PXRD pattern (step 3).
COFs are ideal materials to test our protocol, as their structural characterization is challenging due to often noisy PXRD patterns, owing to a lack of long‐range order and crystallinity in most experimental samples. These promising materials are made up from light, covalently bound, organic constituents, combining low mass densities with a high stability. Potential applications are situated in the field of drug delivery,[ 29 , 30 , 31 ] (photo‐)catalysis,[ 32 , 33 , 34 ] sensing,[ 35 , 36 , 37 ] (opto)electronics[ 38 , 39 , 40 ] and gas/liquid storage and separation.[ 41 , 42 , 43 ] In general, one can distinguish between 3D COFs, which are completely connected by strong covalent bonds, and 2D COFs, which form layered structures whose stacking order is determined by much weaker forces, such as dispersion and Coulomb interactions. [44] Only a handful of SCXRD patterns are available for COFs, which are limited to the strongly connected 3D COFs. [45] Up to now, it is therefore common practice to propose initial structural COF models by choosing a topology based on the size of each of the building blocks, their point symmetry, and their connectivity with neighboring building blocks (see Figure 2 for representative examples), favoring the most symmetric topology when multiple possibilities arise. [46] However, with over 500 different COFs being synthesized, [47] accurate and systematic characterization techniques are crucial to enable rational functional material design.

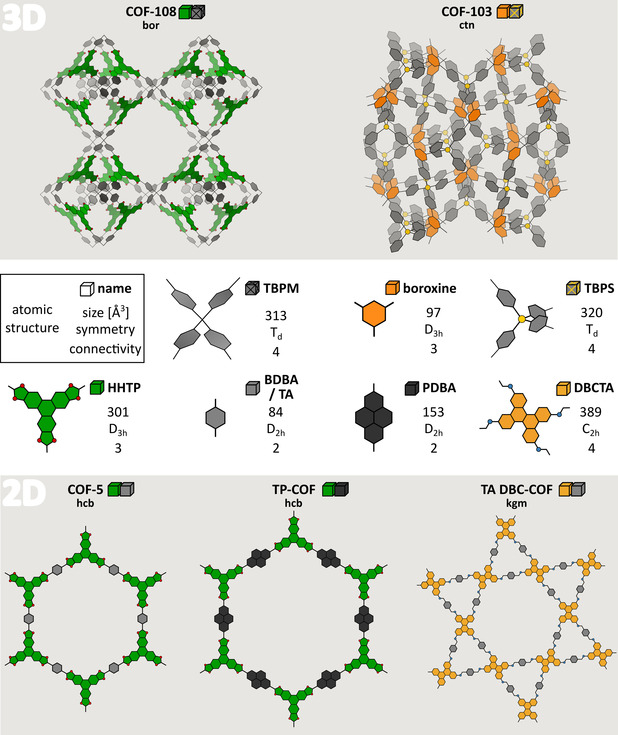
Building blocks and experimentally derived structural models in which they assemble for five experimentally synthesized COFs. The atomic structure and name of each building block (see Table S1 for the abbreviations) are reported, next to their size, symmetry, and connectivity, as expressed by the van der Waals volume, the point group, and number of extension points, respectively.
Results and Discussion
Material Generation
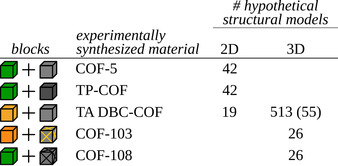
The general applicability of the in silico protocol is illustrated for materials being built from seven different building blocks, illustrated in Figure 2, giving rise to at least five different experimentally characterized COFs. These building blocks were chosen based on their varying sizes, symmetries and connectivities. The two 3D COFs, COF‐103 and COF‐108, were among the first 3D COFs to have ever been synthesized [48] and exhibit the ctn and bor topology, respectively. The bottom panel shows the three 2D COFs. Similar to the chosen 3D COFs, COF‐5 was one of the first ever synthesized COFs, [10] adopting the hcb topology. TP‐COF[ 49 , 50 ] was chosen as an isoreticularly expanded equivalent of COF‐5, whereas TA DBC‐COF [51] was chosen due to its unique kgm topology.
Due to the modular nature of COFs, the seven building blocks of Figure 2 can be assembled in a combinatorial amount of structural models and hence hypothetical COF structures. When considering the five different combinations of two building blocks each that give rise to the five COFs in Figure 2, almost 700 unique structural models can be constructed by only looking at the possible topologies for the co‐condensation of each building block combination. In Table 1, this number is broken down for each building block combination.
Most building block combinations give rise to only a tenfold of structural models due to the assumed rigidity of the building blocks. However, the building block combination that assembles TA DBC‐COF can synthesize in 19 and 513 distinct 2D and 3D topologies, even though only a 2D structural model was resolved experimentally. This huge number of hypothetical models can be attributed to two factors. First, the slight non‐planar character of the DBCTA building block accommodates both 2D and 3D topologies, in contrast to all other building blocks considered here. Second, removing the TA building block would preserve the original topology, similar as for any other twofold connected building block. Consequently, the TA DBC‐COF can hypothetically synthesize in any of the large subset of topologies that contain only fourfold coordinated building blocks. By filtering out the most strained of these structural models, 19 2D and 55 3D hypothetical models are retained for the TA DBC‐COF. For the five building block combinations of Figure 2, step 1 of our protocol hence generates a total of 210 structural models. For each of these models, a fully flexible ab initio based force field was derived using the QuickFF[ 52 , 53 ] protocol (see Section S2) to characterize and validate them with respect to the experimental PXRD patterns.
Automated Model Selection Protocol via Heuristics
An ideal PXRD pattern consists of discrete Bragg reflections, where each peak j is defined by its position θj, intensity Ij and shape, [23] as illustrated in Figure 3 a. These components are uniquely defined for each structural model; deviations between experimental and representative computational PXRD patterns (see Section S1.2) can hence help localize model inaccuracies through these three components. To assess the correspondence among PXRD patterns, a quantitative measure is required, which, in our protocol, relies on the similarity index SI and the weighted profile residual Rwp. A detailed explanation and alternative figures of merit are outlined in Section S1.4. To understand how they penalize differences between two patterns, it is instructive to consider their variations for different types of deviations in either peak or trough regions. To this end, Figure 3 b visualizes four hypothetical PXRD patterns (colored) that are compared to a given reference profile (in gray). Pattern 1 has a low deviation in both the experimental peak and trough regions, whereas pattern 4 has a high deviation in both regions. Pattern 2 exhibits a high deviation in the peak regions of the experimental PXRD pattern but a low deviation in the trough regions, whereas the opposite is true for pattern 3.

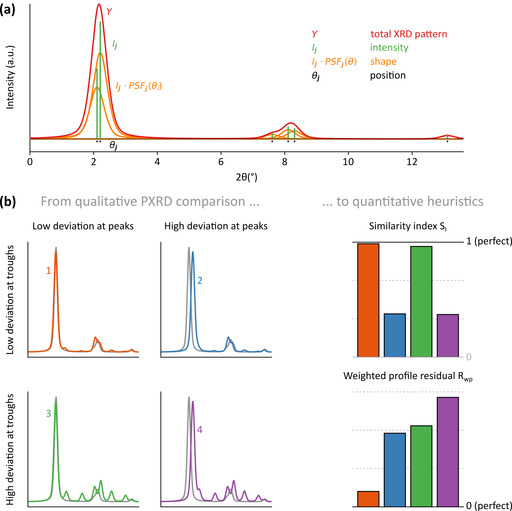
(a) Illustrative PXRD pattern (red) built up from six individual Bragg peaks that are each characterized by their position (black), intensity (green) and shape (orange). (b) Illustration of the figures of merits used in step 3 of the procedure for four hypothetical and representative PXRD patterns.
From Figure 3 b, it is clear that the similarity index SI mainly focuses on the overlap of the peaks, but is largely insensitive to deviations in the trough regions. This results in comparable similarity indices for PXRD patterns 1 and 3, and 2 and 4, which differ only in the trough regions. As SI is normalized to one (see Eq. S1.10), direct comparison between various patterns is possible, in contrast to the Rwp factor. However, Rwp considers relative instead of absolute differences, as each peak is weighted with an uncertainty factor wi that is inversely proportional to the reference profile's height. As a result, Rwp penalizes the mismatch between the profile intensities, both in peak and trough regions, as is evident when considering the similar Rwp factors for patterns 2 and 3. Since the overall relative intensity difference between the reference and the calculated PXRD patterns conveys no physical meaning, we will globally scale each computational pattern to minimize its weighted profile residual when comparing with the full experimental pattern. This will result in a unique Rwp value for each pattern, whereas SI is unaffected as it is scale invariant. Since these figures of merit can vary significantly with the quality of the reference pattern, there is no specific heuristic value at which the agreement is deemed sufficient. However, as the best of two models is defined by a lower value of Rwp, (R wp,ideal=0) and a higher value of SI (S I,ideal=1), the heuristic will allow for a quantitative ordering of which models are most likely to reproduce the experimental data, resulting in an automated model selection criterion.
Finally, the credibility of any figure of merit is significantly influenced by the presence of background noise in the experimental reference patterns. Especially for poorly crystalline COFs, significant background noise is expected, which originates from amorphous regions, and should be filtered. Clearly, a non‐negligible experimental background signal at Bragg angles that correspond to a reflection peak in the computational pattern would artificially improve the figure of merit. As such, eliminating the background profile is essential before employing any PXRD heuristic. This is achieved here using the robust Bayesian analysis method (see Section S1.5), [54] resulting in a protocol that can also be applied if the material contains large amorphous regions. Henceforth, only figures of merit applied on the background filtered profile will be reported, which will be indicated by the “B” subscript.
3D COFs
At first instance, the protocol is applied to the two building block combinations that give rise to the 3D COFs of Figure 2. In the static approach, all potential structural models of Table 1 are optimized towards their equilibrium structure at 0 K and the PXRD patterns of these optimized structures are derived following the procedure outlined in Section S1.3. The resulting likelihood ordering, based on the heuristic value, is visualized in Figure 4 a,b, where the reference experimental PXRD patterns were extracted from ref. [48]. As the heuristic is calculated based on the relative difference between two profile intensities, the 2θ range is limited to the measured experimental data. Consequently, any diffraction peak of our hypothetical models that falls outside this experimental 2θ range is not taken into account when calculating the heuristics. As this can artificially increase the heuristic results for these structural models—it is expected that the experimental pattern has no matching peaks outside the experimental 2θ range—the names of these structural models are indicated by an asterisk (*) in Figure 4 and should be considered with care.

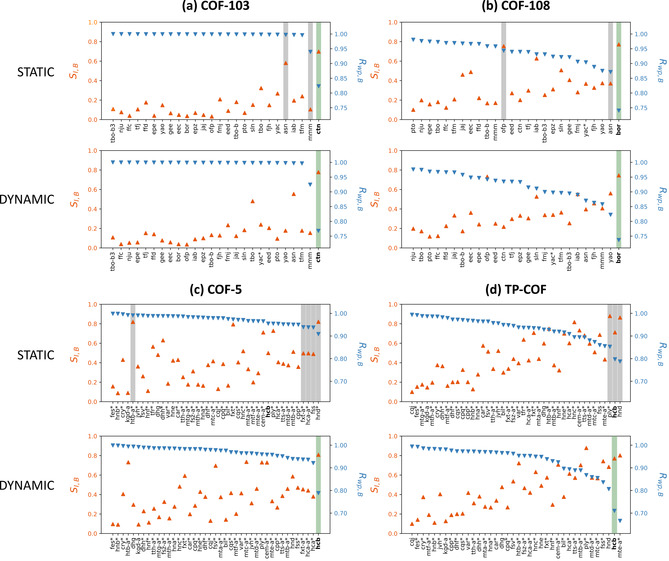
Similarity index S I,B (orange) and weighted profile index R wp,B (blue) ordered as a function of decreasing R wp,B for (a) COF‐103, (b) COF‐108, (c) COF‐5 and (d) TP‐COF, without background noise, using either a (top) static or (bottom) dynamic approach. The green regions indicate a successfully retrieved structural model corresponding to the experimentally reported topology (in bold face), whereas the gray regions correspond to favorable heuristic values that are unsuccessful. An asterisk (*) indicates that the heuristic results for that topology are artificially increased due to significant peaks outside the experimental 2θ range, which are not taken into account when comparing the PXRD patterns.
The green regions in Figure 4 a,b correspond to successfully retrieved experimental structures, whereas the gray regions indicate other likely potential structural models based on the heuristic values. For the 3D‐COFs, COF‐103 and COF‐108, the static approach succeeds in identifying the correct experimentally resolved structural model when taking both the S I,B and R wp,B values into account. The gray zones correspond to structures which might potentially be viable, but it is immediately clear that only one heuristic value is favorable, either S I,B is close to one or R wp,B is close to zero. For COF‐103, shown in Figure 4 a, an appreciable difference is observed between the best ctn topology and the second best mmm topology, facilitating the correct model selection. While our protocol also correctly identifies the experimentally reported topology for COF‐108 (Figure 4 b), the distinction between the best topology (bor, indicated in green) and the second best topology (asn when considering R wp,B and ofp when considering S I,B, indicated in gray) is smaller than for COF‐103 due to the larger residual experimental background for COF‐108 (see Section S1.5). Clearly, the static approach of our protocol is able to correctly identify the most probable structural model for 3D COFs, which are connected through strong covalent bonds and thus less prone to dynamic effects.
2D COFs
Turning our attention to the 2D COFs, visualized in Figure 4 c,d, our static approach is unable to identify the best structural models for COF‐5 and TP‐COF, with no distinct outlier, in contrast to the 3D COFs. The htb‐a, fxt‐a, hca‐a, fss and hnd topologies for COF‐5, and the ply, hcb and hnd topologies for TP‐COF, indicated in gray, have similar S I,B and/or R wp,B values. However, an optimal heuristic combination is missing for the experimentally reported hcb topology of both materials.[ 10 , 50 ] This mismatch originates from the inability of the static approach to account for dynamic averaging at working temperatures, as only one low‐energy structure with a fixed layer inclination is considered (see also Section S5). This limitation is expected to manifest itself for every 2D COF, as their layers are held together by weak, non‐covalent forces. However, for TA DBC‐COF the static approach does predict the correct kgm topology, as in this case the DBCTA building blocks hinder layer shearing due to steric constraints (Figure S18).
To resolve these dynamic effects in structures that have a large intrinsic freedom, characterized by shallow minima on the free energy surface due to the presence of weak interactions, it is necessary to generate PXRD patterns through MD simulations at operando conditions of temperature and pressure (see Figure 1). In this dynamic approach, the PXRD pattern of any structural model is obtained by averaging PXRD patterns collected at different snapshots from the MD trajectory of this structural model. As an example, Figure 5 b visualizes the experimental PXRD pattern of COF‐5 together with (i) the diffraction pattern of the optimized hcb structural model (static approach), (ii) the diffraction patterns corresponding with several snapshots through the MD simulation, and (iii) the diffraction pattern obtained by averaging over the patterns obtained at 50 uniformly distributed MD snapshots, where each snapshot corresponds to an embedding in the hcb topology (dynamic approach). Clearly, the time‐averaged PXRD pattern of the dynamic approach significantly improves the representation of the true atomic structure during measurement, increasing the similarity between the simulated and experimental PXRD patterns.

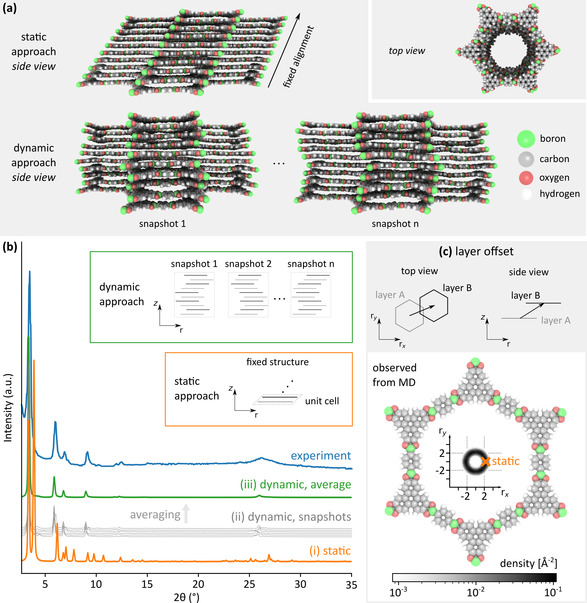
(a) Atomistic representation of the stacking in both the static and dynamic approach, containing two and ten layers, respectively, in their unit cell. (b) Diffraction pattern comparison for COF‐5 using the hcb topology for the optimized structure (static, orange), six representative snapshots taken from the MD trajectory (gray) and the diffraction pattern obtained by averaging over fifty snapshots of the MD trajectory (dynamic, green). (c) Definition of the layer offset between subsequent layers, showing the variation of this offset during an MD simulation as a heatmap.
Turning our attention to the differences between the computational PXRD patterns in Figure 5 b, two observations can be made. First, compared to the PXRD pattern in the static approach, the reflection peaks occurring in the PXRD patterns of the MD snapshots are either shifted towards lower 2θ values or disappear completely, with the exception of the first peak at 2θ=3.4°. While the shift in peak positions indicates an increase in distance between the diffraction planes at finite temperatures, the complete disappearance of peaks indicates that the static structure is too symmetric, featuring extra diffraction planes compared to the experimental structure. This artificial symmetry in optimized structures is a well‐known effect, [55] which is resolved by the MD simulations at finite temperature in our dynamic approach, as demonstrated in Figure 5 b. Second, different MD snapshots give slightly different PXRD patterns. These small deviations are expected, as they correspond to the natural dynamics of the atoms at operando conditions and replace the missing atomic displacement factors in Eq. S1.4. Therefore, the MD‐averaged PXRD pattern obtained in the dynamic approach contains, in a natural way, the broadening effects that are absent in the static approach. As a result, Figure 5 b demonstrates that our dynamic approach leads to a much better correspondence with the experimental PXRD pattern compared to the static approach.
For 2D COFs, the largest discrepancy between the static and dynamic approach finds its origin in the ability to describe the dynamic character of the layer movement, which is evident from Figure 5 a. In a static simulation, the layer offset (see Figure 5 c and Section S1.7) has a fixed magnitude and direction, as defined by the cell vectors. Considering two layers in the optimized structure, they are either aligned, yielding an eclipsed stacking (AA), or displaced with respect to each other, yielding serrated (AB) or inclined stacking configurations, where the latter is illustrated in Figure 5 a. In contrast, in a dynamic simulation, the layer offset fluctuates in both magnitude and direction during the simulation, as shown in Figure 5 a for two snapshots. Moreover, in our dynamic approach, a larger system consisting of ten layers is considered, giving rise to more complex layer behavior. Figure 5 c shows the observed layer offsets both in a static and dynamic approach through a heatmap. Dynamically, a range of offsets is found, all with a magnitude around 2.2 Å without any preferential directionality, whereas in the static approach only one single offset is found with the same magnitude but a fixed direction, which is insufficient to account for the dynamics of the system.
Based on the COF‐5 case study in Figure 5, one expects the dynamic approach to yield a much better heuristic value compared to the static approach for 2D COFs consisting of weakly bound layers. Figure 4 c,d indeed reveals significant alterations when comparing the dynamic with the static approach for 2D COFs. Remarkably, in the dynamic approach, the most likely structural model coincides with the expected topology for COF‐5 and, when ignoring the structural models that contain diffraction peaks outside the experimental 2θ range, also for TP‐COF. We also adopted the dynamic approach for the 3D COFs and TA DBC‐COF, finding no substantial difference with the static approach due to the strong connectivity and steric hindrance in these materials allowing only minimal deviations under finite temperatures and pressures (see Figure 4 a,b and Figure S18). These results illustrate the general applicability of our dynamic protocol to predict the correct structural model.
Model Refinement
While the dynamic approach of the in silico protocol correctly predicts the topology for all COFs considered here, the precise embedding of the building blocks inside the topology can still give rise to different structural models. In turn these can lead to slight variations in the cell vectors and can significantly influence the intensities of the XRD patterns (see Section S1.2). Consider for instance TA DBC‐COF, which assembles in the kgm topology. Even within this topology, different relative orientations of the imine linkages give rise to three different pore structures and distinct diffraction patterns, as illustrated in Figure 6. In other words, the TA building block can be embedded in three different ways, with the imine linkages of TA pointing in opposite directions (kgm1), or with the imine linkages both pointing in the same direction, which is either bent away (kgm2) or towards (kgm3) the smaller triangular pore. These different embeddings can not all be reached during a regular MD simulation as they correspond to different (meta)stable configurations that are separated by too large energetic barriers.

![TA DBC‐COF model refinement for three distinct structural models with the kgm topology but varying orientation of the imine linkage and hence varying embedding, resulting in a different pore geometry and PXRD heuristic value. The PXRD patterns are obtained experimentally
[51]
(gray, background‐filtered) or through our dynamic approach (colored).](/dataresources/secured/content-1766033724066-7ff9d91d-4ebc-49e3-b7df-38e2b7a0b035/assets/ANIE-60-8913-g002.jpg)
TA DBC‐COF model refinement for three distinct structural models with the kgm topology but varying orientation of the imine linkage and hence varying embedding, resulting in a different pore geometry and PXRD heuristic value. The PXRD patterns are obtained experimentally [51] (gray, background‐filtered) or through our dynamic approach (colored).
The heuristic values for the different embeddings reported in this figure demonstrate that the kgm3 model best reproduces the experimental PXRD pattern. Surprisingly, this structural model does not agree with the experimentally proposed model (kgm1), which is illustrated in Figure 2. This experimental model was constructed ad hoc in Material Studio and subsequently refined using the Pawley method, [51] which, however, does not fit the atomic positions, as discussed in Section S1.1. This case study illustrates that, even when the topology is correctly identified, it is instructive to consider whether different embeddings of the building blocks within the topology are possible, at least when multiple (meta)stable configurations exist. From these results it follows that our protocol not only succeeds in finding the optimal structural model for newly synthesized materials, but can also improve upon existing models through refinement of the local geometry and embedding, increasing the similarity between the experimentally observed and calculated diffraction patterns in a quantitative manner.
Conclusion
Crystal structure determination of complex nanoporous materials is key for establishing structure‐function relations in material design. However, finding the atomic‐level structure of experimentally synthesized materials may become a daunting task. This is certainly true for materials that lack long‐range order, such as some COFs, where current techniques struggle to systematically and reproducibly identify the correct structural model as they are highly sensitive to the quality of the experimental data and are prone to confirmation bias. Herein, we presented an in silico protocol that reverses the generally applied strategy of extracting possible models from the observed PXRD peaks. Instead, by generating an exhaustive set of structural models for any given building block combination and generating representative PXRD patterns for each model through a static or a dynamic approach that accounts for the operando experimental conditions, the different structural models are ranked based on intuitive heuristics that unambiguously quantify the correspondence between the computed and experimental PXRD patterns, thereby uniquely identifying the most likely model.
The procedure was validated for several well‐characterized COFs, but is equally applicable to other modular building block materials, such as MOFs and zeolites, in any topology. Starting from seven building blocks, many structural models were proposed, through all possible topologies. For 3D COFs, a static approach without dynamic averaging proved sufficient considering their characteristic strong covalent bonds. However, for 2D COFs, which show a high degree of flexibility due to the weak interaction between the layers, it was essential to account for different dynamically generated snapshots at experimental temperatures. This approach yields a natural analog to experimental XRD measurements and corrects for an artificially too symmetric structure obtained at 0 K in a static approach. Thus, the in silico protocol proposed here can successfully detect experimental crystal structures, even for 2D COFs. Interestingly, our approach also succeeds in showing finer details of the structure. For the TA DBC‐COF, our procedure can distinguish between various structural models that all exhibit the experimental topology but have different orientations of the imine linkages. Such subtleties would easily be overlooked when visually comparing PXRD peak positions.
The presented in silico workflow opens the perspective to systematically screen large databases of materials, to identify their atomic‐level structural models, and establish causal structure‐function relations. We hope that such detailed knowledge will help computational and experimental material scientists alike by opening the door for a more precise design of challenging modular materials for various applications.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
This work is supported by the Research Board of Ghent University (BOF) through a Concerted Research Action (GOA010‐17). S.M.J.R. and J.S.D.V acknowledge the Fund for Scientific Research‐Flanders (FWO) for a postdoctoral fellowship (grant no. 12T3519N) and a strategic basic (SB) research fellowship (grant no. 1S94519N). V.V.S. acknowledges funding from the European Union's Horizon 2020 research and innovation program (consolidator ERC grant agreement no. 647755—DYNPOR (2015–2020)). The computational resources and services used in this work were provided by VSC (Flemish Supercomputer Center), funded by Ghent University, FWO, and the Flemish Government department EWI.
References
1
2
3
4
5
6
7
8
9
10
11
12
13
13
14
15
18
19
20
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
38
39
39
40
41
42
43
44
45
48
49
49
50
51
52
53
54
55
 Quantifying the Likelihood of Structural Models through a Dynamically Enhanced Powder X‐Ray Diffraction Protocol
Quantifying the Likelihood of Structural Models through a Dynamically Enhanced Powder X‐Ray Diffraction Protocol