
- Altmetric
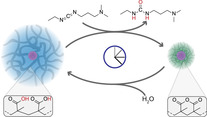
Microgels are soft colloids that show responsive behavior and are easy to functionalize for applications. They are considered key components for future smart colloidal material systems. However, so far microgel systems have almost exclusively been studied in classical responsive switching settings using external triggers, while internally organized, autonomous control mechanisms as found in supramolecular chemistry and DNA nanotechnology relying on fuel‐driven out‐of‐equilibrium concepts have not been implemented into microgel systems. Here, we introduce chemically fueled transient volume phase transitions (VPTs) for poly(methacrylic acid) (PMAA) microgels, where the collapsed hydrophobic state can be programmed using the fuel concentration in a cyclic reaction network. We discuss details of the system behavior as a function of pH and fuel amount, unravel kinetically trapped regions and showcase transient encapsulation and time‐programmed release as a first application.
Moving past classical passive responsive behavior, transient volume phase transitions of poly(methacrylic acid) microgels can be achieved through the use of a chemical fuel. The deswelling creates a transient hydrophobic environment with a lifetime tunable via pH and fuel concentration with possible applications for encapsulation/release.
Introduction
Microgels are a unique class of colloids, consisting of a lightly crosslinked polymer network that swells in water. A key feature of microgels is their ability to reversibly swell and deswell in response to external stimuli such as temperature, [1] pressure, [2] light, [3] presence of ions, [4] or pH, [5] in a process which is commonly referred to as volume phase transition (VPT). This responsive nature enables a wide range of applications, including sensing, [5] photonics [6] and drug delivery. [7] Crucially, so far most microgels systems undergo VPT in a purely responsive manner at or near thermodynamic equilibrium using sequential application of external triggers.
In contrast, biological systems operate out‐of‐equilibrium through the constant input of energy in the form of chemical fuels, which allows for autonomous spatiotemporal control over structures and functionality. [8] In a step towards increasingly autonomous and complex systems, the fields of supramolecular chemistry and DNA nanotechnology have developed a multitude of concepts to enable self‐assembly processes out‐of‐equilibrium by coupling them to chemical reaction networks (CRNs). [8] There are two fundamentally different approaches to realize chemically fueled systems—the activation of the environment surrounding the building blocks and direct activation of the building blocks themselves. [8] Activation of the environment—such as transient pH changes [9] —is very versatile in that it is applicable to the wide array of classical responsive systems that are already available, but often this requires biological components such as enzymes and it is relatively limited in terms of activation/deactivation dynamics since it simultaneously activates all responsive units. In contrast, strategies involving the direct activation of the responsive sites by the CRN require delicate design of the activation and deactivation chemistry, but also offer the potential to have competing activation and deactivation reactions taking place at the same time. [8] While several chemically fueled systems involving polymers as building blocks have been reported, the use of chemical fuels acting directly on polymeric building blocks is still in its infancy, mostly focusing on linear block copolymers.[ 9a , 10 ] Notable exceptions in the field of microgels are the pioneering works using the well‐known oscillating Belusov–Zhabotinsky reaction to enable oscillating swelling/deswelling as well as flocculation/redispersion of PNIPAAm (poly(N‐isopropylacrylamide)) microgels. [11] However, oscillating reactions in closed reactors are poorly tunable and even more difficult to design, [8] and their oscillating nature may be less desirable for applications than a transient, highly programmable change in properties. Strategies for chemical fueling in supramolecular chemistry often rely on the manipulation of charges in the form of carboxylate ions through esterification [12] or anhydride formation, [13] making them inherently compatible with polyacid microgels.
Herein, we report the transient VPT of poly(methacrylic acid) (PMAA) microgels fueled by N‐Ethyl‐N′‐(3‐dimethylaminopropyl)carbodiimide (EDC). Upon its addition, EDC enables two neighboring carboxylic acid groups to form a six‐membered cyclic carboxylic anhydride, while also producing waste in the form of the EDC‐urea (EDU) (Scheme 1 a). Concurrently, hydrolysis of the formed anhydride moieties occurs, and a cyclic CRN develops in balance of EDC‐mediated anhydride formation and water‐induced hydrolysis. We show how the EDC concentration and the pH can be used to tune the lifetime of the fueled, collapsed state (fueling mode I; Scheme 1 b). Moreover, we find that at larger EDC excess, and thus degree of anhydride formation, the microgels aggregate due to reduced electrostatic and steric stabilization, constituting the second fueling mode II (Scheme 1 c). We rationalize the occurring changes by calculations of octanol/water partition coefficients (logP) as a function of the anhydride to gain additional insight into the hydrophobic environments created by the fueling process. Finally, we showcase transient encapsulation of a dye model compound, Nile Red, as a first mimic for time‐programmed encapsulation.

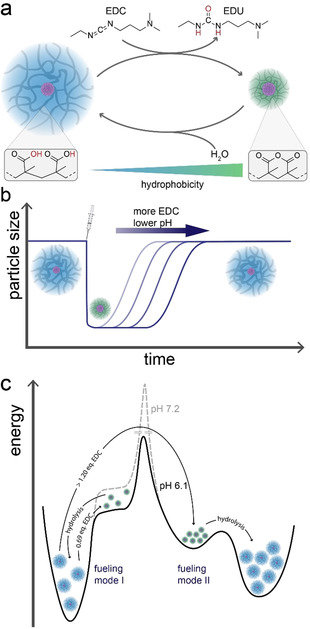
EDC‐fueled, transient deswelling of poly(methacrylic acid) microgels. a) Scheme for the underlying CRN. Upon the addition of EDC, neighboring carboxylic acid groups form cyclic anhydrides, leading to deswelling of the microgels. Following the hydrolysis of the anhydride moieties, the hydrogels swell again. b) Transient size profile of the microgels during the fueling process. c) Energy landscape of fuel‐induced volume phase transition (fueling mode I) and aggregation of particles (fueling mode II).
Results and Discussion
Microgel Synthesis
As a prerequisite, the PMAA microgels should be uniform and narrowly dispersed for accurate analysis of the particle size with dynamic light scattering (DLS), as well as sufficiently large in size at neutral pH in both the swollen and deswollen state to facilitate imaging using confocal laser scanning microscopy (CLSM). We previously reported the synthesis of narrowly dispersed, crosslinked PMAA microgels via emulsion polymerization of t‐butyl methacrylate (tBMA) and divinyl benzene (DVB), and subsequent acidic cleavage of the t‐butyl ester. [14] While this approach offers a high tunability of submicron particles regarding size by changing the surfactant concentration and swelling via adjusting the degree of crosslinking, it is not suited for the synthesis of microgels with micrometer size at neutral pH. As a remedy, we developed a two‐step protocol for the synthesis of larger PMAA microgels featuring a hydrophobic PTFEMA (poly(2,2,2‐trifluoroethyl methacrylate)) core, followed by a shell synthesis of PtBMA as a PMAA precursor and subsequent hydrolysis. PTFEMA is refractive‐index matched to water and provides negligible van der Waals interactions in aqueous dispersions. In more detail, the first step consists of the surfactant free emulsion polymerization (SFEP) of TFEMA and divinyl benzene (DVB; 1 mol %) using potassium persulfate (KPS) as the initiator, followed by the addition of tBMA and DVB (1 mol %) in a one‐pot process (Figure 1 a). Transmission electron microscopy (TEM) (Figure 1 b,c) reveals uniform, narrowly dispersed particles for both the core and core–shell lattices with radii of R TEM,n=77±7 and 174±14 nm, respectively, as determined by statistical image analysis. Consistently, cumulant analysis in DLS gives z‐averaged hydrodynamic radii R H,z=80 nm and R H,z=206 nm for the core and core–shell particles, respectively, with narrow size distributions as evidenced by CONTIN analysis (Figure 1 d). In the second step, acidic cleavage of the tBu esters gives the desired PMAA microgels with a fluorinated PTFEMA core. At pH 6.1 and 7.2 (10 mM MES or MOPS buffer, respectively, 0.2 g L−1 particles)—the conditions relevant for the fueling experiments—the microgels swell significantly, as evidenced in DLS with R H,z=568 nm and 592 nm, respectively. Cryogenic transmission electron microscopy (cryo‐TEM) of the core–shell microgels at pH 6.1 shows a high‐contrast core with R≈100 nm, surrounded by a low‐contrast shell (Figure 2 c). Notably, the core is larger than the size of the PTFEMA‐core (R TEM,n=77±7 nm). This can however easily be rationalized by the faster incorporation of DVB during the polymerization of the shell, [14] which leads to a higher degree of crosslinking in the proximity of the PTFEMA core and thus less swelling of the microgel shell attached to the core. Additionally, cross‐sectional gray scale analysis finds overall particle diameters of approximately 2200 nm (Figure 2 e), much larger than the size measured by DLS (R H,z=568 nm). While cryo‐TEM offers a good way to investigate the structure of the microgels in their native solution state, one needs to keep in mind that the vitrified ice layer confining the microgels is much thinner than the particle diameter. Due to their inherent softness, the microgels adapt to a more oblate structure.

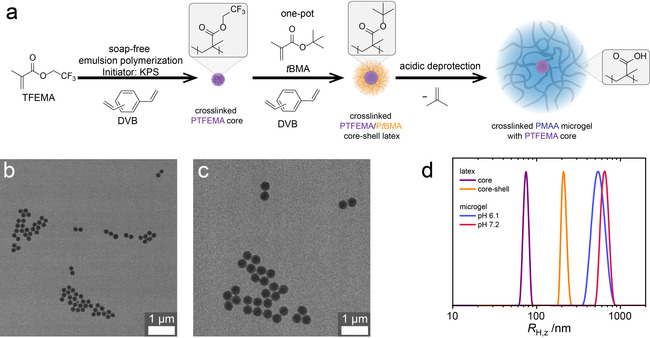
Synthesis of crosslinked PMAA microgels with a PTFEMA core. a) Two‐step approach: featuring the one‐pot soap‐free emulsion polymerization of TFEMA and tBMA using DVB as the crosslinker, followed by acidic cleavage of the t‐butyl ester. b, c) TEM images of the PTFEMA cores and PTFEMA/PtBMA core–shell latex, respectively. d) Size distributions obtained from DLS CONTIN analysis of PTFEMA core, PTFEMA/PtBMA core–shell latices and PMAA/PTFEMA core–shell microgels (10 mM buffer, 0.2 g L−1 particles).

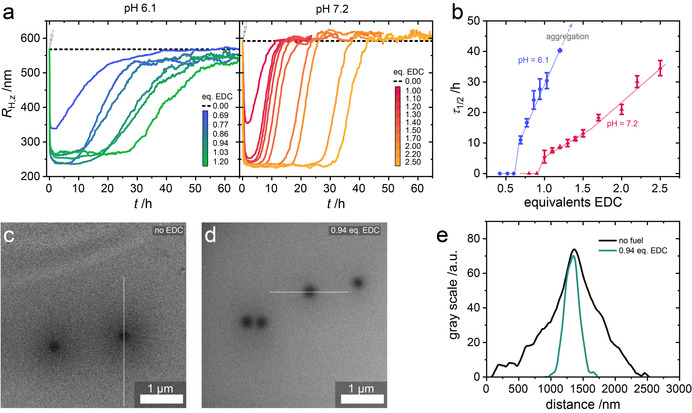
EDC fueling of PMAA microgels. a) Temporal evolution of hydrodynamic radii R H,z obtained from DLS after the addition of EDC at pH 6.1 and pH 7.2. b) Lifetimes τ 1/2 of the deswelling profiles in (a). Error bars represent the standard deviation of three experiments, lines are drawn to guide the eye. c,d) Cryo‐TEM images of the microgels at pH 6.1 in the absence of EDC, and 2 h after the addition of 0.94 equiv. EDC, respectively. e) Gray‐scale analysis of the cross‐sectional profiles indicated in c and d.
Conductometric and potentiometric titration of the core–shell microgels revealed a carboxylic acid content of 83 wt % with an apparent pK a=7.56 (see Supporting Information, Figure S1a). The observed pK a is in line with findings for bulk PMAA gels, [15] and corresponds to 3.4 % (pH 6.1) and 30 % (pH 7.2) dissociation of carboxylic acid groups based on a naïve Henderson‐Hasselbalch approach. It should be noted, however, that for weak polyelectrolyte networks such as the PMAA microgels, dissociation depends on the complex balance of electrostatic interaction, conformation, swelling, and the local distribution of counter‐ and co‐ions. As a result, the actual degree of dissociation can differ from that based on the theory governing small molecules, and significant differences between measured (global) and local pH of up to two pH‐units can occur. [16]
The pH‐dependent swelling of the microgels reflects the complex dissociation behavior of the weak polyelectrolyte network: Above pH 6, the microgels are fully swollen to just below R H,z≈600 nm, further swelling likely being limited by the crosslinking (see Supporting Information, Figure S1b). Below pH 6, the microgels steadily deswell to R H,z≈260 nm at pH 3.2, with significant deswelling occurring in the regime more than two pH units below the pK a, where protonation of the carboxylic acids is quasi‐quantitative. Notwithstanding the inevitable inaccuracies of the pK a determination, general trends based on the influence of degree of dissociation and pH are reasonably expected to remain unaffected.
EDC‐Fueled Volume Phase Transition
While classical approaches towards investigating responsiveness in microgels use acid/base titration or ionic strength effects to change the volume phase behavior of microgles, we herein introduce the coupling to a cyclic CRN that will give rise to autonomous behavior due to the fuel consumption. The chemical fueling process in our system transduces across two main length scales: On a molecular level, the CRN changes the chemical composition of the polymer by transient hydrophobization via anhydride formation, which in course triggers the microgel response on the polymer network level. In contrast to fueled systems of small molecules, established techniques such as time‐resolved 1H‐NMR spectroscopy and HPLC are not suited for the determination of anhydride concentrations in the microgels.[ 13 , 17 ] These analytical limitations are detrimental to the molecular level characterization of the CRN, making analytics on the colloidal level the tools‐of‐choice for the investigation of our system.
In typical EDC‐fueled systems, the kinetic asymmetry between fast anhydride formation and slower hydrolysis leads to the transient buildup of anhydride in the system.[ 13 , 17 ] The maximum molar fraction of the starting material converted to anhydride that is reached depends on the ratio of the rate constants for the activation and deactivation reaction, as well as the amount of EDC present in the system: large kinetic asymmetry and high concentrations of EDC lead to high maximum anhydride conversion. The formation of poly(methacrylic anhydride) from PMAA upon treatment with carbodiimides such as DCC (N,N′‐dicyclohexyl carbodiimide) is well‐known, albeit not in the context of chemically fueled systems. [18] Similar to other polymer analogous reactions involving two neighboring functional groups, the statistical limit for anhydride formation is 83 %, [18] assuming that transacylation reactions that would allow the cyclic anhydride to move along the polymer backbone, do not occur. Experimentally, slightly lower values of 80 % have been found for linear, syndiotactic PMAA. [18] Given the presence of 1 mol % crosslinkers in the PMAA microgels, we expect a limit for maximum anhydride conversion slightly lower than the theoretical one.
To investigate the fueling of the PMAA microgels in dependence of the amount of added EDC, we conducted fueling experiments in 10 mM aqueous buffer (MES and MOPS for pH 6.1 and 7.2, respectively) with microgel concentrations of 0.2 g L−1 which corresponds to a carboxylic acid concentration of 1.92 mM. Since two carboxylic acid moieties react with one fuel molecule, 1.00 equiv. EDC is equivalent to an initial fuel concentration of 0.96 mM. One however needs to keep in mind that for statistical reasons only a maximum PMAA group conversion of below 80 % is possible.
At pH 6.1, upon the addition of 0.69 equiv. EDC, the microgel radius decreases from R H,z=568 nm to R H,z=324 nm within less than 1 h, followed by a full recovery of the initial size over the course of 30 h (Figure 2 a). This stark difference in activation and deactivation time scales reflects the kinetic asymmetry of the EDC chemistry, but is also affected by the swelling and deswelling kinetics of the polymer network. Interestingly, the addition of less than 0.69 equiv. EDC does not lead to a change in size. This indicates the existence of a critical degree of anhydride formation, above which the microgel network undergoes a VPT (Figure 2 b).
Since anhydride formation and hydrolysis are concurrent reactions, not all 0.69 equiv. EDC first form anhydrides which are subsequently hydrolyzed, but the cyclic CRN limits the amount of actually present maximum anhydride fraction. More pronounced deswelling to minimum radii between R H,z≈240—R H,z≈270 nm takes place upon the addition of greater than 0.77 equiv. EDC (as probed up to 1.20 equiv EDC; Figure 2 a). The absence of a further correlation between the minimum radius and amount of fuel indicates that the system enters quasi‐steady states in closed systems where the cyclic CRN operates with concurrent activation and deactivation. In good agreement with DLS, cryo‐TEM analysis of microgels 2 h after the addition of 0.94 equiv. EDC reveals homogeneous particles (Figure 2 d), with a diameter of approximately 500 nm as evidenced by cross‐sectional gray‐scale analysis (Figure 2 e). The lifetime τ 1/2 of the deswollen state—defined as the time after which half of the fuel‐induced decrease in R H,z is recovered—increases linearly with the amount of fuel from τ 1/2=11±1 h at 0.69 equiv. EDC to τ 1/2=28±3 h at 1.20 equiv. EDC (Figure 2 c).
Notably, the speed at which the microgels reswell—given by the slope of the size‐profile after the minimum—is very similar for all EDC concentrations and can be interpreted as an apparent hydrolysis rate, assuming that hydrolysis of the anhydride is rate‐determining for the reswelling process. The increase in lifetime with increasing amount of added EDC is therefore largely a result of the longer plateau time spent in the fully deswollen state. The hydrolysis of anhydride typically is a pseudo‐first order reaction that only depends on the anhydride concentration. [13a] The hydrolysis of anhydride when all the EDC is consumed should thus follow exponential decay, which does not account for a linear increase of τ 1/2 with the amount of added EDC. However, in the presence of excess EDC, when all available carboxylic acids are converted to anhydride, the rates of anhydride formation and EDC consumption are limited by the hydrolysis of anhydride. As the anhydride formation is faster than hydrolysis, the anhydride concentration will be in a steady‐state close to the maximum conversion of approximately 80 % which in turns leads to pseudo‐zero‐order consumption of EDC. We therefore reason that the linear increase in τ 1/2 between 0.77–1.20 equiv. EDC is a result of steady‐state‐limited, zero‐order consumption of EDC. Additionally, similar hydrolysis speeds for all EDC concentrations suggest that the addition of larger amounts of EDC does not introduce significant negative feedback for the hydrolysis of the anhydride. Such negative feedback was reported for the self‐assembly of small molecule building blocks fueled by EDC, and was a result of the creation of hydrophobic barriers shielding the anhydride from water. [13a] The absence of negative feedback in our system is easily rationalized by comparing the size of the PtBMA core–shell lattices before removal of the t‐butyl ester (R H,z=206 nm) to the fueled state of the core–shell PMAA microgels (R H,z≈245 nm). Taking into consideration that roughly 40 % of the PtBMA shell mass is lost in the ester cleavage step, it becomes evident that the microgels still contain considerable amounts of water when fueled, which ensures the hydrolysis of the anhydride.
To elucidate the influence of pH on the fueling process, we performed further experiments at pH 7.2. In analogy to pH 6.1, a critical excess of EDC is necessary to induce the VPT. Upon the addition of 1.00 equiv. EDC, transient deswelling occurs from R H,z=592 nm to R H,z=342 nm (Figure 2 a). With increasing amount of added EDC, the minimum radius that is reached decreases until it plateaus at R H,z=230 nm at 1.50 equiv. EDC. In this regime, the lifetime τ 1/2 increases linearly with EDC concentration from to τ 1/2=6±2 h at 1.00 equiv. EDC to τ 1/2=13±1 h at 1.50 equiv. EDC (Figure 2 c). Notably, at comparable EDC concentrations, τ 1/2 is smaller by a factor of ≈5 than at pH 6.1 and increases more slowly with fuel concentration. When more than 1.50 equiv. of fuel is present, and the deswelling plateaus, τ 1/2 increases faster, but still approximately linearly with increasing fuel concentration. Applying the same arguments as for pH 6.1, we identify the regime above 1.50 equiv. EDC as a steady‐state of quasi‐quantitative anhydride formation, which is not reached between 1.00 equiv. and 1.50 equiv. EDC. The larger amount of EDC necessary to induce the VPT, as well as the shorter lifetimes of the fueled state compared to pH 6.1 are direct consequences of the increase in pH. Mechanistic studies on the reaction of EDC with nucleophiles in aqueous media have shown a decrease in reactivity and thus slower anhydride formation with increasing pH.[ 17 , 19 ] Simultaneously, polymers bearing cyclic anhydrides attached to their backbone undergo anhydride hydrolysis faster at higher pH. [20] The combination of slower activation and faster deactivation of the fueled state leads to a less effective buildup of anhydride, thus requiring larger amounts of fuel to reach comparable degrees of anhydride formation.
Microgel Aggregation and Pathway Complexity
At pH 6.1, but not pH 7.2, a critical transition into fueling mode II occurs when more than 1.20 equiv. of EDC is added. The microgels aggregate and sediment over the course of a few hours, prohibiting further characterization via light scattering (Figure 3 b).

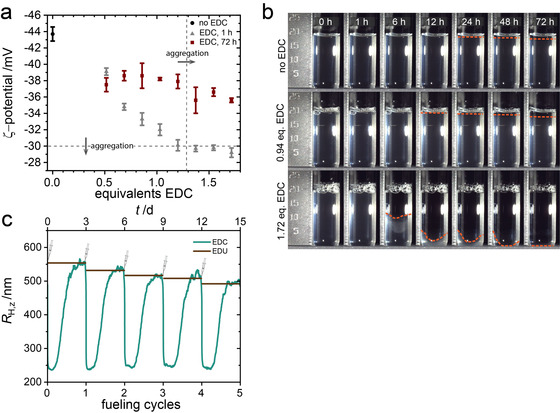
Aggregation (fueling mode II) and refueling of PMAA microgels. a) ζ‐potential of microgels 1 h and 3 d after the addition of EDC (pH 6.1). Error bars represent the standard deviation of three ζ‐potential measurements. The horizontal dashed line indicates the general colloidal stability limit of |ζ‐potential| > 30 mV; the dashed vertical line represents aggregation of the microgels when an excess >1.20 equiv. EDC is added. b) Time series of microgel dispersions (pH 6.1) in the absence of EDC, and after the addition of 0.94 and 1.72 equiv. EDC. c) Temporal evolution of hydrodynamic radii at pH 6.1 for the repeated addition of 0.94 equiv. EDC and influence of the addition of the amount of EDU waste product.
In the unfueled state, because of their large degree of swelling, the microgels are nearly refractive index‐matched, resulting in low vdW‐attraction. Additionally, they are sterically stabilized through dangling chains, as well as electrostatically stabilized by carboxylate and initiator‐derived sulfate groups. The aggregation in the fueled state can be understood as a combination of increased attraction and reduced stabilization. Upon the addition of EDC, vdW‐attraction between the particles increases as the deswelling increases the refractive index mismatch. Additionally, the dangling chains become insoluble and collapse, reducing colloidal stabilization of the deswollen microgels. Finally, the addition of fuel also reduces electrostatic stabilization, as evidenced by ζ‐potential measurements. Before the addition of fuel, the colloids are stabilized well, as indicated by a ζ‐potential of −44 mV (Figure 3 a). In the fueled state (1 h after EDC addition), the ζ‐potential increases steadily with increasing amount of added fuel, up to −30 mV at 1.20 equiv. EDC, before passing the general stability limit for hard colloids (|ζ‐potential| > 30 mV). [21] The increase in ζ‐potential upon the addition of EDC is a direct result of anhydride formation, which reduces the number of available negatively charged carboxylate moieties stabilizing the particles. With increasing EDC concentration, the anhydride conversion in the steady‐state is pushed closer towards the statistical limit, contributing to both decreased electrostatic and steric stabilization.
After completion of the fueling cycle, the ζ‐potential partially recovers to ≈−38 mV, but never reaches the value before the addition of EDC. From control experiments, where we prepared the final composition of the system after completion of the fueling process by directly adding EDU (the EDC‐derived urea), it becomes obvious that this is largely a result of the EDU waste product (see Supporting Information; Figure S2). In general, waste accumulation is a critical challenge in chemically fueled systems, limiting reusability as well as hampering their efficiency. [23] Five consecutive additions of 0.94 equiv. EDC at pH 6.1 show good stability and repeatability of the fueling process. In line with the effects of waste accumulation on the ζ‐potential, the R H,z of the swollen equilibrium state decreases from initially R H,z=568 nm to R H,z=492 nm after five cycles (Figure 3 c). Again, reference experiments using direct waste addition mirror the damping effect in the equilibrium size without going through the fuel cycles (brown line, Figure 3 c). Interestingly, the fact that the addition of a total of 4.70 equiv. EDC in 0.94 equiv. steps induces no aggregation of the microgels, whereas the addition of >1.20 equiv. at once does, constitutes pathway complexity similar to what has been shown for the aggregation of inorganic nanoparticles. [22]
Transient Encapsulation in Hydrophobic Environments
To gain further insight into the nature of the hydrophobic environment created in the fueling process, we calculated changes in hydrophobicity using surface‐area‐normalized octanol/water partition coefficients (logP/SA) (Figure 4 b). These logP/SA values encompass a thermodynamic perspective (i.e. logP) inspired by medicinal chemistry efforts to characterize drug‐like molecules combined with conformational insight via Molecular Dynamics (MD) simulations to apprehend the optimal surface area (SA). [23] Additionally, as suggested by the length scale concept in Lum‐Chandler‐Weeks theory, molecular models were large enough in order that hydrophobicity scaled with SA rather than volume. [24] The resulting combination of theory, MD simulations, and experimental validation facilitates characterization for a variety of macromolecular architectures [25] and polymerization methods. [26] Importantly, positive logP/SA values indicate hydrophobic environments while negative values correspond to hydrophilic environments. [23a]

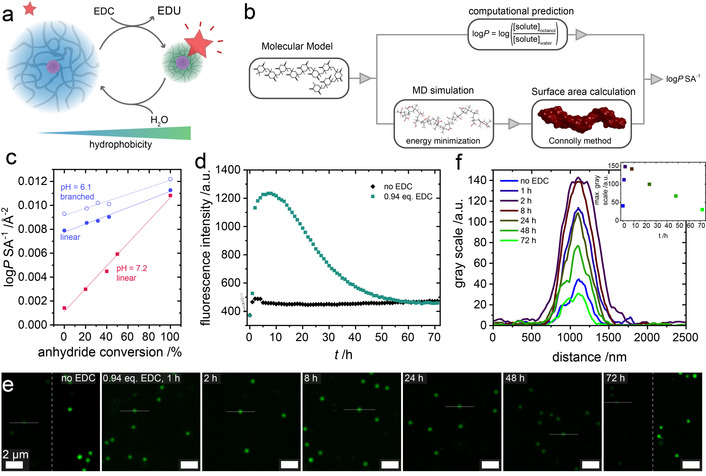
Investigation of hydrophobic environments created in the fueling process. a) Scheme for fueling experiments in the presence of 2.5 μM Nile Red as a solvatochromic probe. b) Flow chart for the calculation of logP/SA values. c) Calculated logP/SA values at pH 6.1 and pH 7.2 depending on anhydride conversion for linear and branched oligomeric models. The lines represent linear regression of the data sets. d) Temporal evolution of fluorescence intensity at λ em=640 nm (λ ex=545 nm) in the absence and upon the addition of 0.94 equiv. EDC at pH 6.1 e) Time series of CLSM images ((λ ex=552 nm) during the fueling process. The right halves of the first and last images (no EDC, 72 h) are contrast‐enhanced for improved visualization of particles. f) Gray‐scale analysis of the cross‐sectional profiles indicated in (e).
Initially, we created a series of oligomeric models to mimic anhydride conversion during EDC‐fueling. Based on the experimentally determined pK a value as well as solution pH, these models contained an appropriate number of ionized carboxylates and represent linear segments (see Supporting Information, Scheme S1) within the microgels as well as branch points (see Supporting Information, Scheme S2–5) where DVB units crosslink the microgels. As such, models for linear segments indicate that the overall degree of hydrophobicity increases linearly as a function of anhydride formation at both pH 6.1 and 7.2 (Figure 4 c). At pH 7.2, hydrophobicity is overall lower, but increases more strongly with increasing anhydride conversion. Notably, logP/SA values are close to zero, yet still positive even in the absence of anhydride groups, suggesting a relatively hydrophobic environment within the microgels. In comparison, branched models indicate DVB locally increases hydrophobicity in proximity to crosslinks, which in turn requires the vicinity surrounding ionized carboxylates to be more hydrophilic. Indeed, analysis of short segments within these oligomeric models demonstrates segments consisting of three and four monomer units could have negative logP/SA values when ionized carboxylates ranged from 50–66 mol % (see Supporting Information, Table S1). We hypothesize these segments with negative logP/SA contribute to swelling and the prevalence of these hydrophilic moieties decreases with increasing conversion as well as decreasing pH. Importantly, the logP/SA calculations are able to qualitatively capture changes in hydrophobicity and thus solubility of chemically fueled polymers. This makes them a promising tool in identifying potential new systems and predicting trends in parameter space.
Next, we conducted fueling experiments in the presence of 2.5 μM Nile Red (NR) to track the changes in hydrophobicity during the fueling process experimentally and identify whether a transient encapsulation of hydrophobic molecules for EDC programmed release could be achieved (Figure 4 a). NR is a strongly solvatochromic dye which exhibits a blue‐shift of its absorption and emission maxima, as well as a pronounced increase in fluorescence with increasing hydrophobicity of the environment. [27] In the absence of EDC, the fluorescence intensity of NR increases slightly over the course of 5 h in presence of the microgels, which we attribute to slight uptake of the poorly water‐soluble dye (Figure 4 d). However, the behavior is drastically different when adding 0.94 equiv. EDC to a NR‐containing microgel dispersion at pH 6.1. Here, the fluorescence intensity increases by a factor of ≈3, reaching a maximum after 8 h, before decaying to a value slightly above the initial intensity within 72 h (Figure 4 d). This transient increase in fluorescence intensity arises from the formation of increasingly hydrophobic environment within the microgels in their deswollen state. Increased NR fluorescence and deswelling are closely linked as indicated by the half‐life—defined as the time after which half of the increase in fluorescence intensity has subsided—of 25 h which is very similar to the half‐life τ 1/2=28 h measured by DLS at identical conditions. Confocal laser scanning microscopy (CLSM) of the NR containing microgel dispersions corroborates the fluorescence spectroscopy findings. In the absence of fuel, the fluorescence is very weak and mainly located in an area corresponding to the PTFEMA‐core and its densely crosslinked vicinity (Figure 4 e). During the fueling cycle, a marked increase in the microgel fluorescence occurs and is followed by slower a decrease. Cross‐sectional analysis of single particle fluorescence intensity reveals a temporal evolution of maximum fluorescence intensity that mirrors the ensemble‐based time profile obtained via fluorescence spectroscopy (Figure 4 f).
Conclusion
In summary, we introduced the first example of chemically fueled VPT in microgel systems, where the non‐equilibrium collapsed state can be induced, maintained and controlled by the availability and transduction kinetics of a chemical fuel. We demonstrated this concept for EDC‐fueled, transient VPT of PMAA microgels, that exploits transient transformation of hydrophilic carboxylic acids into hydrophobic intramolecular anhydrides in the polymer network using a cyclic CRN. The lifetimes of the fueled state are in the range of hours, and are tunable over almost one order of magnitude by variation of the amount of added fuel as well as pH. In contrast to supramolecular systems, no significant negative feedback for the deactivation of the fueled state is observed, and the fueling cycle shows good tolerance towards waste accumulation, allowing use for several cycles. In a second fueling mode, following their double nature as polymer networks and colloids, the PMAA microgels aggregate at high fuel concentration, due to suppression of surface charges, increased vdW attraction and reduced steric stabilization. We rationalized the behavior using hydrophilicity/hydrophobicity calculations based on logP values, that can give guidance for future chemically fueled polymer systems. The chemical fueling strategy offers potential for novel strategies to orchestrate hierarchical self‐assembly of building blocks by transient reduction of (surface) charges, or reduction of hydrophilicity.
While we showcased transient encapsulation of hydrophobic solvatochromic dyes as model systems for programmed release applications, we wish to point to a distinct challenge in future applications. Moving from microgel dispersions presented in this manuscript to true bulk polymer networks is an outstanding challenge for future applications, as it requires the addition of large amounts of fuel, leading to issues with homogenization, salting out, and waste accumulation. The development of strategies that allow for significant changes in material or functional properties, but require only small amounts of fuel will therefore be paramount. Similar to classic responsive polymer systems, this may be achieved by careful choice and combination of fuel‐responsive monomers with unresponsive comonomers, which highlight a significant challenge for polymer science.
Conflict of interest
The authors declare no conflict of interest.
Acknowledgements
This work was supported by the DFG under project WA3084/4‐2. This work made use of the microscopy facilities provided through the Core Facility Imaging of Materials Systems at the FIT, Freiburg University, Germany. RTM thanks the Penn State Institute of CyberScience and the Penn State Materials Research Institute for providing access to Materials Studio 2019. Open access funding enabled and organized by Projekt DEAL.
References
1
2
3
5
6
6
7
9
9b
9b
10
10a
10b
10c
11
11a
11c
11d
12
12
13
13a
15
17
18
19
20
21
22
23
23a
23b
24
24b
25
25a
25b
25c
26
26a
26a
26b
27
 Chemically Fueled Volume Phase Transition of Polyacid Microgels
Chemically Fueled Volume Phase Transition of Polyacid Microgels
