
- Altmetric
The recent discoveries of strikingly large zero-field Hall and Nernst effects in antiferromagnets Mn3X (X = Sn, Ge) have brought the study of magnetic topological states to the forefront of condensed matter research and technological innovation. These effects are considered fingerprints of Weyl nodes residing near the Fermi energy, promoting Mn3X (X = Sn, Ge) as a fascinating platform to explore the elusive magnetic Weyl fermions. In this review, we provide recent updates on the insights drawn from experimental and theoretical studies of Mn3X (X = Sn, Ge) by combining previous reports with our new, comprehensive set of transport measurements of high-quality Mn3Sn and Mn3Ge single crystals. In particular, we report magnetotransport signatures specific to chiral anomalies in Mn3Ge and planar Hall effect in Mn3Sn, which have not yet been found in earlier studies. The results summarized here indicate the essential role of magnetic Weyl fermions in producing the large transverse responses in the absence of magnetization.
The large anomalous Hall (AHE) and anomalous Nernst effects (ANE) in antiferromagnets Mn3Sn/Mn3Ge are considered fingerprints of Weyl nodes residing near the Fermi energy. Here, the authors review the results from previous studies combining with new transport measurements on Mn3Sn/Mn3Ge single crystals, suggesting the essential role of magnetic Weyl fermions in explaining the AHE and ANE.
Introduction
In the field of quantum materials, topology—a mathematical concept that describes the robustness of form—has inspired a new era by introducing novel topological phases of matter1–3. Until recently, most of the associated discoveries take place in weakly interacting materials in which electron correlation effects have only a minor role. Now the hunt for new topological phases is shifting toward strongly correlated electron systems. The notion of strong electronic correlation provides a common thread linking a wide variety of fascinating emergent phenomena in quantum materials, ranging from high-Tc superconductivity to fractional quantum Hall effect. Its convergence with topology affords an exceptional venue to explore topological order in magnetism. A key discovery along this direction is the surprisingly large anomalous Hall effect (AHE) in chiral antiferromagnets4–6, which has triggered extensive research efforts in various fields, ranging from topological condensed-matter physics, spintronics, and energy harvesting technology7–16. A serious challenge facing condensed-matter and material physicists is revolutionizing information technology that breaks through the fundamental limit of Moore’s law, namely, developing strategies that enhance the processing speed and energy efficiency simultaneously. With this regard, spintronics has provided cutting-edge technologies, introducing nonvolatile forms of logic and memory devices. Traditionally focused on ferromagnetic (FM) materials, recent studies have revealed further benefits using antiferromagnets: antiferromagnets possess ultrafast dynamics and are insensitive to stray fields that perturb neighboring cells, allowing them to exceed the capacity of the FM counterparts17,18. Thus, the large AHE in antiferromagnets observed at room temperature may serve as a readout for a spintronic device1,16–18. Another remarkable discovery is the substantial anomalous Nernst effect (ANE) accompanying the large AHE without net magnetization9,13,15,19. This feature indicates that the control of Berry curvature is essential for enhancing the transverse thermoelectric effect, which has inspired new development in thermoelectric converters9,20–23.
Understanding of the mechanism behind the unusually large AHE and ANE in antiferromagnets serve as the basis for their application in modern technologies; this is where the novel topological quasiparticles—Weyl fermions—come into play. In a metallic or semimetallic material, the double electronic band degeneracy enforced by the Kramers theorem is lifted with the breaking of either time-reversal or spatial inversion symmetry (IS). The linearly dispersing touching points of two nondegenerate bands are known as Weyl nodes, around which the Weyl Hamiltonian describes the electronic states24,25. According to the dimensionality of the electronic band touching, the topological states can be classified into topological insulators, nodal points, and nodal lines; the Weyl node is a typical example of the nodal point. In this case, the emergent quasiparticle represents a condensed-matter physics analog of the long-anticipated relativistic Weyl fermion that remains unobserved in high-energy physics experiments. The Weyl nodes carry quantized magnetic charges that act as a source or drain of Berry curvature24. The Berry curvature can be regarded as a fictitious magnetic field in momentum space, as it behaves in the same manner as a real magnetic field under symmetry operations26,27. In contrast with Dirac fermions in graphene, the Weyl node is a three-dimensional object; namely, the corresponding Weyl Hamiltonian involves all three Pauli matrices that form the basis of the Hilbert space. As a result, any perturbation in the form of a linear superposition of the Pauli matrices cannot annihilate the Weyl points but merely shift its position in momentum space. The magnetic charge is protected as in the Gauss’s law for an electronic charge in real space. This topological protection of Weyl nodes against perturbation renders them appealing potential sources of real-life applications.
The Weyl semimetal (WSM) state occurs in two situations, requiring either a broken time-reversal symmetry (TRS) or a broken spatial IS; the latter has been established in weakly interacting electron systems with spectroscopic evidence of Weyl fermions. The experimental quest for a TRS-breaking WSM is far more challenging, yet it features advantageous properties from both fundamental and practical standpoints. The TRS-breaking or magnetic WSM provides the possibility of realizing a model system that exhibits macroscopic spontaneous responses due to Weyl fermions in zero field, which are absent in the IS-breaking WSM. For instance, the substantial net Berry curvature inherent to the Weyl nodes, combined with the magnetism, may yield unusually large anomalous transport and optical properties in TRS-breaking WSMs. Moreover, the magnetic texture provides a handle for manipulating the Weyl fermions4,5,8,28, making the magnetic WSMs particularly attractive in spintronic applications16.
In noncollinear antiferromagnets, the combination of the symmetry of the spin structure and the underlying band topology allows for the realization of a TRS-breaking WSM8,28,29. When the Weyl nodes reside close to the Fermi energy, they may manifest through large intrinsic AHE and ANE due to the significant enhancement in the Berry curvature. In fact, in addition to the chiral anomaly in magnetotransport, the observation of AHE and ANE in antiferromagnets has provided first crucial experimental signatures of magnetic Weyl fermions8. Here, we provide an overview of transport measurements in chiral antiferromagnet Mn3X (X = Sn, Ge) that features unusually large AHE and ANE. Combined with spectroscopic studies and first-principles calculations, the comprehensive set of transport signatures in Mn3X (X = Sn, Ge) serves as an effective probe of magnetic Weyl fermions, paving an important avenue for future identification of the WSM state in strongly correlated materials.
Basic properties of Mn3X (X = Sn, Ge)
Kagome-based metals have recently become a new focus in the field of quantum materials for their topological electronic structures, as well as large electromagnetic and transport responses4–6,9,11,12,15,23,30,31. Mn3Sn and Mn3Ge are hexagonal chiral antiferromagnets (space group P63/mmc) that comprise breathing-type kagome layers of Mn atoms in the ab-plane (Fig. 1a); these kagome planes are stacked along the c-axis32. Neutron diffraction studies in the magnetically ordered phase revealed an inverse triangular spin structure, in which Mn moments are aligned within the kagome layers, forming a 120° ordering with a negative vector chirality and a q = 0 ordering wave vector; the ordered moment is about 3 μB/Mn (μB, Bohr magneton) in Mn3Sn and about 2.5 μB/Mn in Mn3Ge33–36. This chiral spin structure reduces the hexagonal crystal structure to orthorhombic in both compounds. Within each triangular motif, only one of the three Mn moments points along the local easy axis (

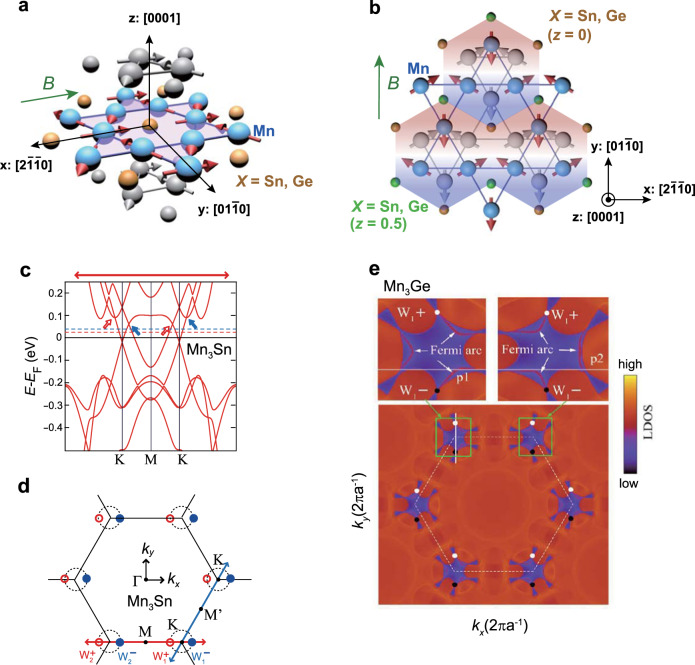
Magnetic structure and theoretically predicted Weyl points of Mn3X (X = Sn, Ge).
a Crystal structure of Mn3X (X = Sn, Ge) and the spin texture under a magnetic field applied along the
The Mn moments residing on an octahedron made of two triangles of neighboring kagome bilayers constitute a cluster magnetic octupole; the inverse triangular spin structure can be viewed as a ferroic order of cluster magnetic octupoles (Fig. 1b)7,44,45. Mn3Sn serves as a textbook example for the developing cluster multipole (CMP) theory, which identifies the symmetry equivalence of noncolinear AFM spin structures with FM states by considering CMP as the order parameter of noncollinear AFM orders44,45. The large magneto-optical Kerr effect has been discovered in Mn3Sn as the first example in the AFM metal and enables visualization of the magnetic octupole domains and their switching under an applied magnetic field7. The interplay between CMP in real-space magnetic domains and the Weyl points in momentum space may yield intriguing topological electric transport that remains to be explored46.
Below the Néel temperature TN ≈ 430 K, Mn3Sn enters the inverse triangular spin state, which is taken over by helical ordering and a cluster glass phase at low temperatures4,9,34,43,47–49, depending on the Mn concentration. In contrast, Mn3Ge retains the inverse triangular spin structure down to at least 0.3 K, as is evident from the magnetization M curves of our newly synthesized Mn3Ge single crystals (Fig. 2e): M undergoes a sharp transition at the Néel temperature TN ≈ 372 K, and no additional transition occurs down to 0.3 K. The in-plane magnetization reaches a saturation value of about 7 mμB/Mn at B = 0.1 T and T < 100 K, which is approximately ten times greater than the magnetization for B || [0001].

Observation of large anomalous Hall and Nernst effects in Mn3Sn.
a Field dependence of the Hall resistivity, ρH (B), observed in Mn3.02Sn0.98 at room temperature under magnetic fields
The hexagonal structure of bulk Mn3Sn and Mn3Ge is stable only in excess Mn4,5,33,35, leading to Mn-substituted Sn/Ge sites. The off-stoichiometry is reflected in a short electronic mean free path of the order several nm at room temperature, comparable to the lattice parameters13,19. This compositional disorder may alter the magnetic and anomalous transport properties of the material and deserves detailed studies. We have recently investigated the behavior of Si-doped Mn3Ge crystals and find that Si doping into the Ge sites provides a means for systematically examining how the physical properties evolve with excess Mn. By doping Si into Ge sites, the level of extra Mn x is enhanced concomitantly; the lattice parameters and the unit cell volume exhibit a slight linear decrease with increasing amount of extra Mn. The volume reduction rate dV/dx (=−39 ~ −48Å3/Mn) in Mn3+x(GeSi)1-x is nearly identical to the value found in Mn3+xGe1-x, implying that Si acts merely as an impurity ion at the Ge site. The magnetization of Si-doped Mn3Ge samples shows temperature variation similar to that of undoped Mn3Ge, while the Néel temperature decreases monotonically with increasing amount of Si doping (Fig. 2e, inset).
Observation of anomalous transport in Mn3X (X = Sn, Ge)
Anomalous Hall effect (AHE)
The AHE is traditionally considered to be proportional to net magnetization, and therefore is expected to arise only in FM materials50. In the past decade, theoretical advances in understanding the mechanism of AHE has established that the intrinsic contribution to the anomalous Hall conductivity (AHC) is the sum of the Berry curvature of all the occupied bands26,27,51, such that:
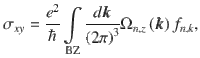
In 2015, the first observation of the large AHE in an antiferromagnet was achieved using the chiral AFMs Mn3X (X = Sn, Ge)4,5. At room temperature, the Hall resistivity ρH of Mn3Sn measured under in-plane magnetic fields
The negligible σxy at high temperatures is in line with the in-plane polarization of the magnetic octupole due to coplanar 120° spin structure, whereas the drastic increase in σxy observed at T < 50 K may involve a topological Hall effect4. For T < 20 K, the Hall measurements in polycrystalline Mn3Sn samples reveal sharp peaks of ρxy (B) at about ±0.8 T, suggesting a topological Hall contribution
In contrast with Mn3Sn, we show that the Hall conductivity σyz of our Mn3Ge single crystals increases on cooling and saturates at ~300 Ω−1 cm−1 below about 100 K (Fig. 2f) owing to the absence of additional magnetic phase transition at low temperatures5,6. Contrary to the FM case, neither of σyz nor σzx follows the behavior of M (T) (Fig. 2e, f), which are consistent with earlier reports5. With a slight increase in the extra Mn concentration, the saturated value of the AHC significantly declines (Fig. 2f), suggesting that the excess Mn controls the number of the conduction electrons and thereby tunes the Fermi level EF, as the electron states at EF are constituted solely by the 3d electrons8,28.
Anomalous Nernst effect (ANE)
The ANE is another key quantity that measures the Berry curvature. Unlike the AHE that involves the Berry curvature over all occupied bands, the ANE is determined by the Berry curvature lying close to the Fermi energy EF9,27,63. The Nernst signal Sji is obtained using the same electrodes as in the Hall effect measurements, by applying temperature gradient instead of charge current; namely, an induced transverse voltage Vj perpendicular to both the magnetic field B and the heat current
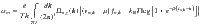
Figure 2d shows the key findings of the substantial room-temperature ANE in Mn3Sn reported by Ikhlas et al.9. Similar to the Hall conductivity ρH and the magnetization M, the field dependence of −Sji is strongly anisotropic; the in-plane field components −Syz and −Szx exhibit sharp hysteretic jump with a substantial zero-field component of about 0.3 μVK−1, more than three orders of magnitude higher than the expected value according to the scaling relation for FM materials (see below), while −Sxy remains zero within experimental resolution without showing any hysteresis. The comparison between the field dependence of −Sji and M helps unveil the driving mechanism behind the ANE. Although −Syz and M measured under
Similar to the case of Mn3Sn, our newly obtained Nernst coefficient −Syz of Mn3Ge single crystals shows a step-like profile with a sizeable zero-field component at room temperature, as shown in Fig. 2g. On cooling, the zero-field components of −Syz and −Szx behave similarly and reach a maximum of about 1.35 μVK−1 near 100 K (Fig. 2h), which is more than twice larger than the value reported for Mn3Sn9. The recent studies by Wuttke et al.15 also find that the temperature dependence of zero-field −Syz and −Szx are nearly identical, with magnitude consistent with our finding. Under a high magnetic field of 14 T, −Syz and −Szx are further enhanced to about 1.5 μVK−1, while the broad peak remains at around 100 K (see below). The out-of-plane field component −Sxy is negligibly small compared to −Syz and −Szx in the studied temperature range. The behavior of Sji observed in Mn3X (X = Sn and Ge) shares remarkable similarities with the low-temperature field-induced ANE of prototypical nonmagnetic WSMs TaAs and TaP, in which the peak position of Sji provides a rough estimate of the lowest Weyl node energy relative to EF64. For T > 50 K, the ANE observed in TaAs and TaP gives way to the B-linear ordinary contribution64, whereas the ANE in Mn3X (X = Sn and Ge) dominates the Nernst signal over a much wider temperature range up to room temperature.
To comprehensively characterize the thermoelectric properties, we have newly measured the longitudinal Seebeck coefficient, Sii (T), of Mn3.04Ge0.96 for
Anomalous thermal Hall effect (ATHE)
As the thermal counterpart of the AHE, the anomalous thermal Hall conductivity,
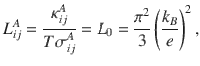

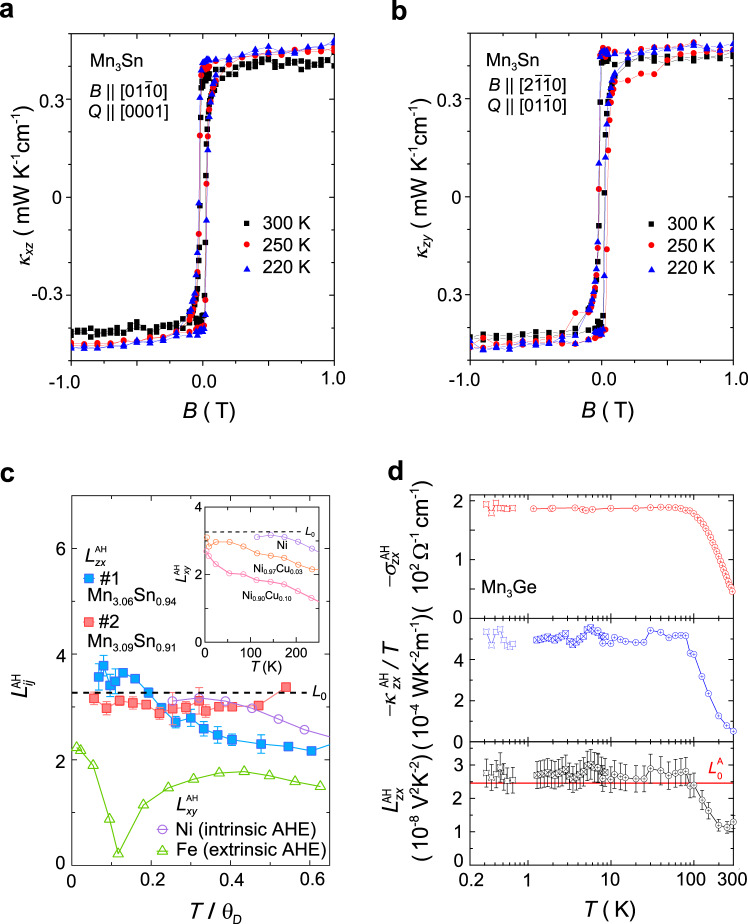
Anomalous transverse Wiedemann–Franz (WF) law found in Mn3X (X = Sn, Ge).
a, b Field dependence of the thermal Hall conductivity κxz (a) and κzy (b). c Temperature dependence of the anomalous Lorentz number
which relates the ratio between anomalous thermal and electrical Hall conductivities with the Sommerfeld number L0. In conventional ferromagnets such as Fe, Ni, and NiCu alloys, the magnitude of
In contrast, the
Evidence for magnetic Weyl fermions
Following the experimental discoveries of the large AHE and ANE, Mn3X (X = Sn, Ge) is proposed as the magnetic version of the WSM (Weyl magnet) based on first principle calculations8,28. The coplanar 120° spin structure of Mn3Sn and Mn3Ge (Fig. 1a, b) lowers the original hexagonal crystal symmetry to orthorhombic, which possesses a nonsymmorphic symmetry and two mirror reflections, MxT and MyT, with time reversal T added. These symmetry properties set strong constraints on the positions of the Weyl points. That is, the mirror symmetries ensure that the Weyl points appear along a k-direction parallel to the local easy magnetization axis, namely, the x-axis for Mn3Sn and y-axis for Mn3Ge; the corresponding k-space location of Weyl points are shown in Fig. 1d, e, respectively7,8. By applying a rotating magnetic field in the xy-plane, one may shift the locations of the Weyl points governed by the underlying spin texture along a hypothetical nodal ring obtained in the absence of the SOC, as illustrated in Fig. 1d.
The calculated band dispersion in both Mn3Sn and Mn3Ge reveals multiple pairs of type-II Weyl nodes at various energies28, which possess finite density of state at the nodal point owing to the touching between electron and hole pockets. Among those, the most relevant to transport properties are the pairs sitting close to the Fermi level EF. In the case of Mn3Sn, the two pairs of Weyl points lying in the vicinity of EF arise from electron-hole band crossings along the K-M-K direction8, as shown in Fig. 1c. Each pair consists of two Weyl points of opposite chirality, with
Analysis of the anomalous transverse coefficients and carrier doping effect
We begin by discussing the temperature variation of the anomalous transverse thermoelectric conductivity72,

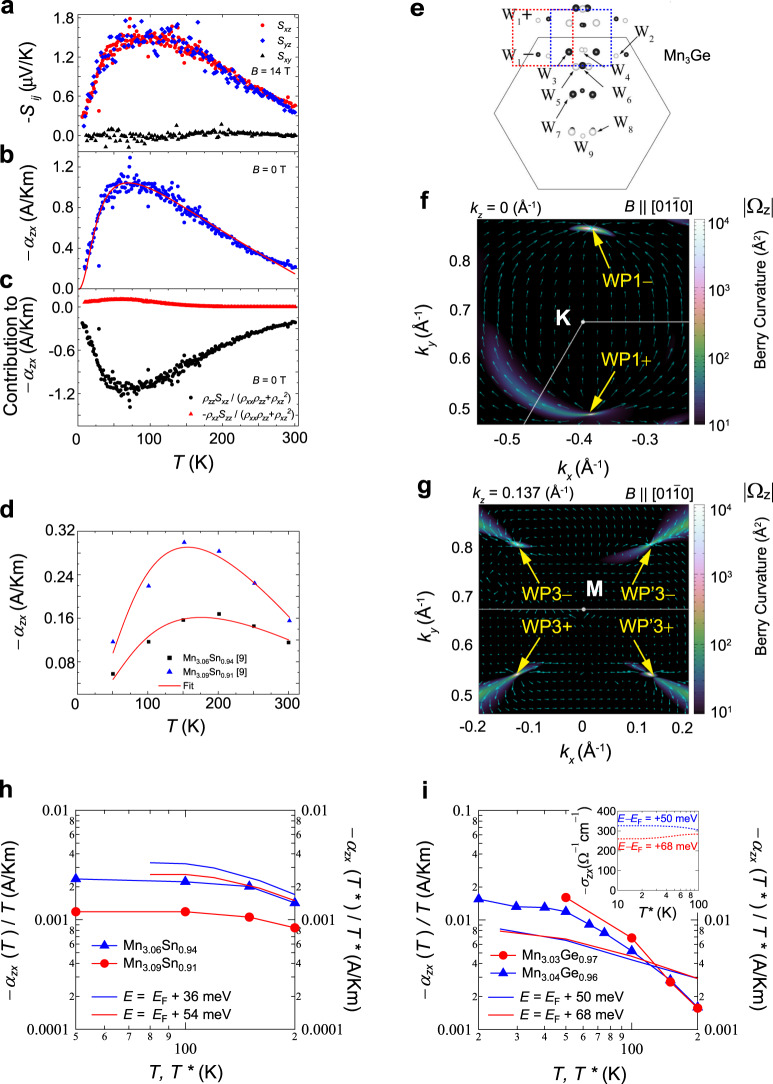
Transverse thermoelectric effects in Mn3X (X = Sn, Ge) and their theoretical analyses.
a–c Temperature dependence of the Nernst coefficient,
We next present a comparison between the experimentally observed −αji in Mn3Sn and Mn3Ge with our DFT calculations. The Mn3Sn and Mn3Ge samples usually contain extra Mn, as mentioned earlier. Since the states at the EF are occupied solely by 3d electrons, a small amount of Mn doping may generate a sizeable shift of the chemical potential relative to the EF of the stoichiometric case. A 1% Mn-doping in Mn3Sn may shift up the chemical potential by about 6 meV from EF; thus, the two Mn compositions, Mn3.06Sn0.94 and Mn3.09Sn0.91, have the chemical potential of E = EF + 36 meV and E = EF + 54 meV, respectively, as confirmed by angle-resolved photoemission spectroscopy (ARPES) measurements7. Moreover, the ARPES study finds a significant bandwidth renormalization and quasiparticle damping. Thus, in the calculation of the anomalous transverse thermoelectric conductivity, we take both the real and imaginary parts of the self-energy into account, such that:
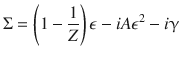
The Z value is estimated to be 0.2 for Mn3Sn according to the renormalization factor estimated by the ARPES and specific heat measurements7,8. Given the larger bandwidth of Mn3Ge in comparison with Mn3Sn44,45, a larger Z value of 0.5 is chosen. The coefficient 1/ZA determines the energy window within which the quasiparticle is well defined. We assume a window size of 40 (100) meV for Mn3Sn (Mn3Ge) based on the ARPES measurement7 of Mn3Sn so that the size covers the energy scale for Weyl fermions relevant for both compounds. Thus, AZ2 = 5 eV−1 for both Mn3Sn and Mn3Ge. The solid curves in Fig. 4h are the calculated −αzx/T for Mn3.06Sn0.94 and Mn3.09Sn0.91 that are dominated by the Berry curvature stemming from the low-energy Weyl points. They reproduce the overall temperature dependence of the experimental −αzx/T yet overestimate the magnitude by nearly a factor of 2. Note that we limit the temperature range for the comparison of theory and experiment up to 200 K; the temperature variation of the magnetization M is negligible in this T regime, and thus the spin fluctuations should have only a minor effect on the transport properties.
In the case of Mn3Ge, our DFT calculations predict the presence of several Weyl points near E – EF = 78 meV (Fig. 4f) and 63 meV (Fig. 4g) under
Spectroscopic investigations of the electronic band structure
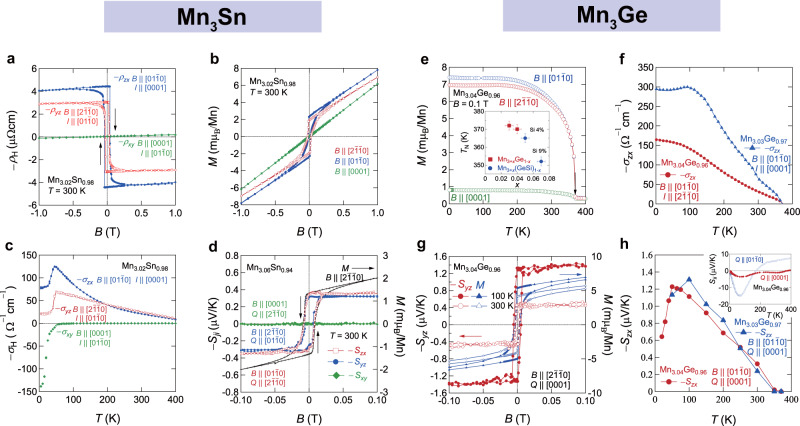
Identification of the band structure and the locations of Weyl points in the momentum space provides direct evidence for the Weyl fermions. In weakly interacting electron systems with broken IS, clear spectroscopic evidence of Weyl points and surface Fermi arcs has been established1,73. The search of Weyl fermions in magnetic materials that breaks TRS is far more challenging because strong correlation effects due to magnetism inevitably lead to diffusive character of the Weyl excitations and prevent their detection by spectroscopic probes. While recent ARPES experiments find some evidence for magnetic Weyl fermions in FM Co-based materials74,75, the present Mn3X (X = Sn, Ge) compounds feature much stronger electron correlations than the Co-based systems, as reflected by the large renormalization factor of five. Such dramatic bandwidth renormalization is comparable to that of high-temperature superconductors and heavy-fermion compounds76, therefore posing an intrinsic challenge for direct observation of Weyl fermions. Figure 5a–c summarizes the ARPES spectra of Mn3Sn reported by Kuroda et al.8. The kz-dispersion of ARPES intensity along the H-K-H high-symmetry direction reveals a quasiparticle peak near EF at a photon energy of

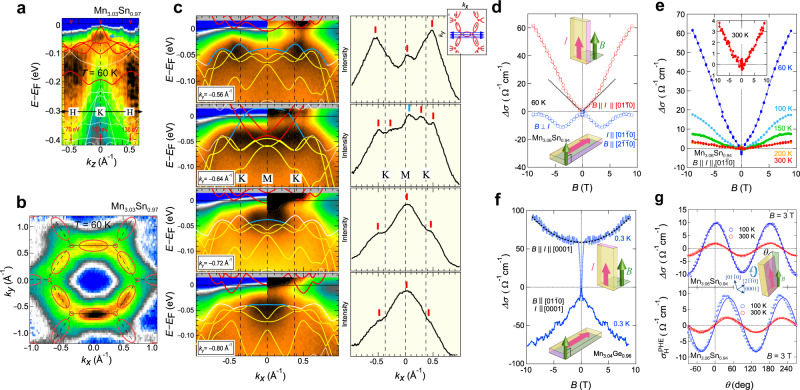
ARPES study and the chiral anomaly in Mn3X (X = Sn, Ge).
a
kz-dispersion along the H-K-H high-symmetry line (black arrows) obtained at 60 K by varying the incident photon energy hν from 50 to 170 eV. The blue arrow marks the quasiparticle peak developed around K point. b ARPES intensity at EF in the kx–ky-plane obtained with hν = 103 eV. The solid curves represent the Fermi surface predicted by the DFT calculation. c ARPES intensity maps in the E–kx-plane along the high-symmetry K-M-K direction at various ky obtained at 60 K. The original spectrum intensity (left) is compared to the intensity divided by the energy-resolution convoluted Fermi–Dirac (FD) function. The solid lines represent the calculated band dispersion, with the red and blue curves marking the electron and hole bands that form the Weyl points. Right: the anomalies in the corresponding momentum distribution curves (MDCs) are marked by the vertical color bars. d Field dependence of the magnetoconductivity in Mn3Sn for B || I (red) and B ⊥ I (blue) under a magnetic field
Chiral anomaly in Mn3X (X = Sn, Ge)
The gapless nature of the Weyl fermions renders their acute responses in low-energy probes, with the hallmark feature in magnetotransport known as the chiral anomaly. In the presence of a high magnetic field, the Weyl crossings are quantized into Landau levels (LLs), with a chiral lowest LL for each Weyl node. Namely, electrons occupying the lowest LL are divided into left- and right-moving groups of opposite chirality. Hypothetically, these two groups do not mix, leading to separate number conservation of the three-dimensional left- and right-handed Weyl fermions. Once an electric field
In this section, we discuss the Weyl-fermion-induced magnetotransport anomalies in Mn3Sn and Mn3Ge. The magnetoconductance obtained for Mn3Sn at 60 K is strongly anisotropic (Fig. 5d)8. When the magnetic field B is applied parallel to the electric field E, a positive magnetoconductance is observed, while a negative magnetoconductance appears in the E ⊥ B configuration. In the low-field regime, the positive LMC for
Unlike the case of Mn3Sn, the ferro-octupole phase in Mn3Ge remains intact further down to 0.3 K, which provides an advantage for discerning the intrinsic effects of Weyl fermions from that of the magnetic spin fluctuations. Figure 5f shows the field dependence of the magnetoconductivity
Apart from the chiral anomaly, other conventional mechanisms may yield positive LMC; one such well-known effect is the current jetting85. High-mobility semimetals may exhibit a very large transverse magnetoresistance relative to the LMR owing to the orbital effect. In such cases, the strongly anisotropic MR may restrict the current to the direction parallel to the field, while the current flow transverse to the field is largely suppressed. This field-induced steering of the current may lead to positive LMC that depends strongly on the sample dimension and geometry. Recent studies have shown that the current-jetting effect serves as the primary mechanism behind the positive LMC observed in several Dirac and WSM candidates85. The carrier mobility of Mn3X (X = Sn, Ge) is considerably lower than that of weakly correlated semimetals and zero-gap semiconductors, with a nearly isotropic magnetoresistance. Therefore, any current-jetting effect is unlikely to occur. Nevertheless, experimental tests were performed to address this concern. The magnetoconductivity measured at different voltage contacts on the sample are nearly identical, and all measured samples display qualitatively the same behavior, indicating that the observed positive LMC of Mn3X (X = Sn, Ge) is intrinsic rather than arising from current inhomogeneities.
Another magnetotransport signature of the chiral anomaly is the planar Hall effect (PHE), which is formulated as follows:


Scaling behavior in Mn3X (X = Sn, Ge)
The results summarized above provide firm evidence for the existence of Weyl nodes near the Fermi energy, which play a central role in generating the AHE and ANE. When the AHE comes from the intrinsic mechanism, the Hall conductivity is independent of the longitudinal conductivity, following the universal scaling law26,87–89. Figure 6a presents the transverse Hall conductivity, σH, as a function of the longitudinal conductivity, σ, for various single crystals of Mn3+xX1-x (X = Sn, Ge) with different composition in comparison with those of FM materials. Here, σ and σH refer to the values obtained at the low temperature limit of the phase where the inelastic scattering is minimized. Notably, for all studied samples, the longitudinal σ is in the range of 5 × 103 Ω−1 cm−1, and the σH value is nearly independent of σ (Fig. 6a, inset). Both features indicate that Mn3X (X = Sn, Ge) sits in the “good metal” regime, where the AHE is governed by the intrinsic mechanism.

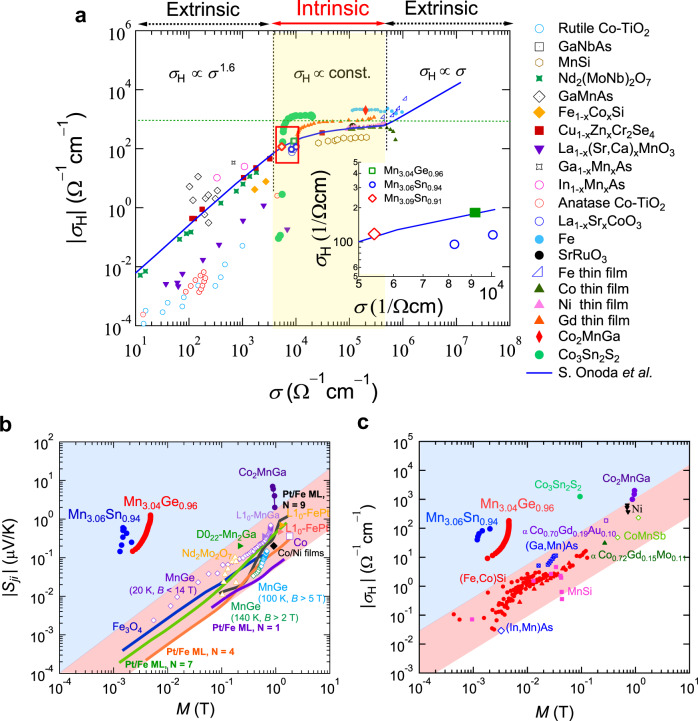
Universal scaling relations for the magnetic Weyl semimetals.
a Universal scaling relation between the Hall conductivity, σH, and the longitudinal conductivity, σ, for Mn3.04Ge0.96 (2 and 10 K), Mn3.06Sn0.94 (60 and 100 K), and Mn3.09Sn0.91 (100 K)4,9, plotted together with the data for various ferromagnets including transition metals (Ni, Gd, Fe, and Co thin films)87, Fe single crystals87, Co3Sn2S231, MnSi89, Fe1-xCoxSi89, perovskite oxides (SrRuO3, La1-xSrxCoO3, La1-x(SrCa)xMnO3)71, spinels (Cu1-xZnxCr2Se4)71, pyrochlore (Nd2(MoNb)2O7)71, and magnetic semiconductor (Ga1-xMnxAs, In1-xMnxAs, anatase–Co–TiO2, rutile–Co–TiO2)71. Within the good metal regime of
Summary and perspectives
The combination of the experimental and theoretical studies on the chiral antiferromagnets Mn3X (X = Sn, Ge) has revealed a comprehensive set of evidence that confirms the presence of Weyl fermions, in particular, the large Berry-curvature-driven AHE and ANE, positive LMC and PHE originated from the chiral anomaly. The large Berry curvature stemming from the Weyl nodes leads to significantly enhanced AHE and ANE in the absence of net magnetization. To further demonstrate this feature, we show a summary comparison of the magnetization dependence of the spontaneous Hall conductivity σH (M) and the anomalous Nernst coefficient Syx (M) obtained in Mn3X (X = Sn and Ge) with those observed for various conventional FM materials (Fig. 6b, c)4–6,9,15,21,23,89. The large σH (M) and Syx (M) of Mn3X manifest themselves beyond the linear relation for the ordinary ferromagnets (red shaded region). Other known members of this regime are the FM cobalt-based WSMs Co2MnGa21 and Co3Sn2S223; in both compounds, recent ARPES studies reveal evidence of Weyl fermions74,75, which are identified as the dominant cause of the unusually large AHE and ANE.
The research on Mn3X (X = Sn, Ge) therefore paves the path for designing and investigating new Weyl magnets with strong electron correlation. The realization of Weyl magnets triggers further exploration of their intriguing properties emerging from the interplay between magnetism and topology, which may cast new light on the fundamental science behind topological quantum states of matter. The great tunability and robustness of Weyl fermions, combined with the unique advantages of the AFM spin structure over FM counterparts, render Mn3X (X = Sn, Ge) remarkable potential to spark advances in spintronics and energy harvesting technologies. Intensive efforts are underway to make the novel properties of Weyl magnets useful for future applications16–18,20–22.
Methods
Single-crystal growth
Single crystals of Mn3Ge were synthesized by the Bridgman and Bi self-flux methods, using high-purity starting materials (Bismuth—99.999%, Manganese and Germanium—99.999%) with an optimized ratio. The Bridgman growth follows a procedure similar to that described in previous studies of Mn3Sn9. The initial step was to obtain polycrystalline samples by melting mixtures of manganese and germanium in an arc furnace under argon atmosphere. Starting from these polycrystalline materials, the single crystals of Mn3Ge were grown using a single-zone Bridgman furnace, by applying a maximum temperature of 1080 °C and a growth speed of 1.5 mm/h. In the case of Si-doped samples, the mixed germanium and silicon are melted with pure manganese in an arc furnace with the stoichiometric ratio. The subsequent Bridgman growth of single crystals was achieved with a lower maximum temperature of 1050 °C and a slower growth speed of 0.5 mm/h. The crystals were then annealed at 740 °C for 3 days.
Crystal characterization
The crystals were characterized by single-crystal X-ray diffraction (RAPID, Rigaku) at room temperature. The lattice parameters are obtained by Rietveld refinement. All the samples were shown to be single phase, with lattice parameters consistent with previous work5. According to the energy dispersive X-ray analysis with a scanning electron microscope, the compositions of crystals obtained by Bi-flux and Bridgman methods are Mn3.03Ge0.97 and Mn3.04Ge0.96, respectively. The oriented single crystals were cut into a bar shape by spark erosion for transport and magnetization measurements.
Magnetization measurements
The magnetization measurements on orientated samples were conducted using a commercial SQUID magnetometer (MPMS, Quantum Design) in the temperature range of 2–400 K.
Electrical resistivity and Hall effect studies
The longitudinal and Hall voltage signals were measured simultaneously in six-probe geometry; contacts to the crystals were made by gluing 20 μm gold wires with silver epoxy or attaching them by spot welding. Measurements at temperatures of 2–400 K were performed in the PPMS system (Quantum Design), and a helium-3 sample-in-vacuum insert system (HelioxVT, Oxford Instruments) was employed for low-temperature measurements at 0.3 K. The Hall contributions to the longitudinal resistivity and vice versa were eliminated by adding and subtracting the resistivity data taken at positive and negative magnetic fields. The uncertainties of the longitudinal resistivity and Hall resistivity are about 1-2%.
Thermoelectric studies
The thermoelectric properties were measured by the one-heater and two-thermometer configuration using the PPMS system (Quantum Design). Bar-shaped samples with a typical dimension of 10 × 2 × 2 mm3 were used for the measurements. By applying a temperature gradient
Density functional theory (DFT) calculations of the band structure
The electronic structure calculations were performed using the Quantum ESPRESSO package90. The exchange–correlation energy functionals were considered within the generalized gradient approximation, following the Perdew–Burke–Ernzerhof scheme91. A 7 × 7 × 7 k-point grid and projector augmented wave pseudopotentials92 were applied for the calculations. The cut-off energies of 80 and 320 Ry were chosen for the wave functions and the charge density, respectively. By using the Wannier90 code93–95, the Wannier basis set was constructed from the Bloch states obtained in the DFT calculation, which includes 292 bands. The Wannier basis mentioned above consists of localized (s,p,d)-character orbitals at each Mn site, and (s,p)-character orbitals at Ge site, which gives 124 orbitals/u.c. in total. The Berry curvature, along with the transverse thermoelectric conductivity63, was calculated using a Wannier-interpolated band structure94 with 70 × 70 × 70 k-point grid and additional adaptive k-point grid of 3 × 3 × 3 in regions where the Berry curvature is large.
Thermoelectric conductivity
To calculate the thermoelectric conductivity, we begin with the calculation of the AHC, σAH, at finite temperature:
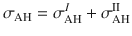
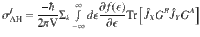
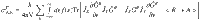
here
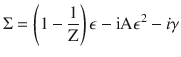
We obtained the thermoelectric conductivity, αji, following the Mott relation, that is:
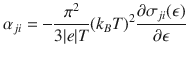
Acknowledgements
This work is partially supported by CREST (JPMJCR18T3), by JST-Mirai Program Grant (JPMJMI20A1), Japan Science and Technology Agency, by Grants-in-Aids for Scientific Research on Innovative Areas (15H05882, 15H05883, and 15K21732) from the Ministry of Education, Culture, Sports, Science, and Technology of Japan, by New Energy and Industrial Technology Development Organization, by Grants-in-Aid for Scientific Research (19H00650) from the Japanese Society for the Promotion of Science (JSPS). The work at the Institute for Quantum Matter, an Energy Frontier Research Center was funded by DOE, Office of Science, Basic Energy Sciences under Award # DE-SC0019331. The work for first-principles calculation was supported in part by JSPS Grant-in-Aid for Scientific Research on Innovative Areas (18H04481 and 19H05825) and by MEXT as a social and scientific priority issue (Creation of new functional devices and high-performance materials to support next-generation industries) to be tackled by using post-K computer (hp180206 and hp190169). M.F. acknowledges support from the Japan Society for the Promotion of Science (Postdoctoral Fellowship for Research in Japan (Standard)). The use of the facilities of the Materials Design and Characterization Laboratory at the Institute for Solid State Physics, The University of Tokyo, is gratefully acknowledged.
Author contributions
S.N. conceived the project and planned the experiments. T.C., T.T., M.F., I.M., and S.N. performed the experiments and analyzed the data. S.M., T.K., M.K., F.I., and R.A. performed the first-principles calculations. D.N.H. and R.I. performed the TEM and ICP measurements and analyses. S.N., M.F., T.T., S.M., and T.C. wrote the paper. All authors discussed the results and commented on the paper.
Data availability
The data that support the findings of this study are available on reasonable request from the corresponding author (S.N.).
Competing interests
The authors declare no competing interests.
References
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
87.
88.
89.
90.
91.
92.
93.
94.
95.
96.
 Anomalous transport due to Weyl fermions in the chiral antiferromagnets Mn3X, X = Sn, Ge
Anomalous transport due to Weyl fermions in the chiral antiferromagnets Mn3X, X = Sn, Ge
