
- Altmetric
In quantum magnets, magnetic moments fluctuate heavily and are strongly entangled with each other, a fundamental distinction from classical magnetism. Here, with inelastic neutron scattering measurements, we probe the spin correlations of the honeycomb lattice quantum magnet YbCl3. A linear spin wave theory with a single Heisenberg interaction on the honeycomb lattice, including both transverse and longitudinal channels of the neutron response, reproduces all of the key features in the spectrum. In particular, we identify a Van Hove singularity, a clearly observable sharp feature within a continuum response. The demonstration of such a Van Hove singularity in a two-magnon continuum is important as a confirmation of broadly held notions of continua in quantum magnetism and additionally because analogous features in two-spinon continua could be used to distinguish quantum spin liquids from merely disordered systems. These results establish YbCl3 as a benchmark material for quantum magnetism on the honeycomb lattice.
Honeycomb lattices with interacting spins can host rich magnetic behaviour; however, typically features are complicated by additional interactions. Here, the authors perform neutron scattering on YbCl3, which exhibits near perfect two-dimensional magnetism, providing a benchmark for other materials.
Introduction
The honeycomb lattice decorated with interacting spins is a particularly fascinating structural motif for the generation of collective quantum behavior. This bipartite lattice geometry has the minimum coordination number of three for a lattice in two dimensions. When the interactions between the spins are strongly anisotropic, as is the case for a growing number of Kitaev materials1–22, the result is strongly frustrating interactions and, hence, the honeycomb lattice is presently thought of as one of the primary contenders to host quantum spin liquids. In the opposite limit of isotropic spin interactions, frustrated quantum magnetism can arise through the competition of nearest neighbor and next-nearest neighbor interactions23–37. Indeed, most honeycomb lattice materials studied thus far require the addition of further neighbor interactions to explain the underlying physical behavior6,8,38–47. Such materials, with a complicated phase diagram as a function of first, second, and third nearest-neighbor interactions, have been fertile ground for exploration.
On the other hand, finding an example of honeycomb lattice magnetism where nearest-neighbor Heisenberg interactions are dominant would provide an important benchmark for studying quantum magnetism in two dimensions. In this instance, due to the bipartite geometry of the honeycomb lattice, the Heisenberg exchange interactions are not frustrated and a Néel ground state is expected25,26,48 at zero temperature. However, long-range order at finite temperature is prohibited by the Mermin–Wagner theorem as long as there are no anisotropic or interlayer interactions. Despite the lack of frustration, in this case, the low connectivity of the honeycomb lattice indicates that collective quantum effects are likely to be observable. Experimental realizations of the ideal honeycomb lattice Heisenberg model (HLHM) are thus attractive as a means of testing fundamental concepts of collective quantum behavior.
For example, quantum effects connected to two-magnon continua, such as magnon decays and renormalizations, have been predicted for a range of two-dimensional lattices49, including the square50,51, triangular52,53, and honeycomb54 lattices. However, while the Van Hove singularities of the two-magnon continua have a crucial role in these quantum effects, the Van Hove singularities themselves have not been experimentally observed despite extensive studies of square lattice55–57 and triangular lattice58–60 quantum magnets. More generally, it is important to distinguish quantum effects that arise entirely due to the honeycomb geometry from those that also require other sources, such as frustration or anisotropic interactions. A further motivation is the identification of a model system where the energy scale of the spin–spin interactions is modest enough to allow the quantum properties to be studied as a function of a relevant tuning parameter, for example, an applied magnetic field54.
Here we focus on the nearly ideal honeycomb lattice material YbCl3 as a potential model quantum magnet in the unfustrated limit. The arrangement of the Yb3+ ions is illustrated in Fig. 1. While YbCl3 is formally monoclinic (space group C12/m1), there is only a very modest distortion (<0.5% difference between Yb–Yb nearest-neighbor distances) from the ideal honeycomb lattice geometry in the ab planes61. YbCl3 has been proposed as a candidate for Kitaev physics62,63, but other studies suggest that YbCl3 is likely to exist in the Heisenberg limit64. Thus, a key question concerning the physical behavior of YbCl3 is the nature of the spin interactions and the manifestation of collective quantum effects. Experimental studies thus far have found a broad signature in the specific heat peaked at 1.8 K that comprises ~99.8% of the entropy of expected for the ground state doublet62. At T = 0.6 K, a weak anomaly in the specific heat is observed. The local crystallographic environment results in easy plane anisotropy of the Yb3+ magnetic moments61. Finally, the polycrystalline averaged magnetic excitation spectrum of YbCl361 is rather different from that of the prototype Kitaev material RuCl317, suggesting that a different set of interactions govern the physical behavior of YbCl3.

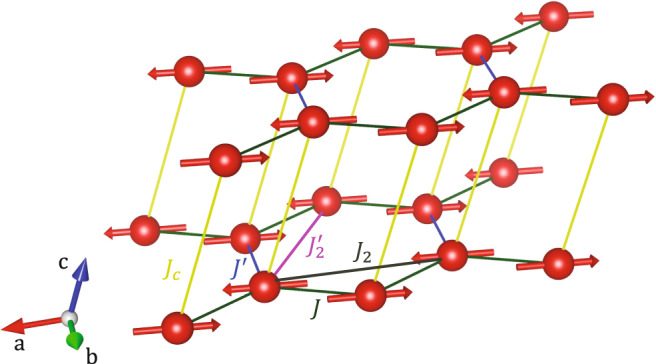
Crystal and magnetic structure of YbCl3.
The monoclinic crystal structure (space group C12/m1) and ordered spin configuration (magnetic space group
In this paper, we study YbCl3 with high-resolution inelastic neutron scattering (INS) measurements of single crystals. In addition to a conventional spin-wave (single-magnon) mode, these measurements show a sharp Van Hove singularity (VHS) within a broad two-magnon continuum that originates from longitudinal (quantum) spin fluctuations. Linear spin-wave theory with a single Heisenberg interaction on the honeycomb lattice reproduces all features of the data, demonstrating the strong quantum and almost perfectly two-dimensional character of YbCl3. Additional support for these conclusions is presented through polarized neutron diffraction and specific heat capacity measurements in conjunction with microcanonical thermal pure quantum state (mTPQ) calculations. Together, these results demonstrate that YbCl3 is an ideal model system of a two-dimensional quantum magnet without frustrated or anisotropic interactions. Being considerably hard to find, such model systems are crucial in quantum magnetism as they enable the controlled experimental investigation of collective quantum behavior. Moreover, on a conceptual level, the observation of a sharp feature within a continuum response demonstrates the coherent origin of the continuum. Therefore, our results for the two-magnon continuum are proof of the principle that similar features within two-spinon continua could be utilized for more unambiguous detection of fractionalized quantum magnets, such as quantum spin liquids.
Results
Inelastic neutron scattering data
We first examine the low-energy magnetic excitation spectra of YbCl3 at 0.24 K. Figures 2a–c and 3a–e show the INS spectra as a function of energy, ℏω, and wave vector, Q, transfer. Figure 2a–f is plotted as the product of the intensity and the energy transfer to emphasize higher energy features in the spectrum. The spectra contain three distinct features: a component characteristic of conventional transverse spin waves (ℏω ≤ 0.6 meV), a continuum or multimagnon component, and a sharper component at higher energies (0.8 ≤ ℏω ≤ 1.2 meV). The spin-wave mode disperses throughout the (HK0) plane with no discernible dispersion along the (00L) direction (see Fig. 3e and Fig. 5 of the Supplementary material). The lack of an observable dispersion along the (00L) direction indicates that the interactions between the honeycomb planes are very weak. Interestingly, the spin-wave mode appears to be broader than the instrumental resolution. While the reason for this broadening is uncertain, it may arise due to domain formation as a result of bond disorder65, interaction with the multimagnon continuum (potentially following a renormalization of the spin-wave spectrum52), or even the inability to fully distinguish the overlapping continuum contribution. We also point out that the T = 3.7 K data in Fig. 3f illustrate a complete lack of well-formed magnetic excitations at higher temperatures. Finally, an important feature of the data is the lack of an appreciable spin gap (see Supplementary material for additional details). This observation suggests that the spins do not possess a significant uniaxial anisotropy, in agreement with the crystal field ground state with easy plane anisotropy determined in ref. 61.

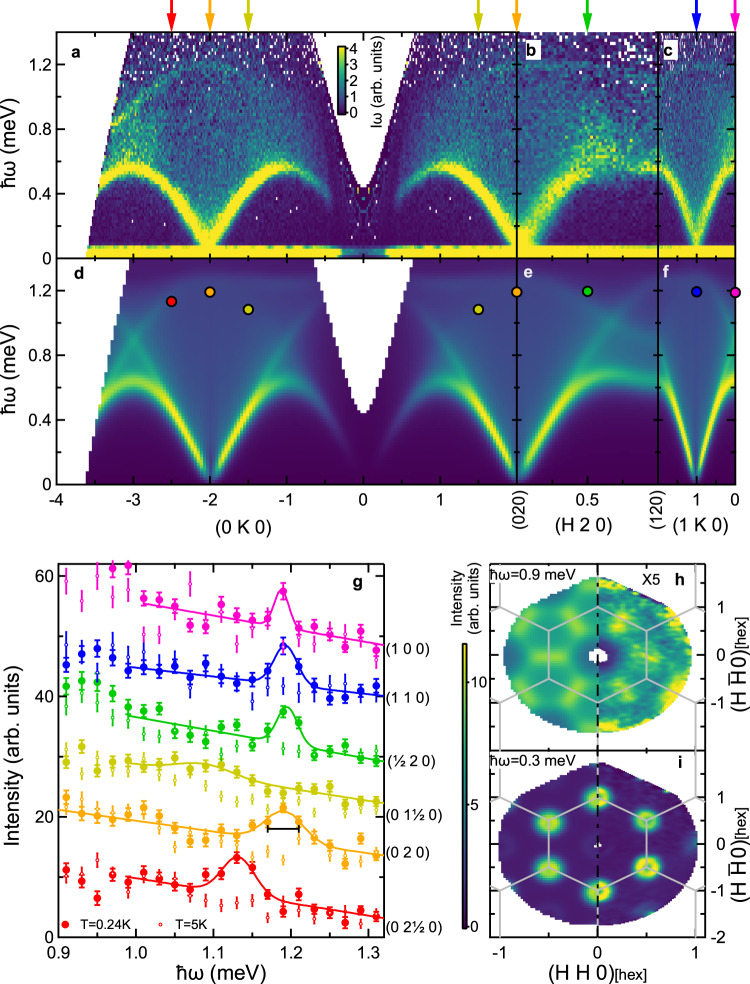
Inelastic neutron scattering data and linear spin-wave theory calculations.
a–c Inelastic neutron scattering data measured at T = 0.24 K using the CNCS instrument. d–f Linear spin-wave calculations including transverse and longitudinal channels for the ideal model (see Eq. (1)) with a fitted value of J = 0.421(5) meV along high symmetry directions in the (HK0) plane. Panels a–f are plotted as the product of intensity and energy transfer (ℏω). The Yb3+ magnetic form factor is included in the calculations. g Intensity as a function of ℏω through the Van Hove singularities at several wave vectors for T = 0.24 K (T = 5 K), marked by solid (open) points. Solid lines are Gaussian lineshapes with a sloping background. The horizontal bar represents the energy resolution at ℏω = 1.19 meV. The color of the data in (g) corresponds to the wave vector indicated by the colored arrow at the top of (a)–(c). Peak positions of the Gaussian lineshapes in (g) are shown as solid circles in (d)–(f). h–i Calculated (left) and measured (right) scattering intensity for ℏω = 0.9 meV (h) and 0.3 meV (i). The data and calculation in (h) have been scaled by a factor of 5 to be on the same intensity scale as (i). Gray lines indicate high symmetry directions of the Brillouin zone. Wave vector transfers are shown in the reciprocal space of the monoclinic lattice in reciprocal lattice units for (a)–(g) and projected into a hexagonal lattice in (h)–(i). Data in (a)–(c) and (g) have been averaged about the H = 0 and K = 0 axes. Data in (h) and (i) have been averaged about the vertical axis.

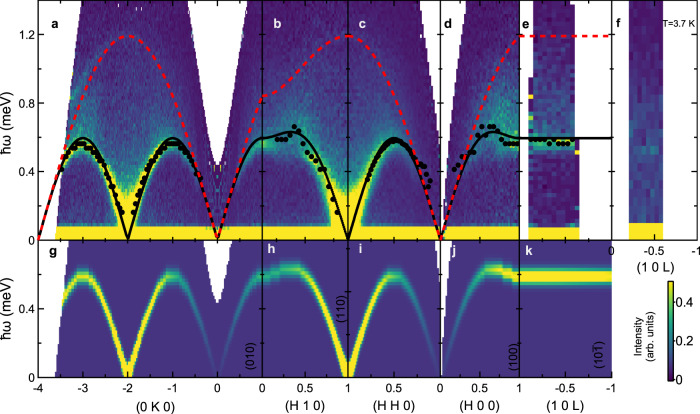
Inelastic neutron scattering data and calculations for YbCl3.
a–e Measured at 0.24 K using the CNCS instrument. f Measured at 3.7 K. Black points are the locations of the absolute peak intensity at different wave vectors. The solid black line is the fitted spin-wave dispersion with a single interaction J = 0.421(5) meV. The dashed red line is the calculated upper boundary of the corresponding two-magnon continuum scattering. g–k Linear spin-wave calculations of the transverse spectrum for interactions J = 0.42(1) meV,
The most unusual part of the spin excitation spectrum is the sharp feature toward the top of the broad continuum. While there is precedence for the observation of spinon and multimagnon continua in one-dimensional66–70 and two-dimensional square and triangular lattice55–60 quantum magnets, the observation of a sharp feature within such a continuum has, to the best of our knowledge, not yet been reported. This sharp multimagnon feature is explored further through constant wave vector scans in Fig. 2g. At energies where the sharp feature is well separated from the most intense parts of the continuum, the width is essentially limited to the calculated energy resolution of the instrument, FWHM = 0.04 meV at ℏω = 1.19 meV. As will be described in more detail below, this result provides an experimental demonstration of how a sharp feature can be generated within a continuum response in a quantum magnet. Note that the hexagonal symmetry of the spin excitations is manifest in both these higher energy features and the transverse spin-wave modes at lower energies, as shown in the right sides of Fig. 2h and i, respectively.
Linear spin-wave theory
To understand the physics begetting the novel spin excitation spectrum of YbCl3, we consider a Heisenberg model on the honeycomb lattice with a single antiferromagnetic exchange interaction J between nearest-neighbor S = 1/2 spins
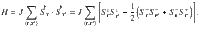
Discussion
Comparison between data and model
The HLHM in Eq. (1) reproduces the experimental data for the transverse spin-wave mode, the broad continuum, and the sharp feature toward the top of the continuum. We first note that, due to the summation over the momentum k, the contribution from the two-magnon states in Eq. (5) results in a broad continuum of scattering. To determine the Heisenberg exchange J, we consider the transverse component of the data. Due to the large scattering intensity of the continuum, we compare the calculated dispersion to the overall maxima in the scattering intensity as a function of q (solid points in Fig. 3a–e). Comparing these values for points restricted to the (HK0) plane yields a Heisenberg exchange of J = 0.421(5) meV, shown as a solid line in Fig. 3a–e. Moreover, we directly compare the data along the (0K0), (H20), and (1K0) directions to the numerical evaluation of Eqs. (3) and (5) convolved with a Gaussian approximation to the instrumental energy and wave vector resolution functions while also including the spherical approximation for the Yb3+ magnetic form factor and an additive background term. The resulting spectra are shown in Fig. 2d–f and h–i; the continuum response and the sharp feature within the continuum are reproduced exceptionally well. (see Supplementary material for additional comparisons between the data and the model.) We remark that the excellent agreement between the experimental data and the ideal HLHM is also in accordance with the prediction of ref. 64.
The sharp feature toward the top of the continuum is a particularly interesting aspect of the spectrum that, to the best of our knowledge, has not been previously observed in a quantum magnet. In the model, such a sharp feature appears within the two-magnon continuum due to a VHS in the joint density of states49,50,52–54. Indeed, on the level of pure kinematics (i.e., ignoring any matrix element effects), the longitudinal two-magnon response in Eq. (5) is proportional to the joint density of states,

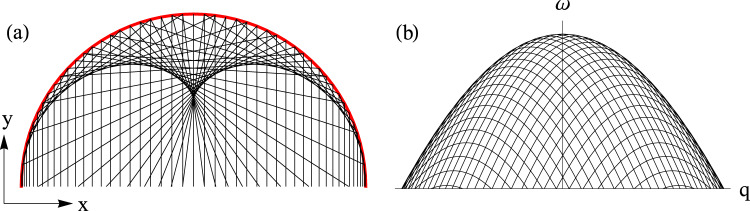
Alternative understanding of Van Hove singularities as caustic features in the collective spin dynamics.
a Caustic features in ray optics. Parallel light rays (black lines) enter an optical system at different positions. When these light rays reflecting from a circular mirror (red line) coalesce, they give rise to caustic features in real space. b Caustic features in a spin response. The two-magnon continuum can be understood as a sum of sharp contributions, ω = εk + εq−k, each corresponding to a fixed momentum k of the first magnon. When these sharp contributions (black lines) coalesce, they give rise to caustic features in the two-magnon continuum. Note that the spin response shown here is for a one-dimensional model system; for the two-dimensional system in consideration, the caustic features appear inside the continuum (not at its edge) and are weaker as they correspond to logarithmic (rather than square-root) singularities.
Upon close examination, the analytic model does not fully capture the intensity and dispersion of the VHS over the entire zone, as can be seen in Fig. 2a–f. By plotting the fitted peak positions of the VHS from Fig. 2g on the calculated spectra in Fig. 2d–f, we notice that there are differences between the calculated and the observed VHS energies near the (100) and
We now explore the potential importance of additional exchange interactions through comparison of the experimental spin-wave dispersion, including points measured along the L direction, to calculations using the SpinW software73. Since there are very small differences in the bond lengths within the honeycomb layers of YbCl3, as described in Fig. 1, we label two of the three nearest-neighbor exchanges as J for the d = 3.884 Å bonds and the third one as
Magnetic moment and Néel temperature
To further check the validity of the ideal HLHM, we have performed polarized neutron diffraction measurements at T = 0.3 K (see Supplementary material for additional details). We observe an antiferromagnetic spin arrangement with a well-defined staggered magnetic moment. By symmetry, this moment can either lie in the ac plane or point along the b axis, i.e., a linear combination of the two directions is not allowed. Our measurements reveal that the magnitude of the ordered moment is 1.06(4) μB and that the moment points primarily along the a axis with only a small deviation of 5(3)° along the c axis. The expected moment from the ground state crystal field doublet is 2.24(5) μB61. The value of the ordered moment is thus ≈47% of the fully polarized moment, which is in excellent agreement with the value of ≈48% obtained from linear spin-wave theory and the value of ≈54% determined by more accurate techniques72,74–77. We emphasize, however, that these theoretical values are extremely sensitive to any interlayer exchange Jc. For example, if we include ∣Jc/J∣ ≈ 4%, corresponding to the detection limit from the INS response (see above), the ordered moment in linear spin wave theory already increases from ≈48% to ≈63%. Therefore, the small value of the experimental moment indicates that the actual value of Jc is significantly below the INS detection limit and further confirms our conclusion that the magnetism in YbCl3 is two dimensional to a very good approximation.
The same conclusion is demonstrated even more strikingly by the very small value of the Néel temperature, TN ≈ 0.6 K62. Theoretically, for a quasi-two-dimensional Heisenberg magnet, the Néel temperature is approximately given by
Heat capacity calculations
Specific heat capacity measurements provide an additional means of examining the HLHM in YbCl3. The experimental specific heat and the entropy of YbCl3 for 0.5 K < T < 8 K are shown in Fig. 5a and b. Between T = 0.5 K and T = 8 K, nearly all of the entropy,

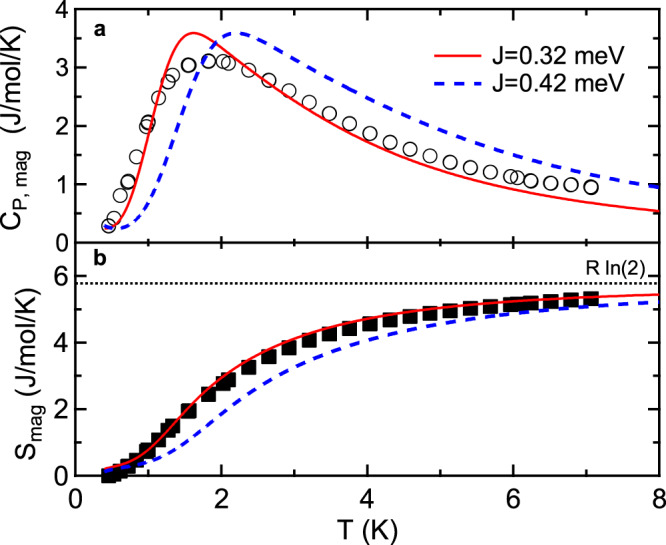
Magnetic specific heat capacity, entropy, and mTPQ calculations for YbCl3.
Specific heat capacity (a) and entropy (b) for YbCl3. The solid red line is the best fit calculation using mTPQ as described in the text. The dashed blue line is the calculated specific heat using mTPQ with the value J = 0.42 meV obtained by fitting the INS data.
We have used INS to investigate the collective magnetic excitation spectrum of YbCl3. In addition to a conventional transverse spin-wave (single-magnon) mode, there is a longitudinal two-magnon continuum harboring a sharp VHS. These components are all reproduced by linear spin-wave theory with a single nearest-neighbor Heisenberg interaction on the honeycomb lattice. The sharp VHS is observable due to the almost perfectly two-dimensional quantum magnetism in YbCl3, which is further reflected in a strongly reduced ordered moment and a very small ordering temperature. Our results establish YbCl3 as an ideal model system to investigate the collective quantum behavior of the honeycomb antiferromagnet in the unfrustrated limit. Finally, we point out that the observation of a VHS in a two-magnon continuum provides a strong indication that a similar observation in the two-spinon spectrum of a two-dimensional quantum spin liquid83,84 is experimentally feasible. Such an observation in a quantum spin liquid would be important in ruling out competing sources of a continuum response, such as quenched disorder or overdamped magnons, and could provide a more unambiguous signature of a long-range-entangled quantum state.
Methods
Single crystals of YbCl3 were grown using the Bridgman technique in evacuated silica ampoules (see Supplementary material and ref. 85 for further details). INS measurements were performed with the cold neutron chopper spectrometer (CNCS)86 at the Spallation Neutron Source at Oak Ridge National Laboratory. Additional measurements were made with the disk chopper spectrometer (DCS) at NIST (see Supplementary material for additional details). The CNCS measurements were performed with a 0.625 g sample oriented with the (HK0) scattering plane horizontal using 2.49 meV incident energy, Ei, neutrons in the high flux configuration of the instrument. To minimize the effects of the modest neutron absorption cross section of Yb and Cl, the sample used at CNCS was constructed of a stack of plates cut to dimensions of 3.2 mm by 3.4 mm. The polarized HYSPEC measurements were performed using the same sample as the CNCS experiment. We employed 3D polarization analysis, i.e., we measured the Px, Py, and Pz spin-flip and non-spin flip channels. Additional details are provided in the Supplementary material.
Supplementary information
Supplementary information is available for this paper at 10.1038/s41467-020-20335-5.
Acknowledgements
We thank C.D. Batista, N.B. Perkins, and S. Do for useful discussions. This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. This research used resources at the Spallation Neutron Source and the High Flux Isotope Reactor, a Department of Energy (DOE) Office of Science User Facility operated by Oak Ridge National Laboratory (ORNL). The research by P.L. and S.O. was supported by the Scientific Discovery through Advanced Computing (SciDAC) program funded by the US Department of Energy, Office of Science, Advanced Scientific Computing Research and Basic Energy Sciences, Division of Materials Sciences and Engineering. This research used resources of the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. G.P. was partially supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4416. The work of G.B.H. was supported by the Laboratory Directed Research and Development Program of Oak Ridge National Laboratory, managed by UT-Battelle, LLC, for the US Department of Energy. This manuscript has been authored by UT-Battelle, LLC under Contract No. DE-AC05-00OR22725 with the U.S. Department of Energy. The United States Government retains and the publisher, by accepting the article for publication, acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. The Department of Energy will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan).
Author contributions
A.D.C. conceived and managed the project. G.S., M.B.S., B.K.R., V.O.G., N.P.B., A.P., G.P., and A.D.C. performed the neutron scattering experiments. G.S. and M.B.S. performed the fits to the neutron scattering data. B.K.R. and A.F.M. synthesized the samples. A.F.M. performed heat capacity measurements. G.B.H. performed the spin wave calculations. P.L. performed the mTPQ calculations. D.S.P. and S.O. provided theoretical input. G.S., M.B.S., A.F.M., G.B.H., and A.D.C. wrote the paper with input from all coauthors.
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information files. Additional data are available from the corresponding author upon reasonable request.
Code availability
All numerical codes used in this paper are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
References
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
75.
76.
77.
78.
79.
80.
81.
82.
83.
84.
85.
86.
 Van Hove singularity in the magnon spectrum of the antiferromagnetic quantum honeycomb lattice
Van Hove singularity in the magnon spectrum of the antiferromagnetic quantum honeycomb lattice
