Introduction

Solvation dictates all chemical transformations in the liquid phase ranging from processes in the living world to production of bulk chemicals on a multi ton scale. Nevertheless, the specific solvent‐solute interactions and their importance on controlling chemical reactions is often underestimated. They can exhibit discrete or bulk effects on molecules and atoms leading to an alteration also of macroscopic properties. In biology, the solvent environment is crucial for the accurate folding and function of proteins. ^[1] In this way, the catalytic activity and stability can be enhanced tremendously. ^[2] But the solvent plays a far greater role than just containing the reactants for a chemical transformation. It can influence the selectivity of a chemical reaction by favouring a certain transition state. ^[3] By the proper selection of the solvent, it is even possible to reverse the enantioselectivity of a reaction. ^[4]

While in most cases the bulk properties of a solvent can be reliably described, direct interactions of solvent molecules with the solute often require sophisticated and expensive computational approaches. Although hydrogen bonding or formation of Lewis pairs are already well predictable by calculations, the weaker van der Waals interactions are often neglected in more complex systems. Accurate computation of non‐covalent interactions and entropies in solution stays a demanding task. Especially, implicit solvent models often show a mediocre correlation with experiments and even explicit methods are in general only slightly better. ^[5] This emphasizes the need for experimental data to predict also subtle solvent effects and to provide a basis for further improvements of computational models, particularly with regard to a growing interest in evaluating subtle preferences of non‐covalent interactions for their consideration in the design of catalysts. ^[6] The proper selection of an ideal solvent can therefore be decisive in controlling certain molecular processes. Understanding solute‐solvent interactions is crucial and promises potential for improvements in industrial solvent purification ^[7] and recovery. ^[8]

In this context, London dispersion slowly starts to gain attention as a means to control selectivities in synthesis. Large and polarizable moieties have proven their applicability as dispersion energy donors ^[9] stabilizing extreme bonding situations. ^[10] They play an important role in the aggregation of aromatic species, ^[11] the formation of organometallic complexes ^[12] and in catalysis. ^[13] However, there are only a few rare investigations of London dispersion interactions between linear alkyl chains.[ ¹⁴ , ¹⁵ ] Flexible n‐alkyl chains can adopt a high number of conformers at elevated temperatures. Due to this fact, an estimation of their dispersion donor abilities is a highly complex task. In recent years numerous computational methods were developed giving access to a comprehensive toolbox for efficiently evaluating the dispersive interactions in molecular systems in the gas phase with high accuracy. ^[16] The strength of London dispersion in solution, however, is subject of current research interests. Some studies address this by investigating the effect of the solvent on conformer or dimer stability.[ ¹⁷ , ¹⁸ , ¹⁹ ]

These approaches were conducted in order to determine the contribution of London dispersion to the stability of their systems. The observed attenuation of the dispersion caused by competitive interactions with the solvent molecules, however, was not complete. For some systems a compensation between 60–80 % was observed.[ ¹⁷ , ²⁰ ] We introduced the azobenzene switch as powerful tool to investigate London dispersion forces. Herein, it was chosen to address these open questions.[ ¹⁹ , ²¹ , ²² , ²³ ]

Methods

The present study aims at systematically exploring the interplay of alkane solvents with different alkyl substituents in meta‐position of the azobenzene by monitoring the thermal Z→E isomerization. During this process, the alkyl‐alkyl and alkyl‐aryl interactions contribute to the stabilization of the Z‐isomer, which is influenced by the solvent environment. Azobenzene can isomerize between two different states—the E‐state and the about 11.7 kcal mol⁻¹ considerably less stable Z‐state (Figure 1). ^[24] Isomerization between the E‐ and Z‐state can be initiated upon irradiation with light. The transition from the Z‐ to the E‐isomer can also be achieved by heating. The distance between the carbon atoms in para‐position of the rings changes from 9.1 Å ^[25] in the E‐isomer to about 6.2 Å ^[26] in the Z‐isomer. In this way, substituents on the azobenzene can be brought in close proximity. Especially substituents in meta‐positions come into a distance, where London dispersion donors stabilize the Z‐isomer of the azobenzene as we could show previously. ^[21] The general effect of the solvent on the isomerization barrier for azobenzenes can be described as a sum of three parameters [Eq. 1]. ^[27] First, the contribution from interactions between the solute and the solvent ΔF _inter. These forces mainly include dispersive and electrostatic interactions. Second, the ΔF _cav term describes the energy necessary to form cavities in the solvent for the solute. Here, the interdependence of solvent surface tension γ and the volume of the solute dominate this parameter. Third, ΔF _red stands for the reduction of intramolecular interactions between molecular groups of the solute, which are altered by the solvent environment.

Figure 1

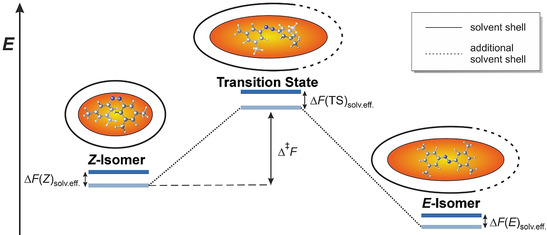
Relative energies for the Z to E isomerization of an azobenzene. Upon isomerization, the solvent accessible surface of the azobenzene increases, leading to increased solute solvent interactions.

The contribution of the solvent on the intramolecular interactions in the Z‐isomer is considered to be constant. This assumption is supported by the fact, that the overall tendency of the half‐lives observed in dependence of the substituents stays very similar in all investigated solvents (see Figure 2 and Supporting Information Figure S2–S8). Due to their apolar character, solvophobic contributions to the thermal Z→E isomerization barrier should play a minor role here.

Figure 2

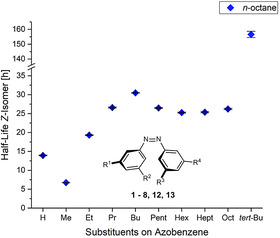
Influence of the substituents on the half‐lives for the Z‐isomers of azobenzenes 1–8, 12 and 13 at 40 °C in n‐octane. The overall tendency of the half‐lives in dependence of the substituents is in most cases minorly affected by the solvent (see also Supporting Information Figure S2–S8).

The utilized azo compounds 1–13 (Scheme 1) for this investigation were prepared by a highly flexible synthesis strategy allowing the introduction of a variety of alkyl substituents (for synthetic details, see Supporting Information). ^[23] To study the varying interactions in several alkane solvents all azobenzenes investigated were switched from the E‐ to the Z‐state by irradiation at 302 nm. The thermally induced back isomerization at 40 °C was measured by UV/Vis spectroscopy. In this way, the influence of subtle changes of the solvent environment on the stability of the Z‐isomer in dependence of the alkyl substituent of the azobenzenes was investigated. In this study, a series of linear alkanes starting from n‐heptane to n‐dodecane, as well as 2,2,4‐trimethylpentane (iso‐octane) and cyclooctane were used as solvents. Concentration as well as temperature were kept constant for these measurements.

Scheme 1

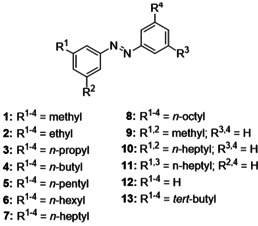
Overview of the investigated azobenzene derivatives with different substitution patterns and sizes.

Results and Discussion

As previously reported ^[23] substitution of the parent azobenzene 12 with methyl substituents leads first to a decrease of the Z‐isomer half‐life, which results from a change in the electronic properties of the azobenzene motif. Further elongation of the alkyl substituents increases the half‐life due to increasing attractive London dispersive interactions with increasing chain length. In the row of all‐meta n‐alkylated azobenzenes 1–8, the highest half‐life is observed for derivative 4 with n‐butyl groups. With longer alkyl chains, the unfavourable entropic contributions lead again to slight decrease of the Z‐isomer stability in 5–8. However, the arrangement of the alkyl groups has a large effect for both the solvent and the substituents on the azobenzene. Replacing the n‐butyl substituents in 4 with tert‐butyl groups in azobenzene 13 leads to a tremendous increase in the half‐life of the Z‐isomer by a factor >4. The reason for this is that all alkyl groups in 13 are now in an optimal distance for establishing attractive alkyl‐alkyl and alkyl‐aryl interactions caused by London dispersion. In 4, the linear alkyl chains bear more conformational flexibility and due to the higher distance from the azobenzene core exhibit weaker attractive interactions in the Z‐isomer.

A surprisingly large increase of the half‐lives for all compounds was determined, when the solvent was changed from n‐octane to iso‐octane. The increase varies between ≈5 % for small azobenzenes to around 20 % for those with larger alkyl substituents (Figure 3. By applying the Arrhenius law, the difference in the activation barrier for the isomerization of 4 for example can be calculated as 0.1 kcal mol⁻¹. This change just derives from replacing the linear alkane n‐octane with the more spherical formed iso‐octane. The opposite effect is observed, when cyclooctane instead of n‐octane is used. Here, the half‐life of the Z‐isomer is reduced between 12 and 21 % compared to n‐octane for all compounds in this study except for azobenzene 13 with the tert‐butyl groups. To evaluate the origin of these solvent effects, the details of the alteration of half‐lives were looked at for the whole series of solvents. The main reason for these observations can be correlated to a change in the solute‐solvent interaction term ΔF _inter or by changes in ΔF _cav.

Figure 3

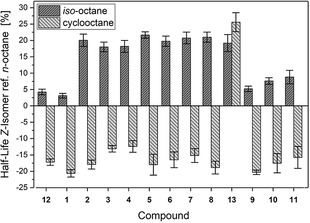
Relative changes of the Z‐isomer half‐lives for the azobenzenes 1–13 with different substituents at 40 °C relative to n‐octane. The highest deviations were observed for iso‐octane and cyclooctane showing increases of the half‐lives up to 20 %.

At first, the influence on the solute‐solvent interactions were examined regarding a change of electrostatic or van der Waals contributions. Especially the Z‐isomer is affected by changes in the electrostatic environment due to the larger dipole. For unsubstituted azobenzene, an increase of the relative permittivity ϵ _r of the solvent environment normally leads to an increase in the half‐life of the Z‐isomer. This was demonstrated by the work of Winkler and co‐workers, who determined the half‐lives of azobenzene (12) for solvents with a relative permittivity ϵ _r between 1.92 and 80.10. ^[28] Most measurements were performed in solvents with a relative permittivity higher than 7. Their results can be explained by a thermodynamic stabilization of the Z‐isomer in a solvent with a substantially higher polarity. This is supported by the findings of Haberfield and co‐workers, ^[29] who calorimetrically investigated the enthalpies for the Z→E isomerization of Z‐azobenzene in cyclohexane and cyclohexanone. Furthermore, an energetic increase of the transition state due to less favoured solute‐solvent interactions was detected.

When the half‐lives in different alkanes as solvents are determined, however, a negative linear dependence on the solvent permittivity is observed for azobenzenes with small alkyl groups (Figure 4 a). In contrast to the investigation of Winkler, a decrease of the half‐lives with increasing permittivity ϵ _r was detected. It can be assumed, that for the investigated permittivity range, destabilization of the Z‐isomer occurs rather than stabilization. The dipole moment of Z‐azobenzene can be calculated with 3.2 D. ^[30] This value is close to the one of acetone with 2.9 D. ^[31] Studies show, that the mixing enthalpy of acetone with n‐alkanes increases with increasing chain length of the n‐alkanes, indicating less favourable interactions between solute and solvent. ^[32] This would also be the case for the Z‐azobenzene, leading to a lowering of the Z→E isomerization barrier by increasing the energy of the Z‐isomer and therefore a shorter half‐life.

Figure 4

The half‐lives of Z‐isomer of azobenzene 1 (a) and 9 and 10 (b) in different alkanes as solvent in dependency of the relative solvent permittivity ^[31] at 40 °C. a Azobenzene 1 still shows a linear dependency on the relative permittivity. b Half‐lives for 9 and 10 show already a higher deviation from linearity for iso‐octane as solvent.

Modification of the degree of substitution of the azobenzene provides further insights: For compounds 9 and 10 the overall relative permittivity dependency of the half‐lives seems to stay the dominant factor, although the course of the half‐lives is less steep (Figure 4 b). This is most likely caused by the changed electron distribution of the azobenzene core, since two alkyl substituents were replaced with hydrogen. However, a deviation from linearity for the measurements in iso‐octane is emerging here, which seems to be even higher for the derivative with the longer alkyl chains 10. For longer alkyl groups, also the linear correlation shows significantly less coherence, indicating a growing influence of other types of interactions.

Since the actual volume or solvent accessible surface of the azobenzenes changes upon isomerization, it is very likely that for larger substituents a greater effect is observed. This will then contribute mainly to the ΔF _cav term, describing the compensation of solvent‐solvent interactions, which have to be overcome to accommodate the solute. The dominant parameter here to describe the changes in the solvent shell is the surface tension. When the half‐lives of the azobenzenes 9 and 10 are plotted against the surface tension γ (Figure 5 a) a linear correlation is again obtained for these solvents with similar γ values. It can be argued, that in solvents with less surface tension, that is, iso‐octane, the dipolar Z‐isomer of the azobenzenes is less destabilized in these apolar solvents, leading to the higher half‐lives. Cyclooctane, however, exhibits very strong internal solvent‐solvent interactions, which can be derived from the rather high melting point of 14.6 °C. ^[31] These forces have to be overcome upon solvation of the azobenzene, resulting in less favouring solute‐solvent interactions. In contrast, iso‐octane might provide a less favourable interaction surface to interact with the linear alkyl substituents due to its more spherical shape. This would lead to a less solvated transition state compared to linear alkanes as solvents resulting in longer half‐lives.

Figure 5

The half‐lives of Z‐isomer of azobenzene 9 and 10 (a), 4 (b), 7 (c) and 13 (d) in different alkanes as solvent in dependency of the surface tension ^[41] at 40 °C. a In contrast to Figure 3 b the half‐lives for 9 and 10 show a better linear correlation with the surface tension of the solvents. This observation goes along with an increasing importance of the ΔF _cav term for these derivatives. b Elongation of the alkyl chains leads to higher fluctuations from linearity for n‐alkanes as solvent. c These data differ also with the chain length of the substituents on the azobenzene. These fluctuations can be contributed to the ΔF _inter term. d This solute‐solvent interaction is also the reasonable cause for the large increase of Z‐isomer stability of 13 in cyclooctane.

For all‐meta alkylated azobenzenes with longer alkyl chains, a higher fluctuation of the half‐lives is observed, though the overall trend of decreasing half‐lives with increasing surface tension remains. The additional methylene units in longer chains bear more degrees of rotational freedom. At such elevated temperatures, already an ensemble of conformers is adopted for these flexible alkyl chains of the substituents but also of the solvents. For n‐octane, already ten conformers are less than 0.6 kcal mol⁻¹ higher in energy than the all‐trans conformer. ^[33] It is not unlikely that discrete solvent‐solute interdependency of the alkyl chains with the solvent lead to a kind of match‐mismatch interaction. This special type of interaction contributes to the ΔF _inter term. The importance of the right geometrical match for such weak London dispersion interactions was just recently demonstrated by Chen and co‐worker, who showed that disadvantageous interaction geometries can exceed the contribution of higher polarizability upon formation of perfluoroalkane‐alkane dimers. ^[15]

The results of azobenzene 4 with n‐butyl chains are not only special for exhibiting the longest half‐lives of all n‐alkyl substituted azobenzenes (Figure 5 b). They further show significant breaks in the tendency of decreasing half‐lives for the row of linear alkane solvents. However, their conformational freedom still seems to be limited enough, so that attractive London dispersive interactions in the Z‐isomer are not overcompensated by entropic contributions in any solvent. The trend of fluctuating half‐lives for the row of linear alkane solvents is continued for other all‐meta n‐alkylated azobenzenes like 7 with n‐heptyl chains in Figure 5 c. The energetic differences in the isomerization barrier for the Z→E isomerization of these derivatives in n‐alkanes are so small that even subtle changes of entropic contributions have a detectable impact. This includes changes in the conformer distribution.

Rigidity can have an advantageous effect for the interactions of two molecular entities. For linear alkyl chains the entropic contributions to the free energy of interaction upon approaching is much higher compared to rigid alkyl structures. They exhibit weaker enthalpic attraction but a much less entropic penalty for association due to their conformational rigidity. ^[34] Therefore, rigid tert‐butyl groups as substituents were introduced with the incentive to evaluate the influence of spatial extent on the solvent effect (Figure 5 d). Azobenzene 13 is the only derivative in this study, for which the half‐life of the Z‐isomer in cyclooctane is higher than in n‐octane and even in iso‐octane. Since the tert‐butyl substituents are isoelectronic compared to n‐butyl, this stability change is most likely based on a structural effect. The predominant conformer of cyclooctane is the boat‐chair, ^[35] which exhibits a very flat interaction surface. The better capability of cyclooctane for interaction with more globular structures is reflected that is, by the lower mixing enthalpy of the more spherical 2,3‐dimethylbutane compared to n‐hexane ^[36] and for other spherical solutes. ^[37] This should in our case then result in an increased interaction of the tert‐butyl groups with the cyclooctane solvent compared to the linear alkanes, leading to a better solvation of the Z‐isomer and, therefore, an increased half‐life.

Computational Conformer Analysis

With the introduction of new sophisticated computational tools, it was possible to evaluate the influence of the conformational and rotational flexibility of the alkyl chains on the stabilisation within the Z‐isomer. The Conformer‐Rotamer Ensemble Sampling Tool (CREST) by Grimme was used to perform such a conformational analysis. ^[38] The structures of the E‐state, the transition state and the Z‐state of azobenzene 1 were first optimized on a PBE0 ^[39] level of theory and used as template for other derivatives. Afterwards, the core structure of the azobenzene was constrained allowing only rotation of the alkyl substituents. In this way, hundreds of conformers for azobenzenes 2, 4 and 7 were computed. Single point energies on the B97‐3c ^[40] level of this conformer ensemble were calculated for allowing a better selection of the relevant structures. Conformers up to 3 kcal mol⁻¹ higher in energy than the lowest energy structure were considered for further analysis.

In the next step, distances between the carbon atoms on opposing alkyl chains were determined to find close contacts for non‐covalent interactions. Results were limited to distances below 5 Å, therefore including H‐H distances of 4.2 Å or lower where dispersive interactions start to contribute significantly to the stability of molecular entities. ^[42] To obtain a more meaningful picture of the contact distribution, the considered conformers were weighed by their single point energies with a Boltzmann distribution. The in this way determined average number of C−C contacts over the conformer ensemble within this 3 kcal mol⁻¹ energy window are listed in Table 1. For compound 2, the distances between the ethyl side chains are too short for relevant attractive interactions between the alkyl chains in the E‐ as well as the transition state. Only in the Z‐state, the ethyl groups mesh well. For longer chains, like n‐butyl in 4, this kind of interactions are also to a minor extent present in the transition state but ≈5.7 times more dominant in the Z‐state. In the n‐heptyl derivative 7, these interactions occur in all three states. While the differences between the E‐state and the transition state are quite small, the number of contacts in the Z‐state are here only ≈3.4 times higher than in the transition state. Noteworthy, that the same number of average interactions are present in the E‐state, supporting the correlation between transition and E‐state projected in the introduction. This analysis emphasizes that the observed kinetic trend for linear alkyl substituted azobenzenes is mainly driven by increased stabilisation of the Z‐isomer up to mid‐length chains. With further increasing chain length, these interactions start to occur also more and more in the transition state and seem to compensate further elongation of the alkyl substituents.

Table 1

Average Number of opposing C−C contacts below 5 Å over all conformers within 3 kcal mol⁻¹.

Cpd	E‐state	Transition state	Z‐state
2	0.00	0.00	0.73
4	0.00	2.04	11.68
7	12.81	12.74	42.70

These interactions can also be visualized by an NCI analysis, which is depicted in Figure 6. ^[43] This non‐covalent interaction analysis indicates the regions in the molecules as isosurfaces, where these contacts occur. The colour code further allows to differentiate between attractive (blue), repulsive (red) and weak interactions (green). In the transition state of derivative 4 weak alkyl‐alkyl interactions start to form as can be seen in the right part of the molecule. In the Z‐state additional alkyl‐aryl interactions emerge, providing a much larger interaction surface leading to a large stabilization of the Z‐state. For the n‐heptyl derivative 7, a similar analysis can be done (see Supporting Information Figure S9 and S10). It has to be pointed out, that the alkyl chains in the Z‐state intercalate with the ones on the opposing aryl ring, leading to larger stabilizing effects on the structure. In the transition state, the alkyl chains tend to preferentially interact with the ones on the same aryl ring due to an unfavourable core geometry of the transition state. These interactions are most likely competing with interactions with solvent molecules due to the less restricted geometry. It can be assumed that specific solute‐solvent interactions mainly affect the transition state.

Figure 6

NCI ^[43] analysis of the optimized structures for the lowest energy conformers of the transition state and the Z‐state of azobenzene 4 [PBE0‐D3BJ/def2‐TZVP].[ ³⁹ , ⁴⁴ ] Visualization was created with VMD. ^[45]

Conclusion

Three main effects governing the London dispersion between alkyl groups and alkyl solvents could be established:

The intramolecular dispersion interactions are only marginally influenced by the solvent since the overall tendency of the half‐lives in dependency of the substituents stays very similar.

It was shown that in solvents with low surface tension, destabilizing contributions due to solvent‐solvent interactions can contribute up to 0.1 kcal mol⁻¹ or an increase of the Z‐isomer half‐life up to 20 %.

Specific individual interactions between the alkyl chains on the azobenzene and those of the solvent lead to additional fluctuations of the half‐lives. These are presumably caused by structural changes of the conformer ensemble both of the n‐alkyl substituents and of the n‐alkanes as solvents.

This investigation using azobenzene as a molecular probe reveals that even small structural changes of an alkane solvent can have substantial effects on the stability of an organic compound. A detailed computational evaluation of the conformer ensemble supports the taken approach. These new insights provide general guidelines to design solvent‐solute interactions for all kinds of processes in the liquid state.

Conflict of interest

The authors declare no conflict of interest.