
The Framingham Heart Study
- Altmetric
Supplemental Digital Content is available in the text.
Intrinsic frequencies (IFs) derived from arterial waveforms are associated with cardiovascular performance, aging, and prevalent cardiovascular disease (CVD). However, prognostic value of these novel measures is unknown. We hypothesized that IFs are associated with incident CVD risk. Our sample was drawn from the Framingham Heart Study Original, Offspring, and Third Generation Cohorts and included participants free of CVD at baseline (N=4700; mean age 52 years, 55% women). We extracted 2 dominant frequencies directly from a series of carotid pressure waves: the IF of the coupled heart and vascular system during systole (ω1) and the IF of the decoupled vasculature during diastole (ω2). Total frequency variation (Δω) was defined as the difference between ω1 and ω2. We used Cox proportional hazards regression models to relate IFs to incident CVD events during a mean follow-up of 10.6 years. In multivariable models adjusted for CVD risk factors, higher ω1 (hazard ratio [HR], 1.14 [95% CI], 1.03–1.26]; P=0.01) and Δω (HR, 1.16 [95% CI, 1.03–1.30]; P=0.02) but lower ω2 (HR, 0.87 [95% CI, 0.77–0.99]; P=0.03) were associated with higher risk for incident composite CVD events. In similarly adjusted models, higher ω1 (HR, 1.23 [95% CI, 1.07–1.42]; P=0.004) and Δω (HR, 1.26 [95% CI, 1.05–1.50]; P=0.01) but lower ω2 (HR, 0.81 [95% CI, 0.66–0.99]; P=0.04) were associated with higher risk for incident heart failure. IFs were not significantly associated with incident myocardial infarction or stroke. Novel IFs may represent valuable markers of heart failure risk in the community.
Numerous studies have identified pulse pressure, an indirect but widely available measure of arterial stiffness, as a novel cardiovascular disease (CVD) risk factor.1–7 Recently, interest has shifted to potential information contained within the waveform features. Several studies have examined various time-domain measures, such as primary wave amplitude, timing of wave reflection, augmented pressure amplitude, and augmentation index.8–11 Some of these features depend on waveform calibration (primary wave amplitude or augmented pressure), whereas others are unitless (augmentation index) or depend only on timing (reflected wave arrival time).
Intrinsic frequency (IF) method is a systems-based approach (based on sparse time-frequency representation) for the analysis of heart and vascular function.12,13 The main advantage of this method is its independency on waveform calibration.12,13 The IF method models the coupled heart-vascular network as an object rotating around an artificial origin where the angular velocity of the rotations during systole and diastole are the IFs (ω1 and ω2). Mathematically speaking, IF method establishes best fit sine waves separately for systole and diastole. The corresponding frequency of these sine waves represents the IF for each phase of the cardiac cycle, with ω1 representing the IF for systole and ω2 for diastole. Recently, Pahlevan et al12,14 extracted the 2 IFs from existing clinical data and showed that ω1 is similar among healthy individuals, but its value increases in patients with left ventricle (LV) systolic dysfunction. Their results indicated that ω2 values were similar among younger participants but gradually diverged with age or progressive disease states.12,15 In addition, the prior theoretical work showed that cardiac pulsatile power reaches a minimum at any given arterial stiffness at a heart rate where the difference between ω1 and ω2 is zero.12 Thus, it was concluded that the total frequency variation (Δω=ω1−ω2) may provide an additional novel measure of optimal ventricular vascular coupling and vascular health.12
Although the aforementioned studies provide a proof of concept for novel cardiovascular indices, the prognostic values of the novel IF measures (ω1, ω2, and Δω) as indicators of cardiovascular health are unknown. Thus, we aimed to examine relations of ω1, ω2, and Δω with incident CVD in the Framingham Original, Offspring, and Third Generation Cohorts. We hypothesized that IF measures are associated with increased risk for incident adverse CVD outcomes.
Methods
The present article adheres to the American Heart Association Journals’ implementation of the Transparency and Openness Promotion Guidelines (available online at http://www.ahajournals.org/content/TOP-guidelines). The procedure for requesting data from the Framingham Heart Study can be found at https://framinghamheartstudy.org/.
Participants
The sample for the present study was drawn from the Framingham Original, Offspring, and Third Generation Cohorts, which have been described.16–18 During Original Cohort examination 26 (1999–2001, N=558), Offspring examination 7 (1998–2001, N=3539), and Gen 3 examination 1 (2002–2005, N=4095), participants underwent a noninvasive assessment of central hemodynamics (successfully obtained in N=293, N=2484, and N=3921, respectively, for a total N=6698). Analysis of waveforms to extract IF measures was successfully performed in 5924 (88.4%) of the 6698 participants. Participants were further excluded for the following reasons: prevalent CVD (n=206), age<35 years (n=981), or missing laboratory or covariate data (n=37). For secondary analyses that assessed relations between IF measures and aortic stiffness, we further excluded participants with missing carotid-femoral pulse wave velocity (N=192). All participants provided written informed consent and protocols were approved by Boston University Medical Center’s Institutional Review Board.
Noninvasive Hemodynamics and Tonometry
Hemodynamic data were acquired as previously described.19 After a 5-minute rest, participants were studied in the supine position. Arterial tonometry with simultaneous electrocardiography was obtained from brachial, radial, femoral, and carotid arteries using a custom tonometer. Tonometric data were digitized during the primary acquisition and transferred to a core laboratory (Cardiovascular Engineering, Inc.) for blinded analyses. Tonometry waveforms were signal-averaged using the electrocardiographic R-wave as a fiducial point.19 Cuff systolic and diastolic blood pressures obtained at the time of tonometry were used to calibrate the peak and trough of the signal-averaged brachial pressure waveform. Diastolic blood pressure and integrated brachial mean arterial pressure were used to calibrate carotid pressure tracings, which represented central aortic pressure.20 Carotid-femoral pulse wave velocity was calculated as previously described accounting for parallel transmission in the carotid artery and aortic arch.21
Intrinsic Frequencies
Derivation of IFs from aortic pressure waveforms, the convergence of its algorithm, and its accuracy has been described previously.12,22 IF method is a new method (based on the sparse time-frequency representation23) for analysis of coupled dynamical systems (See Data Supplement for more details).12,24 IF method models a coupled dynamical system as an object rotating around an origin. The angular velocity of the rotation is the IF. In its simplest form, a coupled dynamical system is composed of 2 systems. One physiological example of a 2-coupled dynamical system is the LV-arterial system. Figure 1 is the visualization of the IF concept.25 IF frequencies are operating frequencies treating the LV combined with the aorta and the remaining peripheral arteries as a coupled dynamical system (heart + aortic tree), which is decoupled upon closure of the aortic valve.12,14,22 It is well known that sparse time-frequency representation based methods, such as IF method, are capable of handling nonlinear and nonstationary signals.12,13,23 Using the IF method, one can extract 2 IF frequencies (ω1 and ω2) from a single arterial blood pressure waveform. The first IF, ω1, describes the dynamics of the systolic phase of the cardiac cycle where the LV and aorta (vasculature) are a coupled system. Therefore, ω1 is dominated by the dynamics of LV systolic function.12,14 The second IF, ω2, belongs to the diastolic phase when the aorta and vascular branches are decoupled from the LV. Hence, ω2 is dominated by the dynamics of the aorta and the rest of the arterial system.12,14,15

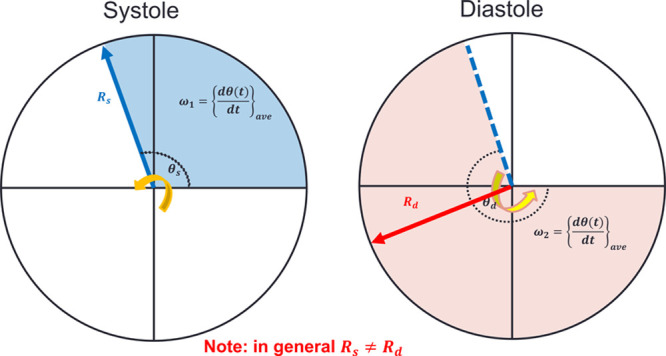
Intrinsic frequency (IF) visualization. ω1 and ω2 are the intrinsic frequencies during systole and diastole, respectively. Rs and Rd are the envelopes of intrinsic frequencies associated with ω1 and ω2, respectively. dθ/dt is the instantaneous frequency. θs and θd are the intrinsic phases during systole and diastole, respectively (see the Data Supplement for details about IF and its relations to instantaneous frequency).
The IF algorithm is based on an L2-minimization that uses a waveform to compute the IF parameters.22 The mathematical formulation is as follows:
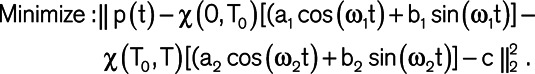
This minimization is subject to periodicity of the waveform (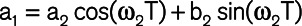 ) and continuity at T0 (
) and continuity at T0 (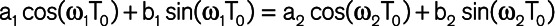 ). Here, χ (a,b) is the indicator function (χ (a,b)=1 if a ≤t≤b and χ (a,b)=0 otherwise), T0 is the dicrotic notch time (end-systolic time), p(t) is the input waveform, and T is the duration of the cardiac cycle. A brute-force algorithm was used to solve this nonconvex and nonlinear optimization problem resulting from the aforementioned L2 minimization formulation.12,22 More details about the mathematical formulation of IF method, its computational procedure, and its convergence/accuracy have been provided previously.12,14,22 Using IF algorithm, we were able to compute the 2 IFs ω1 (IF of the coupled LV and aorta + its vascular branches) and ω2 (IF of the decoupled aorta after the aortic valve closes; Figure 2). Since the goal of the IF method is to find the best fit dominant (single) frequency during systole and diastole (and not to find the best overall fit for the waveform data), the fit figure shows how well the first intrinsic mode functions of the IF represent the actual signal. The notch selection for IF calculation was performed using an automatic algorithm. To find the notch, a first and second derivatives were calculated for the pulse. The algorithm then performed first and second derivative analysis to determine the location of the notch by searching for zero crossings in the first derivative and peaks in the second derivative. Figure S1 in the Data Supplement shows reconstruction of IF with various values of ω1 and ω2 from participants overlaid on top of the original raw carotid pressure. Total frequency variation (Δω) was calculated as the difference between ω1 and ω2.12,25
). Here, χ (a,b) is the indicator function (χ (a,b)=1 if a ≤t≤b and χ (a,b)=0 otherwise), T0 is the dicrotic notch time (end-systolic time), p(t) is the input waveform, and T is the duration of the cardiac cycle. A brute-force algorithm was used to solve this nonconvex and nonlinear optimization problem resulting from the aforementioned L2 minimization formulation.12,22 More details about the mathematical formulation of IF method, its computational procedure, and its convergence/accuracy have been provided previously.12,14,22 Using IF algorithm, we were able to compute the 2 IFs ω1 (IF of the coupled LV and aorta + its vascular branches) and ω2 (IF of the decoupled aorta after the aortic valve closes; Figure 2). Since the goal of the IF method is to find the best fit dominant (single) frequency during systole and diastole (and not to find the best overall fit for the waveform data), the fit figure shows how well the first intrinsic mode functions of the IF represent the actual signal. The notch selection for IF calculation was performed using an automatic algorithm. To find the notch, a first and second derivatives were calculated for the pulse. The algorithm then performed first and second derivative analysis to determine the location of the notch by searching for zero crossings in the first derivative and peaks in the second derivative. Figure S1 in the Data Supplement shows reconstruction of IF with various values of ω1 and ω2 from participants overlaid on top of the original raw carotid pressure. Total frequency variation (Δω) was calculated as the difference between ω1 and ω2.12,25

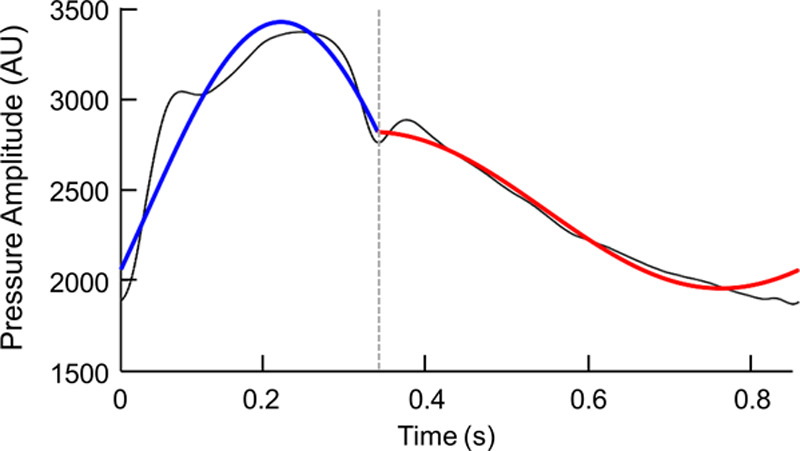
The intrinsic frequency (IF) reconstruction of a carotid pressure waveform. The piecewise reconstruction of a representative pressure wave from a Framingham participant overlaid on top of the original raw carotid pressure waveforms (black) in arbitrary units (AU). The portions of the reconstructed waveform represented by ω1 and ω2 are shown in blue and red, respectively. The location of the dicrotic notch is marked by the vertical gray dotted line.
Incident CVD Outcomes
The criteria for CVD outcomes (CVD-related death, myocardial infarction, ischemic or hemorrhagic stroke, and heart failure [HF]) have been described.26,27 Medical records were obtained for physician and hospital visits related to CVD during follow-up. All outcomes were reviewed by a committee of 3 physician investigators and were adjudicated by using a written protocol. A separate group of neurologists adjudicated cerebrovascular outcomes. Follow-up evaluations were performed on data acquired through October 17, 2014.
Clinical Evaluation and Covariates
Medical history, physical examination, and electrocardiography were performed routinely at each examination.17 Age, sex, use of antihypertensive drugs, and smoking (current versus nonsmoker) were assessed via questionnaires. Height and weight were assessed during the examination. Heart rate, systolic and diastolic blood pressures, and systolic ejection period were assessed during tonometry. Serum cholesterol levels were measured from a fasting blood test. Criteria for diabetes were a fasting glucose ≥126 mg/dL (7.0 mmol/L) or treatment with insulin or an oral hypoglycemic agent. Smoking was defined as self-reported regular use of cigarettes in the year preceding the examination. Body mass index was calculated by dividing weight in kilograms by the square of the height in meters.
Statistical Analyses
Characteristics for the study sample were tabulated. We estimated partial correlations to assess associations among the novel IFs (ω1, ω2, and Δω) and hemodynamic measures (heart rate, systolic ejection period, and systolic and diastolic blood pressures) accounting for age, sex, and cohort. We used Cox proportional hazards models to assess the associations between individual IFs and the time to a first major CVD event. We also assessed the associations between individual IFs and the time to event for each type of CVD event (HF, myocardial infarction, and stroke) separately. We tested the proportional hazards assumption by assessing the significance of time-dependent covariates by creating interactions of each predictor and survival time. Covariates were selected a priori and included components of the Framingham risk score28: age, sex, cohort, body mass index, systolic blood pressure, diastolic blood pressure, total cholesterol, high-density lipoprotein cholesterol, smoking, diabetes, and hypertension treatment as well as additional potential confounders: heart rate and systolic ejection period. To determine whether the relations between IFs and incident CVD outcomes differed by age (segregated by median age) or sex, we included interaction terms for these variables. To further illustrate relations between IFs and CVD outcomes, IF variables that were significantly related to CVD outcomes as continuous variables were categorized into quartiles to construct Kaplan-Meier curves of cumulative probability. Non-CVD death was a censoring event; the curves of cumulative probability were not modified for competing events.
All analyses were performed with SAS version 9.4 for Windows (SAS Institute, Cary, NC). Two-tailed P<0.05 were considered statistically significant, except for the tests of interaction, where P<0.05/48 (Bonferroni-adjusted P=0.001) was considered significant.
Results
Study exclusion criteria resulted in a sample of 4700 participants (2577 [55%] women) The full age range of our sample was 35 to 98 years. Table S1 presents a comparison of baseline characteristics of included and excluded participants. Characteristics of the study sample are presented in Table 1. Our sample was composed of relatively healthy individuals with typical smoking but lower prevalence of diabetes and hypertension treatment. Table 2 provides a partial correlation matrix for the novel IF measures, demographic data, and hemodynamic measures. Partial correlation plots between IF values and hemodynamic measures are presented in Figure S2. Correlations between novel IFs and demographic data are presented in Table S2. Higher ω1 and Δω but lower ω2 were modestly to moderately correlated to higher heart rate and diastolic blood pressure. Lower ω1 and Δω were moderately to strongly correlated to higher systolic ejection period. Additionally, correlations between IFs and systolic blood pressure were modest.

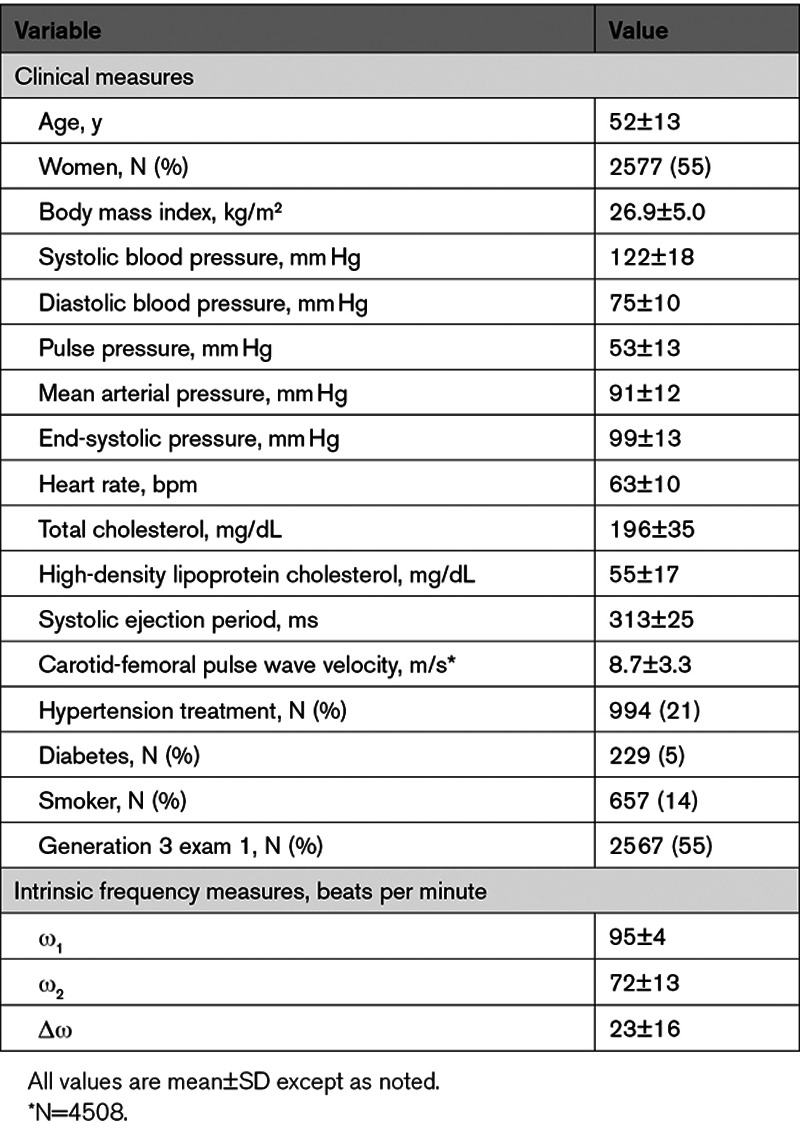

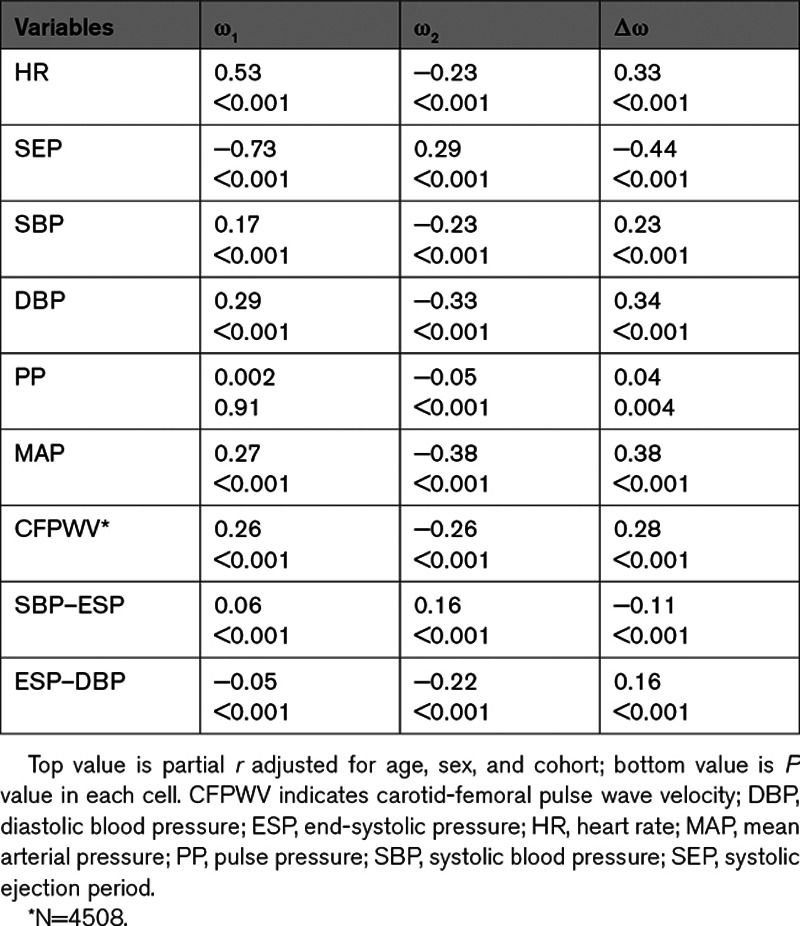
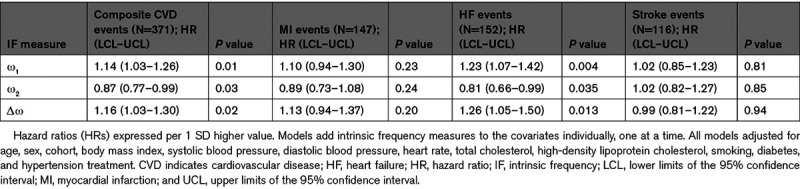
During follow-up (mean 10.6 years; median 10.8 years), we observed CVD events in 371 (7.9%) participants, with 94 events resulting in death. The most common events were myocardial infarction (n=147 [3.1%]), HF (n=152 [3.2%]), and stroke (n=116 [2.5%]); some participants were observed to have multiple CVD outcomes at the time of adjudication. Cox proportional hazards models for individual IF measures as predictors of incident CVD events are presented in Table 3. In multivariable models adjusted for age, sex, cohort, body mass index, systolic blood pressure, diastolic blood pressure, heart rate, total cholesterol, high-density lipoprotein cholesterol, smoking, diabetes, and hypertension treatment, higher ω1 and Δω but lower ω2 were associated with higher risk for incident composite CVD and HF events. In contrast, IFs were not significantly associated with incident myocardial infarction or stroke. Models further adjusted for systolic ejection period were similar (Table S3). We did not observe significant effect modification of IF relations with events by median age or sex (all Bonferroni-corrected P>0.001). We present Kaplan-Meier plots for incident HF events by IF quartile groups in Figure S3.

Discussion
Principal Findings
In the community-based Framingham Heart Study, we investigated relations of novel IFs (ω1, ω2, and Δω) derived from carotid waveforms with risk of incident CVD outcomes, including composite CVD events, myocardial infarction, stroke, and HF. In multivariable models that adjusted for traditional CVD risk factors and heart rate, higher ω1 and Δω (the IF of the coupled heart and vascular system during systole and the total frequency variation, respectively) but lower ω2 (IF of the decoupled vasculature during diastole) were associated with higher risk for incident composite CVD and HF events. None of the IFs were associated with incident myocardial infarction or stroke events alone. Our results are consistent with the hypothesis that IFs are cardiovascular health indicators that are associated with increased risk for HF in the community.
Recent Studies of Waveform Analysis
Novel noninvasive techniques combined with mathematical models that describe pulsatile pressure and blood flow have provided better understanding of cardiovascular pathophysiology and hemodynamics.29–37 To model the complex interactions of the heart and systemic circulation, many investigators have relied on Windkessel and wave transmission theories, which can provide simplified models that explain changes in arterial pressure waveforms due to aging and CVD pathologies. Several recent studies used models that depend solely on assessment and analysis of arterial pressure waves, which provide parameters that are associated with CVD risk. For example, recent population-based studies have derived parameters from carotid arterial waveforms using the reservoir-wave concept, which separates pressure into Windkessel-related (reservoir) and wave-related components.30,31 However, some studies have suggested that the reservoir-wave concept should be abandoned since it introduces error into arterial wave analysis that leads to misconceptions that violate physical principles.38,39 Measures of vascular dysfunction such as excess pressure integral, systolic and diastolic time constants, pulse pressure amplification ratio, and wave reflection index were associated with incident composite CVD events among middle-age and elderly hypertensive patients.30,31,40 In addition, Cheng et al32 performed pulse wave analysis on central arterial pressure waveforms in 2 large, population-based cohorts and showed that novel mechanical parameters independently predicted CVD mortality among presumably healthy participants.32 However, the aforementioned studies were inconsistent in their confounding adjustment and sample sizes. Recently, we investigated the prognostic utility of measures derived from a pressure-only Windkessel wave analysis of central waveforms in a Framingham sample.36 In traditional linear models, Windkessel-derived parameters were not related to incident CVD events; however, in modified models that accounted for nonlinear pressure-dependence of systolic and diastolic time constants, Windkessel parameters were modestly related to events.36
Although parameters derived from pressure-only Windkessel models may have modest utility for risk prediction in the community, they do not consider fully the implications of wave transmission at finite velocity. Therefore, their ability to represent the system dynamics of blood flow and pressure accurately is limited. Other methods for deriving novel arterial pressure parameters are based on frequency- and time-domain methodologies and rely on assessment of both pressure and flow for wave separation analysis. For example, multiple studies have shown a significant relation between backward (reflected) wave and incident CVD outcome.9,41,42 However, these studies did not directly measure central aortic flow but instead relied on various modeling assumptions for wave separation. Previously, we performed wave separation to assess the relative contributions to CVD risk among a comprehensive panel of individual components of mean and pulsatile pressure derived from directly measured central pressure and flow.37 In the forgoing study, forward pressure wave amplitude, but not backward pressure wave amplitude, predicted incident events in models that adjusted for traditional CVD risk factors. Furthermore, primary pressure wave amplitude, a pressure-only surrogate for forward pressure wave amplitude, was not associated with CVD. Thus, these studies emphasize that novel parameters derived from central pressure waveforms alone should be independent of or account for aortic blood flow.
IFs as Novel Markers of HF Risk
The arterial pressure wave is governed by dynamics of the LV, the systemic arteries, and their interactions; therefore, the pressure wave contains information about these separate systems and their optimum coupling during healthy and pathological states. For the heart and arterial system, optimum coupling occurs when minimum energy is wasted to convert LV systolic ejection to forward flow and pressure waves in the systemic circulation for perfusion. In multivariable-adjusted models, higher ω1 (the IF of the coupled heart and arterial system during systole) and higher Δω (total frequency variation) were associated with a higher risk for incident HF. Our observation is consistent with the forgoing theoretical work, which showed that ω1 was higher among a sample of HF patients with systolic dysfunction.12 In addition, Pahlevan et al12 observed that Δω was about zero among young, healthy participants with ideal ventricular-arterial coupling, but Δω was significantly higher among older individuals and among those with prevalent HF.12 During systole, the LV-arterial coupled system has a dominant frequency about which the instantaneous frequency oscillates, which is primarily dominated by cardiac function. Both HF with reduced and preserved systolic function (HFrEF and HFpEF, respectively) are progressive pathological states of aberrant cardiac function and suboptimum ventricular-arterial coupling associated with poor outcomes, including death. In HFrEF, arterial elastance is elevated but LV systolic elastance is reduced, leading to worse ventricular-arterial coupling. For example, Ky et al43 observed that worse ventricular-arterial coupling (assessed via Ea/Ees) predicted death and cardiac hospitalization outcomes among patients with HFrEF.43 Unlike HFrEF, which is characterized by LV dilation (eccentric remodeling) and systolic dysfunction, HFpEF is associated with concentric remodeling, myocardial fibrosis, microvascular rarefaction, and diastolic dysfunction of the LV. In HFpEF, both arterial and ventricular elastances are elevated, which may help to preserve ventricular-arterial coupling.44,45 However, in chronic HFpEF patients (compared with hypertensives without HF and healthy controls), Borlaug et al46 observed impaired dynamic ventricular-arterial coupling (as assessed by Ea/Ees) during exercise. Our data suggest that elevation of ω1 and Δω precedes HF clinical presentation and may represent preclinical markers for HF, indicating nascent impaired coupling of the ventricular-arterial system. Although distinct clinical differences among HF classifications exist, we did not distinguish by severity of HF or between HFrEF or HFpEF events. For example, Ho et al47 showed that incident HFpEF and HFrEF are preceded by different antecedent risk factors. Thus, additional studies should assess the differential relations for IFs at different stages and between participants with and without systolic dysfunction.
After the aortic valve closes, the heart and aorta are decoupled, and the dominant frequency is dictated only by the dynamics of the arterial system. Thus, ω2 represents the IF of the decoupled vasculature during diastole. In an adjusted multivariable model, lower ω2 was associated with higher risk for incident HF. Since the aorta is the largest artery and is coupled directly to the LV, it dominates the wave dynamics (and pulsatile load) that the heart experiences. Pahlevan et al12 observed lower ω2 with increasing age among healthy individuals, and ω2 was significantly lower among those with hypertension and peripheral artery disease (compared with healthy individuals).12 Taken together, these data suggest that lower ω2 may indicate early vascular remodeling associated with age, such as aortic stiffness and hypertension, which can elevate exposure of the heart to pressure pulsatility. Although pulsatile load contributes modestly to the total energy of the heart, multiple studies have shown that abnormal pulsatile load contributes to the development of ventricular remodeling and progression to HF.19,37,48,49 Future studies should examine relations between IFs and excessive pressure pulsatility resulting from abnormal blood pressure elevation and arterial stiffness.
Appropriate and accessible clinical tools are imperative for assessment of markers that may inform clinicians about prevention, diagnosis, and progression of CVD. Deriving well-known hemodynamic measures using time and frequency domain methods is clinically challenging because it requires both pressure and flow waves directly measured at the same site simultaneously. The novel IFs presented herein are derived via a direct time-frequency signal analysis that requires only one uncalibrated arterial pressure waveform.12,50,51 Measurement of carotid pressure via tonometry is noninvasive and easily and safely implemented in a clinical setting with relatively inexpensive equipment and modest training. Ventricular-arterial coupling can be assessed in the pressure–volume plane via analysis of pressure–volume loops. These methods, however, are invasive and limited as they do not characterize aspects of ventricular-arterial interactions, such as systolic loading sequence, that are clinically relevant for individuals at risk of HF or with prevalent HF.52 Thus, assessment of IFs is clinically feasible and may provide a novel method to assess HF risk.
Strengths and Limitations
Our prospective study is observational with many years of follow-up. We included a large, community-based sample consisting of men and women derived from a longitudinally followed cohort from across 3 generations of participants. Contrary to other common impedance and wave intensity methods, which require simultaneous measurement of pressure and flow waves,50,51 our proposed modified sparse time-frequency representation method (the IF method) requires only a central arterial (carotid) pressure waveform to perform the analysis. There are also limitations of our study to consider. We did not account for multiple testing; therefore, our investigation is more susceptible to type-1 error. Finally, our findings may not be generalizable to other racial and ethnic groups since this sample was comprised primarily of white participants of Western European descent.
Perspectives
We observed that novel IFs derived from central carotid waveforms are predictive of incident HF after adjustment for traditional CVD risk factors, heart rate, and systolic ejection period. Although differences in IFs were observed in older individuals and among those with prevalent cardiac and vascular dysfunction,12 we have shown for the first time the prognostic relation between IFs and incident CVD outcomes in a large community-based sample that spans the adult age spectrum. Assessment of IFs is noninvasive and requires only the analysis of a single waveform; therefore, translation to a clinical setting is feasible with relatively inexpensive equipment and modest training. In addition, since these IF measures were only modestly correlated with standard risk factors, they are suitable as potential biomarkers.53 Thus, our observations suggest that these novel IF measures could be used as potential early biomarkers to stratify individual CVD risk. Current preventive measures are targeted toward individuals who are identified as high risk based on traditional CVD risk factors; however, these algorithms fail to detect many individuals who will eventually develop CVD. Identifying this group before clinical manifestations and providing earlier detection and treatment could reduce CVD mortality and morbidity.
Acknowledgments
From the Framingham Heart Study of the National Heart Lung and Blood Institute of the National Institutes of Health and Boston University School of Medicine.
Sources of Funding
This work was supported by the National Heart, Lung and Blood Institute’s Framingham Heart Study (Contracts No. N01-HC-25195 and HHSN268201500001I) and by HL076784, AG028321, HL070100, HL060040, HL080124, HL071039, HL077447, HL107385, HL126136, HL128914, and 2-K24-HL04334.
Disclosures
G.F. Mitchell is owner of Cardiovascular Engineering, Inc, a company that develops and manufactures devices to measure vascular stiffness, serves as a consultant to and receives honoraria from Novartis, Merck, Servier and Philips, and was funded by research grants HL094898, DK082447, HL107385, HL104184, and HL126136 from the National Institutes of Health. N.M. Pahlevan holds equity and has a consulting agreement with Avicena LLC. D.G. Rinderknecht is the Chief Technology Officer for Avicena, LLC. The other authors report no conflicts.
Nonstandard Abbreviations and Acronyms
| CVD | cardiovascular disease |
| HF | heart failure |
| HFpEF | HF with preserved ejection fraction |
| HFrEF | HF with reduced ejection fraction |
| HR | hazard ratio |
| IF | intrinsic frequency |
| LV | left ventricle |
References
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
Novelty and Significance
What Is New?
We have shown for the first time the prognostic relations between novel intrinsic frequencies derived from aortic waveforms and incident cardiovascular disease outcomes in the community.
What Is Relevant?
Blood pressure is a well-known risk factor for cardiovascular disease; however, recent interest has shifted to potential information contained within pressure waveforms.
Assessment of intrinsic frequencies is noninvasive and requires only the analysis of a single waveform; therefore, translation to the clinic is feasible.
Since these intrinsic frequencies are only modestly correlated with standard risk factors, they are suitable as potential biomarkers.
Summary
Intrinsic frequencies are novel cardiovascular health indicators that are associated with increased risk for heart failure in the community.
 Intrinsic Frequencies of Carotid Pressure Waveforms Predict Heart Failure Events
Intrinsic Frequencies of Carotid Pressure Waveforms Predict Heart Failure Events