
- Altmetric
Hyperbolic phonon polaritons have recently attracted considerable attention in nanophotonics mostly due to their intrinsic strong electromagnetic field confinement, ultraslow polariton group velocities, and long lifetimes. Here we introduce tin oxide (SnO2) nanobelts as a photonic platform for the transport of surface and volume phonon polaritons in the mid- to far-infrared frequency range. This report brings a comprehensive description of the polaritonic properties of SnO2 as a nanometer-sized dielectric and also as an engineered material in the form of a waveguide. By combining accelerator-based IR-THz sources (synchrotron and free-electron laser) with s-SNOM, we employed nanoscale far-infrared hyper-spectral-imaging to uncover a Fabry–Perot cavity mechanism in SnO2 nanobelts via direct detection of phonon-polariton standing waves. Our experimental findings are accurately supported by notable convergence between theory and numerical simulations. Thus, the SnO2 is confirmed as a natural hyperbolic material with unique photonic properties essential for future applications involving subdiffractional light traffic and detection in the far-infrared range.
Systems that help to enable nanophotonics in the terahertz region are in demand for developing technologies. The authors introduce and study the photonic properties of tin oxide nanobelts as such a platform, supporting phonon polaritons in the far-IR range.
Introduction
Phonon polaritons (PhPs) result from the coupling of electromagnetic fields and crystal lattice vibrations, creating bosonic quasi-particles analogous to photons that are confined at interfaces of the crystalline lattices having opposite signs of permittivity1. They exist from THz to mid-IR spectral frequencies, within Reststrahlen bands (RBs), situated between transversal and longitudinal
In the mid-infrared (IR), strongly confined hyperbolic phonon polaritons (HPhPs) in hBN12,17 and α-MoO318–20 have gained much attention as they exhibit natural hyperbolicity and, hence, enhanced waveguiding properties. Consequently, the search for quantum materials that can support HPhPs in alternative energy ranges is of considerable interest. In the photonics scope, SnO2 shows negative permittivity in specific spectral ranges, from mid- to far-IR, where different types of polaritons coexist. Accordingly, SnO2 serves as a unique platform to study the optical transport of multimode PhPs. The compelling polaritonic properties of SnO2 stem from its crystalline structure (Fig. 1a) leading to an anisotropic phononic resonant
Here we present SnO2-NBs as a lithography-free nanophotonic platform suitable for cavity confinement of far-IR HPhPs. Assisted by scattering scanning near-field optical microscopy (s-SNOM)36–38 coupled to accelerator-based sources (Fig. 1e, f), we employed broadband IR-THz Synchrotron Infrared Nanospectroscopy (SINS)39–41 and IR-THz free-electron laser s-SNOM narrowband imaging (FEL s-SNOM)42–44 to experimentally access HPhP cavity modes in SnO2-NBs by direct nano-imaging of transverse HPhP standing waves. Our experimental observations are comprehensively described and supported by numerical simulations as well as analytical modeling for the NB as a Fabry–Perot (FP) cavity. Overall, our findings expand the possibilities of SnO2-NBs from an established 1D-semiconductor to a unique multimode hyperbolic material naturally optimized for the realization of subdiffractional resonators and, potentially, waveguiding in the far-IR range.

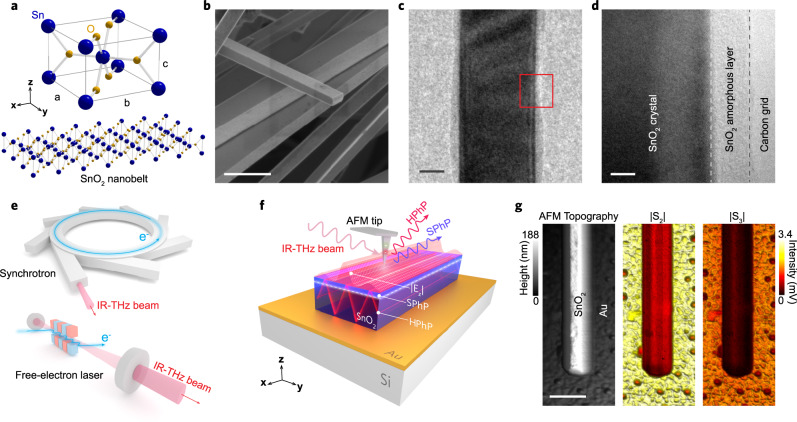
Overview of SnO2-NBs morphology and spectral nano-imaging experiments.
a Schematic of SnO2 unit cell for tetragonal Rutile, and crystalline structure of the nanobelt. Blue and yellow spheres represent tin (Sn) and oxygen (O) atoms, respectively. b SEM image of SnO2-NBs. c TEM image of an isolated nanobelt covered by a thin amorphous layer in a carbon grid. d High-magnification TEM image (red square in c) highlighting the crystalline structure covered by a thin amorphous layer. e Accelerator-based IR-THz sources employed in the spectral nano-imaging experiments. f Experimental schematic showing the IR-THz beam illuminating a metallic AFM tip (nano-antenna) for the s-SNOM experiment. The highly confined and vertically polarized electric fields (Ez) at the tip apex launch surface (SPhPs) and volume (HPhPs) polaritons waves in the SnO2-NB. g Morphology (AFM topography) and broadband reflectivity (|S2| and |S3|) nanoscale images of an isolated SnO2-NB/Au simultaneously measured by SINS. Scale bars in b, c, d, and g represent 1 µm, 50 nm, 5 nm, and 500 nm, respectively.
Results and discussion
Morphology, atomic structure, and broadband nano-reflectivity of SnO2-NBs
Tetragonal Rutile SnO2 (P42/mnm, space group 136) with lattice constants a = b = 0.473 nm and c = 0.318 nm in the form of NBs (Fig. 1a) were morphologically characterized by scanning and transmission electron microscopy (SEM and TEM). Figure 1b shows a SEM image of a set of NBs with a clear view of the smooth surface quality and average rectangular shape of the NBs. Typical transverse dimensions are 50–500 nm wide (w) and a few hundreds of nm thick (t). Lengths can reach up to 50 µm. Figure 1c presents a TEM image of a 120 nm wide isolated SnO2-NB. Figure 1d displays a high-magnification TEM image of the side edge of the NB (red square area in Fig. 1c) with a clear contrast between crystalline and amorphous phases of the nanostructure34. Complementary, SINS broadband imaging (Fig. 1g) unveils morphology (AFM topography) and broadband local reflectivity of a SnO2-NB transferred to Au substrate, a standard configuration for all samples analyzed in this work. The AFM topography corroborates the SEM and TEM morphological analysis, while the s-SNOM amplitude maps highlight broadband reflectivity indicating a preliminary and qualitative view of optical confinement in the NB. |S2| and |S3| represent the 2nd and 3rd harmonics of the s-SNOM tip demodulation, respectively, and confirm the high signal-to-noise ratio and background-free quality of the analysis. This work analyzed three NBs samples with different dimensions (t, w): SnO2-NB1 (93 nm, 350 nm), SnO2-NB2 (130 nm, 200 nm), and SnO2-NB3 (120 nm, 700 nm).
Multimode PhPs in SnO2-NBs: theory and experimental assessments
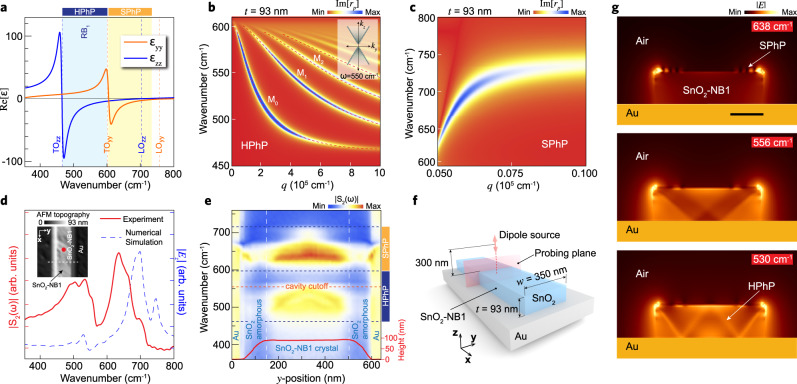
The SnO2 Rutile-type structure is known to exhibit optical phonons in the mid- and far-IR frequency ranges45,46. Thus, the knowledge of these specific phonon frequencies is key to define the photonic suitability of materials. The SnO2 polaritonic properties are defined in terms of the phononic resonant
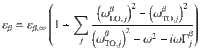

Polaritonic activity in SnO2-NBs.
a Real part components of the electrical permittivity (εyy and εzz) of SnO2 showing the hyperbolic (HPhP) spectral region (light blue-shaded Reststrahlen band type I, RB1) and surface phonon polaritons (SPhP) window (light yellow-shaded). b, c Dispersion relation for volume (HPhPs) and surface (SPhPs) phonon polaritons in SnO2, respectively. False-color plot represents the calculated imaginary part of the complex reflectivity
These phonon modes give rise to the RB, where the real parts of the in-plane and out-of-plane permittivities exhibit opposite signs
Figure 2b, c displays the calculated frequency–momentum (
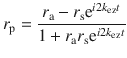
where
For the hyperbolic modes, considering highly confined subdiffractional waves (
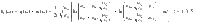
We employed SINS to experimentally access the full spatial-spectral response and imaging of PhPs in SnO2-NBs. Free-space broadband mid- to far-IR synchrotron radiation is strongly confined at the apex of a metallic AFM tip (see “Methods” section) allowing the launching and detection of PhPs waves in SnO2-NBs (Fig. 1f), enabled by the momentum match between the s-SNOM source/probe and these quasi-particles. The full spectral response across the RB1 of the sample SnO2-NB1 is presented in Fig. 2d. The SINS point spectrum, acquired at the center of the NB (red dot in Fig. 2d AFM inset), unveils strong IR activity in the frequency range from 420 to 700 cm−1, which are assigned to Sn–O antisymmetric vibrations. Within that spectral range, the peak at 686 cm−1 is assigned to Sn–O–Sn vibrations, and the bands in the lower frequency range (430–620 cm−1) are attributed to Sn–O stretching vibrations48,49.
To explore the polaritonic response of the SnO2-NB1, we acquired a spectral linescan with 25 nm spatial resolution (Fig. 2e) transverse to the NB (white-dashed line in Fig. 2d inset). Each point over the line carries a normalized amplitude spectrum (|S2| = |SSnO2|/|SAu|), as organized in the distance-frequency map displayed in Fig. 2e. An AFM profile (red line at the bottom) overlaps the |S2| spatio-spectral map allowing for a direct correlation between morphology and optical response of the NB. The AFM profile confirms the dimensions 93 nm × 350 nm (t × w) for the SnO2-NB1 sample. The linescan experiment unveils a complex spatial-frequency |S2| intensity pattern within the crystalline phase of the SnO2-NB, delimited by vertical white-dashed lines. The spectral response observed is consistent with the calculated permittivity and dispersion relations in Fig. 2a–c. In the range above 600 cm−1, a strong and uniform near-field response is attributed to SPhPs, as predicted from the single branch dispersion relation in Fig. 2c. Within the RB1 range, the near-field intensity fringes produce an interference pattern of frequency-dependent standing waves, suggesting transverse volume confinement of HPhP waves inside the NB. The horizontal orange dashed line in Fig. 2e indicates the cutoff frequency for the SnO2-NB1, further discussed in this report.
To support the interpretation of the SINS spatio-spectral analysis, we employed finite-difference time-domain (FDTD) numerical simulations to estimate the mid- to far-IR near-field response of the SnO2-NB. Figure 2f presents the parameter space for the numerical simulation, where the metallic tip was modeled as an ideal dipole source positioned 300 nm above the NB surface (see “Methods” section). A SnO2 nanobelt with dimensions t = 93 nm, w = 350 nm, and infinite length was defined as the polar crystal, analogous to the real morphology of the SnO2-NB1 sample. The substrate was modeled as Au in accordance with the experimental conditions. Figure 2d shows a simulated |Ez| spectrum (blue dashed amplitude profile) reconstructed from the integration of the out-of-plane electric field underneath the model dipole (red-dashed line in Fig. 2f) at the center of the NB. By comparing experiment and numerical simulation in Fig. 2d, a qualitative match is noticed for the central frequency of the main spectral features. In the line shape comparison, there is a fair correspondence between experiment and modeling for the SPhPs (peaks above 600 cm−1), while the HPhP range appears to be less trivial to model since volume waves are highly sensitive to the morphology of the NB. The divergence between simulated and measured spectrum in Fig. 2d can be attributed to realistic experimental aspects not taken into account in the simulation (see “Methods” section). For a better understanding of the volume PhPs in SnO2-NBs, Fig. 2g displays simulated electric field intensity maps from cross-sections of the SnO2-NB1 (probing plane in Fig. 2f) when excited by a broadband dipole source (see “Methods” section). At 638 cm−1 (inside the SPhPs window) there is no evidence of the polaritonic activity below the surface, while in the HPhP window we can clearly notice volume modes at 556 and 530 cm−1. The polaritonic response observed in the SINS spectral linescan (Fig. 2e) and supported by numerical simulations (Fig. 2g) provides a clear indication of the existence of HPhPs standing waves inside the polar crystal, therefore, configuring the SnO2-NB as a transverse FP cavity for PhPs.
We carried out SINS hyperspectral (HS) imaging (see Supplementary Note 2) of the SnO2-NB1 for a real-space visualization of the HPhP cavity modes. Figure 3b presents a series of frequency-selected nano-images inside the SnO2 RB1. These narrowband images were reconstructed from a full HS map in which each pixel of a 2D scanned image contains a full SINS spectrum, as described by the experimental diagram in Fig. 3a. These images covered a full cross-section of the NB enabling the visualization of interference fringes inside the crystal that are strongly dependent on the excitation frequency. The images at 539, 529, and 520 cm−1 unveil a systematic increase in the number of intensity maxima inside the NB (blue arrows in Fig. 3b), while the image at 565 cm−1 displays a flat and relatively weak near-field response, since this last excitation frequency lies well above the cutoff for this cavity (555 cm−1, from Fig. 2e). In contrast to dielectric waveguides where the cutoff frequency is at the lower limit of the waveguide mode dispersion, for the SnO2-NBs the cutoff frequency is at the upper limit since the magnitude of the transversal wavevector increases with decreasing frequency, as a consequence of the band type I dispersion of the SnO2 HPhP modes. Therefore, the HS analysis provides direct experimental evidence for the presence of HPhP cavity modes inside the crystalline phase of the SnO2-NBs.

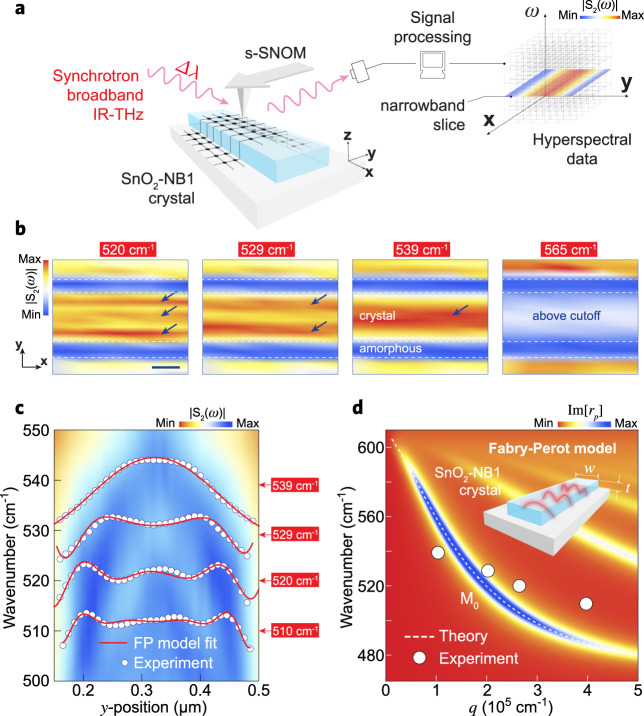
Experimental visualization of cavity modes in SnO2-NBs.
a Schematic of the SINS experiment for broadband IR-THz (Δλ) hyperspectral imaging. b SINS amplitude S2(ω) narrowband maps (10 cm−1 spectral width) reconstructed from a full hyperspectral image of SnO2-NB1/Au for the frequencies 520, 529, 539, and 565 cm−1. Horizontal white-dashed lines delimit crystalline and amorphous phases of the NB. Blue arrows guide the eyes highlighting the interference fringes formed by HPhP waves inside the SnO2-NB1 crystal. Scale bar represents 200 nm. c Spectral linescan (false-color map) superposed by SINS amplitude profiles (white circles) extracted from Fig. 2e. Red solid lines represent the FP model fitting (Eq. 5) of the experimental profiles at 510, 520, 529, and 539 cm−1. Amplitude profiles are in arbitrary units and were vertically offset for clarity. d Dispersion relation for HPhP volume fundamental mode (M0) calculated analytically from Eq. 2 through the imaginary part of the complex reflectivity
Figure 3c shows a spectral linescan (false-color map) of the SnO2-NB1 and respective amplitude profiles extracted at frequencies 510, 520, 529, and 539 cm−1. In order to understand the confining mechanism that regulates the wave patterns observed in Fig. 3b, c, we considered a model where the tip-launched HPhP waves (M0 mode), traveling across the y axis of NB (Fig. 3a), are reflected by its side edges forming a FP cavity (inset Fig. 3d). The mode M0 accumulates a round-trip phase (left part of the Eq. 4) that is equal to multiple integers of 2π (right part of the Eq. 4), thus, satisfying the FP maxima interference condition according to the following equation50,51:
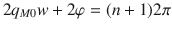
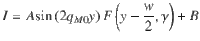
As a further matter, the FP model provided an effective lifetime estimate for the cavity modes of

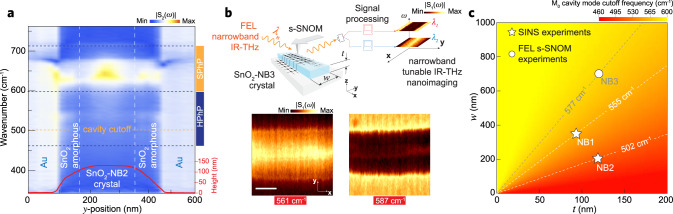
SINS and FEL s-SNOM control measurements outside NBs cavity condition.
a Experimental SINS amplitude S2(ω) spectral linescan across the SnO2-NB2 crystal (t = 130 nm, w = 200 nm). Red line profile at the bottom illustrates the AFM topography profile of the NB. Vertical white-dashed lines delimit amorphous and crystalline SnO2 phases. Horizontal blue dark-dashed lines denote the volume (HPhPs) and surface (SPhPs) phonon polaritons spectral ranges. The horizontal orange dashed line indicates the cutoff frequency for this NB. b (top) Tunable THz-IR (λn) s-SNOM nano-imaging experimental scheme and FEL s-SNOM narrowband maps (bottom) of the SnO2-NB3 (t = 117 nm, w = 700 nm) for the frequencies 561 and 587 cm−1. Scale bar represents 300 nm. c Cavity cutoff frequency map for M0 modes as a function NBs thickness (t) and width (w). Isofrequency diagonal-dashed lines denote M0 mode cavity cutoff for the SnO2-NB1, -NB2, and -NB3, analyzed by SINS and FEL s-SNOM in this work.
Figure 4c illustrates a false-color map of M0 cutoff frequencies as a function of the FP cavity form factor. The red-yellow color scale spans the whole RB1 and the cavity dimensions ranges are defined based on the sample geometries analyzed in this work. Isofrequency diagonal-dashed lines, for the FP cavities experimentally approached, indicate the (w, t) parameters corresponding to
In this work, we introduce SnO2 as a nanophotonic material suitable for multimode polaritonics in the mid- to far-IR frequency ranges. The results reported here place SnO2 in the list of natural anisotropic hyperbolic materials for extreme light confinement (e.g., hBN and MoO3) and extend the range of applications of this class of material towards the THz range. As a further step into applications, we studied the cavity confinement properties of as-grown SnO2-NBs exploring their lithography-free advantage. s-SNOM combined with accelerator-based synchrotron and free-electron laser sources enabled far-IR nanoscale spectral imaging of SnO2-NBs, uncovering an HPhP confinement mechanism consistent to resonant cavities. Hence, our experimental data is interpreted on the basis of a FP model, that consistently explains the measurements. In summary, this work provides a complete nano-optical description of SnO2 as a dielectric and also as a resonator. For a SnO2-NB with 93 × 350 nm2 (t × w) cross-section, we present SnO2’s permittivity and PhPs dispersion relation, covering the RB1 up to the SPhPs ranges, supported by experimental confirmation by SINS point spectra and linescan analyses, respectively. Inputting HPhP volume modes (M0) into the FP model allowed the reconstruction of the dispersion relation for the cavity modes M0, which was further attested by SINS hyperspectral analysis. From the model, we estimate a confinement factor of ∼50 and an effective lifetime of ∼0.10 ± 0.06 ps for the M0 cavity modes. Additionally, we measure two extra NB samples as supplementary evidences for the SnO2 cavity confinement study, including a control experiment using FEL s-SNOM to demonstrate the presence/absence of M0 modes below/above the cutoff frequency. Now confirmed as a hyperbolic medium highly feasible for THz subdiffractional resonators, we foresee SnO2-NBs as an essential building block in modern photonics, opening opportunities for light manipulation in the far-IR range.
Methods
Sample preparation
The SnO2-NBs analyzed in this work were synthesized via gold-catalyst-assisted vapor-liquid-solid (VLS) method21. A suitable amount of pure Sn powder (1 g, 4 N pure) was placed on top of a highly p-doped Si substrate coated with a 300-nm-thick amorphous SiO2 layer. A 5 nm Au layer was previously deposited on the Si/SiO2 substrate, to serve as a catalyst. A tube furnace was heated up to 800 °C in an air/argon atmosphere, and the temperature was kept constant for 2 h. Low O2 concentration on the tube furnace atmosphere is important during growth, in order to create shallow-level defects. After a 2 h cooling, SnO2-NBs were found on the Si/SiO2 substrate surface in a cotton-wool-like form. Finally, the SnO2-NBs were removed from the original substrate, ultrasonically dispersed in isopropanol, and then transferred to a fresh thermally evaporated Au(100 nm)/Si surface by drop coating. In this way, isolated NBs can be individually studied as illustrated in Fig. 1. The structure of the as-grown nanostructures was determined by X-ray diffraction (XRD) measurements34,52. They can be ascribed to the tetragonal Rutile SnO2 structure (P42/mnm, space group 136) with lattice constants a = b = 0.473 nm, c = 0.318 nm, according to the unit cell shown in Fig. 1a.
Scanning electron microscopy (SEM) images of the nanobelts were performed in a FEG Quanta 200 FEI microscope. Transmission electron microscopy (TEM) images of an individual SnO2 nanobelt were performed in a Tecnai G2-20 SuperTwin FEI 200 kV microscope.
Synchrotron infrared nanospectroscopy (SINS)
SINS experiments were performed at the Advanced Light Source (ALS)53 and at the Brazilian Synchrotron Light Laboratory (LNLS)41,54. Both beamlines use a quite similar optical setup comprising of an asymmetric Michelson interferometer mounted into a commercial s-SNOM microscope (NeaSnom, Neaspec GmBH), which can be basically described by an AFM microscope possessing a suited optical arrangement to acquire the optical near-field. In the interferometer, the incident synchrotron IR beam is split into two components by a beamsplitter defining the two interferometer arms formed by a metallic AFM tip and an IR high-reflectivity mirror mounted onto a translation stage. The IR beam component of the tip arm is focused by a parabolic mirror on the tip–sample region. In the experiment, the AFM operates in semi-contact (tapping) mode, wherein the tip is electronically driven to oscillate (tapping amplitude of ~100 nm) in its fundamental mechanical frequency
Free-electron laser scattering scanning near-field optical microscopy (FEL s-SNOM)
FEL-s-SNOM was performed at the free-electron laser FELBE at Helmholtz-Zentrum Dresden-Rossendorf (Dresden, Germany). FELBE provides pulsed narrowband radiation (spectral width of ~1% of central wavenumber) at mid-to-far-IR wavenumbers from 40 to 2000 cm−1 at a repetition rate of 13 MHz55. The IR radiation is focused onto the tip (Pt–Ir-coated Si cantilever) of a home-built s-SNOM setup42–44 that uses a self-homodyne detection scheme, with the latter leading to a mixed response of optical amplitude and phase56. The back-scattered light is detected with a MCT detector. Similar to SINS, demodulation at higher harmonics of the tip-tapping frequency (~160 kHz for our case) is used to differentiate the near-field signal from the far-field background. AFM tapping amplitude was set as ~100 nm peak-to-peak. FEL-s-SNOM 2D |S1| amplitude scans as shown in Fig. 4b are obtained while keeping all FELBE parameters fixed, i.e., at a fixed wavenumber. The spectral response is obtained by repeating the measurements after tuning the FEL to a different wavenumber.
Numerical simulations
The simulation results shown in Fig. 2 were obtained by finite-difference time-domain (FDTD) calculations assisted by the commercial code Lumerical FDTD v8.23. We considered an infinite long rectangular cross-section nanobelt on Au substrate with a thickness (t) and width (w) of 93 and 350 nm, respectively. The Au dielectric function was taken from Palik57. Both axial and transverse components of the SnO2 permittivity,
Additionally, divergences from the simulated to the experimental spectrum in Fig. 2d can be attributed to (i) divergences from the theoretical and the experimental dielectric tensor, (ii) approximation of the
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-021-22209-w.
Acknowledgements
We thank the Brazilian Synchrotron Light Laboratory (LNLS), Advanced Light Source (ALS), and Helmholtz-Zentrum Dresden-Rossendorf (HZDR) for providing beamtime for the experiments. Parts of this research were carried out at ELBE at the Helmholtz-Zentrum Dresden-Rossendorf e. V., a member of the Helmholtz Association. I.D.B., E.R.V., and J.C.G. thank Geraldo M. Ribeiro (UFMG) for preliminary studies of production and characterization of tin oxide nanobelts and A. Gobbi (LNNano), and M.H.O. Piazetta (LNNano) for the support on samples preparation. R.O.F. and I.D.B. thank T.M. Santos (LNLS) and A. Cernescu (Neaspec) for technical assistance. I.D.B. and A.M. acknowledge the financial support from the Brazilian Nanocarbon Institute of Science and Technology (INCT/Nanocarbono). F.C.B.M. and F.H.F. acknowledge the CNPq project 140594/2020-5. R.O.F. and R.A.M. acknowledge the FAPESP project 2019/08818-9. R.O.F. acknowledges the support from CNPq through the research grant 311564/2018-6 and FAPESP Young Investigator grant 2019/14017-9. I.D.B. acknowledges the support from CNPq through the research grant 311327/2020-6. J.C.G. acknowledges the financial support of Brazilian agencies CNPq and FAPEMIG. L.W., L.M.E., and S.C.K. acknowledge funding by the BMBF under grants 05K16ODA and 05K19ODB, as well as by the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter (ct.qmat) and by the TU Dresden graduate academy. E.R.V. would like to acknowledge the CNPq projects 403360/2016-1 and 311534/2017-1, the Center of Microscopy at the Universidade Federal de Minas Gerais (UFMG) and Universidade Tecnológica Federal do Paraná (CMCM-UTFPR-CT) for providing the equipment and technical support for the electron microscopy experiments. This research used resources of the Advanced Light Source, a U.S. DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.
Author contributions
I.D.B. together with E.R.V. and J.C.G. initiated the research. E.R.V. and J.C.G. prepared the samples. A.M. provided the interpretation of the crystalline structure of the nanoblets. I.D.B., H.A.B., F.C.B.M., and R.O.F. carried out the SINS experiments. J.M.K., L.M.E., L.W. , and S.C.K. prepared the instrumentation for the FEL measurements. I.D.B., L.W., and F.C.B.M. carried out the FEL experiments. I.D.B., R.A.M., and F.H.F. performed post-experimental data analysis. I.D.B., R.O.F., F.H.F., and R.A.M. interpreted the theoretical approach of polaritonic modes. R.A.M. developed the FDTD simlulations. All authors took part in the interpretation of the phenomena. I.D.B., F.H.F., R.A.M., and R.O.F. prepared the manuscript.
Data availability
The source data that support the findings of this study are available from the corresponding author upon reasonable request. All these data are directly shown in the corresponding figures without further processing.
Code availability
Scripts for theoretical predictions and contour plot processing are available from the corresponding authors upon reasonable request.
Competing interests
The authors declare no competing interests.
References
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
 Sub-diffractional cavity modes of terahertz hyperbolic phonon polaritons in tin oxide
Sub-diffractional cavity modes of terahertz hyperbolic phonon polaritons in tin oxide
