Outline

In what follows, we first introduce the setup of the problem and the main idea of our method for certifying randomness with the adversarial imperfections discussed above. Our method works in the presence of both the classical and quantum side information of Eve. We then illustrate the performance of our method with simulations, showing the advantage of Eve with an access to quantum side information. Finally, we present our experimental realization of a simple low-latency real-time QRNG enabled by our method.

Setup of the problem

To generate random bits, we consider an experiment with a sequence of n repeated trials. These trials are not necessarily independent or identical. We denote the input (basis choice) and the output (measurement outcome) at the k’th trial by the random variables I_k and O_k, respectively. The inputs and outputs of the experiment are then $$ {\mathbf{I}}_n={\left(I_k\right)}_{k=1}^n$$ and $$ {\mathbf{O}}_n={\left(O_k\right)}_{k=1}^n$$. The amount of randomness in the outputs relative to both the inputs and Eve is quantified by the smooth conditional min-entropy $$ H_{\min }^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$, where ϵ_s is the smoothness error²¹. We consider two alternative smooth conditional min-entropies $$ H_{\min ,\mathrm{c}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$ and $$ H_{\min ,\mathrm{q}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$ in the presence of the classical and quantum side information of Eve, respectively. The ability of Eve to access quantum side information (which is stored in a quantum system $$ \mathsf{E}$$) as compared with classical side information (which is stored in a classical, random variable E) allows attacks that can take advantage of long-term quantum memories^22,23 correlated in a quantum manner with the quantum devices used for the state preparation in the experiment. Our goal is to bound the smooth conditional min-entropies $$ H_{\min ,\mathrm{c}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$ and $$ H_{\min ,\mathrm{q}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$ from below.

For certifying the randomness in the outputs O_n relative to the inputs I_n and Eve, we must assume that the outputs O_n are kept private and not accessible to Eve. We allow Eve to hold classical or quantum side information about the state prepared at a trial. At the same time, we allow Eve to manipulate the distribution of the possible inputs and the specific forms of the associated measurements at the trial, as long as these manipulations satisfy the prespecified imperfection bounds. We assume that by manipulations Eve can access classical side information but not quantum side information about the measurement performed. The method to be presented allows classical correlations between Eve’s side information about the state prepared and Eve’s partial knowledge of the input and measurement used at each trial. That is, the state prepared can be classically correlated with the input selected or the measurement performed. We emphasize that our method cannot be applied in the case where at each trial Eve’s side information about the state is correlated in a quantum manner with Eve’s partial knowledge of the input and measurement. Moreover, although we allow Eve to manipulate the input distribution, we assume that before a trial Eve has no perfect knowledge of which specific input to be selected at the trial. This assumption is required for security analysis; otherwise, Eve can deterministically forecast the output of the trial, and it would be therefore impossible to certify randomness²⁴.

Main idea of our method

For certifying randomness with respect to classical and quantum side information, we construct probability estimation factors (PEFs)^25,26 and quantum estimation factors (QEFs)^27,28, respectively. Both a PEF and a QEF are non-negative functions of the input I and output O of a trial, denoted by F_c(I, O) and F_q(I, O). The key observation is that the smooth conditional min-entropies $$ H_{\min ,\mathrm{c}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$ and $$ H_{\min ,\mathrm{q}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$ can be bounded from below, once we know the respective products $$ {\prod }_{k=1}^n{F}_{\mathrm{c}}\left(i_k,o_k\right)$$ and $$ {\prod }_{k=1}^n{F}_{\mathrm{q}}\left(i_k,o_k\right)$$. Here, i_k and o_k are the observed values of the input and output at the k’th trial. This key observation can be formalized by Theorem 1 and Theorem 2 in the “Methods” section. We emphasize that PEFs and QEFs can use the result of each trial for both verifying and accumulating randomness. Both PEFs and QEFs have been constructed for certifying device-independent randomness^15,25–28. In this work, we develop methods to construct PEFs and QEFs for the scenario of our interest. In particular, the PEFs and QEFs constructed are adapted to the adversarial imperfections in both the state source and the measurement apparatus. Both PEFs and QEFs have the advantage that significantly less data is required in order to certify a fixed amount of randomness. Details for constructing PEFs and QEFs are discussed in the “Methods” section.

After certifying the amount of randomness, we run the randomness extractor developed in ref. ²⁹ with extractor error ϵ_x = ϵ − ϵ_s in order to generate random bits which are within distance of ϵ > ϵ_s from uniform. The distance ϵ is termed the soundness error. For the results presented in this work, we set the smoothness error and the extractor error to be ϵ_s = 0.8ϵ and ϵ_x = 0.2ϵ.

Advantage of quantum adversaries over classical adversaries

We illustrate with simulations the performance of our method in the asymptotic limit, so that one can see the expected behavior of our QRNG scheme. When the trials are identical and n approaches infinity, the amount of randomness certified by our method increases linearly with n. The increasing rate (per trial) is called the asymptotic randomness-generation rate. The rates in the presence of classical and quantum side information, R_c and R_q, certified by our method are optimal (see refs. ^25,27 for general proofs). We can quantify R_c and R_q as functions of the depolarization noise d (as defined in the caption of Fig. 1). The results presented in Fig. 1 clearly indicate that Eve’s access to quantum side information as compared with classical side information results in a reduction of the randomness-generation rate. Such a reduction is an important yet unquantified advantage to Eve.

Fig. 1

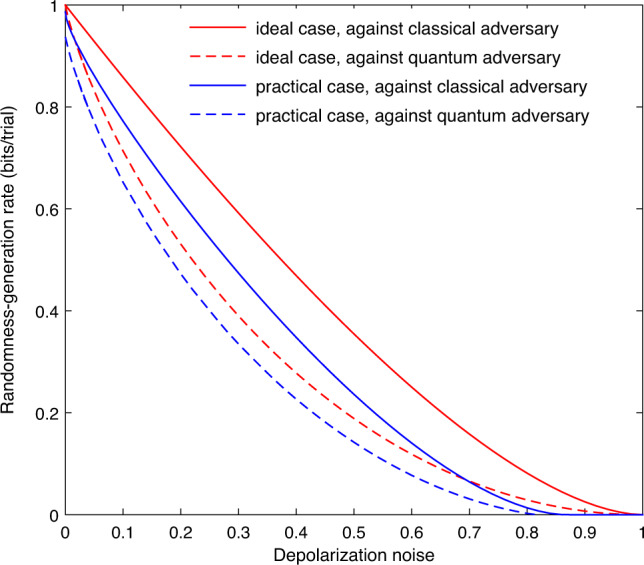
Asymptotic randomness-generation rates R_c and R_q as functions of the depolarization noise d.

For illustration purpose, here we simulate the result at a trial according to either the X-basis or Z-basis measurement on the depolarized single-photon state $$ \left(1-d/2\right)∣0⟩⟨0∣+d/2∣1⟩⟨1∣$$, where $$ ∣0⟩$$ and $$ ∣1⟩$$ are the two eigenstates (in the single-photon subspace) of the Z-basis measurement and d quantifies the depolarization noise. At each trial the X-basis measurement is selected with probability P_X = 0.9999, and so the imbalance τ = (P_X − P_Z)/2 is exactly known. Our method can certify randomness without assuming that the state and measurements are fully characterized. Instead, our method requires only an upper bound δ on the misalignment angle between the two measurement bases and a lower bound q_1,lb on the probability of a single photon in a practical photon source. For the ideal case (the red curves), we set q_1,lb = 1 and δ = 0, while for the practical case (the blue curves), we set q_1,lb = 0.95 and δ = 5^∘.

Experimental realization of a simple low-latency real-time QRNG

To realize a QRNG, we perform measurements on photonic time-bin states, where the quantum information is encoded into the superposition of two different temporal positions (time bins) of an optical pulse. The two time bins are usually called the early and late time bins denoted by t_e and t_l. Time-bin encoding has been widely used especially in fiber-based quantum communication systems³⁰. The advantage of time-bin encoding lies in that both the state source and the measurement apparatus required are easily packaged onto a chip, which is an important factor to consider for practical QRNG use.

To produce randomness, at each trial we attempt to prepare the time-bin qubit state $$ \mid 1_{t_e}⟩\otimes \mid 0_{t_l}⟩$$, where $$ ∣j_t⟩$$ represents the j-photon state located at the time bin t ∈ {t_e, t_l}. After passing it through an unbalanced Mach–Zehnder interferometer (MZI), we measure the time-bin qubit, as depicted in Fig. 2. The difference in photon transit time between the two unbalanced paths of the MZI matches the separation between t_e and t_l. Therefore, a photon can come out from the MZI at the early, middle and late time bins denoted by $$ t_e^{\prime }$$, $$ t_m^{\prime }$$ and $$ t_l^{\prime }$$, respectively. If the photon comes out at $$ t_e^{\prime }$$ or $$ t_l^{\prime }$$, then the Z-basis (time-bin basis) is passively selected. In this case, the arrival time indicates the measurement outcome. If the photon comes out at $$ t_m^{\prime }$$, then the X-basis (superposition basis) is passively selected. In this case, the two output ports of the MZI indicate which measurement outcomes are observed. Note that if the first beam splitter in the MZI has the 50:50 splitting ratio, the two measurement bases are uniformly randomly selected. In this sense, the first beam splitter in the MZI acts effectively as a physical but uncertified random number generator³¹.

Fig. 2

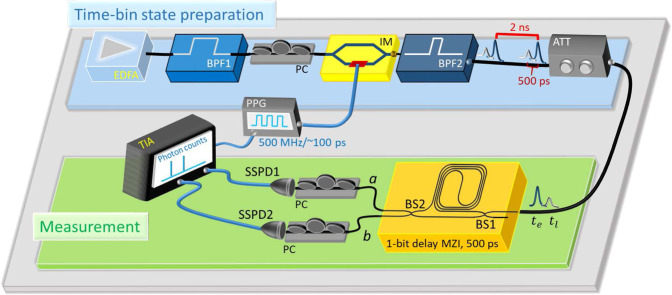
Schematic diagram of our experimental setup.

First, the time-bin state $$ \mid 1_{t_e}⟩\otimes \mid 0_{t_l}⟩$$, where there is a single photon at the early time bin t_e and no photon at the late time bin t_l, is prepared in the ideal case. Second, after passing over an unbalanced Mach–Zehnder interferometer (MZI), the optical pulse is detected by two superconducting nanowire single-photon detectors (SSPDs). The MZI is composed of two beam splitters, BS1 and BS2, and has two output ports a and b. In the diagram the abbreviations have the following meanings. EDFA: erbium-doped fiber amplifier, BPF: band-pass filter, PC: polarization controller, IM: intensity modulator, ATT: optical attenuator, PPG: pulse pattern generator, TIA: time-interval analyzer. See the “Methods” section for details.

In practice, the source emits zero photon with a non-zero probability at each trial, and threshold detectors (which cannot resolve photon number) of finite efficiency are employed. Moreover, a photon can be lost over the transmission from the source to the detectors. Therefore, not all trials have detector clicks. For security analysis, we assume that the trials with detector clicks are a fair sample of all trials. Accordingly, no-click events do not affect the security analysis of randomness generation but only the rate and latency achieved in practice.

Now for certifying randomness, we must take into account the adversarial imperfections in our setup. Neither of the two beam splitters, BS1 and BS2, in the MZI has the ideal 50:50 splitting ratio. In addition, the two detectors at the output ports a and b may have different efficiencies η_a and η_b. These facts induce not only an imbalance between the probabilities P_X and P_Z of selecting the X-basis and Z-basis but also a misalignment between the two bases. Based on a calibration of our measurement apparatus, we found that the splitting ratios of BS1 and BS2 are 53.8:46.2 and 46.9:53.1, respectively, and that the ratio η_a: η_b is 1.024:1. Consequently, the imbalance τ = (P_X − P_Z)/2 and misalignment δ satisfy the conditions ∣τ∣ ≤ 0.041 and δ ≤ 3.565^∘. Moreover, we estimated that the single-photon component of the optical pulse contributes at least 99.3% of all click events. More details behind the above characterizations are available in Supplementary Note 3. Accordingly, we conservatively assume that ∣τ∣ ≤ 0.06, δ ≤ 6^∘, and q_1,lb = 0.98 in our security analysis, specifically, for constructing PEFs and QEFs to guarantee certifiable randomness generation.

Based on a set of calibration data, we estimated the expected number, k_exp, of random bits certifiable every 0.1 s runtime at a soundness error ϵ varying from 10⁻⁵ to 10⁻³⁰. The dependence of k_exp on ϵ in the presence of either quantum or classical side information is illustrated in Fig. 3. As expected fewer number of random bits can be certified with respect to quantum side information than with respect to classical side information. However, the number of certifiable bits in each situation is not significantly affected by the soundness error in the range considered.

Fig. 3

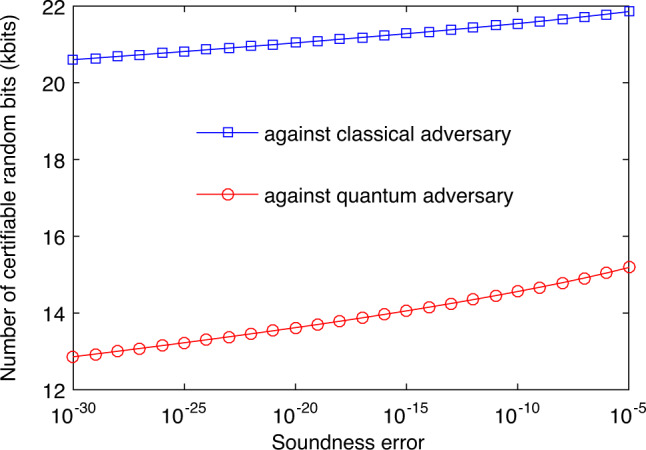
Trade-off between the soundness error ϵ and the expected number of random bits certifiable from the measurement outcomes observed every 0.1 s runtime.

The results in the presence of classical and quantum side information are shown as the blue and red curves, respectively.

We finally consider a request for a block of 8192 (or 2 × 8192) random bits in the presence of quantum (or classical) side information and with soundness error bounded by 2⁻⁶⁴ ≈ 5.42 × 10⁻²⁰. The results in Fig. 3 strongly suggest that our QRNG can successfully fulfill the request every 0.1 s runtime. Indeed, the success probability is estimated to be at least 1 − 2⁻³⁸⁰ (or 1 − 2⁻⁴⁷⁸) in the presence of quantum (or classical) side information (see Supplementary Note 4 for details). We further demonstrate this repeated fulfillment in experiment. For this, before the experiment we fixed the PEF and QEF used, as well as several other parameters used in our security analysis, based on the above calibration data (see Supplementary Note 4). Then we ran the experiment for 420 s and processed the data block obtained every 0.1 s runtime successively. For each data block, we certified a lower bound on the number of random bits extractable with soundness error 2⁻⁶⁴ and with respect to either quantum or classical side information. If the certified lower bound exceeds the request threshold, the instance of our QRNG succeeds. Conditional on success, we run the randomness extractor developed in²⁹ to generate the final random bits. The randomness extractor is seed-efficient and requires an additional processing time: for extracting 8192 (or 2 × 8192) random bits it takes 0.02 s (or 0.04 s), respectively. Totally we ran 4200 instances of our QRNG. The analysis results summarized in Fig. 4 show the success of each instance.

Fig. 4

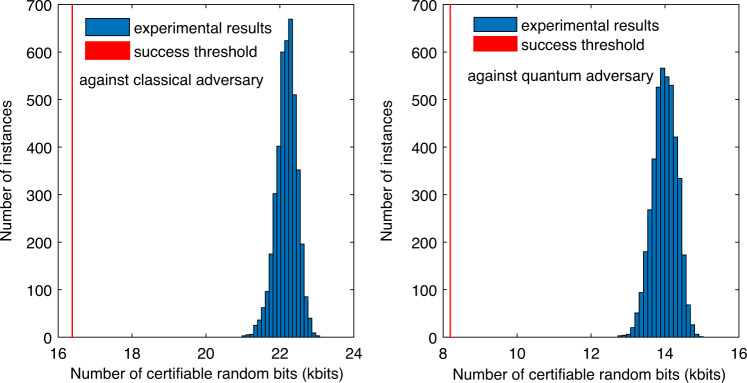
Histogram of the numbers of random bits certifiable with soundness error 2⁻⁶⁴ from 4200 instances of our QRNG: the left and right panels are for certifying randomness with respect to classical and quantum side information, respectively.

Each instance of our QRNG uses a data block obtained in 0.1 s runtime. In each panel, the experimental results are shown as blue bars, while the success threshold is shown as the red line.

Outline

Here we provide details of our experimental setup for realizing a simple low-latency real-time certifiable quantum random number generator. We also introduce the general framework of probability estimation (or quantum probability estimation) for certifiable randomness generation in the presence of classical (or quantum) side information. Further, we discuss the details of implementing these general frameworks in the presence of the adversarial imperfections considered in both the state source and the measurement apparatus.

Experimental implementation

Our experimental setup is shown in Fig. 2. To generate time-bin states, amplified spontaneous emission from an erbium-doped fiber amplifier (EDFA), which has a broad spectrum and thus can be regarded as inherently dephased, is used as a light source. After reducing its bandwidth by a band-pass filter (BPF1) of 1551.1 ± 1.2 nm, the light from the EDFA is sent into an intensity modulator (IM) to generate (in the ideal case) the time-bin qubit state consisting of the single-photon pulse $$ \mid 1_{t_e}⟩$$ and the vacuum pulse $$ \mid 0_{t_l}⟩$$. A pulse pattern generator (PPG) is used to modulate the IM at a repetition rate of 500 MHz using a pulse of width approximately 100 ps. The same modulation signal is also sent to the time-interval analyzer (TIA), to synchronize the IM and TIA. A BPF2 of 1551.1 ± 0.44 nm is then used to further surpress the noise outside of the bandwidth. With the help of an optical attenuator (ATT), we then adjust the average photon number per pulse to a value of approximately 0.0035. Finally, we launch the time-bin pulse into an unbalanced Mach–Zehnder interferometer (MZI), which is fabricated using planar lightwave circuit technologies³⁵. The path difference of the unbalanced MZI is 500 ps, the same as the time separation between the early and late time bins. The insertion loss of the MZI is approximately 2.0 dB. The photons from the output ports of the MZI are detected by two superconducting nanowire single-photon detectors (SSPDs), where the detection events are recorded by the TIA. The system detection efficiency of each SSPD is about 59%, and the dark count rate of each SSPD is less than 40 s⁻¹. A few polarization controllers (PCs) are inserted before the IM and SSPDs in order to adjust the polarization of photons. We measure that roughly 470,000 trials with detector clicks are generated per second.

Certifiable randomness generation in the presence of classical side information

To certify randomness with respect to the classical side information of Eve, we apply the framework of probability estimation as developed in refs. ^25,26. For this, we need to characterize each trial of the experiment by a classical model. In the scenario of our interest, the model is adapted to the adversarial imperfections considered. Given the model, we construct probability estimation factors (PEFs) which can certify randomness with respect to classical side information. Below we first introduce the concepts of classical models and PEFs, and then present the main result of probability estimation for randomness generation.

Let us focus on a generic trial in the experiment with an input I and an output O. We omit the trial index for generic trials. As is conventional, we denote a random variable and its possible value by an upper-case letter in regular math font and the corresponding lower-case letter. The classical side information E of Eve can be correlated with the trial input I and trial output O. This correlation is described by a joint probability distribution $$ \mathbb{P}\left(I,O,E\right)$$. However, in practice we cannot access the classical side information E held by Eve. Therefore, we can characterize only the distribution of I and O conditional on each possible value e of E, denoted by $$ \mathbb{P}\left(I,O\mid E=e\right)$$. The set of conditional distributions $$ \mathbb{P}\left(I,O\mid E=e\right)$$, for all possible e, achievable at a trial is defined to be the classical model $$ \mathcal{C}$$ for the trial. For simplicity we make the condition on Eve’s classical side information implicit in the rest of the paper, and so the classical model $$ \mathcal{C}$$ specifies the set of probability distributions $$ \mathbb{P}\left(I,O\right)$$ achievable at a trial. To certify randomness in the output O conditional on the input I and on the classical side information E, we consider a class of non-negative functions F_c: (i, o) ↦ F_c(i, o), called PEFs for the classical trial model $$ \mathcal{C}$$. A PEF with a positive power β_c is a non-negative function F_c: (i, o) ↦ F_c(i, o) which satisfies the PEF inequality

The number of near-uniform random bits extractable from the outputs O_n given the inputs I_n and the classical side information E of Eve is quantified by the classical smooth conditional min-entropy $$ H_{\min ,\mathrm{c}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$²¹. Here, the smoothness error ϵ_s measures the total-variation distance between the actual distribution and an ideal distribution of I_n, O_n and E (see Definition 9 of ref. ²⁶). Suppose that each trial of an experiment is characterized by the classical model $$ \mathcal{C}$$. Denote the PEF with power β_c at the k’th trial by F_c,k, which is a function of I_k and O_k, and let the variable T_c,n be the product of PEFs up to the n’th trial, that is, $$ T_{\mathrm{c},n}={\prod }_{k=1}^n{F}_{\mathrm{c},k}$$. In practice, the input at a trial is independent of the outputs of the previous trials conditionally on the classical side information E and the inputs of the previous trials. Under this conditional-independence condition, probability estimation can certify randomness with respect to classical side information according to the following theorem:

Theorem 1 (Theorem 1 of ref. ²⁶): Let 1 ≥ κ, ϵ_s > 0 and 1 ≥ p ≥ 1/∣Rng(O_n)∣, where ∣Rng(O_n)∣ is the number of possible outputs after n trials. Define Φ to be the event that T_c,n≥ 1/($$ p^{{\beta }_c}$$ϵ_s). For each joint probability distribution $$ \mathbb{P}\left({\mathbf{I}}_n,{\mathbf{O}}_n,E\right)$$, either the probability of the event Φ is less than κ or the classical smooth conditional min-entropy, when the event Φ happens, satisfies

The event Φ can be interpreted as the event that the experiment succeeds. When the experiment succeeds, we compose the classical smooth conditional min-entropy bound in Eq. (2) with a classical-proof strong extractor of error ϵ_x (in total-variation distance), in order to obtain random bits which are within soundness error (in total-variation distance) ϵ = ϵ_s + ϵ_x from uniform in the presence of classical side information. See Sect. IV C of ref. ²⁵ for the details of the end-to-end randomness generation. Note that an extractor is strong if the joint of its output and the seed is nearly uniform, while an extractor is classical-proof if it works in the presence of classical side information. In our experiment, we used Trevisan’s extractor³⁶ as implemented by Mauerer, Portmann, and Scholz²⁹, which we refer to as the TMPS extractor. The TMPS extractor is an efficient classical-proof strong extractor that requires few seed bits^29,36. The way of running the TMPS extractor for our case is the same as for the case of device-independent randomness generation with respect to classical side information studied in refs. ^13,25.

Certifiable randomness generation in the presence of quantum side information

To certify randomness with respect to the quantum side information of Eve, we apply the framework of quantum probability estimation as developed in refs. ^27,28. For this, we need to characterize each trial of the experiment by a quantum model. In the scenario of our interest, the model is adapted to the adversarial imperfections considered. Given the model, we construct quantum estimation factors (QEFs) which can certify randomness with respect to quantum side information. Below we first introduce the concepts of quantum models and QEFs, and then present the main result of quantum probability estimation for randomness generation.

Consider a generic experimental trial which has a classical input I and a classical output O. Suppose that Eve holds a quantum system $$ \mathsf{E}$$, which carries the quantum side information about the experiment. So, the quantum system $$ \mathsf{E}$$ is correlated with the trial input I and trial output O. The correlation between $$ \mathsf{E}$$ and (I, O) can be described by a classical-quantum state

The number of near-uniform random bits extractable from the outputs O_n given the inputs I_n and the quantum side information carried by the system $$ \mathsf{E}$$ of Eve is quantified by the quantum smooth conditional min-entropy $$ H_{\min ,\mathrm{q}}^{{ϵ}_s}\left({\mathbf{O}}_n\mid {\mathbf{I}}_n,\mathrm{Eve}\right)$$²¹. Here, the smoothness error ϵ_s measures the purified distance between the actual state and an ideal state of I_n, O_n and $$ \mathsf{E}$$ (see Sect. IV of ref. ²⁸). Suppose that each trial of an experiment is characterized by the quantum model $$ \mathcal{Q}$$. Denote the QEF with power β_q at the k’th trial by F_q,k, which is a function of I_k and O_k, and let the variable T_q,n be the product of QEFs up to the n’th trial, that is, $$ T_{\mathrm{q},n}={\prod }_{k=1}^n{F}_{\mathrm{q},k}$$. In practice, the input at a trial is independent of the outputs of the previous trials given the quantum side information in $$ \mathsf{E}$$ and the inputs of the previous trials. Under this conditional-independence condition, quantum probability estimation can certify randomness with respect to quantum side information according to the following theorem:

Theorem 2 (Theorem 3 of ref. ²⁸): Let 1≥κ, ϵ_s, p > 0. Define Φ to be the event that $$ T_{\mathrm{q},n}\ge 1/\left(\right)p^{{\beta }_{\mathrm{q}}}\left({ϵ}_s^2/2\right)\left)\right)$$. For each classical-quantum state $$ {\rho }_{{\mathbf{I}}_n{\mathbf{O}}_n\mathsf{E}}$$, either the probability of the event Φ is less than κ or the quantum smooth conditional min-entropy, when the event Φ happens, satisfies

The event Φ can be interpreted as the event that the experiment succeeds. When the experiment succeeds, we compose the quantum smooth conditional min-entropy bound in Eq. (6) with a quantum-proof strong extractor of error ϵ_x (in trace distance), in order to obtain random bits which are within soundness error (in trace distance) ϵ = ϵ_s + ϵ_x from uniform in the presence of quantum side information. See Sect. V of ref. ²⁸ for the details of the end-to-end randomness generation. Note that an extractor is quantum-proof if it works in the presence of quantum side information. As the TMPS extractor^29,36 is a quantum-proof strong extractor³⁷, we use this extractor for randomness extraction. The way of running the TMPS extractor for our case is the same as for the case of device-independent randomness generation with respect to quantum side information studied in refs. ^15,27,28.

Constructions of PEFs and QEFs with adversarial imperfections

Both probability estimation and quantum probability estimation are general frameworks for certifying randomness; however, their implementations are case-dependent as both the classical and quantum models for a trial depend on the case of interest. For the case of device-independent randomness generation, both frameworks have been implemented, see refs. ^15,25–28. In this work we would like to apply probability estimation and quantum probability estimation for randomness generation with partially characterized quantum devices. For this, we need to  first construct the classical model $$ \mathcal{C}$$ and the quantum model $$ \mathcal{Q}$$ for an experimental trial in the scenario of our interest, and then construct the corresponding PEFs and QEFs. Below we provide an overview of our constructions. Details are presented in Supplementary Notes 1 and 2.

To construct the models $$ \mathcal{C}$$ and $$ \mathcal{Q}$$ for the scenario of our interest, we observe that although the measurements along the X-basis and Z-basis are difficult to be precisely characterized, both of them are block-diagonal with respect to various photon-number subspaces. Therefore, the model $$ \mathcal{C}$$ (or $$ \mathcal{Q}$$) can be expressed as a convex combination (or a direct sum) of sub-models $$ {\mathcal{C}}_j$$ (or $$ {\mathcal{Q}}_j$$), where the sub-models $$ {\mathcal{C}}_j$$ and $$ {\mathcal{Q}}_j$$ are the classical and quantum models conditional on the number of photons j emitted from the source. So, we need only to construct the sub-models $$ {\mathcal{C}}_j$$ and $$ {\mathcal{Q}}_j$$ individually, which is discussed in the next two paragraphs.

To construct the sub-models $$ {\mathcal{C}}_1$$ and $$ {\mathcal{Q}}_1$$ when a single photon is emitted (i.e., j = 1), we take into account of the bounds on the adversarial misalignment and on the adversarial imbalance between the X-basis and Z-basis, and consider all the possible single-photon states which may be correlated with the side information of Eve. We assume that the measurements in the single-photon subspace are projective, although these measurements are not precisely characterized. So, the misalignment and imbalance are sufficient for characterizing these imperfect measurements. The above assumption can be relaxed to some degree as explained in Supplementary Notes 1 and 2. When Eve can manipulate the misalignment or imbalance depending on the auxiliary degrees of freedom of the single photon such as spatial mode, frequency or polarization, we need to represent the single-photon state and the associated measurement operators in a Hilbert space describing not only the time-bin degree of freedom for information encoding but also the auxiliary degrees of freedom manipulable by Eve. In this case, we take advantage of the assumption that the coherent superposition of states for an auxiliary degree of freedom manipulable by Eve does not play a role throughout the measurement process. (Such assumption has been exploited for verifying entanglement³⁸ and further for proving the security of quantum key distribution³⁹ in the presence of side channels that can induce detection-efficiency mismatch.) This assumption can be justified if in the setup for time-bin measurements there is no quantum interference between any pair of states for the auxiliary degree of freedom manipulable by Eve (which is true in practice as we think). In addition, the above assumption is consistent with the assumption specified in the Results section that by manipulations Eve can access classical side information but not quantum side information about the measurement performed. Therefore, each measurement operator on a single photon is block-diagonal with respect to various states for the auxiliary degrees of freedom, where each block is described by a qubit measurement. As a consequence, for constructing the sub-models $$ {\mathcal{C}}_1$$ and $$ {\mathcal{Q}}_1$$ the single-photon state and the associated measurement operators can be treated without loss of generality as living in a two-dimensional Hilbert space, even in the general case where Eve’s manipulations can depend on the auxiliary degrees of freedom of the single photon. We note that for security analysis in the above general case, the bounds on the misalignment and on the imbalance between the X-basis and Z-basis should be satisfied by the measurement operators in each two-dimensional Hilbert space obtained by projecting onto each particular state for the auxiliary degrees of freedom manipulable by Eve.

On the other hand, when multiple photons are emitted (i.e., j > 1) we construct the sub-models $$ {\mathcal{C}}_j$$ and $$ {\mathcal{Q}}_j$$ in a device-independent way (i.e., without using any information about the multiphoton state prepared or measurements performed). By the device-independent constructions of sub-models $$ {\mathcal{C}}_j$$ and $$ {\mathcal{Q}}_j$$ with j > 1, we pessimistically allow Eve’s classical or quantum side information to be perfectly correlated with the trial output O given the trial input I and j > 1. Consequently, we choose to not certify the randomness contributed by the multiphoton events, and so our security analysis is robust against photon-number splitting attacks. We emphasize that even with the device-independent constructions of sub-models $$ {\mathcal{C}}_j$$ and $$ {\mathcal{Q}}_j$$ with j > 1, the resulting models $$ \mathcal{C}$$ and $$ \mathcal{Q}$$ still behave well for certifying randomness as the probability of emitting a single photon at each trial is assumed to be bounded from below no matter how Eve manipulates the photon-number distribution.

Once the classical model $$ \mathcal{C}$$ and the quantum model $$ \mathcal{Q}$$ are constructed, we can construct the corresponding PEFs and QEFs. Since the classical model (or the quantum model) for each trial is the identical $$ \mathcal{C}$$ (or $$ \mathcal{Q}$$), we can use the same PEF F_c(I, O) (or the same QEF F_q(I, O)) for each trial. According to Theorem 1 (or Theorem 2), the amount of classical (or quantum) ϵ_s-smooth min-entropy in the outputs O_n certifiable conditionally on the inputs I_n and on the side information E (or $$ \mathsf{E}$$) is determined by the product $$ {\prod }_{k=1}^n{F}_{\mathrm{c}}\left(I_k,O_k\right)$$ (or $$ {\prod }_{k=1}^n{F}_{\mathrm{q}}\left(I_k,O_k\right)$$). Before the experiment we need to choose a PEF (or a QEF) such that the expected amount of certifiable classical (or quantum) ϵ_s-smooth min-entropy is as large as possible. At the same time, a PEF (or a QEF) satisfies a set of linear constraints imposed by each member of the model $$ \mathcal{C}$$ (or $$ \mathcal{Q}$$). Therefore, we can formulate the constructions of PEFs and QEFs as constrained optimization problems. To solve these optimization problems, we provide effective outer-approximations of the models $$ \mathcal{C}$$ and $$ \mathcal{Q}$$. We note that the outer-approximations of $$ \mathcal{C}$$ and $$ \mathcal{Q}$$ provided by us include the convex closures of $$ \mathcal{C}$$ and $$ \mathcal{Q}$$, respectively. Therefore, in view of the remarks below Eqs. (1) and (5), the constructed PEFs and QEFs can certify randomness even when Eve’s side information about the state is classically correlated with Eve’s partial knowledge of the input and measurement at a trial.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.