Introduction

Enzymes catalyse a wide variety of reactions with near perfect enantioselectivity as a result of a precisely tuned network of attractive non‐covalent interactions (NCI) between the substrate and the enzyme binding pocket. ^[1] Thus, selectivity is mainly achieved by selective rate acceleration of the desired enantiomer whereas the role of repulsive steric interactions to retard transformation of the minor enantiomer is negligible. ^[2] In contrast, steric repulsion traditionally served as a key guiding principle in the design of asymmetric catalysts, ^[3] for example, by using large “blocking groups”. ^[4] This does not necessarily exclude the simultaneous influence of attractive interactions as highlighted in studies by, for example, Hawkins, ^[5] Corey, ^[6] Noyori, ^[7] Sharpless, ^[8] or Fuji. ^[9] Thus, small‐molecule catalysts can induce enantioselectivity through a combination of several attractive NCIs[ ^3a , ¹⁰ ] such as aromatic interactions. ^[11] Accordingly it was found that the role of attractive London dispersion forces ^[12] on chemical reactivity, catalysis and stability was traditionally underestimated. ^[13] These analyses were helped by the development of dispersion‐corrected DFT ^[14] and linear scaling coupled cluster theories, ^[15] both of which facilitate the quantification of NCIs in extended molecular systems. ^[16] Most of this progress in elucidating the role of NCIs in asymmetric catalysis is based on theoretical studies,[ ¹⁶ , ¹⁷ ] either alone or in combination with NMR‐ or X‐ray‐ based structure analyses. ^[18] While the influence of NCIs on ground state properties has recently been studied thoroughly, ^[19] most experimental studies on enantioselective catalysis restrict themselves to the determination of the stereoselectivity factor s. This latter quantity is defined as the ratio of rate constants for conversion of the faster and slower reacting isomer, respectively (s=k _major/k _minor). However, the s values themselves cannot answer the question whether selectivity results from the acceleration of the major enantiomer through attractive NCIs or a deceleration of the minor enantiomer through repulsive steric interactions. Surprisingly, kinetic studies on this question are very rare. ^[20] This is likely due to the fact that acceleration or deceleration has to be measured relative to a system with “zero” steric repulsion or attraction. Elimination of groups that induce steric hindrance and attraction is, unfortunately, linked to possible changes of electronic, kinetic and thermodynamic properties. Herein we present a different approach where the aromatic side chains of alcohol substrates are increased systematically such that no additional effective degrees of freedom are introduced. ^[21] It should be added that the term “effective” implies that the conformational space available to all substrates is practically identical and that the term “size” always refers to the dimensions of the aromatic side chains. From the rate data measured for these reactions we can infer how increasing substrate size impacts k _major and k _minor. This novel approach allows us to elucidate the origin of enantioselectivity through direct kinetic measurements. Initial acylation experiments were performed with fluxionally chiral N,N‐dimethylaminopyridine (DMAP) derivative 3 developed by Sibi et al. ^[22] This catalyst displays moderate selectivity for the acylation of 1‐phenylethanol 1 a (s=7) with isobutyric anhydride (2), while a much larger selectivity was found for the larger substrate 1‐(2‐naphthyl)ethanol (1 b) with s=39.

Results and Discussion

Experimental studies

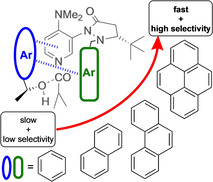
In order to precisely determine relative rates and ensure comparable reaction conditions competition experiments for the acylation of 1:1 mixtures of racemic 1 b as reference and racemic 1 a,c,d (see Figure 1) were performed and monitored by chiral HPLC. Enantioselectivity values s of (pseudo)‐first order kinetic resolution experiments are commonly calculated by Kagan's formulas ^[23] from the enantiomeric excess (ee) of products and reactants at a single conversion point. It should be emphasized that the reliability of this approach is very limited for higher s values and neither the internal consistency nor the preconditions for the Kagan equation can be controlled by a single measurement (for a detailed analysis see Supporting Information (SI)). ^[24] Thus, herein all enantioselectivity values were determined by the more accurate linear regression analysis method ^[25] (see Figure 2). Through simultaneous determination of chemoselectivity values for the two (R)‐enantiomers relative rates for all four alcohols are obtained as shown in Figure 1 a. The reliability of this approach was validated by reproducibility measurements and by comparison to literature data. ^[22a] In an appropriate model system for measuring the size‐dependence of reaction rates aromatic side chains should be increased systematically without adding unfavourable interactions (e.g. 1,5‐interactions).[ ²¹ , ²⁶ ] That alcohols 1 a–d represent a suitable series for such a purpose is supported by the following characteristics: a) The calculated reaction free energies for the acylation with anhydride 2 were found to be almost identical for all four alcohols 1 a–d. b) The same calculations indicate that the partial charge on the alcohol oxygen atom and the acidity of the hydroxy group is very similar for all four systems. c) Reaction rates for the acylation of alcohols 1 a–d with anhydride 2 are almost identical when using tri(n‐butyl)‐phosphine (NBP, 6) as the catalyst (Figure 1 b). This may be due to the large conformational flexibility of this catalyst, which is incapable of differentiating the substrate alcohols on the basis of size (or any other intrinsic property). In sharp contrast, reaction rates between the largest alcohol 1 d and the smallest alcohol 1 a differ by a factor of 10.1 when using DMAP (5) as the acylation catalyst. These reactivity differences are likely due to cation–π interactions in the respective transition states.[ ²⁶ , ²⁷ ] These measurements have been repeated for different DMAP concentrations in order to verify that there is basically no uncatalyzed background reactivity of the respective substrates. With these results in hand, relative rate constants k _rel for the acylation of 1 a–d with anhydride 2 catalysed by chiral DMAP derivative 3 were evaluated. Enantioselectivity values for this reaction increase by a factor of 9 from s=7 for 1‐phenylethanol (1 a) to 66 for 1‐(2‐pyrenyl)ethanol (1 d). Relative rates in Figure 1 using alcohol (S)‐1 a as the reference show that the reaction of both (S)‐ and (R)‐enantiomers is notably accelerated with the growing aromatic side chain. However, while the rate constant for (S) ‐1 d increased by a factor of 4.6 relative to (S) ‐1 a, alcohol (R) ‐1 d reacts 40 times faster than (R) ‐1 a! The size‐induced rate acceleration is thus significantly larger for the (R)‐ than for the (S)‐alcohols and is also about four times larger for chiral catalyst 3 as compared to DMAP (5). Based on these findings we explored whether suitably modified catalysts can further increase the selectivities obtained with catalyst 3. Sibi et al. have already reported that enantioselectivity decreases if the naphthyl moiety in 3 (s=23 at 0 °C) is replaced by both phenyl (s=15) or 9‐anthracenyl (s=14). ^[22a] The first result is in agreement with the above‐mentioned mechanism for size selection. The comparatively low selectivity for the 9‐anthracenyl substituent is likely due to unfavourable 1,5‐interactions that have already burdened other systematic studies of size effects. ^[21] We therefore synthesized 1‐pyrenyl‐substituted DMAP derivative 7 as a possibly even more size‐selective catalyst (see SI). Repeating the acylation reactions of alcohols 1 a–d with anhydride 2 and catalyst 7 under otherwise identical conditions we find generally increased selectivities for all substrates, the largest selectivity for alcohol 1 d now amounting to approx. s=250 (Figure 1). For a quantitative analysis, the size of the alcohol reagents was calculated as the volume of the van der Waals cavity used in the SMD solvation model at the B3LYP‐D3/6‐31+G(d) level of theory. As shown in Figure 3, the molecular volume strongly correlates with ln(k _rel) for the acylation of (R)‐alcohols with catalysts 3, 7, and DMAP (5). The slope of the correlations is notably higher for the chiral catalysts 3 and 7 than in the case of DMAP (5). Thus, the bulky substituents in 3 and 7 further increase the size‐acceleration of the reaction rates.

Figure 1

a) Setup of competitive kinetic resolution experiments: 0.01 mmol of catalyst, 0.05 mmol of (rac)‐1 b and (rac)‐1 a,c,d were dissolved in 2 mL diethyl ether. At −50 °C 0.15 mmol of 2 was added. After defined periods of time 0.05 mL of the reaction mixture was quenched and analysed by chiral HPLC. Relative rates were then determined by linear regression analysis and chemoselectivity calculation (for more details see SI). b) Relative rates for the acylation of alcohols 1 a–1 d with catalyst 3 and 5–7. Values are averaged over two independent runs. Experimental reference was (R)‐1 b, rates are displayed relative to (S)‐1 a for ease of discussion. HPLC traces, linear regression analysis, simulations and reliability analysis are provided in the SI.

Figure 2

Linear regression analysis for the competitive acylation of (rac)‐1 b and (rac)‐1 d with anhydride 2 catalysed by 3. Conversion c was calculated as (ee _alcohol)/(ee _alcohol+ee _ester). ^[23] Results of two independent measurements are presented. The slope of the linear correlations corresponds to selectivity value s.

Figure 3

Correlation of ln(k _rel) for the different catalysts and alcohols with the molecular volume of the reagents calculated at the B3LYP‐D3/6‐31+G(d) level of theory.

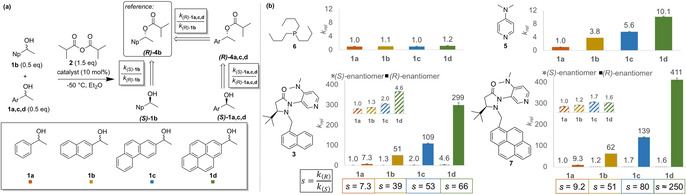
Furthermore, reagent volume V also correlates positively with ln(k _rel) of the minor (S)‐enantiomer, which is contrary to expectation if repulsive steric effects were to control the stereoselectivity. The correlation slope decreases from DMAP (5) to catalyst 3 and becomes quite flat for catalyst 7. Alternative correlations with similar trends for the calculated polarizability of the reagents (see SI) highlight the crucial role of dispersion forces. It can thus be concluded that enantioselectivity improvements result from a rate acceleration of the major enantiomer through reinforced dispersion interactions if simultaneously the structure of the loaded catalyst minimizes the rate accelerations for the minor enantiomer.

Computational studies

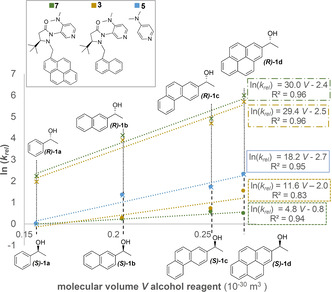
The acylation of 1 b with anhydride 2 catalysed by DMAP‐derivative 3 was investigated computationally. Geometry optimizations and frequency analyses were performed at SMD(Et₂O)/B3LYP‐D3/6‐31+G(d) ^[28] level of theory, followed by single point calculations at the DLPNO‐CCSD(T)/def2‐TZVPP level.[ ¹⁵ , ²⁹ ] In accordance with recent results of Wheeler et al. ^[30] the energy profile of the reaction (see SI) implies that loading of the catalyst 3 through a first transition state TS1 is rate limiting, followed by the selectivity‐determining acylation of alcohol 1 b through transition state TS2. To ensure a comprehensive and systematic conformational search for TS2, the conformational space was partitioned into eight geometrical classes as a function of three criteria (Figure 4): The Re or Si face attack of the alcohol substrate; orientation of the pyrazolidinone side chain; and the relative orientation of the isobutyryl group.

Figure 4

Relative free energies at the SMD(Et₂O)/B3LYP‐D3/6‐31+ G(d) level of theory for TS2 of (S)‐1 b (red circles) and (R)‐1 b (blue crosses). TS conformers are categorized by Re/Si face attack of 1 b, pyrazolidinone side chain orientation and relative position of the isobutyryl group (see bottom left). Structures of the best conformers for (R)‐ and (S)‐1 b are presented (for others see SI).

Due to its absolute configuration alcohol (R) ‐1 b attacks the acyl‐catalyst intermediate preferentially from the (Si) face, while alcohol (S) ‐1 b shows the opposite preference. For both alcohols we find a preference for a trans‐conformation of the isobutyryl and pyrazolidinone side chain. Thus, all conformations populated by more than 1 % are either in class I ((R)‐1 b) or in class III ((S)‐1 b). Conformations for (S) ‐TS2 are best described as “triple‐sandwich” structures of the aromatic alcohol side chain, catalyst pyridinium core, and catalyst sidechain. Wheeler et al. found geometrically similar conformations governing the kinetic resolution of biaryl substrates by catalyst 3. ^[30] In the best (R) ‐TS2, in contrast, attack occurs from the crowded side of the catalyst resulting in a cage structure of the three aromatic rings. A similar structure for (S) ‐1 b is strongly disfavoured by the absolute configuration of the tert‐butyl group of 3. The difference in free energy (ΔΔG ^≠ ₂₂₃=+8.6 kJ mol⁻¹) on single point level for the energetically best conformers of each enantiomer (R)‐TS2_1 and (S)‐TS2_1 is in good accordance with the experimental enantioselectivity value. In order to identify the origin of this selectivity the respective free energy difference ΔΔG ^≠ ₂₂₃ (black bar in Figure 5) was decomposed into its contributors. Surprisingly, the solvation energy (blue bar in Figure 5) stabilizes all of the relevant (S) conformers relative to (R)‐TS2_1. Thus, solvation is a counterplayer of enantioselectivity. Hence, we also found a very good negative correlation of experimental ln(s) values and solvent polarity parameter E _T (30) ^[31] (see SI). To further distinguish the impact of NCIs involving the aromatic moiety of the alcohol, relative single point energies were calculated for TS2_HC structures, wherein the naphthyl moiety of 1 b was replaced by a hydrogen atom (see Figure 5). ^[32] While almost no energy difference is found for the H‐capped structures TS2_HC (green bars in Figure 5), the NCI energy contribution (yellow bar in Figure 5) is very significant at −10.9 kJ mol⁻¹ and thus the dominant component for the preference of the (R)‐TS2_1. Similar trends were found for all of the other relevant conformers (see SI). A local energy decomposition analysis ^[33] confirmed that the intermolecular dispersion energy of alcohol and loaded catalyst in (R)‐TS2_1 is 6.7 kJ mol⁻¹ more stabilizing as compared to (S)‐TS2_1. Thus, stronger dispersive interactions of catalyst and alcohol are indeed the crucial factors in determining the enantioselectivity for this system. A qualitative NCI analysis by the Atoms In Molecules (AIM) ^[34] method as well as NCI plots ^[35] indicate that for both TS2 structures pyridinium‐naphthyl stacking orientations are present. However, (R)‐TS2_1 is further stabilized by additional CH–π‐ and tilted π–π‐stacking interactions (see Figure 6) of catalyst sidechain and alcohol moiety.

Figure 5

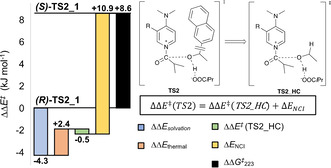
Energy decomposition Scheme for (S)‐TS2_1 relative to (R)‐TS2_1. Solvation energies and thermal corrections were calculated at the SMD(Et₂O)/B3LYP‐D3/6‐31+G(d) level of theory. The differences between DLPNO‐CCSD(T)/def2‐TZVPP single point energies for TS2 and TS2_HC yield NCI energies.

Figure 6

Non‐covalent bond paths between alcohol 1 b and loaded catalyst analysed by AIM analysis ^[36] with relevant distances in pm. Right‐hand structures are printed for orientation only. For full results see SI.

Conclusion

The enantioselectivity of acylation reactions catalysed by chiral DMAP derivates increases systematically with increasing size of the aromatic side chains in the alcohol substrates. Rate measurements for alcohols with different‐sized aromatic side chains reveal that reaction rates for the major enantiomer are increased more than 40 times by substitution of phenyl by pyrenyl. These rate acceleration correlates with the polarizability and volume of the reagents. When also increasing the size of the catalyst side chain in a similar manner, enantioselectivity values of up to s=250 have been obtained. Computational studies show that alcohol attack from the more crowded side of the loaded catalyst is most favourable and stabilized by CH–π‐stacking interactions. In combination with the results of kinetic measurements this implies that the selectivity values obtained result from a targeted rate acceleration of the transformation of the major enantiomer through dispersive interactions and not from steric hindrance of the minor enantiomer. The approach for elucidating the origins of enantioselectivity described in this study should also be useful for the analysis and systematic improvement of catalyst performance in other cases.

Conflict of interest

The authors declare no conflict of interest.