Preparation of giant multi-molecular and confined monomolecular toroids

Bacteriophages T5st(0) (Genbank Acc AY692264) and Lambda are obtained by infection of Escherichia coli K12 and E. coli R594 (cI857 S7) strains respectively, purified on cesium chloride gradients, and extensively dialyzed during several days against NaCl 100 mM, MgCl₂ 1 mM, CaCl₂ 1 mM, Tris 10 mM pH 7.6. Stock suspensions are stored at 4°C. FhuA and LamB receptors are purified respectively from the strain E. coli AW740 and pop 154 from K12 in which the lamB gene is transduced from Shigella sonnei, as described earlier (37–39). FhuA and LamB solubilized in NaCl 100 mM, MgCl₂ 1 mM, CaCl₂ 1 mM, LDAO 0.03% (FhuA) or oPOE 1% (LamB), Tris 10 mM pH 7.6 are stored at −80°C. DNA ejection from phages is triggered by mixing the phage stock solution with 110 FhuA/120 LamB molecules per infective phage (T5/Lambda respectively), in the presence of 0.03% LDAO (w:w), and 4 or 40 mM spermine. Bacteriophages are incubated with 4 or 40 mM spermine about 20–30 min prior to the addition of the receptor. Although spermine distribution in the sample is not known, it was previously shown, using similar equilibration time, that spermine-induced DNA condensation inside capsids follows the spermine/DNA phosphate charge ratio (36), showing that spermine equilibrates in less than 30 min. The ionic environment is kept constant at all stages of the preparations. The phage concentration is adjusted so that the final global DNA concentration C_DNA = 4 mg/ml. For ejection, the sample is transferred at 37°C during 90 min, and transferred back to room temperature before freezing for cryo-EM observation. To obtain multi-molecular giant toroids outside phage capsids, the ejection is simply allowed to proceed until completion (90 min). To obtain monomolecular confined toroids, DNAse (Invitrogen, 20–25 ue/μl) is added to the sample at t = 5–10 min after the addition of FhuA/LamB.

Cryo electron microscopy

3 μl of the toroid suspension are deposited onto a glow-discharged holey carbon grid (Quantifoil R2/2), blotted with a filter paper for 4 s, and plunged into liquid ethane cooled down by liquid nitrogen, using a Vitrobot Mark IV (ThermoFisher) operated at room temperature and 100% relative humidity. Frozen samples are transferred and observed in a cryo-TEM, either a JEOL 2010F or a Titan Krios (ThermoFisher) equipped with a Cs corrector, a Quantum GIF energy filter (Gatan, slit width set to 20 eV) and a Volta Phase Plate (VPP), operated at 200 and 300 kV, respectively. Images are recorded either at a nominal defocus of 900 nm on Kodak SO163 negative films (JEOL 2010F acquisitions) or close to focus on a Gatan K2 summit camera (Titan Krios with VPP acquisitions). Negative films are developed in full strength Kodak D19 for 12 min, and scanned with a Coolscan 9000 (Nikon) at a resolution of 4000 pixels per inch. Images recorded on the JEOL 2010F are denoised by wavelet filtration using ImageJ (‘A trous filter’ plugin, k₁ = 20, k_{n > 1} = 0). In all cases, micrographs are calibrated using full T5st(0) phages imaged in the same conditions. The DNA hexagonal lattice spacing in fully filled phages is measured on line profiles, and the image scale is calculated from the known value previously recorded by X-ray scattering (40). Line profiles are recorded using imageJ, with a line width of 5 nm (giant toroids) or 2.65 nm (confined toroids).

Statistical analysis

We use Mathematica 12.0 (41) for the statistical analysis of the spacing datasets. In particular, we use the MannWhitneyTest routine to compare the spacing datasets from small and giant toroids, and the NonLinearFit routine to fit our model to the data.

We use DNA ejection from phages to produce small confined DNA toroids and giant unconfined DNA toroids

The phage/receptor system has previously been used to produce DNA toroids, from small monomolecular toroids consisting of a portion of the phage genome confined within its capsid (35) to giant assemblies of multiple DNA molecules ejected from many phages (34). Inspired by these works, we produce toroids of variable curvature using two phage species (T5 and Lambda) with different capsid sizes. We trigger DNA ejection in the presence of spermine to condense DNA and form toroids. In some experiments, we add DNAse at different times corresponding to different stages of the DNA ejection process. DNAse degrades the already-ejected fraction of the DNA molecule outside the capsid and interrupts the transfer. The remaining DNA is condensed into a toroid confined inside the capsid. In other experiments where DNAse is absent, the genome is fully transferred out (42,43) and the molecules from several phages aggregate into giant unconfined toroids typically wrapped around one of the capsids.

Cryo-EM examination reveals the variety of toroids thus generated outside phage capsids (Figure 1A, B), as well as confined toroids generated inside them (Figure 1C, D). Small confined toroids have their outer radius R_out fixed by the species-dependent capsid size, namely 36−37 nm in phage T5 (Figure 1C) and 26 nm in phage Lambda (Figure 1D). The inner radius of small toroids is unconstrained and on average slightly smaller in Lambda. Conversely, in giant toroids, the capsid fixes the inner radius $$ (mean ± std.dev., N = 39), and $$ (mean ± std.dev., N = 16), while the outer radius is unconstrained. Note that freestanding giant toroids, without capsid at their core, are also observed, though less frequently. In these cases, the toroids kink and avoid curvature as shown in Supplementary Information SI-1. Giant toroids are relatively monodisperse in all conditions, with outer radii R_out = 153 ± 15 nm (mean ± std.dev., N = 76), with no significant difference between toroids obtained from phages T5 and Lambda.

Figure 1.

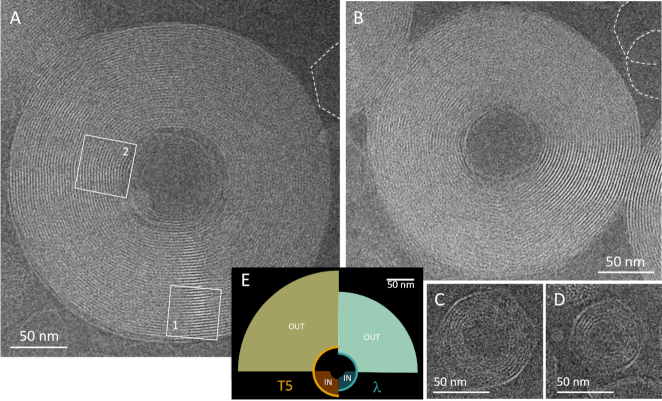
CryoEM imaging of the different types of toroids obtained by DNA ejection from phages in the presence of condensing amounts of spermine. Toroids are here observed in top views. (A, B) Giant unconfined toroids formed outside phage capsids after the ejection of multiple DNA molecules from phage T5 (A) or Lambda (B). A capsid is located at the core of both giant toroids. Empty capsids are visible in the periphery of the image and are outlined by white dashed contours. C_spermine = 40 mM. In (A), the ejection is not complete for the capsid located at the core of the giant toroid and the remaining segment inside is condensed into a small confined toroid. The two sub-regions (1) and (2) are analyzed in Figure 6 (C, D). Small confined toroids trapped in after partial DNA ejection in the presence of DNAse in the external medium, for phage T5 (C) and Lambda (D). C_spermine = 4 mM. (E) Sketch of the different toroid populations: giant external toroids with fixed inner boundary and small confined ones with fixed outer boundary. In all cases, the radius of the fixed boundary is dictated by the radius of the phage capsid, i.e. the phage species: here T5 (orange) and Lambda (cyan).

The wide range of well defined toroid sizes generated by our approach allows us to access curved DNA configurations with radii of curvature varying continuously from 7 to 375 nm, as sketched in Figure 1E.

Inter-helix spacing is larger in highly curved regions of either types of toroids

Both global and local measurements of inter-helix spacing are possible from the analysis of cryo-electron micrographs. As already shown by other cryo-EM studies of DNA toroids (35,44), toroids observed in top views exhibit concentric striated patterns (Figure 2A). The local hexagonal packing of DNA is visualized in side views (Figure 2B and Supplementary Information SI-2). Wherever we find striations in top views (Figure 2B’), we observe the hexagonal structure along the direction of one of its lattice planes. The striation spacing is $$, where a_H is the interhelix spacing between DNA segments, as sketched in Figure 2B”. We do not observe striations along the whole circumference of the toroid (Figure 2A, asterisk) due to the rotation of the hexagonal lattice in this direction (35) and other defects (44).

Figure 2.

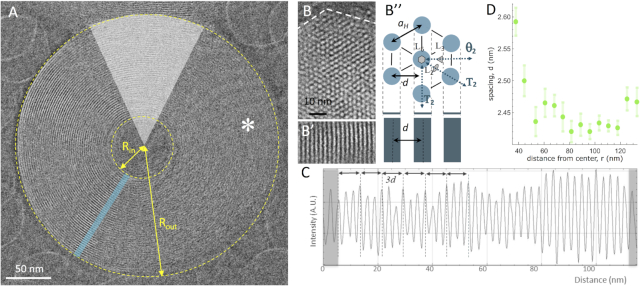
Filament spacing measurements on cryo-EM images (here giant toroids). (A) Top view of a toroid. The inner and outer radii R_in and R_out are outlined by yellow dotted lines. The asterisk highlights a region devoid of striations. An example of a line profile used for our analysis is given in cyan. The pale gray overlay highlights a sector whose outer boundary is constrained by a contact with another toroid, and is therefore excluded from our analysis. (B) Side view of a giant toroid showing the arrangement of its DNA filaments into a triangular lattice in its cross-section. Similar pictures for small tori are available in the Supplementary Information (SI-2). (B’) Detail of the striations observed in a top view projection along a T₂ projection axis. (B”) Corresponding sketch of the hexagonal lattice in transverse view with its symmetry axes: 2-fold axes (L₂, T₂, θ₂), 3-fold axes (L₃) and 6-fold axes (L₆), showing its projection along a T₂ axis into parallel stripes. d is the striation spacing and a_H the interhelix spacing. (C) Plot of the line profile shown in (A). The striation spacing d is measured from averages over 3 layers. The inner and outer layers (gray overlay) are discarded. (D) Variation of d as a function of r, averaged over 10 line-profiles recorded on the toroid shown in (A). Error bars correspond to standard errors of the mean. Note that a weak increase of the lattice spacing occurs at very large radii. This can be attributed to peripheral fluctuations (45) that may slightly propagate inwards beyond the peripheral layer itself, over a few additional layers. In many samples, this increase is not observed (see Figure 3).

To measure the average striation spacing $$, we record line profiles on top views of toroids (Figure 2A, cyan line) and divide the profile length by the number of layers (Figure 2C). We find $$ in small toroids and $$ in giant ones (Supplementary Information SI-3). This suggests an increase of $$ with increasing curvature. The small difference in radii between T5 and Lambda capsids does not lead to any noticeable difference between the two species. Increasing the spermine concentration from 4 to 40 mM does not significantly affect the striation spacing (Supplementary Information SI-3). A similar independence on spermine concentration was previously observed in dense packings of short DNA fragments in the presence of (relatively) high amounts of monovalent cations (≥50 mM) (12). In the following we thus pool the data obtained under these two spermine concentrations together, and conduct a detailed analysis of seven small toroids (five at 4 mM spermine in T5 and Lambda, two at 40 mM spermine in T5) and nine giant ones (eight at 40 mM spermine, T5 and Lambda; one at 4 mM, T5) (Supplementary Information SI-4).

To access local variations of the spacing d beyond the mean estimate $$, we measure peak-to-peak distances on line profiles. To reduce noise, we take advantage of the large number of layers in giant toroids and average spacings over three layers. On account of the small number of layers in small toroids, the spacings are not averaged there, resulting in noisier data. In all cases, we exclude from the measurements the DNA layers constituting the inner and outer boundaries of the toroids (innermost and outermost layers, shadowed in grey in Figure 2C) to eliminate the influence of the peripheral fluctuations due to the reduced number of neighboring filaments (45). In giant toroids, we do not collect data from regions where the toroid is potentially perturbed by a contact with a neighbor (Figure 2A, pale grey overlay). For each toroid, we record several line profiles (from 8 to 13 in giant toroids, 3 to 6 in small confined ones) and average d values. We plot the resulting d values as a function of the radius r (Figure 2D). We show the complete datasets in Figure 3(A, B). The spacing dataset from small toroids (median at 2.6 nm, 38 points) is shifted upwards compared to the dataset from giant toroids (median at 2.5 nm, 111 points), as confirmed by a Mann–Whitney test (46) (p ≃ 10⁻⁹) and shown in the box-and-whisker plot in Figure 3C.

Figure 3.

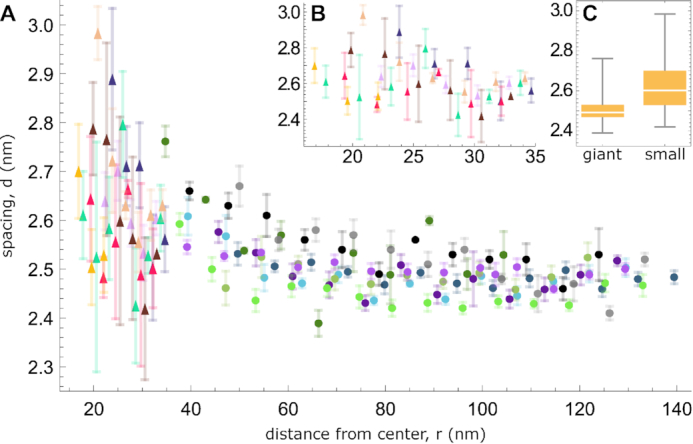
Experimental data about local spacing in DNA toroids. (A) Complete dataset for small toroids (triangles) and giant ones (circles). The spacing d decreases with increasing distance from the toroid center r under all conditions examined. Error bars represent a standard error of the mean (for details, see Supplementary Information SI-4). Colors and symbols are consistent with Supplementary Information SI-4, as well as with Figures 2D and 5. (B) Close-up of the small toroid data. Axes and units are the same as in (A). (C) Box-and-whisker plot of the distribution of d values for the two types of toroids. The vertical axis is the same used in (B).

The result of these local measurements confirms the trend observed for the mean estimates $$, indicating an increase in spacing with increasing curvature. The analysis of giant toroids moreover suggests that this dependence is only relevant at high enough curvatures, as d appears roughly constant for curvature radii r larger than 75 nm.

A mathematical model based on the helices’ bending energy accounts for the observed variable spacing

To understand the local correlation between inter-helical spacing and curvature, we develop a mathematical model based on the competition between inter-helical electrostatic interactions and DNA bending rigidity. Qualitatively, imposing curvature on DNA has a high bending energy cost. To relieve this cost, DNA tends to move away from the highly curved inner regions of the toroid to regions with milder curvatures. Due to this tendency to move, we expect DNA to be more closely packed on the outside of the toroid, as observed experimentally. In the presence of strong inter-helical interactions imposing a well-defined value of the inter-helical spacing, these variations tend to be small. Conversely, a relatively large variability in the packing density indicates a loose inter-filament interaction. Our model harnesses this correspondence to infer the inter-filament interaction strength from the spatial variation of their spacing.

We consider a simplified two-dimensional model comprised of concentric DNA circles, reminiscent of the striations appearing in toroid top views (Figure 2A). The smallest (largest) circle has a radius R_in (R_out). Denoting the capsid radius by R_c, we have R_out = R_c in small confined toroids while R_in = R_c in giant unconfined toroids. We model DNA as a semi-flexible polymer, implying that the bending energy per unit length of a filament reads

Since the typical inter-helical spacing in our set of circles (2.5−3 nm) is much smaller than the toroid size, we take the continuum limit of the set of circles and assimilate it to a hollow disk parametrized by the radial coordinate r ∈ [R_in, R_out] (Figure 4). We use the state where the DNA filaments are uniformly spaced by d = d₀ as our reference state. There, the number of circles between r and r + dr is dr/d₀. When k_b > 0, DNA filaments resist the bending associated with this state by relaxing their local curvature such that the local radius of curvature goes from r to r + U(r), where the displacement U(r) characterizes the magnitude of the deviation of the filament positions from the reference state. In this final state, the spacing depends on the position r and reads d(r) = d₀[1 + U′(r)] (Figure 4), where the prime denotes differentiation with respect to r.

Figure 4.

Two-dimensional model of small confined (left) and giant unconfined (right) DNA toroid. Fixed boundaries are colored in red. Both models represent continuum limits for a dense set of concentric circles (cyan). Dashed box: close-up showing two circles, located at r and r + dr in the reference state and spaced by d(r) = d₀[1 + U′(r)] in the final state.

The relatively small deviations of our filament spacings from a homogeneous distribution (of the order of $$—see Figure 3) may be expressed as U′(r) ≪ 1, and suggests that bending effects are weak compared to interactions. We formalize this observation by introducing a dimensionless small parameter $$ that quantifies the magnitude of the DNA bending stiffness relative to the inter-filament interactions. We assume ε ≪ 1 and write U(r) = εu(r) in the following. The two energetic contributions detailed in Equations (1) and (2) thus yield a continuum free energy

We compute the equilibrium filament displacement u(r) by minimizing the free energy functional of Equation (3) (see Supplementary Mathematical Modelling SMM-2). To leading order in ε, we obtain for small toroids

Thus in both small and giant toroids, our model predicts that the spacing d decreases with increasing distance r from the center. While this finding is consistent with the data presented in Figure 3, another prediction of our model appears at odds with our experimental observations. Indeed, our model predicts $$, implying $$ in small toroids, while $$, implying $$ in giant ones. By contrast, our experimental data show $$. These statements can only be reconciled by assuming that the optimal spacing d₀ has a different value for small vs. giant toroids.

Fitting of the model’s parameters reveals differences in interactions in small and giant tori

To understand the effect of confinement-induced high curvatures on DNA–DNA interactions, here we extract the values of the optimal spacings $$ and $$ as well as the interaction parameter γ from the data presented in Figure 3. We illustrate how our model fits two datasets from small and giant toroids in Figure 5A, B. Rather than fitting the individual d = d(r) curves, we exploit our model to collapse datasets collected on toroids of different sizes into a universal curve on which we perform a global fit.

Figure 5.

Fitting our model elucidates the dependence of the filament spacing on position and toroid geometry. (A) Example for a single giant toroid (same dataset as in Figure 2D). The line is the fit of the theoretical model $$, with $$ given by Equation (6). The inferred parameters are d₀ = 2.42 ± 0.01 nm and ε = 0.11 ± 0.02 (expected value ± st. error). (B) Example for a single small toroid. The line is the fit of the theoretical model $$, with $$ from Equation (5). The inferred parameters are d₀ = 3.32 ± 0.16 nm and ε = 0.12 ± 0.02 (expected value ± st. error). (C) Filament spacing d for small (giant) toroids collapses onto a single master curve when expressed as a function of $$ ($$). Note that Equation (5) implies that $$ cancels at $$, while Equation (6) implies that $$ cancels at $$. The solid (dashed) line is the fit to the model of the giant (small) toroid data. The inferred model’s parameters corresponding to the dashed and the solid lines are provided in Table 1. (D) Close-up of the giant toroid data in panel C. All colors, symbols and error bars are consistent with Figure 3 and Supplementary Information SI-4.

While the curves presented in Figure 3 are all qualitatively similar, our model predicts that the detailed dependence of the spacing d on the radius r depends on the toroid-specific parameters R_in and R_out, preventing a collective fit of all our datasets. Conveniently however, within our small parameter expansion, d is an affine function of u′(r), with parameters ε and d₀. We thus plot d as a function of u′ for all our T5 capsid datasets in Figure 5C, D, using our measurements of the inner and outer radii (Supplementary Information SI-4) for the values of $$ and $$ in the expression of u′ [Equation (5) and (6)]. We exclude from the analysis the two Lambda data sets because we only have two of them (one confined, one unconfined) and that accounting for two different values of capsid radius would complicate the extrapolation of γ in the following. We further exclude an outlier dataset (Supplementary Mathematical Modelling SMM-3), which leads to a large statistical error on the slope of the linear fit, and whose outlier nature is probably due to an incorrect assessment of its inner and outer radii, as discussed in Supplementary Mathematical Modelling SMM-4. Note that the following results are robust to the experimental fluctuations of the inner and outer radii, and we can get to similar conclusions even by assuming the same values of $$ and $$ for all toroids belonging to the same category, either small or giant (Supplementary Mathematical Modelling SMM-4).

The theory predicts that the dependence of spacing d on strain u′ should be affine, and we find that our data on small and giant toroids are each separately compatible with this prediction. Consistent with our earlier comment that the same optimal spacing d₀ cannot be used for both giant and small toroids, the same affine function clearly cannot be used to fit the two datasets in Figure 5C. To determine the d₀ associated with each dataset, we perform separate least-square fits on small (u′ < 0) and giant (u′ > 0) toroids, using ε and d₀ as free parameters, and plot the resulting affine dependencies as dashed and solid lines in Figure 5(C, D). We present the inferred values of the free parameters in Table 1. Note that the 95% Confidence Intervals (95% CIs) of $$ and $$ do not intersect, suggesting a statistically significant difference between the two. Conversely, the 95% CIs of ε_small and ε_giant have a broad intersection, suggesting that the two are statistically indistinguishable. We compute $$ using $$, T = 298 K and ℓ_p = 40 nm [which is reasonable under our salt conditions (47)], and find γ_small = 0.15 ± 0.02 pN nm⁻², γ_giant = 0.17 ± 0.03 pN nm⁻² (where uncertainties are standard errors). We obtain two statistically compatible values of γ from small and giant toroids, between 0.1 and 0.2 pN nm⁻². Nevertheless, the relatively large uncertainty on ε prevents us from resolving γ with the same accuracy as that of d₀, therefore we cannot exclude variations of that order going from small to giant toroids.

Table 1.

Inferred model parameters: best-fit value (value), standard error (SE), 95% confidence interval (95% CI)

	Value	SE	95% CI
Small toroids
d 0 (nm)	2.98	0.08	[2.82, 3.14]
ε	0.08	0.01	[0.05, 0.10]
Giant toroids
d 0 (nm)	2.47	0.01	[2.46, 2.48]
ε	0.10	0.02	[0.07, 0.13]

Conversely, we find that the equilibrium spacings d₀ differ significantly between small and giant toroids, shifting from 2.98 to 2.47 nm, respectively. This suggests that the interactions between DNA helices depend on their curvature, and favor smaller spacings in giant than in small toroids.

Alignment of neighboring DNA helices depends on local curvature

We speculate that the different inter-helical interactions found in small and giant toroids may be related to a different relative alignment of neighboring DNA helices in small and giant toroids. Indeed, the inhomogeneous helical charge distribution of phosphate groups and counter-ions causes DNA helices packed at high density to order longitudinally through an ‘electrostatic zipper’ mechanism (48). Such longitudinal correlations of the helices have been characterized using X-ray diffraction patterns (49) and cryo-EM imaging (35). Consistent with our proposal, these correlations were found to differ in highly curved small toroids and straight bundles (35). Specifically, while helices in straight DNA bundles were found to align in register (major grooves of one helix facing the minor grooves of its nearest neighbors in all three directions of the lattice), alternating longitudinal orientations were found in small confined toroids. We hypothesize that out-of-register helices found in curved bundles may not interlock as efficiently as in-register helices, which might prevent the former from lying as close to each other as the latter and hence produce the curvature-dependent d₀ reported here. This possibility is further supported by previous suggestions that helical correlations may vary with interaxial separation (49,50), as well as with the lattice geometry (50).

To confirm our hypothesis, we investigate helical correlations in giant toroids as was done for straight bundles and small confined toroids (35). We record Fourier transforms (FT) in striated regions of the toroids, i.e. projection views along a T2 axis of the hexagonal lattice (Figures 1A, 6A, B). FT patterns show equatorial Bragg peaks corresponding to the lattice spacing d and the meridional layer line n = ±1, whose position relates to DNA helical pitch (49,51). For external regions of the toroids, we measure d = 2.45−2.5 nm, in good agreement with line profile measurements and h = 3.3−3.5 nm, as expected for B-DNA. The position of the peaks on the n = ±1 layer line depends on the correlations between DNA helices (49). Outer regions of giant toroids generally show FT patterns similar to that observed for straight bundles (35), typical of in-phase alignment of molecules (35,49). This observation is consistent with our hypothesis that correlations in giant toroids differ from those in small confined toroids where an out-of phase alignment was reported (35). Yet, data are noisy and not all FT patterns can be interpreted. We cannot exclude that other phasing angles may occur in some places. In inner regions of higher curvature, the analysis of the FT is made more complex by curvature (Bragg peaks transform into arches); yet the position of the peak on the n ± 1 line is different (Figure 6B2). We suspect that the situation there is closer to that of small confined toroid, with out of phase alignment in the curvature direction as described in (35). The transition takes place at r = 80 nm, where d plateaus at d₀, supporting the link between lattice spacing, curvature and helical correlations.

Figure 6.

Correlations between DNA helices are analyzed in two striated domains (labelled 1 and 2) of the giant toroid seen on Figure 1A. Corresponding Fourier transforms are given in (B). The equatorial peaks correspond to d (lattice spacing), and the meridional position of the first layer line (n = ±1) is related to the DNA helical pitch h. The peaks on the first layer line (white circles) reveal correlations of the helices between lattice planes. The position of the peaks on the first helical layer line differ in (1) and (2), indicating of different types of correlations. (C) Possible alignments of DNA helices in regions 1 (in phase) and 2 (out of phase, shift by half the helical pitch of the molecule). Redrawn from (35).