Methods

The study of complex networks has incorporated the analysis of systems, for which, multiplex modelling is more suitable. In these cases nodes are located in layers with connections among them and the nodes are common to all layer-networks. A number of real-world and simulated multilayer networks have been studied in contexts such as finance and economics [17–19], social systems [20, 21], synchronization [22] and linguistics [12].

In this study, we plan to analyze the multiplex language network which consists of an orthographic network and phonological network (see Fig 1 for a schematic representation). For the orthographic network, we construct a network at word-level G^[O] = (V^[O], E^[O]), where nodes are words and a link between two nodes is defined if the DL distance, described later, is smaller or equal than a threshold value ℓ. Similarly, a phonological network G^[P] = (V^[P], E^[P]) is constructed where the nodes represent words which were translated to the international phonological alphabet (IPA), and edges are defined if the DL, is smaller or equal than a given threshold ℓ. To generate a multiplex language network at word-level, the orthographic and phonological networks are combined to form a two-layer word-level network, denoted by $$ G_L^{\left[\alpha \right]}=(V^{\left[\alpha \right]},E^{\left[\alpha \right]})$$, with α = O, P. Here, the adjacency matrix for the multiplex network is given $$ a_{ij}^{\left[\alpha \right]}$$, where $$ a_{ij}^{\left[\alpha \right]}=1$$ indicates that there is a link between node (word) i and node (word) j at layer α. More formally, the adjacency matrix associated with each layer is defined as: $$ a_{ij}^{\left[\alpha \right]}=\Theta (\ell -d(w_i^{\left[\alpha \right]},w_j^{\left[\alpha \right]}))-{\delta }_{ij}$$, where Θ(−) represents the Heaviside function, δ_ij is the Kronecker delta and $$ d(w_i^{\left[\alpha \right]},w_j^{\left[\alpha \right]})$$ the DL distance between word i and word j at layer α.

Fig 1

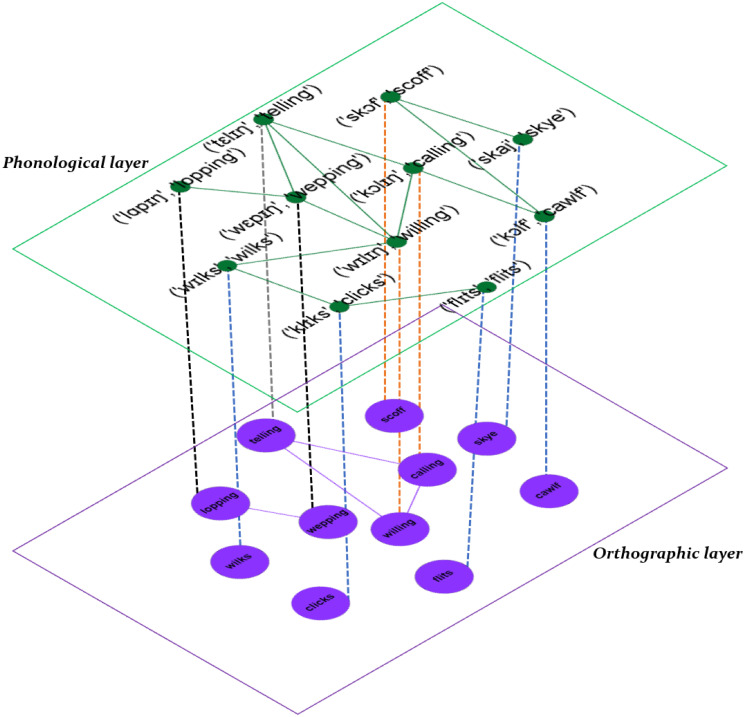
Construction of the multiplex language network.

Schematic illustration of the construction of a multiplex language network for English based on an orthographic-distance and phonological-distance similarity networks. In the orthographic and phonological layers nodes are words and there is a link if the Damerau-Levenshtein distance is smaller than a given threshold ℓ. Notice that words in the phonological layer were translated into the International Phonetic Alphabet and then the DL was calculated.

Regarding the distance condition between two words, as we mentioned in the Introduction, the distance similarity between two strings A and B can be defined as the minimum number of edit operations needed to transform A into B. These operations are: (1) substitute a character in A to a different character, (2) insert a character into A, (3) delete a character of A, and (4) transpose two adjacent characters of A. The Damerau-Levenshtein (DL) distance is then defined as the length of the optimal edit sequence. For instance, the Levenshtein distance is the length of the shortest sequence of substitutions, insertions, and deletions needed to transform string A into string B. In our analysis, we adopt the DL distance ℓ as a threshold value to define a link between two words.

Databases

The corpus of words were constructed from written texts (books) freely available at Gutenberg project www.gutenberg.org. The written texts were pre-processed to remove function words, stop words and any mark symbol. The titles of the written texts and the resulting corpus are described in https://doi.org/10.6084/m9.figshare.12735380.v4 [23]. The final corpora contain 10⁴ words with their corresponding translation to the international phonetic alphabet for four languages (transliterated by the epitran library of Python version 3.6.8).

Topological properties of single-layer and multiplex networks

Our initial analysis is focused on the basic topological characteristics of two individual networks, and then to proceed to investigate similarities and differences of the two layers. The single-layer-network measures (of a network with N nodes) in a multiplex network that have been initially evaluated are [24]:

Density. The density of a layer α, ρ^[α], is given as:


where m^[α] is the number of actual connections within the layer α.

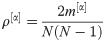
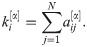
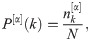
Degree distribution. The degree $$ k_i^{\left[\alpha \right]}$$ of a node i is the number of links outgoing (or incoming) to that node,


The degree distribution for layer α is then defined as the fraction of nodes in the network with degree k,

where $$ n_k^{\left[\alpha \right]}$$ is the number of nodes with degree k.

Clustering Coefficient. Measures the degree of transitivity in connectivity among the nearest neighbors of a node i within the layer α. $$ C_i^{\left[\alpha \right]}$$ is calculated as [25],


where $$ E_i^{\left[\alpha \right]}$$ is the number of links between the $$ k_i^{\left[\alpha \right]}$$ neighbors of the node i within the layer α.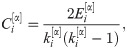

Average Nearest-Neighbor Degree. Measures the average of the neighbors of a node [25]. The 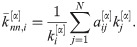$$ {\overline{k}}_{nn,i}^{[\alpha ]}$$ is calculated as:



Modularity. Given 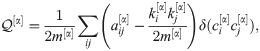$$ c_i^{\left[\alpha \right]}$$ the community associated to the node i within the layer α, where $$ c_i^{\left[\alpha \right]}\in \{1,2,\dots ,P\}$$, with P a natural number. The modularity, Q^[α] of a given layer α is given by [24]:


where δ is the Kronecker delta. We use the Louvain algorithm [26] to perform a greedy optimization of the modularity.

In order to get insight on our study, we plan to characterize structural network properties and information-based quantities from the following perspectives: (i) presence of similarities across 4 linguistics families (Romance, Germanic, Slavic and Uralic), (ii) increase of the size of the number of words (corpus) from 10⁴ to 50 × 10³, and (iii) robustness of the networks. Regarding (i), we will analyze to what extent the topological single-layer and multiplex network properties exhibit similarities and differences quantified by means of correlation measures and information-theory-based metrics for 12 natural languages which belong to 4 linguistic families. To reinforce the characterization of the grouping patterns of nodes of the network, we will consider multilayer community detection algorithms [27] to determine the presence of clusters across layers. These procedures will help us in the understanding of local and global network properties of the orthographic-phonological variations across several languages. With respect to (ii), we plan to increase the size of the corpus to 50 × 10³ in the number words for all languages in our study. The results for this size will confirm the validity of our preliminary results for 10⁴ words, and also will permit to evaluate the concordance of our findings with previous results. Concerning (iii), the robustness of the single-layer and multiplex network will be evaluated by means of two well-recognized strategies: random removal of fraction of nodes and edges and directed attacks [28]. Moreover, a randomized version of the networks will be also considered to repeat all the calculations in our study.

Initial analyses for 4 natural languages and 10⁴ words

We have started our analyses working with 4 languages (Spanish, English, German and Russian) with corpus containing 10⁴ words each one. Table 1 concentrates the results of the calculations for the basic structural properties of the orthographic network, the phonological network and the multiplex one. These preliminary results of topological features indicate that there are common properties at local and global scales. Interestingly, the results for the average clustering for Spanish, in the case of the phonological layer with ℓ = 2, is concordant with the value reported for phonological networks [16], where the authors used a different corpus and assumed an edge between words if the differ by a single phoneme or sound segment. In order to get a better understanding of the patterns of the connectivities in both layers, we proceed to construct the degree distribution for different threshold values of the DL distance ranging form 1 to 3. Fig 2 shows the cases of the degree distributions of G^O and G^P for Spanish, German, English and Russian and DL distances from 1 to 3. It is visually apparent that, for the 4 languages, as the DL distance increases, the distributions change from an approximately exponential regime (ℓ = 1) to a combination of an exponential and power law behavior (ℓ ≥ 2). It is likely that the best fit would be obtained by means of a truncated power law function, which has been suggested to fit phonological networks [16]. In our initial estimation of the best fit of the distributions, we only consider the power law behavior at the tails, P(k) ∼ k^−γ, where γ is an exponent which characterizes the connectivities. For instance, for a DL distance ℓ = 3 and the phonological layer, the estimated γ-exponents (1.12) for the power law degree distribution is concordant to the value reported in [16] for Spanish. Additional tests are needed in order to get a better description of the distributions, and also for the behavior of the other topological metrics as a function of the degree.

Fig 2

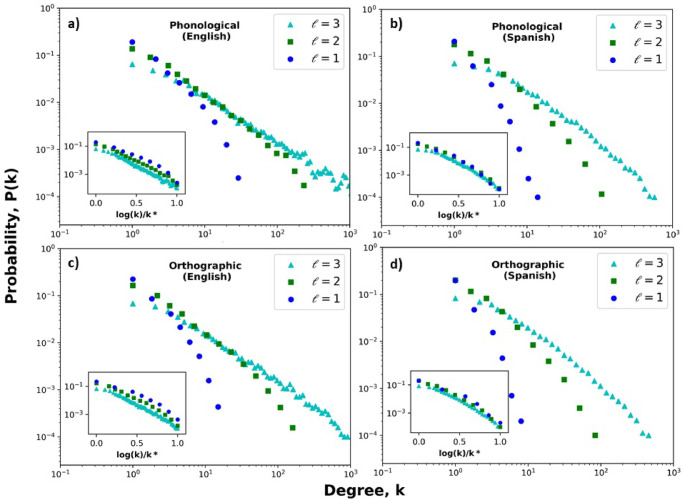
Degree distributions for phonological and orthographic networks and several DL distance thresholds.

a) Phonological (English). b) Phonological (Spanish). c) Orthographic (English). d) Orthographic (Spanish). For a better comparison of the data, the insets of each plot show the corresponding degree distribution for normalized degrees, where k* = max(log(k)).

Table 1

The basic topological network quantities are listed for the ortographic (G^O) and phonological (G^P) networks.

Language	Network	GO			GP
	Metric
	Threshold	ℓ = 1	ℓ = 2	ℓ = 3	ℓ = 1	ℓ = 2	ℓ = 3
English	Density	0.60(10−3)	1.98(10−3)	10.23(10−3)	0.86(10−3)	3.18(10−3)	15.42(10−3)
	Average degree $$	2.03	13.74	91.53	1.24	3.41	16.78
	Clustering $$	0.12	0.22	0.29	0.03	0.12	0.21
	Nearest neighbor $$	2.51	19.31	137.66	0.46	4.57	24.92
	Maximum modularity Q	0.91	0.55	0.35	0.99	0.77	0.49
	Fit exponent γ	2.57 ± 0.57	1.31 ± 0.25	1.02 ± 0.16	2.08 ± 0.56	1.22 ± 0.24	0.96 ± 0.18
	Average cluster size	4.26	13.76	58.10	5.24	17.35	60.07
German	Density	0.59(10−3)	1.05(10−3)	4.29(10−3)	0.81(10−3)	1.61(10−3)	5.70(10−3)
	Average degree $$	1.47	5.73	32.23	1.93	8.53	42.24
	Clustering $$	0.10	0.22	0.27	0.14	0.22	0.29
	Nearest neighbor $$	1.72	7.77	48.76	2.35	11.36	61.48
	Maximum modularity Q	0.98	0.67	0.45	0.94	0.64	0.47
	Fit exponent γ	3.14 ± 0.48	1.82 ± 0.42	1.20 ± 0.21	2.47 ± 0.47	1.57 ± 0.37	1.15 ± 0.12
	Average cluster size	2.94	8.05	21.83	3.68	8.56	23.49
Russian	Density	0.64(10−3)	0.65(10−3)	2.68(10−3)	0.74(10−3)	0.65(10−3)	2.16(10−3)
	Average degree $$	1.22	3.73	22.27	1.24	3.42	16.78
	Clustering $$	0.06	0.19	0.25	0.07	0.19	0.25
	Nearest neighbor $$	1.35	5.06	33.92	1.37	4.57	24.92
	Maximum modularity Q	0.99	0.74	0.43	0.99	0.78	0.5
	Fit exponent γ	4.17 ± 0.50	2.09 ± 0.35	1.31 ± 0.25	3.64 ± 0.34	2 ± 0.26	1.39 ± 0.22
	Average cluste size	2.40	6.18	25.52	2.40	5.24	17.31
Spanish	Density	0.52(10−3)	0.86(10−3)	4.14(10−3)	0.52(10−3)	1.11(10−3)	5.59(10−3)
	Average degree $$	1.41	5.87	37.36	1.68	8.07	51.53
	Clustering $$	0.06	0.21	0.27	0.09	0.23	0.28
	Nearest neighbor $$	1.66	8.18	56.69	2.01	11.28	77.20
	Maximum modularity Q	0.98	0.65	0.41	0.95	0.59	0.39
	Fit exponent γ	3.26 ± 0.53	1.90 ± 0.46	1.19 ± 0.31	2.98 ± 0.49	1.77 ± 0.43	1.12 ± 0.30
	Average cluster size	2.87	10.21	60.49	3.36	12.72	83.75

Notes. Topological metrics of the orthographic network and the phonological network. Here we present the average values of the degree (k_i), clustering (c_i) and nearest neighbor (k_nn,i). We observe that the density, $$ \overline{k}$$, $$ \overline{c}$$ and $$ \overline{k_{nn}}$$ exhibit an increasing behavior for the four languages and the two layers, with some similarities such as it occurs for $$ \overline{c}$$ in both layers and distances ℓ = 2, 3. For the modularity and the average cluster size, we observe they exhibit opposite trends, while the modularity decreases as ℓ increases, the average cluster size increases because a larger number of nodes tends to be connected to a giant component.