Material Properties.

Developing CNS tissue is soft and pliable (SI Appendix, Topic 1) and grows in an incompressible fluid environment. Except for the pia mater and arterial and venous linings, its extracellular matrix (ECM) largely lacks components such as collagen that stiffen peripheral tissues (91011–12). Three types of biomechanical properties relevant to morphogenesis can be assayed in tissues, cells, or molecules by measuring physical deformation (strain) in response to applied force (stress) (13): 1) Elasticity (compliance) and its inverse, stiffness, reflect linear, time-independent deformation measured under linearly aligned stress (tensile and compressive stiffness) or more complex stress configurations (bending and shear stiffness). Purely elastic material returns to its original configuration after force removal. 2) Viscosity reflects fluid resistance to flow in response to applied pressure, manifested by a time-dependent displacement under constant force. 3) Plastic behavior involves nonelastic deformation without recovery after force release. Developing neurons and neural tissue commonly display viscoelastic and plastic behavior.

Forces.

Five types of physical force are especially relevant to CNS morphogenesis: 1) Omnidirectional fluid pressure arising from macroscopic fluid production (e.g., intraventricular CSF) or from osmotic imbalance across a cell’s plasma membrane spreads in all directions until reaching a diffusion barrier. 2) Surface tension and interfacial tension are tangential forces that strive to reduce the surface area of an interface between two materials. In biology, fluid pressure across an epithelium sealed by tight junctions causes macroscopic interfacial tension. Microscopic surface tension arises at the plasma membrane lipid/aqueous interface and is enhanced by interfacial tension from an underlying actin-rich cytoskeletal “cortex” (14). 3) Microscopic directed pressure can be highly anisotropic, but only when cellular components (e.g., bundled filaments) have high bending stiffness as they push. 4) Axial tension occurs when elongated cellular components actively generate a longitudinal shortening force or when elastic or viscoelastic components are passively stretched while anchored at both ends. 5) Adhesiveness reflects the tendency of a cellular constituent to stick to something else, including molecules in the ECM that surrounds CNS cells and has its own distinctive material properties (15), even when forces are trying to pull the components apart.

Tensegrity.

A tensegrity structure, as promulgated by Buckminster Fuller (16) for architecture and by Donald Ingber (17, 18) for cell biology, attains stability by having some components under tension and others under compression, rather than the predominantly compressive forces that support conventional buildings. In a geodesic dome the distribution of struts under tension vs. compression depends on external forces (e.g., gravity and wind) and can change rapidly (e.g., in a storm). In cell biology, focal adhesions to external substrates can transfer tension and strongly influence cell geometry (19). Living cells are not floppy bags of molecular and macromolecular soup but rather “prestressed” tensegrity structures responsive to dynamic developmental and environmental forces.

Biomechanics of Tissue Expansion.

Key aspects of tissue growth in developing CNS tissue can be considered in relation to a schematic 3D grid of small volume elements (“voxels” in Fig. 1). Tissue expansion in a given voxel is indicated by a tiny “growth bubble” whose size reflects the net change in volume per unit time (from expansion of existing cells and ingrowth of new cells, less any material loss; see also figures 1.5 and 12.1 in ref. 20). If tissue compliance is isotropic and there is no external pressure differential, expansion will also be isotropic, represented by a spherical growth bubble and equal-sized green expansion arrows (Fig. 1A). Anisotropic tissue compliance such as that caused by radially biased tension (Fig. 1B, red arrows) leads to anisotropic tissue expansion—an ellipsoidal growth bubble (of equal volume) and unequal green expansion arrows (Fig. 1B). Importantly, these tissue expansion patterns are independent of the direction of cellular migration or ingrowth. Thus, growing axons do not push tissue “ahead” to form a gyrus (as suggested in ref. 21), and migrating neurons do not push cells “to the side” (as suggested in ref. 22).

Fig. 1.

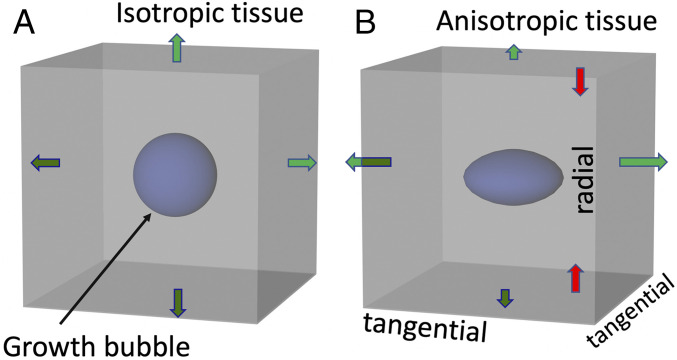
(A) Spherical growth bubble and isotropic expansion (green arrows) in a cubical tissue “voxel” with isotropic compliance. (B) Oblate spheroidal growth bubble in a voxel with radially biased tension (red arrows) and hence anisotropic compliance and expansion.

It is also important to consider asymmetric or anisotropic forces external to a given tissue compartment that can modify cellular architecture (see below). External forces that fold a thick viscoelastic slab generate compressive forces near the fold’s interior crease, tensile (stretching) forces near its exterior margin, and shearing stresses throughout (23).

Cytoskeletal and Related Components.

Neuronal morphology in its magnificent diversity is established, maintained, and modified mainly by the cytoskeleton. Fig. 2 schematizes how four cytoskeletal macromolecules play dominant roles in cellular force generation and transmission in seven common events during neural development. 1) Filamentous actin (F-actin) is a polarized filament whose length is dynamically regulated by polymerization of globular actin (G-actin) subunits at one end and depolymerization at the other. F-actin can be cross-linked into stiff bundles (e.g., in growth cone filopodia), an irregular mesh (in lamellopodia), or ring-like structures in axons (242526–27). 2) Many myosin subtypes interact with F-actin to generate force via multiple mechanisms (14, 2829–30). 3) Microtubules are tubular, larger in diameter than F-actin, lengthened via subunit assembly at one end, and shortened by disassembly at the other (31). They can be cross-linked into stiff bundles (32), and sliding between microtubules can generate a pushing force mediated by molecular motors (28, 33). 4) Anchoring molecules, particularly transmembrane integrins, mediate focal adhesion to the plasma membrane (26, 34, 35) by anchoring F-actin, microtubules, and other filaments internally and binding externally to the ECM, a network of proteins, proteoglycans, and other molecules that occupy interstitial space and also constitute the basal lamina (basement membrane) at the pial surface (36). Another subsystem regulates osmotic pressure across the plasma membrane by transmembrane transport of ions, water, and other constituents (37).

Fig. 2.

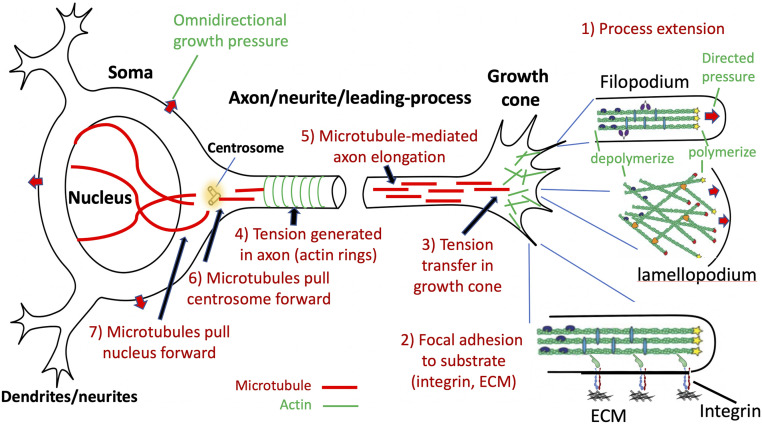
Key events and cellular components in a prototypical developing neuron during axonal/neurite outgrowth and cell migration. These events may occur concurrently or in any sequence.

Growth Cones.

Growth cones enable axons, dendrites, and migrating cells to advance, retract, or turn based on local chemical and mechanical cues. Actin polymerization in lamellopodia and filopodia can push the plasma membrane forward by directed pressure (red arrows, event 1 in Fig. 2) (27, 38). Adhesion of the growth cone tip to ECM molecules (event 2) enables actomyosin-mediated traction to advance the growth cone (39, 40) and transfer tension to the growth cone rear (event 3) (27).

Axons and Neurites.

“Neurites” (not explicitly classified as axons or dendrites) studied in vitro commonly exhibit three key characteristics: resting tension, retraction on tension release, and elongation when pulled (“towed growth”). Resting tension has been demonstrated in vitro for many neuronal types and species and in vivo for invertebrate axons (4142–43). Tension magnitude varies widely (13), but should suffice to drive morphogenesis in highly compliant neural tissue (SI Appendix, Topic 1). Axons can transfer tension from the growth cone (event 3 in Fig. 2) and also generate tension along their length (event 4 in Fig. 2) by an actomyosin-based process likely involving circumferential F-actin rings (6, 24, 44). When tension is relaxed, retraction commonly occurs (45). Towed growth can increase axonal length dramatically while maintaining diameter (46, 47), likely involving pushing from microtubule sliding (event 5 in Fig. 2) (48, 49).

Glial and Dendritic Processes.

Evidence for resting tension in glial cell processes comes from tissue cuts in developing cerebellum (50) and viscoelasticity observations in retina (51). Resting tension in dendrites has been challenging to demonstrate directly but is consistent with dendritic elongation via growth cones (52), the presence of dendritic actin–spectrin rings (53) akin to those implicated in axonal tension, plus indirect evidence discussed below.

Migration and Cytokinesis.

Neurons often migrate considerable distances from birthplace to destination (54). In radial migration, a leading process growth cone crawls along an anchored radial glial scaffold and passively pulls the centrosome via microtubule assemblies (event 6 in Fig. 2); the nucleus may be pulled passively via microtubules (event 7) or pushed by myosin-based squeezing (54). Tangentially migrating neurons lack a glial scaffold, but their leading processes (54) may advance by latching onto the ECM of vascular endothelial cells (55). During cytokinesis of glial and neural progenitors, nuclear translocation can occur along processes anchored to the ventricular (apical) and/or pial (basal) surfaces (56), likely involving microtubule-mediated pulling of the centrosome and nucleus (events 6 and 7 in Fig. 2) (5758–59).

Tissue Growth and Mechanics.

The embryonic mammalian forebrain gives rise to cerebral cortex plus many subcortical nuclei via an intricately choreographed process involving multiple proliferative zones and other transient structures. This section emphasizes key events in human and macaque forebrain development but also draws on findings in ferret and mouse.

Forebrain Vesicles and Ventricles.

The telencephalic and diencephalic vesicles arise and become inflated by virtue of 1) rapid neuroepithelial cell proliferation in the anterior neural tube, 2) sealing of the anterior neuropore to impede CSF efflux, 3) actomyosin-based constrictions that separate embryonic vesicles (60), and 4) a pressure differential across the tight-junction–coupled neuroepithelium driven by ion pumps and protein and proteoglycan secretion (37) (SI Appendix, Topic 1). The choroid plexus emerges as a vascularized structure whose epithelial layer produces CSF (61) plus growth factors that promote neuroepithelial proliferation (62), and the forebrain vesicles differentiate into ventricles proper. In humans, the lateral ventricles expand rapidly along with the thin cortical sheet (Fig. 3A).

Fig. 3.

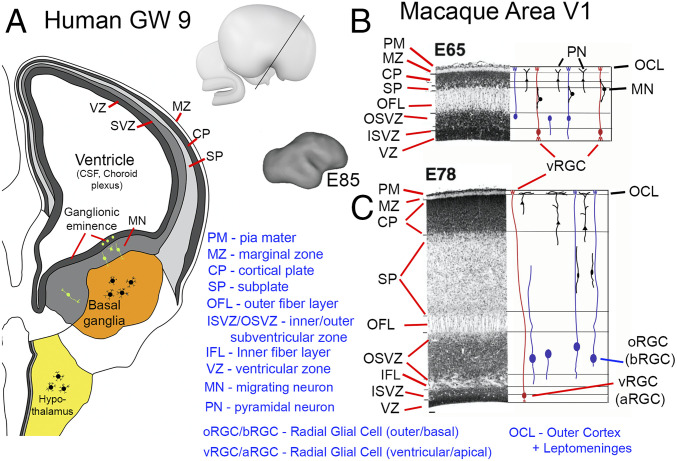
Primate forebrain development. (A) Schematic of human coronal section at GW9. Copyright (2006) from ref. 63. Reproduced by permission of Taylor and Francis Group, LLC, a division of Informa plc. (B and C) Nissl-stained sections from macaque cortical area V1 at embryonic days E65 and E78, respectively, with schematics of glial and neuronal morphologies. Reprinted from ref. 65, by permission of Oxford University Press.

Subcortical Nuclei.

Forebrain subcortical nuclei arise from the ventricular germinal zone of the diencephalon and ventromedial telencephalon (63). Postmitotic diencephalic neurons migrate mainly laterally and settle in nearby target regions that become specific thalamic and hypothalamic nuclei, each generally compact but irregularly shaped (yellow in Fig. 3A). The diencephalic vesicle collapses into the narrow third ventricle lined by a thick gray matter wall. In the telencephalon, the blob-like ganglionic eminence bulges into the lateral ventricle. Many postmitotic neurons from the ganglionic eminence migrate ventrally and coalesce to form the basal ganglia nearby (orange in Fig. 3A).

Tension Explains Quasi-Isotropic Subcortical Expansion.

Neurons in forebrain subcortical nuclei typically develop multipolar, irregularly oriented dendrites (64) intertwined with one another and with highly branched intrinsic and afferent axons. If these dendrites and local axons are under tension, their quasi-isotropic morphology should result in quasi-isotropic subcortical tissue compliance and tissue expansion (as in Fig. 1A), thereby accounting for their mostly blob-like adult shapes (1). Alternative morphogenetic mechanisms have not to my knowledge been proposed for the shapes of typical subcortical nuclei. SI Appendix, Topic 2 addresses an outlier case, explaining why the tail of the caudate nucleus in primates has a uniquely elongated shape and an associated architectural anisotropy discernible using diffusion MRI.

An Extended Proliferative Period for Cerebral Cortex Neurons.

Cerebral cortical neurons greatly outnumber subcortical neurons, especially in gyrencephalic species, as a consequence of several developmental factors: 1) The balloon-like ventricular expansion (Fig. 3A) preferentially increases the surface area of the cortical portion of the proliferative ventricular zone. 2) Cortical germinal layers add inner subventricular zones (ISVZ) and outer subventricular zones (OSVZ), increasing the proliferative pool (65). 3) A prolonged neuronal proliferation period (red bars in Fig. 4 A and B) allows many rounds of mitosis. In macaque area V1, neurons are born during the 2 mo between approximately embryonic day 45 (∼E45) and ∼E102 (66, 67). Neuronal proliferation for human cortex is even longer, extending from approximately gestation week 6 (∼GW6) into the third trimester (68). As proliferation subsides, the ventricular zone becomes an ependymal cell layer (69) no longer sealed by tight junctions (70, 71), thus facilitating CSF seepage through the brain parenchyma. SI Appendix, Topic 3 discusses why, from evolutionary and computational perspectives, cerebral cortex remains thin but expands disproportionately with brain size.

Fig. 4.

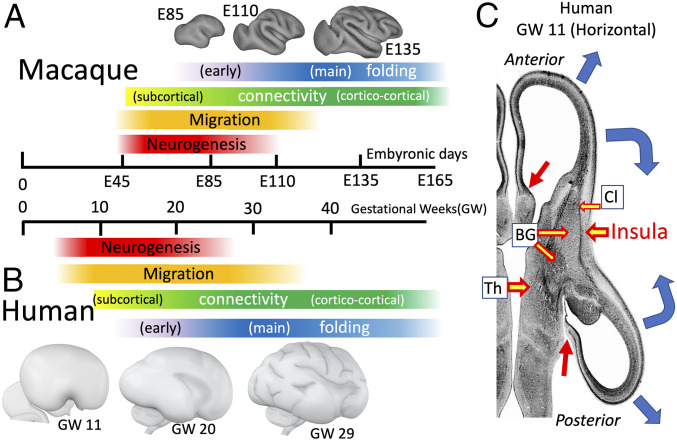
(A and B) Timing of major events in macaque (A) and human (B) cortical development. (C) Location of future insular cortex relative to claustrum (Cl), basal ganglia (BG), thalamus (Th), and lateral ventricles in human at GW11. Blue arrows, cortical expansion trajectories; red arrows, junction between neocortex and subcortical medial wall. (A) Macaque surface models are reprinted from ref. 106, which is licensed under CC BY 4.0. (C) Republished with permission of Taylor & Francis Group LLC – Books, from ref. 63; permission conveyed through Copyright Clearance Center, Inc.

Radial and Tangential Migration.

Postmitotic excitatory neurons born in the ventricular zone migrate radially along a scaffold of ventricular radial glial cells (vRGC) (a.k.a. apical RGC [aRGC]) anchored at ventricular and pial surfaces. In primates, neuronal proliferation in the subventricular zones, especially the OSVZ, continues beyond that of vRGCs (68) and involves multiple outer radial glial cell subtypes (oRGC) (a.k.a. basal RGC [bRGC]) whose processes extend apically and/or basally (Fig. 3C) (56, 7273–74). Later-born neurons migrate mostly along radially oriented oRGC basal processes, many of which are likely anchored within the OSVZ as well as at the pial surface and are under tension as the cerebral wall expands (72, 75). Neurons reaching the cortical plate migrate past deeper (earlier-born) cortical neurons and settle superficially, just below the marginal zone (MZ) that contains early-arriving Cajal–Retzius cells and later becomes layer 1 (76, 77). Migration (orange bars in Fig. 4 A and B) extends well beyond the neural proliferation period.

Excitatory pyramidal cells extend a descending axon plus an apical dendrite, typically with an apical tuft in the MZ (25, 65, 76). As additional migrating neurons settle more superficially in the cortical plate, the apical dendrites of deeper-layer pyramidal cells remain anchored in the MZ and presumably lengthen by towed growth akin to that observed in vitro (Fig. 3C) (77, 78). Inhibitory interneurons migrate tangentially from the ganglionic eminence (54). In the macaque, glial cells arise mainly from the OSVZ as neuronal proliferation winds down (79).

The Outer Cortex + Leptomeningeal Layer.

The outer (basal) cortical surface is bounded by the pia mater, which includes a thin layer of pial cells; an acellular and stiff basal lamina containing collagen, laminins, etc. (80); an ECM that may extend into the arachnoid layer; and a vasculature that early on contains a plexus of pial capillaries (81). The MZ (later layer 1), pia mater, and adjacent arachnoid layers are anatomically distinct, but are considered here as an outer cortical + leptomeningeal (OCL) zone/layer (Fig. 3B) that works in concert to generate tangential morphogenetic forces.

Cortical Subplate and Fiber-Rich Zones.

The cortical subplate (SP) (Fig. 3), between the cortical plate and the outer fiber layer (OFL), is a transient but at times thick layer (63, 65, 82, 83). It is fiber rich but contains migrating neurons plus a sparse but persistent population of morphologically heterogeneous neurons (84, 85), and it serves as a transient waiting zone for thalamocortical and and cortico-cortical projections (86, 87) (but see ref. 88). The initially thin OFL thickens and transitions to WM along with the subplate and OSVZ. The subcortical WM core and its precursors are considered a single layer in the current framing of the DES+ model despite its multilaminated fibrillar and cellular strata (63, 82, 89).

Connectivity and Gyrification.

In humans, early-forming long-distance fiber pathways involving cerebral cortex (Fig. 4B, yellow portion of connectivity bar) include the internal capsule (starting ∼GW8) and corpus callosum (starting ∼GW13.5) (82). Cortical synapse formation and WM expansion involving cortico-cortical and cortico-subcortical pathways occur throughout the third trimester (68) (green portion of connectivity bar) and match the main period of gyrification (blue portion of folding bar) (82). In the macaque (Fig. 4A), long-distance cortico-cortical connections reach the subplate and/or cortical plate beginning ∼E106 for area V4 (87) and ∼E108 for V1-V2 (90). This overlaps with the main gyrification period (∼E100 to ∼E135) (9192–93). Axons tend to run in parallel in the developing white matter, forming numerous long-distance fiber tracts. However, extensive crossing of fiber bundles must occur to achieve the brain’s enormous wiring complexity (e.g., an average of >50 input and output pathways to each cortical area in the macaque) (94). Hence, white matter wiring must have high topological complexity, which has important implications for aggregate wiring length as the brain grows (see below).

Three-Dimensional Landscape Prior to Gyrification.

The insula and Sylvian fissure profoundly impact overall cerebral shape in primates. Insular cortex arises early from a specialized germinal region (95) and is anchored by its connections with the adjacent slow-growing claustrum and basal ganglia (Fig. 4C). Neighboring neocortex expands rapidly (blue arrows), surrounding the insula by GW20 and forming a complete Sylvian fissure by GW29 (Fig. 4 B, Bottom row). Near the midline the cortical sheet merges with subcortical structures (red arrows in Fig. 4C); the noncortical “medial wall” occupies the gap. At GW20, the 3D landscape is generally smooth but curved to varying degrees: rounded like a ball near occipital and frontal poles, quasi-cylindrical in some temporal and peri-Sylvian regions, and saddle shaped in a few locations. These 3D features may bias the axis of cortical folding (see below and ref. 96).

Early Cortical Folds.

An important but understudied early phase of cortical folding occurs in primates (purple portion of folding bars in Fig. 4). Most strikingly, the calcarine sulcus (CaS) appears by GW13.5 in humans (82) (Fig. 5 A and B) and by E85 in macaques (91). The associated cerebral wall is notably thin (red arrows) except for the marginal zone (green arrows) and protrudes deeply into the ventricle.

Fig. 5.

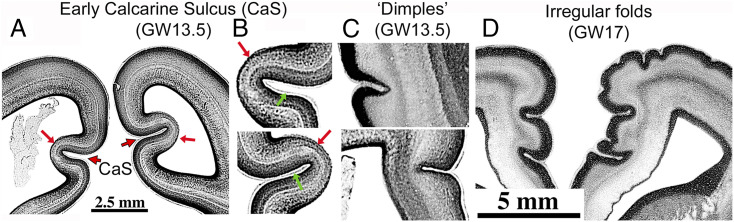
Early-forming cortical sulci in humans. (A and B) Calcarine sulcus at GW13.5 (coronal). (C) “Dimples” in lateral temporal (Top) and medial frontal (Bottom) GW13.5 cortex. (D) Early irregular folds in frontal cortex at GW17. Republished with permission of Taylor & Francis Group LLC – Books, from ref. 82; permission conveyed through Copyright Clearance Center, Inc.

Also appearing early in the second trimester in humans are small dimples and wrinkles (Fig. 5 C and D) that are irregular in location and spacing and might only be transient (82). Importantly, invaginations are typically most pronounced in superficial layers, suggesting they are initiated by superficial morphogenetic forces. Remarkably, addition of several ECM components to human organotypic neocortical slice cultures induces invaginations that are most pronounced in superficial layers and include basal lamina “fingers” extending into each invagination (97) (SI Appendix, Topic 4). These observations help motivate the proposed role of the OCL in the DES+ model.

Key Folding and Thickness Characteristics.

Models of cortical expansion and folding should aim to account for many observations, including the following: 1) Folding and folding-function consistencies: In moderately gyrencephalic species, cortical folding is consistent across individuals and is closely correlated with areal boundaries (folding-function consistency), as demonstrated most clearly in the macaque (1, 98, 99). 2) Folding and folding-function variability: In contrast, human cortex shows much greater individual variability in folding and folding-function correlations, although regularities persist for primary folds (99100–101). 3) Folding-related architectonic distortions: Cortical folding is associated with systematic distortions of laminar and radial organization and cellular morphology (75, 102, 103). In gyral crowns, radial axes diverge from the base; deeper layers are thicker and have tall, narrow dendritic arbors vs. short, wide arbors in thinner superficial layers. In sulcal fundi, the pattern is reversed. 4) Cross-sulcal adherence: In countless published human structural MRI images and in gently processed histological sections from healthy adult brains, apposed banks of sulci generally are contiguous with one another along the pia mater over extended regions, except where blood vessels intervene (SI Appendix, Topic 2 and Fig. S1). This adherence may be mediated by a thin intervening ECM layer, as occurs in other tissues, where apposed basal laminae may adhere to or slide past one another (104). 5) Cortical thickness: Cortex tends to be thinner in sulcal fundi and thicker in gyral crowns (75). Also, each cortical area has a characteristic thickness, which in adult humans varies approximetaly twofold across cortical areas (105). 6) Folding abnormalities: Folding abnormalities occur in many human brain disorders (e.g., lissencephaly, polymicrogyria) and should be explicable in terms of altered folding mechanisms (SI Appendix, Topic 5).

The DES+ Model.

Fig. 6 schematizes major morphogenetic forces proposed for each layer. The model’s core tenets represent mechanistically distinct components that can operate in concert and presumably contribute to different degrees according to region and developmental stage.

Tenet 1. Radially biased tension promotes tangential cortical expansion and is supplemented by CSF pressure at early ages. Initially, tension along radial processes of neuroepithelial and radial glial cells combines with elevated CSF pressure to expand the nascent cerebral wall and keep it thin, akin to inflating a balloon. Once migrating neurons establish the cortical plate, tension along pyramidal cell apical dendrites anchored by apical tufts in the MZ and by cell bodies and basal dendrites in deeper layers (red arrows) make CGM stiffer along radial vs. tangential axes (pink elliptical growth bubbles) (cf. Fig. 1), thus promoting tangential expansion.

Tenet 2. Differential tangential expansion along the cortex/core boundary promotes folding. Except for the medial wall gap (Fig. 4C), cerebral cortex surrounds a subcortical core that includes WM, ventricles, and forebrain subcortical nuclei in adults, plus subplate, fibrous, and proliferative zones at earlier stages. The pattern of subcortical core expansion should reflect integrated growth across the volume, schematized by the magnitude and orientation of local growth bubbles. Cortex remains smooth if the expanding exterior of this core matches tangential cortical expansion, as occurs early in development in all mammals and into adulthood in lissencephalic species. In gyrencephalic species, instabilities arise along the cortex/core boundary once cortical surface area expands beyond that needed to enshroud a smooth core. Tension along axons and glia that cross this boundary prevents overt separation between the CGM and core. Instead, the exterior of the subcortical core must expand by folding to match that of the adjacent cortical sheet. This can be manifested in two distinct ways in terms of the location and pattern of folding.

Tenet 2A. Pathway-specific tension promotes gyral folds. Pathway-specific tension along axons interconnecting nearby cortical areas tends to bring strongly connected regions close together, forming a gyrus in between. Importantly, interareal connections tend to be strongest between nearby areas, and on average connectivity declines exponentially with distance (via WM) between areas (107). Given this distributional bias, pathways linking nearby areas should strongly influence folding patterns unless these pathways selectively lack tension (see below).

Tenet 2B. Tethering tension promotes buckling along the cortex/core boundary. Axons and radial glial processes whose trajectories include a strong component oriented toward deeper parts of the subcortical core generate tethering tension that anchors the cortical sheet to the interior and promotes buckling once instabilities arise along the cortex/core boundary, rather than allowing fluid-filled “blisters” to form along the boundary. The distinction between tethering and pathway-specific tension is not an all-or-nothing dichotomy; many axons likely contribute to both processes.

Tenet 3. Tangential tension in the OCL layer and transsulcal pial adhesion promote buckling and sulcal invagination. Candidate sources of tangential tension in the OCL layer include 1) obliquely and tangentially oriented apical tufts of pyramidal cell apical dendrites; 2) tangentially oriented axons from extrinsic and intrinsic cortical neurons; 3) axons and dendrites of Cajal–Retzius cells; and 4) passive stretching of the acellular, stiff basal lamina induced by CGM expansion. In addition, adhesion between pial surfaces on opposing sulcal banks may promote sulcal “zipping.”

OCL tension may account for cortical dimples occurring early in normal development (Fig. 5 C and D) and after experimental induction (97). As schematized on the right in Fig. 6, instabilities may arise when a local invagination (“puckering”) alters local forces and/or material properties to promote further invagination (e.g., by inducing a nonlinear increase in OCL tension). When invagination brings the basal lamina on opposite sides of a crease into contact, adherence between opposing pial surfaces (via adhesive ECM intermediates) (SI Appendix, Topic 4) may stabilize the crease and also tend to “zip up” the interface and thereby deepen the invagination (Fig. 6, Inset). Other factors such as increased cortical plate compliance at the fundus of nascent sulci (97) might further promote invagination.

Fig. 6.

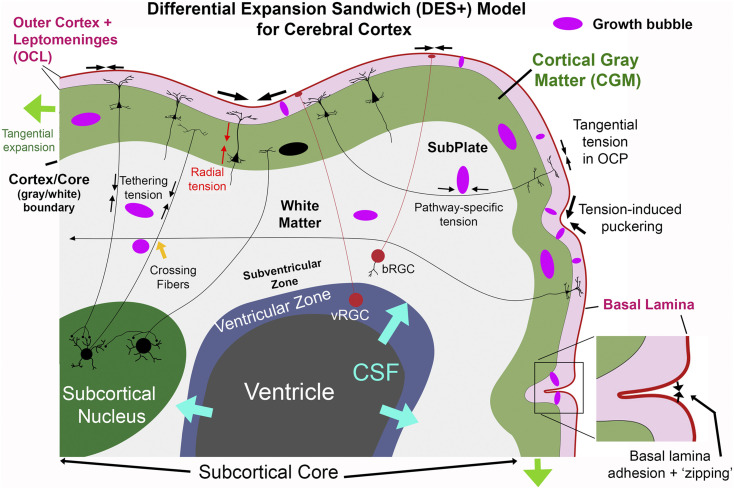
Schematic of the DES+ model for cerebral cortex. See main text for explanation.

For the human CaS (Fig. 5 A and B) tensile and adhesive forces in the thick OCL might interact with mechanical properties of the much thinner subjacent layers of the cerebral wall to promote early and deep sulcal invagination into the ventricle. This distinctive internal bulge persists in adults as the calcar avis of the lateral ventricle (108).

Tenet 4. Three-dimensional geometry biases the location of folds and the axis of folding. The main period of gyrogenesis begins on a relatively smooth but complex 3D landscape generated by differential proliferation, migration, and differentiation (Fig. 4). In regions of locally elevated proliferation and migration the subcortical core will tend to bulge outward, as will the overlying CGM with its elevated number of neurons, setting up a bias for a gyral fold (109, 110). Regions that are curved in a quasi-cylindrical way (vs. flat, quasi-spherical, or saddle shaped), may be biased to fold along their long axis (96), as occurs most prominently in the temporal lobe (Figs. 4B and 7).

Tenet 5. Tension reduces wiring length and interstitial space. Resting tension along dendrites, axons, and glial processes should cooperatively make white and gray matter compact: 1) Axonal and dendritic tension takes up available slack and reduces wiring length throughout. 2) Brain growth is accommodated by tension-induced elongation that protects against axonal breakage. Importantly, wiring-length reduction must respect topological constraints imposed by crossing fiber bundles established prior to gyrification (SI Appendix, Topic 6). 3) Tension along all processes squeezes excess interstitial fluid out of CNS tissue (as in a sponge under pressure), with the pial basal lamina acting as a “shrink-wrapping” outermost layer. This prevents fluid accumulation from steady seepage of CSF through the brain parenchyma driven by ventricular CSF production (blue arrows in Fig. 6).

Fig. 7.

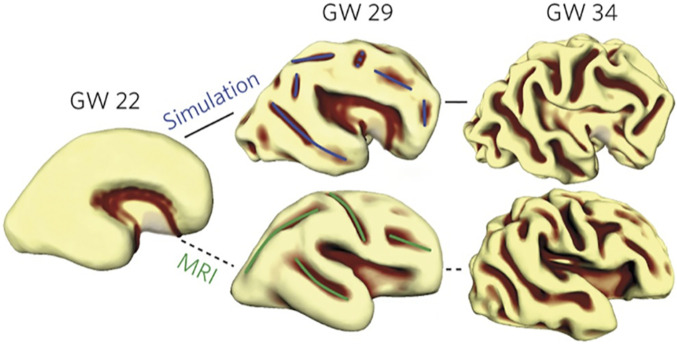
Observed and simulated patterns of cortical folding. Starting from the 3D shape of a GW22 human fetal brain, the gel-brain simulation (Top row) and observed anatomical folding pattern (Bottom row) show striking similarities. Reprinted by permission from ref. 96 Springer Nature: Nature Physics, copyright 2016.

Correlative Evidence Supporting the DES+ Model.

The DES+ model qualitatively accounts for several previously noted characteristics of cortical folding: 1) Folding-vs.-function consistencies can be explained by pathway-specific axonal folding forces that bias the location of gyral folds. In the macaque, gyri typically lie between nearby strongly connected areas (e.g., areas V1 and V2) (1, 98). However, detailed quantitative analyses have not been reported for any species. 2) Folding and folding-vs.-function variability in humans may reflect multiple factors. Individual differences in cortical area size (105) and connectivity (SI Appendix, Topic 7) may result in pathway-specific folding that varies across individuals. Greater tethering tension in the core and/or tangential tension in the OCL may increase buckling or quasi-random invaginations and thus folding-vs.-function variability. 3) Folding-related architectonic distortions: The aforementioned gyral vs. sulcal differences in laminar thickness and dendritic profiles qualitatively match the predicted internal strain patterns when external forces cause a slab to fold; the differences in cell morphology likely reflect dendritic lengthening via towed growth when stretched (tangentially or radially) and shortening by retraction when compressed. 4) Cortical thickness increases markedly during development (65) (Fig. 3 B and C) and correlates with a progressive decline in an initially high radial anisotropy (92). However, the tendency for cortex to be consistently thicker in gyral crowns and thinner in sulcal fundi (75) may involve a different mechanism (111).

Evidence for and against the Model from In Vitro Tissue Cuts.

Tissue cuts made in brain slices of adult mice (112) and developing and adult ferrets (113) provide direct tests for tension in different brain locations. Cuts in deep cerebral white matter caused gaps indicative of resting tension in long-distance axons that presumably mediate tethering. Radial cuts in ferret cortex caused a gap in superficial but not deep layers, consistent with tangential tension in the OCL layer. However, counter to the DES+ model, tangential cuts in ferret CGM (113) failed to reveal resting radial tension. In white matter blades separating gyral folds, gaps occurred for cuts orthogonal but not parallel to the blade, suggesting that pathway-specific tension was selectively lacking in short-pathway cortico-cortical axons between opposing gyral banks. A critical issue is whether these ex vivo observations apply to developing cortex in vivo. This need not be the case, because tension ex vivo may have been partially obscured by tissue edema in and near metabolically active gray matter, stemming from osmotic shock and other side effects of slice preparation. Indeed, glutamate receptor activation and oxidative stress cause edema in brain slices (114, 115), strengthening the plausibility of this confound.

The apparent lack of radial tension within CGM and lack of axonal tension across gyral blades are both puzzling because, as discussed below, no biologically plausible alternative mechanisms have been proposed for preferential tangential expansion or for consistent gyral folding between strongly connected nearby cortical areas. Experiments to resolve these issues are proposed below.

A Complementary Gel-Brain Bilayer DTE Model.

A striking physical and computational two-layer DTE model is based on a gel brain with an elastomer inner core shaped like an early (GW22) human fetal brain coated with a thin, softer outer layer (96). Immersion in a solvent (and running a matched computer simulation) caused the thin outer layer to expand faster, resulting in folding that broadly mimicked human cortical folding (Fig. 7). Importantly, the gel-brain and the DES+ models are strongly complementary. The gel-brain model explains the orientation of major folds as reflecting a smooth linear instability combined with a nonlinear sulcification instability operating on mechanical stress fields arising from the initial 3D brain shape (96). These folding biases are consistent with DES+ tenet 4 but are not predicted by it in detail. On the flip side, the DES+ model explains five major phenomena not explicitly addressed by the gel-brain model but compatible with its framework: 1) Correlations between folds and areal boundaries and how these differ across species are explained by pathway-specific tension pitted against tethering tension and OCL tension (tenets 2 and 3). 2) Regulation of cortical thickness was constrained in the simulation to increase parametrically over time. Tenet 1 acccounts for thickness changes based on temporal and spatial patterns of radially biased tension. 3) Cohesion at the cortex/core boundary is achieved in the simulation by assumed physical continuity and in tenet 2 by tension along processes crossing this boundary. 4) Tangential cortical expansion exceeding growth of the subcortical core is achieved in the simulation by explicit growth equations and in tenets 1 and 5 by preferential tangential expansion of the CGM and compact wiring of the subcortical core. 5) Early cortical folds and dimples, neither reported nor excluded by the gel-brain simulation, are explained by tension fluctuations along the OCL layer and adhesiveness of the pial complex (tenet 3). Thus, a hybrid approach that incorporates the strengths of both the DES+ and gel-brain simulation models offers a promising avenue of exploration.

Comments on Other Models.

Two other models of cortical expansion and folding do not explicitly invoke tension but, like the gel-brain simulation, are compatible with the DES+ model and appear to need tension to attain a biologically plausible instantiation. One is the radial intercalation model (22) for preferential tangential expansion. Another is a model of differential proliferation underneath gyral vs. sulcal regions leading to tangential dispersion of neurons in presumptive gyral regions as explanations for both preferential tangential expansion and cortical folding (110, 116, 117). SI Appendix, Topic 8 explains how these models can both be subsumed by tenet 1, argues that tangential dispersion is a consequence rather than a cause of tangential expansion, and critically evaluates a superficial-vs.-deep layer model of cortical buckling (118) and a “free energy” model of cortical folding (4).

Proposed Tests of the DES+ Model.

The seven approaches outlined below highlight promising ways to address key open questions pertaining to the DES+ model: 1) Photoablation of cellular processes: A potentially powerful approach would be to focally photoablate individual fluorescently labeled dendrites, axons, and/or glial processes in mammals, as has been done in invertebrate axons (119), and then test for resting tension in different regions (CGM, OCL, gyral WM blades), orientations (radial vs. tangential), species, developmental ages, and in vivo (likely feasible in mice and ferrets) or in brain slices that are protected from edema (likely necessary for macaque studies). The magnitude and rate at which cut ends of a photoablated process retract may correlate with tension magnitude and might reveal any radial vs. tangential biases at each location. 2) Gyrification in mouse mutants and in vitro: Model systems for mechanistic studies of cortical gyrification include mutant mice (120, 121), human cerebral slice cultures (97), and stem-cell–derived cerebral organoids (122, 123). In such models it is important to distinguish between “bona fide” folding (with a smooth underlying ventricular suface) and wrinkling that includes all layers of the cerebral wall (75, 109) (SI Appendix, Topic 9). 3) Pial complex adhesion: In vitro experiments (e.g., using organotypic slice culture and free-floating tissue culture (97)) may enable analyses of the molecular basis of adhesion between apposed pial surfaces in nascent cortical sulci. Perturbation experiments akin to those in other model systems (104) may reveal effects of pial adhesions on other aspects of folding (SI Appendix, Topic 4). 4) Computational modeling: Aspects of cortical folding have been modeled using a variety of computational approaches. An attractive option involves computational simulations that incorporate neurobiologically realistic constraints. For example, a finite-element approach akin to that used for the gel-brain DTE model (96) might be adapted to incorporate biologically plausible pressure and tension as predicted by the DES+ model. 5) Biomechanical measurements of tissue properties: Recent methods such as magnetic resonance elastography (MRE) combined with focused ultrasound (FUS) might in principle test for the anisotropic compliance predicted by the DES+ model in white matter, and even CGM if sufficiently high spatial resolution can be achieved (SI Appendix, Topic 10). 6) Folding abnormalities in human brain disorders: Cortical folding abnormalities are profound in some disorders (e.g., lissencephaly) but modest or subtle in others such as Williams syndrome (124) and autism (125). Diverse mechanisms are likely involved in different disorders, including some that can be plausibly explained in terms of specific tenets of the DES+ model (SI Appendix, Topic 5). However, elucidation of disease mechanisms at cellular, molecular, and genetic as well as biomechanical levels will surely remain a major challenge for each disorder. 7) Possible roles of the vasculature in formation and/or stabilization of cortical folds should be explored, given that blood vessels undergo extensive modifications during gyrogenesis (126), including larger vessels embedded in the arachnoid that extend branches into apposed sulcal banks.

Cerebellar Cortical Organization and Development.

Cerebellar cortex is thin (approximately one-third of cerebral cortical thickness), comparable to one cerebral hemisphere in surface area, and tightly folded like an accordion (127). The mammalian cerebellum has 5 cardinal lobes (separated by 4 fissures), 10 lobules, and many finer-grained lamellae and folia in large-brain species (128, 129). Key features of adult cerebellar architecture (Fig. 8A) include a thin layer of Purkinje cells (PCs, red) and Bergmann radial glial cells (BGCs, green) above a dense layer of granule cells (GCs, blue) that have stubby, quasi-isotropic dendrites (128). GC axons ascend to the molecular layer (ML) and bifurcate into parallel fibers that synapse onto trellis-like PC ascending dendritic arbors. The thin cerebellar white matter contains three main axonal types: ascending mossy fibers (from the pons and other subcortical structures onto GCs), climbing fibers (from the inferior olive onto PCs), and Purkinje cell axons projecting to cerebellar nuclei (128, 130). Direct cerebellar cortico-cortical connections via white matter have not been reported. As with cerebral cortex, pial surfaces on apposed cerebellar folds typically abut one another directly (Fig. 8C) and appear to be adherent (SI Appendix, Topic 4 and Fig. S4). Finally, the granule cell layer (GCL) is thicker in gyral crowns and thinner in sulcal fundi, whereas the ML is thicker in sulci than in gyri, similar to the pattern for layer 1 vs. deep layers of neocortex.

Fig. 8.

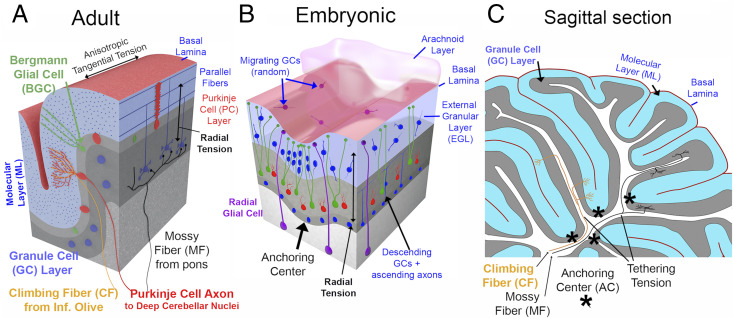
Cerebellar circuits, development, and morphogenetic forces. (A) Adult cerebellar layers and input/output cell types (interneurons excluded). (B) Schematic of key developmental features at an early developmental stage (∼E17.5 in mouse). (C) Adult mouse parasagittal section drawing, with putative tethering forces provided by input axons.

Cerebellar cortical development differs dramatically from that of cerebral cortex, although there are also important similarities. The earliest cerebellar neurons migrate from the rhombic lip anteriorly and then ventrally to form the cerebellar nuclei (131). The massively proliferating granule cell precursors (GCPs, blue) in the external germinal layer (EGL) also originate from the rhombic lip (132) (Fig. 8B). Above the EGL are the pia mater with basal lamina plus an arachnoid layer that (in contrast to cerebral cortex) is notably thick in humans and extends deep into cerebellar folds (133). PCs originate in the ventricular zone, migrate along radial glial cells (RGCs, purple) past the cerebellar nuclei (131) and settle below the EGL. Many RGCs lose their connection with the ventricular surface, migrate to the PC layer, and extend multiple processes to the pial surface (134) to become BGCs that are analogous to bRGCs in cerebral cortex (131, 135). Within the mouse EGL, GCPs have short leading and trailing processes and take divergent movement trajectories (50) as in a “can of worms.” Postmitotic GCs extend processes medially and laterally, becoming parallel fibers that elongate within a rapidly thickening ML below the EGL. GCs migrate down BGC processes (with the GC ascending axons trailing behind) past the PC layer and settle in the inner granular layer (IGL) that becomes the GCL. In mice, major folds are initiated by “anchoring centers” (ACs) that are associated with 1) clustering and elongation of postmitotic GCs in the EGL, 2) maturation and invagination of PCs, and 3) convergence of BGC processes (136) (Fig. 8B). As the cortex expands tangentially, ACs remain anchored at the base of fissures and major folds (asterisks in Fig. 8C).

Mechanisms and Models of Cerebellar Development.

Important mechanistic insights come from tissue cuts in embryonic mouse cerebellar slices (50). Radial tissue cuts into the EGL and underlying core result in wide gaps indicative of “circumferential” (tangential) tension in the EGL and PC layers. Horizontal cuts in the central core between EGL and ventricular zone result in wide gaps indicative of radial tension, likely involving RGCs and descending and ascending axons. These observations inspired a “multiphase wrinkling” model (50) that invokes 1) tangential expansion of the EGL driven by competition between radial and circumferential tension (perhaps generated in part by the meninges) and 2) folding mediated in part by differential radial tension related to the distribution of RGCs and BGCs. This model (137) has an elastic core surrounded by a fluid-like “film”; interactions between film-spanning and full-radius elastic fibers can account for why the outer film is relatively thick at the base of folds and relatively thin at the crowns (at least for the EGL). A proposed three-layer model (138) is based on differential stiffness of the ML, PC, and IGL; however, the ML is not yet present when folding is initiated. None of these models account for the accordion-like pattern of parallel cerebellar folds.

Here, I propose a cerebellar multilayer sandwich (CMS) model for cerebellar cortex that invokes additional features while sharing similarities with the above multiphase-wrinkling and three-layer models, the cerebral DES+ model, and my original cerebellar TBM model (1). The CMS model involves up to five layers, but fewer at early and late developmental stages, and includes five major tenets. Tenet 1, radially biased tension, generated early on mainly by BGC and RGC processes reaching the pial surface and later by PC dendrites and GC ascending axons reaching the ML, should keep cerebellar cortex thin and promote tangential expansion of the IGL, PC, ML, and EGL layers. Tenet 2, anisotropic tangential tension in the ML along parallel fibers, should promote folding along the parallel fiber axis (as in a package of spaghetti noodles) and thereby account for accordion-like cerebellar folding (1) and also elongation of the unfolded cerebellum in macaques and humans (127) along the higher-compliance axis (mainly antero-posterior) compared to the stiffer axis (mainly medio-lateral). Tenet 3, tangential tension in the meningeal layers, may come from stretching of the pial basal lamina and thick arachnoid layer. The transient EGL might also contribute if GCP leading processes are under tension as they migrate in quasi-random directions. Tenet 4, tethering tension in cerebellar input (CF and MF) and output (PC) axons, should keep cerebellar WM compact (Fig. 8C), leading to a thin, highly convoluted cerebellar cortex enshrouding thin WM blades. Tenet 5, transsulcal adhesion, would link opposing sulcal banks, initially by the thick but transient arachnoid (133) and later by ECM linking apposed basal laminae, promoting further invagination by a zipping mechanism akin to that proposed for neocortex. Importantly, the current cerebellar CMS model lacks a clear mechanism to account for ACs and the formation of primary fissures.

Testing the CMS Model.

Several approaches proposed above for the cerebral DES+ model may be adaptable for testing the CMS model: 1) Use photoablation to test for anisotropic tension in parallel fibers; PC dendrites; BGC and RGC radial processes; GC ascending axons; and CF, MF, and PC axons. 2) Analyze cerebellar gyrification mutants (e.g., ref. 139) as model systems for mechanistic analyses. 3) Examine pial and arachnoid mechanical properties and adhesive interactions using in vitro methods, including organotypic cerebellar cultures (140). 4) Biomechanical measures: Does the ML layer show anisotropic compliance along vs. across the parallel fiber axis as predicted by the CMS model (SI Appendix, Topic 10)? 5) Critically evaluate computational models that incorporate biologically plausible tension patterns predicted by the CMS model.