Syntheses, Crystal Structures and Spectroscopic Data

The reactions of RSiCl₃ with R=phenyl (Ph, I), naphthyl (Np, II), and styryl (Sty, III) with Na₂S discussed herein are summarized in Scheme 1.

Scheme 1

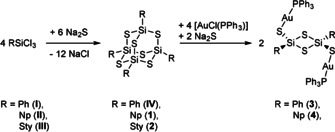
Summary of reactions done to produce compounds IV and 1–5.

While synthesizing NpSiCl₃ (II) as a precursor for [(NpSi)₄S₆] (1), single crystals were obtained upon distillation, and the molecular structure (Figure 1, left) was determined via single crystal X‐ray diffraction. As expected, the Si atom exhibits a trigonal pyramidal coordination environment. Furthermore, π‐interactions between the naphthyl substituents are observed in the unit cell, alternating between parallel‐displaced π‐stacking and T‐shaped CH/π‐interactions (Figure 1, right). The distance between the adjacent naphthyl rings with π‐stacking is slightly larger (3.4397(18) Å) than the distance between the layers in graphene (3.35 Å), ^[9] whereas the distance between the center of one of the naphthyl rings to the closest H atom of the next perpendicular naphthyl ring (2.9371(1) Å) is in the typical range of strong CH/π‐interactions. ^[10]

Figure 1

Molecular structure (left) and crystal structure (right) of II. Ellipsoids drawn at 50 % probability level. H atoms omitted for clarity; π‐stacking and CH/π‐interactions are indicated as dashed lines. Selected distances and angles [Å, °]: Si−Cl 2.0313(7)–2.0385(7)), Si−C 1.8426(18); Cl−Si−Cl 106.42(3)–107.58(3), Cl−Si−C 111.42(6)–112.56(6), C_Np⋅⋅⋅π (red) 3.4397(18), C_Np‐H⋅⋅⋅π (blue) 2.9371(1). ^[15]

The reaction of II with 1.5 equivalents of Na₂S affords a crystalline, colorless solid. Upon dissolution in toluene and cooling to −25 °C, single crystals of [(NpSi)₄S₆]⋅0.5 C₇H₈ (1⋅0.5 C₇H₈) suitable for X‐ray diffraction were obtained. The molecular structure of 1 is shown in Figure 2. 1 crystallizes in the triclinic space group P $\bar{1}$ with two molecules per asymmetric unit. Like [(PhSi)₄S₆], 1 is an adamantane‐type Si/S cluster with four organic substituents, each bound to one Si atom. The molecule shows minor deviations from T_d symmetry, due to slightly different angles in the inorganic core and different orientations of the organic substituents. Furthermore, the two individuals differ greatly in the orientation of the organic substituents (see Figure 2, bottom), indicating a very low energy barrier for rotation of the organic substituents about the Sn−C bond, which in most cases leads to intrinsic amorphousness. Notably, while both [(PhSn)₄S₆] and [(NpSn)₄S₆] are amorphous (with the Np compound comprising a considerable amount of order according to its optical response, see also below), ^[7b] the two Si analogs are crystalline. Initially, this was ascribed to the smaller radius of the Si/S core with respect to the Sn/S core only, as the corresponding smaller volume per given number of cluster molecules causes the aromatic rings of neighboring clusters to approach more closely overall, and thus form more efficient π‐stacking interactions. In this work, we present a refined version of this interpretation (see below).

Figure 2

Molecular structure of 1 (top) and visualization of the two different orientations of the organic substituents in the two individuals within the asymmetric unit (bottom); the structure at the top refers to the bottom right individual. Ellipsoids drawn at 50 % probability level. H atoms omitted for clarity. Selected distances and angles [Å, °]: Si−S 2.111(3)–2.153(3), Si−C 1.837(8)–1.876(8); Si−S−Si 103.42(11)–105.64(13), S−Si−S 110.31(12)–113.28(12), S−Si−C 104.1(3)–110.1(2). ^[15]

The reaction of StySiCl₃ (III) with 1.5 equivalents of Na₂S should proceed similarly and lead to the formation of [(StySi)₄S₆] (2). However, only the crude product could be isolated upon evaporation of the solvent in form of a colorless “solid” with the consistency of cotton candy or honey—depending on the duration of the reaction and drying process. We attribute this to the high polymerization tendency of the styryl substituents, and the corresponding oligomerization/polymerization that proceeds visibly as time goes by. Notably, this was not the case for the Sn analogs, which we take as a further hint for the correlation of the nature of the T/E cluster core with the properties of the organic substituents: in the Sn/S clusters, the styryl substituents of neighboring cluster units are obviously not close enough to allow for a chemical reaction of neighboring vinyl groups. As a consequence of the different situation with an underlying Si/S cluster core, 2 could neither be obtained as single crystals, nor could individual clusters be detected by means of liquid injection field desorption/ionization (LIFDI) or electrospray ionization (ESI) mass spectrometry. However, we were able to collect ²⁹Si NMR data of a freshly prepared sample of 2 that turned out to be sufficiently soluble. A downfield shift of ≈9 ppm of the observed singlet with respect to the precursor signal is in accordance with the NMR data of other Si/S adamantane‐type clusters and their corresponding organosilicon trichloride precursors reported previously, such as [(EtSi)₄S₆]/EtSiCl₃, [(PhSi)₄S₆]/PhSiCl₃, or [(CH₂=CHSi)₄S₆]/CH₂=CHSiCl₃. ^[11] Another indication is given by the ¹H and ¹³C NMR spectra, which clearly show the signals of the styryl substituent at a significant downfield‐shift compared to the starting compound III, with the ipso‐ and meta‐atoms being the most affected, which indicates a reaction at the Si atom to have taken place. Hence, the NMR data indicate the formation of a compound comprising individual adamantane‐type clusters [(StySi)₄S₆]. Yet we assume that they start to unstoppably form oligo‐/polymers shortly upon synthesis.

Further studies on the reactivity of the adamantane‐like organosiliconsulfide clusters were undertaken. The addition of Na₂S and [AuCl(PPh₃)] leads to the fragmentation of the clusters and the formation of the four‐membered rings [{RSi(μ‐S)}₂{AuPPh₃(μ‐S)}₂] (3: R=Ph, 4: R=Np). Colorless single crystals of 3⋅CH₂Cl₂ and 4 were obtained by layering the respective reaction solutions with n‐hexane. Their molecular structures are shown in Figure 3. 3⋅CH₂Cl₂ crystallizes in the monoclinic space group C2/c, and 4 crystallizes in the triclinic space group P $\bar{1}$ , both with half a molecule per asymmetric unit. The molecules in these compounds have an inversion center in the center of an {RSi(μ‐S)}₂ ring, with nearly linear {Au(PPh₃)(μ‐S)} substituents attached to the Si atoms. Although the structural parameters of the central unit in both compounds are quite similar, they differ significantly in the orientation of the {Au(PPh₃)(μ‐S)} units: whereas they point away from the central {Si₂S₂} ring in 3 with a C1−Si1−S2−Au1 cis arrangement, the corresponding atoms in 4 show a trans arrangement. Thus, while the interatomic distances in these compounds are similar, the Si1−S2−Au1 and S2−Au1−P1 bond angles are different. Homologous Sn/S compounds exhibiting this structural motif as well as a cis or trans arrangement depending on the organic moiety at the tetrel atom were described previously, showing the same trends in the T−S−Au and S−Au−P bond angles. ^[12]

Figure 3

Molecular structure of 3 (left) and 4 (right) Ellipsoids drawn at 50 % probability level. H atoms and P‐bound phenyl groups omitted for clarity. Selected distances and angles [Å, °]: 3: Si−S 2.091(2)–2.144(2), S−Au 2.3136(16), Au−P 2.2534(16), Si−C 1.870(7); Si−S−Si 82.40(9), S−Si−S 97.60(9)–115.54(10), Si−S−Au 90.97(7), S−Au−P 178.03(6). 4: Si−S 2.095(2)–2.1589(3), S−Au 2.297(2), Au−P 2.256(2), Si−C 1.865(8), Si−S−Si 82.58(10), S−Si−S 97.42(10)–115.64(10), Si−S−Au 103.57(9), S−Au−P 173.35(7). ^[15]

Upon fragmentation of the adamantane‐type cluster and formation of 4, a further downfield shift by 5.6 ppm was observed in the ²⁹Si NMR spectrum. Table 1 summarizes the respective NMR data for compounds I–IV, 1, 2, and 4. Note that NMR data of compound 3 were not obtained owing to very poor solubility of the crystals.

Table 1

²⁹Si NMR shifts of compounds I–IV, 1, 2, and 4 reported in this work.

Compound	I	II	III	IV	1	2	4
δ (29Si)/ppm	−0.9	−0.4	−0.9	10.9	6.8	8.7	12.4

Quantum Chemical Investigation of Structural Features

It was experimentally shown, that [(PhSi)₄S₆] (IV) and [(NpSi)₄S₆] (1) are observed in a crystalline phase, while [(PhSn)₄S₆] and [(NpSn)₄S₆] are intrinsically amorphous. Nevertheless, it was suggested that [(NpSn)₄S₆] features a structure with a higher amount of order compared to [(PhSn)₄S₆], owing to more efficient π‐stacking interactions between the Np substituents as compared to the Ph substituents. ^[7] This assumption was based on the different nonlinear optical responses of the two compounds, which showed SHG (requiring phase matching) for the Np compound but not for the Ph analog, for which WLG was reported.

To explain the general difference observed in the [(RSn)₄S₆] and [(RSi)₄S₆] cluster compounds with R=Ph, Np, one may consider the smaller radius of the {Si₄S₆} core with respect to the {Sn₄S₆} core to enable a stronger interaction of the neighboring clusters through more efficient π‐stacking interactions. To investigate this hypothesis, quantum chemical calculations of the interaction in cluster dimers as a minimal model were carried out, which already provide valuable insights into the cluster interaction that can be transferred to the extended crystalline or amorphous material.

In order to classify the flexibility of the substituents, we initially calculated the rotation barriers of the substituents for both cluster cores. Rotation barriers of the substituent at the single cluster are hardly present (<1 kJ mol⁻¹) for the clusters with phenyl substituents, while for the clusters with naphthyl substituents, a barrier height of 17 kJ mol⁻¹ is obtained for the [(NpSi)₄S₆] cluster and 9 kJ mol⁻¹ for the [(NpSn)₄S₆] cluster (see Figure 4 and Figure S12). The larger rotation barrier for the cluster with an {Si₄S₆} core as compared to the cluster with an {Sn₄S₆} core can indeed be explained by the smaller core radius. The smaller Si−C distance in this cluster (1.889 Å) in comparison with the corresponding Sn−C distance (2.088 Å) increases the barrier by a stronger interaction between the hydrogen atom of the substituent and the sulfur atoms of the cluster. The relative positions of S and H atoms at the rotation barrier are visualized in Figure 5.

Figure 4

Scan of the phenyl group (top) and naphthyl group (bottom) rotations by variation of the dihedral angle for corresponding clusters [(PhSi)₄S₆] and [(NpSi)₄S₆] calculated at the BP86‐D3/cc‐pVDZ(‐PP) level of theory. Structures at the minimum and maximum positions of the scan are shown on the right hand side. The corresponding scans for the Sn/S core cluster analoges are given in Figure S12.

Figure 5

Comparison of the S−H distances at the energetic maximum of the rotational scan for [(NpSi)₄S₆] (left) and [(NpSn)₄S₆] (right), calculated at the BP86‐D3/cc‐pVDZ(‐PP) level of theory.

Furthermore, the substituent–substituent interaction can increase the rotation barrier, but this is of minor importance for the considered conformers. In summary, the calculations indicate a high orientational flexibility for phenyl substituents on both Si/S and Sn/S clusters, as opposed to a comparatively lower freedom of orientation for naphthyl substituents. The latter show a higher orientational flexibility for the cluster with larger core radius (Sn/S) than for those with smaller core radius (Si/S), which is in agreement with the tendency for (a) higher order in compounds with R=Np than in compounds with R=Ph, and (b) higher order in {Si₄S₆}‐based clusters than in {Sn₄S₆}‐based clusters.

The investigation of the cluster dimer structures was performed to analyze the interaction between the molecules with different cluster cores and substituents. The cluster dimer structures were determined by two computational approaches and their results were combined to obtain a larger number of possible conformers. The dissociation energies of all cluster dimers are plotted against their core–core distance in Figure 6, and selected cluster dimer structures are plotted in Figure 7.

Figure 6

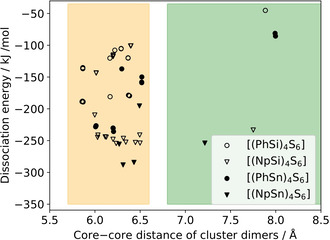
Dissociation energy of cluster dimers, plotted against the corresponding core–core distance calculated at the BP86‐D3/cc‐pVDZ(‐PP) level of theory. Medium core–core distances are indicated by an orange background, large core–core distances by a green background. The region of small core–core distances is plotted in Figure S13.

First, we discuss the obtained cluster dimers in regard of their core–core distances and geometric structures. Most of the cluster dimers have a distance of the two adamantane cores between 5.9 and 6.5 Å (orange region in Figure 6). The [(PhSi)₄S₆] cluster dimers show a core–core distance range that is shifted to slightly smaller values than the range calculated for [(NpSi)₄S₆]. The same trend, but even more pronounced, is observed for the {Sn₄S₆}‐based cluster dimers. Cluster dimers in this region of inter‐cluster distances yielded stacked or alternating substituents and different orientations of the cluster cores (Figure 7). In all of them, a minimum of two substituents of one cluster interact with at least two substituents of the other cluster. In the “stacked dimer” conformers, the substituents are arranged directly towards each other. In the “alternating dimer” conformers, the substituents of one cluster are located in a void between the substituents of the other cluster. Interestingly, the “alternating dimer” structure is slightly preferred on average for clusters with phenyl substituents, while for naphthyl substituents the “stacked dimer” structure is slightly preferred. The core–core distances between Si/S and Sn/S clusters, respectively, differ only slightly for analogous cluster dimers (by ≈0.15 Å on average). The “alternating dimers” show a high similarity to the arrangement of the cluster in the crystal structures, as demonstrated for [(PhSi)₄S₆] in Figure 8. Although similar structural units are present, the core–core distance in the crystal structure (closest core–core distances: 7.05–7.46 Å in IV, 7.44–7.58 Å in 1) is much larger (by 0.5 to 1.0 Å) as compared to the calculated cluster dimers, as in the crystal, the interaction is shared between more than two clusters. Besides the majority of cluster dimers with a core–core distance between 6.0 and 6.5 Å, there are a few cluster dimers with core–core distances between 7.2 and 8.0 Å, with a poor relative orientation of the clusters to each other (green region in Figure 6; example of a structure shown in Figure 7, top). The Si/S cluster dimers with phenyl and naphthyl substituents listed in this green region show larger core–core distances than the corresponding crystal structures. On the other hand, for some of the Sn/S‐based cluster dimers, we found a fusion of cluster structures (purple region in Figure S13). Since we do not consider them to be relevant for the solid‐state structures of this study, we have not considered the fused clusters further.

Figure 7

Examples for cluster dimers emerging from the calculations, shown for dimers of [(PhSi)₄S₆] calculated at the BP86‐D3/cc‐pVDZ(‐PP) level of theory. Top: cluster dimer with a large core–core distance. Centre: cluster dimer with medium core–core distance and alternating substituents (two views). Bottom: cluster dimer with medium core–core distance and stacked substituents (two views).

Figure 8

Comparison of the relative orientation of [(PhSi)₄S₆], as an example of the generated dimer structures (green, core–core distance 6.37 Å) calculated at the BP86‐D3/cc‐pVDZ(‐PP) level of theory, and a dimer extracted from the crystal structure of [(PhSi)₄S₆] ^[7a] (blue, core–core distance 7.05 Å), indicating the good agreement of the model with the experimental data.

Second, we discuss the obtained cluster dimers depending on their dissociation energy. Considering each individual cluster composition, the majority of dimer clusters with core–core distances between 5.9 and 6.5 Å yield higher absolute dissociation energies as compared to the absolute dissociation energies of the cluster dimers with core–core distances between 7.2 and 8.0 Å. The difference in dissociation energies between the medium and large core–core cluster dimers is smaller for clusters with Np ligands than for those with Ph ligands.

Considering the cluster dimers with core–core distances between 5.9 and 6.5 Å, there are 2–3 regions of dissociation energies for the individual cluster compositions in Figure 6, each of which correlates with a certain number of substituents interacting with each other. Thus, the highest dissociation energies were obtained for cluster dimers in which three substituents of one cluster interact with three substituents of the other one. The “stacked dimer” and “alternating dimer” conformers for individual cluster compositions yield similar dissociation energies. Among the cluster dimers with highest dissociation energies, [(NpSi)₄S₆] exhibits a dissociation energy that is by about 65 kJ mol⁻¹ higher than that of [(PhSi)₄S₆]. A similar, but slightly smaller, difference in dissociation energies is calculated for the corresponding {Sn₄S₆}‐based cluster dimers (≈53 kJ mol⁻¹). Obviously, the larger Np substituents lead to a stronger interaction between cluster dimers than Ph substituents. Other than originally anticipated, the investigation of the cluster dimers did not indicate larger dispersive interaction for clusters comprising a smaller radius of the cluster core. The {Sn₄S₆}‐based clusters have a higher absolute dissociation energy than the {Si₄S₆}‐based cluster dimers, which illustrates a stronger interaction overall. To understand this result, we performed a decomposition analysis of the cluster dimer binding energy contributions into the substituent–substituent interaction, the substituent–core and core–core interaction (see Figure 9).

Figure 9

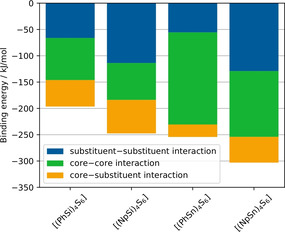
Decomposition of the binding energy contributions of cluster dimers into substituent–substituent interaction, the substituent–core and core–core interaction calculated at the BP86‐D3/cc‐pVDZ(‐PP) level of theory.

The decomposition of the binding energy reveals similar substituent–substituent binding energies for cluster dimers with the same substituent. The larger naphthyl substituents show a higher binding energy than the smaller phenyl substituents due to larger dispersive interactions. In contrast, the core–core binding energy is larger for the Sn/S‐based cluster dimers than for the Si/S based cluster dimers due to the larger adamantane core. This stronger core–core interaction for the larger Sn/S‐based cluster dimers leads to higher absolute values of the dissociation energies than observed for the Si/S‐based analogs. For the cluster dimers with larger core–core distances (green region in Figure 6), the same trend in dissociation energies is observed, although larger core–core distances are found here than for crystalline [(PhSi)₄S₆] and [(NpSi)₄S₆]. We therefore believe that these insights can be transferred to crystalline and amorphous cluster materials with core–core distances between the medium and large core–core distance regions of Figure 6.

In conclusion, we propose that the predominance of the relatively isotropic core–core interactions in [(PhSn)₄S₆] outplay the rather directional interactions involving the substituents, which explains why this compound shows a distinctly lower tendency for order in the solid than the crystalline {Si₄S₆}‐based homologue. This trend is also visible for the clusters with Np substituents, yet for [(NpSn)₄S₆] the relatively similar strengths of core–core and substituent–substituent interactions allow for a higher degree of intermolecular order, which is in agreement with the (virtually contradicting) experimental findings: the powder produces SHG (as a sign of phase matching) in spite of an apparently amorphous nature according to X‐ray diffraction. The results of this study thus contribute significantly to the overall understanding of the origin of (dis)order in compounds of the type [(RT)₄E₆] (T=Si, Ge, Sn; E=S, Se, Te).

Optical Properties

We explored the optical response of compounds 1–4 by optical spectroscopy. The absorption and emission spectra are summarized in Figure 10.

Figure 10

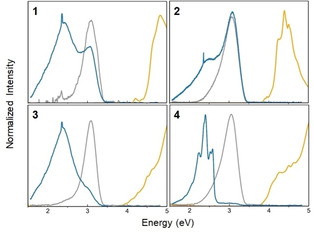
Linear absorption spectra in solution (yellow line) and photoluminescence spectra (solid=blue line, solution=gray line) of compounds (1–4).

Clearly, the emission and absorption data are mirror‐image‐like for the solution data. The emission spectra of the solid phase show an additional resonance about 500 meV below the emission maximum in solution. Such features are commonly attributed to excitons or an ensemble thereof. Notably, the higher‐energy emission maximum persists in the condensed matter phase for all samples. However, it is significantly quenched by the existence of Au/S moieties in compounds 3 and 4 in contrast to 1 and 2. This apparently enhances the lower‐energy emission channels. In particular, for compound 4, several distinct emission channels are observed which are tentatively attributed to transitions involving atomic orbitals of the Au^I atom.

The crystalline compound 1 shows a clear nonlinear optical response. In agreement with the observation made for IV, ^[7b] we observe SHG here in spite of the centrosymmetric space group, which therefore is attributed to surface effects or defects of the crystal (see Figure 11). The other compounds, in general, do not show a nonlinear response that is clearly distinguishable from luminescence effects owing to chemical transformations. Hence, we can neither confirm nor exclude that the adamantane‐based compound 2 exhibits WLG, but its significantly higher chemical sensitivity to oxygen and humidity as compared to the heavier homologue hampers a clear statement to date (note that it is technically not possible to prevent that the samples are exposed to air for a very short moment prior to the measurement).

Figure 11

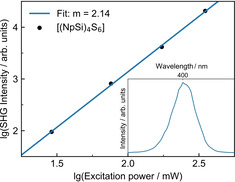
Nonlinear optical response of compound 1. Excitation power dependency of SHG. SHG spectrum from excitation at 800 nm (inset).

Calculation of Optical Properties

We investigated the role of the substituents (phenyl vs. naphthyl) on the optical response of the molecular clusters. Thereby, we modeled two of the synthesized clusters with the same core but different substituents, [(PhSi)₄S₆] and [(NpSi)₄S₆]. The structural relaxation of single clusters and molecular crystals performed by the plane‐wave implementation of the DFT within the periodic supercell method leads to geometries of the same symmetry and in overall close agreement with the structures calculated with a localized basis. The optimized geometries were employed for the calculation of the electronic and optical excitations.

Figure 12 shows the relaxed geometry as well as the HOMO and LUMO states for the [(PhSi)₄S₆] and [(NpSi)₄S₆] clusters. The structural differences between the cluster cores of the two molecules are limited. The Si−S distance amounts to 2.15 Å in both clusters, while the S−C bond length is 1.87 Å in [(PhSi)₄S₆] and 1.88 Å in [(NpSi)₄S₆]. However, the different substituents have a deeper impact on the molecular electronic structure. The (degenerate) HOMO of the [(PhSi)₄S₆] molecule is localized at the S atoms in the cluster core, while the HOMO of the [(NpSi)₄S₆] cluster is localized on the naphthyl rings. The LUMO of both systems is similar and localized on the substituents (see Figure 12). Thus, the DFT‐calculated HOMO–LUMO gap of the two systems is rather different and amounts to 3.76 eV for [(PhSi)₄S₆] and 2.96 eV for the [(NpSi)₄S₆] cluster. Quasiparticle effects, calculated in an approximate manner by the ΔSCF method as described in Ref. [13], open up the fundamental independent‐particle‐approximation (IPA) gap to a value of 6.54 eV for [(PhSi)₄S₆] and 5.09 eV for the [(NpSi)₄S₆] cluster (see Figure S15 in the Supporting Information). The energy of the lowest excitonic excitation, describing the transition of one electron to the LUMO leaving a hole behind in the HOMO, is calculated following the procedure described in Ref. [13]. Excitonic excitations of 3.92 eV for [(PhSi)₄S₆] and 2.89 eV for the [(NpSi)₄S₆] cluster, respectively, are predicted. These energies are rather close to the HOMO–LUMO gap, suggesting that the quasiparticle shifts are nearly canceled out by the electron‐hole attraction. Thus, as many‐body effects due to the electron‐electron and the electron‐hole interaction counterbalance, the IPA‐calculated optical excitation spectra are expected to yield a reasonable description of the measured optical response, at least for the low‐energy excitations.

Figure 12

Optimized molecular structures and orbital characters of the HOMO and LUMO states of [(PhSi)₄S₆] (left) and [(NpSi)₄S₆] (right) single clusters.

The extinction coefficient of [(PhSi)₄S₆] (blue line) and [(NpSi)₄S₆] (black line) single clusters is shown in Figure 13. The components of the dielectric tensor are averaged to allow for a direct comparison with experimental data later in the manuscript. The general shapes of the dielectric functions are rather different, although the structures of the two clusters are similar. In order to rationalize these differences and understand their origin, we analyzed the electronic transitions of the two clusters. Indeed, spectral resonances can be directly related to electronic transitions between occupied and empty states at the IPA level.

Figure 13

Extinction coefficients calculated in the independent‐particle approximation for isolated [(PhSi)₄S₆] (blue line) and [(NpSi)₄S₆] (black line) clusters.

The onset of the optical absorption corresponds exactly to the DFT‐calculated HOMO–LUMO transition in the case of the [(NpSi)₄S₆] cluster (black line). Structures in the first peak match quite well the energy of the HOMO–LUMO+1,2 (degenerate) and HOMO–LUMO+3. The main peak at about 4 eV is mainly due to transitions from the HOMO to a group of energetically close states localized at the C atoms of the naphthyl rings. Instead, in the case of the [(PhSi)₄S₆] cluster (blue line), the onset of the optical absorption is located at much higher energies than the DFT‐calculated HOMO–LUMO difference. Indeed, the HOMO–LUMO transition probability is small, due to the different spatial localization and orbital character of the two states. We assign the first spectral peak to transitions from the HOMO to three molecular orbitals about 4.4 eV above the HOMO and with a spatial extension partially overlapping the HOMO. Summarizing, the absorption spectra of [(PhSi)₄S₆] and [(NpSi)₄S₆] clusters are rather different concerning the positions and line shapes of the spectral features. The deviations in the optical response originate from the qualitatively different and differently localized electronic states involved in the transitions resulting in the main spectral peaks of the two compounds.

The optical answer of the isolated clusters represents the basis for understanding the absorption spectra of the solid material comprising the molecules. According to the calculations, which started from the experimental crystal data, the optimized geometries show only small modifications of the geometrical parameters determined for the isolated molecules. The largest bond length deviation is 1.4 pm, while the bond angles of the substituents are rotated by 13.2° with respect to the single molecules due to the presence of toluene. When the single clusters aggregate to form the crystalline material, the discrete energy levels broaden to become energy bands. These have been calculated in the IPA approximation along the directions in reciprocal space shown in Figure S16, and are illustrated in Figure 14. The electronic band gap of the crystals is slightly smaller than the HOMO–LUMO energy differences of the corresponding molecules; however, the orbital characters of valence and conduction band edges closely resembles those of the HOMO and LUMO of the parent molecules (see Figure 12). As the band dispersion is rather flat and no major rearrangement is expected upon inclusion of quasiparticle effects, self‐energy correction mainly serves to widen the band gap, and may be replaced by a numerically less costly scissors‐shift for the calculation of the optical response.

Figure 14

Electronic structure of the crystals comprising [(PhSi)₄S₆] and [(NpSi)₄S₆] molecules calculated within the IPA. The fundamental band gap is indicated in yellow.

We then proceeded with the optical characterization of the synthesized crystalline compounds. Owing to the synthesis method, the experimental crystal structure of [(NpSi)₄S₆] (1) comprises toluene molecules (0.5 C₇H₈ per formula unit of 1, see Table S1). As illustrated in Figure S17, the extinction coefficient calculated with and without toluene does not substantially differ, demonstrating that the optical response of the molecular cluster is not affected by the presence of solvent. The extinction coefficient calculated within the IPA for the [(PhSi)₄S₆] (IV) derived and [(NpSi)₄S₆] (1) derived molecular crystals is shown in Figure 15.

Figure 15

Extinction coefficient of the [(PhSi)₄S₆] derived (blue line) and [(NpSi)₄S₆] derived (black line) molecular crystals calculated within the IPA at the DFT equilibrium geometry.

For both compounds, the spectral signatures of the isolated clusters are clearly recognizable in the optical answer of the corresponding molecular crystals. They barely shift in energy, and the relative intensity compares well with that predicted for the single clusters. It can thus be concluded that the transitions leading to the absorption peaks of the single clusters are chiefly responsible for the major peaks in the dielectric function of the semiconducting crystals. The main difference between molecules and crystals comprising these molecules is that the crystal absorption features are broadened with respect to the molecular peaks due to the energy dispersion of the molecular states upon aggregation. As the onset of the molecular and crystalline absorption coincides, we can exclude new intermolecular low‐energy electronic transitions to occur when the clusters aggregate to form crystals. Thus, for the investigated compounds, the molecules seem to individually interact with light rather than jointly. However, the relative orientation of the molecules in the solids (ordered vs. non‐ordered) controls the nature of the nonlinear optical response (with or without phase matching).

In order to compare the calculated spectra of the crystalline material comprising [(NpSi)₄S₆] cluster (1) with the measured data, we accounted for many‐body effects in an approximated manner by means of a scissors‐shift. ^[14] We chose a scissor‐shift of 0.7 eV, correcting the DFT underestimation of the experimentally measured band gap of the molecular crystals. The corresponding results are shown by the blue line Figure 16 together with experimental results (yellow line) from Figure 10. The comparison with the experimental data shows that calculations at the IPA level with scissors‐shifts already agree with the measurements.

Figure 16

Extinction coefficient of the crystals comprising [(NpSi)₄S₆] molecules, calculated within the IPA with scissor‐shifts of 0.7 eV (blue line). The measured curve (yellow line) as well as the IPA calculation without scissors‐shift (gray line) are shown for comparison.

The calculations fairly describe the main absorption peak, originating from transitions between the valence band edge and bands localized at the C atoms of the naphthyl rings, including the shoulder observed at about 4.6 eV. However, the intensity of the peak at about 3.5 eV corresponding to the transition from the valence band maximum to the conduction band minimum is overestimated in the calculations in comparison with the measured spectra. More refined and computationally demanding approaches accounting for quasiparticle effects in a perturbative manner and accounting for the electron‐hole attraction by means of the Bethe‐Salpeter equation might further improve the agreement with the experiment.

The calculation of the second‐order polarizability tensor for the crystalline phases of [(PhSi)₄S₆] (IV) and [(NpSi)₄S₆] (1) shows vanishing optical nonlinearities for all tensor components, as expected for a centrosymmetric crystal structure. Deviations from this behavior in experiments thus arise from structural defects and amorphous regions in the samples, as well as from surface‐related contributions. At least for centrosymmetric crystals, they are not inherent bulk properties.