Experiments

We conducted 24 experiments where adult zebrafish individually swam in the flow. In order to understand the role of vision in the fish swimming mechanism, we considered two experimental conditions on groups of 12 individuals: Bright and Dark. In Bright, fish swam with standard illumination (250 lx), and in Dark they swam in the darkness.

Based on related studies, we anticipated that vision would play an important role on rheotaxis [20, 26]. In particular, we expected zebrafish to reduce rheotactic behavior in the darkness when compared to standard illumination conditions [20, 25, 27]. In addition, we anticipated that, even when deprived from vision, fish would still be able to engage in counter flow swimming. In fact, touch and hydromechanical cues along with information from the vestibular system could be integrated to perform rheotaxis [17, 27]. In summary, we made the following hypotheses: (i) zebrafish would still be able to perform rheotaxis in the absence of visual cues, and (ii) the lack of illumination would decrease the ability of zebrafish to perform rheotaxis.

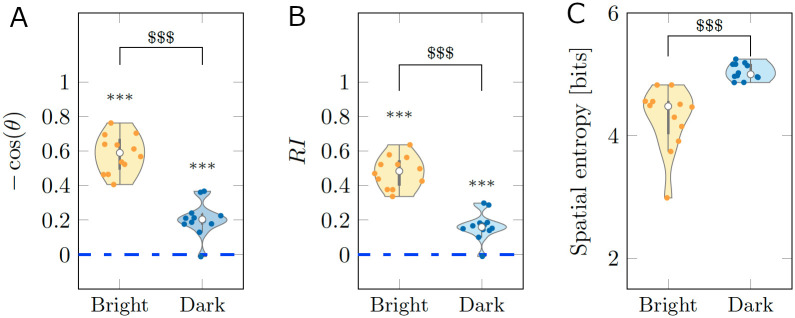
Using an automatic tracking software, we obtained time series for the position of the fish centroid and heading angle as described in Materials and methods. To quantify rheotaxis, we compared the scoring of two different metrics, the mean of (negative) cosine of the heading and the mean rheotaxis index (RI); see Materials and methods for a mathematical definition. Both metrics take values between −1 and 1 corresponding to biased headings towards downstream and upstream, respectively. A zero value represents the case in which a fish does not have a preference to swim either upstream or downstream.

From the results in Fig 1, we determined that the cosine of the heading was different from chance in both Bright (V = 78;p < 0.001) and Dark (V = 71;p < 0.010). Likewise, for RI, we registered significant differences from chance in both Bright (V = 78;p < 0.001) and Dark (V = 68;p = 0.050). These findings support the first hypothesis that fish can perform rheotaxis independent of the illumination conditions. In agreement with the second hypothesis, pairwise comparisons between Bright and Dark identified a superior rheotactic response for animals swimming in standard illumination conditions, with respect to the cosine of the heading (W = 134;p < 0.001) and RI (W = 134;p < 0.001).

Fig 1

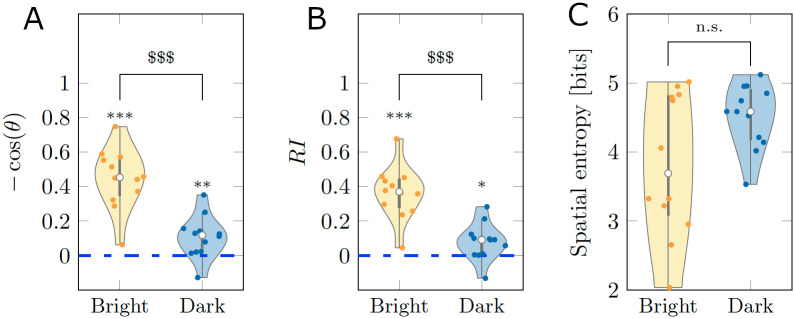
Average scoring of three behavioral metrics for real experiments.

(A-B) Rheotactic metrics taking values between −1 and 1 corresponding to biased headings downstream and upstream, respectively. (C) Spatial entropy, measuring the exploratory behavior across the test section. The average was taken over the entire time series of 9, 000 points for each experimental subject. The gray bar in each violin plot details median (white dot), first and third quartiles, and lower and upper adjacent values. The colored area of a violin plot corresponds to the probability density of the data. Symbols *, ** and *** indicate significant differences from zero with p < 0.050, p < 0.010, and p < 0.001, respectively. Symbol $$$ indicates significant difference between conditions with p < 0.001.

Finally, to measure locomotory activity of the animal in the form of exploration of the entire test section, we calculated the spatial entropy; see Materials and methods for a mathematical definition. The comparison between the two conditions suggests the presence of a weak trend, with fish swimming in the dark displaying a higher locomotory activity than subjects swimming in standard illumination conditions (W = 47;p = 0.160). This weak trend was accompanied by a significant difference of the variance of the spatial entropy between conditions (F = 13.497;p < 0.010), with animals swimming in the dark displaying a lower variability.

Zebrafish swimming as a finite-dipole

We treat a zebrafish as a self-propelled body swimming in two dimensions within a uniaxial inviscid flow (see Fig 2). Here, (x(t), y(t)) are the coordinates of the fish centroid in the global reference frame ($$ \mathcal{X},\mathcal{Y})$$, where t is the time variable. The angle θ(t) ∈ [−π, π) represents the fish heading. For θ = −π the fish is heading upstream, while for θ = 0 it is heading downstream. Following [47, 48], we assimilate the fish to a finite-dipole, consisting of a pair of point vortices separated by a distance l, corresponding to the fish thickness. These two point vortices of circulation strengths Γ_l(t) and Γ_r(t) describe the fish self-induced propulsion. The fish thickness is about 5mm for adult zebrafish, which is much smaller than either dimensions of the water channel, 2x_max and 2y_max.

Fig 2

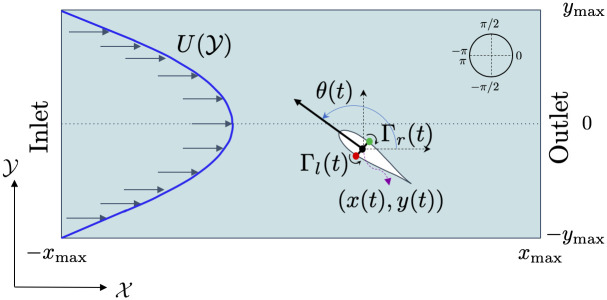
Modeling zebrafish swimming in a flow as a finite-dipole.

$$ U\left(\mathcal{Y}\right)$$ is the profile of the uniaxial background flow. The black dot and arrow denote the fish centroid position (x(t), y(t)) and heading angle θ(t), with respect to the global reference frame ($$ \mathcal{X},\mathcal{Y}$$). The green and red dots represent the left and right location of the vortices of circulation strengths Γ_l(t) and Γ_r(t), respectively.

Hence, the time evolution of the fish position and heading angle can be described by the following set of ODEs:

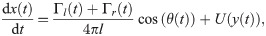
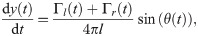
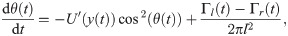
The vortex strengths encapsulate the self-propelling mechanism along with the feedback contributions for controlling both heading and speed. In particular, Γ_l(t)>Γ_r(t) indicates that the fish performs a counterclockwise turn, while the opposite, Γ_r(t)>Γ_l(t), refers to clockwise turns. For Γ_l(t) = Γ_r(t), the fish swims straight. The fish relative speed with respect to the background flow is (Γ_l(t) + Γ_r(t))/(4πl).

Modeling the time evolution of the vortex strengths

In general, the distributions of Γ_l and Γ_r are highly correlated suggesting that these processes are not independent. In particular, the processes unfold around the line Γ_l = Γ_r with random fluctuations corresponding to turning maneuvers. This behavior shares similarities with phase plots of diffusively coupled dynamical systems, often studied in the context of synchronization [49–51]. Just as oscillators tend to synchronize their phase against noise [52], the two vortices seek to match their circulation strengths against random fluctuations (see Supporting information S1 Fig).

We approximate the vortex strengths Γ_l(t) and Γ_r(t) by a Gamma distribution [53]. Based on the analogy with diffusively coupled systems, we propose the following pair of coupled Cox–Ingersoll–Ross processes [54] to model the time evolution of the vortex strengths:

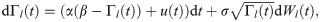
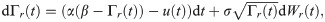
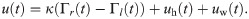
The feedback term u(t) acts differentially on Γ_l(t) and Γ_r(t), that is, it takes opposite signs in Eqs (2a) and (2b) to produce adequate turning maneuvers. For instance, when the fish performs clockwise turns, the vortex strengths should satisfy Γ_l(t) > Γ_r(t). Then, the feedback would tend to increase the circulation of the vortex on the left and decrease the circulation of the one on the right. The first term on the right hand side of Eq (3) corresponds to a classic bidirectional diffusive coupling, with κ[1/s] being the coupling strength [51, 52]. This positive parameter is associated with the ability of a fish to resume straight swimming after a maneuver. The diffusive coupling forces both processes to evolve along the synchronization manifold Γ_l(t) = Γ_r(t). The terms u_h(t) and u_w(t) capture the hydromechanical orientation mechanism and wall interactions through visual cues, respectively. Tactile interactions with the walls are separately addressed by modifying Eqs (2a) and (2b) to account for collisions.

Hydromechanical feedback mechanism

Here, we model the feedback process allowing zebrafish to gather information from hydrodynamic cues and use them to orient in the flow, that is, modulating the vortex strengths through the term u_h(t) in Eq (3). Similar to zebrafish larvae [25], we propose that adult zebrafish perform rheotaxis on the basis of an estimate of the local vorticity field. We compute the circulation of the background flow around a circle $$ \mathcal{C}$$ with radius r centered at (x(t), y(t)), which approximates the fish perimeter (see Fig 3A),

Fig 3

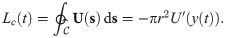
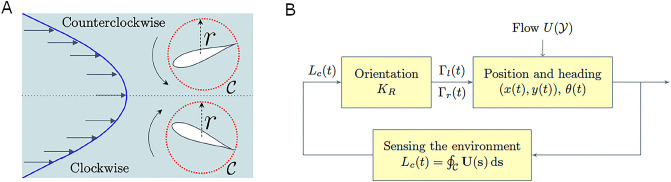
Hydromechanical feedback mechanism.

(A) Example of rotation induced by a parabolic flow; the red circle of radius r is the approximation used for the fish perimeter in the computation of the local circulation of the background flow. (B) Block diagram describing the feedback mechanism to orient in the flow and perform rheotaxis.

Here, U(s) = [U(s_y), 0] is the vector-field of the uni-axial background flow and the last equality is true up to the order $$ \mathcal{O}\left(r^4\right)$$; see Materials and methods for details on the derivation. We set r = 1/2BL, with BL = 3.6 mm being the average fish body length. Positive values of L_c(t) indicate that the background flow induces counterclockwise rotations, while negative values refer to clockwise rotations. The value of the local circulation L_c(t) depends on the fish position in the swimming channel.

We consider the hydromechanical feedback u_h(t) in Eq (3) to be a linear function of the local circulation of the background flow,

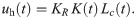
Here, K_R [1/s] is a positive parameter weighting the hydrodynamic information, as illustrated in Fig 3B, and K(t) is a Boolean random variable. K(t) = 1 represents the case when the fish tracks the local circulation L_c(t) to maneuver, while for K(t) = 0 this information is not utilized. The switching mechanism was introduced to model uncertainty in the rheotactic response, where fish alternates between time intervals following and ignoring the local circulation (see model calibration in Materials and methods for details on the estimation of K(t)). We model K(t) as a continuous-time Markov chain given by

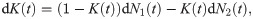
Wall interaction: Visual and tactile feedback

Here, we study the interaction of a fish with the walls, which comprises two different feedback mechanisms using vision and touch. Visual feedback is captured through u_w in Eq (3). Tactile feedback instead is modelled as a collision that modifies the evolution of the vortex strengths with respect to Eqs (2a) and (2b), as the fish collides with the walls.

Inspired by [34, 36], we quantified the wall effect by measuring the projected distance d and angle of collision ϕ which is measured from the wall axis to the projected heading vector (see Supporting information S2 Fig). We only considered those instances when the centroid was within 1 BL range from the wall.

The results indicate that a zebrafish rotates according to the sign of the angle ϕ when interacting with a wall (see Supporting information S2 Fig). Following [35], we model the visual feedback as a function of the projected distance and angle of collision which is given by

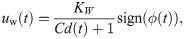
To further delve into how fish interacts with the wall, we examined only instances when they were in close proximity or in direct contact to a wall. In these instances, the animal could exploit other sensing mechanisms beyond vision to avoid the wall. Our experimental results suggest that fish rotation in the vicinity of a wall depends on the sign of the angle ϕ (see Supporting information S2 Fig). We model the tactile component of turning in the vicinity of a wall, which is crucial for describing the wall interaction of the fish in the dark. In the vicinity of a wall, turns are captured through

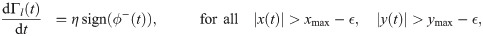
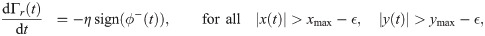
There is an additional consideration to make for the right wall which corresponds to the test section outlet, shown in Fig 2. In this case, the fish experiences suction forces and could hit the wall while heading in a direction opposite to it, thereby preventing the use of Eqs (8a) and (8b) for capturing the impact. To account for this case and counter-balance the suction force, we should modify Eqs (8a) and (8b) as follows:

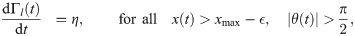
Here, the constraint on the heading angle guarantees that the animal is heading in the opposite direction to the right wall. Also, the signs in Eqs (9a) and (9b) are both positive, indicating that the interaction with this particular wall is repulsive to counter the suction force.

Model validation: Comparison between real and in-silico experiments

We calibrated our model using experimental data, as detailed in Material and methods; the resulting parameter values are shown in Fig 4 for both conditions Bright and Dark. We found that the condition significantly influenced the baseline value of the circulation strengths β (W = 3;p < 0.010). We did not register a significant difference on the linear rate of decay of the vortex strengths α(W = 93;p = 1.000), the intensity of added noise σ (W = 56;p = 1.000), the coupling strength κ (W = 50;p = 1.000), hydrodynamic feedback gain K_R (W = 66;p = 1.000), λ₁ (W = 72;p = 1.000), and λ₂ (W = 27;p = 0.196).

Fig 4

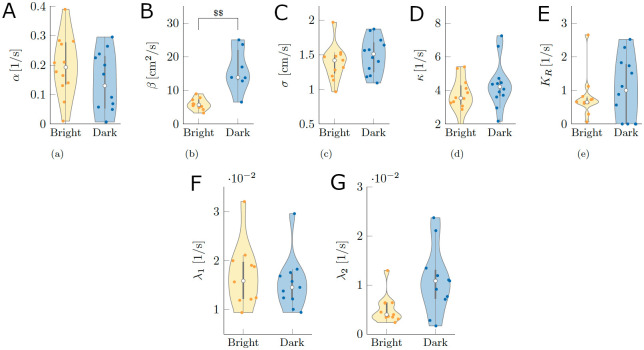
Calibrated model parameters for conditions Bright and Dark.

(A) Linear rate of decay of the vortex strengths. (B) Baseline value of the vortex strengths. (C) Intensity of the noise added to the time-evolution of vortex strengths. (D) Coupling gain between vortex strengths associated with the ability of a fish to resume straight swimming after a maneuver. (E) Hydrodynamic feedback gain. (F-G) Rates of transitioning from dismissing to using information about the local circulation and vice versa. The gray bar in each violin plot details median (white dot), first and third quartiles, and lower and upper adjacent values. The colored area of a violin plot corresponds to the probability density of the data. Symbol $$ indicates a significant difference between conditions with p < 0.010.

In order to validate the predictive power of our model, we conducted in-silico experiments consisting of 12 trials for each condition: Bright and Dark, as in the real experiment. In-silico experiments predicted relationships analogous to real experiments as shown in Fig 5. The cosine of the heading differed from chance in both Bright (V = 78;p < 0.001) and Dark (V = 77;p < 0.001). Similarly, RI registered significant differences in both Bright (V = 78;p < 0.001) and Dark (V = 77;p < 0.001). Pairwise comparisons between Bright and Dark indicated significant differences for the cosine of the heading (W = 144;p < 0.001), RI (W = 144;p < 0.001), and spatial entropy (W = 0;p < 0.001), while we only identify a weak trend for the variance of spatial entropy (F = 3.669;p = 0.068). Supporting information S2 Video and S3 Video show exemplary instances of rheotactic behavior predicted by the mathematical model in conditions Bright and Dark, respectively.

Fig 5

Average scoring of three behavioral metrics for in-silico experiments.

(A-B) Rheotactic metrics taking values between −1 and 1 corresponding to biased headings downstream and upstream, respectively. (C) Spatial entropy, measuring the exploratory behavior across the test section. The average was taken over synthetic time series of 9, 000 points for each experimental subject. The gray bar in each violin plot details median (white dot), first and third quartiles, and lower and upper adjacent values. The colored area of a violin plot corresponds to the probability density of the data. Symbol $$$ indicate significant difference between conditions p < 0.010, respectively.

Ethics statement

Experiments were performed in accordance with the guidelines and regulations approved by the University Animal Welfare Commitee (UAWC) of New York University under protocol number 13-1424.

Animal care and maintenance

A total of 24 wild-type adult zebrafish (Danio rerio), 12 male and 12 female, were used in this study. The fish were purchased from Carolina Biological Supply Co. (Burlington, NC, USA), and housed in a 615 L vivarium tank divided into two compartments to mantain sexes separated. Fish were kept under a 12 h light/12 h dark photo-period and fed with commercial flake food once a day, approximately at 7 PM. Water parameters of the holding tanks were regularly checked, and temperature and pH were maintained at 26°C and 7.2, respectively. Prior to the beginning of the experiments, fish were acclimatized in the holding facility for one month.

Experimental apparatus

The experimental set-up (see Fig 6A) consisted of a 151 L Blazka-type water channel (Engineering Laboratory Design Inc., Lake City, MI, USA), a video camera (Logitech C910 HD Pro Webcam without infrared filter, Logitech, Switzerland) located at the bottom of the channel, an array of lights, and black curtains to minimize outside visual stimuli. We used two different lighting systems for the Bright and Dark conditions. In particular, for the Bright condition, we used a pair of fluorescent lamps (Aqueon Full Spectrum Daylight T8, Aqueon, USA) located at the top of the channel along with a white plexiglass sheet to dim the light intensity and provide a homogeneous light background of 250 lx. For recording fish swimming in the dark, we used infrared lights (Iluminar IRC99 Series, Iluminar, Irvine, CA) with wavelength 940 nm, which is greater than the adult zebrafish threshold of spectral sensitivity [66]. Two pairs of infrared lights were located at the bottom and top of the water channel to provide a clear background for recording videos in the dark.

Fig 6

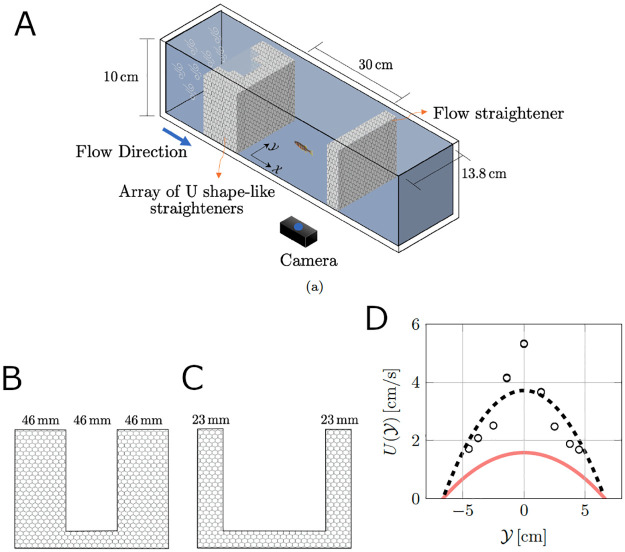
Experimental set-up.

(A) Overview of the experimental apparatus. (B,C) U shape-like honeycomb grids for straightening the flow in the water channel. (D) Measurements of the flow velocity profile (black circles) and parabolic fit (black dash line) at the mid-span using laser Doppler velocimetry, along with the parabolic fit of flow profile from fish locomotion (solid red line).

A test section of 30 cm × 13.8 cm (2x_max × 2y_max) at a water height of 10 cm was arranged within the channel using flow straighteners, as shown in Fig 6A. The flow profile was created using an array of U-shaped flow straighteners with different opening sizes to manipulate the flow speed (see Fig 6B and 6C). We estimated the axial flow velocity utilizing the fish swimming trajectories for each experimental subject based on the following steps. First, we limited our analysis to instances when sin(θ(t)) ≠ 0, such that Eq (1) could be inverted to obtain $$ U\left(y\left(t\right)\right)=\frac{\mathrm{d}x\left(t\right)}{\mathrm{d}t}-\frac{\mathrm{d}y\left(t\right)}{\mathrm{d}t}\frac{cos\left(\theta \right(t\left)\right)}{sin\left(\theta \right(t\left)\right)}$$. Second, we utilized a standard least squares method in Matlab (R2019b) to fit each data set with a parabola. By averaging the 24 fish, we determined a flow profile $$ U\left(\mathcal{Y}\right)=-0.036{\mathcal{Y}}^2+1.584$$ (with units in cm and cm/s; see Fig 6D).

Interestingly, the advective velocity experienced by the fish was less than the velocity in the middle of the water height (5 cm from the bottom) through laser Doppler velocimeter (BSA, F50, Dantec, Denmark). Through velocimetry, we obtained five velocity measurements for nine different points across the test section ($$ \mathcal{Y}$$-coordinate). The fitted parabolic flow profile is shown in Fig 6D, for completeness. This discrepancy between identified data and velocimetry experiments is due to the fact that fish can swim along the z-axis, not only in the plane. We confirm this reduction along and across the tunnel by conducting finite element (FE) simulations of the fluid flow within the test section in the commercial FE software Comsol Multiphysics (see Supporting information S3 Fig).

Experimental procedure

Two different illumination conditions were tested, namely Bright and Dark. Each trial consisted of three main phases. The first two phases were introduced for habituation to the new environment and the flow, while the third phase was the actual testing. Only the last phase was recorded. At the beginning of the trial, the animal was transferred from the vivarium to the water tunnel (using a hand net) and kept there for five minutes of habituation with the water velocity set to zero. Then, the water flow was turn on for two minutes of further habituation and five minutes of testing. A total of 24 naïve adult fish were tested, 12 (6 male and 6 female) for each condition (Bright and Dark).

Tracking

A total of 300 s were recorded for each trial at 30 frames per second. All videos were post-processed using a foreground detection algorithm in Matlab (R2019b) for highlighting the animal shape on the image and improve the tracking process [67]. The resulting images were input to a slightly modified version of the multi-target tracking algorithm Peregrine [68], accounting for manual repairs in body shape tracking mode. The software fitted a parabola on the fish blob and returned: the fish centroid position (x(t), y(t)) with their respective velocities, shape parameters (coefficients of the parabola), and heading vector h(t) = [cos(θ(t)), sin(θ(t))], from which the heading angle and turn rate were calculated. For each experiment, we obtained time series of centroid coordinates, heading, and turn rate, consisting of 9, 000 samples corresponding to the total experimental time. All data can be found in the Supporting Information file S1 Data set.

Statistical analyses and behavioral scoring

All statistical analyses were performed with the statistics software R (version 3.6.1). We used the Wilcoxon signed-rank test and the Mann-Whitney U test (Wilcoxon rank sum), with a significance level of 0.050, for comparing one-sample and two-sample data, respectively [69]. For testing the equality of two-sample data variances we use the Levene’s test [70] with a significance level of 0.050. To study rheotaxis, we averaged the time series of −cos(θ(t)) in each trial, and we scored RI, defined as the difference between the cumulative distribution functions of the absolute value of the heading and a uniform random variable [27]. More specifically, $$ RI=1-(2/\pi ){\int }_0^{\pi }\Lambda \left(\right|\theta \left|\right)\mathrm{d}\theta $$, with Λ(⋅) being the empirical cumulative distribution function. Here, π/2 represents the area under the curve of an empirical cumulative distribution function of a uniform random variable over the interval [0, π].

We further quantified the fish exploratory behavior in the test section through spatial entropy. This quantity was measured by first dividing the test section in 10 × 4 squares of approximately 3cm × 3.45cm each, corresponding to a grid of 1 BL in size. Then, using the centroid trajectory (x(t), y(t)), we estimated the probability of occupying each boxes in the grid, p_i. The spatial entropy is then given by $$ -{\sum }_{i=1}^{40}{p}_i{log}_2\left(p_i\right)$$.

Comparisons of calibrated model parameters were conducted to elucidate the role of illumination thus reducing the number of model parameters and avoiding overfitting of the data. Comparisons were performed using seven independent Mann-Whitney U tests. Because hypotheses were not defined a priori on the parameter comparisons, we corrected for multiple comparisons using a Bonferroni adjusted significance level of 0.05/7 [71].

In-silico experiments

We replicated the real experiment by considering 24 trials, 12 for Bright and 12 for Dark. We numerically integrated Eqs (1), (2), (3), (5) and (7) using the Euler-Maruyama scheme with a time step of 1/30 s [72], matching the sampling rate of the tracked data. To ensure convergence to a steady state probability distribution, we chose a simulation time of six times the experimental time (6 × 300 s), and we only considered the last 300 s. The parameter values α, σ, κ, K_R, λ₁, and λ₂ were taken from Gaussian distributions corresponding to the data shown in Fig 4 across all 24 trials (Bright and Dark). Because the parameter β was significantly different between Bright and Dark, its value was drawn from two different Gaussian distributions corresponding to the data of each condition shown in Fig 4B. Given that the test section is rectangular, unrealistic turns or oscillations might arise on the corners due to their discontinuous nature [36]. To avoid this problem, we kept the angle to collision constant when the fish was inside a square region of 1cm² on the corners.

Derivation of the governing equations of the finite-dipole model

The zebrafish dipole representation is depicted in Fig 2. By adapting the equation set (2) from [48], the centroid position and heading angle can be obtained by integrating the following set of ODEs:

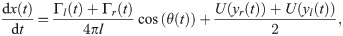
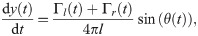
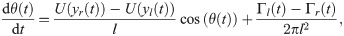
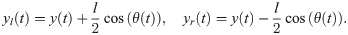
Considering that the animal thickness, l ∼ 5 mm, is small with respect to the dimensions of the water channel, we expand the velocity field at the location of the two vortices, U(y_r(t)) and U(y_l(t)), around the centroid coordinate y(t) using a Taylor series, yielding

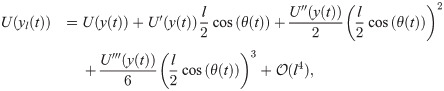
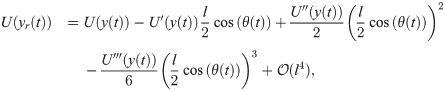
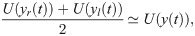
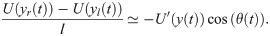
Finally, replacing Eqs (13a) and (13b) in Eqs (10a) and (10b) yields Eqs (1a)–(1c).

Estimation of the circulation strengths from experimental time series

To estimate the circulation strengths we used experimental data of the fish centroid position (x(t), y(t)), heading angle θ(t), and turn rate ω(t). Using a first order approximation, Eqs (10a) and (10b) can be written as

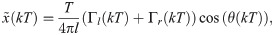
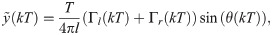
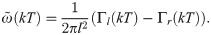
Here, k = 1, 2, …, N − 1 is the time step, T = 1/30 s is the video-camera sampling period, N = 9000 is the total number of samples, and

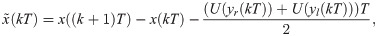
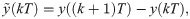
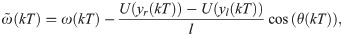
By squaring both sides of (14a) and (14b), we determine that

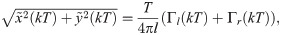
Finally, from Eqs (14c) and (16) we obtain the sought expression of the circulations strengths as function of fish motion

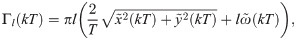
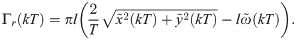
Expansion of the line integral for the local circulation

The fish perimeter is approximated by a circle $$ \mathcal{C}$$ around the fish centroid (x(t), y(t)) defined by

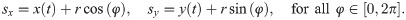
The line integral in Eq (4) is thus given by

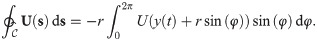
By a using a Taylor expansion of the velocity around y(t), we establish

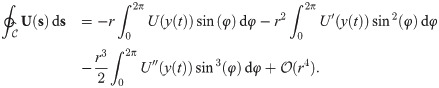
Finally, from the fact that $$ {\int }_0^{2\pi }sin\left(\phi \right)d\phi =0$$, $$ {\int }_0^{2\pi }{sin}^2\left(\phi \right)d\phi =\pi $$, and $$ {\int }_0^{2\pi }{sin}^3\left(\phi \right)d\phi =0$$ we derive Eq (4).

Model calibration

We began by approximating the solutions of the stochastic differential equations in Eqs (2a) and (2b) away from the wall (neglecting u_w), using the Euler-Maruyama method, thereby yielding the following Markov chain:

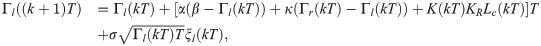
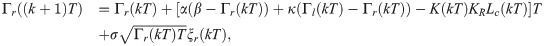
To estimate K(kT), we quantified the level of synchronization between the turn rate of the fish ω_a(kT) = Γ_l(kT) − Γ_r(kT) and L_c(kT). We first normalized both time-series on the interval [−1, 1] by dividing each of them by the maximum absolute value over the entire time span yielding $$ {\widehat{\omega }}_a\left(kT\right)$$ and $$ {\widehat{L}}_c\left(kT\right)$$. Next, we smoothed $$ {\widehat{\omega }}_a\left(kT\right)$$ utilizing a moving average filter in Matlab (R2019b) to attenuate noise. Then, we assessed synchronization by defining the synchronization error $$ e\left(kT\right)=\sqrt{{({\widehat{\omega }}_a\left(kT\right)-s\left(kT\right))}^2+{({\widehat{L}}_c\left(kT\right)-s\left(kT\right))}^2}$$ with $$ s\left(kT\right)=({\widehat{\omega }}_a\left(kT\right)+{\widehat{L}}_c\left(kT\right))/2$$ being the average signal. By manually inspecting all 24 trials, we found that e(kT)<0.35 over a time window greater than 2 s corresponded to instances in which the fish tracked the local circulation, that is, it performed a complete turning maneuver following the rotation indicated by the circulation. Hence, we imposed K(kT) = 1 if e(kT)<0.35 for all the frames within any 2s-window containing instant kT. The use of a continuous window allows for mitigating the effect of chance, whereby the fish may inadvertently follow the circulation during its swimming, despite not using it for decision-making.

After some algebraic manipulations, Eqs (21a) and (21b) can be rewritten as

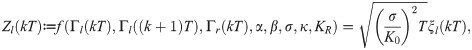
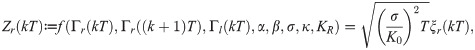
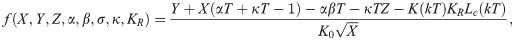
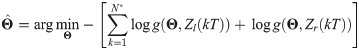
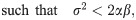
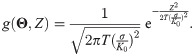
Next, to estimate the parameters λ₁ and λ₂ of the continuous-time Markov chain in (6), we counted the number of transitions of K(kT) from ignoring the circulation to following it and vice versa. The estimated parameters are shown in Fig 4 for the 24 experimental trials.

Moreover, for calibrating the wall parameters in Eq (7), we implemented the following steps:

(i)We first extracted instances when the fish turns according to the opposite sign of the angle to collision ϕ, that is, blue points (Γ_l − Γ_r > 0) for ϕ < 0 and red points (Γ_l − Γ_r < 0) for ϕ > 0 as shown in Fig 7A. To undertake this step, we utilized a cutoff function, which was informed by the following rationale. As the angle ϕ approaches ±π/2 or the distance to collision d increases, fish turns becomes less predictable. Hence, we retained pairs (ϕ, d) such that |g_ϕ(ϕ) − d|<δ and |ϕ|<ϕ₀, where ϕ₀ and δ are cutoff parameters and $$ g_{\varphi }\left(\varphi \right)=a_g+b_g{e}^{-{(\varphi /c_g)}^2}$$ (Black curve in 7a). By manually examining the 12 trials in Bright, we found that setting ϕ₀ = 1, a_g = 2.8 cm, b_g = 27.2 cm, c_g = 0.26, and δ = 1 was a valid choice to extract all relevant maneuvers.

(ii)To understand how fish turn based on the vicinity to a wall, we defined G_ϕ as the quantity collecting the values of the difference of circulation strengths (Γ_l − Γ_r), corresponding to the points (ϕ, d) obtained from the previous step. For the example shown in Fig 7A, the points G_ϕ correspond to black dots. Next, we used a non-parametric locally weighted least squares (LOESS) filter in Matlab (R2019b) with a 5% span on the absolute value of G_ϕ to smoothen the data. The results are the green dots shown in Fig 7B;

(iii)The output of the LOESS filter, y_d, was utilized as input to fit the wall function K_W/(Cy_d + 1) using the nonlinear least-squares solver of Matlab (R2019b). The fitted function corresponds to the red curve in Fig 7B and

(iv)Because we used the difference of circulation strengths for the fitting, the estimate of K_W should be corrected to obtain the true amplitude of turns corresponding to each circulation strengths. Hence, we computed the maximum value of Γ_l and Γ_r across all time instances near a wall. K_W was selected as the maximum between the values obtained in (iii) and (iv). Results are reported in Table 1.

Fig 7

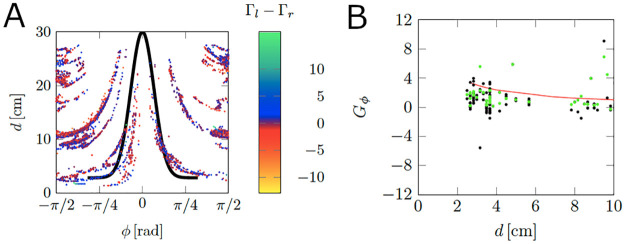
Illustration of the wall calibration process.

(A) Two-dimensional projection of the difference of vortex strengths Γ_l − Γ_r, as a function of the projected distance, d, and angle to collision, φ, for one trial from Bright. The black curve is a normal function utilized to select relevant values of (φ, d) associated with those instances when the fish turns according to the angle to collision ϕ. (B) Example of calibration of the wall function. Black dots correspond to G_ϕ and green dots correspond to the filtered output of |G_ϕ|. The red line is the fitted wall function.

Table 1

For experiments in the dark, K_W is set to zero and this form of interaction is absent.

Calibrated wall parameters for the 12 fish tested in standard illumination (condition Bright).

Trial	KW [1/s]	C [cm]
1	23.727	-
2	48.112	2.172
3	63.173	2.237
4	23.170	-
5	29.646	2.195
6	78.167	2.196
7	21.005	-
8	33.066	-
9	32.606	2.194
10	39.661	2.502
11	33.658	2.158
12	32.696	-
Mean	38.224	2.236
Median	32.881	2.195

We remark that our model is calibrated by splitting our data set into two: (i) data of fish interacting with the wall, and (ii) data of fish swimming away from walls. We set 1 BL of distance from the wall as a threshold to split the data set. This separation provides enough data points for the condition of fish swimming away from the wall, needed to guarantee convergence of the optimization problem in Eq (25). This distance, however, could be within the capabilities of zebrafish to detect walls [74]. We verified that the calibrated parameters values do not change considerably by slightly increasing this threshold to 1.2 BL (∼4 cm) and 1.4 BL (∼5 cm).