
Competing Interests: The authors have declared that no competing interests exist.
- Altmetric
One-to-multiple path analysis model describes the regulation mechanism of multiple independent variables to one dependent variable by dividing the correlation coefficient and the determination coefficient. How to analyse more complex regulation mechanisms of multiple independent variables to multiple dependent variables? Similarly, according to multiple-to-multiple linear regression analysis, multiple-to-multiple path analysis model was proposed in this paper and it demonstrated more complex regulation mechanisms among multiple independent variables and multiple dependent variables by dividing the generalized determination coefficient. Differently, three other types of paths were generated in multiple-to-multiple path analysis model in that the correlation among multiple dependent variables was considered. Then, the decision coefficient of each independent variable was constructed for dependent variables system, and its hypothesis testing statistics were given. Finally, the research example of the wheat breeding rules in arid area demonstrated that the multiple-to-multiple path analysis considering more correlation information can get better results.
1 Introduction
The regression analysis, as one of the most widely used statistical methodologies, focuses on studying the relations between dependent variables and independent variables. However, the regression analysis worries less about the correlation mechanisms that may exist among the independent variables [1]. In 1918–1921, the issue was addressed by the biological geneticist Sewall Wright through developing the path analysis method [2, 3]. Sewall Wright’s path analysis mainly emphasizes decomposing the correlation and total determination in terms of model parameters, and drawing the path diagram. The path diagram is a pictorial representation of a system of simultaneous equations, which presents the picture of the relationships that are assumed and is more clearly than the equations [4]. The concrete decomposition result is to distinguish the three types of effects: direct, indirect and total effects, which can lead to a more comprehensive understanding of the relation between variables. Usually, the indirect effects of a variable are mediated by at least one intervening variable [4]. In fact, the decomposed indirect effects quantify the regulation of variables with correlation. The quantitative expression of regulatory mechanism can make the analysis more thorough and clear. Therefore, the path analysis was later applied in multiple science research fields, such as behavioural science, social science, economics, biology, agriculture, medical science and so on [5–18]. This method seems to be more and more widely used at present.
In terms of methodology research, the path analysis was generalized to the structural equation models (SEMs) through combining the principle of factor analysis and was used to analyse the relations between multivariate blocks of data [19, 20]. The decision coefficient was constructed in the specified path analysis model with no latent variables, which included one dependent variable (as result) and multiple independent variables (as causes), based on the decomposition of total determination coefficient [21]. Here, the specific path analysis model was called one-to-multiple path analysis model with the nature of standard multiple linear regression. The decision coefficient of each independent variable equals to the sum of its direct determination and the correlation indirect determination with the other independent variables. The decision coefficient can express the magnitude and direction of each independent variable influencing the variation of dependent variable. Still further, the importance of each independent variable for dependent variable can be ranked according to the decision coefficient result, which shows that the decision coefficient has the significance of making decisions. Subsequently, the statistical test of the decision coefficient was proposed [22]. The decision coefficient improves the one-to-multiple path analysis model to a certain extent. Later, the one-to-multiple path analysis model was applied in the lint yield of upland cotton research and the KEGG gene pathway regulation mechanisms research [23–25].
However, the causal system including multiple independent variables (as “causes”) and multiple dependent variables (as “results”) are often encountered in practice research. For instance, the different pathways contain the same genes in the KEGG pathway, which demonstrated that the same genes can lead to the different gene functions. Here, multiple identical genes and multiple different gene functions constitute a multiple-to-multiple system. Analysis of the regulatory relationship between genes and gene functions is helpful to the modification and change of gene structure. Similar to this, in breeding field, multiple biological shapes to multiple yield indicators also constitute a multiple-to -multiple system. Determining the importance of multiple biological shapes to multiple yield indicators is helpful to improve the yield and quality of crops. It is assumed that such a causal system does not contain latent variables. Then, the one-to-multiple path analysis model can be used to analyse the importance of each independent variable to one dependent variable and the regulations among multiple independent variables. But, it is frustrating that the results of multiple single one-to-multiple path analysis are often contradictory, so that decision makers feel confused when making decisions. Therefore, it is urgent to find a more suitable model to provide more clear decision-making suggestions for decision-makers in such a more complex system.
In this paper, we attempt to propose the multiple-to-multiple path analysis model according to the multiple-to-multiple linear regression analysis, including multiple independent variables and multiple dependent variables and no latent variables. This model considers the correlation among multiple dependent variables caused by multiple common independent variables on the basis of one-to-multiple path analysis model. The other three types of paths generated besides the two types of paths in one-to-multiple path analysis model. The decomposition of the generalized determination coefficient showed the regulation mechanisms among the multiple independent variables and multiple dependent variables along these five types of paths. And the decision coefficient of each independent variable was used to judge its importance for all dependent variables system. Finally, the effectiveness of the model was verified by an example of the wheat breeding rules in arid area.
2 Method
2.1 Equations and models
The multiple-to-multiple linear regression model is the basis of the multiple-to-multiple path analysis, so it was introduced firstly. Define the following assumptions: the dependent variable of linear regression is Y = (Y1,Y2,⋯,Yp)T and the independent variable is X = (X1,X2,⋯,Xm)T. Suppose the joint distribution of and
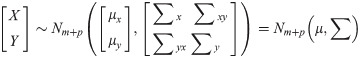
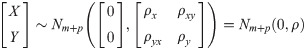
Among them, ρx, ρxy and ρy are the correlation arrays of X,X and Y,Y respectively. ρ is the correlation matrix of [XT,YT]T. Under the above assumption, the normalized multiple-to-multiple linear regression model is:
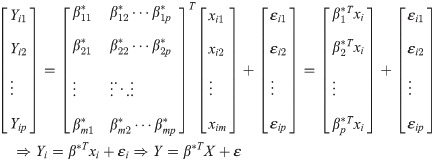
In (3), Yi = [Yi1,Yi2,⋯,Yip]T, xi = [xi1,xi2,⋯,xim]T, β* is the regression parameter of the model, i = 1,2,⋯,n. Let n be the number of observations. We assumed that ε~Np(0,∑e) is the regression residual and has nothing to do with the value of X.
2.2 Regression hypothesis testing
Path analysis can only be carried out when the standardized regression equation is significant. Therefore, we need to perform the following four types of hypothesis tests for regression analysis before path analysis.
2.2.1 Hypothesis testing of generalized complex correlation coefficient rxy
In multiple-to-multiple standardized linear regression equations, the joint distribution of X and Y is showed as formula (2), then the generalized determination coefficient is defined as [26]:
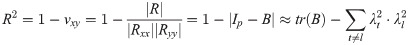
In Eq (4), vxy is the likelihood ratio statistics for testing independence of X and Y. And
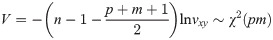
2.2.2 Hypothesis testing of regression equation y ^ α = b α * T x ( α = 1 , 2 ⋯ , p )
The invalid hypothesis is
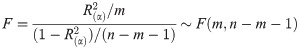
2.2.3 Hypothesis testing of components b j α * b α *
The invalid hypothesis is
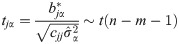
In (7),
2.2.4 Hypothesis testing of b x j y *
The invalid hypothesis is
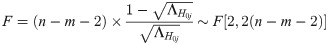
In (8),
2.3 Path analysis of Y α = β α * T x + ε α ( α = 1 , 2 , ⋯ , p )
The first step of multiple-to-multiple path analysis is to conduct one-to-multiple path analysis for each dependent variable and all independent variables. According to the established multiple-to-multiple linear regression equation, the path analysis model is performed. The correlation coefficient
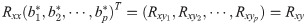
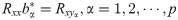

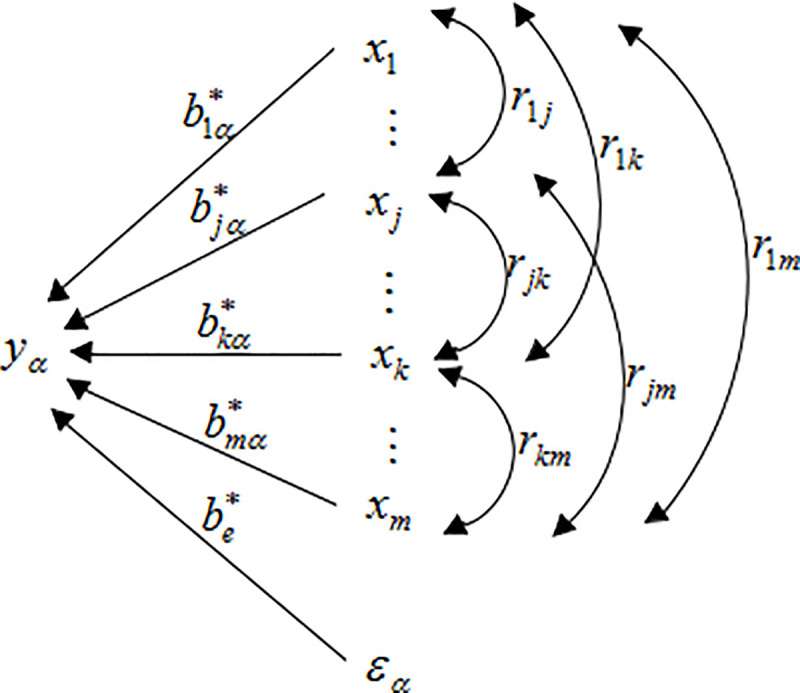
One-to-multiple path analysis diagram.
2.3.1 The division and path of r j y α
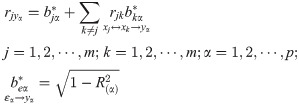
Obviously, the correlation efficient
2.3.2 The division and path of
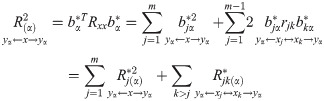
Among (11):
2.3.3 The decision coefficient Rα(j) and hypothesis test [22]
The comprehensively determine ability of xj to yα can be represented by the decision coefficient based on the division of
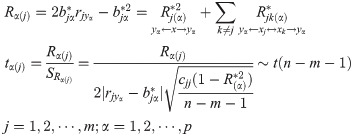
The definition indicates that Rα(j) equals to the sum of the direct determination coefficient
2.4 Multiple-to-multiple path analysis central theorem
The second step is to conduct multiple-to-multiple path analysis. And the innovation is that the correlation between Y caused by the common cause X is considered and three other types of paths are generated. For convenience of observation, let p = 3, m = 3 as an example to make a multiple-to-multiple path analysis diagram as Fig 2. But, the theoretical analysis is based on m independent variables and p dependent variables.

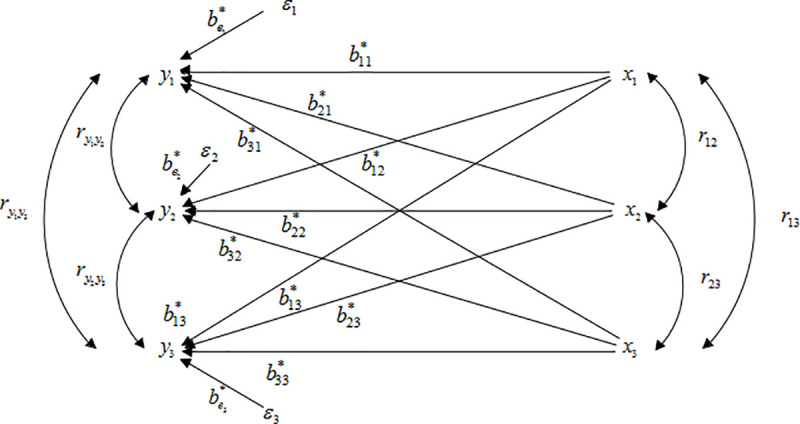
Multiple-to-multiple path analysis diagram.
The multiple-to-multiple path analysis model considered the correlation among different dependent variables compared to the one-to-multiple path analysis model. Accordingly, the central theorem of multiple-to-multiple path analysis is proposed. Based on model (3), for two different Yα and Yt, their models are:
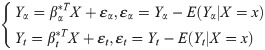
In (13), εα and εt are independent of each other and have nothing to do with the value of X. Since Yα, Yt and X have been standardized, the correlation coefficients of Yα and Yt, and the corresponding path theoretically is:
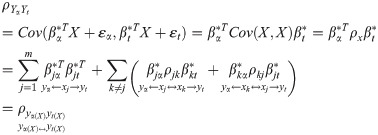
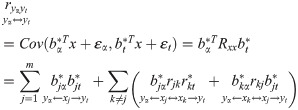
Among them, j = 1,2,⋯,m; k = 1,2,⋯,m; and α = 1,2,⋯,p; t = 1,2,⋯,p. Eq (14) and Eq (15) are called the central theorem of multiple-to-multiple path analysis.
The central theorem demonstrated that
In fact, the correlation coefficient in the multiple-to-multiple path analysis central theorem is theoretically the regression square sum matrix U in multiple-to-multiple standardized linear regression. Under the least squares estimation, U can be expressed as follows [16]:
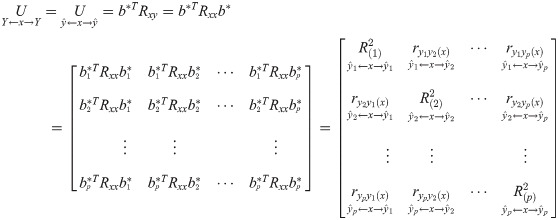
In (16),
2.5 The division of R2≈tr(B) and its corresponding path
The generalized determination coefficient has been defined using formula (4) before, which was used to reflect the comprehensive determination of all independent variables to all dependent variables [26]. Because the non-zero eigenvalue
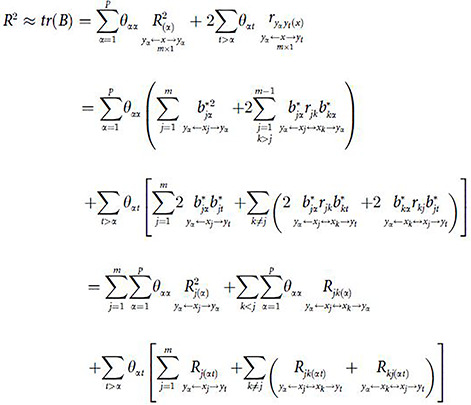
Among (17), θαt is the element in matrix
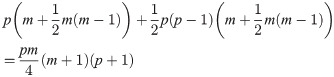
Formula (17) demonstrates that the generalized determination coefficient R2 was divided successfully along the five types of paths stated in multiple-to-multiple path analysis central theorem. The specific path vector structure is:
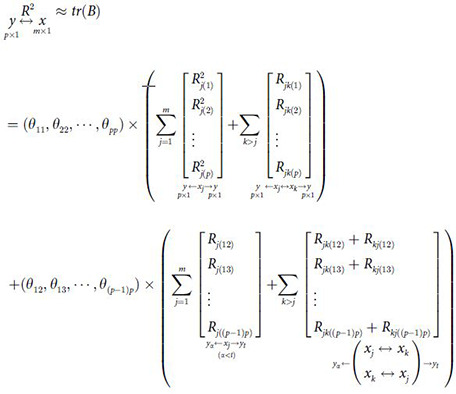
2.6 The generalized decision coefficient Ry(j)
2.6.1 The definition of Ry(j)
In order to describe the comprehensive decision-making ability of xj to Y, the generalized decision coefficient Ry(j) was defined as follows:
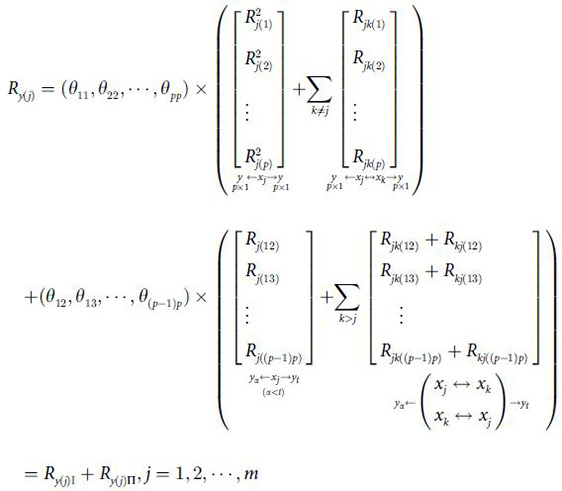
Obviously, the generalized decision coefficient is the sum of the products of
2.6.2 The hypothesis testing of Ry(j)
The invalid hypothesis is H0:E(Ry(j)) = 0 and the corresponding t test statistic is:
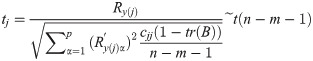
3 Application
3.1 Datasets
In order to demonstrate the effectiveness of the multiple-to-multiple path analysis, the wheat data in arid areas to explore breeding rules was selected to discuss. In detail, the wheat data included thirty-five varieties. These data were obtained in a completely randomized block test, and each sample was set with three repetitions [28]. In multiple-to-multiple path analysis, three indexes closely related to wheat yield was selected as dependent variables: panicles per plant (y1), grain number per panicle (y2) and 1000-grain weight (y3), and three other indexes were selected as independent variables: bio-mass per plant (x1), single stem grass weight (x2) and economic coefficient (x3). Here, economic coefficient refers to the ratio of economic yield to biological yield of wheat.
3.2 Calculation and results
Firstly, the phenotypic correlation matrix of the sample was calculated and expressed as Eq (21). The number of observations for each variable is n = 105.
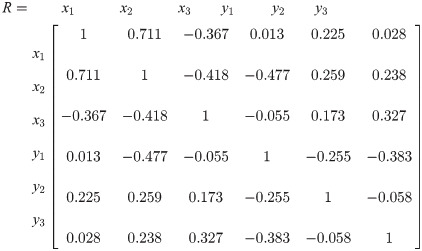
Then, we establish a multiple-to-multiple standardized multiple linear regression equation and calculate the corresponding parameters, the results were written as follow:
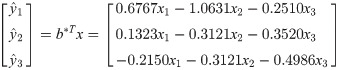
The hypothesis testing of generalized complex correlation coefficient rxy.
Likelihood ratio statistics of X and Y is vxy = 0.2987, so χ2 = 121.4357**>χ2(3×3), and R2 = 1−vxy = 0.7013,
The hypothesis testing of regression equation
The values of F test statistics are F1 = 37.9188**, F2 = 25.394**, F3 = 14.408**, respectively. They were all greater than F0.01(3,101) = 4.007, which showed that each standardized regression equation was extremely significant.
The hypothesis testing of components
The results of hypothesis testing of components

| y1 | y2 | y3 | |
|---|---|---|---|
| x1 | 6.8994** | 1.0212 | -1.8092 |
| x2 | -105852** | 2.3527** | 4.9257** |
| x3 | -3.3060** | 3.5101** | 5.4202** |
Among them, except x1 was not significant to y2 and y3, the others were extremely significant.
4The hypothesis testing of
The results are F1 = 8.670**, F2 = 25.394**, F3 = 10.384**, and the test results were all extremely significant.
Except x1 is not significant to y2 and y3, the above test results showed that the established multiple-to-multiple standardized linear regression equations were extremely significant. The path analysis and decision analysis can be performed subsequently.
Secondly, one-to-multiple path analysis of

| xj to yα | Direct effect | xj↔yα |  | Indirect effect |  | Total effect | |
|---|---|---|---|---|---|---|---|
| x1 to y1 | 0.6767** | x1↔x2→y1 | -0.7559 | -0.66638(3) | 0.2328(1) | 0.013(1) | |
| x1↔x3→y1 | 0.0921 | ||||||
| 1 | x2 to y1 | -1.0631** | x2↔x1→y1 | 0.4811 | 0.5860(1) | -0.3115(3) | -0.477(3) |
| x2↔x3→y1 | 0.1049 | ||||||
| x3 to y1 | 0.251** | x3↔x1→y1 | -0.2483 | 0.1960(2) | 0.1970(2) | -0.055(2) | |
| x3↔x2→y1 | 0.4444 | ||||||
| x1 to y2 | 0.1323(3) | x1↔x2→y2 | 0.2219 | 0.0927(1) | 0.0455(2) | 0.225(2) | |
| x1↔x3→y2 | -0.1292 | ||||||
| 2 | x2 to y2 | 0.3121(2) | x2↔x1→y2 | 0.0941 | -0.0530(2) | 0.0914(1) | 0.259(1) |
| x2↔x3→y2 | -0.1471 | ||||||
| x3 to y2 | 0.3520(1) | x3↔x1→y2 | -0.0486 | -0.1791(3) | -0.2763(3) | 0.173(3) | |
| x3↔x2→y2 | 0.1305 | ||||||
| x1 to y3 | -0.2150*(3) | x1↔x2→y3 | 0.4262 | 0.2432(1) | -0.074(2) | 0.028(3) | |
| x1↔x3→y3 | -0.1830 | ||||||
| 3 | x2 to y3 | 0.5994**(1) | x2↔x1→y3 | -0.1529 | -0.3613(3) | 0.1757(1) | 0.238(2) |
| x2↔x3→y3 | -0.2084 | ||||||
| x3 to y3 | 0.4986**(2) | x3↔x1→y3 | 0.0789 | -0.1716(2) | -0.3914(3) | 0.327(1) | |
| x3↔x2→y3 | -0.2505 |

| yα←xj→yα | Direct determination | yα←xj↔xk→yα |  | indirect determination | Decision coefficient | |
|---|---|---|---|---|---|---|
| y1←x1→y1 | 0.4579 | y1←x1↔x2→y1 | -1.0230 | -0.8983 | -0.4404**(3) | |
| y1←x1↔x3→y1 | 0.1247 | |||||
| 1 | y1←x2→y1 | 1.1302 | y1←x2↔x1→y1 | -1.0230 | -1.2461 | -0.1159(2) |
| y1←x2↔x3→y1 | -0.2231 | |||||
| y1←x3→y1 | 0.0630 | y1←x3↔x1→y1 | 0.1247 | -0.0984 | -0.0354(1) | |
| y1←x3↔x2→y1 | -0.2231 | |||||
| y2←x1→y2 | 0.0175 | y2←x1↔x2→y2 | 0.0587 | 0.0245 | 0.0420*(2) | |
| y2←x1↔x3→y2 | -0.0342 | |||||
| 2 | y2←x2→y2 | 0.0974 | y2←x2↔x1→y2 | 0.0587 | -0.0331 | 0.0643**(1) |
| y2←x2↔x3→y2 | -0.0918 | |||||
| y2←x3↔x1→y2 | -0.0342 | |||||
| y2←x3→y2 | 0.1239 | -0.1260 | -0.0021(3) | |||
| y2←x3↔x2→y2 | -0.0918 | |||||
| y3←x1→y3 | 0.0462 | y3←x1↔x2→y3 | -0.1833 | -0.1046 | -0.0584(2) | |
| y3←x1↔x3→y3 | 0.0787 | |||||
| y3←x2↔x1→y3 | -0.1833 | |||||
| 3 | y3←x2→y3 | 0.3593 | -0.4331 | -0.0738(3) | ||
| y3←x2↔x3→y3 | -0.2498 | |||||
| y3←x3↔x1→y3 | 0.0787 | |||||
| y3←x3→y3 | 0.2486 | -0.1711 | 0.0775*(1) | |||
| y3←x3↔x2→y3 | -0.2498 |
The t test statistics values of decision coefficient hypothesis testing were listed in Table 4.

| y1 | y2 | y3 | |
|---|---|---|---|
| x1 | -3.39774** | 2.3205* | -1.2288 |
| x2 | -0.74458 | 4.5633** | -0.7716 |
| x3 | -0.9793 | -0.0636 | 2.4488* |
In one-to-multiple path analysis, the results of correlation coefficient division showed that the total effect of biomass per plant (x1), single stem grass weight (x2) and economic coefficient (x3) are all positive and the largest to panicles per plant (y1), grain number per pancicle (y2), 1000-grain weight (y3), respectively. Differently, the direct effect of x1 to y1 is the positive and the largest, while the indirect effect is negative and the smallest. The direct effect of x2 to y2, x3 to y3 are not the largest, but the total effect becomes the largest through the correlation regulation by the indirect effect. The results of the determination coefficients division and the decision coefficients showed that for y1, x1 is a very significant restrictive factor; for y2, x2 is a very significant positive factor and x1 is a significant positive factor; for y3, x3 is a significant positive factor. These results meant that single stem grass weight (x2) and economics coefficient (x3) need to be increased in order to increase grain number per pancicle (y2) and 1000-grainweight (y3), but panicles per plant (y1) will decrease according due to the negative correlation x2, x3 and y1. Meanwhile, biomass per plant (x1) should be decreased in order to increase the panicles per plant (y1), but grain number per pancicle (y2) will decrease here. The contradictory decision-making results of different independent variables (xi) to different dependent variables (yi) often lead to the confusion of breeders.
Therefore, after the one-to-multiple path analysis, the multiple-to-multiple path analysis was practiced by taking into account the correlation between the dependent variables. According to formula (17–19), the generalized determination coefficient R2 was divided and the results were listed in Table 5.

| a | yα←xj→yt | direct determination | yα←xj↔xk→yα |  |
|---|---|---|---|---|
| y1←x1→y2 | 0.1791 | y1←x1↔x2→y2 | 0.3003 | |
| y1←x1↔x3→y2 | -0.1748 | |||
| 1 | y1←x2→y2 | -0.6636 | y1←x2↔x1→y2 | -0.2000 |
| y1←x2↔x3→y2 | 0.3128 | |||
| y1←x3→y2 | -0.1767 | y1←x3↔x1→y2 | 0.0244 | |
| y1←x3↔x2→y2 | 0.0655 | |||
| y1←x1→y3 | -0.2910 | y1←x1↔x2→y3 | 0.5768 | |
| y1←x1↔x3→y3 | -0.2477 | |||
| 2 | y1←x2→y3 | -1.2744 | y1←x2↔x1→y3 | 0.3253 |
| y1←x2↔x3→y3 | 0.4431 | |||
| y1←x3→y3 | -0.2503 | y1←x3↔x1→y3 | -0.0396 | |
| y1←x3↔x2→y3 | 0.1258 | |||
| y2←x1→y3 | -0.0569 | y2←x1↔x2→y3 | 0.1128 | |
| y2←x1↔x3→y3 | -0.0484 | |||
| 3 | y2←x2→y3 | 0.3741 | y2←x2↔x1→y3 | -0.0955 |
| y2←x2↔x3→y3 | -0.1301 | |||
| y2←x3→y3 | 0.3510 | y2←x3↔x1→y3 | 0.0556 | |
| y2←x3↔x2→y3 | -0.1764 |
The specific calculation of path vector structure is as follows:

From the previous calculation, we can get tr(B) = 0.8671. The above division of the generalized coefficient of determination is reasonable according to R2≈tr(B). The decision analysis of the model was carried out continually. The decision coefficient of each independent variable to Y = (y1,y2,y3)T was calculated as follows:
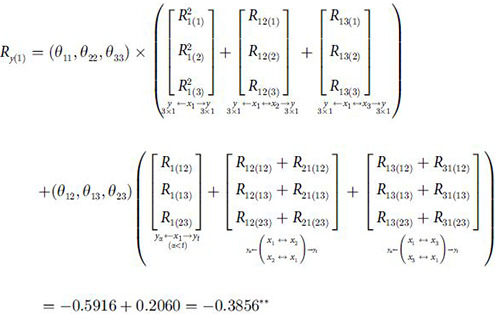
Similar available: Ry(2) = −0.1157, Ry(3) = 0.0906*. According to the decision coefficient, the t test about Ry(j) is further conducted, and the result is t1 = −4.3943**, t2 = 0.9293, t3 = 2.0785**. In addition, it should be noted that the determination coefficients of xj and xj↔xk to yα have been calculated by one-to-multiple path analysis model (Table 3). The comparison of the results of Table 3 and those of Table 5 demonstrated that great changes have taken place in the regulation of xj to Y when the correlation among dependent variables was considered. Firstly, the direct and indirect regulations of xj, xj↔xk to Y also were greatly affected by the correlation among Y because of common X. As shown in Table 3, the direct determination of x2 to y1, y2 were both positive, respectively (
4 Discussion
In this article, the multiple-to-multiple path analysis model was proposed based on multivariate linear regression analysis, which can be regarded as a generalization of one-to-multiple path analysis model based on univariate linear regression analysis. The innovation of this model is the multiple-to-multiple path analysis central theorem. The correlation among Y caused by common X was considered in the system analysis including multiple independent variables and multiple dependent variables. As Fig 2 shown, the other three types of paths (yα←xj→yt, yα←xj↔xk→yt, yα←xk↔xj→yt) generated in multiple-to-multiple path analysis model besides the two types of paths (yα←xj→yα, yα←xj↔xk→yα) in one-to-multiple path analysis. Along these five types of paths, the generalized determination coefficient R2 was divided into the direct determination and the indirect determination according to R2≈tr(B). This division can clearly show the complex regulatory mechanisms among variables. Still further, the generalized decision coefficient Ry(j) was constructed by synthesizing all the items related to xj, which was used to express the comprehensive decision-making ability of xj to Y = (Y1,Y2,⋯,Yp)T. In fact, the direct and indirect determinations all were products of corresponding path coefficients. The quantitative expression of the regulation among variables is helpful for decision makers to make more reasonable and optimized decision suggestions for target variables. The analysis results of the wheat data in arid areas strongly confirm this. It is worth mentioning that the path analysis of any closed system can be made according to the multiple-to-multiple path analysis central theorem. However, the application of multiple-to-multiple path analysis model still has some limitations. Firstly, the model is only applicable to the causal relationship analysis among multiple dependent variables and independent variables with correlation. Secondly, the difference between the generalized determination R2 and tr(B) is relatively large when the correlation among variables is very strong in multiple-to-multiple linear regression analysis, that is, the value of the correlation coefficient in correlation matrix is almost 1. Here, the division of the generalized determination coefficient R2 based on R2≈tr(B) is very different from the actual result. Therefore, other division methods need to be further considered.
5 Conclusion
In the multiple-to-multiple path analysis model, the correlation among dependent variables caused by common independent variable is considered, besides the correlation among independent variables. Taking into account more correlation information analysis makes the results more practical and instructive.
References
1
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
 Multiple-to-multiple path analysis model
Multiple-to-multiple path analysis model
