Biological summary

Angiogenic sprouting is initiated when an active cytokine, such as VEGF, reaches the existing vasculature and activates quiescent ECs. Active ECs express proteases that degrade the basement membrane (BM) so that EC extravasation and migration can occur [44, 45]. In vivo and in vitro, coordinated migration is guided by local chemical and mechanical cues [42, 46, 47]. While VEGF-activated ECs at the front of the vascular network explore new space and anastomose, to form branching patterns, previously created vascular sprouts mature, form lumens and, with the help of murine cells (pericytes and smooth muscle cells), stabilise [48]. In our mathematical model, we focus on EC migration, and its regulation by local environmental (mechanical and chemical) cues. Due to the short time scales considered in the model, processes such as proliferation, vessel maturation and lumen formation are neglected.

VEGF-induced actin polymerisation and focal adhesion assembly result in substantial cytoskeletal remodelling as required for cell migration [49]. This includes actin remodelling to form filopodia and lamellipodia, stress fibre formation, and focal adhesion turnover [41]. A crucial consequence of such remodelling is that ECs acquire front-to-rear polarity which coincides with the direction of their migration [50]. Membrane protrusions, such as filopodia and lamellipodia, increase the cell surface area at the leading edge. More VEGF receptors and integrins, which bind to ECM components, become activated at the cell front to further reinforce the cytoskeleton remodelling and polarisation [51]. This mechanism is known as taxis (e.g. chemotaxis, haptotaxis) and allows ECs to sense extracellular cues and migrate towards them. The cells’ chemotactic sensitivity leads to the so-called brush-border effect which is characterised by increased rates of branching and higher EC densities closer to the source of the VEGF stimulus which can be sensed by cells and biases their migration towards higher VEGF concentrations.

Whilst interactions with ECM components play a central role in EC polarisation and movement, EC migration, in turn, reorganises and remodels the ECM [45]. Prior to assembly of the basement membrane of the newly formed vessels, the ECM microenvironment consists mostly of collagen I and elastin fibers. Activated ECs secrete matrix type 1 metalloproteinases (MT1-MMPs) that degrade the ECM [44, 46, 52]. This process generates ECM-free tunnels into which the sprouts can elongate [52]. As sprouts grow, they assemble a basement membrane which contains, among other things, fibrous components (collagen IV, fibronectin and various laminins [44]) that are secreted by the ECs and whose function is to promote cell-cell and cell-ECM contact and to limit EC migration [46].

Further matrix reorganisation occurs in response to the mechanical forces generated by migrating cells as they realign the collagen fibrils of the ECM. Several experiments have shown that cells with extended filopodia and lamellipodia form focal adhesions with the ECM components and realign them by pulling in the direction parallel to their motion [39, 40, 51, 53]. They also move the fibrils from the local neighbourhood closer to their surfaces. As a result, collagen fibrils accumulate and align along the direction of sprout elongation. Since cell-followers form focal adhesions with these aligned fibrils they automatically polarize and migrate in the direction of sprout elongation [42, 46, 47]. In this way sprout integrity is maintained and the coordinated motion of ECs emerges.

The default phenotype of an EC that has been activated by VEGF is a “tip” cell [12, 13]. Tip cells are characterised by exploratory behaviour and low proliferative activity. Thus, although the ECM regulates EC behaviour to a great extent [45], if all cells were to move at the same time in an exploratory fashion, sprout integrity would be lost. In non-pathological angiogenesis, typical vascular network morphology is obtained when EC proliferation and migration (i.e. the exploration of space by active ECs in response to signalling cues) are properly balanced. This balance is mediated by the Delta-Notch signalling pathway, which provides ECs with a contact-dependent cross-talk mechanism by which they can acquire a “stalk” cell phenotype [12, 13]; stalk cells are characterised by reduced migratory and higher proliferative activities. In this way, cell-cell communication allows cells to adjust their gene expression patterns (and, hence, phenotype) and to coordinate their behaviour [54]. The processes influenced by cell phenotype in our model are illustrated in Fig 1A. The ratio between the number of tip and stalk cells during sprouting plays a key role in the integrity of the developing vascular network and its functionality. This was confirmed by experiments in which Notch activity was inhibited or completely blocked. This caused all cells to adopt a tip cell phenotype and led to pathological network formation [7].

Fig 1

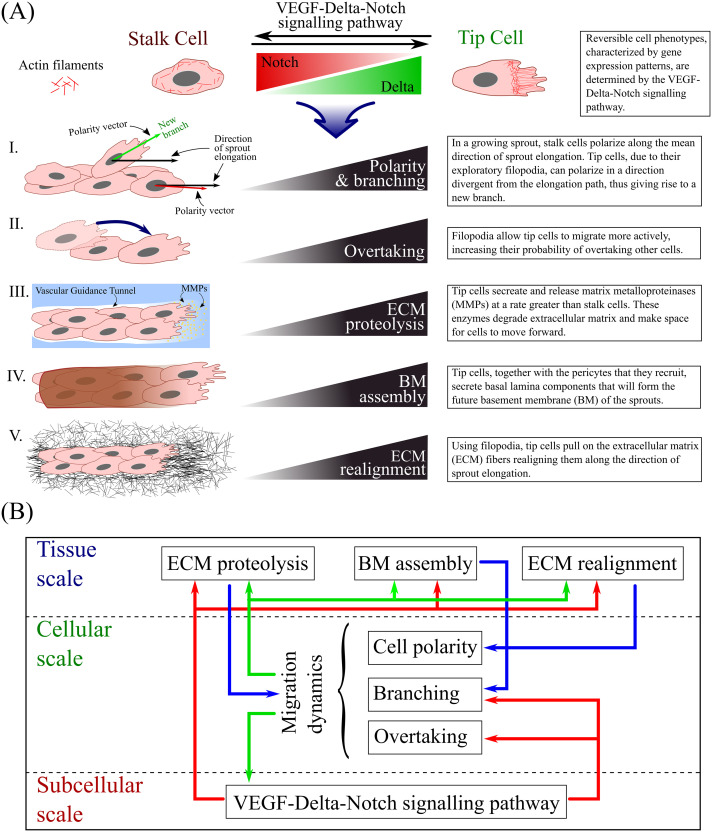
Schematic summary of our model.

(A) The gene expression profile of each cell (and, hence, its phenotype) is accounted for at the subcellular scale of our model. It influences such processes as I. cell polarity and branching, II. overtaking, III. extracellular matrix (ECM) proteolysis, IV. basement membrane (BM) assembly and V. ECM realignment. The cartoons on the left illustrate each process, whereas the text-boxes on the right provide brief descriptions of how they are influenced by tip and stalk cells. (B) The structure of our multiscale model. The diagram illustrates the processes that act at each spatial scale. Arrows illustrate coupling between the scales.

Mathematical modelling of random cell migration

Stochastic approaches have been successfully used to mathematically model systems with random, heterogeneous behaviour, including spatially extended systems [27, 55–64]. We model cell migration at the cellular scale stochastically to account for random cell motility, cell mixing, and branching dynamics. This approach allows us to compare our model with in vitro experiments which, as any biological system, are noisy.

Within the context of spatially extended systems, a stochastic model can be formulated as an individual-based, or a compartment-based, model. In the former approach, the Brownian dynamics of each individual agent (cells, molecules, etc.) are simulated, which becomes computationally expensive as the number of agents increases. The latter is more numerically efficient for the purpose of simulating small vascular networks containing at most hundreds of cells. In this method the domain is partitioned into non-overlapping compartments, or voxels so that the position of each agent is known up to the voxel size. Agents within the same voxel are considered indistinguishable and reactions between them occur independently of those in other compartments. Movement of agents between the voxels is modelled as a continuous time random walk (RW). This is also known as the Reaction Diffusion Master Equation (RDME) approach.

A weakness of the RDME approach is that it does not converge to its individual-based Brownian dynamics in dimensions greater than one for compartments with size less than a specific lower bound (of the order of the reaction radius in the Smoluchowski interpretation) [65]. The RDME breaks down as the voxel size tends to zero because the waiting time for multi-molecular reactions becomes infinite. One strategy to address this problem, the so-called convergent RDME (cRDME), is an approximation of Doi’s model for the binary reactions of the form A + B → C proposed in [66]. In the cRDME, agents from different voxels may interact via multi-molecular reactions provided they lie within a predefined interaction radius. In this way the artefact of vanishing reaction rates as voxel size tends to zero is avoided.

We formulate the cellular scale of our model using the cRDME approach. We introduce an interaction radius, R_c, within which cells are assumed to interact. This approach also fits naturally with the VEGF-Delta-Notch driven cell cross-talk that we incorporate at the subcellular scale of our multi-scale model (see below).

For the numerical implementation of the cRDME we use the Next Subvolume (NSV) method [67], which is a computationally efficient implementation of the standard Stochastic Simulation Algorithm [68] to simulate RDME/cRDME.

Summary of the multiscale model

The model we develop is a two-dimensional stochastic multiscale model of migration-driven sprouting angiogenesis. Its structure is shown in Fig 1B. Briefly, the model operates on three distinct spatial scales:

The subcellular scale defines the gene expression pattern of individual cells. Since ECs contain a finite number of proteins, some level of noise is always present in the system. Thus, we implement a stochastic model of the VEGF-Delta-Notch signalling pathway to describe the temporal dynamics of the number of ligands/receptors for each cell. This pathway is known to produce bistable behaviour. Cells exhibit either high Delta and VEGFR2, and low Notch levels (the tip phenotype) or low Delta and VEGFR2, and high Notch levels (the stalk phenotype). Stochasticity allows random transitions between these phenotypes in regions of bistability, behaviour which cannot be achieved in a deterministic model.

The cellular scale accounts for cell migration. It is formulated as a variant of an on-lattice persistent random walk (PRW) of ECs.

The tissue scale keeps track of the local ECM environment of the cells. Local ODEs track the evolution of the concentrations of the existing ECM and BM components, whereas ECM fibril alignment driven by EC movement is updated using a phenomenological model.

An illustration of the model geometry can be found in Fig 2.

Fig 2

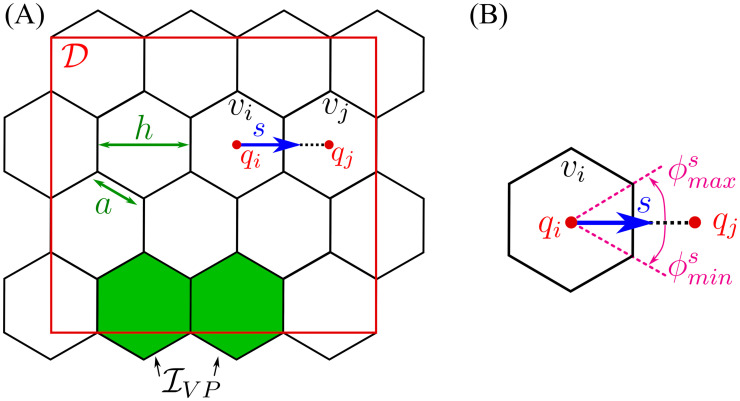
Model geometry.

(A) To account for cell migration in the framework of a PRW, we cover the domain, $$ \mathcal{D}\subset {\mathbb{R}}^2$$, by a uniform lattice $$ \mathcal{L}=\{v_k:{\bigcup }_{k=1}^{N_I}{v}_k\supset \mathcal{D}\}$$ of non-overlapping hexagonal voxels, v_k, of width h (or hexagon edge, a, $$ h=\sqrt[]{3}a$$). We denote by $$ \mathcal{I}=\{k={(k_x,k_y)}^T:v_k\in \mathcal{L}\}$$ the set of 2D indices, with cardinal, $$ \left|\mathcal{I}\right|=N_I$$. The coordinates of the centre of voxel v_k are denoted by $$ q_k={(q_k^x,q_k^y)}^T$$. We assume that there is a constant supply of ECs to the domain, coming from the vascular plexus. These ECs enter the domain at fixed boundary voxels, defined as a set, $$ {\mathcal{I}}_{VP}$$ (coloured in green). (B) A detailed illustration of an individual voxel, v_i. s = h⁻¹(q_j − q_i) denotes a normalised vector of the migration direction between neighbouring voxels, v_i and v_j. There are at most 6 possible migration directions for each hexagonal voxel. Each migration direction, s, can be characterised by an equivalent angle interval $$ [{\varphi }_{min}^s,{\varphi }_{max}^s]$$.

In general, an EC has an arbitrary shape which depends on its cell-cell and cell-matrix focal adhesions. In our model we do not keep track of the exact cell shape and assume that cell position is known up to the position of its nucleus. Thus, when referring to a cell position, we refer to the position of its nucleus and assume that the cell has some arbitrary shape centred on the voxel containing its nucleus (see Fig 3A). A consequence of this approach is that, since cells can extend membrane protrusions and interact with distinct cells beyond their first neighbours, interactions between cells in our model are non-local. We introduce two interaction radii, R_s and R_c, for the subcellular and cellular scales, respectively, and assume that a cell can interact with any neighbouring cell partially overlapped by a circular neighbourhood of these interaction radii (see Fig 3A). In particular, at the subcellular scale trans-binding between a Delta ligand on one cell and a Notch receptor on another can occur if the distance between their cell centres is less than the interaction radius, R_s. Thus, the total amount of ligand/receptor (belonging to a neighbour/neighbours) to which a cell is exposed is proportional to the surface area of the overlap region between the circular neighbourhood and the neighbouring voxel/voxels (not necessarily first neighbours). A similar modelling technique is employed at the cellular scale with the interaction radius, R_c, which we use to account for cell-cell adhesion. These radii are not necessarily equal (although they are of the same order of magnitude) since different types of interactions are considered at each scale.

Fig 3

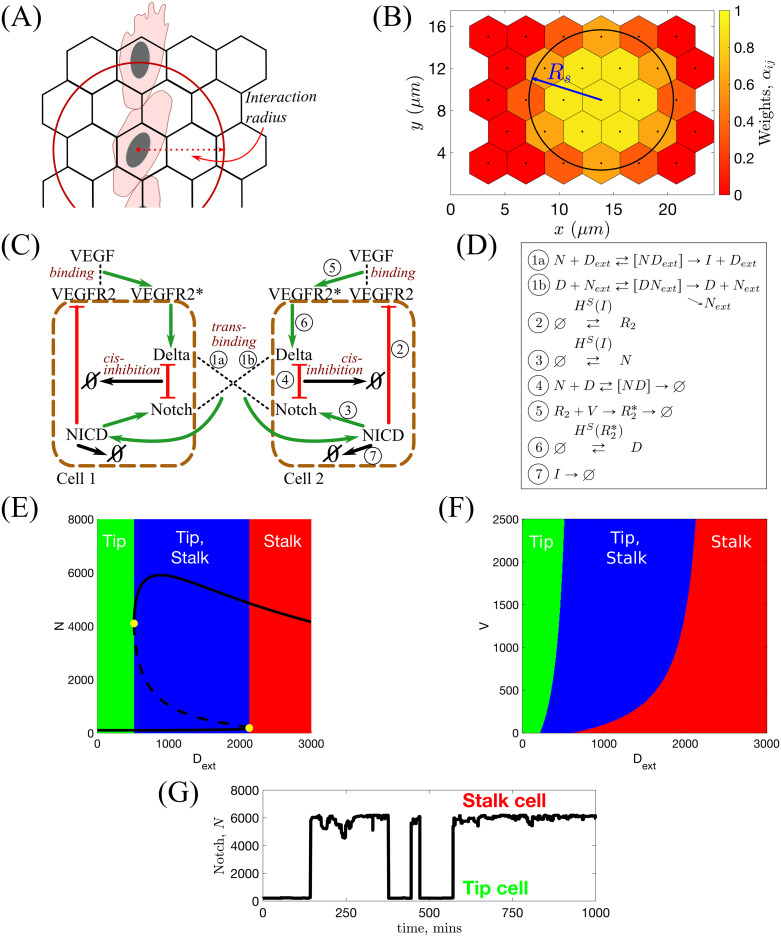
Illustrations for the subcellular scale of the model.

(A) Since we track the position of cells only up to the positions of their nuclei, interactions are assumed to be non-local within some interaction radius. The subcellular and cellular scale interaction radii are denoted by R_s and R_c, respectively. (B) Illustration of values of the weight coefficients, α_ij (see Eq (5)). (C) Schematic illustration of the VEGF-Delta-Notch signalling pathway. NICD stands for Notch intracellular domain, VEGFR2 for VEGF Receptor 2 and VEGFR2* for activated, i.e. bound to VEGF, VEGFR2. In this case, the local environment of Cell 2 is Cell 1, and D_ext and N_ext correspond, respectively, to the Delta and Notch concentrations in Cell 1 (and vice versa). Circled numbers correspond to the kinetic reactions listed in (D). (D) Kinetic reactions used for the VEGF-Delta-Notch pathway. See Table 1 for description of the model variables. H^S(var) indicates that the transition rate of gene expression of a protein is transcriptionally regulated by the signalling variable, var. Here, H^S(⋅) is the shifted Hill function (see caption of Table 2). Simple arrows indicate reactions with constant rates. (E) Bifurcation diagram of Notch concentration, N, as a function of external Delta ligand, D_ext, corresponding to the system of equations Eq (1). Full lines denote stable steady states; dashed lines—unstable steady state; yellow filled dots—saddle-node bifurcation points. (F) Phenotype diagram as a function of external Delta, D_ext, and external VEGF, V, corresponding to the system of equations Eq (1). (G) In simulations, the local environment of a cell (Delta and Notch levels in a neighbourhood of the cell, D_ext and N_ext (Eq (6))) dynamically changes with time due to cell migration. This leads to phenotype switches.

We perform our numerical simulations over time periods that are commensurate with the duration of in vitro experiments (hours) and for which proliferation is negligible [2, 7, 54]. For these reasons the model focuses only on the coordinated migration of ECs and assumes that proliferation occurs only at the vascular plexus [54], the initial vascular bed. This effect is implemented by introducing ECs into the domain at a specific set of boundary voxels, $$ {\mathcal{I}}_{VP}$$ (see Fig 2A).

Since the experimental data we use for model calibration and validation were extracted from experiments carried out with constant VEGF concentration supplied externally, we assume that the distribution of VEGF is maintained at a (prescribed) constant value at all times.

Interested readers will find more detail on model formulation later in this section and in S1 Text.

We list the variables of our multi-scale model in Table 1.

Table 1

The variables in the table are organised by spatial scales. Subcellular variables, used to simulate the VEGF-Delta-Notch signalling pathway, define the gene expression pattern of individual cells (their phenotypes). Cellular scale variables define the occupancy of the lattice by ECs. Tissue scale variables define the composition and structure of the ECM. Bold letters denote vector variables specifying variable configuration for the whole lattice; normal font letters correspond to the variables associated with a particular voxel, the index of which is specified by a subscript.

The description of the model variables.

	Variable	Description
Subcellular scale	$$	The distribution of Notch receptor among voxels. If there is no cell nucleus in a voxel vi, i.e. Ei = 0, then Ni = 0.
	$$	The distribution of Delta ligand among voxels. If there is no cell nucleus in a voxel vi, i.e. Ei = 0, then Di = 0.
	$$	The distribution of Notch intracellular domain (NICD) among voxels. If there is no cell nucleus in a voxel vi, i.e. Ei = 0, then Ii = 0.
	$$	The distribution of VEGFR2 receptor among voxels. If there is no cell nucleus in a voxel vi, i.e. Ei = 0, then R2i = 0.
	$$	The distribution of activated VEGFR2 receptor (VEGFR2 bound to extracellular VEGF) among voxels. If there is no cell nucleus in a voxel vi, i.e. Ei = 0, then $$.
Cellular scale	$$	The distribution of EC nuclei among voxels. Ei = 1 if a cell nucleus is present in the voxel vi, Ei = 0, otherwise. At most one cell nucleus is allowed per voxel.
	$$	The neighbourhood nucleus distribution. This variable is completely defined by the configuration of E. Each $$, where $$, $$ is a circular neighbourhood of interaction radius, Rc, centred in the voxel vi, and ∣⋅∣ denotes area.
Tissue scale	$$	The ECM density, consisting mostly of collagen I and elastin fibers. It is degraded by cells via a process termed ECM proteolysis (Fig 1A III.). We assume 0 ≤ ci ≤ cmax for all $$, where cmax > 0 is a parameter characterising the maximum density of the ECM.
	$$	The concentration of basal lamina components (collagen IV, fibronectin and various laminins) newly deposited by cells that are used for BM assembly (Fig 1A IV.). We assume 0 ≤ mi ≤ 1 for all $$; mi = 0 if no BM components have been deposited yet, whereas mi = 1 if a BM has been assembled around the sprout segment situated in voxel vi.
	$$	The orientation landscape (OL) variable representing the alignment of ECM fibrils (Fig 1A V.) within the voxel. For a hexagonal lattice $$ for all possible jumping directions $$ (r—right, ur—upward-right, ul—upward-left, l—left, dl—downward-left, dr—downward-right), $$ (see Fig 2). An example of possible orientation landscape configurations is shown in Fig 5A.

Individual cell system

The kinetic reactions acting on individual cells system are illustrated in Fig 3D. We account for trans-activation of Notch receptor (production of an NICD) when it trans-binds to a Delta ligand belonging to a neighbouring cell, D_ext (reaction 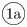$$). If a Delta ligand trans-binds to a Notch receptor on a neighbouring cell, N_ext, it is either endocytotically recycled or degraded (reaction $$). In this reaction, we assume that the active Notch signal is produced in the neighbouring cell, the dynamics of which are irrelevant for the cell of interest. Once cleaved from the Notch receptor, active Notch signal, NICD, is translocated to the cell nucleus where it down-regulates gene expression of VEGFR2 (reaction ②) and up-regulates gene expression of the Notch receptor (reaction ③). Cis-inhibition is accounted for in reaction ④ in which mutual inhibition is assumed for a Delta ligand and a Notch receptor interacting within the same cell. External VEGF, V, can bind to and activate a VEGFR2 (reaction ⑤). This leads to up-regulation of Delta production (reaction ⑥). Reaction ⑦ corresponds to degradation of NICD.

An essential feature of our subcellular model is that it exhibits bistability. To demonstrate this, we derived the mean-field limit equations associated with the kinetic reactions shown in Fig 3D (see Eq (1) in Table 2) and performed a numerical bifurcation analysis (see S1 Table for a list of the parameter values). The results presented in Fig 3E show how the steady state value of the Notch concentration, N, changes as the concentration of external Delta ligand, D_ext, varies. For small (large) values of D_ext, the system supports a unique steady-state corresponding to the tip (stalk) phenotype. For intermediate values of D_ext, the system is bistable: both phenotypes coexist. The combined effect of the external VEGF, V, and D_ext on the system is shown in Fig 3F. We see that varying V does not alter the qualitative behaviour shown in Fig 3E, although the size of the bistable region decreases as V decreases.

Table 2

Here H^S(⋅) is the so-called shifted Hill function [78]. Its functional form is given by $$ H^S\left(X\right)=H^S(X;X_0,{\lambda }_{X,Y},n_Y)=\frac{1+{\lambda }_{X,Y}{({}^X/{}_{X_0})}^{n_Y}}{1+{({}^X/{}_{X_0})}^{n_Y}}$$, where X₀, λ_X,Y and n_Y are positive parameters (see S1 Text for more details). Description and values of parameters can be found in S1 Table.

Mean-field equations associated with the stochastic system of the VEGF-Delta-Notch signalling pathway for the individual cell system (left column) and the multicellular system (right column).

Individual cell system (1)	Multicellular system (2)
$$	$$

The stable states of the subcellular system are characterised by distinct gene expression patterns (for example, high (low) Delta level, D, corresponds to tip (stalk) phenotype). Thus, one variable suffices in order to effectively define the phenotypes. We use Delta level, D, as a proxy variable in the following way

where b_D is baseline gene expression of Delta ligand in ECs (see S1 Table).

Multicellular system

In order to account for cell-cell cross-talk via the VEGF-Delta-Notch pathway, we extend the individual cell system (see Fig 3D) to a multicellular environment by specifying for each cell the external (i.e. belonging to neighbouring cells) amount of Delta and Notch to which it is exposed. As mentioned above, since cell positions in our model are only known up to the position of their nuclei, we assume non-local interactions between cells within a reaction radius, R_s. Thus, we define the local environment of a cell whose nucleus is situated in voxel v_i as the set of voxels with a non-zero overlap region with a circular neighbourhood of radius R_s centred at voxel v_i, $$ {\mathcal{B}}_{R_s}\left(i\right)$$,

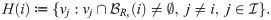
The weights, α_ij, assigned to each voxel v_j ∈ H(i), (see Fig 3B) are defined as follows

where ∣⋅∣ denotes 2D area.

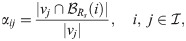
The external Delta (Notch) concentration, D_ext (N_ext), for a cell situated in a voxel v_i is defined as follows:

where D_j (N_j) denotes the Delta (Notch) concentration in voxel v_j.

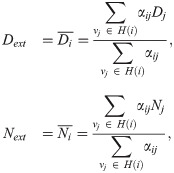
Therefore, our multicellular stochastic system at the subcellular scale consists of the same kinetic reactions as in Fig 3D formulated for each voxel v_i, $$ i\in \mathcal{I}$$ with D_ext, N_ext given by (6). It is important to note that, in simulations of angiogenic sprouting, the quantities D_ext and N_ext dynamically change due to cell migration, thus leading to phenotype re-establishment (see Fig 3G).

When simulated within a two-dimensional domain, our multicellular system produces an alternating pattern of tip/stalk phenotypes. As the reaction radius, R_s, changes the system dynamics do not change but the proportion of tip and stalk cells does. To illustrate this, we ran simulations of the stochastic multicellular system for a 10 × 12 regular monolayer of cells for different values of the interaction radius, R_s (see S1 Fig). These simulations revealed that the distance between tip cells increases (i.e. the proportion of tip cells decreases) as R_s increases. We also investigated how phenotype patterning changes within a monolayer as cis-inhibition intensity varies (see S1 Text). For low values of the cis-inhibition parameter, κ_c, typical chessboard tip-stalk pattern is produced; as κ_c increases, ECs with tip phenotype can become adjacent to each other, thus increasing the time to patterning, since the lateral inhibition is weakened (see S1 Text).

The mean-field equations associated with the multicellular stochastic system are given by Eq (2) in Table 2.

More detail on the derivation and analysis of the subcellular model can be found in S1 Text.

Cellular scale. Persistent random walk and cell overtaking

At the cellular scale we account for EC migration and overtaking. In more detail, we consider a compartment-based model of a persistent random walk (PRW) [79], in which transition rates depend on the phenotypic state of individual cells and their interactions with ECM components.

We denote by $$ s=h^{-1}(q_j-q_i)\in \mathcal{S}$$ the migration direction, as a unit vector pointing from q_i towards q_j, the centres of neighbouring voxels v_i and v_j, respectively (see Fig 2B). In order to formulate the PRW of ECs, we introduce, ω(i → j), to denote the probability that a cell moves from voxel v_i to a neighbouring voxel v_j (i.e. along the direction s) where

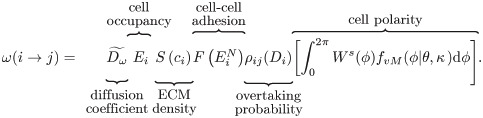
We explain below each of the terms that appears in Eq (7) (see also Fig 4 for a graphical illustration and Table 1 for a description of the model variables).

Fig 4

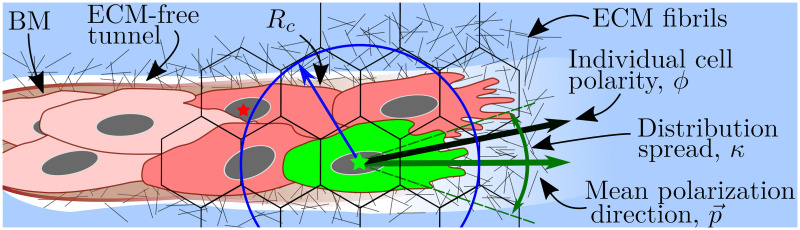
A cartoon illustrating cell migration.

Migration transition rate (Eq (7)) is illustrated for a cell coloured in green. Its nucleus is marked with a green star. The motility of this cell depends on the ECM density, c_i, in the voxel where its nucleus is situated (accounted for by the S(⋅) function (Eq (8)). The green cell forms cell-cell adhesions with other cells coloured in red. In this work, we assume a circular neighbourhood for cell-cell interactions within the so-called interaction radius, R_c, for the cellular scale (here it is drawn to have the same value as in our simulations, R_c = 1.5h, where h is the voxel width). This allows cells to interact beyond their immediate neighbours as, for example, the cell with the nucleus marked by a red star and the focal green cell. Other geometries (e.g. elliptical neighbourhood aligned with cell polarity vector) are unlikely to alter the model behaviour significantly since, in sprouting structures, lateral regions of the circular neighbourhood, which would be ignored by an elliptic neighbourhood, are typically empty. Cell-cell adhesion is accounted for by the neighbourhood function, F(⋅), Eq (9). The individual cell polarity, ϕ, is sampled from the von Mises distribution (Eq (12)) with the mean value given by the mean polarization direction, $$ \overrightarrow{p}$$ (calculated as a function of local ECM fibril alignment, l_i, Eq (13)). The distribution spread, κ, is assumed to depend on the focal cell phenotype and the concentration of the BM components, Eq (14).

ECM density

The function S(c_i) accounts for the effect of the local ECM density, c_i, on cell motility. In general, S(⋅) is a decreasing function of its argument. We assume further that ECs cannot move if the ECM concentration exceeds a threshold value, c_max (S(c_i) = 0 for c_i ≥ c_max). In our simulations we fix

Cell-cell adhesion

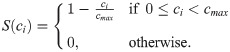
The effect of cell-cell adhesion on cell migration is incorporated via the so-called neighbourhood function, $$ F\left(E_i^N\right)$$. Its argument, $$ E_i^N$$, represents the number of ECs in a cell’s local neighbourhood (red-coloured cells in Fig 4). The functional form of the neighbourhood function was chosen in order to phenomenologically capture the way in which EC behaviour depends on the cell-cell contacts (see Fig 5E). In biological experiments, it was shown that when a cell loses contact with its neighbours (laser ablation experiments in [8]) it halts until the following cells reach it. This is captured by the increasing part of $$ F\left(E_i^N\right)$$; when the number of neighbours around a cell is below the first threshold, E_F1, the probability of cell movement decreases rapidly to zero, thus the migration transition (Eq (7)) goes to 0 as well. Similarly, when there are many ECs in a cell’s neighbourhood, its movement slows down. This is accounted for by the decreasing part of $$ F\left(E_i^N\right)$$ when the number of neighbouring cells exceeds the second threshold value, E_F2, cell movement is slowed down and eventually halts in regions of high cell density.

where (x)⁺ = max(0, x), and the parameters E_F1, E_F2, s_F1 and s_F2 characterise the shape of the curve.

Fig 5

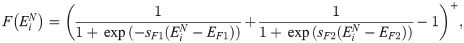
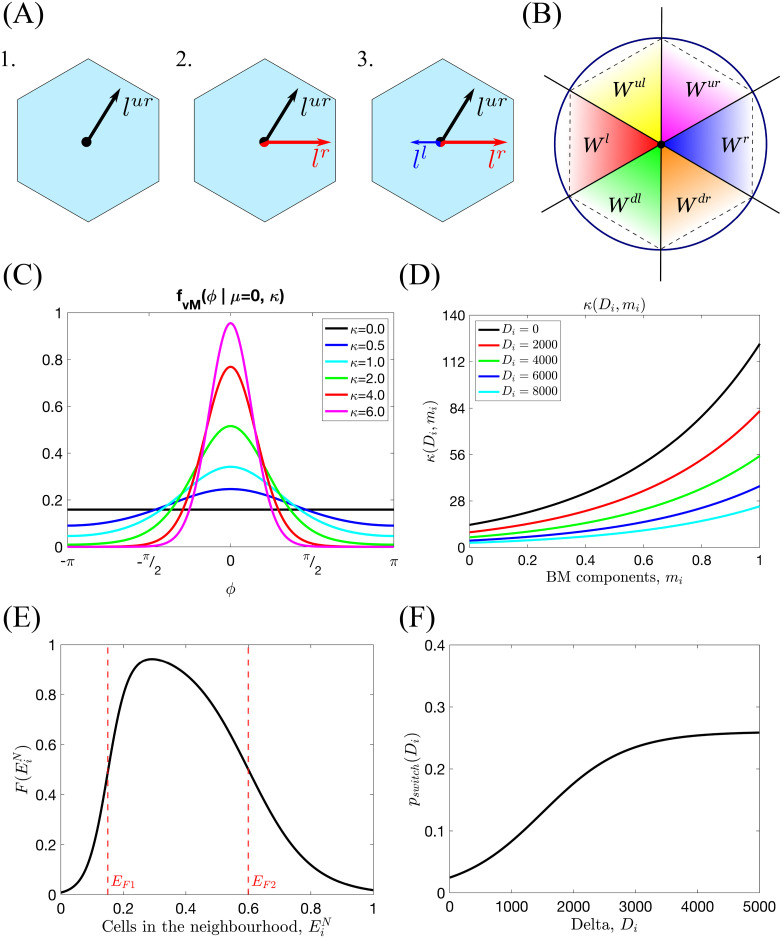
Series of sketches illustrating the components of the cellular scale persistent random walk.

(A) An example of the orientation landscape, l, configurations for a hexagonal lattice. 1. All fibrils are aligned in the upward-right direction; this would be an example of a strongly aligned part of the ECM. 2. Half of the fibrils are aligned to the right, half in the upward-right direction. This would correspond to a branching point. 3. As in 2. but with some additional fibrils aligned in the left direction. (B) The window function, W^s(ϕ), (Eq (15)) has been defined as an indicator function over an angle interval corresponding to each possible migration direction $$ s\in \mathcal{S}$$ (lattice-dependent). The diagram illustrates these intervals for a hexagonal lattice. (C) Illustration of the probability distribution function of the von Mises distribution, f_vM(x|μ, κ), centred at μ = 0 for different fixed κ (Eq (12)). (D) Illustration of the κ function as a function of local Delta ligand level, D_i, and concentration of BM components, m_i, (Eq (14) with K = 13.6, k_m = 2.2 and k_D = 0.0002). (E) An example of the neighbourhood function, $$ F\left(E_i^N\right)$$ (Eq (9), with E_F1 = 0.15, E_F2 = 0.6, s_F1 = 30, s_F2 = 10). (F) A sketch showing how the switching probability, p_switch(D_i), changes with the level of Delta in voxel v_i, D_i (Eq (10) with p_max = 0.26, s_p = 0.0015, D_p = 1500).

Overtaking probability

This term accounts for cell overtaking and excluded volumes. A jump occurs with overtaking probability, ρ_ij(D_i) = 1, if the target voxel, v_j, is empty (E_j = 0). Otherwise, the cells in voxels v_i and v_j switch their positions with probability ρ_ij(D_i) = p_switch(D_i). We consider this probability to be phenotype dependent. In particular, we assume that tip cells (see Eq (3)) are more motile because their filopodia are stronger (see Fig 1A II.). Thus, the switching probability, p_switch(D_i), is assumed to be an increasing function of the Delta level, D_i, of the migrating cell

where

the parameters s_p and D_p characterise, respectively, the slope and position of the sigmoid, and p_max denotes its maximum value (see Fig 5F).

Cell polarity

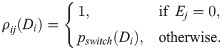
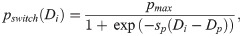
Prior to migration, cells develop a polarity which depends on their local environment. Following [81, 82], we consider the local cell polarity, ϕ, (see Fig 4) to be a random quantity sampled from the von Mises distribution. The probability density function (pdf) of the von Mises distribution reads

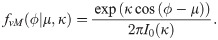
Its shape is characterised by two parameters: the mean value, μ, and the distribution spread, κ (see Fig 5C for a sketch of this pdf for different values of κ). I₀ is the modified Bessel function of the first kind of order 0.

In the context of EC migration, we view μ as the mean polarisation angle, and κ as cell exploratoriness. We integrate ECM structure and composition and cell phenotype into our cell migration model by assuming that μ and κ depend on these quantities. In particular, we assume that the mean polarisation angle, μ, depends on the ECM fibril alignment which is represented in our model by the orientation landscape variable, l_i (see Table 1). From a biological point of view, this is substantiated by experimental observations of cells forming focal adhesions with ECM fibrils and, consequently, aligning along them [43]. We introduce the mean polarisation direction vector, $$ \overrightarrow{p}\in {\mathbb{R}}^2$$, and compute μ as its principle argument (see Fig 4)

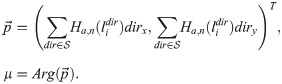
In Eq (13) the summation is taken over all possible directions for movement, $$ dir={(di{r}_x,di{r}_y)}^T\in \mathcal{S}$$ (in a hexagonal lattice there are at most 6 possible directions, see Fig 5A). The Hill function, H_a,n(⋅), is used to reflect the natural saturation limit to alignment and deformation of the ECM fibrils, with a and n being fixed positive parameters. Details about how fibril orientation (orientation landscape, l_i) is calculated are given below.

Cell exploratoriness, κ ≥ 0, is directly related to the EC phenotype (see Fig 1A I.). If κ ≈ 0, then the effect of polarity on migration is weak, and cells can explore many directions (this behaviour is typical of exploratory tip cells, see Eq (3)). By contrast, when κ ≫ 1, the von Mises pdf is concentrated around μ (this behaviour is characteristic of stalk cells, see Eq (3)). To account for such phenotype-dependent behaviour, we assume κ to be a monotonic decreasing function of D_i, the Delta level of the migrating cell. Similarly, increased concentration of the BM components deposited by ECs (see Fig 1A IV.) reduces the exploratory capability of both tip and stalk cells. We therefore propose κ to be an increasing function of the local concentration of the BM components, m_i. Combining these effects, we arrive at the following functional form for κ = κ(D_i, m_i):

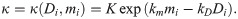
Here K, k_m, k_D are positive parameters (see Fig 5D for a sketch of κ(D_i, m_i)).

Since our model of cell migration is formulated on a lattice, transition rates of type ω(i → j) (jumps from v_i into v_j, in the direction $$ s\in \mathcal{S}$$) are associated with an angle interval $$ [{\varphi }_{min}^s,{\varphi }_{max}^s]$$ (see Fig 2B). This corresponds to the angle between the vectors connecting the centre of the voxel v_i with the endpoints of the voxel edge shared by v_i and v_j. For example, in a hexagonal lattice, the right direction, $$ r\in \mathcal{S}$$, is associated with an interval $$ [{\varphi }_{min}^r,{\varphi }_{max}^r]=[-{}^{\pi }{/}_6,{}^{\pi }{/}_6]$$. Therefore, we restrict the von Mises pdf, f_vM(⋅), in Eq (7) to this interval by multiplying it by a corresponding indicator function, W^s(ϕ),

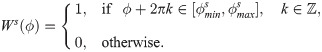
This function is 2π-periodic due to the fact that its argument is an angle. We refer to W^s(ϕ) as the window function (see Fig 5B).

Tissue scale. Modelling cell environment: ECM structure and composition

We account for the alignment of ECM fibrils, l, density of the ECM, c, and concentration of the basal lamina components, m (see Table 1) in the following way.

Local alignment of the ECM fibrils, l, serves as a scaffold for the orientated migration of ECs [43]. Thus, we refer to l as the orientation landscape. Traction forces exerted by migrating ECs realign the ECM fibrils, so that they move closer to the growing sprouts. Furthermore, since tip cells have more filopodia than stalk cells, they exert a greater influence on the orientation landscape [39] (see Fig 1A V.). We account for phenotype-dependent ECM realignment by assuming active stretching and accumulation of the fibrils upon cell movement between the voxels i → j (in the direction $$ s\in \mathcal{S}$$), i.e. when a transition of type ω(i → j) occurs,

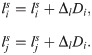
Here, the parameter Δ_l > 0, which quantifies the linear response of ECM fibrils to cell migration, depends on the substrate stiffness.

Besides active stretching induced by cell locomotion, we also consider passive relaxation of the orientation landscape. We assume that relaxation follows a simple elastic model so that the orientation landscape decays exponentially at a constant rate, η_l,

where τ is the waiting time of the occurred migration transition and the update is done for all voxels $$ i\in \mathcal{I}$$ and all directions $$ s\in \mathcal{S}$$.

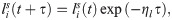
The time evolution of the ECM density, c, and BM components, m, is modelled via local ODEs. We assume phenotype-dependent ECM proteolysis induced by ECs (see Fig 1A III.). Since tip cells exhibit higher proteolytic activity than stalk cells [83, 84], we assume that the ECM at voxel v_i is degraded at rate η_c(D_i), which is an increasing function of its argument

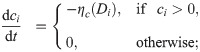
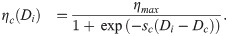
Here, in order to account for the natural saturation in EC proteolytic ability, we assume a sigmoidal functional form for η_c(D_i) with positive parameters D_c and s_c (which correspond to the threshold level of Delta for initiation of ECM proteolysis and sharpness of EC response, respectively) and maximum value η_max.

Similarly, BM assembly (i.e. deposition of basal lamina components), is assumed to be phenotype-dependent (see Fig 1A IV.). Tip cells are known to secrete BM components and to recruit and activate pericytes which secrete basal lamina components around the sprout [83, 84]. Thus we assume that the rate of secretion of BM components, γ_m(D_i), is an increasing function of D_i

where, again, a sigmoidal functional form is assumed for γ_m(D_i) with positive parameters D_m and s_m (which correspond to the threshold level of Delta for initiation of BM assembly and sharpness of EC response, respectively) and maximum value γ_max. Here we assume the decay of BM components is negligible on the timescale of our simulations.

Description of quantitative metrics

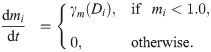
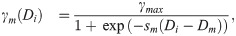
In order to calibrate and compare our simulation results to experimental data (see [2, 8]), we computed a number of metrics defined below.

Mixing measure

This metric is motivated by the experimental observation that the trajectories of individual ECs, which initially form clusters with their immediate neighbours (see Fig 6 for an illustration), at later times diverge so that cells can find themselves at distant regions of the angiogenic vascular network [2, 8]. This metric is introduced to quantify the cell rearrangements. Cell rearrangements are a key driver of sprout elongation during the early stages of vasculature formation and, as such, are directly related to network growth patterns. Later in this work, we will show how the mixing measure varies for different patterns of vascular network formation.

Fig 6

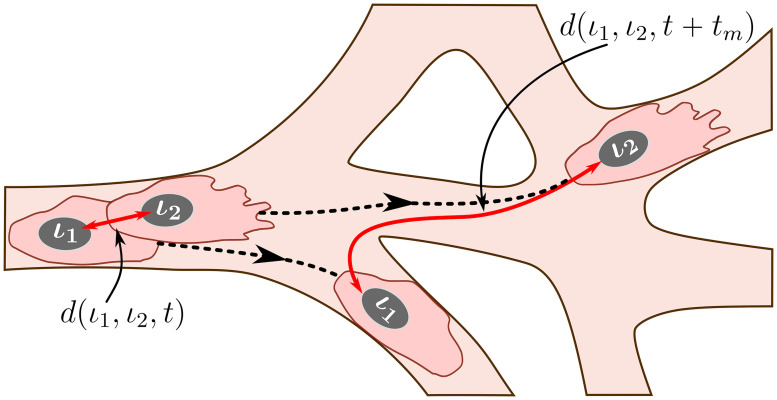
An illustration of the mixing measure.

Two cells, labelled by ι₁ and ι₂, are located at the positions corresponding to the set $$ {\mathcal{I}}_{cluster}$$ at time t. We track their trajectories in the simulated vascular network (dashed black lines) during time t_m. The mixing measure is defined as the difference between the distances between these cells at times t and t + t_m, d(ι₁, ι₂, t) and d(ι₁, ι₂, t + t_m), respectively, normalised by the number of cells considered and the maximum distance it is possible to travel in the simulated network. The distance function is defined as a distance within the simulated network (see S1 Text for details).

Briefly, during simulations, we assign a label to each EC, ι, and record its position in the system at time t, $$ p(\iota ,t)\in \mathcal{I}$$. We specify a set of voxels that form a cluster of nearest neighbours in the lattice, $$ {\mathcal{I}}_{cluster}$$. At the end of the simulation, using recorded cell trajectories, we compute how far away (in a pair-wise fashion) cells that were situated at the voxels in $$ {\mathcal{I}}_{cluster}$$ at time t have moved away from each other during time interval of duration t_m. Normalising this quantity by the cardinal of $$ {\mathcal{I}}_{cluster}$$, $$ \mid {\mathcal{I}}_{cluster}\mid $$, and the maximum possible travel distance in the system, d_max, we obtain the mixing measure at time t, $$ \mathcal{M}\left(t\right)$$, defined as

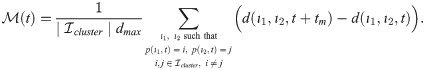
Here d(ι₁, ι₂, t) is the distance between cells with labels, ι₁ and ι₂, at time t. It is computed as a distance in a manifold of the simulated vascular network (see Fig 6). This is due to the fact that ECs do not migrate randomly but rather within ECM-free vascular guidance tunnels of the generated vascular network.

The distance, d_max, in Eq (22), is the maximum distance in the simulated vascular network, defined as follows

where T_max is the final simulation time.

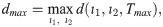
Detailed descriptions of all the metrics and computational algorithms that we used are given in S1 Text.

Emergent qualitative features: Branching and VEGF sensitivity

Our model exhibits two characteristic features of functional angiogenic structures, namely, branching and chemotactic behaviour. A novel aspect of our multiscale model is that these features are emergent properties of its dynamics rather than being hardwired into the model.

Specifically, branching is a direct consequence of the phenotype-dependent polarity of individual cells. When a stalk cell within a sprout undergoes a phenotype switch and assumes a tip identity, its exploratoriness, increases (i.e. κ, decreases). This enables the cell to develop a polarity angle that departs from the mean elongation direction of the sprout, μ. As a consequence, a new branch forms. In our model, new branches are typically initiated by cells exhibiting the tip cell phenotype (see S1 Movie). This behaviour is characteristic of ECs observed in biological experiments [7, 9]. Figs 7 and 8 illustrate the branching phenomenon and stabilisation of the network structure (due to accumulation of BM components deposited by ECs) in single realisations of numerical simulations of the model for uniform VEGF distribution at concentrations of 5 and 50 ng/ml (see also S1 and S4 Movies). Note that in all our simulations “gaps” within sprouts can arise since we track the positions of cell nuclei and do not account for their true spatial extent.

Fig 7

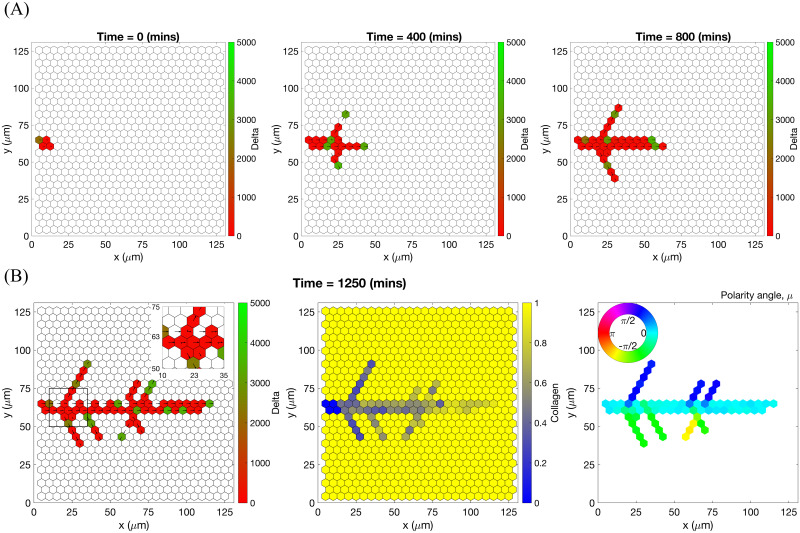
An example of an individual vascular network generated during simulation of our model with uniform VEGF = 5 ng/ml.

(A) Temporal evolution of a simulated vascular network captured at 0 mins, 400 mins and 800 mins in an individual realization of our model for uniform VEGF = 5 ng/ml. The colour bar indicates level of Delta, D, (green colour corresponds to tip cells, red—to stalk cells). Arrows indicate the configuration of the orientation landscape, l. (B) The final configuration of the simulated vascular network at 1250 mins (corresponds to the final simulation time, t = T_max = 2.5). The leftmost panel shows the concentration of Delta, D. Higher concentration (green colour) corresponds to tip cell phenotype, low concentration (red colour)—to stalk. On this plot, arrows correspond to the orientation landscape configuration, l. The central panel shows the final concentration of the ECM, c. The rightmost panel shows the final distribution of the polarity angle, μ, variable. Numerical simulation was performed using Setup 1 from S4 Table. Parameter values are listed S1 and S2 Tables for subcellular and cellular/tissue scales, respectively. For a movie of the numerical simulation, see S4 Movie, left panel.

Fig 8

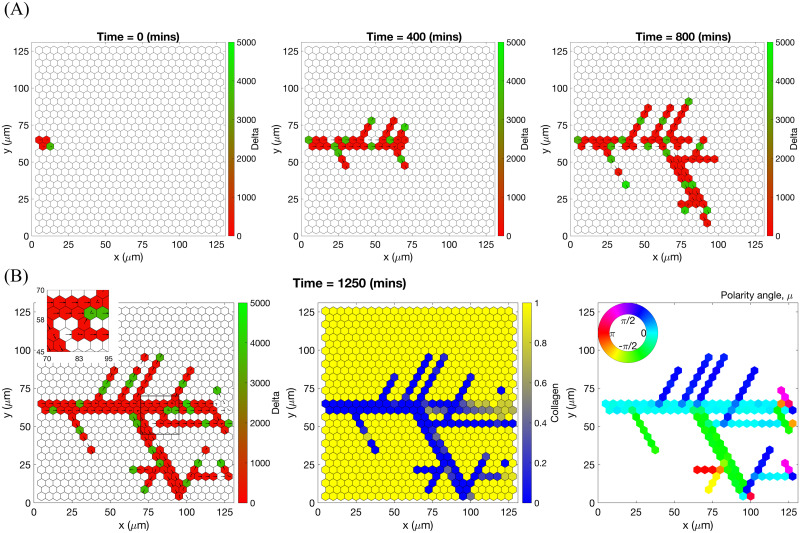
An example of an individual vascular network generated during simulation of our model with uniform VEGF = 50 ng/ml.

(A) Temporal evolution of a simulated vascular network captured at 0 mins, 400 mins and 800 mins in an individual realization of our model for uniform VEGF = 50 ng/ml. The colour bar indicates level of Delta, D, (green colour corresponds to tip cells, red—to stalk cells). Arrows indicate the configuration of the orientation landscape, l. (B) The final configuration of the simulated vascular network at 1250 mins (corresponds to the final simulation time, t = T_max = 2.5). The leftmost panel shows the concentration of Delta, D. Higher concentration (green colour) corresponds to tip cell phenotype, low concentration (red colour)—to stalk. On this plot, arrows correspond to the orientation landscape configuration, l. The central panel shows the final concentration of the ECM, c. The rightmost panel shows the final distribution of the polarity angle, μ, variable. Numerical simulation was performed using Setup 1 from S4 Table. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively. For a movie of the numerical simulation, see S1 Movie.

Chemotactic sensitivity in our model is a direct consequence of cell interactions with the ECM. In biological experiments, proteolytic activity of cells was observed to increase as expression levels of Delta rise [83, 84]. In our model, increased levels of extracellular VEGF, V, up-regulate subcellular levels of Delta. As a result, an EC’s ability to degrade the ECM and invade it at a faster rate is enhanced where VEGF levels are high. This can be seen by comparing networks generated at different uniform VEGF concentrations (see Figs 7 and 8). The network generated at VEGF = 5 ng/ml is small (Fig 7B, leftmost plot), and the vascular guidance tunnels created via proteolysis (middle plot) are not fully formed. By contrast, the simulated network for VEGF = 50 ng/ml (Fig 8B, leftmost plot) has a greater spatial extent, since collagen-free vascular tunnels (Fig 8B, middle plot) facilitate cell migration within them, increasing sprouting and cell persistence (see ECM density term in Eq (7)).

Our model also exhibits the brush-border phenomenon [11, 85]. We performed a numerical simulation experiment of sprouting initialised from an initial vessel placed in a matrix with linearly increasing VEGF gradient. Fig 9 shows the evolution of the network at different times. The brush-border effect is evident at later times and characterised by increased cell numbers and branches in the top regions of the domain where VEGF levels are high.

Fig 9

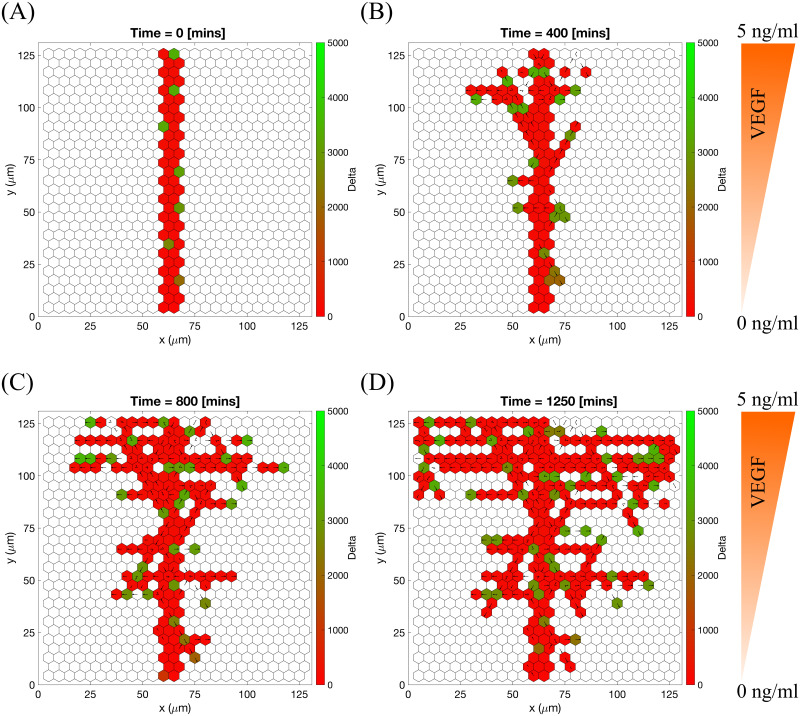
Sprouting in static VEGF gradient.

Snapshots at different times of a vascular network growing in linear VEGF gradient increasing from VEGF = 0 ng/ml to VEGF = 5 ng/ml. (A) Time = 0 mins, initial setup. (B) Time = 400 mins, new branches appear from the initial sprout mostly in the upper half of the domain (higher VEGF concentration). ECs with lower positions have lower Delta level. (C) Time = 800 mins, the effect of the VEGF gradient can be seen clearly. (D) Time = 1250 mins, the final configuration of the simulated V-shaped (opening towards higher VEGF concentrations) network. Colour bar shows the level of Delta, D. Numerical simulation was performed using Setup 2 from S4 Table with final simulation time, T_max = 2.5. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively.

Model calibration

Having established that our model exhibits the essential features of branching and chemotactic behaviour observed in experiments, we next compared our simulations with experimental results from [2, 8, 38]. This enabled us to estimate baseline parameter values for processes at the cellular and tissue scales (estimated values of parameters associated with processes acting at the subcellular scale are taken from previous works, see S1 Table).

We ran 100 model simulations for uniform VEGF concentrations of 0, 5 and 50 ng/ml (Setup 1, see S4 Table, with final simulation time, T_max = 2.5, equivalent to 1250 mins, i.e. ≈ 20.8 h) and computed three metrics, namely, displacement, orientation and directionality (see Materials and methods for definitions) as was done in [2, 8]. The results presented in Fig 10 show that our simulations reproduce general trends of angiogenic sprouting reported in [2, 8]. Specifically, regarding the displacement statistic (Fig 10A), agreement is very good, except for the inconsistency at displacement = 0 μm, i.e. cells that did not move during the considered time interval (15 minutes). This inconsistency arises because we do not include the vascular bed from which cells migrate (we account for it via a boundary condition; see Fig 2A and S1 Appendix). By contrast, in [8], cell displacements from the embedded aortic ring assay were included in the sample (these ECs are mostly quiescent). Similarly, results regarding the orientation statistic (Fig 10B and 10C) are in good agreement with the experimental results. In particular, in our model ECs are more oriented, i.e. more persistent, in higher VEGF concentrations, which is a feature also observed in [2]. Concerning the directionality statistic (Fig 10D–10F), we note that when VEGF = 0 ng/ml the numbers of anterograde and retrograde cells in the experiments [2] (Fig 10F) and numerical simulations (Fig 10E) are approximately equal. In this scenario, ECM proteolysis is slow and cell migration is mostly constrained to existing sprouts. Thus, any anterograde movement is an overtaking event in which the overtaken cell has to perform a retrograde displacement. As the VEGF concentration increases, ECM proteolysis (see Eqs (18) and (19)) increases and more cells at the leading edge of sprouts can invade the surrounding ECM, elongating the sprouts. This leads to an increase in the ratio of anterograde to retrograde moving cells with the VEGF concentration.

Fig 10

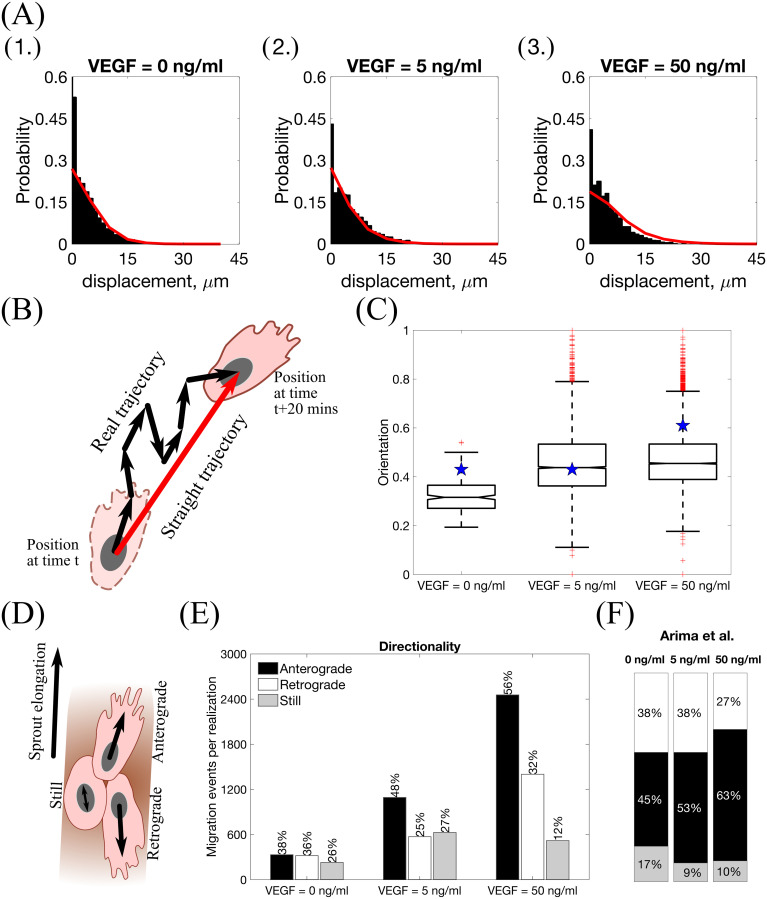
Statistics extracted from simulations of our model.

(A) Histograms of cell displacements during a 15 minute time period for (1.) VEGF = 0 ng/ml, (2.) VEGF = 5 ng/ml and (3.) VEGF = 50 ng/ml. Black histograms correspond to the experimental data taken from the Supplementary Material of [8], red lines correspond to displacement curves for each VEGF concentration extracted from our model simulations. (B) A cartoon illustrating the orientation statistic, which is defined as a ratio between the net trajectory and the actual trajectory of a cell during simulation. (C) Box plots of the orientation statistic extracted from model simulations with VEGF = 0, 5, 50 ng/ml. Red crosses indicate box plot outliers. Orientation statistics obtained from experimental data from [2] are shown by blue stars on each box plot. (D) A cartoon illustrating the directionality statistic. (E) The directionality statistics for model simulations with VEGF = 0, 5, 50 ng/ml. (F) The directionality statistics extracted from experimental data in [2]. Numerical simulations were performed using Setup 1 from S4 Table and T_max = 2.5. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively. All statistics were computed for 100 realisations.

Further evidence of agreement with experimental data is found by performing numerical simulations imitating the experimental setup of [38]. We performed simulations of sprouting from a cell bead embedded into the ECM (see Setup 3 from S4 Table) with varying collagen density (which corresponds to the initial ECM concentration, c_max, in our model) and a static linear VEGF gradient. Results from single realisations of different values of c_max are presented in Fig 11 (see also S2 Movie). These results show free cell migration with no preferred direction for low c_max values, typical angiogenic morphology for intermediate values of c_max, and poorly elongating sprouts for higher values of c_max. These findings are consistent with the experimental observations reported in [38]. Furthermore, we note that the “sweet spot” of ECM concentration is related to EC ability to form typical angiogenic sprouting structures rather than to their ability to invade the ECM which decreases as the ECM concentration, c_max, increases (see Fig 11).

Fig 11

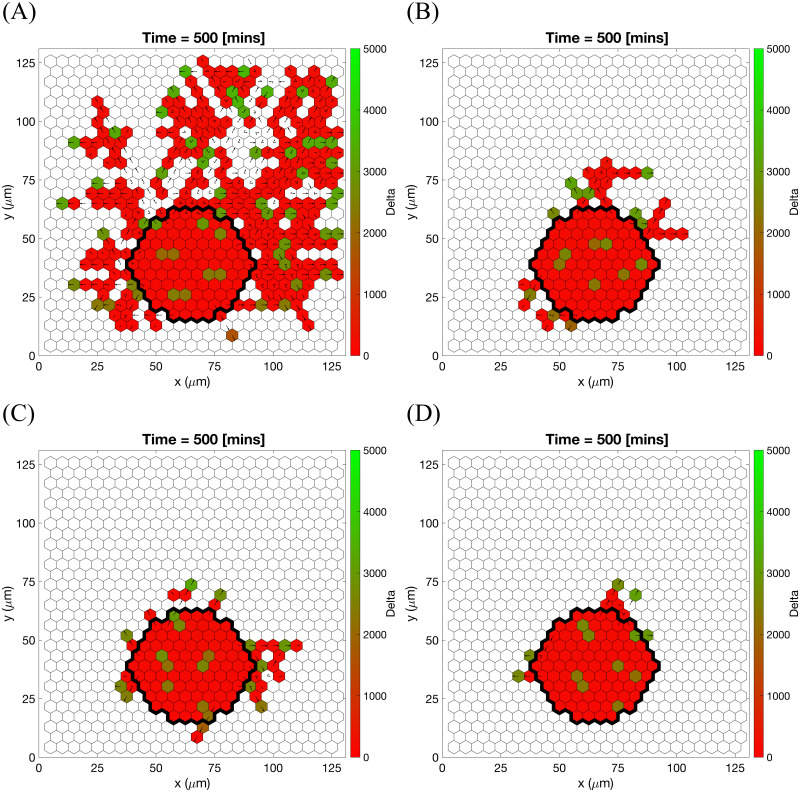
Cell migration from a cell bead in substrates of different collagen density.

Final configurations of simulated vascular networks at time T_max = 1.0 (corresponding to 500 minutes) of individual simulations used in reproducing the results of the polarisation experiment in [38]. Maximum collagen density (A) c_max = 0.1, (B) c_max = 1.0, (C) c_max = 1.7, (D) c_max = 3.0. The VEGF linear gradient starts with 0 ng/ml at y = 0 and increases up to 5 ng/ml at y = 125 μm. Central bead initial and basement membrane conditions, $$ {\mathcal{I}}_{BM}={\mathcal{I}}_{init}$$, are outlined by a black thick line on each plot. Colour bars indicate Delta ligand concentration. Numerical simulations were performed using Setup 3 from S4 Table. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively. For a movie of the numerical simulation, see S2 Movie.

We note that the results presented in this section were generated using a fixed set of parameter values, except for the concentration of VEGF, V, and the concentration of collagen, c_max. Henceforth, we use these values as baseline parameter values (see S2 Table).

Further model validation

In this section we validate our model by comparing its predictions with experimental results detailing the behaviour of certain VEGF receptor mutant cells (VEGFR2^+/- and VEGFR1^+/- mutants with halved gene expressions of VEGFR2 and VEGFR1, respectively), studied by Jakobsson et al. in [7] and described in S1 Appendix.

In order to ascertain whether our model can quantitatively reproduce competition between cells of different lineages (wild type (WT) and mutant cells) for the position of the leading cell in a sprout, we designed a series of numerical experiments which mimic the biological experiments reported in [7]. We start by simulating of EC competition within linear sprouts that are devoid of collagen matrix (Setup 4 in S4 Table), to ensure proteolysis-free random shuffling of cells within the sprout. We randomly initialise the sprout with cells of two chosen types with probability 50% (50% of WT cells and 50% of a specific mutant cell type) (see Fig 12, left column). Cells are then allowed to shuffle within the sprout, overtaking each other. For each realisation we record the total amount of time for which WT and mutant cells occupy the position of the leading cell.

Fig 12

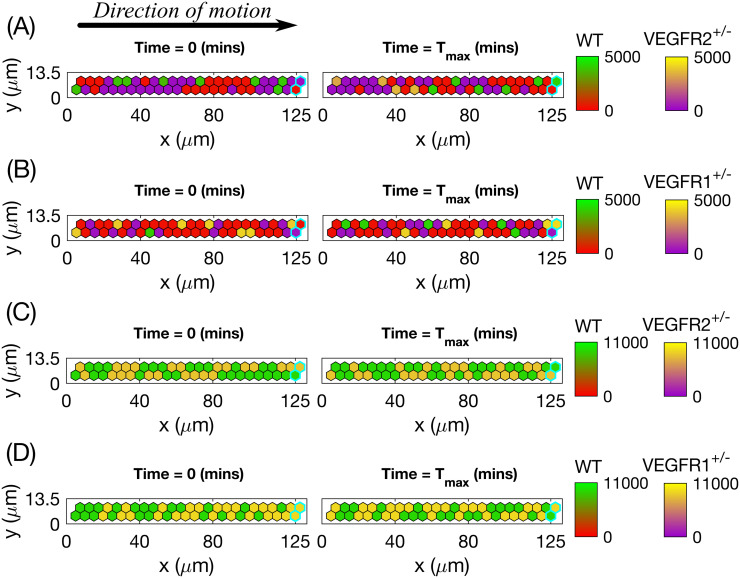
Initial and final configurations of single realisations of cells shuffling within a linear sprout when two given cell lines are mixed 1:1 (50% to 50%).

Left column corresponds to the initial (random, 1:1) distribution of cells, right column—to the final one. The colour bar for Delta level of the WT goes from red colour (stalk cell) to green (tip cell), whereas for the mutant cells the bar goes from purple colour (stalk cell) to yellow (tip cell). (A) 50% of WT cells mixed with 50% of VEGFR2^+/- mutant cells, no DAPT treatment. (B) 50% of WT cells mixed with 50% of VEGFR1^+/- mutant cells, no DAPT treatment. (C) 50% of WT cells mixed with 50% of VEGFR2^+/- mutant cells, both DAPT-treated. (D) 50% of WT cells mixed with 50% of VEGFR1^+/- mutant cells, both DAPT-treated. Voxels corresponding to the leading edge of a sprout are outlined by thick cyan lines on each plot. Numerical simulations were performed using Setup 4 from S4 Table. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively, except for the changed parameters for the mutant cells listed in S1 Appendix. Final simulation time, T_max = 50.0. For a movie of the numerical simulations, see S3 Movie.

As a control, we ran simulations in which two identical cell lines with parameters corresponding to WT lineage were mixed in a 1:1 ratio. As expected, the contribution of each WT cell to the leading cell position was approximately 50% (see Table 3).

Table 3

Since as an initial setup of simulations we considered a sprout of width 2 (two voxels), there are two equivalent leading positions (Position 1 and Position 2) (outlined on each plot by cyan lines in Fig 12). The results are reported as mean value ± standard deviation for samples obtained from 100 realizations for each experimental scenario. Numerical setup is as specified in Fig 12.

Contribution of WT cells to the leading cell position when mixed 1:1 (50%: 50%) with another type of cell (equivalent WT or specified mutant).

Experiment	Position 1	Position 2	Ref. value [7]
WT:WT	51.1±16.4%	53.3±20.6%	45.8%
WT:VEGFR2+/-	93.6±7.1%	90.4±14.8%	87.0%
WT:VEGFR1+/-	19.5±9.8%	20.5±17.8%	30.0%
WT:VEGFR2+/- +DAPT	51.5±13.7%	52.9±17.8%	47.0%
WT:VEGFR1+/- +DAPT	50.3±14.3%	47.6±16.7%	40.6%

We then performed competition simulations in which WT cells were mixed with the different mutant cell lines in a 1:1 ratio (i.e. mixing 50% of WT cells with 50% of mutant cells). We repeated these numerical experiments in the presence of DAPT inhibitor which abolishes Notch signalling. The results of individual realisations presented in Fig 12 (see also S3 Movie), illustrate features of the different competition scenarios. For the WT:VEGFR2^+/- scenario (see Fig 12A) when the mutant cells compete with WT cells, they almost never acquire the tip phenotype. Consequently, they are rapidly overtaken by WT cells and accumulate far from the leading edge of the sprout (outlined in cyan on each plot). The leading cell positions are thus occupied predominately by WT cells. By contrast, in the WT:VEGFR1^+/- scenario (Fig 12B), mutant cells acquire the tip phenotype more often than WT cells, and thus contribute more significantly to the leading cell position. Treatment with DAPT forces all ECs (WT, VEGFR2^+/- and VEGFR1^+/-) to acquire the tip cell phenotype (which is the default when Notch signalling is abolished [12, 13]). Consequently, in these cases both treated mutants have a 50% likelihood of occupancy of the leading position (Fig 12C and 12D).

We have also collected statistics from 100 realisations for each scenario and compared the results to the quantitative estimates provided in [7]. The results reported in Table 3 show that the contribution of WT cells to the leading cell position in each scenario is in good agreement with experimental values from [7]. In our simulations, VEGFR2^+/- cells are less likely to stay at the leading position than WT cells: they occupy the leading position approximately 7% of the time. By contrast, VEGFR1^+/- cells occupy the leading cell position approximately 78% of the time. DAPT restored the balance between the cells of different lineages so that they were on average equally mixed. Since the only parameters that we have modified are those used to mimic mutant cell gene expression and DAPT inhibition of Notch signalling (see S1 Appendix) our model provides possible explanation for overtaking dynamics of ECs in angiogenesis.

Sensitivity analysis

To ascertain how variation in the baseline parameter values of our model affects the behaviour of the system, we have performed an extensive sensitivity analysis. Since the subcellular VEGF-Delta-Notch model has already been calibrated and validated independently [76], we have focused our analysis on the cellular and tissue scale parameters (see S2 Table). Briefly, we have performed our analysis by fixing all the parameters except one at their baseline values, and then vary the focal parameter by ±0.1%, ±5%, ±10%, ±15%, and ±20%. This procedure is repeated for each of the tissue and cellular scale parameters. In order to quantify the impact of the variation of each parameter on both EC behaviour and network structure we have measured the following quantities:

anterograde cell proportion (directionality metric);

orientation;

displacements;

number of branching points per 100 μm² of vascular network area;

number of vessel segments;

vessel segment lengths.

Each of these metrics has been measured over 100 realisations of the multiscale system. For a full account of the details, see S1 Text.

The results of our sensitivity analysis are summarised in Fig 13 and S2 Fig. Our analysis shows that system behaviour is robust to variations in most of the model parameters considered. This is indicated by the central cluster in Fig 13 and S2 Fig, highlighted in magenta, which represents those scenarios that exhibit very small deviations from the baseline behaviour. By contrast, variations of a small number of parameters produce significant deviation from the baseline behaviour (see Table 4 and Fig 13 and S2 Fig).

Fig 13

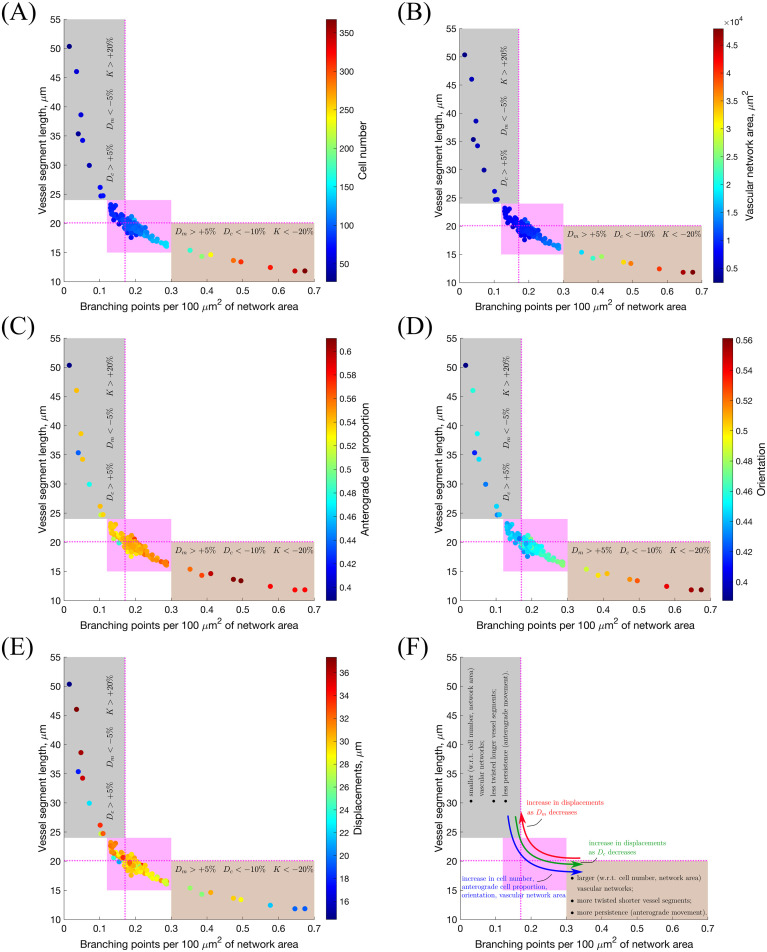
Sensitivity analysis: Branching vs. vessel elongation.

The results of the sensitivity analysis are represented as scatter plots of the mean number of branching points per 100 μm² of vascular network area vs. mean vessel segment length, with colouring indicating mean (A) cell number; (B) vascular network area; (C) anterograde cell proportion; (D) orientation and (E) displacements. On these plots, dashed magenta lines indicate the point corresponding to the default parameter values (see S2 Table); magenta highlights the region of the main point clustering. The grey-coloured outlier region corresponds to vascular networks with few branching points and long vessel segments (hypo-branching), whereas the brown outlier region is characterised by short vessel segments and greater number of branching points (hyper-branching). Variations of the parameters that push the system towards one of the outlier regions are indicated on each plot. Panel (F) provides a general summary of these results. Simulation setup as in Setup 1, S3 Table, with T_max = 2.5. The results are averaged over 100 realisations for each scenario. The subcellular parameters are fixed at their default values in all experiments (see S1 Table).

Table 4

↓ stands for decrease of the focal parameter, ↑—increase of the focal parameter.

Sensitivity analysis: Parameters producing significant deviation in system behaviour from the baseline scenario.

Par.	Description	Ref. equation	Metrics affected	Effect
Dc	Threshold of level of Delta for initiation of ECM proteolysis	Eq (19)	All	Hyper-branching: Dc↓; hypo-branching: Dc↑
Dm	Threshold of level of Delta for initiation of BM assembly	Eq (21)	All	Hypo-branching: Dm↓; hyper-branching: Dm↑
K	Cell exploratoriness, i.e. controls the variance of the von Mises distribution	Eq (14)	All	Hyper-branching: K↓; hypo-branching: K↑
EF1	Threshold of the level of cell-cell contact necessary for cell movement initiation	Eq (9)	Orientation, directionality	Hyper-branching: EF1↓
EF2	Threshold of the inhibitory effect of crowding on cell movement	Eq (9)	Orientation, directionality	Hypo-branching: EF2↓

Specifically, we observe that an increase in D_m and a decrease in both D_c and K induce excessive branching, with shorter average vessel length (see Fig 13, hyper-branching region highlighted in brown). By contrast, a decrease in D_m and an increase in both D_c and K induce less branched networks, with longer average vessel length (see Fig 13, hypo-branching region highlighted in grey). These results are in agreement with well-known features of tumour vasculature, where the tumour microenvironment inhibits vessel stabilisation; specifically, it hinders the formation of the basal membrane in tumour vasculature, yielding aberrant, excessively branched, networks [86]. This phenomenon can be realised by increasing D_m. Furthermore, proteolysis is also up-regulated during tumour-induced angiogenesis due to secretion of MMPs by cancer cells. Proteolysis reduces the resistance experienced by the ECs as they migrate towards the tumour [86]. This effect can be accounted for phenomenologically by a reduction in D_c. Increased stimulation with growth factors that can also bind to VEGF receptors (as in pathological angiogenesis [86, 87]) can reduce the response of the ECs to chemotactic stimuli, due to high occupancy of receptors all over the cell membrane, thus shifting cell behaviour to chemokinesis (non-directional cell migration) [88, 89]. In our model, this transition is controlled by the cell exploratoriness, κ (see Eq (14)): for high values of κ (i.e. higher values of K) cell migration is directed along the sprout elongation vector, whereas for small values of κ (i.e. smaller values of K) cells exhibit exploratory behaviour corresponding to chemokinesis.

Our model thus predicts that changes in D_c, D_m and K are likely to occur in tumour-induced angiogenesis. This prediction is supported by current knowledge regarding the effects of the presence of a tumour in the microenvironment [86–88].

Model predictions: Network structure and cell mixing

We also simulated the growth of vascular networks formed by a single mutant cell line (VEGFR2^+/- or VEGFR1^+/-) in the presence/absence of DAPT and compared our findings with the results from Jakobsson et al. who observed that in the absence of DAPT mutant cells mix with WT cells to form normal networks [7]. By contrast, the addition of DAPT leads to unstructured growth [7]. This is consistent with our simulation results (see S3–S6 Figs). Specifically, simulations with VEGFR2^+/- mutant cells in the absence of DAPT (see S3 Fig and S4 Movie) suggest that the rate of network growth of VEGFR2^+/- is slower than for their WT counterparts (see Figs 7 and 8 and S7 Fig). Since Delta levels in VEGFR2^+/- cells are lower than in WT cells, they are less able to degrade and invade ECM, and deposit BM components than WT cells. This results in slower sprout elongation and increased branching (see S7 Fig). By contrast, VEGFR1^+/- mutant cells possess higher levels of Delta and thus degrade the ECM more efficiently and invade the matrix more quickly than the WT cells (see S5 Fig and S4 Movie). Likewise, since the rate of segregation of BM components, γ_m, increases with Delta (Eq (21)), VEGFR1^+/- cells are more persistent than WT cells. As a result, VEGFR1^+/- ECs form less branched networks, with longer sprouts (see S7 Fig). Regarding networks grown with DAPT, since DAPT treatment abolishes all Notch signalling, all cells in the simulations with DAPT acquire the tip cell phenotype (S5 and S6 Figs), which produces unstructured growth.

Since a cells’ ability to compete for the leading position, or, equivalently, cell shuffling, is altered in mutant cells, we sought to understand how cell rearrangements influence the structure of a growing vascular network. To quantify cell rearrangements, we introduce a metric, which we refer to as mixing measure, $$ \mathcal{M}\left(t\right)$$ (see Eq (22)). In Fig 14A, we plot the dynamics of the mixing measure, $$ \mathcal{M}\left(t\right)$$, obtained by averaging over 100 WT simulations. As the vascular network grows and new sprouts form (see Fig 14C), $$ \mathcal{M}\left(t\right)$$ increases over time.

Fig 14

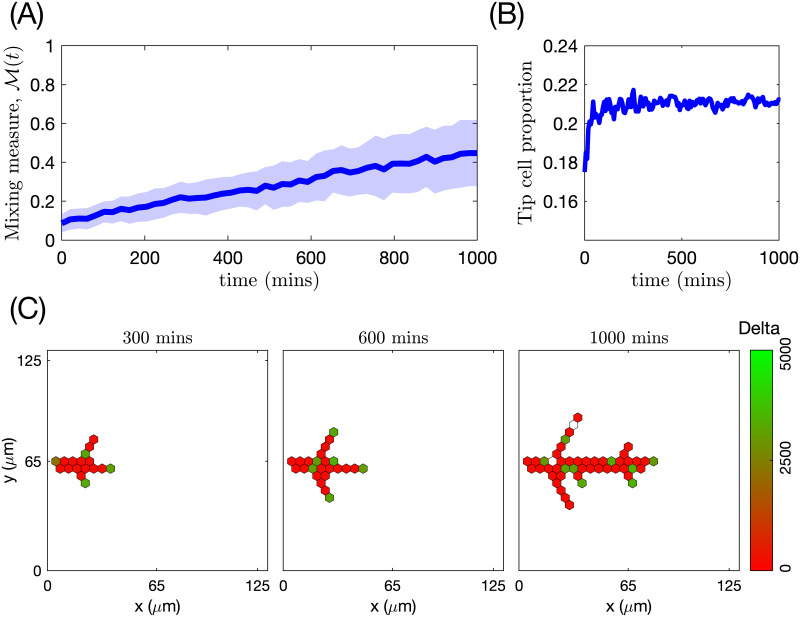
Temporal evolution of mixing measure, tip cell proportion and branching structure in a simulated vascular network formed by WT cells.

(A) The mixing measure, M(t), as a function of time (the mean value is indicated by a thick line and standard deviation is shown by a colour band). The results are averaged over 100 realisations. (B) Evolution of tip cell proportion as a function of time. The results are averaged over 100 realisations. (C) Snapshots from a single realization of our model simulating a vascular network formed by WT cells at 300, 600 and 1000 minutes. Colour bar indicates the level of Delta. The numerical simulation setup used is Setup 1 from S4 Table with final simulation time T_max = 2.5. VEGF distribution was fixed uniformly at 5 ng/ml. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively.

The time evolution of the mixing measure varies for different cell lines. For VEGFR2^+/- mutant cells it increases more slowly (Fig 15A), than for the WT cells (Fig 14A). VEGFR2^+/- mixing arises more from branching than sprout elongation (see Fig 15C). A similar trend is seen for the VEGFR1^+/- cells (compared to WT cells) (Fig 15A). However, contrary to VEGFR2^+/-, this is due to high migration persistence of VEGFR1^+/- ECs (see Fig 15D). A slower increase in the mixing measure for mutant cells correlates with slower stabilisation of tip cell proportion around its steady state in vascular networks formed by mutant cells (see Figs 14B and 15B for WT and mutant cells, respectively). This supports our hypothesis that cell shuffling is directly related to the phenotypic specifications of ECs. Thus, we note that the cell rearrangement phenomenon is not a cell-autonomous decision but rather a result of contact-dependent EC cross-talk, which leads to EC phenotype specification.

Fig 15

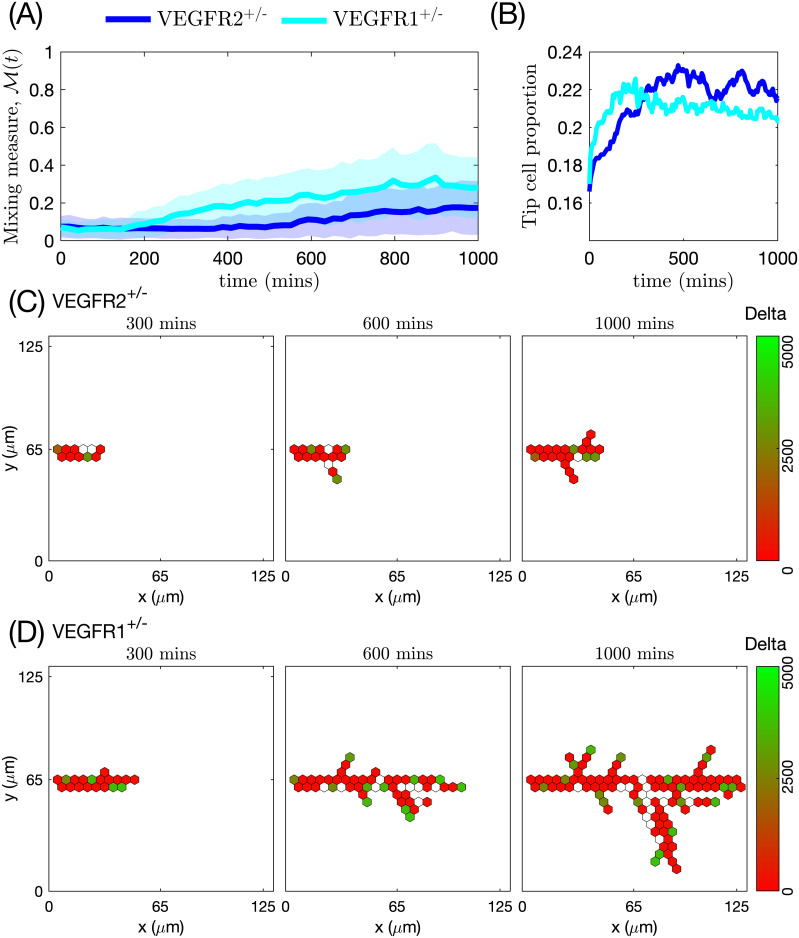
Temporal evolution of mixing measure, tip cell proportion and branching structure in simulated vascular networks formed by VEGFR2^+/-and VEGFR1^+/- mutant cells.

(A) The mixing measure, M(t), as a function of time (the mean value is indicated by a thick line and standard deviation is shown by a band of the corresponding colour). The results are averaged over 100 realisations. (B) Evolution of tip cell proportion as a function of time. The results are averaged over 100 realisations. (C) Snapshots from a single realization of our model simulating a vascular network formed by VEGFR2^+/- mutant cells at 300, 600 and 1000 minutes. Colour bar indicates the level of Delta. (D) Snapshots from a single realization of our model simulating a vascular network formed by VEGFR1^+/- mutant cells at 300, 600 and 1000 minutes. Colour bar indicates the level of Delta. The numerical simulation setup used is Setup 1 from S4 Table with final simulation time T_max = 2.5. VEGF distribution was fixed uniformly at 5 ng/ml. Parameter values are listed in S1 and S2 Tables for subcellular and cellular/tissue scales, respectively, except of those changed for mutant cells (see S1 Appendix).

In all cases, regardless of the cell type and VEGF concentration, the mixing measure increases towards a steady state value (see S8 Fig, left panels). Furthermore, the steady state value of the mixing measure is independent of cell type ($$ \mathcal{M}\left(t\right)\approx 0.385$$ as t → ∞, see S9 Fig). This is a result of the fact that, as the vascular network reaches a sufficient size, cells perform proteolysis-free random shuffling within the manifold of the developed sprouts [52]. The rate of this proteolysis-free random shuffling does not depend on the cell line but rather on the tip-to-stalk ratio in the vasculature, which evolves to a steady state regardless of cell type and VEGF concentration (see S8 Fig, right panels). We conclude that the temporal evolution of the mixing measure characterises the resulting network structure to a larger degree than its steady state.