INTRODUCTION

DNA and RNA have divergent biological roles despite seemingly minor variations in the chemical structures of their nucleotide components. To rationalize this remarkable fact, xeno nucleic acids (XNAs), which consist of chemically modified backbones, are increasingly being explored (1,2). In the origin of life field, XNAs are explored as more primitive, self-assembling polymers (3). XNAs are also being studied in the field of synthetic biology as alternative information carriers capable of evolution (4–6), and are also being pursued for their biomedical and material applications (7–13).

XNAs display a wide range of physical and chemical properties (1,2). For example, glycol nucleic acids (GNA) (14) comprise a flexible three-carbon sugar in the backbone, while the locked nucleic acid (LNA) (15) backbone is highly restrained. Peptide nucleic acids (PNA) (16) have an electrostatically neutral backbone with amide linkages instead of phosphodiester linkage. These variations in the backbone properties drastically impact the structure and stability of XNAs and tune their ability to self-hybridize or to pair with their natural counterparts (1,2). The structures of XNAs vary from those resembling the canonical A- and B-forms of RNA and DNA (2) to those adopting other types of helices, such as the P-helix in PNA (17) and the N- and M-helices in GNA (18). Modifying the nucleobases is another dimension for exploring nucleic acid analogs (8). It ranges from limited alteration of the nucleobases, such as methylating atom 5 in cytosine which occurs naturally (19), to introducing new nucleobases and expanding the genetic alphabet (20,21).

The search for alternative nucleic acids may also be extended to examining the self-assembly of alternative nucleobases or the interaction between natural and synthetic nucleobases. For example, poly-adenosine strands have been shown to self-assemble in the presence of cyanuric acid, in a proposed hexameric pattern (22). Furthermore, alternative nucleobases aminopyrimidine and cyanuric acid, among others, have been shown to self-assemble into hexad structures (23–27). Figure 1 shows various examples of nucleic acid analogs.

Figure 1.

Chemical structures of the canonical and selected alternative nucleic acids. (A) Examples of alternative nucleic acid backbones. (B) The canonical nucleobases and two examples of alternative nucleobases that can be incorporated into a nucleic acid duplex. (C) The hypothetical assembly of three adenosine oligomers and an alternative nucleobase, cyanuric acid, in a hexad geometry. (D) The assembly between oligomers of two alternative nucleobases and the formation of a hexameric structure. (LNA: locked nucleic acid; CeNA: cyclohexene nucleic acid; GNA: glycol nucleic acid; PNA: peptide nucleic acid; P: 6-amino-5-nitro-2(1H)-pyridone; Z: 2-amino-imidazo[1,2-a]-1,3,5-triazin-4(8H)-one; I: cyanuric acid; E: aminopyrimidine).

Many software programs for general analysis and prediction of DNA and RNA structures are available to nucleic acid researchers (28–41). In contrast, computational investigation of alternative nucleic acids has largely been limited to the study of specific XNA systems, e.g. through molecular dynamics simulations (42–54). Broad explorations using coarse grained modeling (55) and chemoinformatic tools (56) have only recently been utilized. However, no general purpose software for modeling alternative nucleic acids is available to the scientific community. The availability of computational tools for modeling alternative nucleic acids will help accelerate the search for viable candidates and guide the experimental and computational design of nucleic acids with desired properties. For example, Open Babel can build DNA and RNA structures with a user-specified number of bases per turn, and using a fixed nucleotide geometry for the canonical nucleobases (57). 3DNA can construct various pre-defined nucleic acid models (34). It can also construct sequences of nucleobases with user-defined helical parameters and an approximate DNA or RNA backbone. The Nucleic Acid Builder is a language that can be used to construct complex nucleic acid structures (58). However, these tools are designed for modeling DNA and RNA and do not support the modeling of nucleic acid analogs.

In this article, we present the proto-Nucleic Acid Builder (pNAB), a free and open-source software tool for constructing alternative nucleic acid structures with arbitrary backbone-nucleobase combinations (available at: https://github.com/GT-NucleicAcids/pnab). The key feature of the proto-Nucleic Acid Builder is the addition of a backbone candidate onto a pre-existing core of nucleobases (or their analogs). The initial construct is further subjected to a structural optimization through a conformational search, and a discrimination of the backbone candidate. Thus, the construction of the polymers might be viewed as being ‘inside-out’, allowing for various backbones to be attached to the same core of the stacked nucleobases (or their analogs).

The program constructs nucleobases with user-defined helical parameters. It then performs a conformational search over non-restricted dihedral angles of the putative nucleic acid backbone to find conformations compatible with the helical structures using one of several available search algorithms. General force fields are used to evaluate the energies of proposed nucleic acid candidates. We discuss the algorithm and software implementation, and then present a few examples of the utility of the program for constructing structures of nucleic acid analogs. We show that the program can reasonably reproduce experimental structures and can correctly predict expected trends for the correlation between the helical configurations of DNA and RNA and their backbone conformations.

MATERIALS AND METHODS

The general algorithm is illustrated in Figure 2A. Details on the search algorithm are available in the Supplementary Information (SI). Briefly, the user provides the three-dimensional (3D) chemical structures of the building blocks for the polymers (nucleobases or their analogs and putative backbone linkers) as input and indicates the linking atoms (Supplementary Figure S-1). The user also defines fixed and variable helical parameters that describe the orientation of nucleobases in nucleic acid strands (59–61) (Supplementary Figure S-2) and can optionally fix any torsion in the backbone. Lastly, the user specifies the conformational search algorithm options, the desired sequence, and the number of strands. The program then initiates a torsion-driven search for backbone conformations that are compatible with the given helical configuration. Once a plausible backbone conformer is obtained, the program generates a 3D structure of an oligomer (of a given length and sequence) and evaluates its energy. The methodology can be used to construct single-stranded and duplex structures as well as more complex structures up to hexads.

Figure 2.

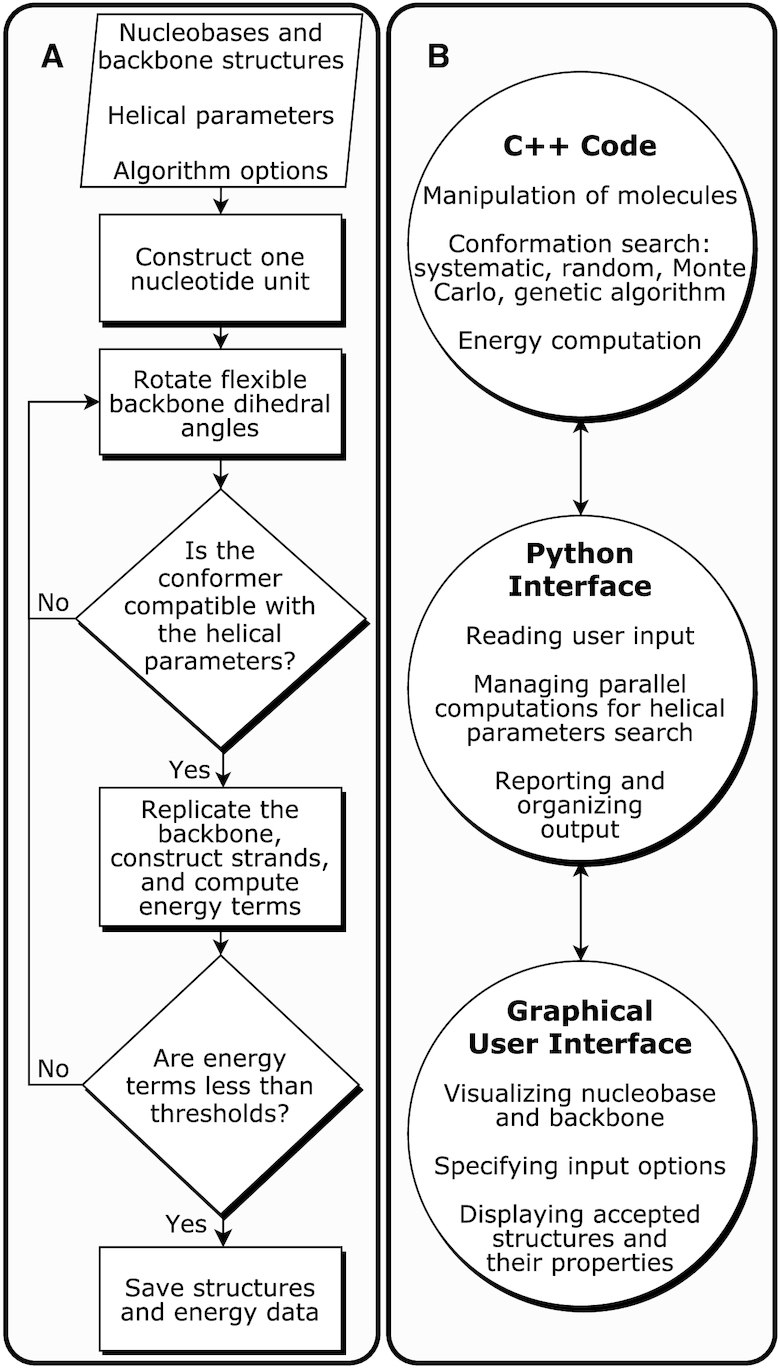
(A) The algorithm implemented within the Builder for predicting alternative nucleic acid structures. (B) The architecture of the proto-Nucleic Acid Builder software.

Several torsion-driven conformation search algorithms are implemented in the program, including the systematic, random, Monte Carlo, and genetic algorithms (62). General force fields are used to evaluate the energy of plausible candidates (63,64). Candidates are accepted or rejected depending on whether they satisfy five energy terms: The energy of (i) the bonds and (ii) angles between the nucleotides; (iii) the energy of flexible torsions in the backbone; (iv) the van der Waals energy of the whole system; and (v) the total energy of the whole system.

The main limitation of the algorithm is that the program can only generate a regular structure with identical helical parameters and backbone conformations across the strand. Thus, it is not possible to generate irregular helical structures with the current program. Additionally, effective sampling of the backbone conformation is limited to a small number of rotatable dihedral angles in the backbone.

SOFTWARE IMPLEMENTATION

The proto-Nucleic Acid Builder is a free and open-source program licensed under the GNU GPL license. It is available in the public GitHub repository at https://github.com/GT-NucleicAcids/pnab, which includes the source code, code documentation, and a user manual. The program can be installed using the conda package manager, and all the dependencies can be satisfied through conda. It is available for the Linux, MacOS, and Windows operating systems. The program provides a library of the coordinates of the canonical nucleobases in their standard frame of reference and the coordinates for the canonical DNA and RNA backbones. It also provides coordinates for the non-canonical nucleic acids discussed below. Example input files to generate the structures discussed below are also included with the package. Users can use an online server for trying the package or quickly constructing starting models without having to install the program.

As shown in Figure 2B, the program consists of three components: (i) A C++ library for the manipulation of the molecules and computation of energies, utilizing tools from the Open Babel program (57), (ii) A Python library for managing the computations and reporting the results, interfaced with the C++ code using pybind11 (65) and (iii) a Jupyter notebook (66) graphical user interface for specifying user-input and visualizing the results, utilizing the NGLView library (67) (Supplementary Figure S-3). The graphical interface can be tried online using the binder project (68). Details on these three components are available in the SI.

RESULTS AND DISCUSSION

Here we present proto-Nucleic Acid Builder modeling results for DNA and RNA, as well as for several non-canonical nucleic acid analogs. The chemical structures of the monomers used for the example calculations are provided in Figure 1. The majority of examples presented here can be compared against experimentally determined structures that are available in the Protein Data Bank (69). We have tested and benchmarked various backbone torsion search algorithms for their efficiency and accuracy. Structures generated by the Builder were superimposed with the experimental structures, when available, using the PyMol program (70). Images were generated using the VMD program (71). Input files to generate these structures are included with the package. Overall, the results of modeling demonstrated that the Builder is capable of sampling the backbones and generating the oligomeric structures with a good accuracy against the experimental structures. Thus, the modeling capabilities can potentially be expanded to building blocks consisting of arbitrary nucleobases and backbone linkages with random nucleobase sequences.

We also performed an in-depth examination of the conformational searches for the canonical RNA and DNA, and explored the sampling of various helical parameters for these two systems and the role of the geometrical constraints imposed by the sugar puckers of the (deoxy-)ribose phosphate backbone linker. Our results show the significant effect of the input sugar pucker on the final conformation of the output backbone. The correlation between the pucker and the overall helical conformation (A- or B-forms) indicates a strong coupling between the backbone and helical parameters. Additionally, we modeled two examples of non-conventional nucleic acid analog structures that have been proposed to adopt a hexad geometry (Figures 1C and D).

For comparing the conformation search algorithms, we have used the systematic search algorithm with a 2° angular resolution to exhaustively sample the backbone conformations. For the other search algorithms, we terminated the search after 10⁸ steps. The running time can take from seconds to hours depending on the search algorithm and the system. Identical energy and distance criteria were used for all the search algorithms, and all the conformations that have satisfied the criteria, whose numbers vary depending on the algorithm, were stored and analyzed. Supplementary Table S-1 lists the force field and the distance and energy thresholds used for the various systems. The total energy threshold was set to a large value in all cases. The thresholds for a given force field were kept identical across the various systems to illustrate the impact of the threshold on accepting candidates of different systems. The torsional threshold for PNA was increased because it has more flexible torsions in the backbone than other systems. Benchmarking the performance of the various search algorithms in terms of the number of conformation search steps required for finding acceptable candidates is shown in Supplementary Figure S-4.

Predicting the helical structures of DNA and RNA

We first analyze the conformations predicted by the proto-Nucleic Acid Builder for the canonical B-DNA and A-RNA structures (Figure 3). A fixed set of helical parameters corresponding to the canonical DNA and RNA structures are used in this example. The polar plots (Figures 3B and D) show the distribution of unrestricted torsional angles of the backbone in the accepted candidates sampled during the conformation search using a variety of conformational search algorithms. As can be seen from the polar plots, all search algorithms converge to the same set of solutions, but with a varying number of accepted candidates found in the specified number of steps. Such a convergence in the solutions obtained by various methods illustrates that the torsion-driven approach is robust and suitable for finding plausible backbone conformations, provided that suitable energy thresholds are chosen. It also shows that alternative search algorithms can be used instead of the more demanding systematic search algorithm. Furthermore, as the backbone conformations are similar in the accepted candidates when only one family of solutions is accessible (e.g. Figure 3B), users might find it sufficient to terminate the search after finding a few candidates or to lower the number of conformation search steps.

Figure 3.

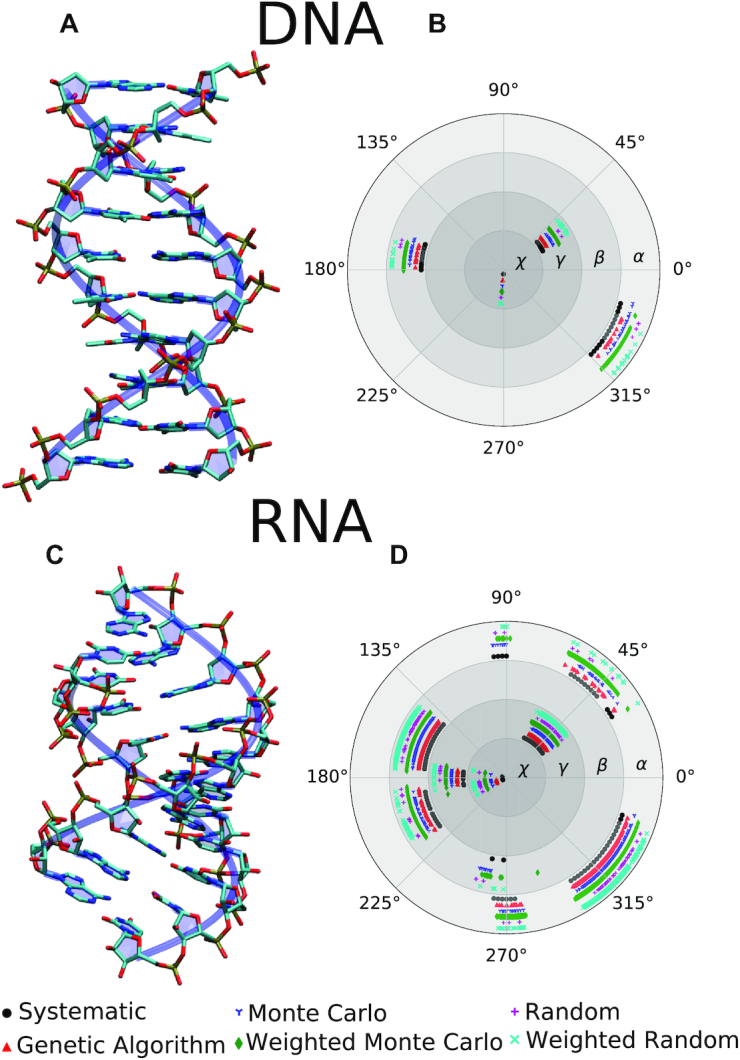
DNA and RNA structures. Panels (A) and (C): Predicted structures for the B-DNA and A-RNA conformations, respectively. The displayed structures for DNA and RNA represent one example out of the many possible structures shown in panels (B) and (D). Panels (B) and (D): Polar plots displaying the distribution of rotatable torsional angles in the backbone for the accepted candidate structures obtained using various conformation search algorithms. The lack of points for a given algorithm indicates its failure to find a solution in the specified number of steps. The angles are defined in Supplementary Figure S-1.

Notably, the polar plots also show the varying flexibility of the backbone torsional angles. For both DNA and RNA, the glycosidic torsion χ (see Supplementary Figure S-1) is the most constrained angle, as it largely determines the orientation of the nucleic acid backbone (72). The program has identified multiple discrete families of solutions for the torsional angles of RNA for the given energy thresholds. The variations in acceptable dihedral angles can be controlled by tightening the energy thresholds, if desired.

Having confirmed that the search algorithms were reliable for predicting the backbone structure for B-DNA and A-RNA when the nucleobase helical parameters are known, we tested the potential for the Builder to correctly predict the helical parameters of nucleic acids based on only the conformational compatibility between the nucleobase orientation and the backbone conformation. To evaluate this potential capability, we performed a helical parameter search for the DNA and RNA helical structures using (deoxy-)ribose-phosphate backbones with various sugar puckers. DNA and RNA are intrinsically optimized to adopt the canonical B- and A-forms, in which the sets of the helical parameters and the backbone conformations are mutually consistent. RNA has a strong preference for the A-form, and DNA is predominantly found in the B-form but can also adopt the A-form.

The backbone of both the A- and B-forms contains deoxyribose in two distinct conformations determined by the sugar pucker: C3′-endo for the A conformation and C2′-endo for the B conformation. As the dihedral angle δ is excluded from the rotomeric search algorithms due to the structural constraints, the (deoxy-)ribose-phosphate backbone is supplied to the Builder in a given pucker state that cannot be altered upon simulations. In terms of the helical parameters, these two forms are predominantly discriminated by three parameters: the helical rise, x-displacement and inclination. Therefore, we included these parameters as searchable variables, while the y-displacement, helical twist, tip, and base-pair parameters were assigned the middle values between the A-form and B-form of DNA as reported previously (60), and remained constant. For each combination of rise, x-displacement and inclination, we supplied a backbone candidate with a fixed sugar pucker and performed a conformation search using the systematic search algorithm with a 2° step size. Duplex structures with d(CGTA)₂ sequence for DNA and r(CGUA)₂ sequence for RNA were analyzed.

As shown in Figure 4, the DNA helical structure is highly sensitive to the type of sugar pucker used for deoxyribose (C2′-endo versus C3′-endo). Using the two different sugar puckers, we find accepted candidates that are clustered around the A-form or the B-form depending on the sugar pucker, with a greater flexibility for the C2′-endo pucker. As a characteristic difference between the A- and B-forms, the glycosidic angle χ, shown in the color plot, varies from approximately −90 to −190° for the B- and A-forms, respectively. These observations agree with experimental x-ray structures obtained for the DNA transition from the B- to A-form (73). Indeed, the χ angle has been shown to vary continuously from roughly −80° to −180° as DNA transitions from the B-form to the A-form. This change in the torsional angle is accompanied by a change in the pucker state from C2′-endo to C3′-endo through intermediate O4′-endo states (73). The coupling between χ and the helical parameters has also been observed previously (72). Compared to DNA, RNA adopts a far more restricted helical parameter space for the same energy thresholds and sugar pucker conformation. Our previous work on the energetics of DNA and RNA nucleobase stacking interactions has indicated the greater influence of the RNA backbone compared to the DNA backbone in dictating the helical structures adopted by these nucleic acids (74).

Figure 4.

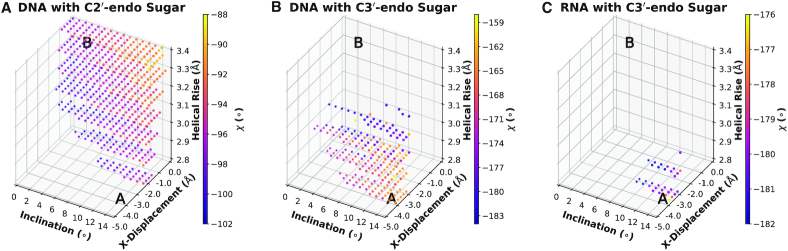
Helical parameter search for DNA and RNA over the helical rise, x-displacement, and inclination with two sugar puckers. Each dot corresponds to an accepted candidate. The color of the dots indicates the value of the glycosidic bond torsion χ for the accepted candidate. The energy thresholds are 0.5, 2.0, 3.5 and 30 kcal mol⁻¹ nucleotide⁻¹ for the bond, angle, torsion and van der Waals terms, respectively.

Overall, this example shows that by simple consideration of van der Waals contacts and the energies of key covalent bonds and torsional angles, the Builder can provide significant limits on the space of acceptable structures for nucleic acid backbones, and in doing so potentially find sets of mutually compatible helical parameters for the nucleobase core and the backbone conformation that, at least in the case of DNA and RNA, are consistent with known experimental structures. The spread of DNA structures can be further limited by tightening the energy thresholds. The precise ranking of the structures in terms of the total energy of the conformers may require specialized force fields and more advanced simulations.

Predicting duplex structures of nucleic acid analogs

We further modeled and analyzed several XNA structures and one example of an RNA:XNA duplex as depicted in Figure 5. Each of these structures contains a set of canonical nucleobases and a modified backbone. The backbone modifications range from substituting a hydroxyl group by a fluoro group in FRNA, to replacing the sugar in LNA and CeNA, to replacing the entire sugar-phosphate backbone in PNA. For these models, the helical parameters for the nucleobases were taken from the experimental structure and the Builder was used to find favorable backbone solutions. In all cases, the predicted and experimental structures have good agreement (RMSD < 1.0 Å). The FRNA polar plot shows discrete families of acceptable backbone conformations and a wide range of accessible dihedral angles. In contrast, LNA, which has a constrained sugar, shows a narrow window of acceptable backbone orientations for the same energy thresholds. The energy thresholds can be tuned to refine the space of accessible configurations and to determine the most plausible backbone conformations.

Figure 5.

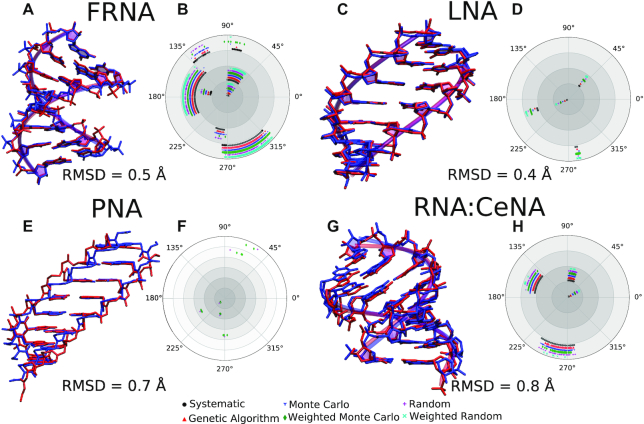
XNA structures. Panels (A), (C), (E) and (G): Experimental structures for FRNA duplex (PDB: 3P4A) (75), LNA duplex (PDB: 2X2Q) (76), PNA duplex (PDB: 3MBS) (77) and RNA:CeNA duplex (PDB: 3KNC) (78), respectively, are superimposed with the structures generated by the program with the indicated RMSD values. The theoretical structure with the lowest total energy is used for comparison. The theoretical and experimental structures are blue and red, respectively. Panels (B), (D), (F) and (H): Polar plots displaying the distribution of rotatable torsional angles in the backbone obtained using various conformation search algorithms. For the RNA:CeNA structure, the distribution is shown for the CeNA strand. The lack of points for a given algorithm indicates its failure to find a solution in the specified number of steps.

Unlike the other examples which have four rotatable torsions in the backbone, PNA contains seven rotatable bonds, posing a challenge for the conformational search algorithms. For example, a dihedral step size of 2° would require 6 × 10¹⁵ steps to systematically sample the entire torsional space for this system, which is impractically large. In such cases, the program allows users to fix certain dihedral bonds in the backbone (e.g. the amide bond in the PNA backbone, which is known to have values around 180°). Furthermore, the alternative conformation search algorithms outlined previously can be used to sample dihedral conformations more efficiently. In contrast to other systems, the large number of independent search parameters (or degrees of freedom) in PNA results in the failure of several algorithms to find backbone candidates in the specified number of steps (10⁸). Consequently, a longer search is required for systems with large numbers of rotatable bonds in the backbone, such as PNA, to effectively sample the conformation space.

Finally, we have also modeled a hetero-duplex between CeNA and RNA, which is shown in Figure 5G. The program does not currently support directly building hetero-duplexes because this requires simultaneous conformation search for two different backbones. However, the program allows users to choose whether to build the primary strand only or the complimentary strand only. Thus, users can easily construct hetero-duplexes by combining the geometry of one strand with the geometry of the complimentary strand with a different backbone. Energy evaluations for the two strands are performed independently. Even with this less automated approach, the RMSD between the modeled and the experimental structures is only 0.8 Å.

Figure 6 shows nucleic acid structures with modified or alternative nucleobases. The 5MC structure (panels A and B) shows a system where cytosine is replaced by 5-methylcytosine in a DNA duplex. The ZP structure (panels C and D) shows a DNA duplex where six of the base pairs are formed by the non-canonical nucleobases Z and P. The energy thresholds used for ZP (Supplementary Table S-1) appear to be too tight, so that even the systematic search with a 2° resolution fails to find accepted candidates. Increasing the angular resolution to 1°, which corresponds to a 16-fold increase in the number of grid points for the ZP system with 4 degrees of freedom, enables the program to find acceptable candidates using the systematic search algorithm as shown in Supplementary Figure S-5. This particular test case illustrates that the energy thresholds are system-dependent and highlights the effectiveness of alternative search algorithms in finding acceptable backbone conformations.

Figure 6.

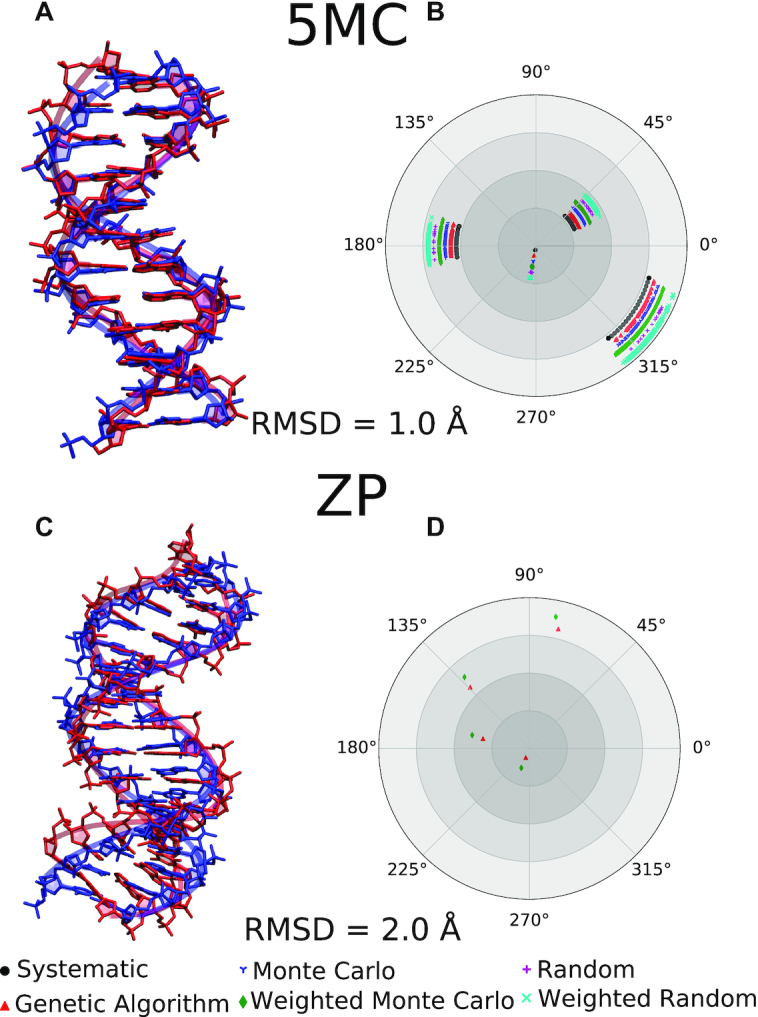
Nucleic acid structures with alternative nucleobases. Panels (A) and (C): Experimental structures for a DNA containing 5-methylcytosine, 5MC, (PDB: 4GJU) (79) and Z-P base pairs (PDB: 4XNO) (21), respectively, are superimposed with the structures generated by the program with the indicated RMSD values. The theoretical structure with the lowest total energy is used for comparison. The theoretical and experimental structures are blue and red, respectively. Panels (B) and (D): Polar plots displaying the distribution of rotatable torsional angles in the backbone obtained using various conformation search algorithms. The lack of points for a given algorithm indicates its failure to find a solution in the specified number of steps.

Predicting hexameric structures

In addition to the standard single-stranded and double-stranded geometries, the program can build more complex assemblies containing multiple strands, up to a hexad. Here we demonstrate the constructions of such assemblies by modeling two systems that were proposed to adopt a hexameric geometry (Figure 7). Unlike for the double stranded examples, considered above, the helical parameters of the hexads only contain two variables (twist and rise) due to their intrinsic symmetry. Since the rise parameter is determined by the stacking interactions, it was maintained constant at a value of 3.4 Å throughout all hexad simulations. Thus, only the dihedral angles of the backbone and the helical twist were optimized during the conformational searches performed on the hexad systems. In the first example, we build a polymer illustrating the self-assembly of three poly-adenosine strands in the presence of an intermediary molecule, cyanuric acid, a pattern proposed previously (22). In the second example, we report a plausible structure for a hexameric polymer that has been proposed as a precursor to modern RNA and DNA (26).

Figure 7.

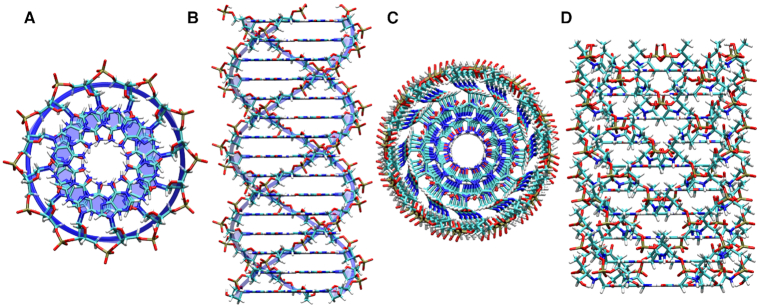
Hexameric nucleic acid structures. (A) Top and (B) side views of the hexad structure depicted in Figure 1C with three adenosine oligomers with a DNA backbone interacting with cyanuric acid nucleobases. (C) Top and (D) side views of the hexad structure depicted in Figure 1D constructed by cyanuric acid and aminopyrimidine with an acyclic threoninol nucleic acid backbone.

Panels A and B of Figure 7 show a system consisting of an adenosine oligomer interacting with cyanuric acid in a hexad geometry. We probed a deoxyribose-phosphate in a B-DNA sugar pucker conformation as a possible backbone candidate. While the program is designed to generate oligomeric strands, it can be ‘tricked’ to build systems with mixed oligomers and free nucleobases. In this example, the geometry of an adenine–cyanuric acid base pair was provided instead of providing the geometries of adenine and cyanuric acid independently. In turn, the program was instructed to build every other strand.

Panels C and D of Figure 7 show top and side views of hexameric oligomers of cyanuric acid and aminopyrmidine with a threoninol nucleic acid backbone. When we replaced aminopyrmidine with 2,4,6-triaminopyrimidine, we noticed some increase in the steric repulsion between the base and the backbone due the proximity of the amino groups to the backbone. The calculations indicated the preference for forming a helical structure, as the program did not find any solution around zero twist angle.

CONCLUSION

The current work describes the proto-Nucleic Acid Builder (pNAB), a free and open-source program for constructing nucleic acid analogs. The program is aimed to generate all-atom 3D models for canonical or alternative nucleic acids, with periodic helical parameters and backbone conformations, for arbitrary backbone/nucleobase combinations. The program is written in C++ and Python and has a graphical user interface utilizing the Jupyter notebook. It can be accessed online at https://github.com/GT-NucleicAcids/pnab, and it can be used in the Windows, MacOS and Linux platforms.

Several examples have also been provided that demonstrate modeling of the 3D structures for the canonical DNA and RNA as well as for duplexes of various nucleic acid analogs with varying backbones, base sequences and helical parameters. Nucleic acids with modified nucleobases or with an expanded set of non-canonical nucleobases can also be generated by the Builder. Additionally, 3D models for nucleic acids analogs with alternative topologies, such as hexad-based polynucleotides, can be constructed within the framework of the program. The predicted structures agree well with the experimentally reported structures (when available), demonstrating that the torsion-driven approach adopted in the conformation search algorithms is reliable in predicting correct backbone conformations.

In-depth simulations on the RNA and DNA systems, for which the backbone and helical parameters are tightly coupled, demonstrated a proper selection of the helical parameters for a given state of the sugar pucker of the (deoxy)ribose phosphate backbone. Thus, by examining the structure of DNA using two different sugar puckers (from the canonical A- and B-forms) and at varying helical configurations, the Builder obtained the conformations where the values for the helical parameters, the glycosidic torsion χ (characteristic for the A- and B-forms), and the sugar pucker are mutually consistent. Thus, the program can correctly predict accessible helical and backbone conformations.

As research on alternative nucleic acids advances, the Builder is intended to provide a service to the community of theoretical and experimental chemists to facilitate the exploration of nucleic acid analogs (XNAs). Specifically, researchers in the fields of origins of life and synthetic biology should find the Builder valuable for initial ‘in silico’ construction of 3D structures for alternative informational polymers to predict their feasibility for adopting stable helical structures before investing substantial experimental resources. Computational chemists can use the Builder to generate initial models and test their stability using more advanced MD simulations. Educators can also use this program for visualizing the helical structures of DNA and RNA and other alternative nucleic acid systems. Overall, this program can highlight the factors governing the stability of DNA, RNA and nucleic acid analogs, and can likely accelerate the search for novel nucleic acid analogs with desired properties.

DATA AVAILABILITY

The code and example input files are available at: https://github.com/GT-NucleicAcids/pnab.