Introduction

There are several different settings for the compatibility of states, measurements, and channels that are considered in this paper. The interested reader is referred to the reviews in refs. ^1–4 for further discussions on these topics.

The quantum state marginal problem ^5–8 is one of the most fundamental problems in quantum theory and quantum chemistry. One version of this problem is the following problem. Given a collection of systems $$ {\mathcal{X}}_1,\dots ,{\mathcal{X}}_n$$ and a collection of density operators ρ₁, …, ρ_m—each acting on some respective subset of subsystems $$ S_1,\dots ,S_m\subseteq {\mathcal{X}}_1\otimes \cdots \otimes {\mathcal{X}}_n$$—determine whether there exists a state ρ on $$ {\mathcal{X}}_1\otimes \cdots \otimes {\mathcal{X}}_n$$ which is consistent with every density operator ρ₁, …, ρ_m. For example, if ρ₁ acts on S₁, then ρ must satisfy

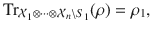
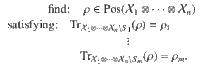
Note that the condition that ρ has unit trace is already enforced by the constraints. In the case where the systems $$ {\mathcal{X}}_2=\cdots ={\mathcal{X}}_n$$ and density operators σ: = ρ₂ = ⋯ = ρ_n are identical (where we omit ρ₁ for indexing convenience), we remark that, for the choice of subsystems $$ S_i={\mathcal{X}}_1\otimes {\mathcal{X}}_i$$ for each i ∈ {2, …, n}, one obtains the so-called (n − 1)-symmetric-extendibility condition for σ. This is closely related to separability testing ¹¹.

There is an analogous task for quantum measurements called the measurement compatibility problem (see ^12,13 for POVMs (positive operator-valued measures) and ^14,15 for the special case of qubits). This task can be stated as follows. Two POVMs {M₁, …, M_m} and {N₁, …, N_n} are said to be compatible if there exists a choice of POVM {P_i,j: i ∈ {1, …, m}, j ∈ {1, …, n}} that satisfies

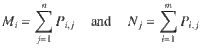
Determining the compatibility of the two POVMs above can be solved via the following semidefinite programming feasibility problem:

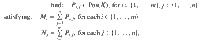
This notion of compatibility for measurements generalizes the concept for commuting measurements. Indeed, if [M_i, N_j] = 0 holds for each choice of indices i and j then the measurement operators P_i,j defined as P_i,j = M_iN_j form a compatibilizing POVM. This does not hold generally, as the operators M_iN_j need not even be Hermitian if M_i and N_j do not commute. Nevertheless, one can study Hermitian versions of these matrices using Jordan products, as is discussed below.

The Jordan product of two square operators A and B is defined as

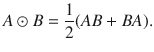
This is Hermitian whenever both A and B are Hermitian. The Jordan product can be used to study the compatibility of measurements (see ^24,25). In particular, for POVMs {M₁, …, M_m} and {N₁, …, N_n}, note that the operators defined as

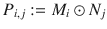
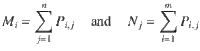
Before discussing the quantum channel marginal problem, we take a slight detour and discuss the no-broadcasting theorem. A quantum broadcaster for a quantum state $$ \sigma \in \mathrm{Pos}\left(\mathcal{X}\otimes \mathcal{Y}\right)$$ is a channel that acts on the $$ \mathcal{X}$$ subsystem of σ and outputs a state $$ \rho \in \mathrm{Pos}\left({\mathcal{X}}_1\otimes {\mathcal{X}}_2\otimes \mathcal{Y}\right)$$ that satisfies

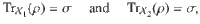
The task of determining compatibility of quantum channels, which has been studied recently (see, e.g. ^31–35), can be stated as follows. Given two quantum channels, Φ₁ from $$ \mathcal{X}$$ to $$ {\mathcal{Y}}_1$$ and Φ₂ from $$ \mathcal{X}$$ to $$ {\mathcal{Y}}_2$$, one determines if there exists another channel Φ from $$ \mathcal{X}$$ to $$ {\mathcal{Y}}_1\otimes {\mathcal{Y}}_2$$ that satisfies

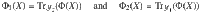
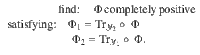
The condition that Φ is trace-preserving follows from the constraints. The channel compatibility problem (in either the no-broadcasting formulation or in the general form given in Eq. (10)) is an essential component of research in quantum cryptography. For example, if two parties, say Alice and Bob, decide to communicate via some channel Φ₁, an eavesdropper Eve may use any channel Φ₂ compatible with Φ₁ to obtain partial information about the communication between Alice and Bob.

To see how the channel and state versions of the marginal problem are generalizations of each other, we may consider the Choi representations of the channels. It is not hard to see ^32,36 that the conditions for the compatibility of Φ₁ and Φ₂ is equivalent to the following conditions on the Choi matrices:

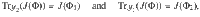
To see how the channel compatibility problem is a generalization of the measurement compatibility problem, consider the following reduction. For the POVMs {M₁, …, M_m} and {N₁, …, N_n}, define the channels

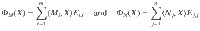
The result above also holds in more general settings. In particular, a similar result holds for measure-and-prepare channels in the case when the choice of state preparations are distinguishable. However, if the preparations are chosen in a general way, then this equivalence breaks down. To be precise, consider the channels defined as

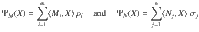
Another notion of channel compatibility that we consider in this paper concerns the case when Φ₁ = Φ₂ = Φ for some fixed channel Φ (i.e., when the channels are the same). A channel Φ that is compatible with itself is said to be self-compatible.

One may also consider—for some other positive integer k > 2—whether some choice of k channels Φ₁, …, Φ_k are compatible. If k copies of some fixed channel are compatible—i.e., Φ₁ = ⋯ = Φ_k = Φ are all equal to some fixed channel Φ—then we say that Φ is k-self-compatible.

In this work, we prove several results about channel compatibility. First, we show that the channel compatibility problem is equivalent to the quantum state marginal problem, i.e., every quantum state marginal problem can be recast as the compatibility of two channels, and vice versa. Second, we show that compatible measure-and-prepare channels (i.e., entanglement-breaking channels) do not necessarily have a measure-and-prepare compatibilizing channel. Third, we extend the notion of the Jordan product of matrices to quantum channels and present sufficient conditions for channel compatibility. These Jordan products and their generalizations might be of independent interest. Lastly, we formulate the different notions of compatibility as semidefinite programs and numerically test when families of partially dephasing-depolarizing channels are compatible.

Results

We examine the quantum channel marginal/compatibility problem using several different perspectives. Here we provide an overview of our results, which are stated in an informal manner. Precise definitions and theorem statements can be found in Supplementary information.

On the compatibility of measure-and-prepare

We first note that every measure-and-prepare (i.e., entanglement-breaking) channel is self-compatible. Indeed, for measure-and-prepare channel Φ there exists a POVM {M₁, …, M_m} and a collection of density matrices ρ₁, …, ρ_n such that

for all X. Now consider the channel

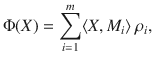
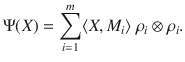
This channel clearly compatibilizes two copies of Φ. (Moreover, one can easily modify Ψ above such that it compatibilizes k copies of Φ. Hence every measure-and-prepare channel is also k-self-compatible for all k.)

The task of determining whether two distinct measure-and-prepare channels Φ₁ and Φ₂ are compatible, however, is not so straightforward. From the discussion in the previous paragraph, if Φ₁ and Φ₂ are expressed as measure-and-prepare channels such that the prepared states are distinct computational basis states, it can be seen that the notion of channel compatibility is equivalent to that of measurement compatibility. However, this is not the case for all measure-and-prepare channels. For instance, there may be multiple ways to express the measurements and/or preparations for a particular measure-and-prepare channel. One might guess that any channel which compatibilizes two measure-and-prepare channels must also be measure-and-prepare and can only exist if all three sets of measurements satisfy some conditions. However, we show that this is not the case, as described below. Note that similar result was also recently obtained in a different context in ³⁷.

Result 2 (See Supplementary Note 3 for details.) There exists a pair of compatible measure-and-prepare channels with no measure-and-prepare compatibilizer.

The two channels were found using semidefinite programming formulations of channel compatibility and the notion of positive partial transpose (PPT).

Jordan products of quantum channels

The Jordan product of two channels, Φ₁ from system $$ \mathcal{X}$$ to system $$ {\mathcal{Y}}_1$$ and Φ₂ from $$ \mathcal{X}$$ to $$ {\mathcal{Y}}_2$$, is the linear map Φ₁ ⊙ Φ₂ from the system $$ \mathcal{X}$$ to the system $$ {\mathcal{Y}}_1\otimes {\mathcal{Y}}_2$$ whose Choi representation is given by

where E_i,j is the matrix whose (i, j)-entry is 1 and has zeros elsewhere, i.e., one can also think of E_i,j as $$ ∣i⟩⟨j∣$$ in Dirac notation, and ⊙ on the right-hand side denotes the Jordan product of matrices as defined in Eq. (5). It is straightforward to see that the map Φ = Φ₁ ⊙ Φ₂ satisfies

for every choice of X. The map Φ₁ ⊙ Φ₂ might not be completely positive, as the corresponding Choi representation in Eq. (16) might not be positive semidefinite. However, if Φ₁ ⊙ Φ₂ is completely positive—and thus a channel, since it is trace-preserving by Eq. (17)—then this linear map is a compatibilizing channel for the channels Φ₁ and Φ₂. The condition that Φ₁ ⊙ Φ₂ be completely positive is therefore a sufficient condition for the channels Φ₁ and Φ₂ to be compatible. If Φ₁ ⊙ Φ₂ is not completely positive, one can use the lowest eigenvalue of the Choi matrix of Φ₁ ⊙ Φ₂ to estimate the amount of noise needed to add to the channels Φ₁ and Φ₂ to make them compatible. This amount of noise is closely related to the resource theory of compatibility and to the robustness of incompatibility of quantum channels ³⁸. One may also use the equivalence of the channel compatibility and quantum marginal problems from Result 1 to apply the Jordan product to the quantum marginal problem.

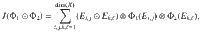
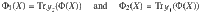
It is known that for projection-valued measures (PVMs)—that is POVMs where every operator is a projection—the Jordan product provides a necessary and sufficient condition for the compatibility of a PVM with any POVM ²⁶. It is therefore natural to consider whether the Jordan product of channels similarly provides necessary and sufficient conditions for a PVM-measurement channel to be compatible with another arbitrary channel. Namely, for a PVM {Π₁, …, Π_m}, let Δ_Π be the corresponding measurement channel defined as

for every choice of X. One may ask whether complete positivity of the Jordan product Δ_Π ⊙ Φ is always equivalent to the compatibility of Δ_Π and Φ, for any other choice of channel Φ. This is indeed the case, as described below.

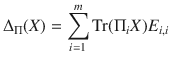
Result 3 (Informal, see Supplementary Note 4 for a formal statement.) Δ_Π is compatible with Φ if and only if Δ_Π ⊙ Φ is completely positive.

To tackle more general cases, we describe how to relax the sufficient condition that the Jordan product be completely positive. Note that the Choi representation of the Jordan product as provided in Eq. (16) can be expressed as

where A_JP is the Choi representation of the Jordan product of two identity channels. By replacing A_JP in Eq. (19) with another matrix $$ A\in \mathrm{Herm}\left(\mathcal{X}\otimes {\mathcal{X}}_1\otimes {\mathcal{X}}_2\right)$$ satisfying

one obtains another linear map—which we denote by Φ₁ ⊙ _AΦ₂. Each such matrix A provides another potential compatibilizing channel, so long as the corresponding map Φ₁ ⊙ _AΦ₂ is completely positive. If there exists at least one choice of Hermitian matrix A satisfying Eq. (20) such that the map Φ₁ ⊙ _AΦ₂ is completely positive, we say that the channels are Jordan compatible. What is surprising is that this sufficient condition is also necessary in most cases, as described in the following two results.

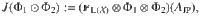
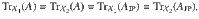
Result 4 (Informal, see Supplementary Note 4 for a formal statement.) If the channels Φ₁ and Φ₂ are invertible as linear maps, then they are compatible if and only if they are Jordan compatible. (Note that the inverses do not have to be quantum channels themselves.)

The requirement that both channels are invertible is not too restrictive, as indicated by the following result.

Result 5 (Informal, see Supplementary Note 5 for a formal statement.) The set of Jordan-compatible pairs of channels has full measure as a subset of all compatible pairs.

Semidefinite programs for channel compatibility

The task of determining whether two channels Φ₁ and Φ₂ are compatible can be formulated as the following semidefinite programming feasibility problem:

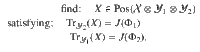
This formulation can be found by using the Choi representations of each channel and their compatibilizer (where X is the Choi representation of the desired compatibilizer).

The Jordan-compatibility of two channels can be similarly determined via the following semidefinite programming feasibility problem:

where A_JP is the matrix as determined in the discussion around Eq. (19).

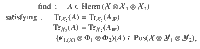
The formulation in Eq. (21) has the advantage of being linear in the Choi representations of the channels—one could therefore keep them as variables and impose affine constraints on the channels. As a concrete example, one may ask whether there exist two qubit-to-qubit channels that are compatible and both unital. (We know that two identity channels do not satisfy these two conditions, but an identity channel and a completely depolarizing channel does.)

We use duality theory to show a few theorems of the alternative for the cases of compatibility and Jordan compatibility. For an example, we present one of the two versions for compatibility, below.

Result 6 (Informal, see Supplementary Note 6 for a formal statement.) Φ₁ and Φ₂ are compatible if and only if there does not exist Z₁ and Z₂ such that

(Note that we define formally what the adjoint of the partial trace is later, but for now it can simply be viewed as a linear map.)

Numerically testing qubit-to-qubit channels

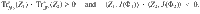
We test various notions of compatibility for certain classes of qubit-to-qubit channels using the semidefinite programming formulations shown above. The family of channels that we consider are the partially dephasing-depolarizing channels defined as

for parameters p, q ∈ [0, 1]. Here $$ {\mathbb{1}}_{\mathrm{L}\left(\mathcal{X}\right)}$$ is the identity channel, Δ is the completely dephasing channel, and Ω is the completely depolarizing channel, which are defined by the equations

holding for all operators X, where $$ {\mathbb{1}}_{\mathcal{X}}$$ is the identity matrix.

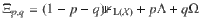
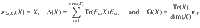
We investigate the values (p, q) ∈ [0, 1] × [0, 1] for which the channel Ξ_p,q is k-self-compatible for k ∈ {1, …, 10} ∪ {∞}. (Recall that the condition that Ξ_p,q is measure-and-prepare is equivalent to the condition that it is k-self-compatible for all k.)

We also examine the values of (p, q) ∈ [0, 1] × [0, 1] for which Ξ_p,q ⊙ Ξ_p,q is completely positive. This region turns out to be marginally smaller than the region where Ξ_p,q is self-compatible, thus reinforcing the need for our generalization of the Jordan product. In fact, the channel Ξ_p,q is invertible when p, q > 0 satisfies p + q < 1, so self-compatibility for this channel can be examined using (generalized) Jordan products for almost all values of p and q.

Finally, we investigate the region of values (q₀, q₁) ∈ [0, 1] × [0, 1] for which the pairs of channels $$ \left({\mathrm{\Xi }}_{0,q_0},{\mathrm{\Xi }}_{0,q_1}\right)=\left({\mathrm{\Omega }}_{q_0},{\mathrm{\Omega }}_{q_1}\right)$$ are compatible and when the Jordan product $$ {\mathrm{\Omega }}_{q_0}\odot {\mathrm{\Omega }}_{q_1}$$ is completely positive. It turns out that the values of (q₀, q₁) for which $$ {\mathrm{\Omega }}_{q_0}\odot {\mathrm{\Omega }}_{q_1}$$ is completely positive contains some nontrivial instances while simultaneously missing other trivial instances of compatible pairs. This illustrates that the (standard) Jordan product provides an interesting sufficient condition for compatibility.

Discussion

In this work, we studied the quantum channel marginal problem (i.e., the channel compatibility problem)—which is the task of determining whether two channels can be executed simultaneously, in the sense that afterwards, one can choose which channel’s output to obtain. We showed how to decide this via semidefinite programming and presented several other key properties such as its equivalence to the quantum state marginal problem.

We also studied a generalization of the Jordan product to quantum channels, and in turn, generalized it further such that it captures the compatibility of invertible channels. This Jordan product may be of independent interest.

There are many open problems concerning the compatibility of channels. We briefly mention a few which we think are interesting.

One immediate open problem is the question of whether compatibility and Jordan compatibility are equivalent. We conjecture that they are equivalent based on the fact that the set of pairs of compatible channels that are not Jordan compatible must have zero measure when the output and input spaces have the same dimension. On this note, it would be interesting to see if the resolution to this conjecture depends on the dimensions of the input and output spaces.

Another interesting problem is to examine the computational complexity of determining compatibility for a given pair of channels. Since it is equivalent to the quantum state marginal problem, we suspect that there are versions of this problem which are QMA-hard (although the equivalence is a mathematical one, and may or may not translate into efficient algorithmic reductions).

Another open problem is whether one can extend this work to study the compatibility of other quantum objects, such as quantum strategies ^39–41, combs ^42,43, or even channels in other generalized probabilistic theories.

Lastly, there might be a relationship between channel compatibility and cryptography. For example, symmetric extendibility is closely related to quantum key distribution, since you do not want Alice to be just as correlated/entangled with Bob and she is with Eve. Since quantum channel compatibility generalizes symmetric extendibility, perhaps there is another cryptographic setting in which the notion of channel compatibility translates into (in)security.