Epidemic spreading on heterogeneous dynamical networks

We consider an activity-driven network model with attractiveness, taking into account both the temporal dynamics of social contacts and the heterogeneity in the propensity to establish social ties^33–36. Each susceptible node S is assigned with an activity a_S and an attractiveness parameter b_S, drawn from the joint distribution ρ(a_S, b_S): the activation rate a_S describes the Poissonian activation dynamics of the node; the attractiveness b_S sets the probability $$ p_{b_{\mathrm{S}}}\propto b_{\mathrm{S}}$$ for a node to be contacted by an active agent. At the beginning all nodes are disconnected and when a node activates it creates m links with m randomly selected nodes (hereafter we set m = 1); then all links are destroyed and the procedure is iterated. The functional form of ρ(a_S, b_S) encodes the correlations between activity and attractiveness in a population with a given distribution of activity. It has been observed that several social systems feature positive correlations between activity and attractiveness and a broad power-law distribution of activity^33–39:

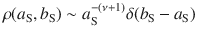
On top of the activity-driven dynamics, we consider a compartmental epidemic model which includes the main phases of clinical progression of the SARS-CoV-2 infection^6,40–42, also applicable to other infectious diseases with asymptomatic and presymptomatic transmission. The model is composed by five compartments: S susceptible, P presymptomatic, A infected asymptomatic, I infected symptomatic, R recovered. A contagion process (see Fig. 1a) occurs with probability λ when a link is established between an infected (either P, A, and I) and a susceptible node S (contact-driven transition): a node has probability δ to become presymptomatic after infection and probability (1 − δ) to become asymptomatic, thus $$ S\stackrel{\lambda \delta }{\to }P$$ and $$ S\stackrel{\lambda \left(1-\delta \right)}{--\to }A$$. A presymptomatic node spontaneously develops symptoms with rate γ_P = 1/τ_P, thus with a Poissonian process $$ P\stackrel{{\gamma }_P}{\to }I$$; both asymptomatic and symptomatic nodes spontaneously recover respectively with rate μ = 1/τ and with rate μ_I = μγ_P/(γ_P − μ), so that the average infectious period for both symptomatic and asymptomatic is τ. We neglect states of hospitalization and consider recovery without death: this choice does not affect the infection dynamics.

Fig. 1

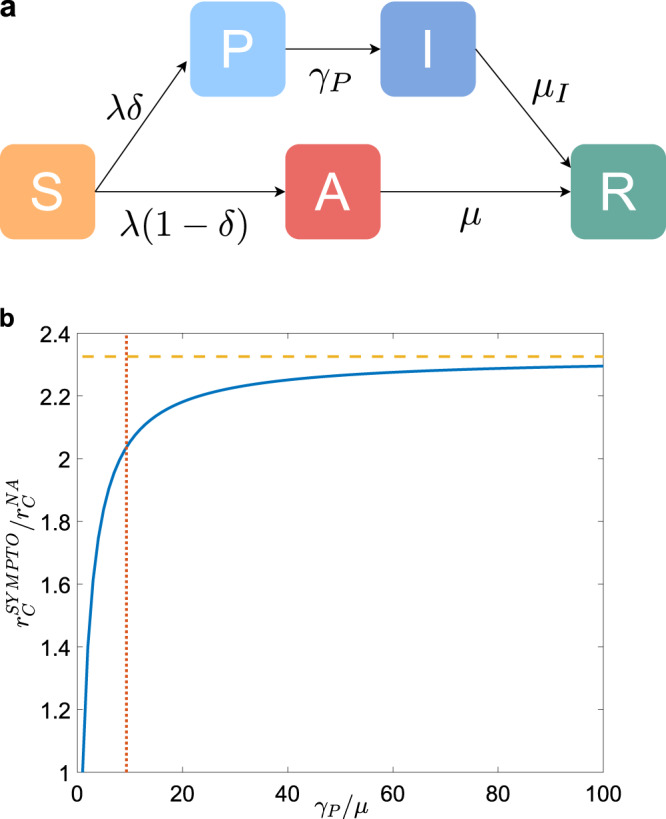
Epidemic model without contact tracing.

a Diagram of the compartmental epidemic model without CT. b We plot, as a function of γ_P/μ, the ratio between the epidemic threshold $$ r_{\mathrm{C}}^{\mathrm{SYMPTO}}$$ when symptomatic nodes are isolated and the epidemic threshold of the non-adaptive case $$ r_{\mathrm{C}}^{\mathrm{NA}}$$. The horizontal dashed orange line indicates the value of $$ r_{\mathrm{C}}^{\mathrm{SYMPTO}}/r_{\mathrm{C}}^{\mathrm{NA}}$$ for γ_P = ∞ (instantaneous onset of symptoms). The vertical red dash-dotted line indicates the value of γ_P/μ we consider in the rest of the paper. We set ρ(a_S, b_S) = ρ_S(a_S)δ(b_S − a_S). The curve does not depend on the specific form of ρ_S(a_S).

Adaptive behavior of populations exposed to epidemics can be modeled within the activity-driven network framework: infected nodes experience a reduction in activity, due to isolation or the appearance of symptoms; similarly, other individuals undertake self-protective behavior to reduce the probability of contact with an infected node, and this is modeled as a reduction in the attractiveness of infected nodes^43–45. We assume that symptomatic infected nodes I are immediately isolated (a_I, b_I) = (0, 0), therefore not being able to infect anymore. On the contrary, we assume that recovered R, asymptomatic A, and presymptomatic P individuals behave as when they were susceptible (a_A, b_A) = (a_P, b_P) = (a_R, b_R) = (a_S, b_S). The adaptive behavior is implemented without affecting the activity of nodes which are not isolated⁴⁴.

The control parameter r = λ/μ is the effective infection rate, whose critical value r_C—the epidemic threshold—sets the transition point between the absorbing and the active phase of the epidemic. The increase in the value of r_C is an indicator of the effectiveness of mitigation strategies. Within the adaptive activity-driven framework, the epidemic threshold can be calculated analytically via a mean-field approach (see Methods).

The effect of isolating symptomatic nodes as the only containment measure is shown in Fig. 1b. We compare the epidemic threshold r_C, obtained with the isolation of symptomatic nodes only, with the epidemic threshold $$ r_{\mathrm{C}}^{\mathrm{NA}}$$ of the non-adaptive (NA) case, in which no containment measures are taken on infected individuals, as a function of γ_P/μ (see Methods for the explicit expression). In the case of instantaneous symptoms development (γ_P/μ → ∞), the threshold is increased by a factor of 1/(1 − δ), while for smaller γ_P/μ the gain is reduced. For example, for (1 − δ) = 0.43, that is 43% of asymptomatic individuals, τ_P = 1.5 days and τ = 14 days as observed for SARS-CoV-2 (see Methods for details on the parameters used in all figures), the threshold is doubled by the isolation of symptomatic nodes. This is the baseline reference for the evaluation of the performance of CT strategies.

Manual and digital contact tracing protocols

The CT protocols differ in their practical implementation as well in their exploration properties.

Manual tracing is performed by personnel who, through interviews, collects information, contacts individuals who may have been infected and arranges for testing. In manual CT, as soon as an individual develops symptoms (i.e., P → I), her contacts in the previous T_CT days are traced with recall probability ϵ(a_S), where a_S is the activity of the symptomatic individual. A traced contact is tested and, if found in state A (infected asymptomatic), isolated (a = b = 0): the average time between the isolation of the symptomatic individual and the isolation of her asymptomatic infected contacts is τ_C. Such delay can be quite large, due to the time required for the collection of the diary, the execution of the diagnostic test and the subsequent isolation^2,17. Moreover, the manual protocol depends on ϵ(a_S), which takes into account the limited resources allocated for tracing and the limited memory/knowledge of symptomatic individuals in reconstructing their contacts. Low activity nodes make few contacts over time and a fraction of their contacts will be traced; on the other hand high activity nodes will only remember a finite number of their contacts so that, also because of limitations of the tracing capacity, we expect that at most a number k_c of contacts can be traced^46,47. This translates into the limited scalability property:

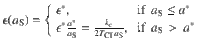
Digital CT is based on the download of an app which allows the tracing of close contacts equipped with the same app. We assume that each of the individuals has a probability f to download the app before the epidemic starts. As soon as an individual develops symptoms (i.e., P → I), if she downloaded the app, her contacts are traced only if they downloaded the app as well. A traced contact is tested and, if found in state A (infected asymptomatic), is isolated (a = b = 0). The time passing between the isolation of a symptomatic individual and the isolation of her asymptomatic infected contacts is taken to be 0, thus assuming an idealized scenario of instantaneous notification and isolation. We finally consider a more realistic scenario where the two procedures are combined into a hybrid protocol in which digital CT supports manual CT, potentially reaching individuals not traced manually^19,25,29. See Methods for details on the implementation of the CT protocols.

Stochastic vs. prearranged sampling

We first compare the manual and digital CT protocols in the case of a population with homogeneous activity and attractiveness, ρ(a_S, b_S) = δ(a_S − a)δ(b_S − b), without delay even in manual CT, i.e., τ_C = 0. We set ϵ = f² so that the probability that a single contact is traced in the two protocols is the same. However, it should be emphasized that typical values of f² range between 0.01 and 0.1 in many countries^30–32, while ϵ is usually larger (≈0.3−0.5), since typically 30−50% of contacts are close and occur at home, at work, or at school and thus are easily traceable^48,49. An exact analytical estimate of the epidemic threshold is obtained through a linear stability analysis around the absorbing state (see Methods for explicit expressions and Supplementary Method 1 for detailed derivation): in Fig. 2a we compare the threshold for manual and app-based CT, compared to the NA case, for realistic COVID-19 parameters. Both protocols feature the same epidemic threshold when ϵ = f = 0 and ϵ = f = 1: indeed the former corresponds to the isolation of symptomatic individuals only, without CT, while the latter limit corresponds to the case in which all contacts are traced. For intermediates values of ϵ = f ², manual tracing is strongly and surprisingly more effective than digital tracing, as it increases significantly the epidemic threshold, compared to the app-based protocol. Since we are considering no heterogeneity or delays, the difference is due only to sampling effects in the CT dynamics. In practice, in app-based CT the population to be tested is prearranged, based on whether or not the app was downloaded before the outbreak started. On the contrary, manual CT performs a stochastic sampling of the population: the random exploration can potentially reach the entire population, since anyone who has come in contact with a symptomatic node can be traced. The simplest example of the difference in tracing multiple infections processes in the two protocols is illustrated in Fig. 2b.

Fig. 2

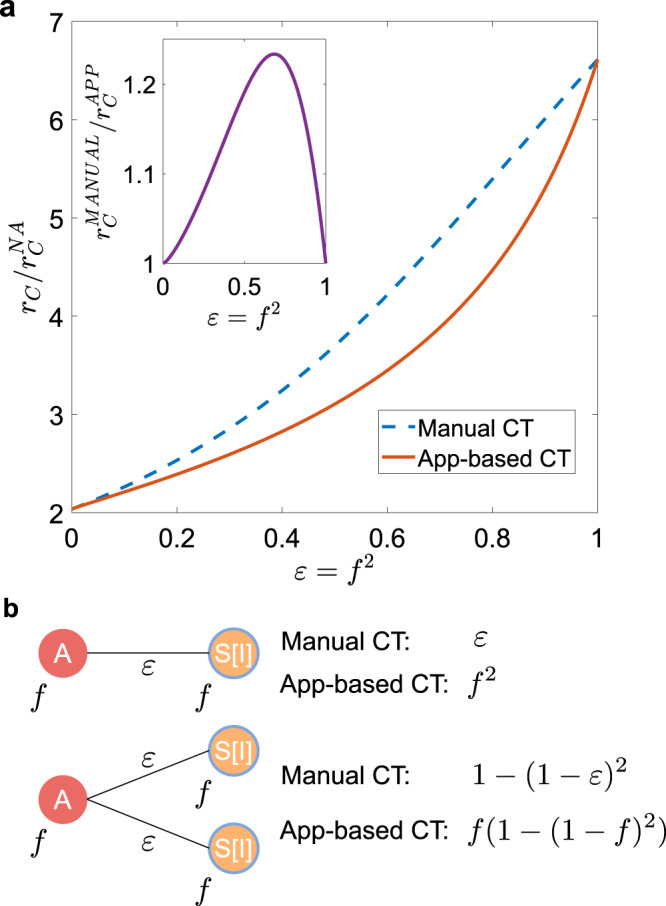
Stochastic vs. prearranged sampling in contact tracing.

a Plot, as a function of ϵ = f², of the ratio between the epidemic threshold r_C in the presence of CT protocols and the epidemic threshold of the non-adaptive case $$ r_{\mathrm{C}}^{\mathrm{NA}}$$. In the inset we plot the ratio between the epidemic threshold of the manual CT $$ r_{\mathrm{C}}^{\mathrm{MANUAL}}$$ and that of the app-based CT $$ r_{\mathrm{C}}^{\mathrm{APP}}$$, as a function of ϵ = f². We consider homogeneous activity and attractiveness, setting ρ(a_S, b_S) = δ(a_S − a)δ(b_S − b). b If an asymptomatic node A infects a single susceptible node S (which subsequently becomes symptomatic, I), the infector is traced with probability ϵ in the manual CT and with probability f² in the digital CT. Thus the probability is the same if we impose f² = ϵ. However, if an asymptomatic node infects two susceptible nodes (which subsequently become symptomatic), the probability of tracing the infector with the manual protocol is 1 − (1−ϵ)² = 2f² − f⁴ (still considering ϵ = f²). This value is always larger than that of the digital protocol f(1 − (1−f )²) = 2f² − f³.

Effects of heterogeneous activity

We now consider a heterogeneous activity distribution, as observed in several human systems, and we consider a positive activity-attractiveness correlation, as defined in Eq. (1)^{33–35,37–39}. The power-law distribution for the activity implies the presence of hubs with high activity and high attractiveness. We investigate the pure effect of heterogeneities in CT^12,27 setting now ϵ(a_S) = ϵ, ∀ a_S and not considering delays in manual CT, τ_C = 0. We perform again a mean-field approach, obtaining an analytical closed form for the epidemic threshold (see Methods and Supplementary Method 1): in Fig. 3 we compare the epidemic threshold with the two protocols as a function of the exponent ν of the activity distribution, for realistic parameters and setting an average activity $$ \overline{a_{\mathrm{S}}}=6.7$$ days^−143,48. Both protocols are more effective in heterogeneous populations, that is at ν ~ 1−1.5. Note that due to the cut-offs and the constraint on the average, the fluctuations of the activity distribution are maximum for ν = 1, and the epidemic thresholds depend both on activity fluctuations and higher order moments of ρ_S(a_S) (see Methods and Supplementary Method 1 for details). However heterogeneity greatly amplifies stochastic effects, further increasing the advantage of the manual tracing over the app-based prearranged protocol. Indeed, in heterogeneous populations nodes with high activity and attractiveness (super-spreaders) drive and sustain the spread of the epidemic. Manual CT is far more effective in identifying and isolating them than app-based CT: in digital CT, hubs which have not downloaded the app will never be traced, despite the high number of their contacts. On the contrary, manual CT is very effective in tracing super-spreaders, because they are engaged in many contacts and are traced very effectively by stochastic exploration.

Fig. 3

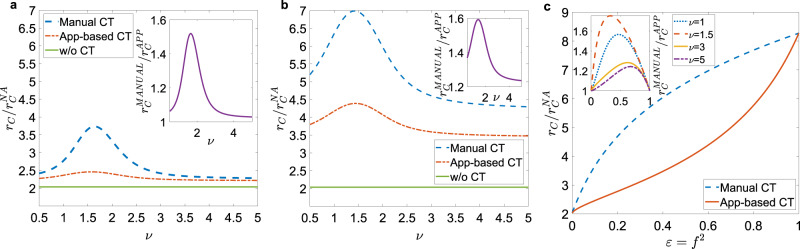
Effects of heterogeneity.

a Plot, as a function of the exponent ν, of the ratio between the epidemic threshold r_C in the presence of CT protocols and the epidemic threshold of the non-adaptive case $$ r_{\mathrm{C}}^{\mathrm{NA}}$$. We set ϵ = f² = 0.1 (f ≈ 0.316). In the inset we plot the ratio between the epidemic threshold of the manual CT $$ r_{\mathrm{C}}^{\mathrm{MANUAL}}$$ and that of the app-based CT $$ r_{\mathrm{C}}^{\mathrm{APP}}$$, as a function of ν. b Same plot as a with ϵ = f² = 0.6 (f ≈ 0.775). c The ratio $$ r_{\mathrm{C}}/r_{\mathrm{C}}^{\mathrm{NA}}$$ is plotted as a function of ϵ = f² for both CT protocols, with ν = 1.5. In the inset we plot the ratio $$ r_{\mathrm{C}}^{\mathrm{MANUAL}}/r_{\mathrm{C}}^{\mathrm{APP}}$$ as a function of ϵ = f² for several ν values. In all panels the distribution ρ(a_S, b_S) is given by Eq. (1).

Limited scalability and delay in manual CT

We now consider some features of manual CT that can reduce its effectiveness: the limited scalability of the tracing capacity^46,47 and the delays in CT and isolation^2,23,28. We set ϵ(a_S) as in Eq. (2) and consider a large delay τ_C = 3 days² in manual CT. In Fig. 4 we compare the epidemic threshold for the two CT protocols, setting equal probabilities of tracing a contact $$ \overline{ϵ}=f^2$$, where $$ \overline{ϵ}=\int d{a}_{\mathrm{S}}ϵ\left(a_{\mathrm{S}}\right){\rho }_{\mathrm{S}}\left(a_{\mathrm{S}}\right)$$. For small values of $$ \overline{ϵ}$$ (note that this however corresponds to a quite large adoption rate $$ f=\sqrt{\overline{ϵ}}\approx 0.316$$) manual CT is still more effective (see Fig. 4a): the delay in isolation and the limited scalability are not able to significantly reduce the advantage provided by the stochastic exploration of contacts. Figure 4b shows that digital CT can become more effective than manual CT, but this occurs only for very large values of f ² and τ_C. This indicates that for realistic settings, the advantage of the manual protocol over the app-based protocol is robust even including delays and limited scalability. Figure 4c further illustrates for which (unrealistically large) values of f ² and τ_C, digital CT outperforms manual CT. Note that realistic values of f correspond to f ² at most of the order of 0.1. Hence, an extremely high adoption of the app is necessary in order to obtain an effective advantage of the digital CT.

Fig. 4

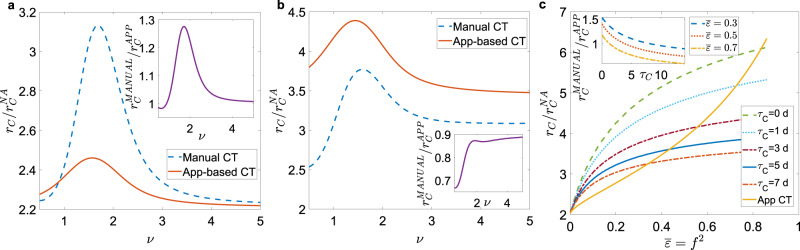
Effects of limited scalability and isolation delay in manual contact tracing.

a Plot, as a function of the exponent ν, of the ratio between the epidemic threshold r_C in the presence of CT protocols and the epidemic threshold of the non-adaptive case $$ r_{\mathrm{C}}^{\mathrm{NA}}$$, with limited scalability and delay in manual CT. We set $$ \overline{ϵ}=f^2=0.1$$ (f ≈ 0.316), τ_C = 3 days. In the insets we plot the ratio between the epidemic threshold of the manual CT $$ r_{\mathrm{C}}^{\mathrm{MANUAL}}$$ and that of the app-based CT $$ r_{\mathrm{C}}^{\mathrm{APP}}$$, as a function of ν. b Same plot as a with $$ \overline{ϵ}=f^2=0.6$$ (f ≈ 0.775), τ_C = 5 days. c Plot of the ratio $$ r_{\mathrm{C}}/r_{\mathrm{C}}^{\mathrm{NA}}$$ as a function of $$ \overline{ϵ}=f^2$$ for both CT protocols, setting ν = 1.5 and for several values of τ_C. In the inset we plot the ratio $$ r_{\mathrm{C}}^{\mathrm{MANUAL}}/r_{\mathrm{C}}^{\mathrm{APP}}$$ as a function of τ_C for several $$ \overline{ϵ}$$ values. In all panels the distribution ρ(a_S, b_S) is given by Eq. (1).

Manual and app-based CT in the epidemic phase

We now explore with numerical simulations (see Methods, Supplementary Method 2) the effects of manual and digital CT protocols in the active phase of the epidemic. We consider an optimistic value of f = 0.316, setting $$ \overline{ϵ}=f^2=0.1$$ that is a very low value for the recall probability, and we consider the system above the epidemic threshold r > r_c, in the conditions of Fig. 4a. Figure 5 shows that the infection peak with manual tracing is lower than the app-based one. Moreover, in the manual CT the duration of the epidemic is reduced: this strongly impacts on the final epidemic size, which is about half of the one observed in the app-based CT. We also plot the temporal evolution of the average activity of the system 〈a(t)〉 and of the fraction of isolated nodes Iso(t) (see inset). In general, the average activity 〈a(t)〉 features a minimum, however its value remains very large (about 98% of the case without any tracing measure). This implies that both protocols do not disrupt the functionality of the system. Interestingly, the fraction of isolated nodes is coherent with the infection peak, and in particular it is lower when the infection peak is lowered. This means that the most effective procedure, i.e., manual CT for realistic values of the parameters, not only lowers the infection peak but it is also able to isolate a smaller number of nodes, a key feature of any effective CT strategy.

Fig. 5

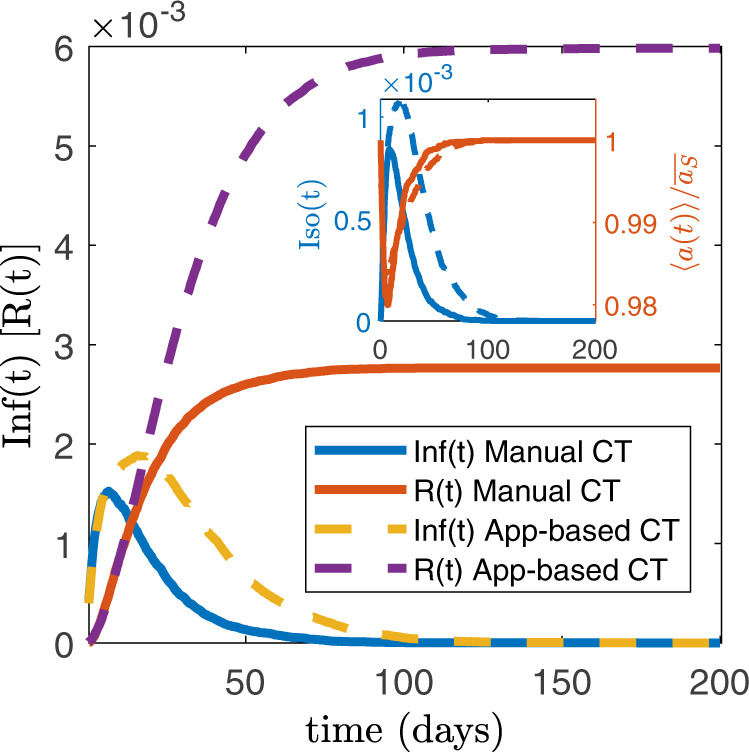
Effects of manual and digital contact tracing on the epidemic active phase.

We plot the temporal evolution of the fraction of infected nodes $$ \mathrm{Inf}\left(t\right)$$, i.e., infected asymptomatic and infected symptomatic, and of the fraction of removed nodes R(t), for both manual and digital CT. In the inset we plot the temporal evolution of the fraction of isolated nodes Iso(t) (right y-axis) and of the average activity of the population 〈a(t)〉 (left y-axis), normalized with $$ \overline{a_{\mathrm{S}}}$$. All curves are averaged on several realizations of the disorder and of the temporal evolution. We set $$ \overline{ϵ}=f^2=0.1$$, τ_C = 3 days, $$ r/r_{\mathrm{C}}^{\mathrm{NA}}=3.1$$ and N = 5 × 10³. The distribution ρ(a_S, b_S) is given by Eq. (1), with ν = 1.5. The curves for digital and manual CT are averaged respectively over 554 and 681 realizations and the errors, evaluated through the standard deviation, are smaller or comparable with the curves thickness.

Robustness

In the Supplementary Notes we show that the advantage of the manual CT is robust with respect to the relaxation of several assumptions and to changes of parameters. In particular, we consider the case where all nodes have equal attractiveness ρ(a_S, b_S) = ρ_S(a_S)δ(b_S − b), we take into account very long delays τ_C and we change the maximum number of traceable contacts k_c. We also show that the advantage of manual CT in the presence of heterogeneous activity is robust, if one takes into account that contacts belonging to the close social circle of the index case (same household) are always traced and isolated manually, also in the digital protocol. This can be verified by using a hybrid procedure with a fixed small number of contacts always traced (see Supplementary Notes).

Hybrid CT protocols: manual plus digital CT

We now consider the implementation of a realistic hybrid CT protocol with manual and digital CT working at the same time. We assume that each individual has downloaded the app with probability f before the epidemic starts. As soon as an individual with activity a_S develops symptoms (i.e., P → I), CT is activated with reference to the previous T_CT days: if the infected individual and also her contact downloaded the app, the contacted agent is immediately traced and isolated with no delay. Otherwise, the contact can only be traced manually, with probability ϵ(a_S) (as in Eq. (2)) and, if found in state A, the contact is isolated with a delay τ_C. We set a realistically large delay τ_C = 3 days.

The threshold in the hybrid case can be determined through the solution of a complex set of equations, that we solve numerically in Supplementary Method 1. In the presence of heterogeneous activity (i.e., super-spreaders), starting form a purely digital protocol (Fig. 6b, c) the addition of manual CT rapidly increases the threshold, leading to an improvement by a large factor (about 80%), for realistic values $$ \overline{ϵ}\gtrsim 0.3$$. Instead, starting from a realistic manual CT setup $$ \overline{ϵ}\gtrsim 0.3$$, a significant improvement (i.e., a 50% of threshold increase) is obtained by implementing a digital CT only if f  ≳ 0.60−0.75 (Fig. 6a, c). These values are consistent with other results in the literature^2,9,23; however, in most countries, the app adoption rates do not reach these values^30–32.

Fig. 6

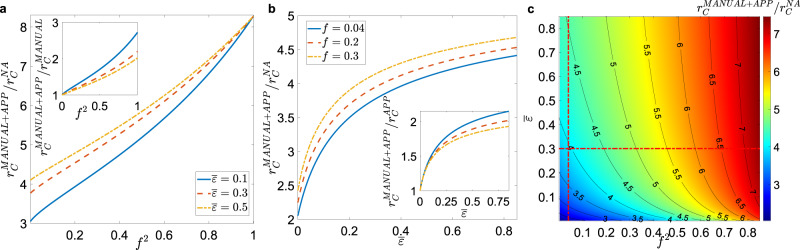
Effects of hybrid contact tracing protocol.

a Plot, as a function of f², of the ratio between the epidemic threshold in the presence of a hybrid CT protocol, $$ r_{\mathrm{C}}^{\mathrm{MANUAL}+\mathrm{APP}}$$, and the epidemic threshold of the non-adaptive case, $$ r_{\mathrm{C}}^{\mathrm{NA}}$$, for realistic values of $$ \overline{ϵ}$$ (see legend). In the inset we plot, as a function of f², the ratio between $$ r_{\mathrm{C}}^{\mathrm{MANUAL}+\mathrm{APP}}$$ and the epidemic threshold when only manual CT is implemented, $$ r_{\mathrm{C}}^{\mathrm{MANUAL}}$$. b Plot of the ratio $$ r_{\mathrm{C}}^{\mathrm{MANUAL}+\mathrm{APP}}/r_{\mathrm{C}}^{\mathrm{NA}}$$ as a function of $$ \overline{ϵ}$$, for realistic app adoption levels f (see legend). In the inset we plot, as a function of $$ \overline{ϵ}$$, the ratio between $$ r_{\mathrm{C}}^{\mathrm{MANUAL}+\mathrm{APP}}$$ and the epidemic threshold when only app-based CT is implemented, $$ r_{\mathrm{C}}^{\mathrm{APP}}$$. c The ratio $$ r_{\mathrm{C}}^{\mathrm{MANUAL}+\mathrm{APP}}/r_{\mathrm{C}}^{\mathrm{NA}}$$ is plotted as a function of f² and $$ \overline{ϵ}$$, through a heat map: the red dash-dotted lines are plotted for $$ \overline{ϵ}=0.3$$ and f = 0.2, i.e., they correspond to the red dashed curves of panel a and b. In all panels the distribution ρ(a_S, b_S) is given by Eq. (1), the manual CT features a delay of τ_C = 3 days and limited scalability is considered.

Mean-field equations and implementation of CT protocols

We consider an activity-attractiveness based mean-field approach, dividing the population into classes of nodes with the same activity a_S and attractiveness b_S and treating them as if they were statistically equivalent. For each class (a_S, b_S) we consider the probability that at time t a node is in one of the epidemic compartments. For arbitrary ρ(a_S, b_S) distribution and arbitrary functional form of f(a_S) and ϵ(a_S) we build the mean-field equations which describe the temporal evolution of the network, the epidemic spreading and the adaptive behavior due to isolation and CT. In particular, in order to model the manual and app-based CT we introduce two further compartments: T traced asymptomatic and Q isolated asymptomatic. An asymptomatic individual became traced T when infected by a presymptomatic node or when she infects a susceptible node that eventually develops symptoms. In the manual case the tracing is effective with probability ϵ(a). In the app-based case, tracing occurs only if both nodes involved in the contact downloaded the app. A traced node is still infective (a_T, b_T) = (a_S, b_S) and with rate γ_A = 1/τ_A ≫ μ it is quarantined, $$ T\stackrel{{\gamma }_A}{\to }Q$$; while a quarantined node is no more infective since (a_Q, b_Q) = (0, 0). In order to take into account the delay in the manual CT we set: τ_A = τ_C + τ_P for the manual case and τ_A = τ_P for the app-based process. See Supplementary Method 1 for the detailed equations of manual, digital, and hybrid CT protocols.

Epidemic thresholds

We perform a linear stability analysis of the mean-field equations around the absorbing state obtaining the conditions for its stability and then the epidemic threshold r_C (see Supplementary Method 1 for details). For the NA case, when infected individuals do not modify their behavior, the threshold is equal to the one obtained in refs. ^35,44. Indeed, setting ρ(a_S, b_S) = ρ_S(a_S)δ(b_S − a_S) we obtain:

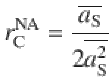
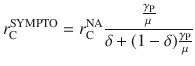
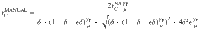
Model parameters

Figures present results where one of the model parameters is varied and all the others are fixed. Here we report the parameter values used throughout the paper, unless specified otherwise. They are tailored to describe the current COVID-19 pandemic.

The fraction of infected individuals who develop symptoms is δ = 0.57¹. The time after which a presymptomatic individual spontaneously develops symptoms is τ_P = 1.5 days^6,41,49, while infected individuals recover on average after τ = 14 days^42,50. The time window over which contacts are reconstructed is T_CT = 14 days⁴⁹: it is fixed equal to τ to track both nodes infected by the index case in the presymptomatic phase (forward CT) and the primary case who infected the index case (backward CT)¹². The maximum number of contacts engaged in T_CT by a single individual that can be reconstructed with the manual CT procedure is k_C = 130, according to reasonable estimates of the number of contacts manually traced for very active individuals⁴⁹. Moreover, fixing k_C = 130 and for realistic $$ \overline{ϵ}~0.1-0.5$$⁴⁸, the average number of traced contacts for each index case is approximatively 10−60, consistently with reported data on manual CT and with estimates for resources allocation^46,49,56,57 (see Supplementary Notes for the distribution P(k_T) of contacts k_T traced manually by each index case). The activity-driven network parameters are fixed so that the average value of the activity is always the same, i.e., $$ \overline{a_{\mathrm{S}}}=6.7$$ days^−143,48. In particular for a power-law distribution $$ {\rho }_{\mathrm{S}}\left(a_{\mathrm{S}}\right)~a_{\mathrm{S}}^{-\left(\nu +1\right)}$$, the values of a_S are constrained between a minimum and a maximum value (a_m < a_S < a_M). We keep a_M = 10³a_m and then we tune a_m to set $$ \overline{a_{\mathrm{S}}}$$.

Numerical simulations

We perform numerical simulations of the epidemic model on the adaptive activity-driven network: the network dynamics and epidemic spreading are implemented by a continuous time Gillespie-like algorithm. We consider an activity-driven network of N nodes. The results are averaged over several realizations of the disorder and of the dynamical evolution, so that the error on the infection peak height is lower than 6%. The initial conditions are imposed by infecting the node with the highest activity a_S and the CT protocols are immediately adopted. A detailed description of the simulations is reported in Supplementary Method 2.