
Recent experiments demonstrate the control of chemical reactivities by coupling molecules inside an optical microcavity. In contrast, transition state theory predicts no change of the reaction barrier height during this process. Here, we present a theoretical explanation of the cavity modification of the ground state reactivity in the vibrational strong coupling (VSC) regime in polariton chemistry. Our theoretical results suggest that the VSC kinetics modification is originated from the non-Markovian dynamics of the cavity radiation mode that couples to the molecule, leading to the dynamical caging effect of the reaction coordinate and the suppression of reaction rate constant for a specific range of photon frequency close to the barrier frequency. We use a simple analytical non-Markovian rate theory to describe a single molecular system coupled to a cavity mode. We demonstrate the accuracy of the rate theory by performing direct numerical calculations of the transmission coefficients with the same model of the molecule-cavity hybrid system. Our simulations and analytical theory provide a plausible explanation of the photon frequency dependent modification of the chemical reactivities in the VSC polariton chemistry.
Vibrational strong coupling controls the ground-state reactivity of molecules in optical cavities, but the underlying theory is still elusive. The authors analyze a molecular system coupled to a cavity mode and find that the reaction rate is suppressed for a particular cavity frequency, related to the topology of the reaction barrier region, analogously to a solvent caging effect.
Polariton Chemistry is an emerging field1–5 that provides opportunities for new chemical reactivities or selectivities by coupling molecular systems to quantized radiation fields inside an optical cavity. By hybridizing electronic excitation of the molecule and the photonic excitation of the radiation inside the cavity, new light-matter entangled states, so-called polariton states are generated. Recent experimental and theoretical works have demonstrated the possibility of changing photo-isomerization reactivities3,6–9, modifying electron transfer kinetics10–12, and remotely controlling chemical reactions13. These new polaritonic photochemical reactivities are attributed to the modification of the excited state landscape1,3,6–9,11,12 due to the formation of the polariton states.
Similarly, hybridizing molecular vibrations and the photonic excitations inside an optical cavity14,15 forms vibrational polaritons (Fig. 1a). For the vibrational polaritonic hybrid system, it is a well-known result that the Rabi splitting observed in the infrared (IR) spectrum (due to light-matter couplings) scales as with N as the number of molecules14,15 inside the cavity. Whether or not such a collective effect also manifests itself into chemical kinetics has been a subject of a debate16–19. Recent experiments have demonstrated that it is possible to suppress20–24 or enhance25,26 the ground-state chemical reactivities by placing an ensemble of molecules in an optical microcavity through the resonant coupling between the cavity and vibrational degrees of freedom (DOF) of the molecules. This so-called vibrational strong coupling (VSC) regime5 operates in the absence of any light source21,22, and was hypothesized to utilize the hybridization of a vibrational transition of a molecule and the zero-point energy fluctuations of a cavity mode21,22. This new strategy of VSC, if feasible, will allow one to bypass some intrinsic difficulties (such as intramolecular vibrational energy transfer) encountered in the mode-selective chemistry that uses IR excitation to tune chemical reactivities, offering a paradigm-shift of synthetic chemistry through cavity enabled bond-selective chemical transformations21,22.
Unfortunately, a clear theoretical explanation of such remarkable VSC ground-state reactivities remains missing, including explaining both (i) the collective (N-dependent) effects on chemical reaction rates, and (ii) the resonant effect where the suppression of the rate is achieved with a particular cavity photon frequency. Recent theoretical works that use simple transition state theory (TST) suggest that there is no collective effect nor resonant effect in VSC polariton chemistry17–19,27. On the other hand, both effects do show up in a VSC non-adiabatic electron transfer reaction28, with an enhancement of the rate upon resonant coupling between molecular vibration and the cavity, although the applicability of this theory on the VSC ground-state adiabatic reactions remains an open question.
In this work, we provide a different perspective on understanding the resonant effect of the VSC ground-state reactivities. Note that we refer to the photon frequency-dependent modification of the ground-state kinetics as the resonant effect. Through both analytical theory and numerical simulations, we demonstrate that the non-Markovian nature of a cavity radiation mode leads to significant suppression of the chemical reaction rate constant at a particular photon frequency that is related to the reaction barrier frequency. At such a “resonant” frequency, the cavity radiation mode induces the dynamical caging effect29,30, such that the molecular reaction coordinate becomes trapped in a narrow “photonic solvent cage” near to the top of the barrier region, leading to a suppression of the chemical kinetics. Such effects are dynamical and are not captured within a simple transition state theory. This work underscores the importance of “dynamical solvent effect” of the cavity radiation modes and provides an understanding of the VSC polariton chemistry, paving the way toward an ultimate theoretical understanding of VSC polariton chemistry.
The model QED Hamiltonian used in this work is expressed as31–33


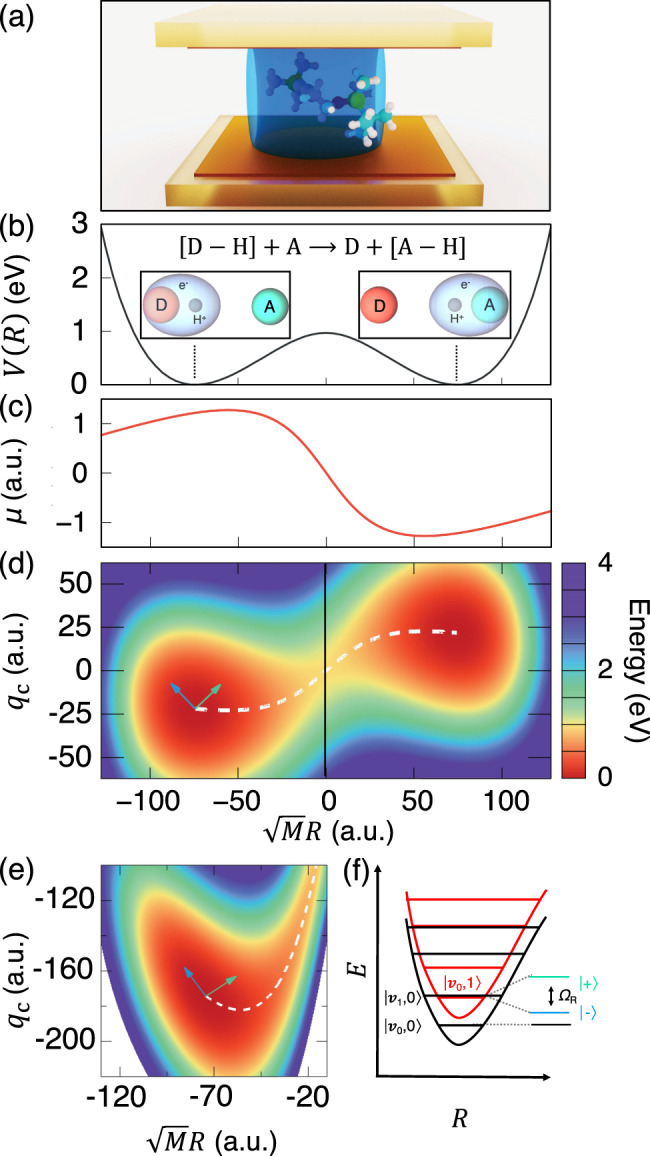
Vibrational strong coupling (VSC) regime in polariton chemistry.
a Schematic representation of a molecule placed inside an optical cavity. b Proton-coupled electron transfer reaction of a Shin–Metiu model. Ground-state potential energy surface (PES) of the molecule as a function of the mass-weighted proton coordinate
At the equilibrium position of the reactant R0, one can approximate the permanent dipole as
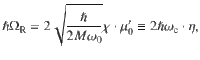

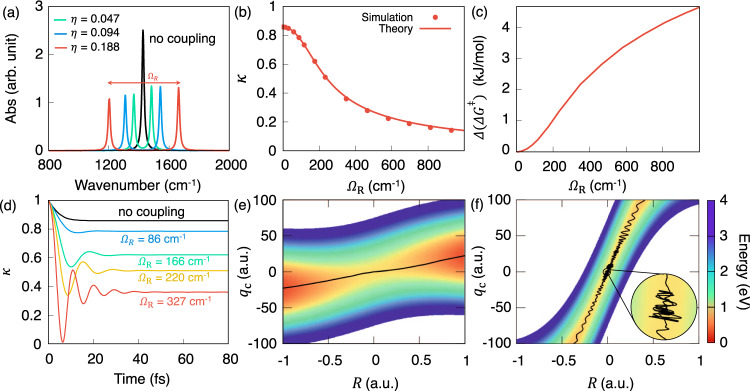
Decrease in the rate constant as increasing light-matter couplings.
a Infrared absorption spectrum by changing the normalized light-matter coupling strength η (see Eq (2)). b The transmission coefficient κ (under the limit t → tp) under various light-matter coupling strength (indicated by ΩR) at the resonant frequency ℏωc = ℏω0 = 0.1706 eV. c The "effective change" of the Gibbs free energy barrier Δ(ΔG‡) with respect to the coupling strength ΩR at 300 K. d Time-dependent transmission coefficient κ(t) at various light-matter coupling strengths at the resonant frequency ℏωc = 0.1706 eV. e, f Cavity Born–Oppenheimer surfaces
The VSC polariton chemical kinetics can be viewed as a barrier crossing process on the cavity Born–Oppenheimer surface (CBO)17,31,35
It is formally rigorous to express the rate constant as the TST rate kTST and the transmission coefficient κ as follows
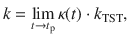
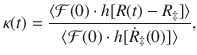
To obtain a more intuitive understanding of how VSC light-matter interactions influence κ, let us consider a simplified model,
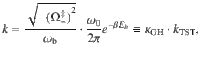

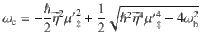
With the above analysis, we conjecture that the cavity radiation mode inside the optical cavity is effectively acting as a “solvent” degree of freedom (DOF) that is coupled to the molecular reaction coordinate R, such that the presence of photonic coordinate enhance the recrossing of the reaction coordinate and reduces the transmission coefficients. A similar phenomenon is commonly referred to as the “dynamical caging” regime in simple organic reactions30,47,48 and enzymatic catalysis49–51, which have been successfully explained by the GH theory. Due to the low frequency of the photonic cavity mode (which is in the same range of the vibrational frequencies), we treat both R and qc as the classical DOFs17–19, and use the GH theory to explore the role of the cavity mode on reaction dynamics.
Figure 2 presents the influence of increasing light-matter coupling η (thereby increasing ΩR) on the reaction transmission coefficient κ with the model Hamiltonian presented in Eq. (1). Figure 2a presents the IR spectrum computed based on the quantum light-matter interaction (Eq. (13) in “Methods”). The numerically exact Rabi splitting ℏΩR is slightly deviated from 2ℏωc ⋅ η (as indicated by Eq. (2)) due to the linear approximation (
Figure 2c presents another interesting result in this work. For the PF Hamiltonian description that explicitly includes the DSE term, there is no change in kTST because there is no change of potential energy barrier (see Fig. 1d) nor free energy barrier18. The only change in the rate comes from κ. However, one can back out the “effective change” of the free energy barrier height due to the changing κ. To this end, we use the Eyring rate equation (see “Methods”) to convert the change of rate from κ into an effective Δ(ΔG‡). The 4 times decrease in κ presented in Fig. 2b results in ~4 kJ/mol change in “effective” Δ(ΔG‡) in Fig. 2c at ~700 cm−1 of ΩR. We emphasize that this is not the real change of the free energy barrier height, but rather an “effective” change of ΔG‡ according to the change of κ based on our theoretical analysis. Interestingly, the experimentally measured results of Δ(ΔG‡) (Fig. 3C in ref. 22, for example) closely resemble our theoretical finding in Fig. 2c, with the key difference that our theoretical results suggest that these are not the actual free energy barrier changes, but entirely due to the change of κ, i.e., kinetics. Note that if one hypothesizes that an unknown mechanism to force the upper or lower vibrational polariton states to be a gateway of VSC polaritonic chemical reaction52, then the activation energy change should shift linearly18 with ΩR. The experimental results, on the other hand, demonstrate a non-linearity of reaction barrier22. Our theory indicates a non-linear increase of the “effective” Δ(ΔG‡) as increasing ΩR due to the change of κ, closely resembles the experimental discoveries (Fig. 3C, D in ref. 22).
Figure 2d presents the time-dependent simulation of the transmission coefficient κ(t) defined in Eq. (4). With an increasing light-matter coupling hence a larger ΩR, the plateau value of κ(t) keeps decreasing, and at the same time, κ(t) becomes more oscillatory. This is a typical behavior of the reaction dynamics in the solvent caging regime53. As the coupling between qc and R increase, the non-Markovian dynamics of qc can significantly influence the recrossing dynamics of the reaction coordinate R, from the “non-adiabatic” limit of a weak coupling regime to the “dynamic caging” of a strong coupling regime39,53.
To clearly demonstrate the difference between these two regimes, we further present the Cavity BO surface
Figure 3a presents the transmission coefficient κ (when t → tp) as a function of the photon frequency ωc with three normalized coupling constant η (defined in Eq. (2)). The results are obtained from the GH theory (solid line) as well as the direct numerical simulation of Eq. (4) (filled circles). One can clearly see a resonant behavior of κ when changing the photon frequency, agreeing with the analytical result (Eq. (7)) of a simpler model. These findings in Fig. 3a closely resemble recent experimental results of desilylation reaction (Fig. 3A in ref. 21, Fig. 3B in ref. 20), aldehyde/ketone Prins cyclization (Fig. 3 in ref. 24), and enzymatic reaction in pepsin (Fig. 3C in ref. 23). Note that under a relatively small light-matter coupling η = 0.047 (green), the resonant frequency that gives a minimal κ is close to ωb, which is also close to the reactant equilibrium frequency of the reactant ω0 in our SM model. For the parameter regime η < 0.1 (not entering into the USC), we find that the resonant condition (based on Eq. (7)) is close to ωb.

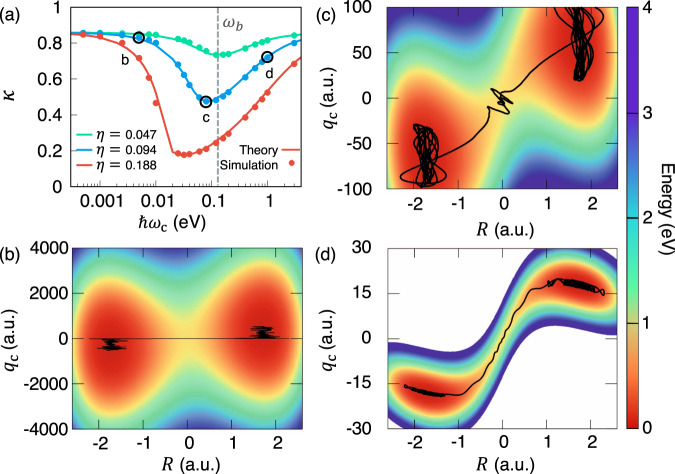
Resonant effect in vibrational strong coupling regime of polariton chemistry.
a Transmission coefficient κ as a function of the photon frequency at three different values of the coupling strength η. b–d The cavity Born–Oppenheimer surfaces VCBO(qc, R) under the normalized coupling strength η = 0.094 (corresponding to the blue solid line in panel (a)) at the photon frequency b ℏωc = 2.5 meV, c 80 meV, and d 1.0 eV, with the representative reactive trajectories indicated with black solid curves.
Note that experimentally, one often plot the cavity frequency-dependent reaction kinetics against the absorption curve of vibrational polariton. With our theoretical understanding and model calculations, we conclude that these two resonant behavior have two different origins and resonant frequencies. The resonant condition observed in the IR spectrum for Rabi Splitting requires ωc = ω0, whereas the resonant effects for a minimum of the rate constant require ωc ≈ ωb. However, it is possible for a given molecular system which has ω0 ≈ ωb. For example, in a theoretical work (at the level of MP2 perturbation theory) by Merkel and co-workers57, a well-studied SN2 reaction (CH3F+ H− → CH4+F−) has a ωb = 975.5 cm−1, which is close to one ground-state vibrational frequency ω0 = 978.7 cm−1. In fact, this reaction could be also an ideal one subject to future investigations of VSC modifications of reactivities. On the other hand, there are also cases where ω0 and ωb are different. For example, in an SN2 reaction involving a Si–C bond cleavage in 1-phenyl-2-trimethylsilylacetylene, we find (using the geometries reported in ref. 58 at the same level of electronic structure theory) that the computed imaginary barrier frequency to be ωb ≈ 74 cm−1, whereas the Si–C stretching frequency in the reactant well58 is ω0 ≈ 860 cm−1.
When increasing the coupling strength to the USC regime (0.1 < η < 1.0), the resonant frequency is significantly red-shifted from ωb. For example, when η = 0.188 (red curve), the resonant condition for reaching a minimum value of κ is 25 meV. Nevertheless, in the range of 10 meV < ℏωc < 100 meV, κ remains a very low value around 0.2, similar to the value at ωc = ωb. This red-shift of resonant frequency at which the rate constant is most significantly reduced has not been observed experimentally. Our theory predicts that if VSC experiments can reach the ultra-strong coupling regime, then the resonant frequency will be significantly shifted.
The origin of this resonant behavior in VSC chemical reaction rate constant (as indicated in Eq. (7)) can also be intuitively understood by examining representative trajectories (black solid curves) on the cavity BO potential energy surfaces presented in Fig. 3b–d, with the black solid lines, indicate representative trajectories. At a very low frequency ℏωc = 2.5 meV shown in Fig. 3b, the photon coordinate essentially remains frozen compared to the dynamics of the reaction coordinate R during the course of the reaction. As a result, under this frozen solvent limit, the transmission coefficient remains close to the no-coupling scenario. At ℏωc = 80 meV in Fig. 3c, with
In this work, we provide a theoretical explanation of the resonant VSC polariton chemistry reactivities. We demonstrate that the resonant suppression of the reaction rate constant using the analytical GH rate theory as well as performing numerical calculations for a SM model molecular system coupled to a single-radiation mode inside an optical cavity. As opposed to the previous theoretical studies17–19,27 that only focuses on the transition state theory, our investigation suggests that the coupling between a cavity photonic mode and a molecule leads to the suppression of the transmission coefficient of the rate constant, exhibiting the resonant behavior which can be explained by simple GH rate theory. Through both analytical theory and numerical simulations, we demonstrate that the cavity photon mode acts like a “solvent” DOF which influences the chemical kinetics and leads to the suppression of the transmission coefficient. Such an effect is purely dynamical and is not captured within a simple transition state theory.
Further, our theoretical hypothesis provides a plausible explanation to the observed resonant effects of the electronically adiabatic ground-state reactions coupled to an optical cavity, whereas previous theoretical studies17–19,27 based upon a simple TST always conclude a frequency-independent VSC rate constant. The suppression of the rate constant is sensitive to the photon frequency, such that the maximum suppression is achieved when the photon frequency is close to the barrier frequency in the vibrationally strong coupling regime when η < 0.1 and is red-shifted in the vibrationally ultra-strong coupling regime when 0.1 < η < 1. Our results indicate that the resonant condition for achieving the Rabi splitting in the IR spectrum and the resonant condition for achieving a maximum suppression of the reaction rate constant are fundamentally different. While the former is related to the frequency of the reactant, the latter is related to the top of the barrier frequency and the molecule-cavity coupling strength.
We want to remind the reader that the present work is limited to a single molecule coupled to a single radiation mode, whereas the experimentally observed frequency-dependent modification of the chemical kinetics in the collective coupling regime. It was suggested in ref. 19 that the resonant effects will disappear under the N → ∞ limit, where N is the number of molecules coupled to the cavity. However, we believe that the effect we have seen will be present under the few N limit (in the current paper, N = 1). Whether our current theory can also be extended to the collective regime remains an open question. The present formalism can be extended to include cavity losses and their impact on the caging effect. The VSC experiments often use low-quality factor cavities, where the cavity loss should also be explicitly included. Interestingly, these far-field modes which are responsible for the cavity loss can be modeled as dissipative modes coupled to the quantized modes of a cavity, providing an additional dissipative environment for the hybrid system. The frequency dependence as well as the collective phenomenon might also emerge when cavity loss is explicitly included60.
Overall, our work emphasizes the importance of the dynamical effect induced by the cavity photon modes on chemical kinetics to explain new chemical reactivities observed in recent experimental studies on vibrational strong coupling of molecules and cavity. Future investigations will focus on understanding the collective VSC reactivities by coupling many molecules with the cavity18,19.
The minimal coupling QED Hamiltonian in the Coulomb gauge (the “p ⋅ A” form) is expressed as
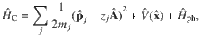
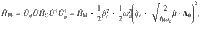
In multidimensional transition state theory, the reactant to product rate constant is given as40,44–46
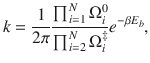
Considering a simplified (classical) model of the molecule-cavity hybrid system,

When considering the phonon bath

The potential energy surface (PES) and permanent dipole moment are taken from a SM model66, which is illustrated in Fig. 1. The SM model is a one-dimensional molecular system that describes a proton-coupled electron transfer reaction between a donor and an acceptor ion. The model consists of a transferring proton, an electron, and two fixed ions. The molecular Hamiltonian is
In addition,

| ℏω0 (meV) | ℏωb (meV) | ||
|---|---|---|---|
| 170.6 | 162.05 | 0.225 | −1.887 |
All simulations were performed under T = 300 K by evolving the classical dynamics governed by H(R, qc) in Eq. (1). Langevin dynamics is used to model the influence of Hvib on the light-matter hybrid system, whereas qc is explicitly propagated in time and treated as a non-Markovian “solvent” DOF. The friction constant in the Langevin dynamics was chosen to be ζ = 400 cm−1 according to the spectral density of the
To account for the “effective change” of the Gibbs free energy barrier Δ(ΔG‡) corresponding to the changes in κ, we consider the Eyring rate equation
We employ a simple approach67 to compute the absorption spectrum of the molecule-cavity hybrid system. The absorption cross section
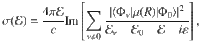
The online version contains supplementary material available at 10.1038/s41467-021-21610-9.
This work was supported by the National Science Foundation CAREER Award under Grant No. CHE-1845747 and “Enabling Quantum Leap in Chemistry” program under a Grant number CHE-1836546, as well as by a Cottrell Scholar award (a program by of Research Corporation for Science Advancement). Computing resources were provided by the Center for Integrated Research Computing (CIRC) at the University of Rochester.
X.L., A.M. and P.H. designed the research. X.L. performed the transmission coefficient simulations. X.L. and A.M. set up the model for molecule-cavity system and performed the absorption spectrum simulations. A.M. performed analytical derivations of the GH rate theory. X.L. and A.M. contributed equally on analyzing the data. X.L., A.M. and P.H. wrote the manuscript.
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon a reasonable request.
The source code for simulating the polariton eigenstates, the absorption spectrum, and the transmission coefficients are available from the corresponding authors upon a reasonable request.
The authors declare no competing interests.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.