Structure search

The model of ZB, RS, and CsCl structures are displayed in Fig. 1a, where the ZB lattice can either adopt an 8-atom cubic cell (left) or a smaller 4-atom unit cell (right). First, we select superalkali NH₄ and superhalogen BCl₄ for constructing a supersalt NH₄BCl₄, where both superatoms are non-centrosymmetric compared with isotropic single atoms, as shown in Fig. 1b. After an extensive structure search using the CALYPSO code, we obtain a series of low-energy structures listed in Table S1. The ground state structure of supersalt NH₄BCl₄ displayed in Fig. 1c is non-centrosymmetric with independent superalkali NH₄ and superhalogen BCl₄ ions. It is a distorted zinc-blende (dZB) structure where the lattice constants (|a|:|b|:|c| = 1.46:1.46:1) are relatively doubled in |a| and |b| (or contracted by half in |c|) compared with the 4-atom unit cell of standard ZB (|a|:|b|:|c|=1:1:1.37). This structure is 0.039 and 0.745 eV/f.u. lower in energy compared with corresponding RS and CsCl structures, respectively. To exclude other polymorphic structures during the synthesis of the ground state dZB phase, temperature and pressure can be controlled, making use of the difference in entropy and density. Choosing proper substrate with perfect lattice match may also facilitate the growth of certain phases while excluding others.

Fig. 1

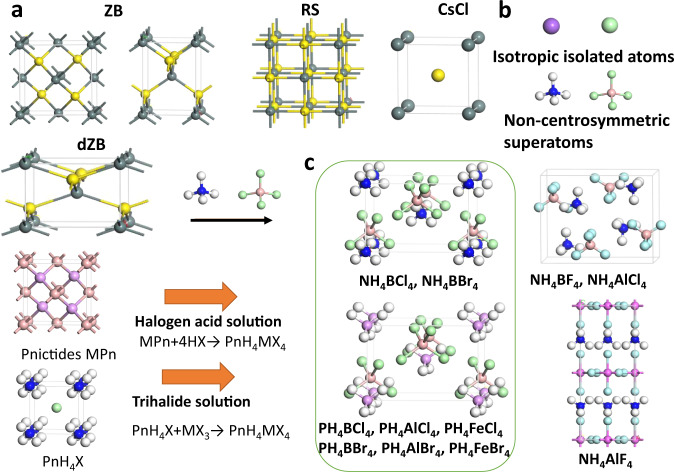
Design of supersalts PnH₄MX₄.

a Structures of ZB, dZB, RS, and CsCl phase, where dark green and yellow spheres, respectively, denote cations and anions. b Non-centro-symmetric superalkali and superhalogen compared with isotropic isolated atoms. c Several typical structures of supersalts PnH₄MX₄, which may be synthesized by reactions MPn+4HX → PnH₄MX₄ or PnH₄X + MX₃ → PnH₄MX₄. White, pink, blue, purple, and light green spheres denote H, B, N, P and halogen atoms, respectively.

Similar to ZB phase, each superalkali cation in the dZB supersalt is tetrahedrally bonded with four adjacent superhalogen anions and vice versa, akin to sp³ hybridization of covalent bonding, which are also connected by weak H…Cl hydrogen bonds (with bond length ~2.4 Å). The energy release computed for a hypothetical reaction BN + 4HCl → NH₄BCl₄, is as high as 1.10 eV/f.u. (i.e., ΔE = −1.10 eV/f.u.), which may enable its solution-processed synthesis via etching of boron nitride by acid. We also examined the following reactions:

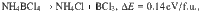
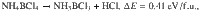
These hypothetical decompositions are all endothermal, which confirm the chemical stability of NH₄BCl₄ and impedes the formation of other products like NH₄Cl or NH₃BCl₃ during the synthesis. However, the strong covalent B–N bonding of BN may lead to high-energy cost to break those bonds, so we cannot guarantee that the formation BN + 4HCl → NH₄BCl₄ would spontaneously proceed at ambient conditions. On the other hand, the reaction NH₄Cl + BCl₃ → NH₄BCl₄ might be a more feasible route for the fabrication of NH₄BCl₄. For the same group pnictides like BP, AlN, the bonding is weaker. The larger hollow space may enable protons or halogen anions to permeate from the surface to inside, which should facilitate similar formations of supersalts. Hence, we further searched for a series of low-energy structures for NH₄MX₄/PH₄MX₄ supersalts, as listed in Table S1. As shown in Fig. 1c, the ground state of NH₄BBr₄ shares the same type of dZB structure with NH₄BCl₄, which is similar to the case for PH₄BCl₄, PH₄AlCl₄, PH₄BBr₄, PH₄AlBr₄, with a slight difference in the relative angles between the cation tetrahedrons and anion tetrahedrons. The 3d metal like Fe may also be used to construct superhalogen like FeCl₄, and the corresponding supersalts like PH₄FeCl₄ and PH₄FeBr₄ turn out to possess similar dZB ground state structures. Their formations are all energetically favorable, with positive energy releases as listed in Table 1. There are a few exceptions like NH₄BF₄ and NH₄AlCl₄ that prefer to form structures where each superalkali cation is hydrogen-bonded to eight adjacent superhalogen anions and vice versa, while NH₄AlF₄ forms a layered perovskite structure, as shown in the right panel of Fig. 1c.

Table 1

The polarization of PnH₄MX₄ and the energy change for the reaction PnH₄X + MX₃ → PnH₄MX₄, where negative values indicate exothermal.

	NH4BCl4	NH4BBr4	PH4BCl4	PH4AlCl4	PH4FeCl4	PH4BBr4	PH4AlBr4	PH4FeBr4
ΔE (eV/f.u.)	−0.14	−0.05	−0.23	−0.55	−0.63	−0.12	−0.48	−0.89
P(µC/cm2)	13.8	12.4	13.1	11.7	11.7	11.8	10.6	10.7

Ferroelectricity

Next, we focus on the polar dZB structures in Fig. 1c, which could be ferroelectric as long as their polarizations are switchable. In previous studies³⁷, the computed switching barriers for ZB structures like CuCl and ZnO can be over 0.30 eV/f.u., so their polarizations are difficult to reverse under ambient conditions. Compared to the breaking of covalent bonds in those structures during polarization switching, the energy barrier for ion displacement in ionic supersalts should be much lower. Taking NH₄BCl₄ shown in Fig. 2a as the paradigmatic case, if all the NH₄ cations at the initial ground state (I) are simultaneously displaced by 2.63 Å along –y direction, with the rotation of all superatoms by a certain angle along –y axis, an equivalent structure (III) with a reversed polarization can be obtained. The reversed polarization turns out to be of a considerable value, namely, 13.8 µC/cm² as listed in Table 1. Its band structure in Fig. 2b reveals that the system is insulating with a large bandgap over 5 eV, which should result in high dielectric breakdown voltage. The ferroelectric switching pathway is computed by SSNEB calculations in Fig. 2c, with a symmetric state as the intermediate state (II), revealing a switchable barrier of only 0.13 eV/f.u. (0.013 eV/atom). Such a high ion displacement with such a small switching barrier is unimaginable in traditional ferroelectrics. For example, the ion displacement in PbTiO₃ during ferroelectric switching is below 1 Å, while the barrier is even larger (~0.15 eV/f.u., i.e., 0.03 eV/atom)³⁸.

Fig. 2

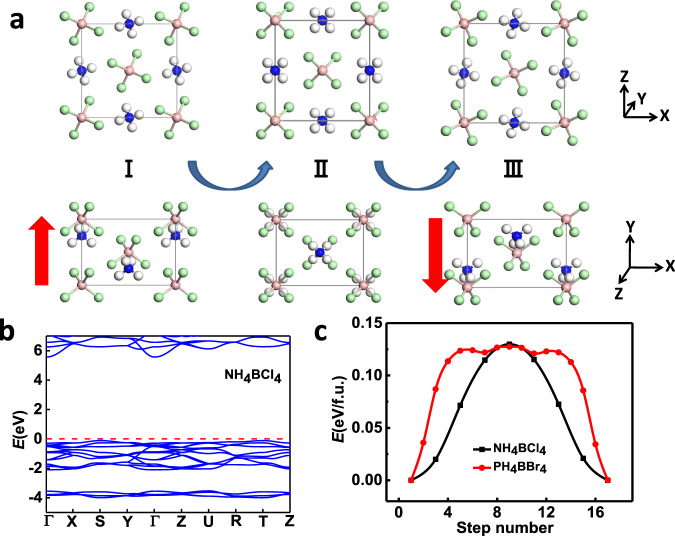
Ferroelectricity.

a Illustration of ferroelectric switching pathway for NH₄BCl₄ and b its band structure. c Comparison of ferroelectric switching pathway between NH₄BCl₄ and PH₄BBr₄. The polarization directions are denoted by the red arrows.

The dynamical stability of the polar ground state for NH₄BCl₄ is further verified by the phonon spectra in Fig. S1, which shows no imaginary frequencies in all vibration spectra. For the nonpolar intermediate state II (paraelectric phase), the imaginary soft optical modes will lead to both rotation and translational displacement of NH₄ cations and BCl₄ anions away from the centrosymmetric position, giving rise to the spontaneous symmetry-breaking below the Curie temperature. Born–Oppenheimer molecular dynamics simulations are also performed to check its thermal stability. Snapshots of the equilibrium structure for NH₄BCl₄ at 300 K and at the end of 5 ps are shown in Fig. S2, suggesting the robustness of its ferroelectricity at ambient conditions. Similar mechanism of ferroelectric switching can be applied to other supersalts like PH₄BBr₄ via the displacement of cations and anions (2.86 Å along –y direction). The switching barrier in this case is also around 0.13 eV/f.u. (i.e., 0.013 eV/atom, as shown in Fig. 3c). The only difference is the rotational mode of superatoms during ferroelectric switching, as displayed in Fig. S3.

Fig. 3

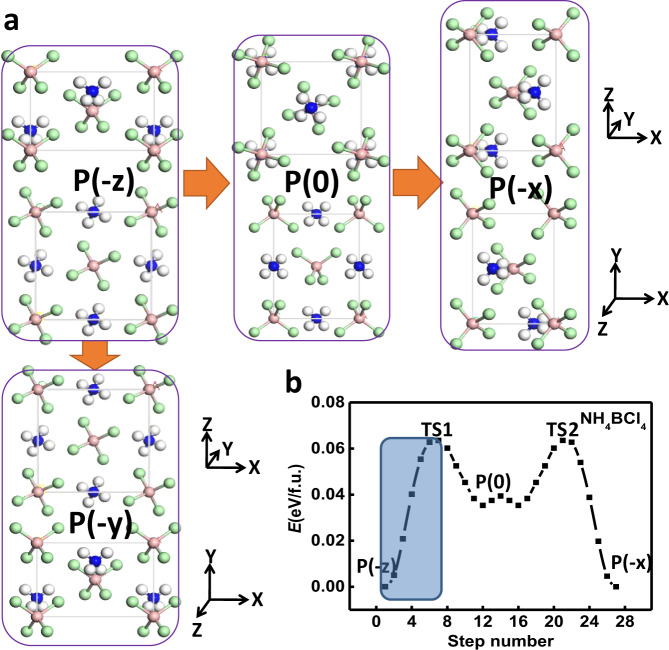
Ferroelasticity.

a Ferroelastic switching for NH₄BCl₄ with its polarization initially along –z direction switched to either –x or –y direction. b Computed ferroelastic switching pathway via SSNEB.

Ferroelasticity

We note that the dZB structure is relatively elongated in two directions, i.e., contracted in the third direction compared with standard ZB phase, which is actually a spontaneous strain that might be switched via stress. The pathway for such ferroelastic switching for NH₄BCl₄ is calculated by SSNEB method, where a symmetrical nonpolar state P(0) can be the intermediate state as its polarization switched from –z direction at the initial P(−z) state to –x/–y direction at the final state P(−x)/P(−y), as shown in Fig. 3a, b. Here, the superiority of ionic ferroelastics with long-range Coulomb interactions between ions should be highlighted, as a barrier of only 0.065 eV/f.u. (i.e., 0.0065 eV/atom) is required for reversing such a high ferroelastic strain (defined as (|b|/|c|−1) × 100%) more than 40%. For high-strain (>20%) ferroelastics predicted in previous reports^39–42, the switching barriers (up to 0.5 eV/atom) almost orders of magnitude higher may induce fracture, which can be attributed to the distinct features of covalent bonds in those systems. As revealed by the pathway in Fig. 3c, during the ferroelastic switching, the structure of P(−z) will be transformed into transition state TS1 that is 0.065 eV higher in energy, and then automatically transformed into metastable phase with lower energy, and symmetrically to another high-energy transition state TS2 followed by another equivalent ground state P(−x) or P(−y). Our calculated stress–strain curve in Fig. S2(c) shows that the highest stress during ferroelastic switching is below 1 GPa (close to the stress induced by a small tensile strain of only 1% applied on zinc-blende ZnS). A snapshot of this point with the highest stress at 300 K and at the end of 5 ps indicates that fracture should not take place during switching. Moreover, the ferroelectric polarization is also rotated by 90 degree upon ferroelastic switching. Such 90-degree polarization switching can also be achieved if an external electric field is applied along –x or –y direction. Hence, the ferroelectricity and ferroelasticity are coupled, so we can use strain to control the polarization direction and electric field to control strain. Due to the low barrier, the required electric field or stress for reversing such a large strain can be greatly reduced. It is noteworthy that a tensile strain is usually applied by clamping on the surface of a material, which is likely to induce non-uniformity, facilitating fracture. In contrast, the electrical force applied on those ferroelectric and ferroelastic supersalts will be much more uniform.

Triferroicity

Supersalts with 3d magnetic ions like PH₄FeBr₄ also possess similar coupled ferroelectricity and ferroelasticity. Moreover, their magnetism can also be coupled. We have checked different possible spin configurations (see Table S1) for PH₄FeBr₄. The ground state is displayed in Fig. 4a, which is antiferromagnetic where the spins of two Fe ions in the unit cell are in the opposite direction, while the spins on the same lines along –x, –y or –z axes are in the same direction. Further, noncollinear spin calculations reveal a magnetic anisotropy energy of 0.4 meV for the spin of each Fe atom, where the spins are preferably aligned along –y direction, the “contracted” direction in Fig. 4a. However, as the “contracted” direction is switched to –x direction upon ferroelastic switching, i.e., 90-degree ferroelectric switching, the magnetization easy axis is also switched from –y to –x direction. Equivalently, it might also be switched to –z direction via a strain or electric field along –z direction. Compared with NH₄BCl₄, the switching barrier of PH₄FeBr₄, according to the calculated pathway in Fig. 4b, is larger (~0.13 eV/f.u.), while the bandgap is much more reduced (~1 eV, see Fig. 4c) to a desirable range for nanoelectronics. Hence, magnetism is also coupled with ferroelectricity and ferroelasticity in PH₄FeBr₄, which can be viewed as a multiferroic material with “triferroic” coupling. Such coupling may render electrically controlled giant anisotropic magnetoresistance for nonvolatile memories, which is highly desirable but still challenging in the current developing field of antiferromagnetic spintroincs⁴³.

Fig. 4

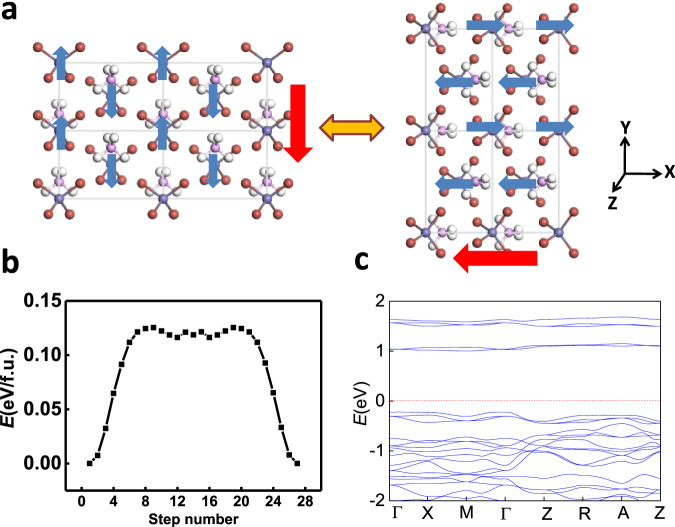
Triferroic coupling.

a Spin switching upon ferroelastic switching (90-degree ferroelectric switching), b ferroelastic switching pathway calculated by SSNEB method, and c the band structure for PH₄FeBr₄. Red and blue arrows denote polarization and spin directions, respectively.