Experimental lineup

The experimental lineup used to scrutinize the aforementioned aspects is schematically illustrated in Fig. 1. Local spins coupled to an electron bath are characterized by a magnetic exchange term JS with J being the s–d exchange coupling of the localized spin of the impurity S, carried here by d-electrons, and the conduction electrons of the substrate. Its effects are expected to manifest in three distinct ways, schematically illustrated in panels a–c. In the superconducting regime, it represents a scattering potential breaking Cooper pairs and giving rise to in-gap YSR states (Fig. 1a). In addition, it is expected to directly affect the superconducting order parameter by suppressing the strength of the pairing interaction, resulting in a reduction of the Josephson current flowing between superconducting electrodes (Fig. 1b). Finally, a strong coupling between magnetic impurities and the electron bath can open additional tunneling channels. These result from inelastic spin excitations induced by the magnetic anisotropy, which opens a gap in the spectra and are experimentally signaled by a step-like increase in the experimentally detected local density of states (LDOS), as sketched in (Fig. 1c)³⁵. As described in the following, instead of the usual two steps expected at positive bias and negative bias voltage, the inelastic spectra can display an unconventional shape, in accordance with recent predictions^33,34.

Fig. 1

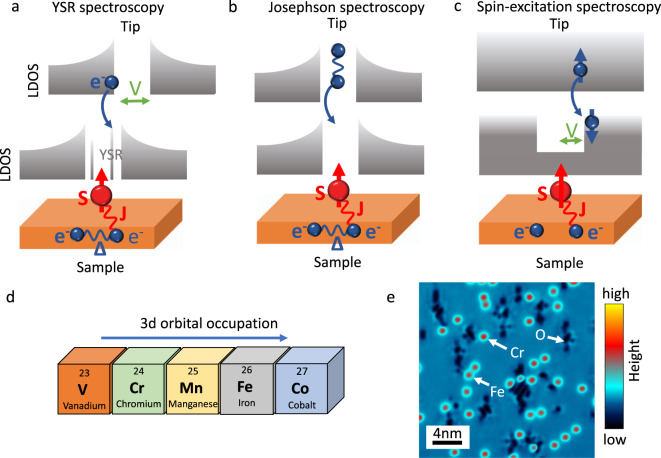
Experimental lineup.

Schematic illustration of (a) Yu–Shiba–Rusinov (YSR), (b) Josephson, and (c) spin-excitation spectroscopy. These three different spectroscopic modes can be used to provide a complete spectroscopic characterization of spin-related effects in the superconducting as well as in the metallic regimes. V corresponds to the bias applied across the tunneling junction, J indicates the exchange coupling of the localized spin of the impurity S, while Δ is the superconducting energy gap of electrons e⁻ condensing into Cooper pairs, (d) 3d elements scrutinized in the present study, (e) topographic image showing Cr and Fe single atoms coupled to the Nb(110) surface. Scanning set-point: V = −300 meV, I = 300 pA.

Figure 1d illustrates the portion of the periodic table of the 3d elements investigated in this study. By scrutinizing the 3d occupation scenario adding one electron at a time, it is possible to analyze the role of orbital occupation in determining the magnetic impurity–superconductor interaction strength. As superconducting material, we choose niobium single crystals which have been prepared according to the procedure described in ref. ³⁶. Niobium represents an optimal choice compared to other superconductors such as Pb^14,15, Re^37,38, and Ta¹⁸ used in previous studies. Indeed, by having the highest transition temperature (T = 9.2 K) among all elemental superconductors, it allows to clearly disentangle in-gap states from superconducting gap thermal broadening effects. Panel e shows a topographic image where different magnetic impurities (Fe and Cr) have been deposited onto the clean Nb(110) surface prepared according to the procedure described in “Methods” and Supplementary Fig. 1. The very same approach has been used for all atomic species, i.e., V, Cr, Mn, Fe, and Co (see Supplementary Fig. 2 for the determination of the adsorption sites). To investigate their impact on the superconducting condensate, full spectroscopic maps have been acquired at temperature T = 1.9 K using superconducting Nb tips. Compared to conventional metallic tips, their use brings two crucial advantages: (i) they allow to enhance the energy resolution while simultaneously (ii) opening the fascinating possibility to measure the Josephson effect at the atomic scale.

YSR spectroscopy

Figure 2 reports the spectroscopic characterization of the superconducting gap obtained by positioning the tip directly on top of the different magnetic perturbations. As described in Supplementary Fig. 3, the use of superconducting tips shifts the "zero energy” by ± Δ_tip with respect to the Fermi level, Δ being the superconducting energy gap. Hence, the single-particle coherence peak appears at energies ± (Δ_tip + Δ_sample). In this case, this corresponds to ~± 3 meV, with slight variations resulting from tips characterized by different Nb clusters at their apex (see Supplementary Fig. 4). An inspection overview of Fig. 2 allows us to immediately identify the existence of an oscillatory behavior that directly correlates with the filling of the 3d orbitals. In particular, V and Co do not show any impact on the superconducting properties, with scanning tunneling spectroscopy spectra taken by positioning the tip over the adatoms (orange line) perfectly overlapping, within our experimental resolution, the spectra taken over the bare Nb substrate (black dashed line). Despite no difference in the dI/dU curves, a very weak $$ d_{z^2}$$-derived YSR state can be detected for V, which is energetically overlapping with the single-particle coherence peak at the edge of the superconducting gap. These results suggest a very small and vanishing magnetic moment for both V and Co, respectively which are located at the opposite extremes of the 3d orbital scenario analyzed in the present study. Both elements are characterized by a partially filled 3d shell, this behavior might appear surprising and it highlights how the hybridization with the substrate can dramatically impact the magnetic properties. Similar to our finding, Co adatoms can be nonmagnetic on Re surface as revealed by a YSR study limited to Mn, Fe, and Co impurities³⁸. As described in the following, the trend unveiled by our experiments is confirmed by ab initio calculations (see subsection “Ab initio simulations”).

Fig. 2

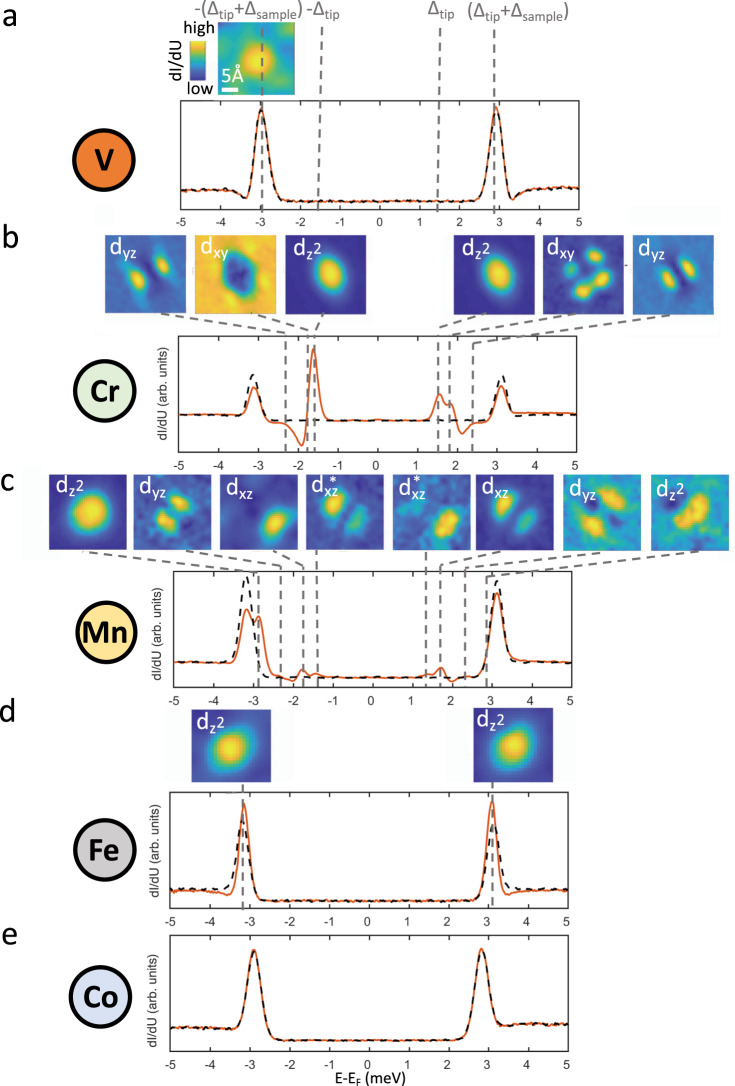
Yu–Shiba–Rusinov (YSR) spectroscopy.

a–e Scanning tunneling spectroscopy for V, Cr, Mn, Fe, and Co. While no YSR state is detected for V and Co, a rich set of in-gap states emerge for Cr, Mn, and Fe. The insets show the spatial distribution of the YSR states, which reflect their orbital character and allows one to quantify their spatial extension. Stabilization parameters: V = 5 meV, I = 500 pA.

In contrast, well-defined YSR states emerging within the superconducting gap are visible for Cr, Mn, and Fe. As expected, all YSR states appear in pairs symmetrically located around the Fermi level. Their energy position ϵ within the superconducting gap is generally described considering pure magnetic scattering mechanisms, being determined by the strength of the exchange coupling terms J through the following expression:

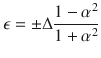
In the case of Fe, a single pair of YSR states is detected. It energetically overlaps with the single-particle coherence peaks visible at the edge of the superconducting energy gap. Spatially mapping its intensity allows one to assign it to a $$ d_{z^2}$$ scattering orbital (see colormaps in Fig. 2d). Cr and Mn show a more complicated spectrum supporting multiple YSR pairs. As for Fe, a $$ d_{z^2}$$ scattering orbital is clearly visible, which moves towards smaller binding energies by progressively decreasing the atomic number. The additional YSR pairs are located at different energies within the superconducting gap. Their spatial distribution is far from being isotropic, resembling well-defined d-level symmetries. These observations prove that the magnetic exchange scattering potentials are strongly orbital-dependent¹⁷. Interestingly, in Fig. 2c, the Mn d_xz-derived Shiba pair show distinct spectral maps at positive and negative energies, signaling a strong particle–hole asymmetry in the wavefunctions, similarly to $$ d_{z^2}$$ YSR-bound states. An additional pair is visible at energies ± (Δ_tip − ϵ). These states correspond to the thermal replica of the d_xz-derived Shiba pair: they become populated by particles and holes due to their proximity to the Fermi level. This assignment is further confirmed by their shape, which energetically mirrors that of the original states¹⁷.

Interestingly, these results allow to systematically follow the evolution of the $$ d_{z^2}$$-derived YSR state, visualizing how it progressively moves toward higher binding energies by increasing the 3d orbital occupation. Within the generally assumed framework of competing singlet-formation mechanism, i.e., Kondo vs. Cooper pairs, this is expected to result in Kondo resonances becoming progressively stronger by moving from Cr to Mn, and, Fe. However, as demonstrated in the following, this is far from being the case (see section “Spin excitations and related discussion”).

Josephson spectroscopy

Although YSR measurements can be effectively used to infer important information on the magnetic coupling strength, they are characterized by a strong fundamental limitation: they can not visualize the effect of magnetic impurities on the superconducting order parameter. Indeed, the local pairing suppression which is expected to take place in presence of magnetic perturbation can not be directly reflected in the YSR spectra. As illustrated in Fig. 2, these show a suppression in the intensity of the coherence peaks at the edge of the superconducting gap, their spectral weight being redistributed to the in-gap bound states, but without any energy shift of their position as compared to the substrate. This distinction between detecting the effects of magnetic impurities on the local density of states and on the superconducting order parameter is well-known and consistent with theoretical expectations³⁹.

To overcome this limitation, we perform scanning Josephson spectroscopy measurements which allow, by measuring the tunneling between Cooper pairs in superconducting electrodes, to directly extract information on the local variation of the superconducting pairing amplitude at the atomic scale. Results for all investigated impurities are summarized in Fig. 3, with left panels showing the I–V characteristics and the right ones reporting their respective dI/dU signal. The orange and dashed black lines have been acquired by positioning the tip atop the magnetic impurities and on the bare substrate, respectively. While no difference with respect to the bare Nb substrate is detected for Co, a small reduction of the Josephson current is observed for V. This effect becomes stronger for all other impurities according to the following order: Fe, Mn, and Cr. These results confirm the oscillatory magnetic behavior visualized in Fig. 2: the magnetic moment becomes strongly suppressed at the opposite extreme of the 3d filling, while Fe, Mn, and Cr preserve a substantial magnetic character. The effect of the different magnetic impurities on the superconducting order parameter can be quantitatively analyzed based on the fact that both the maximum Cooper pairs current I_max as well as the intensity of the dI/dU peak are proportional to the square of the intrinsic Josephson current I_c²⁷. A direct comparison among the different adatoms evidences a suppression of the Cooper pairs tunneling, an effect directly linked to the reduction of the superconducting order parameter, which becomes progressively stronger by moving from Fe to Mn and, finally, Cr. In agreement with theoretical expectations, the same trend is consistently found for both I_max (Fig. 3g) and the dI/dU peak intensity (Fig. 3h)²⁷. Although different magnetic impurities have a different apparent height, as shown in panel e, we can safely exclude that our observations are related to tip-height artifacts. Indeed, despite having Co an apparent height of ~0.7 Å, Josephson currents are not altered when compared to the case when the tip is positioned over the bare substrate. Furthermore, Cr, which shows the strongest perturbation on the superconducting order parameter, has an apparent height that is smaller than Mn. Additional experimental evidence ruling out tip-height effects is provided in Supplementary Fig. 5 where, by using atomic manipulation techniques, we create a Cr dimer. Although being apparently higher than a single Cr adatom, the dimer does not have any impact on the superconducting order parameter, an observation consistent with its antiferromagnetic ground state resulting in a total spin S = 0. Consequently, our measurements directly fingerprint effects induced by a finite spin onto the superconducting order parameter, suggesting a progressively increasing magnetic moment while moving from Fe to Mn and finally Cr. As discussed in the following, these results follow the same trend of the magnetic moments obtained by our theoretical calculations and highlight the very high sensitivity of our measurement protocol.

Fig. 3

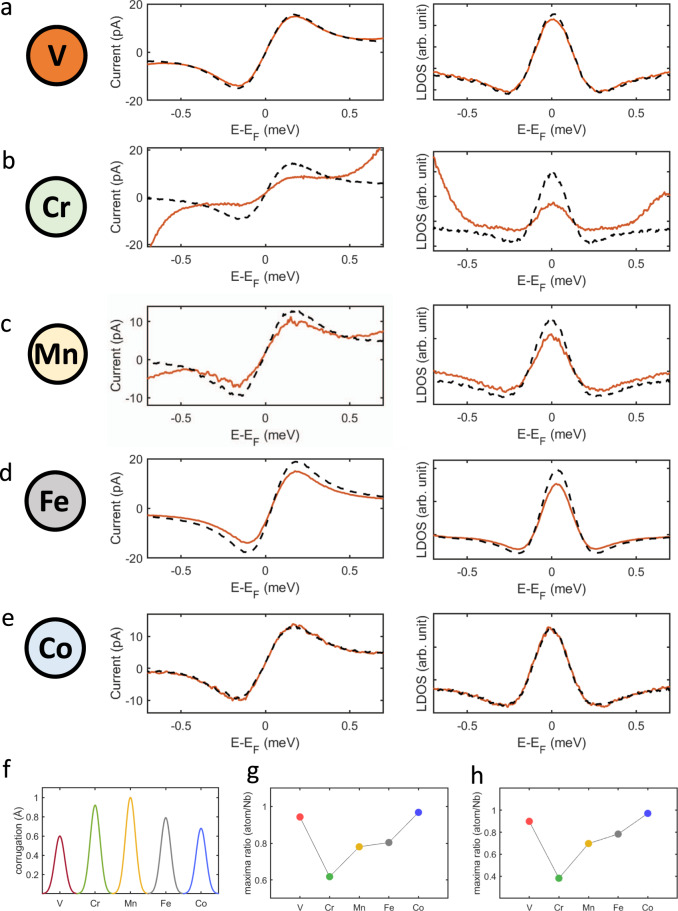
Scanning Josephson spectroscopy.

a–e I − V characteristics (left panels) and respective dI/dU signals (right panels) for all elements. f Apparent heights of the adatoms. g, h Reduction induced by the different magnetic perturbations in the maximum Cooper pairs current I_max and intensity of the dI/dU peak, respectively, both showing the same trend. Stabilization parameters: V = 5 meV, I = 15 nA.

Ab initio simulations

The theoretical interpretation of the trends observed in both YSR and Josephson spectra requires detailed knowledge of the spin-resolved orbital structure of the adatoms and their coupling to the substrate. This is analyzed in the following on the basis of ab initio simulations of the 3d series of adatoms deposited on Nb(110) surface (see Supplementary Notes 1–3 for more details). Figure 4a reports the spin-resolved local density of states (LDOS) for V, Cr, Mn, Fe, and Co with upper and lower panels corresponding to minority- and majority-spin channels, respectively. The LDOS broadening is a direct consequence of the crystal field, which splits the degeneracy of the different 3d orbitals. A detailed discussion is provided in Supplementary Notes 1–3. Its inspection immediately reveals the appearance of a well-defined trend: a substantial imbalance between majority- and minority-spin resonances is found for Cr, Mn, and Fe, while the difference between majority- and minority-spins is found negligible for V and totally absent for Co. These results follow the usual inverse parabolic behavior across the 3d series, with spin magnetic moments reaching a maximum in the middle followed by a decrease toward the end of the series. In agreement with our experimental observations, only four adatoms remain magnetic, with elements at half-filling of the d-states carrying the largest moments (V: ~1.2 μ_B; Cr: ~3.5 μ_B; Mn: ~3.6 μ_B; Fe: ~2.0 μ_B) while Co is nonmagnetic. Note that a non-negligible magnetic moment is induced in the bare Nb substrate at the vicinity of the adatoms, to which it generally couples antiferromagnetically, except for V. This effect modifies the total adatoms–substrate complex spin moments, resulting in V: ~1.4 μ_B, Cr: ~3.3 μ_B, Mn: ~3.0 μ_B, and Fe: ~1.5 μ_B. These values correlate well with the trend visualized by Josephson spectroscopy measurements reported in Fig. 2, allowing to establish a direct link between the magnitude of the magnetic moment and the induced suppression of Cooper pairs supercurrents.

Fig. 4

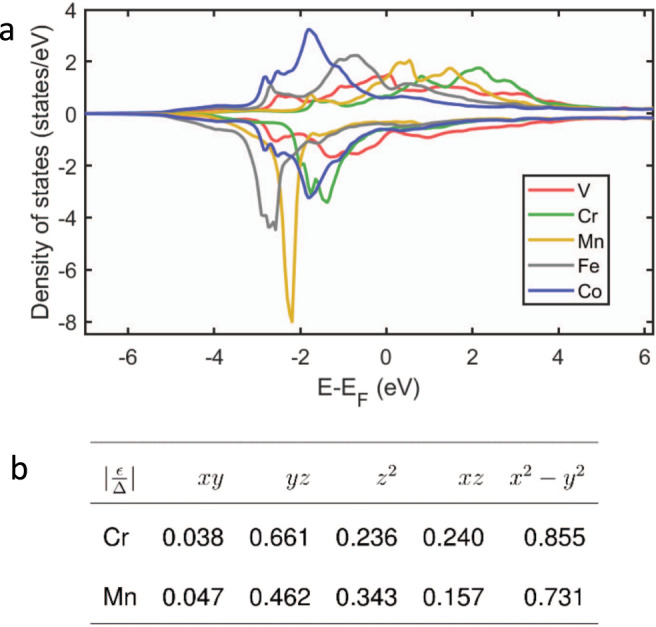
Local density of states and energies of YSR states.

a Spin-resolved electronic structure for V, Cr, Mn, Fe, and Co—upper (lower) panel for minority- (majority-) spin channel. b Theoretically obtained table of orbital-dependent energies of YSR states normalized by the superconducting gap.

The strength of the orbital-average impurity-substrate hybridization, Γ, between adatoms and substrate is rather large for all the adatoms, and it decreases by increasing the 3d orbital occupation, i.e., by moving from left to right across the 3d series (V:1.11 eV; Cr: 0.98 eV; Mn: 0.88 eV; Fe: 0.72 eV; Co: 0.57 eV). This trend is related to the contraction of the 3d states of the atoms when increasing their atomic number, which disfavors hybridization with neighboring atoms. While the hybridization strength is paramount for the description of YSR-bound states, it is worth stressing that its effect can be counteracted by the exchange splitting, 2U, and the energy of orbital m, E_m. A full ab initio description of the YSR states is currently challenging. Here, we follow a simplified model where the aforementioned quantities encode the magnitude of the orbital- and spin-dependent impurity-substrate s–d interaction $$ {\mathcal{I}}_m^{\sigma }$$, where σ = ± depending on the spin of conducting electrons. By virtue of the Schrieffer-Wolff transformation⁴⁰, $$ {\mathcal{I}}_m^{\sigma }=\left(V_m+\sigma J_{m}S\right)$$, with V_m and J_m corresponding to nonmagnetic and magnetic scattering contributions, respectively. The energies of the YSR states can then elegantly be cast into^13,41:

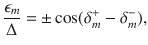
This approach is capable of mapping the scattering phase shifts and the YSR energies directly from our ab initio results (see Supplementary Notes 2 and 3). The complexity of the problem is directly related to the very different energy scales coming into play: the interactions J and V depend on quantities of the eV range, while the energies of the YSR states are of the order of meV and sub-meV. This impedes a perfect one-to-one comparison between all the theoretically calculated and experimentally measured spectra. However, our approach is effectively capable of capturing the observed experimental trends, as discussed in the following. The theoretically predicted energy position for Cr and Mn YSR states is summarized in Fig. 4b.

The Cr $$ d_{z^2}$$ Shiba state is predicted to be located at lower energy than that of Mn, in agreement with the experimental data (see Supplementary Note 3 for a detailed discussion on the role of nonmagnetic and magnetic impurity-substrate interactions in determining the energies of the YSR states). Similar to what is observed in Fig. 2, the d_yz state of Cr is theoretically expected at higher energy than the YSR state of $$ d_{z^2}$$-symmetry, while for Mn the two states are found around the same energy. The calculated d_xz state is located at lower energy than the $$ d_{z^2}$$ state for both Cr and Mn. While this is confirmed experimentally for the d_xz state of Mn, it was not detected for Cr, the corresponding peak being either too weak or difficult to disentangle from the adjacent dominant resonances. Note that all YSR states are characterized by a finite broadening which is related to both the experimental energy resolution and their intrinsic lifetime. This explains why, although ab initio simulations predict that each of the orbitals of Cr and Mn adatoms carries a spin moment, resulting in five distinct YSR states, not all of them are detectable experimentally, as shown in ref. ¹⁴. Fe and V, on the other hand, are found to have a colossal adatom-substrate interactions, which is favored by the LDOS resonances located at the Fermi energy. In both cases, because of the very strong interaction for all orbitals, all YSR features are expected to appear at the edge of the SC gap, with the $$ d_{z^2}$$ orbital dominating the scene because of its larger extension into the vacuum, which facilitates its experimental detection, in agreement with our tunneling spectra.

Spin excitations

The interaction of magnetic impurities with superconducting condensates is generally described within the framework of competing singlet-formation mechanisms, i.e., Kondo screening vs. Cooper pairs. This competition is captured within a phase diagram where the magnetic impurities can be either in a Kondo-screened or free-spin state depending on the impurity–superconductor coupling strength. In the strong coupling regime, k_BT_K ≫ Δ, with k_B being the Boltzmann constant and T_K the Kondo temperature, while in the weak coupling regime k_BT_K ≪ Δ. A quantum phase transition between these two regimes takes place for k_BT_K ≈ Δ, i.e., when Kondo screening and the superconducting gap are characterized by similar energies²⁹. To scrutinize these aspects, a magnetic field has been applied perpendicular to the sample surface in order to quench the superconducting state. Note that all elements are characterized by a well-defined $$ d_{z^2}$$-state, which allows to precisely map its evolution. This is found to progressively move towards the single-particle coherence peak located at the edge of the superconducting gap by increasing the orbital occupation, which should result in a progressively stronger Kondo resonance while moving from Cr to Mn and Fe. However, our measurements clearly reveal that this is far from being the case. As illustrated in Fig. 5, our data reveal a strong zero-bias anomaly (ZBA) with a step-like feature for Cr adatom, also observable in the superconducting phase as shown in Supplementary Fig. 6. Similar behavior is observed for Mn and Fe although the signal is much weaker than for Cr (see Supplementary Fig. 7 for a direct overlap of Cr, Mn, and Fe spectra) and becomes progressively broader. Finally, V and Co spectra appear totally flat.

Fig. 5

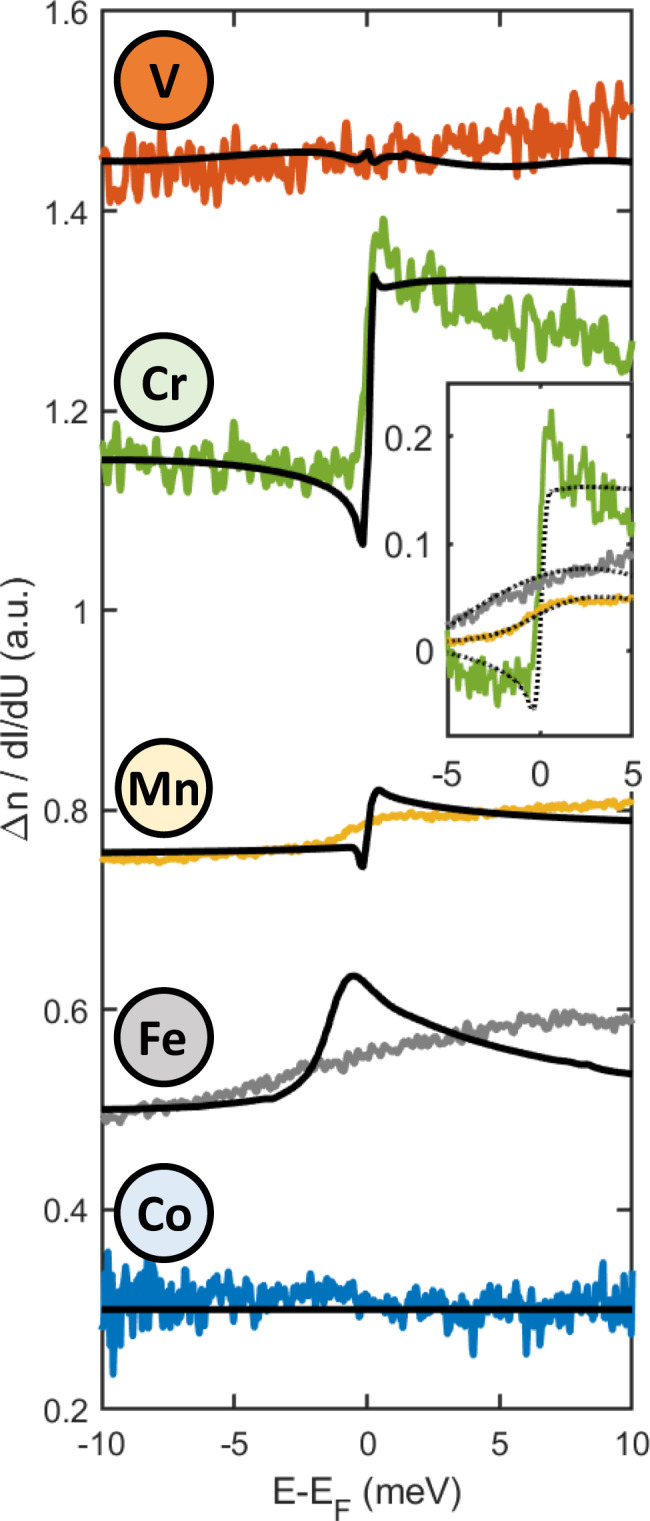
Spin-excitation spectroscopy.

For all adatoms, the experimentally obtained spectra are reported as solid lines following, for each element, the same color-coding scheme used across the manuscript. To exclude spurious effects related to the use of different microtips, all spectra are normalized to the substrate. To drive the system into a metallic state, a magnetic field has been applied perpendicular to the sample surface. All spectra are overlapped with the theoretically calculated spin-excitation spectra (solid black line). The inset shows the theoretical spectra with an artificial Gaussian broadening of 0.20 meV, 1.98 meV, and 7.78 meV for Cr, Mn, and Fe, respectively (dashed lines). Stabilization parameters: Cr, Fe, Mn: V = 10 meV, I = 500 pA; V, Co V = 10 meV, I = 1 nA.

It has recently been predicted that inelastic spin excitations can also lead to unconventional spectral shapes centered around the Fermi level³⁴. To verify if this is the case, the experimental data are compared to relativistic first-principles simulations, combining TD-DFT with MBPT (see “Methods” and Supplementary Notes 4 and 5), reported as solid black lines in Fig. 5. The theoretical inelastic spectra qualitatively reproduce the experimental features (more details on the origin of the step-shapes is provided in the Supplementary Notes Notes 4 and 5) Cr has a weak MAE leading to small excitation energies. The amount of electron–hole excitations responsible for the damping of the ZBA are therefore weak, which favors the observation of the inelastic features. Electron–hole excitations are proportional to the MAE and to the product of the density of states of opposite spin-character at the Fermi energy^31,32. Therefore, although V has a weak MAE, its small exchange splitting leads to a large LDOS at the Fermi energy and a consequent number of electron–hole excitations, heavily decreasing the lifetime of the spin excitations. The interplay of these two mechanisms, MAE and LDOS, broadens the features obtained for Mn and Fe as well. The experimental ZBA of the latter adatoms seems broader than those calculated, which can be resulting from a slight theoretical underestimation of the spin-excitation energy or of the electron–hole excitation energies as shown in Supplementary Fig. 12. Here, we account for this underestimation by broadening the theoretical spectra using a Gaussian broadening, which is shown in the inset of Fig. 5. For the three shown cases of Cr, Mn, and Fe, we used a broadening of 0.20 meV, 1.98 meV, and 7.78 meV, respectively, to match the theoretically predicted spectra with the experimental spectra.

Sample and tip preparation

Nb(110) single crystals (Surface Preparation Laboratory) have been prepared in ultra-high vacuum conditions and measured using a Tribus STM head (Scienta Omicron) operated at T = 1.9 K. The samples have been flashed hundreds of times at a temperature T = 2300 K for 12 s using an home-built electron-beam heater. As illustrated in the Supplementary Information, this procedure is necessary to progressively reduce the oxygen contamination, resulting in clean surfaces. The high quality of the surface is further confirmed by scanning tunneling spectroscopy measurements showing, in agreement with theoretical calculations, a sharp peak energetically located at E = −0.45 eV below the Fermi level which originates from a surface resonance of $$ d_{z^2}$$ character. Single magnetic adatoms have deposited onto the Nb(110) surface using an electron-beam evaporator while keeping the sample at T = 10 K. Superconducting Nb tips have been prepared by indenting electrochemically etched W tips inside the Nb(110) for several nanometers. dI/dU spectra were measured using a lock-in technique, modulating the sample bias with 50 μV (r.m.s.) ac bias at a frequency 733 Hz. More experimental details are given in Supplementary Figs. 1–7.

Ab initio

The ground-state properties of the adatoms deposited on Nb(110) were calculated in a two-pronged approach based on density functional theory (DFT). First, the Quantum Espresso^42,43 package was utilized for geometrical optimization of the adatom-substrate complexes. A 4 × 4 supercell is considered with three Nb layers and a k-mesh of 2 × 2 × 1 is used. Exchange and correlation effects are treated in the generalized gradient approximation using the PBEsol functional⁴⁴, and we used ultrasoft pseudopotentials from the pslibrary⁴⁵ with an energy cutoff of 500 Ry. Second, the calculated positions were then used in the simulations based on the full-electron scalar-relativistic Korringa–Kohn–Rostoker (KKR) Green function including the spin–orbit interaction self-consistently^46,47. KKR permits the embedding of single adatoms in an otherwise perfect substrate. We assume the local spin density approximation (LSDA)⁴⁸ and obtain the full charge density within the atomic sphere approximation. The angular momentum cutoff of the orbital expansion of the Green function is set to ℓ_max = 3 and a k-mesh of 600 × 600 is considered. The trend of the atomic relaxations obtained with Quantum espresso agrees with the simulations (Cr: 17%; Mn: 18%; Fe: 29%; Co: 29% of the Nb bulk interlayer distance), except for V where the theory predicts a relaxation of 22%, while from the corrugation shown in Fig. 3f, we expect a possible extra relaxation of 10%. The energies of the YSR states of the adatoms are modeled by a realistic tight-binding model with parameters from DFT. The model considers the d orbitals of the adatoms and accounts for the Nb substrate via an effective Hamiltonian construction. Further details can be found in ref. ⁴⁹ and Supplementary Note 2.

The spin excitations were investigated utilizing a framework based on time-dependent density functional theory (TD-DFT) ^30–32 including spin–orbit interaction. Many-body effects triggered by the presence of spin excitations are approached via many-body perturbation theory³³ extended to account for relativistic effects³⁴. The single-particle Green functions pertaining to the ground state are employed for the calculation of the bare Kohn–Sham dynamical magnetic susceptibility, $$ {\underset{\_}{\chi }}_{\mathrm{KS}}\left(\omega \right)$$. The latter is renormalized to $$ \underset{\_}{\chi }\left(\omega \right)$$ via the Dyson-like equation to account for many-body effects

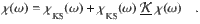
The self-energy describing the interactions of the electrons and the spin excitations is calculated from a convolution of the Green function, G, and susceptibility, $$ \underset{\_}{\mathrm{\Sigma }}\propto \underset{\_}{\mathcal{K}}\underset{\_}{\chi }\underset{\_}{G}\underset{\_}{\mathcal{K}}$$ in refs. ^33,34,54,55. The impact of spin–orbit coupling is incorporated as described in ref. ³⁴. The self-energy is then used to renormalize the electronic structure to account for the presence of spin excitations by solving the Dyson equation g = G + GΣg.

The theoretical spectra shown in Fig. 5 are local densities of states calculated the vacuum above the adatoms, which on the basis of the Tersoff-Hamann approach⁵⁶ correspond to the differential conductance measured by STM. More details on the simulations are provided in Supplementary Notes 1–5.